![]() 5.1.1 Binære trærs egenskaper
5.1.1 Binære trærs egenskaper
Binære trær (eng: binary tree), og trær generelt, er en viktig datastruktur.
I Delkapittel 1.2
brukte vi turneringstrær, i
Delkapittel 1.3
beslutningstrær og i
Delkapittel 1.5
rekursjonstrær. Hos oss er et binærtre en datastruktur og har selvfølgelig lite med
et botanisk tre å gjøre. Men vi låner begreper både fra botaniske trær og fra slektstrær.
I dette delkapitlet skal vi først og fremst diskutere de grunnleggende egenskapene til binære trær. Disse egenskapene inngår når vi senere skal diskutere binære trær med mer spesielle egenskaper - f.eks. binære søketrær, komplette minimumstrær, Huffmantrær, venstretunge trær, balanserte trær (f.eks. rød-svarte trær), multidimensjonale trær (f.eks. B-trær), osv.
Definisjon Et binærtre består av en samling noder (eng: node/nodes) (muligens en tom samling) og en samling kanter (eng: edge/edges) som forbinder par av noder:
- Hvis treet ikke er tomt, har det en rotnode. Kalles også treets rot (eng: root).
- Til enhver node Y, unntatt rotnoden, hører det nøyaktig én node X som vi kaller dens foreldernode eller bare forelder (eng: parent). Det går en kant mellom noden Y og dens forelder X. Omvendt sier vi at Y er et barn (eng: children) til X. En node kan ha to, ett eller ingen barn. Det er kun mellom nodepar av typen barn/forelder det går kanter.
- Hvis en node har to barn er det ene venstre barn og det andre høyre barn. Hvis noden har bare ett barn defineres det enten som venstre barn eller som høyre barn.
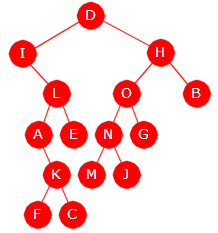
Tegningen under viser et binærtre med 22 noder, og alle har en bokstav som verdi. Det er noden med verdi A (eller A-noden) som er rotnode og den har som vi ser ingen forelder.
 |
| Figur 5.1.1 a) : Et binærtre med 22 noder |
Vi tegner normalt et binærtre opp-ned, dvs. rotnoden øverst og de andre nodene nedover. Det er også vanlig å la nodene være sirkelformede. Kanten fra en forelder til et barn tegnes på skrå - på skrå ned til venstre for et venstre barn og på skrå ned til høyre for et høyre barn. Det betyr at på Figur 5.1.1 a) er B et venstre barn og C et høyre barn til A.
Nivå (eng: level) brukes vanligvis i forbindelse med høyder og høydeforskjell. Havnivå og nivåkurver er kjente uttrykk. Her skal vi bruke begrepet på en tilsvarende måte. Rotnoden er på nivå 0. Vi assosierer vanligvis en rot med noe som er nede i bakken og dermed er det rimelig å si at en rot befinner seg på 0-nivået. (En bør være klar over at i enkelte fremstillinger sies rotnoden å være på nivå 1.) Barna til rotnoden er på nivå 1, barnebarna på nivå 2, osv. Det er vanlig å tegne alle nodene som hører til samme nivå på en og samme (vannrette) rad. I Figur 5.1.1 a) tilhører f.eks. nodene D, E, F og G samme nivå, dvs. nivå 2.
Begrepet generasjon henter vi fra slektstrær. Der kalles gjerne rotnoden for stamforelder (stammor eller stamfar) og nivåene svarer til generasjoner. Forskjellen er at stamforelder vanligvis kalles 1. generasjon. Dermed vil generasjon k være det samme som nivå k − 1.
Hvis alle nivåene i treet har så mange noder som det er plass til, sier vi at treet er perfekt (eng: a perfect binary tree). I et binærtre er det plass til 1 node på nivå 0, 2 noder på nivå 1, 4 på nivå 2, 8 på nivå 3, osv. Generelt er det plass til 2k noder på nivå k.
Slektskap Det er ikke bare begrepet generasjon vi låner fra slektstreet. Vi bruker også begreper som barn og forelder, barnebarn og besteforelder, oldebarn og oldeforelder, etterkommer (eng: descendant, successor) og forgjenger (eng: ancestor, predecessor). Det burde være innlysende hva disse begrepene står for i et binærtre. To noder kalles søsken (eng: sibling) hvis de har samme forelder. En node (forskjellig fra rotnoden) kalles enebarn hvis den ikke har søsken. En node kalles barnløs hvis den ikke har barn.
Subtrær Enhver node kan ses på som rotnode i sitt eget tre, dvs. det
treet som består av noden og alle dens etterkommere (barn, barnebarn, osv). En node
har alltid to subtrær - et venstre subtre og et høyre subtre
- der ett eller begge kan være tomme. Venstre subtre til en node er (hvis det ikke er tomt)
det treet som har venstre barn som sin rotnode. Det blir tilsvarende for høyre subtre.
 |
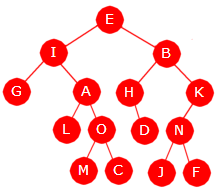
| Figur 5.1.1 b) : Begreper som rot, blader og forgreninger er hentet fra botaniske trær. |
Bladnoder og indre noder Nodene kan deles opp i to typer - bladnoder og indre noder (eng: leaf node, inner node). En bladnode (eller et blad) er en node som ikke har barn, eller som har to tomme subtrær om en vil. Alle andre noder er indre noder. Det betyr at en indre node har ett eller to barn. I Figur 5.1.1 a) ser vi fort at nodene O, P, Q, R, S, L, T, U og V er bladnoder, og dermed at resten er indre noder.
En vei Vi kan orientere alle kantene i treet ved å si at en kants retning
er fra forelder til barn, dvs. nedover. Vi sier at det går en vei (eng: path)
mellom to noder X og Y hvis det er mulig å komme fra X til
Y ved å følge kanter. Spesielt får vi at Y er en etterkommer av X
hvis det går en vei fra X til Y, eller omvendt at X er en forgjenger
til Y. Veilengden er antallet kanter på veien. I
Figur 5.1.1 a)
går det f.eks. en vei med lengde 4 fra noden A til noden V. Men det går
f.eks. ingen vei fra noden L til noden V.
Avstand Hvis det går en vei fra noden
X til noden Y (eller fra Y til X) sier vi at avstanden
mellom dem er lik veilengden. Hvis det ikke går en vei mellom dem, må de ha en nærmeste felles
forgjenger Z. Da sier vi at avstanden mellom X og Y er lik avstanden
mellom Z og X pluss avstanden mellom Z og Y. I
Figur 5.1.1 a) er C nærmeste forgjenger
til L og V og avstanden mellom dem blir dermed 2 + 3 = 5.
Høyden til et binærtre er lengden på den lengste veien i treet. Treet i
Figur 5.1.1 a)
har dermed høyde 4. Den lengste veien må nødvendigvis starte i rotnoden A, og vi ser
at ingen vei er lengre enn 4. En annen måte å si det på er at høyden er det samme som det
største nivået i treet. Treet
i Figur 5.1.1 a)
har 4 som største nivå - altså er høyden 4. Et binærtre med bare én node har
høyde 0 og spesielt skal vi si at et tomt tre har høyde −1.
Høyden til en node X er høyden til det subtreet som har X som rotnode. Rotnodens høyde blir dermed det samme som høyden til hele treet.
Dybden til en node X er avstanden mellom rotnoden og noden X. Dermed kan vi si at høyden til et binærtre er dybden til den «dypeste» noden. I treet i Figur 5.1.1 a) er det mange noder som er «dypest». Det er alle nodene på den nederste nivået.
Retninger Vi tegner som sagt et binærtre opp-ned. Dermed vil oppover og nedover bli det omvendte av det normale med tanke på et botanisk tre. Nedover betyr nå i retning vekk fra roten. Tilsvarende blir oppover retning mot roten. Et uttrykk som «langt nede i treet» vil nå bety langt fra roten. Bunnen av et tre betyr så langt ned en kan komme. I Figur 5.1.1 a) går vi nedover når vi starter i rotnoden A og f.eks. går mot noden S.
En gren i treet består av alle nodene fra rotnoden og ned til en bladnode. Det
betyr at det er like mange grener i treet som det er bladnoder.
I treet i Figur 5.1.1 a) er
det 9 bladnoder og dermed 9 grener. Venstre gren er den som ender i den bladnoden som ligger
lengst til venstre og høyre gren den som ender i den bladnoden som ligger lengst til
høyre. I treet i Figur 5.1.1 a)
blir det grenene (venstre) A, B, D, H, O og (høyre)
A, C, G, N, V. (En node ligger til venstre for en annen
node hvis den første kommer foran den andre i inorden. Se definisjonen av
inorden). Høyden i treet
blir det samme som lengden på lengste gren.

|
| 1. |
a) Hvor mange nivåer har treet? b) Skriv opp alle nodene på nivå 2. c) Skriv opp alle nodene på nivå 3. d) Hvor mange flere noder kan nivå 3 inneholde? e) Hvor mange flere noder kan nivå 4 inneholde? f) Hvem er etterkommere til A-noden? g) Hvem er forgjengere til A-noden? h) Hvilke noder er besteforeldre? i) Er det noen enebarn? j) Hva er treets høyde? k) Hva er dybden til D-noden? l) Hvilke høyder har I-nodens to subtrær? m) Hvor mange bladnoder er det? n) Hvor mange indre noder er det? o) La et binærtre ha n noder. Hva er minste og største antall bladnoder et binærtre kan ha? | |
| 2. |
a) Hvor mange nivåer har treet? b) Skriv opp alle nodene på nivå 2. c) Skriv opp alle nodene på nivå 3. d) Hvor mange flere noder kan nivå 3 inneholde? e) Hvor mange flere noder kan nivå 4 inneholde? f) Hvem er etterkommere til A-noden? g) Hvem er forgjengere til A-noden? h) Hvilke noder er besteforeldre? i) Er det noen enebarn? j) Hva er treets høyde? k) Hva er dybden til D-noden? l) Hvilke høyder har I-nodens to subtrær? m) Hvor mange bladnoder er det? n) Hvor mange indre noder er det? | |
| 3. |
Gjør flg. for treet i Oppgave 1:
a) To noder kalles søskenbarn hvis de har samme besteforelder,
men ikke samme forelder. Skriv opp de nodene som har minst ett
søskenbarn. Hvor mange søskenbarn kan en node ha? b) To noder kalles tremenninger hvis de har samme oldeforelder, men ikke samme forelder eller besteforelder. Skriv opp alle noder som har minst en tremenning. Hvor mange tremenninger kan en node ha? | |
| 4. | Gjør som i Oppgave 3, men bruk treet i Oppgave 2. | |
| 5. |
Det går en vei mellom to noder X og Y hvis det er mulig
å komme fra X til Y ved å følge kanter i kantenes retning
(dvs. nedover).
Hvis det går en vei fra X til Y eller omvendt, sier vi at
avstanden mellom X og Y, avstand(X,Y), er lengden
på veien. Hvis det ikke går noen vei mellom X og Y må de to ha
en nærmeste felles forgjenger Z. Da definerer vi avstanden mellom
X og Y som avstand(Z,X) + avstand(Z,Y).
Diameter til et binærtre er definert som den største mulige avstanden
mellom to noder. Svar på flg. spørsmål:
a) Hva er diameter til trærne i Oppgave 1 og Oppgave 2? | |
| 6. | Skriv opp verdiene i hver av grenene i trærne i Oppgave 1 og Oppgave 2. | |
| 7. | Les mer om treet Yggdrasil! Søk på internett! |
![]() 5.1.2 Antallet forskjellige trær
5.1.2 Antallet forskjellige trær
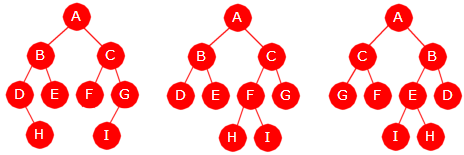 |
| Tre 1 Tre 2 Tre 3 |
| Figur 5.1.2 a) : Tre forskjellige binære trær |
Vi vil vanligvis si at to binære trær er like hvis de både har samme form og samme innhold. Med samme innhold menes at de har parvis like verdier på de samme stedene. Figur 5.1.2 a) viser tre trær som inneholder bokstavene fra A til I. Vi ser at Tre 1 er forskjellig fra Tre 2 siden de ikke har samme form. Men også Tre 2 og Tre 3 er forskjellige. Begge har samme form, men ikke samme innhold. Bokstavene fra A til I er ikke på de samme stedene.
I dette avsnittet skal vi se bort fra nodenes eventuelle verdier. Vi skal kun se på
trærnes form. To trær som har samme form kalles isomorfe. Ordet isomorf kommer
fra gresk. Iso betyr lik og morf betyr form. Spørsmålet vi nå ønsker
å finne svaret på er: Hvor mange isomorft
forskjellige binære trær med n noder finnes det?
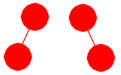 |
| Figur 5.1.2 b): Trær med 2 noder |
Et tre uten noder kalles det tomme treet. Med andre ord finnes det kun ett tomt tre. Antallet forskjellige trær med 0 noder er derfor 1. Det finnes bare ett tre med én node og antallet er også her lik 1. Hvis treet har 2 noder må den ene være rotnoden. Den andre kan da enten være venstre barn eller høyre barn. Det gir 2 isomorft forskjellige trær med 2 noder. Figur 5.1.2 b til venstre viser de to trærne.
Hvis antall noder er 3, får vi litt flere muligheter. Tegningen under (Figur 5.1.2 c) viser at det er 5 isomorft forskjellige binære trær med 3 noder.
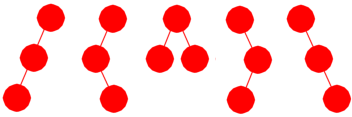 |
| Figur 5.1.2 c) : 5 forskjellige trær med 3 noder |
La C(n), n ≥ 0, være antallet isomorft forskjellige binære trær med n noder. Dermed:
C(0) = 1 C(1) = 1 C(2) = 2 C(3) = 5
Et binærtre med n noder (n > 0) består av en rotnode og av rotnodens to subtrær. La v og h være antallet noder i venstre og høyre subtre. Da må
n = v + h + 1
Hvor mange trær med n noder finnes det som har v noder i venstre og h noder i høyre subtre? Det finnes C(v) trær med v noder og C(h) trær med h noder. Svar: C(v) · C(h). Vi kan nå se på alle tilfellene. Først v = 0 og h = n − 1, så v = 1 og h = n − 2, osv. Til slutt blir det v = n − 1 og h = 0. Dermed kan C(n) regnes ut ved hjelp av flg. differensligning:
(*) C(n) = C(0) · C(n-1) + C(1) · C(n-2) + . . . + C(n-1) · C(0)
Eksempel: Vi vet (se over) at C(3) = 5, men differensligningen (*) gjør at vi kan finne C(3) ved hjelp av C(2), C(1) og C(0). Deretter kan vi finne C(4) når vi kjenner C(3), osv.
C(3) = C(0) · C(2) + C(1) · C(1) + C(2) · C(0) = 1 · 2 + 1 · 1 + 2 · 1 = 5
C(4) = C(0) · C(3) + C(1) · C(2) + C(2) · C(1) + C(3) · C(0)
= 1 · 5 + 1 · 2 + 2 · 1 + 5 · 1 = 14
Det finnes en formel for C(n) (se Avsnitt 5.1.19) der binomialkoeffisienten inngår:
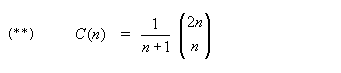 |
Vi kan bruke (**) til å finne C(4) slik:
C(4) = (1/5) · (8 · 7 · 6 · 5)/(4 · 3 · 2 · 1) = 14
Tallene C(0), C(1), . . . kalles Catalan-tall
etter matematikeren E.Catalan (1814 - 94). De 10 første Catalan-tallene er:
1 1 2 5 14 42 132 429 1430 4862
| 1. | Finn C(5) og C(6) ved hjelp av differensligningen (*) og så ved hjelp av formelen (**). |
| 2. | Tegn de 14 forskjellige trærne med 4 noder. |
| 3. | Hvor mange forskjellige av trærne med n noder er det der ingen av nodene har to barn? Figur 5.1.2 b) og Figur 5.1.2 c) viser at svaret er 2 for n = 2 og 4 for n = 3. |
| 4. | La n = 2k + 1 være et oddetall.
Hvor mange fulle
trær med n noder finnes det? Tegn alle forskjellige fulle trær med 7 noder.
|
| 5. | Tallene C(n) kalles Catalan-tall.
Lag metoden public static long catalan(int n). Den skal returnere det n-te
Catalan-tallet. Gjør det på disse måtene:a) Bruk differensligningen (*) til å lage en rekursiv versjon av metoden. Forklar så hvorfor dette vil bli en ekstremt ineffektiv algoritme. b) Bruk differensligningen (*), men lag metoden iterativ. Bruk en lokal hjelpetabell med navn f.eks. lik c, la c[0] = 1 og c[1] = 1, og fyll ut c fortløpende, dvs. c[n] kan regnes ut når c[k] er kjent for alle k mindre enn n. c) Lag metoden ved å bruke formelen (**). |
| 6. | Tall multipliseres to og to. Med tre tall, f.eks. a · b · c, må det settes parenteser og det kan gjøres på to måter: a(b · c) eller (a · b)c. Med fire tall, a · b · c · d, kan det gjøres på fem måter: ((a · b)c)d, (a(b · c))d, (a · b)(c · d), a((b · c)d) og a(b(c · d)). Vis at C(n) er lik antallet måter det kan gjøres når det er n + 1 tall. |
| 7. | Catalan-tallene dukker opp i mange sammenhenger. Finn mer om dette på internett. Start
f.eks. med siden
Catalan-tall.
|
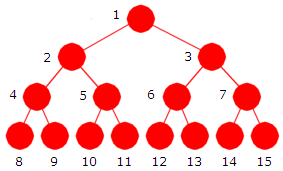 |
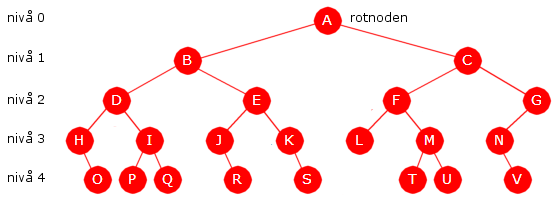
| Figur 5.1.3 a) : Nodeposisjoner i et perfekt binærtre |
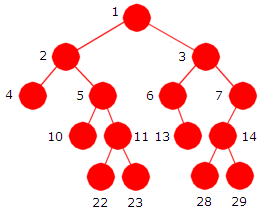 |
| Figur 5.1.3 b) : Posisjoner i et generelt binærtre. Barna til k er 2k og 2k + 1. |
I Figur 5.1.3 b) til venstre har vi et mer generelt binærtre. Vi kan finne posisjoner som i et perfekt tre. Roten har alltid posisjon 1. Men vi må hoppe over de tallene som representerer manglende noder. Nodene har posisjoner 1, 2, 3, 4, 5, 6, 7, 10, 11, 13, 14, 22, 23, 28 og 29. Tallene 8, 9 og 12 (og enda flere) mangler fordi nodene som hører til de posisjonene ikke er i treet.
Flg. regel er enklere: Hvis en node har posisjon k, så har de to barna posisjonene 2k (venstre) og 2k + 1 (høyre). Dette gjelder fra og med rotnoden (posisjon 1). Ta f.eks. noden med posisjon 5. De to barna har posisjoner 2·5 = 10 og 2·5 + 1 = 11.
Det er en tilsvarende regel motsatt vei: Hvis en node har posisjon k (k ≠ 1), så er ⌊k/2⌋ posisjonen til foreldernoden. Ta f.eks. noden med posisjon 5. Det gir posisjon ⌊5/2⌋ = 2 for forelderen. Obs: Vi kan skrive k/2 istedenfor ⌊k/2⌋ hvis vi tolker divisjonen som heltallsdivisjon.
Konklusjon Vi kan bruke flg. regel for å bestemme nodeposisjoner: Rotnoden har posisjon 1. Deretter brukes «barnereglen»: Barna til en node med posisjon k har henholdsvis 2 k (venstre) og 2 k + 1 (høyre) som posisjonstall.
La T være et binærtre og la P (T) være mengden av posisjonstall. Hvis T er et tomt, blir P (T) den tomme mengden. Hvis f.eks. T er treet i Figur 5.1.3 b), vil P (T) = {1, 2, 3, 4, 5, 6, 7, 10, 11, 13, 14, 22, 23, 28, 29}. I Avsnitt 5.1.2 så vi på isomorft forskjellige binære trær. Ved hjelp av mengden P (T) kan vi nå presist definere hva det vil si at to binære trær er isomorfe (har samme form) og at de er like. La v(k) være verdien til noden med posisjon k :
To binære trær T1 og T2 er isomorfe hvis og bare hvis P (T1 ) = P (T2 ).
er lik v(k) i T2 for alle k i P (T1 ) = P (T2 ).
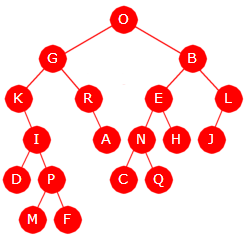
Eksempel: La T1 og T2 være trærne i Figur 5.1.3 a) og b). Vi ser umiddelbart at trærne ikke har samme form. Dette kan vi også se ved å sette opp elementene i de to mengdene P (T1 ) og P (T2 ). Vi vil da se at de er ulike som tallmengder.
 |
|
| Tre 1 Tre 2 | |
| 1. | Sett på ved alle nodene, i både Tre 1 og Tre 2, nodenes posisjonstall. |
| 2. | Finn det største posisjonstallet i Tre 1 (og Tre 2) og sett det på binær form. Det er kjent at høyden i et tre er én mindre enn antallet signifikante binære siffer i treets største posisjonstall. Sjekk at det stemmer i Tre 1 (og Tre 2). |
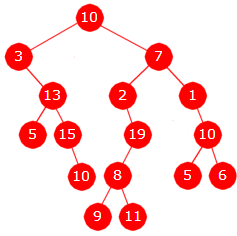
| 3. | La P (T) = {3, 13, 7, 26, 2, 1, 6, 27} være posisjonstallene til et binærtre. Tegn dette treet. Her ser vi bort fra nodeverdier. |
| 4. | La P (T) = {1, 2, 5, 10, 20, 21, 3, 6, 13, 26, 27}. Gjør som i Oppgave 3. |
| 5. | Finnes det et binærtre som har flg. mengde av posisjonstall: {1, 2, 3, 5, 10, 11, 12}. |
| 6. | Finnes det binære trær der mengden av posisjonstall kun inneholder oddetall? |
| 7. | I Avsnitt 5.1.2 ble de fem forskjellige trærne med fire noder satt opp. Sett opp mengden av posisjonstall for hvert av dem. |
| 8. | Et binærtre har en node med posisjonstall 90. Hvilke andre posisjonstall må da treet inneholde? Hva hvis treet også har en node med posisjon 55? Tegn det minste mulige binærtreet som har 90 og 55 som posisjonstall. |
| 9. | P (T) = {3,13,7,26,2,1,6,27} og P(S) = {2,13,1,27,6,3,26,7} er posisjonstallene til trærne T og S. Er de isomorfe? Svar på spørsmålet uten å tegne trærne. |
| 10. | Lag metoden public static boolean girBinærtre(int[] a). Den skal returnere true
hvis tallene i a utgjør posisjonstallene til et binærtre og false ellers. Da må for
det første tallene være positive og forskjellige. Videre må 1 være med og for hvert tall k i a
forskjellig fra 1 må k/2 (heltallsdivisjon) være med i a. |
| 11 | Lag public static int[] utvid(int[] a) der a kun har positive og
ulike tall. Den skal returnere posisjonsmengden til det minstre treet som omfatter a.
Se Oppgave 8. |
| 12 | Lag metoden public static boolean girFulltBinærtre(int[] a). Den skal returnere true
hvis tallene i a utgjør posisjonstallene til et fullt binærtre og false ellers. Bruk først
girBinærtre() til å sjekke at tallene i a er posisjonstallene til et tre. |
| 13 | Lag public static boolean girIsomorfeTrær(int[] a, int[] b). Den skal returnere true
hvis a og b inneholder posisjonstallene til to isosmorfe binærtrær.
|
| 14 | Metoden public static void preSorter(int[] a) (a skal utgjøre
posisjonstallene til et binærtre) skal sortere tallene leksikografisk som bitsekvenser. Da vil f.eks.
5 (= 101) være mindre enn 3 (= 11). Bruk metoden toBinaryString()
fra klassen Integer.
|
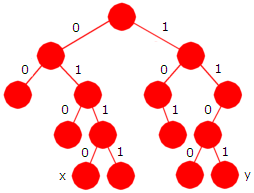 |
| Figur 5.1.4 a) : Tre med binære siffer |
Noden med posisjon 22 er markert med x. Hvis vi starter med et 1-tall (et 1-tall for rotnoden) og så går nedover ved å følge kantene fra rotnoden ned til x-noden, får vi følgende binære sekvens: 10110. Denne sekvensen er nettopp tallet 22 på binærform.
Noden med posisjon 29 er markert med en y. Binærformen til 29 er 11101 og det får vi (bortsett fra den første 1-eren) ved å følge kantene nedover fra rotnoden og ned til y-noden.
Java inneholder metoder for å finne de binære sifrene til et heltall. Flg. kode finner sifrene i tallet 29 (som '0'- eller '1'-tegn i en tegnstreng):
String siffer = Integer.toBinaryString(29);
System.out.println(siffer); // utskrift: 11101
Obs: Hvis det er aktuelt med posisjonstall som er for store for datatypen int
kan vi bruke typen long eller eventuelt
BigInteger.
Det blir nå enkelt å finne frem til en node eller sette inn en node på en oppgitt posisjon hvis posisjonstallet er gitt. La k være et posisjonstall. Hvis k er 1, svarer det til rotnoden. Hvis ikke, finner vi først de binære sifrene til k, ser bort fra den ledende 1-eren, starter i rotnoden, følger de binære sifrene, dvs. går til venstre når det er 0 og til høyre når det er 1.
Vi får flg. oppsummering:
- Hver node i et binærtre har en entydig posisjon (eller et posisjonstall) og det er nodens plassering i treet som bestemmer dette tallet.
- Rotnoden har alltid posisjon 1.
- Hvis k, k > 1, er posisjonen til en node, så er ⌊k/2⌋ posisjonen til nodens forelder.
- Hvis en node med posisjon k har et venstre barn, så er ventrebarnets posisjon lik 2k.
- Hvis en node med posisjon k har et høyre barn, så er høyrebarnets posisjon lik 2k + 1.
- Hvis k, k > 1, er en posisjon i binærtreet, så gir de binære sifrene til k oss veien fra rotnoden ned til denne posisjonen. Vi hopper over det ledende 1-tallet. Deretter går vi til venstre når det er 0 og til høyre når det er 1.
- Høyden i et tre er én mindre enn antallet binære siffer i treets største posisjonstall.
Det å kunne bruke posisjonstall for noder er nyttig i mange sammenhenger. Spesielt er
det viktig i forbindelse med komplette binærtrær og heaper. Det tas opp
i Delkapittel 5.3.
| 1. | Tegn et perfekt binærtre med 15 noder, sett på 0 og 1 på kantene og posisjonstall ved nodene, og bruk dette til å sette opp alle heltallenen fra 1 til 15 på binærform. |
| 2. | Lag et program som skriver ut tallene fra 1 til 15 på binærform ved
å bruke metoden toBinaryString() fra klassen Integer.
|
| 3. | Gjør det samme som over, men bruk bit-operatorer. Se
Delkapittel 1.7.
|
![]() 5.1.5 Datarepresentasjon av noder og binære trær
5.1.5 Datarepresentasjon av noder og binære trær
En klasse for et generisk binærtre må ha en indre nodeklasse med tre instansvariabler (en verdi
og to nodereferanser), konstruktører og metoder som gjør det mulig å bygge opp et tre:
public class BinTre<T> // et generisk binærtre { private static final class Node<T> // en indre nodeklasse { private T verdi; // nodens verdi private Node<T> venstre; // referanse til venstre barn/subtre private Node<T> høyre; // referanse til høyre barn/subtre private Node(T verdi, Node<T> v, Node<T> h) // konstruktør { this.verdi = verdi; venstre = v; høyre = h; } private Node(T verdi) { this.verdi = verdi; } // konstruktør } // class Node<T> private Node<T> rot; // referanse til rotnoden private int antall; // antall noder i treet public BinTre() { rot = null; antall = 0; } // konstruktør public final void leggInn(int posisjon, T verdi) {} // kode utelatt public int antall() { return antall; } // returnerer antallet public boolean tom() { return antall == 0; } // tomt tre? } // class BinTre<T> Programkode 5.1.5 a)
Metoden void leggInn(int posisjon, T verdi) skal legge en verdi
på et oppgitt sted i binærtreet, dvs. gitt ved hjelp
av en nodeposisjon k. Se også Oppgave 11.
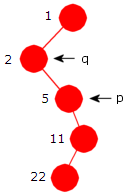 |
| Figur 5.1.5 a) : En gren i treet |
Til venstre har vi en del av et binærtre. Det skal være en verdi i hver node, men
det er utelatt på tegningen. Ved siden av hver node står posisjonstallet.
Det er ikke en del av treet, men er lagt inn
på tegningen for at det skal være lettere å se hva som foregår.
Anta at en ny node skal legges inn som høyre barn til 22-noden, dvs. i posisjon 2·22 + 1 = 45. Binærsifrene til 45 er 101101, men det er bare de 5 siste vi bruker, dvs. 01101. På tegningen ser vi øyeblikkelig hvor den nye noden skal ligge, men når dette skal kodes må vi starte i rotnoden og bruke binærsifrene til å manøvrere oss ned til rett plass.
Det er vanlig å bruke to hjelpereferanser p og q der p i
utgangspunktet settes til rotnoden. Deretter flyttes p ned til venstre
hvis det er et 0-siffer og ned til høyre hvis det er 1-siffer. Hensikten med q er at den hele tiden
skal ligge ett nivå over p, dvs. at q går til forelder til p.
Vi starter i rotnoden med 01101 og kommer ned til 22-noden ved hjelp av 0110 (dvs. venstre,
høyre, høyre, venstre). Men det står igjen et 1-tall i 01101 og dermed går p til slutt ned til høyre
og blir null. Men q, som skal ligge ett nivå over p, vil stoppe
på 22-noden. Den nye noden må da legges som høyre barn til q.
Det må stilles bestemte krav til posisjonstallet. For det første må
det være positivt. Hvis det finnes en node fra før med oppgitt posisjon, kunne
en innlegging tolkes som en oppdatering. Men til det formålet
er det mer naturlig å ha en egen metode. Derfor krever vi her at
den ikke må finnes fra før. En ny node i et ikke-tomt tre må alltid legges
inn som et barn til en eksisterende node. Det betyr at treet må ha en node
med posisjon/2 fra før, men ikke en node med
posisjon. Det bør kastes et unntak hvis posisjon har en ulovlig verdi.
Vi trenger de binære sifrene i posisjon. Det mest optimale er å bruke bitoperatorer.
La f.eks. posisjon = 45 = 101101. Da vil Integer.highestOneBit(posisjon) >> 1
gi tallet 16 = 10000. Vi kaller dette tallet et filter. Da blir første aktuelle siffer 0 hvis
posisjon & filter er lik 0 og lik 1 hvis
posisjon & filter ikke er 0. Vi finner neste siffer i posisjon ved å bitforskyve
filter og sammenligne på nytt.
Det er antallet binære siffer i posisjon som bestemmer antallet iterasjoner metoden
må gjøre for å finne rett plass i treet. Det betyr at metoden vil bli av orden
log2 (posisjon).
public final void leggInn(int posisjon, T verdi) // final: kan ikke overstyres { if (posisjon < 1) throw new IllegalArgumentException("Posisjon (" + posisjon + ") < 1!"); Node<T> p = rot, q = null; // nodereferanser int filter = Integer.highestOneBit(posisjon) >> 1; // filter = 100...00 while (p != null && filter > 0) { q = p; p = (posisjon & filter) == 0 ? p.venstre : p.høyre; filter >>= 1; // bitforskyver filter } if (filter > 0) throw new IllegalArgumentException("Posisjon (" + posisjon + ") mangler forelder!"); else if (p != null) throw new IllegalArgumentException("Posisjon (" + posisjon + ") finnes fra før!"); p = new Node<>(verdi); // ny node if (q == null) rot = p; // tomt tre - ny rot else if ((posisjon & 1) == 0) // sjekker siste siffer i posisjon q.venstre = p; // venstre barn til q else q.høyre = p; // høyre barn til q antall++; // en ny verdi i treet } Programkode 5.1.5 b)
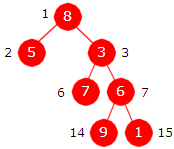 |
| Figur 5.1.5 b) |
Eksempel 5.1.5 a) I Figur 5.1.5 b) er heltall nodeverdier. Ved hver node står posisjonstallet. Treet konstrueres slik:
BinTre<Integer> tre = new BinTre<>(); // T = Integer int[] posisjon = {1,2,3,6,7,14,15}; // posisjoner int[] verdi = {8,5,3,7,6,9,1}; // verdier for (int i = 0; i < verdi.length; i++) tre.leggInn(posisjon[i],verdi[i]); // autoboksing
Typeparameteren i BinTre<Integer> sier at verditypen er Integer. Verditabellen
er imidlertid av typen int. Men det går bra pga. autoboksingen.
Nodene kan ikke settes
inn i tilfeldig rekkefølge. For hver node må foreldernoden være på plass først.
I tabellene v og p er verdiene og posisjonene satt opp i nivåorden
og dermed kommer forelder før barn.
Det kan være praktisk å ha en konstruktør som har posisjons- og verditabellene som parametere. Da kan
leggInn-metoden isteden kalles inne i konstruktøren:
public BinTre(int[] posisjon, T[] verdi) // konstruktør { if (posisjon.length > verdi.length) throw new IllegalArgumentException("Verditabellen har for få elementer!"); for (int i = 0; i < posisjon.length; i++) leggInn(posisjon[i],verdi[i]); } Programkode 5.1.5 c)
Eksempel 5.1.5 b) Figur 5.1.5 c) under er en kopi av Figur 5.1.1 a) - med posisjonstall i tilegg. Da er det enkelt å sette opp to tabeller - en tabell for posisjoner og en for verdier:
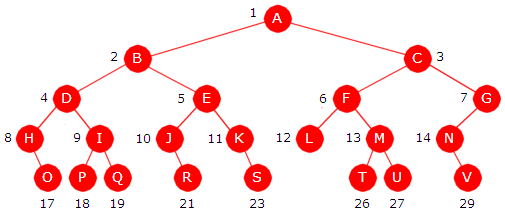 |
| Figur 5.1.5 c) : Et binærtre med tegn som nodeverdier |
Nodeverdiene er tegn, men vi kan ikke bruke datatypen char direkte siden det ikke er
en referansetype. Vi bruker isteden typen Character. Da kan vi ramse opp alle bokstavene
som tegn (char) og la autoboksingen ta seg av konverteringen fra char til Character:
int[] posisjon = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29}; Character[] verdi = {'A','B','C','D','E','F','G','H','I','J','K', 'L','M','N','O','P','Q','R','S','T','U','V'}; BinTre<Character> tre = new BinTre<>(posisjon, verdi); // den nye konstruktøren Programkode 5.1.5 d)
Det er også mulig å se på hvert tegn som en tegnstreng med bare ett tegn. Da kan vi sette opp
nodeverdiene i en tabell av tegnstrenger og la String være datatypen for treet:
int[] posisjon = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29}; String[] verdi = {"A","B","C","D","E","F","G","H","I","J","K", "L","M","N","O","P","Q","R","S","T","U","V"}; BinTre<String> tre = new BinTre<>(posisjon, verdi); // den nye konstruktøren Programkode 5.1.5 e)
Det er imidlertid tungvint å sette opp hver bokstav separat i en tabell enten bokstaven settes opp som tegn
eller som en tegnstreng med ett tegn. Vi kan isteden bruke metoden
split()
fra klassen String på en litt uortodoks måte. Metoden har flg. signatur:
public String[] split(String regex);
Ved å bruke en tom streng (dvs. "") som regulært uttrykk, får vi splittet opp tegnstrengen i
enkelttegn. Dette, sammen konstruktøren
fra Programkode 5.1.5 c), gir oss flg. enkle kode:
int[] posisjon = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29}; String[] verdi = "ABCDEFGHIJKLMNOPQRSTUV".split(""); BinTre<String> tre = new BinTre<>(posisjon, verdi); // den nye konstruktøren Programkode 5.1.5 f)
Vi kan også splitte opp en tegnstreng i enkelttegn ved hjelp av metoden
toCharArray()
fra klassen String. Men da blir resultatet en char-tabell og siden det ikke er en
tabell av referansetyper, kan den ikke inngå som parameter i
konstruktøren fra Programkode 5.1.5 c).
Da må vi isteden bygge opp treet ved å legge inn ett og ett tegn fra tabellen. Det vil virke siden en char-verdi da blir
konvertert (autoboksing) til en Character:
int[] posisjon = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29}; char[] verdi = "ABCDEFGHIJKLMNOPQRSTUV".toCharArray(); BinTre<Character> tre = new BinTre<>(); for (int i = 0; i < posisjon.length; i++) { tre.leggInn(posisjon[i],verdi[i]); } Programkode 5.1.5 g)
Vi har nå sett på flere måter som treet i Figur 5.1.5 c)
kan bygges opp. Verdiene er bokstavene fra A til V. Hvis vi har fortløpende verdier, f.eks. bokstaver,
kan vi genere dem ved hjelp av en løkke. I flg. eksempel lages et
komplett
binærtre (treet i Figur 5.1.5 c) er ikke komplett)
med n bokstaver
fra A og utover.
Med n = 22 blir det fra A til V:
BinTre<Character> tre = new BinTre<>(); // et tomt tre int n = 15; // komplett tre med n verdier for (int i = 0; i < n; i++) { tre.leggInn(i + 1,(char)('A' + i)); } Programkode 5.1.5 h)
Trær blir først interessante når vi også kan få utført andre typer operasjoner enn bare innlegginger. Her er et knippe metoder som et binærtre bør ha:
public boolean finnes(int posisjon) // finnes posisjon fra før? public T hent(int posisjon) // verdien i noden med gitt posisjon public T oppdater(int posisjon, T verdi) // ny verdi i noden med gitt posisjon public T fjern(int posisjon) // fjerner noden med gitt posisjon public boolean inneholder(T verdi) // avgjør om verdi er i treet public int posisjon(T verdi) // posisjonen til verdi
Metodene finnes(), hent(), oppdater() og
fjern() har en posisjon
som parameter. Vi lager en hjelpemetode som finner (søketeknikk som i
Programkode 5.1.5 b) noden med den posisjonen. Dermed kan de
fire metodene kodes vha. den:
private Node<T> finnNode(int posisjon) // finner noden med gitt posisjon { if (posisjon < 1) return null; Node<T> p = rot; // nodereferanse int filter = Integer.highestOneBit(posisjon >> 1); // filter = 100...00 for (; p != null && filter > 0; filter >>= 1) p = (posisjon & filter) == 0 ? p.venstre : p.høyre; return p; // p blir null hvis posisjon ikke er i treet } public boolean finnes(int posisjon) { return finnNode(posisjon) != null; } public T hent(int posisjon) { Node<T> p = finnNode(posisjon); if (p == null) throw new IllegalArgumentException("Posisjon (" + posisjon + ") finnes ikke i treet!"); return p.verdi; } public T oppdater(int posisjon, T nyverdi) { Node<T> p = finnNode(posisjon); if (p == null) throw new IllegalArgumentException("Posisjon (" + posisjon + ") finnes ikke i treet!"); T gammelverdi = p.verdi; p.verdi = nyverdi; return gammelverdi; } Programkode 5.1.5 j)
| 1. | Kopier klassen BinTre over til deg. Legg
den under package hjelpeklasser.
Legg metodene i Programkode 5.1.5 b),
c)
og j)
inn i klassen. Lag et program som kjører
Programkode 5.1.5 c) og
d).
|
| 2. | Lag kode som bygger opp trærne fra Oppgave 1 og 2 i Avsnitt 5.1.1. |
| 3. | Gjør som over for Tre 1 og Tre 2 fra Oppgave 1 i Avsnitt 5.1.3. |
| 4. | La {5,23,2,10,3,11,47,1,22,44} være posisjonstallene for nodene i et binærtre og {4,8,2,5,3,6,10,1,7,9} de tilhørende nodeverdiene i samme rekkefølge. Dvs. noden med posisjon 5 skal ha nodeverdi 4, osv. Tegn treet. Lag så kode som bygger treet. |
| 5. | Lag kode som bygger et perfekt tre med 15 noder og med verdiene 1 - 15 i nivåorden. |
| 6. | Lag kode som bygger et tre med 15 noder der nodene har verdiene 1, 2, . . , 15 i nivåorden. Ingen noder i treet skal ha høyre barn. Tegn treet først. |
| 7. | Lag kode som bygger et tre med 15 noder der nodene har verdiene 1, 2, . . , 15 i nivåorden. Rotnodens to subtrær skal begge ha 7 noder. I det venstre subtreet skal ingen noder ha høyre barn og i det høyre subtreet skal ingen node ha venstre barn. Tegn treet først slik at du ser hvilke noder og posisjonstall du må ha. |
| 8. | Lag metoden public int nodetype(int posisjon) i klassen BinTre. Den skal returnere 1 hvis
posisjon hører til en bladnode, returnere 0 hvis posisjon hører til
en indre node og -1 hvis posisjon ikke er i treet. Bruk metoden
finnNode() i kodingen din.
|
| 9. | Lag metoden public T fjern(int posisjon).
Kun bladnoder kan fjernes. Hvis en indre node fjernes vil ikke treet lenger
henge sammen. Verdien i den fjernede noden returneres. Hvis
posisjon ikke svarer til en bladnode skal det kastes et unntak.
|
| 10. | Lag et binætre som inneholder 31 noder slik at ingen node har høyre barn. La nodene få tallene 1, 2, 3, . . . , 31 som verdier. Blir det noen problemer her hvis du øker antallet med en slik at treet får 32 noder og ingen av dem har høyre barn? Se da Oppgave 11. |
| 11. | Hvis en trenger nodeposisjoner som er større enn datatypen
int tillater, kan en bruke long eller eventuelt
BigInteger.
Lag egne versjoner (Java: overload) av leggInn() og de andre metodene der et heltall inngår som
parameter eller er returverdi, for disse to typene. Da vil signaturen
bli: public void leggInn(long posisjon, T verdi) og
public void leggInn(BigInteger posisjon, T verdi).
|
| 12. | Bruk metoden som bruker long i Oppgave 11 og lag et binærtre som inneholder 63 noder slik at ingen node har høyre barn. La nodene få tallene 1, 2, 3, . . . , 63 som verdier. Blir det noen problemer her hvis du øker antallet med en slik at treet får 64 noder og ingen av dem har høyre barn? Se da Oppgave 13. |
| 13. | Bruk metoden som bruker BigInteger i Oppgave 11 til å lage et binærtre som inneholder 64 noder
slik at ingen node har høyre barn.
|
| 14. | Metodene boolean inneholder(T verdi)
og int posisjon(T verdi) er også satt
opp som aktuelle metoder i et binærtre. Har du noen forslag til hvordan de skal kodes?
|
![]() 5.1.6 Traverseringer - nivåorden
5.1.6 Traverseringer - nivåorden
I binære trær trenger vi ofte, på lik linje med andre datastrukturer, å kunne gå gjennom
samtlige noder eller verdier. Aktuelle oppgaver kunne være å finne antallet verdier av en
bestemt type, skrive ut alle verdiene til konsollet (eller en fil), kopiere verdiene
over i en tabell eller annen datastruktur eller andre aktuelle
ting. Vi trenger derfor teknikker som gjør oss i stand til å «reise gjennom»
treet, dvs. besøke alle nodene etter tur og da vanligvis i en bestemt rekkefølge.
Dette kalles å traversere treet (eng: traverse).
Vi har to hovedtyper av traverseringer. Vi kan for hver node gå
til siden før vi går nedover, dvs. «bredde først» (eng: breadth-first). Alternativt
kan vi gå nedover før vi går til siden, dvs. «dybde først» (eng: depth-first).
Vi skal se på én traversering av typen «bredde først» og tre forskjellige av typen
«dybde først». De har navn etter den orden eller rekkefølge som nodene besøkes.
Rekkefølgen nivåorden er av typen «bredde først» og preorden,
inorden og postorden er alle av typen «dybde først».
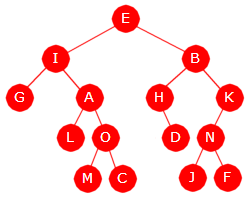
|
| Figur 5.1.6 a) |
Det kalles nivåorden når nodene «besøkes» nivå for nivå, fra rotnoden og nedover,
og for hvert nivå fra venstre mot høyre. I Figur 5.1.6 a) til venstre vil en
oppramsing av nodeverdiene i nivåorden gi oss denne rekkefølgen: E, I, B, G, A, H, K,
L, O, D, N, M, C, J og F. Dette blir en «bredde først»-traversering.
Traversering av typen «bredde først» utføres ved hjelp av
en kø.
I «dybde først» brukes enten rekursjon eller en stakk.
Metoden nivåorden(), som skal ligge i BinTre-klassen
(Programkode 5.1.5 a ), benytter
en kø (Delkapittel 4.2).
Den skriver ut verdiene i nivåorden og med én verdi for hver iterasjon. Det
betyr at den er av orden n der n er antall noder.
Obs: Det er instanser av Node<T> som legges inn i køen:
public void nivåorden() // skal ligge i class BinTre { if (tom()) return; // tomt tre Kø<Node<T>> kø = new TabellKø<>(); // Se Avsnitt 4.2.2 kø.leggInn(rot); // legger inn roten while (!kø.tom()) // så lenge som køen ikke er tom { Node<T> p = kø.taUt(); // tar ut fra køen System.out.print(p.verdi + " "); // skriver ut if (p.venstre != null) kø.leggInn(p.venstre); if (p.høyre != null) kø.leggInn(p.høyre); } } Programkode 5.1.6 a)
Hvordan virker Programkode 5.1.6 a)? Bruk treet i Figur 5.1.6 a) som eksempel. Først legges rotnoden (E-noden) i køen. Så går while-løkken så lenge som køen ikke er tom. Tabellen i Figur 5.1.6 b) under viser de 6 første iterasjonene.
| Runde | Ut av køen | Inn i køen | Køens innhold |
| 1 | E | I , B | I , B |
| 2 | I | G , A | B , G , A |
| 3 | B | H , K | G , A , H , K |
| 4 | G | A , H , K | |
| 5 | A | L , O | H , K , L , O |
| 6 | H | D | K , L , O , D |
| Figur 5.1.6 b) : De 6 første iterasjonene | |||
|---|---|---|---|
Vi bruker treet Figur 5.1.6 a).
Metoden leggInn() krever at forelder må være på plass før noden. Programkode 5.1.6 b)
under har tabeller med nodeposisjoner og verdier. Sjekk at
de er korrekte, at rekkefølgen i tabellene er den samme og at
foreldre legges inn før barn:
int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29}; // posisjoner og String[] verdi = "EIBGAHKLODNMCJF".split(""); // verdier i nivåorden BinTre<String> tre = new BinTre<>(posisjon, verdi); // en konstruktør tre.nivåorden(); // Utskrift: E I B G A H K L O D N M C J F Programkode 5.1.6 b)
Metoden nivåorden() er noe fastlåst. Den skriver til konsollet.
Hva med utskrift til fil? Eller noe helt annet.
Det kan løses ved å «instruere» traverseringsmetoden om hva den skal gjøre
gjennom et generisk funksjonsgrensesnitt Oppgave:
@FunctionalInterface public interface Oppgave<T> // legges under hjelpeklasser { void utførOppgave(T t); // f.eks. utskrift til konsollet } Programkode 5.1.6 c)
Oppgave kalles et funksjonsgrensesnitt siden det er nøyaktig én
abstrakt metode. En metode i et grensesnitt er automatisk både public og abstract.
Dermed er det unødvendig å skrive det eksplisitt.
Vi må endre metoden nivåorden() fra Programkode 5.1.6 a)
for å kunne benytte en Oppgave.
Nedenfor er endringene/tilleggene markert med rød skrift:
public void nivåorden(Oppgave<? super T> oppgave) // ny versjon { if (tom()) return; // tomt tre Kø<Node<T>> kø = new TabellKø<>(); // Se Avsnitt 4.2.3 kø.leggInn(rot); // legger inn roten while (!kø.tom()) // så lenge køen ikke er tom { Node<T> p = kø.taUt(); // tar ut fra køen oppgave.utførOppgave(p.verdi); // den generiske oppgaven if (p.venstre != null) kø.leggInn(p.venstre); if (p.høyre != null) kø.leggInn(p.høyre); } } Programkode 5.1.6 d)
Et grensesnitt er bare en samling metodesignaturer. Det vi normalt må gjøre er å lage en klasse som implementerer
grensesnittet. Der bestemmes hva metodene skal gjøre. Oppgave
er et funksjonsgrensesnitt.
Dermed kan vi bruke et lambda-utrykk til å bestemme hva metoden utførOppgave() skal gjøre. Samtidig definerer
lambda-utrykket en instans av en navnløs (anonym) klasse. Vi gjør det slik:
Oppgave<Character> oppgave = c -> System.out.print(c + " "); // lambda-uttrykk oppgave.utførOppgave('A'); // instansen oppgave har metoden utførOppgave Programkode 5.1.6 e)
I Programkode 5.1.6 e) blir oppgave en instans av en anonym klasse som implementerer
Oppgave. Vi bruker tegnet 'A' som argument i utførOppgave('A').
Det er ok siden Character er datatypen.
System.out.print(c + " ");
blir «innmaten» i metoden utførOppgave. Derfor blir resultatet at bokstaven A skrives til konsollet.
Den nye versjonen av nivåorden() har Oppgave som argument. Den kan brukes i eksemplet
i Programkode 5.1.6 b) hvis vi bytter ut setningen
tre.nivåorden(); med flg. setning:
tre.nivåorden(c -> System.out.print(c + " ")); // lambda-uttrykk som argument Programkode 5.1.6 f)
Legg merke til at i Programkode 5.1.6 f) er lambda-uttrykket argument. Med andre ord er det ikke nødvendig å gjøre som i
Programkode 5.1.6 e), dvs. å lage en instans først.
De lamda-uttrykkene vi kan bruke som en Oppgave, må være på formen: t -> f(t) der f(t) er
en funksjon eller et funksjonsuttrykk. Se også Oppgave 5. Legg merke til
at variabelen kan hete t,
c, x eller hvilket navn vi måtte ønske. Generisk brukes t siden det henger sammen
med typen T. Navnet c ble brukt i Programkode 5.1.6 f) siden Character er datatypen.
Vi tar et eksempel til på hvordan en lambda-uttrykk brukes. Nå skal nivå-traverseringen sørge for at hver verdi legges inn i en liste.
Listens leggInn-metode er egentlig ikke en void-funksjon. Men det gjør ikke noe så lenge dens returverdi
(en boolean) ikke brukes:
Liste<Character> liste = new TabellListe<>(); // en liste tre.nivåorden(c -> liste.leggInn(c)); // lambda-uttrykk som argument System.out.println(liste); // skriver ut listen Programkode 5.1.6 g)
Det å skrive til konsollet er noe vi ofte gjør. Derfor vil det være praktisk om det var en forhåndsdefinert oppgave for dette. Det
kan vi få til ved å la grensesnittet
Oppgave ha en statisk metode som genererer en konsollutskrift:
@FunctionalInterface public interface Oppgave<T> // en utvidelse av Oppgave { void utførOppgave(T t); // en abstrakt metode public static <T> Oppgave<T> konsollutskrift() // en konstruksjonsmetode { return t -> System.out.print(t + " "); // et lambda-uttrykk } } // Oppgave Programkode 5.1.6 h)
Vi kan nå bruke flg. argument når metoden nivåorden kalles:
tre.nivåorden(Oppgave.konsollutskrift()); // den forhåndsdefinerte oppgaven
Det kan være aktuelt å utføre en serie oppgaver. En
default-metode i grensesnittet Oppgave kan brukes til det, dvs. å sette sammen oppgaver:
@FunctionalInterface public interface Oppgave<T> // en ny utvidelse av Oppgave { void utførOppgave(T t); // en abstrakt metode public static <T> Oppgave<T> konsollutskrift() // en konstruksjonsmetode { return t -> System.out.print(t + " "); // et lambda-uttrykk } default Oppgave<T> deretter(Oppgave<? super T> oppgave) { return t -> { utførOppgave(t); oppgave.utførOppgave(t); }; } } // Oppgave Programkode 5.1.6 i)
Oppgaven konsollutskrift() gir et mellomrom etter verdien (dvs. t + " "). Hvis vi f.eks. skulle ønske ytterligere et mellomrom, kan
vi gjøre det på denne måten:
tre.nivåorden(Oppgave.konsollutskrift().deretter(c -> System.out.print(' '))); Programkode 5.1.6 j)
Legg merke til at i lambda-uttrykket: c -> System.out.print(' ') som ble brukt over, inngår ikke
c på høyre side av funksjonspilen ->. Det ble sagt tidligere at lambda-uttrykket måtte være på formen: c -> f(c) der f(c)
er void (funksjon eller funksjonsuttrykk). Men det går bra med en funksjon uten argument og med en funksjon med returtype.
Vi kunne ha brukt en Consumer
istedenfor en Oppgave. Se Oppgave 6.
Vi kan finne ut mer om et tre gjennom en nivåtraversering. Se på treet i Figur 5.1.6 a). Tabellen i Figur 5.1.6 b) viste hva køen inneholdt i løpet av de seks første iterasjonene. Vi utvider tabellen til også å innholde den 8. iterasjonen:
| Runde | Ut av køen | Inn i køen | Køens innhold |
| 1 | E | I , B | I , B |
| 2 | I | G , A | B , G , A |
| 3 | B | H , K | G , A , H , K |
| 4 | G | A , H , K | |
| 5 | A | L , O | H , K , L , O |
| 6 | H | D | K , L , O , D |
| 7 | K | N | L , O , D , N |
| 8 | L | O , D , N | |
| Figur 5.1.6 c) : De 8 første iterasjonene | |||
|---|---|---|---|
I treet i Figur 5.1.6 a) er E, I, G, L og M første (fra venstre) node på hvert sitt nivå. Ta f.eks. G som er første node på nivå 2 (rotnoden E er på nivå 0). Tabellen over viser at den tas fra køen i 4. iterasjon. Men etter 3. og før 4. iterasjon innholder køen G, A, H og K og det er nodene som hører til nivå 2 i treet. Vi ser at det samme skjer når L tas ut av køen. L er den første noden på nivå 3 og rett før den tas ut inneholder køen nodene L, O, D og N og det er nettopp nodene på nivå 3.
Disse observasjonene kan vi utnytte. Før første iterasjon inneholder køen rotnoden E. Køens antall-metode
gir da 1 som verdi. Dermed tar vi ut 1 node i neste runde og legger de to barna I og B i køen.
Neste runde starter med at vi lar køens antall-metode fortelle hvor mange som ligger der. Så tar vi så mange ut av køen.
Osv. Det betyr at hver runde innledes med at vi kaller antall-metoden og så tar vi fra køen nøyaktig så mange som den sier.
Det betyr at vi tar ut alle nodene på det nivået.
Hvis vi for hver runde lagrer i en tabell de tallene antall-metoden gir oss, kan den tabellen etterpå gi oss informasjon om
treet, f.ek. både treets bredde og treets høyde. Vi lager derfor en metode som returnerer en slik tabell:
public int[] nivåer() // returnerer en tabell som inneholder nivåantallene { if (tom()) return new int[0]; // en tom tabell for et tomt tre int[] a = new int[8]; // hjelpetabell Kø<Node<T>> kø = new TabellKø<>(); // hjelpekø int nivå = 0; // hjelpevariabel kø.leggInn(rot); // legger roten i køen while (!kø.tom()) // så lenge som køen ikke er tom { // utvider a hvis det er nødvendig if (nivå == a.length) a = Arrays.copyOf(a,2*nivå); int k = a[nivå] = kø.antall(); // antallet på dette nivået for (int i = 0; i < k; i++) // alle på nivået { Node<T> p = kø.taUt(); if (p.venstre != null) kø.leggInn(p.venstre); if (p.høyre != null) kø.leggInn(p.høyre); } nivå++; // fortsetter på neste nivå } return Arrays.copyOf(a, nivå); // fjerner det overflødige } Programkode 5.1.6 k)
Bredden til et binærtre kan defineres til å være antallet noder på det nivået som har flest. Hvis vi har en tabell med antall noder på hvert nivå, kan den brukes til finne bredden. Treets høyde er én mindre enn antall nivåer, dvs. høyden vil være én mindre enn nivåtabellens lengde. Følgende eksempel viser hvordan Programkode 5.1.6 k) kan brukes:
int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29}; // nodeposisjoner String[] verdi = "EIBGAHKLODNMCJF".split(""); // verdier i nivåorden BinTre<String> tre = new BinTre<>(posisjon, verdi); // en konstruktør int[] nivåer = tre.nivåer(); // bruker Programkode 5.1.6 k) System.out.print("Nivåer: " + Arrays.toString(nivåer)); System.out.print(" Treets bredde: " + nivåer[Tabell.maks(nivåer)]); System.out.println(" Treets høyde: " + (nivåer.length - 1)); // Utskrift: Nivåer: [1, 2, 4, 4, 4] Treets bredde: 4 Treets høyde: 4 Programkode 5.1.6 l)
| 1. | De to første oppgavene i Avsnitt 5.1.1 inneholder trær. Skriv opp verdiene i nivåorden. |
| 2. | Gjør som i Oppgave 1 for de to trærne Avsnitt 5.1.3. |
| 3. | Flytt grensesnittet
Oppgave over til deg og
legg den nye versjonen
av nivåorden inn i BinTre-klassen. Sjekk så at Programkode 5.1.6 b)
virker ok etter at setningen tre.nivåorden(); byttes ut først med det i
Programkode 5.1.6 f), så det i
Programkode 5.1.6 g) og til slutt det i
Programkode 5.1.6 j).
|
| 4. | I Programkode 5.1.6 g) legges verdier inn i en liste. Når den skrives ut kommer resultatet innrammet med [ og ] og med komma og mellomrom mellom verdiene. Gjør om dette slik at det direkte konstrueres en tegnstreng med samme innhold. Bruk en StringJoiner. |
| 5. | Et lambda-uttrykk kan, istedenfor et kall på en funksjon, ha et funksjonsuttrykk, dvs. koden til en funksjon. Koden kan da inneholde variabler og programsetninger. Disse må imidlertid «rammes inn» med krøllparenteser. Gjør som i Oppgave 4, men bruk i tillegg en if-test slik at strengen kun vil komme til å innholde verdier større enn D. |
| 6. | La klassen BinTre også ha metoden
public void nivåorden(Consumer<? super T> oppgave).
Da må det stå: import java.util.function.*; øverst. I koden bytter du ut
utførOppgave med accept. Hva sier kompilatoren hvis et program inneholder koden
tre.nivåorden(c -> System.out.print(c + " "));?
|
| 7. | La Oppgave
også ha den statiske metoden konsollutskrift(String format) der format
er en formateringsstreng. Utskriften skal utføres ved hjelp av printf(format, t).
Bruk så den for å få samme effekt som Programkode 5.1.6 j).
|
| 8. | Lag et lambda-uttrykk til å finne største verdi i treet fra Programkode 5.1.6 b). |
| 9. | I Oppgave 4 skal alle verdiene legges over i en tegnstreng ved hjelp av en StringJoiner. Hvis
dette skal gjøres på en generisk måte, er enklere å lage en klasse som implementerer Oppgave<T>
og så bruke en instans av klassen som argument i metoden nivåorden. La
klassen hete ToString<T>. Den skal i tillegg ha en toString-metode som
returnerer tegnstrengen. Lag så ToString uten typeparameter. Da må den implementere
Oppgave<Object>. Sjekk at begge måtene vil virke.
|
| 10. | Metoden nivåer() testes i
Programkode 5.1.6 l). Sjekk at metoden
virker korrekt også for andre trær. Tegn noen trær, sett inn verdier, lag en posisjonstabell og
en verditabell og bygg treet. Da må du kanskje gjøre noe små endringer i måten treet bygges
opp i Programkode 5.1.6 l).
|
![]() 5.1.7 Preorden, inorden og postorden
5.1.7 Preorden, inorden og postorden
Vi skal her se på de tre vanlige «dybde først»-traverseringene, dvs. preorden (eng: preorder), inorden (eng: inorder)
og postorden (eng: postorder). «Dybde først» betyr at vi går nedover før vi går til siden. Hver av de
tre typene traversering kan defineres ved hjelp av en enkel geometrisk regel. Se på flg. eksempel:
|
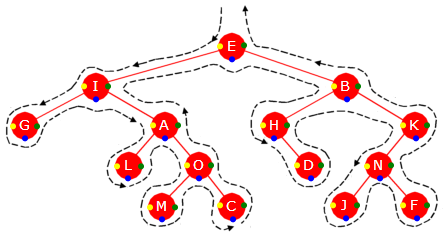
| Figur 5.1.7 a) : Et binærtre med konturkurve |
Figur 5.1.7 a) over viser det samme treet som i
Figur 5.1.6 a). Det er bare
tegnet litt bredere. I tillegg er det tegnet en stiplet strek eller kurve som starter rett opp til venstre for
rotnoden. Videre bukter den seg rundt nodene, går inn mellom forgreningene og ender rett opp til høyre for rotnoden.
Vi kaller det treets kontur eller konturkurve. Pilene gir kurven en retning. I tillegg har
venstre side, undersiden og høyre side av hver node blitt markert med en farget
«prikk» der fargene er gul (venstre side), blå (undersiden) og grønn (høyre side).
I Figur 5.1.7 a) passerer konturkurven hver farget «prikk» nøyaktig én gang. Se f.eks. på I-noden. Der går kurven først forbi på venstre side (gul «prikk»), gjør en runde og kommer tilbake på undersiden (blå «prikk»), gjør en ny runde og kommer deretter forbi på høyre side (grønn «prikk»). I en bladnode som f.eks. G-noden, går konturkurven direkte forbi «prikkene» uten noen mellomliggende runder.
Hvis vi starter ved rotnoden, følger konturkurven og skriver ut nodeverdiene ved passering av en farget «prikk», får vi flg. tre tilfeller:
- Skriver vi ut nodeverdien
når den
gule«prikken» passeres, får vi verdiene ipreorden. For treet i Figur 5.1.7 a) blir det E, I, G, A, L, O, M, C, B, H, D, K, N, J, F. Rotnoden kommer alltid først i preorden! - Skriver vi ut nodeverdien når den
blå«prikken» passeres, får vi verdiene iinordenog dermed G, I, L, A, M, O, C, E, H, D, B, J, N, F, K for treet i Figur 5.1.7 a). Noden nederst til venstre kommer alltid først i inorden! - Skriver vi ut nodeverdien når den
grønne«prikken» passeres, får vi dem ipostorden. Det blir da G, L, M, C, O, A, I, D, H, J, F, N, K, B, E. Rotnoden kommer alltid sist i postorden!
Begrepene pre-, in- og postorden er blitt definert på en uformell og geometrisk måte.
Vi trenger en mer formell definisjon. For det
første betyr ordet orden det samme som rekkefølge og de tre forstavelsene
pre, in og post betyr foran, mellom og etter.
Preorden Det er lettest å definere denne traverseringsrekkefølgen rekursivt:
- Vi starter i rotnoden.
- Videre gjelder for alle noder at først «besøker» vi noden, så dens venstre barn hvis den har et venstre barn og så dens høyre barn hvis den har et høyre barn.
Eksempel: Som allerede nevnt vil dette gi oss verdiene i treet i
Figur 5.1.7 a)
i denne rekkefølgen: E, I, G, A, L, O, M, C, B, H,
D, K, N, J, F.
En enkel huskeregel for preorden er: node, venstre, høyre
Definisjonen av preorden kan lett oversettes til en rekursiv metode. Vi utfører en «oppgave» for hver node vi «besøker». Det kan f.eks. være å skrive ut nodeverdien. Dette bestemmes imidlertid når metoden kalles. Da må oppgaven være bestemt.
Vi lager to metoder - en privat hjelpemetode som
gjør rekursjonen og en offentlig metode som kaller hjelpemetoden. Begge
må legges i class BinTre. Grensesnittet
Oppgave er definert i
Avsnitt 5.1.6:
private static <T> void preorden(Node<T> p, Oppgave<? super T> oppgave) { oppgave.utførOppgave(p.verdi); // utfører oppgaven if (p.venstre != null) preorden(p.venstre,oppgave); // til venstre barn if (p.høyre != null) preorden(p.høyre,oppgave); // til høyre barn } public void preorden(Oppgave<? super T> oppgave) { if (!tom()) preorden(rot,oppgave); // sjekker om treet er tomt } Programkode 5.1.7 a)
Eksempel 5.1.7 a): Vi kan bruke preorden med en Oppgave
i Programkode 5.1.6 b).
Binærtreet som lages der er det samme treet som i
Figur 5.1.7 a)
og programutskriften skal derfor bli E, I, G, A, L, O, M, C, B, H,
D, K, N, J, F. Denne gangen lar vi oppgaven være å bygge opp en tegnstreng innrammet med [ og ] og med
komma og mellomrom mellom hvert tegn. Til det kan vi f.eks. bruke en StringJoiner:
int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29}; // posisjoner og String[] verdi = "EIBGAHKLODNMCJF".split(""); // verdier i nivåorden BinTre<String> tre = new BinTre<>(posisjon, verdi); // en konstruktør StringJoiner s = new StringJoiner(", " ,"[", "]"); // StringJoiner tre.preorden(tegn -> s.add(tegn)); // tegn = String System.out.println(s); // Utskrift: [E, I, G, A, L, O, M, C, B, H, D, K, N, J, F] Programkode 5.1.7 b)
I Programkode 5.1.7 a)
testes det på om parameterverdien er forskjellig fra
null før metoden preorden kalles. I en slik situasjon har vi egentlig
to muligheter. Vi kan teste verdien til parameteren før metoden kalles - slik som i
Programkode 5.1.7 a)
- eller vi kan ha en test som første programsetning i
metoden. Hvis innkommet parameterverdi p da er null, skal metoden
avslutte. Vi kan med andre ord lage metoden preorden på denne
måten:
private static <T> void preorden(Node<T> p, Oppgave<? super T> oppgave) { if (p != null) // metoden returnerer hvis p == null { oppgave.utførOppgave(p.verdi); preorden(p.venstre,oppgave); preorden(p.høyre,oppgave); } } public void preorden(Oppgave <? super T> oppgave) { preorden(rot,oppgave); } Programkode 5.1.7 c)
Spørsmålet blir nå hvilken som er best av versjon 1 (Programkode 5.1.7 a ) og versjon 2 (Programkode 5.1.7 c )? Det er to viktige hensyn vi må ta når en metode skal kodes: 1) koden skal være effektiv og 2) den bør være oversiktlig, forståelig og lett lesbar. Ofte står disse to hensynene i motsetning til hverandre. Enkel og lett forståelig kode er ikke alltid effektiv. Men hvis det kun er marginal forskjell på effektiviteten bør vi normalt velge den koden som er lettest å forstå.
Det er liten eller ingen forskjell på versjon 1 og versjon 2 når det gjelder lesbarhet og forståelighet. Spørsmålet er da om effektivtetene er forskjellige?
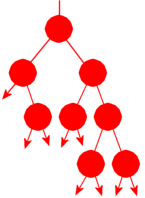 |
| Figur 5.1.7 c) |
Treet i Figur 5.1.7 c) til venstre har 8 noder. Et binærtre
med n noder har en referanse til rotnoden og videre to referanser ut av hver
node - tilsammen 2n + 1. Det er nøyaktig n referanser som
ikke er null siden det går én referanse inn i hver node. Resten av referansene,
dvs. n + 1 stykker, er null-referanser. På tegningen er de 8 + 1 = 9
null-referansene markert med små piler.
Både i versjon 1 og versjon 2 blir alle referansene testet. Det betyr at det begge steder utføres 2n + 1 sammenligninger. Metodene er derfor likeverdige med hensyn på antall sammenligninger. Det er mulig at sammenligningene i versjon 1 er litt mer kostbare enn de i versjon 2. Det er kanskje mer effektivt å arbeide direkte med en referanse p enn å arbeide med p.venstre og p.høyre.
Er det forskjell på antall metodekall i de to versjonene? I versjon 2 skjer sammenligningen etter at metoden er kalt og dermed blir antall sammenligninger og metodekall det samme, dvs. 2n + 1. I versjon 1 kalles metoden kun når referansen ikke er null, dvs. bare n metodekall. Det betyr halvparten så mange metodekall i versjon 1 som i versjon 2. I teorien burde derfor versjon 1 være mest effektiv. Vi kan gjøre testkjøringer for å avgjøre det. Da vil det nok vise seg at versjon 1 bare er marginalt bedre. Konklusjonen blir likevel at vi bruker versjon 1 siden koden er like lesbar og forståelig som i versjon 2. Begge versjonene er av orden n der n er antallet noder.
I versjon 1 er det også brukt et viktig prinsipp (som vi også kjenner fra dagliglivet): «Det er bedre å være føre var enn etter snar». Det bedre å teste på eventuelle feilsituasjoner på forhånd enn å teste på om det kan oppstå en feilsituasjon inne i metoden.
Både nivåorden og preorden har den egenskapen at når en node
(forskjellig fra rotnoden) besøkes er nodens forelder allerede besøkt.
I Eksempel 5.1.7 a) ble
verdiene i tabellene v og p satt inn i nivåorden siden
leggInn-metoden krever at når et node legges inn i treet må nodens forelder
allerede være på plass. Verdiene i v og p
kunne isteden være satt inn i preorden og vi ville fått det samme treet.
Inorden Dette definerer vi også rekursivt:
- Vi starter i rotnoden.
- Videre gjelder for alle noder at først «besøker» vi nodens venstre barn hvis den har et venstre barn, så noden og så dens høyre barn hvis den har et høyre barn.
Eksempel: Hvis vi igjen bruker treet i
Figur 5.1.7 a) gir den
rekursive definisjonen av inorden at verdiene vil komme slik:
G, I, L, A, M, O, C, E, H, D, B, J, N, F, K.
En enkel huskeregel for inorden er: venstre, node, høyre
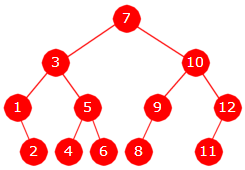 |
| Figur 5.1.7 d: Et sortert binærtre |
Koden for en inordentraversering er maken til den for preorden (se Programkode 5.1.7 a ). Det er bare å bytte ut metodenavnene og flytte oppgavekallet mellom de to rekursive kallene. Husk at pre betyr foran, dvs. oppgavekallet skal stå foran de to rekursive kallene, mens in betyr mellom, dvs. at oppgavekallet skal være mellom de to kallene.
I treet i Figur 5.1.7 d) er verdiene sortert i inorden. Trær med den egenskapen ser vi på
i Delkapittel 5.2.
Flg. metode er som preorden-metoden, av orden n:
private static <T> void inorden(Node<T> p, Oppgave<? super T> oppgave) { if (p.venstre != null) inorden(p.venstre,oppgave); oppgave.utførOppgave(p.verdi); if (p.høyre != null) inorden(p.høyre,oppgave); } public void inorden(Oppgave <? super T> oppgave) { if (!tom()) inorden(rot,oppgave); } Programkode 5.1.7 d)
Eksempel 5.1.7 b):
Vi kan bygge opp treet i Figur 5.1.7 d)
og så bruke inorden-metoden med konsollutskrift som oppgave:
int[] posisjon = {1,2,3,4,5,6,7,9,10,11,12,14}; // posisjonene og Integer[] verdi = {7,3,10,1,5,9,12,2,4,6,8,11}; // verdiene i nivåorden BinTre<Integer> tre = new BinTre<>(posisjon, verdi); // konstruktør tre.inorden(Oppgave.konsollutskrift()); // skriver ut // Utskrift: 1 2 3 4 5 6 7 8 9 10 11 12 Programkode 5.1.7 e)
Postorden En rekursiv definisjon:
- Vi starter i rotnoden.
- Videre gjelder for alle noder at først «besøker» vi nodens venstre barn hvis den har et venstre barn, så dens høyre barn hvis den har et høyre barn og så «besøker» vi noden.
Eksempel: Også her gir den rekursive definisjonen at verdiene i treet i Figur 5.1.7 a) vil komme i den rekkefølgen som ble annonsert ovenfor (i forbindelse med konturkurver): G, L, M, C, O, A, I, D, H, J, F, N, K, B, E.
En enkel huskeregel for postorden er: venstre, høyre, node
I postorden vil en nodes to subtrær allerede være «besøkt»
når noden selv skal «besøkes». Dette kan utnyttes til å lage korte
og enkle algoritmer for f.eks. det å finne høyden og antall noder i et tre
(se Avsnitt 5.1.12) og
for metoden nullstill().
Kode for en traversering
i postorden lages på samme måte som for preorden og inorden. Se
Oppgave 7 og 8.
Metoden toString() arves fra basisklassen Object og vi må
overskrive (eng: override) den. Vi kan f.eks. la strengen inneholde verdiene i inorden. Det
får vi til ved en enkel anvendelse av metoden
inorden(). Den må ha en oppgave som
argument (et lambda-uttrykk) og det kan f.eks. være å legge
inn verdiene i en
StringJoiner
(se også Oppgave 10):
public String toString() { StringJoiner s = new StringJoiner(", ", "[", "]"); if (!tom()) inorden(x -> s.add(x != null ? x.toString() : "null")); return s.toString(); } Programkode 5.1.7 f)
En kan få verdiene i preorden, postorden og nivåorden på samme måte, dvs. å bruke metoden som traverserer. Se Oppgave 10.
Den første I noen situasjoner trenger vi den første noden/verdien. Hvis det er i preorden, er det enkelt siden
rotnoden alltid er først i preorden. I inorden er det litt annerledes. I
Figur 5.1.1 a) kommer H-noden
først i inorden siden det der heter «venstre - node - høyre». Med andre ord finner vi
den første i inorden ved å gå mot venstre så langt det går. Kode for å finne den første noden og dermed den
første verdien i inorden, blir slik:
public T førstInorden() { if (tom()) throw new NoSuchElementException("Treet er tomt!"); Node<T> p = rot; while (p.venstre != null) p = p.venstre; return p.verdi; } Programkode 5.1.7 g)
Hvis en ønsker å finne den siste i inorden, er det bare å gå motsatt vei, dvs. til høyre så langt det går. Se Oppgave 16. Det å finne den første i postorden er litt mer komplisert. I postorden heter det «venstre - høyre - node». Det betyr at den første noden i postorden er den der det ikke er mulig å gå til venstre eller til høyre. Med andre ord er det den bladnoden som ligger lengst til venstre i treet. I Figur 5.1.1 a) blir det O-noden. Dette kan vi kode slik:
public T førstPostorden() { if (tom()) throw new NoSuchElementException("Treet er tomt!"); Node<T> p = rot; while (true) { if (p.venstre != null) p = p.venstre; else if (p.høyre != null) p = p.høyre; else return p.verdi; } } Programkode 5.1.7 h)
Det å finne den siste i postorden er lett. Det er jo rotnoden. Men hva blir den siste i preorden? I neste avsnitt (Avsnitt 5.1.8) diskuterer vi begrepene speilvendt og omvendt orden. Den siste i preorden er lik den første i speilvendt postorden. Dermed finner vi den ved å bytte venstre og høyre i Programkode 5.1.7 h). Se Oppgave 17.
Den neste
Hvis vi står på en node, kan det være aktuelt å finne den neste (eller den forrige) i preorden, inorden
eller postorden. Men det kan by på problemer. I vår datastruktur
er det ikke mulig å gå oppover i treet - kun nedover. I flere tilfeller må vi imidlertid kunne gå oppover for å finne den neste.
En mulig teknikk, som er ineffektiv, er isteden å starte i roten
og så gå nedover ved hjelp av nodeposisjoner. Se Oppgavene 18 - 20.
Hvis vi utvider datastrukturen, f.eks. ved å la hver node ha en forelderreferanse
(se Avsnitt 5.1.15), kan vi finne den
neste på en effektiv måte.
Anta at p er en node i binærtreet som ikke er null. Da gjelder flg. regel for
den neste.
Preorden:
- Hvis
phar et venstre barn, så er det barnet den neste. - Hvis
pikke har et venstre barn, men et høyre barn, så er det barnet den neste. - Hvis
pikke har barn, dvs.per en bladnode, så må vi først til den nærmeste (oppover mot roten) nodenqsom har et høyre barn og som harpi sitt venstre subtre. Den neste tilper da det høyre barnet tilq. - Hvis det ikke finnes noen slik
q, erpden siste i preorden.
Inorden:
- Hvis
phar et ikke-tomt høyre subtre, så er den neste den noden som kommer først i inorden i det subtreet. - Hvis
phar et tomt høyre subtre, er den neste den nærmeste noden oppover mot roten som harpi sitt venstre subtre. - Hvis det ikke finnes noen slik node, er
pden siste i inorden.
Postorden:
- Hvis
pikke har en forelder (per rotnoden), så erpden siste i postorden. - Hvis
perhøyrebarn til sin forelderf, er forelderenfden neste. - Hvis
pervenstrebarn til sin forelderf, gjelder:- Hvis
per enebarn (f.høyreernull), er forelderenfden neste. - Hvis
pikke er enebarn (dvs.f.høyreer ikkenull), så er den neste den noden som kommer først i postorden i subtreet medf.høyresom rot.
- Hvis
Reproduksjon av trær Anta at vi har bygget opp et binærtre og så skrevet ut nodeverdiene i
en eller annen rekkefølge (nivå-, pre-, in- eller postorden). Hvis vi så fjerner treet, er det
da mulig å bygge det opp igjen kun med den informasjonen som ligger i utskriften?
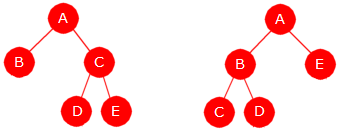 |
| Figur 5.1.7 e) : Forskjellige trær som er like i preorden |
Svaret er nei! Figur 5.1.7 e) inneholder to ulike trær som begge har
A, B, C, D, E som utskrift i preorden. Tilsvarende kan vi finne to ulike trær som har samme utskrift
i hhv. nivå-, in- og postorden. Se Oppgave 29.
Men hvis vi har utskrift i to forskjellige rekkefølger, vil det kunne være annerledes. Dette gjelder f.eks.
preorden og inorden (se også Oppgave 31):
Setning 5.1.7
Gitt to binære trær der ingen av dem har like verdier.
Hvis verdiene til de to trærne er like i preorden og like i inorden, så er de like.
Her er verdiene fra treet i Figur 5.1.5 c) på
tabellform - preorden først og så inorden:
| A | B | D | H | O | I | P | Q | E | J | R | K | S | C | F | L | M | T | U | G | N | V |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| H | O | D | P | I | Q | B | J | R | E | K | S | A | L | F | T | M | U | C | N | V | G |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Figur 5.1.7 f) : Verdiene fra treet i Figur 5.1.5 c) i preorden (øverst) og inorden | |||||||||||||||||||||
Ved hjelp av disse to tabellene er det mulig å gjenskape treet. Den første verdien i preorden
(dvs. A) er rotverdi. Vi finner den i posisjon 12 i inorden. Det betyr at
verdiene i intervallet inorden[0:11] hører til venstre subtre til A og
verdiene i inorden[13:21] til høyre subtre. Den neste i preorden er B og siden venstre
subtre til A ikke er tomt, må B være rotverdi i det subtreet. Videre, siden dette subtreet har
11 - 0 + 1 = 12 verdier, må verdien i posisjon 12 + 1 = 13 (bokstaven C) være rotverdi til høyre subtre til
A, osv.
Generelt: La rot være en indeks.
Hvis verdi = preorden[rot] er
rotverdien til subtreet med verdier i inorden[v:h] og
k er indeksen til verdi i
inorden[v:h],
så vil preorden[rot + 1] være
rotverdien til venstre subtre til verdi og
preorden[rot + 1 + k - v] den til høyre subtre.
Dette kan vi kode rekursivt (metodene hører til klassen
BinTre):
private static <T> Node<T> trePreorden(T[] preorden, int rot, T[] inorden, int v, int h) { if (v > h) return null; // tomt intervall -> tomt tre int k = v; T verdi = preorden[rot]; while (!verdi.equals(inorden[k])) k++; // finner verdi i inorden[v:h] Node<T> venstre = trePreorden(preorden, rot + 1, inorden, v, k - 1); Node<T> høyre = trePreorden(preorden, rot + 1 + k - v, inorden, k + 1, h); return new Node<>(verdi, venstre, høyre); }
public static <T> BinTre<T> trePreorden(T[] preorden, T[] inorden) { BinTre<T> tre = new BinTre<>(); tre.rot = trePreorden(preorden, 0, inorden, 0, inorden.length - 1); tre.antall = preorden.length; return tre; } Programkode 5.1.7 i)
I flg. eksempel bygger vi opp treet i Figur 5.1.5 c) ved
hjelp av to tabeller. Den ene med verdiene i preorden og den andre med dem i inorden. Treet skrives så ut i
nivåorden:
String[] preorden = "ABDHOIPQEJRKSCFLMTUGNV".split(""); String[] inorden = "HODPIQBJREKSALFTMUCNVG".split(""); BinTre<String> tre = BinTre.trePreorden(preorden,inorden); tre.nivåorden(Oppgave.konsollutskrift()); // Utskrift: A B C D E F G H I J K L M N O P Q R S T U V Programkode 5.1.7 j)
Mer om funksjonsgrensesnitt Grensesnittet Oppgave med
utføroppgave() som abstrakt metode, er en konsument (eng: consumer) siden metoden tar imot et argument,
men ikke returnerer noe. Det er slik
Consumer
i java.util.functions er. Der heter metoden accept(). Våre
traverseringer kunne derfor bruke en
Consumer
istedenfor en Oppgave:
private static <T> void preorden(Node<T> p, Consumer<? super T> oppgave) { oppgave.accept(p.verdi); if (p.venstre != null) preorden(p.venstre,oppgave); if (p.høyre != null) preorden(p.høyre,oppgave); } public void preorden(Consumer<? super T> oppgave) { if (!tom()) preorden(rot,oppgave); } Programkode 5.1.7 i)
Vi vil imidlertid kunne få et problem hvis vi bruker flg. programsetning:
tre.preorden(x -> System.out.print(x + " ")); // lambda-uttrykk som argument
Hvis vi i BinTre-klassen har begge versjonene - både den fra Programkode 5.1.7 i) og den fra
Programkode 5.1.7 a), vil ikke kompilatoren kunne avgjøre hvem av dem som skal brukes. Hvis kun den ene er tilgjengelig, vil dette virke.
Se Oppgave 22.
I Programkode 5.1.7 i) er det nodeverdien som er argument i
opgave.accept(p.verdi).
Men hver node har også en posisjon. Rotnoden har posisjon 1 og hvis en node har posisjon k, vil barna ha posisjoner
2k og 2k + 1. Vår nodeverdi er en generisk type, mens posisjonen er et heltall.
java.util.functions har funksjonsgrensesnittet
ObjIntConsumer. Metoden heter fortsatt
accept, men har nå to argumenter. Vi bruker dette i flg. versjon av preorden:
private static <T> void preorden(Node<T> p, int k, ObjIntConsumer<? super T> oppgave) { oppgave.accept(p.verdi, k); if (p.venstre != null) preorden(p.venstre, 2*k, oppgave); if (p.høyre != null) preorden(p.høyre, 2*k + 1, oppgave); } public void preorden(ObjIntConsumer<? super T> oppgave) { if (!tom()) preorden(rot, 1, oppgave); // roten har posisjon 1 } Programkode 5.1.7 j)
Denne versjonen av preorden kan f.eks.
kunne brukes slik (se også Oppgavene 23 - 27):
int[] posisjon = {1,2,3,6,7,12,13,26,27}; // posisjoner String[] verdi = "ABCDEFGHI".split(""); // verdier BinTre<String> tre = new BinTre<>(posisjon,verdi); // konstruktør // bruker v for verdi og p for posisjon som variabelnavn tre.preorden((v,p) -> System.out.print("(" + v + "," + p + ") ")); // Utskrift: (A,1) (B,2) (C,3) (D,6) (F,12) (G,13) (H,26) (I,27) (E,7) Programkode 5.1.7 k)
| 1. | Skriv opp verdiene i pre-, in- og postorden i trærne i oppgave 1 og 2 i Avsnitt 5.1.1. |
| 2. | Gjør som i Oppgave 1 for de to trærne Avsnitt 5.1.3. |
| 3. | Tegn et komplett binærtre som inneholder som verdier tallene fra 1 til 20. a) Legg dem inn slik at i en preorden traversering vil de komme sortert. b) Gjør det samme, men slik at de i en inorden traversering kommer sortert. c) Gjør det samme, men nå i postorden. |
| 4. | Hvis en i et vilkårlig binærtre skriver ut bladnodeverdiene først i preorden, så i inorden og til slutt i postorden, vil en se at det alle de tre tilfellene gir samme rekkefølge. Tegn noen trær og sjekk at det stemmer. Hvis du ser på hvordan de tre rekkefølgene er definert ved hjelp av konturkurven, vil du forstå hvorfor dette alltid er tilfelle. |
| 5. | Gjør om koden i Eksempel 5.1.7 a) slik at treet får samme form, men at verdiene ligger sortert i preorden i treet. Sjekk resultatet ved å lage en preorden utskrift. |
| 6. | Gjør om koden i Eksempel 5.1.7 a) slik at treet får samme form, men at verdiene ligger sortert i inorden i treet. Sjekk resultatet ved å lage en inorden utskrift. |
| 7. | Lag metoden postorden. Den skal traverserer et binærtre i
postorden. Lag en privat rekursiv metode og en offentlig metode som
kaller den private. Se koden for preorden og
inorden.
Metoden skal legges i klassen BinTre.
|
| 8. | Lag metoden public void nullstill(). Den skal nulle alle referanser og alle verdier.
Lag en privat rekursiv metode og en offentlig metode. Bruk postorden i traverseringen.
|
| 9. | Gjør om koden i Eksempel 5.1.7 a) slik at treet får samme form, men at verdiene ligger sortert i postorden i treet. Sjekk resultatet ved å lage en postorden utskrift. |
| 10. | Metoden toString() er kodet ved hjelp av
den generiske inorden-metoden. Det å legge inn verdiene i en StringJoiner
er «oppgaven». Dette fungerer utmerket, men vi må «betale» litt for den enkle koden.
Lag isteden en egen rekursiv versjon av toString() der verdiene fortløpende legges inn
i en StringBuilder. Da må du passe på å ordne det slik at «skillesekvensen» (dvs.
komma og mellomrom) kun kommer mellom verdier.
|
| 11. | Lag metodene toPreString(), toPostString() og
toNivåString().
|
| 12. | Lag metoden public int[] posisjonerPreorden() i BinTre-klassen. Metoden
skal returnere en tabell med treets nodeposisjoner i preorden. Her kan det imidlertid
bli problemer hvis treet har nodeposisjoner som er for store for datatypen int. Da
kunne vi la metoden isteden returnere en long-tabell eller eventuelt en
BigInteger-tall. Hvilken høyde må treet minst ha for at det skal ha nodeposjoner for
store for typen int?
|
| 13. | Som Oppgave 12, men nodeposisjonene i nivåorden. |
| 14. | Ta utgangspunkt i Programkode 5.1.7 b). Opprett
en liste, lag et lambda-utrykk for preorden-versjonen i
Programkode 5.1.7 a) som legger treets verdier inn i listen.
Skriv ut listen. Se Programkode 5.1.6 g).
|
| 15. | Ta utgangspunkt i Programkode 5.1.7 b). Opprett
en StringBuilder, lag et lambda-utrykk for preorden i
Programkode 5.1.7 a) som legger verdiene i
din StringBuilder og lag så en tegnstreng (String) som inneholder treets verdier.
Det skal være komma og mellomrom mellom verdiene og hakeparenteser på hver side.
Skriv ut tegnstrengen.
|
| 16. | Som Oppgave 14, men bruk en StringJoiner istedenfor en StringBuilder.
|
| 17. | Lag metoden public T sistInorden(). Den skal returnere den siste verdien i inorden.
|
| 18. | Lag public T sistPreorden(). Den skal returnere den siste verdien i preorden.
|
| 19. | Metoden public void preorden(ObjIntConsumer<? super T> oppgave)
bruker rekursjon. Lag en iterativ versjon.
Vi starter i roten som har posisjon 1. Gitt så at
vi står på en node p. Hvis p har venstre barn, er det den neste. Hvis p ikke har venstre
barn, men et høyre barn, er det neste. Hvis p er en bladnode, må vi oppover. Gitt at k er posisjonen
til p. Da kan vi gå fra roten nedover til p ved hjelp av de binære sifrene til k. På veien
får vi tak i den neste. Metoden vil få orden n·log(n) hvis treet er noenlunde balansert. Vi skal finne mer effektive
måter å traversere iterativt på senere. Se f.eks. Avsnitt 5.1.10 og
Avsnitt 5.1.15.
|
| 20. | Lag metoden public void inorden(ObjIntConsumer<? super T> oppgave). Den skal gå gjennom treet i inorden
iterativt, dvs. uten rekursjon. Bruk en tilsvarende teknikk som i Oppgave 19. Men husk at det nå er inorden.
|
| 21. | Lag metoden public void postorden(ObjIntConsumer<? super T> oppgave). Den skal gå gjennom treet i postorden
iterativt, dvs. uten rekursjon. Bruk en tilsvarende teknikk som i Oppgave 19. Men husk at det nå er postorden.
|
| 22. | La din BinTre-klasse inneholde både Programkode 5.1.7 a) og
Programkode 5.1.7 i). Lag så en kodebit
der du bygger opp et binærtre. Avslutt kodebiten med følgende setning:
tre.preorden(c -> System.out.print(c + " "));
Dette vil du få en feilmelding på. Hva sier feilmeldingen? Kommenter vekk den ene. Da blir det ok og kjørbart. Kjør programbiten.
Ta den ene tilbake og kommenter vekk den andre. Hva skjer da?
|
| 23. | Legg inn versjonen av preorden i Programkode 5.1.7 j)
i din BinTre-klasse. Sjekk så at
preorden i Programkode 5.1.7 k) virker.
|
| 24. | Gjør om programkode
Programkode 5.1.7 k) slik at resultatet
blir en liste med nodeverdier og en liste med nodeposisjoner. Gjør det ved hjelp av et lamda-uttrykk.
|
| 25. | Gjør om programkode
Programkode 5.1.7 k) slik at du til en
gitt bokstav skriver ut hvilken posisjon bokstaven har i treet.
Gjør så omvendt. Dvs. til en gitt posisjon skal du skrive ut bokstaven i den posisjonen i treet.
|
| 26. | Gjør om programkode
Programkode 5.1.7 k) slik at du finner
den største verdien i treet og samtidig hvilken posisjon den har.
|
| 27. | Gjør om programkode
Programkode 5.1.7 k) slik at du finner
treets høyde. Obs: høyden er én mindre enn antall binære siffer i største posisjonstall.
|
| 28. | En BiConsumer
har to generiske parametere. Vi kan bruke den til å oppnå det samme som en
ObjIntConsumer
hvis vi lar den andre generiske parameteren være Integer. Lag en versjon av preorden der den
brukes. Ta utgangspunkt i Programkode 5.1.7 j) og gjør de
nødvendige endringene. Hva vil skje hvis du har begge versjonene i din BinTre-klasse (både den med
ObjIntConsumer og den med BiConsumer) og har et program med setningen:
tre.preorden((d, k) -> { } ); i koden din? Kommenter vekk så den versjonen som bruker en ObjIntConsumer.
Sjekk at da vil Programkode 5.1.7 k) virke og gi samme resultat som sist.
|
| 29. | Lag to forskjellige binære trær som begge inneholder bokstavene fra A til E som verdier (som i Figur 5.1.7 e), slik at de kommer i samme rekkefølge i inorden. Gjør så det samme med postorden og nivåorden. |
| 30. | Lag treet i Figur 5.1.7 a)
(se første del av Programkode 5.1.7 b).
Lag så kode som genererer to String-tabeller preorden og inorden med
nodeverdiene i henholdsvis preorden og inorden. Bruk så dem til å bygge opp en kopi av treet ved
hjelp av metoden i Programkode 5.1.7 i).
Skriv så ut verdiene i nivåorden i begge trærne.
|
| 31. | Setning 5.1.7 er også sann hvis vi erstatter
preorden med postorden. Det kommer av at omvendt postorden er det samme som speilvendt preorden -
se Avsnitt 5.1.8. Med andre ord kan vi traversere
en postordentabell baklengs og dermed bygge opp det speilvendte treet på samme måte som i
Programkode 5.1.7 i). Men vi kan få
det ordinære treet hvis vi passer på å bytte venstre og høyre i den rekursive metoden. Lag kode
som gjør dette. Bruk navnet trePostorden både den private rekursive metoden og den
offentlige metoden.
|
![]() 5.1.8 Speilvendt og omvendt orden
5.1.8 Speilvendt og omvendt orden
Et binærtre speilvendes ved å rotere det om en vertikal
linje gjennom roten, dvs. venstre og høyre barn bytter plass i alle noder.
Trærne i figuren under er speilvendte av hverandre:
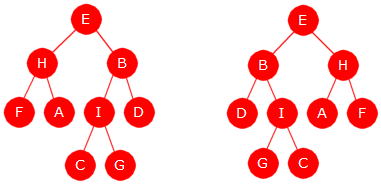 |
| Figur 5.1.8 a) : Det ene treet er det speilvendte av det andre |
En speilvendingsmetode kan vi lage ved å traversere treet og bytte om barna til nodene.
private static <T> void speilvend(Node<T> p) { if (p == null) return; // tomt subtre Node<T> q = p.venstre; p.venstre = p.høyre; p.høyre = q; // bytter speilvend(p.venstre); speilvend(p.høyre); } public void speilvend() { if (antall() > 1) speilvend(rot); } Programkode 5.1.8 a)
Speilvendt nivåorden er det samme som nivåorden i det speilvendte treet eller
at nodene «besøkes» nivå for nivå, fra rotnoden og nedover, og for hvert nivå fra
høyre mot venstre.
I flg. eksempel bygges først treet til venstre i Figur 5.1.8 a), verdiene skrives ut i nivåorden og det speilvendes. En nivåorden utskrift i det speilvendte treet vil gi speilvendt nivåorden:
int[] posisjon = {1,2,3,4,5,6,7,12,13}; // posisjonene og String[] verdi = "EHBFAIDCG".split(""); // verdiene i nivåorden BinTre<String> tre = new BinTre<>(posisjon, verdi); // konstruktør tre.nivåorden(Oppgave.konsollutskrift()); // nivåorden System.out.print(" - "); tre.speilvend(); // speilvender tre.nivåorden(Oppgave.konsollutskrift()); // speilvendt nivåorden // Utskrift: E H B F A I D C G - E B H D I A F G C Programkode 5.1.8 b)
I Programkode 5.1.8 b) er treet blitt endret. Egentlig burde vi speilvende en gang til for å få treet tilbake til opprinnelig form. Men det skal ikke være nødvendig å speilvende et tre for å kunne få verdiene i speilvendt nivåorden. Vi lager isteden en egen metode. Da er det bare å bytte om to setninger i Programkode 5.1.6 d):
public void speilvendtNivåorden(Oppgave<? super T> oppgave) { if (tom()) return; // tomt tre Kø<Node<T>> kø = new TabellKø<>(); // Se Avsnitt 4.2.3 kø.leggInn(rot); while (!kø.tom()) { Node<T> p = kø.taUt(); oppgave.utførOppgave(p.verdi); // den generiske oppgaven if (p.høyre != null) kø.leggInn(p.høyre); // tar høyre først if (p.venstre != null) kø.leggInn(p.venstre); } } Programkode 5.1.8 c)
Omvendt nivåorden er det samme som nivåorden i omvendt (eller baklengs) rekkefølge.
Ta utgangspunkt
i det venstre treet i Figur 5.1.8 a).
I nivåorden kommer verdiene i rekkefølgen: E , H , B ,
F , A , I , D , C , G.
Det omvendte av dette er da: G , C , D ,
I , A , F , B , H , E.
Det er ikke mulig å lage en algoritme som starter i den siste noden i nivåorden og som så beveger seg
gjennom treet nivå for nivå oppover mot roten. Men vi kan få det til ved at vi
traverserer treet i nivåorden og legger verdiene (eller nodene) fortløpende i en datastruktur som
det er mulig å traversere baklengs. Se Oppgave 2.
Speilvendt preorden,
inorden og postorden er det samme som henholdsvis
preorden, inorden og postorden i det speilvendte treet. Men slike traverseringer kan
vi selvfølgelig få til uten å måtte speilvende treet først. Det gjøres rett og slett ved å
bytte om venstre og høyre. For preorden blir det: node, høyre,
venstre. Koden blir slik:
private static <T> void speilvendtPreorden(Node<T> p, Oppgave<? super T> oppgave) { oppgave.utførOppgave(p.verdi); if (p.høyre != null) speilvendtPreorden(p.høyre,oppgave); // høyre først if (p.venstre != null) speilvendtPreorden(p.venstre,oppgave); // så venstre } public void speilvendtPreorden(Oppgave<? super T> oppgave) { if (!tom()) speilvendtPreorden(rot,oppgave); } Programkode 5.1.8 d)
Det omvendte av preorden, inorden og postorden får vi rett og slett ved å gå omvendt vei
i forhold til den ordinære veien.
Ta som eksempel utgangspunkt i treet i Figur 5.1.8 b) under til venstre. Nodeverdiene i preorden blir:
E, H, F, A, B, I, C,
G, D og i omvendt (eller reversert) rekkefølge blir det:
D, G, C, I, B, A, F,
H, E. Tar vi nodeverdiene i speilvendt postorden
får vi faktisk den samme rekkefølgen, dvs: D, G, C, I, B, A, F,
H, E. Dette er ikke tilfeldig. Omvendt preorden og speilvendt postorden
blir alltid det samme.
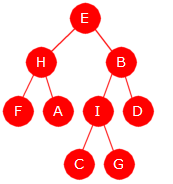 |
| Figur 5.1.8 b) : Et binærtre |
Det er også andre sammenhenger mellom rekkefølgene. I tabellen under er treets verdier satt opp i ordinær, omvendt og speilvendt orden for alle de tre typene:
| Ordinær | Omvendt | Speilvendt | |
| Preorden | E H F A B I C G D | D G C I B A F H E | E B D I G C H A F |
| Inorden | F H A E C I G B D | D B G I C E A H F | D B G I C E A H F |
| Postorden | F A H C G I D B E | E B D I G C H A F | D G C I B A F H E |
| Tabell 5.1.8: Ordinær, omvendt og speilvendt rekkefølge | |||
|---|---|---|---|
Det som vi ser i Tabell 5.1.8 over, gjelder generelt:
- Omvendt preorden er det samme som speilvendt postorden
- Omvendt postorden er det samme som speilvendt preorden
- Omvendt inorden er det samme som speilvendt inorden
| 1. | Ta utgangspunkt i treet i Figur 5.1.1 a). Skriv opp nodeverdiene i 1) nivåorden, 2) omvendt nivåorden, 3) speilvendt nivåorden, 4) inorden, 5) omvendt inorden, 6) speilvendt inorden, 7) preorden, 7) omvendt preorden, 9) speilvendt preorden, 10) postorden, 11) omvendt postorden og 12) speilvendt postorden. |
| 2. | Lag metoden public void omvendtNivåorden(Oppgave<? super T> oppgave).
a) Gjør det først ved å traversere i nivåorden (ved hjelp av en kø) og fortløpende legge verdiene på en stakk. Så
hentes verdiene fra stakken. b) Gjør det så ved å traversere ved hjelp av en tabellstruktur
(f.eks. en TabellListe) istedenfor en kø. Deretter traverserer tabellstrukturen baklengs.
Lag et testprogram for metodene.
|
| 3. | Lag metoden public void speilvendtInorden(Oppgave<? super T> oppgave)
ved å bruke en rekursiv hjelpemetode.
Se koden for speilvendtPreorden.
|
| 4. | Lag metoden public void speilvendtPostorden(Oppgave<? super T> oppgave)
ved å bruke en rekursiv hjelpemetode.
Se koden for speilvendtPreorden.
|
| 5. | Lag metoden public void omvendtPreorden(Oppgave<? super T> oppgave).
|
| 6. | Lag metoden public void omvendtPostorden(Oppgave<? super T> oppgave).
|
| 7. | Bevis teoretisk at omvendt preorden er lik speilvendt postorden og at omvendt postorden er lik speilvendt preorden. Bruk f.eks. konturkurver. Se Figur 5.1.7 a). |
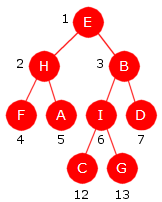 |
| Figur 5.1.9 a): Posisjoner |
Setter vi opp binærkoden for hvert tall, får vi denne rekkefølgen i preorden: 1, 10, 100, 101, 11, 110, 1100, 1101, 111. Dette svarer til en leksikografisk sortering av binærkodene som bitsekvenser. F.eks. er 13 = 1101 og 7 = 111, men leksikografisk kommer 1101 foran 111. Dette betyr at hvis vi kun har nodeposisjonene til et binærtre og ikke treet, kan vi likevel få satt opp nodeposisjonene i preorden. I flg. eksempel bruker vi nodeposisjonene fra treet i Figur 5.1.5 c). Bitkodene sammenlignes leksikografisk:
Integer[] p = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29};
Tabell.innsettingssortering(p, Comparator.comparing(Integer::toBinaryString));
for (int k : p) System.out.print(k + " ");
// Utskrift: 1 2 4 8 17 9 18 19 5 10 21 11 23 3 6 12 13 26 27 7 14 29
Programkode 5.1.9 a)
Programkode 5.1.9 a) er enkel og elegant, men ikke spesielt effektiv. Det kommer av at tallene (Integer)
først må konverteres til tegnstrenger som så blir sammenlignet. Det koster en del. Det er mer effektivt å arbeide på bitnivå i
et int-format. Se Oppgave 3.
Det er også mulig å sortere nodeposisjoner i postorden. To forskjellige nodeposisjoner a
og b vil ha en nærmeste felles forfeder c. Den kan vi f.eks. finne ved
å gå fra a og b oppover mot roten. Dermed kan vi
å bestemme forholdet melom a og b:
Integer[] p = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,17,18,19,21,23,26,27,29};
Comparator<Integer> c = (x,y) ->
{
int a = x, b = y; // går over til int-format
if (a == b) return 0;
while (true)
{ // går oppover ved hjelp av halveringer
while (a > b) a >>= 1; if (a == b) return -1;
while (b > a) b >>= 1; if (a == b) return 1;
}
};
Tabell.innsettingssortering(p, c);
for (int k : p) System.out.print(k + " ");
// Utskrift: 17 8 18 19 9 4 21 10 23 11 5 2 12 26 27 13 6 29 14 7 3 1
Programkode 5.1.9 b)
I komparatoren c i Programkode 5.1.9 b) går vi fra a
og b oppover mot roten. Men det hadde vært bedre å starte i roten og gå nedover mot a
og b. Det er i gjennomsnitt mer effektivt. Se Oppgave 4.
Det er også mulig å bruke toBinaryString - se Oppgave 5.
En komparator (et lambda-uttrykk) for inorden tas opp i Oppgave 6.
| 1. | Tallene som sorteres i preorden slik som de i Programkode 5.1.9 a), behøver ikke være nodeposisjoner i et binærtre. Det kan være hvilke som helst tall så sant de er positive. La tabellen i Programkode 5.1.9 a) inneholde tallene 3, 8, 14, 5, 10, 18, 7, 13, 20, 11. Hvordan blir de sortert. Tegn det minste binærtreet som har disse nodeposisjonene og sjekk hva en preorden traversering gir når kun nodene med disse posisjonene tas med. |
| 2. | Gjør om koden i Programkode 5.1.9 a) slik at det blir en speilvendt postordensortering. Husk at speilvendt postorden er det samme som omvendt preorden. |
| 3. | Lag en komparator (et lambda-uttrykk) for preorden der alt arbeidet foregår i int-format. Start med
første binære siffer i a og i b, fortsett så lenge
sifrene er like eller inntil et av dem ikke har flere siffer. Gjør dette ved hjelp av
binære operatorer.
|
| 4. | Lag en komparator (et lambda-uttrykk) for postorden på samme måte som i Oppgave 3. |
| 5. | Lag en komparator (et lambda-uttrykk) for postorden der du bruker toBinaryString
for å få tak i «bitene» en Integer.
|
| 6. | Lag en komparator som sorterer i inorden. Den skal ordne positive tall etter inorden i et binærtre. Alle posistive tall kan ses på som nodeposisjoner i et tenkt tre. Ta utgangspunkt i Programkode 5.1.9 b). Fasit får en ved å traversere treet i Figur 5.1.5 c) inorden. |
![]() 5.1.10 Traversering uten rekursjon
5.1.10 Traversering uten rekursjon
Traverseringene preorden, inorden og postorden kunne
programmeres på en enkel, elegant og effektiv måte ved hjelp av rekursjon.
Se Avsnitt 5.1.7. Har det da noen
hensikt å lage metoder som gjør dette uten bruk av rekursjon? Svaret er ja! For det første
vil en iterativ metode kunne gi innsikt i hvordan rekursjon fungerer.
For det andre vil det være situasjoner der det ikke er gunstig eller ikke mulig
å bruke rekursjon. Det gjelder f.eks. hvis en traversering skal kunne stoppes
midlertidig og så startes igjen der den stoppet. Dette får vi blant annet bruk for når
vi skal konstruere iteratorer.
Den rekursive metoden preorden i
Programkode 5.1.7 a) så slik ut:
private static <T> void preorden(Node<T> p, Oppgave<? super T> oppgave) { oppgave.utførOppgave(p.verdi); if (p.venstre != null) preorden(p.venstre, oppgave); if (p.høyre != null) preorden(p.høyre, oppgave); } Programkode 5.1.10 a)
I metoden over blir oppgaven utført på noden p, så kalles metoden med p.venstre og deretter med p.høyre som parameter. Her er det programstakken (eng: the runtime stack) som «husker» at når programeksekveringen returnerer fra det første kallet, så er det det andre kallet som skal utføres. Denne «hukommelsen» kan vi få til ved å bruke en stakk.
Legg merke til at det i Programkode 5.1.10 a)
er et rekursivt kall i siste programsetning. Dette kalles halerekursjon
(eng: tail recursion). Et slikt kall kan alltid erstattes med en løkke siden et rekursivt
kall i siste programsetning kun har som effekt at eksekveringen av metodens
setninger starter, med endret parameterverdi, fra toppen igjen.
Se Oppgave 1.
I et første forsøk på å lage en iterativ preorden, legger vi først p.høyre på
stakken og deretter p.venstre. Dermed vil p.venstre ligge høyere opp
enn p.høyre og vil bli tatt ut først av de to. Det gir derfor samme rekkefølge som
i den rekursive metoden:
public void preorden(Oppgave<? super T> oppgave) // iterativ versjon { if (tom()) return; // tomt tre Stakk<Node<T>> stakk = new TabellStakk<>(); // en stakk stakk.leggInn(rot); // starter med å legge rot på stakken while (!stakk.tom()) { Node<T> p = stakk.taUt(); // henter fra stakken oppgave.utførOppgave(p.verdi); // utfører oppgaven if (p.høyre != null) stakk.leggInn(p.høyre); // først høyre if (p.venstre != null)stakk.leggInn(p.venstre); // så venstre } } Programkode 5.1.10 b)
Legg merke til at Programkode 5.1.10 b) har samme oppbygging som den iterative
metoden nivåorden i Programkode 5.1.6 d).
Vår første versjon av iterativ preorden kan effektiviseres noe. Ser vi nøyere
på while-løkken, ser vi at det som legges på toppen av stakken blir tatt ut igjen rett etterpå.
Det kan vi forbedre.
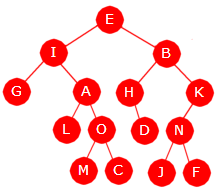 |
| Figur 5.1.10 a) : Et binærtre |
I figuren til venstre starter vi i rotnoden, dvs. i E-noden. Etter at oppgaven er utført på den, skal vi videre til venstre, dvs. til I-noden. Men først må vi legge B-noden på stakken siden vi skal dit etterpå. Fra I-noden skal vi videre til G-noden, men først må A-noden legges på stakken. Osv.
Generelt gjør vi det slik: Hvis vi står på en node p, så sjekker vi om p.venstre finnes. Hvis ja, legger vi p.høyre (hvis den ikke er null) på stakken. Hvis nei (dvs. p.venstre ikke finnes) sjekker vi om p.høyre finnes. Hvis ja, går vi dit. Hvis nei, tar vi noden som ligger øverst på stakken siden det er neste i preorden.
Når er traverseringen ferdig? På figuren over ser vi at F-noden er siste node i preorden. Referansen p skal fortløpende gå til nodene i preorden. Vi ser dermed at traverseringen er ferdig når p hverken har venstre eller høyre barn og stakken er tom.
public void preorden(Oppgave<? super T> oppgave) // ny versjon { if (tom()) return; Stakk<Node<T>> stakk = new TabellStakk<>(); Node<T> p = rot; // starter i roten while (true) { oppgave.utførOppgave(p.verdi); if (p.venstre != null) { if (p.høyre != null) stakk.leggInn(p.høyre); p = p.venstre; } else if (p.høyre != null) // her er p.venstre lik null { p = p.høyre; } else if (!stakk.tom()) // her er p en bladnode { p = stakk.taUt(); } else // p er en bladnode og stakken er tom break; // traverseringen er ferdig } } Programkode 5.1.10 c)
Er det stor effektivitetsforskjell mellom den rekursive
og de iterative versjonene? Og hvilken av de to iterative er best? Dette kan vi finne ut ved
å lage et stort og tilfeldig binærtre og så traversere det mange ganger. Det vil kunne gi
et målbart tidsforbruk. Det å lage tilfeldige trær tas opp i
Avsnitt 5.1.13. I flg. eksempel brukes metoden
Programkode 5.1.13 a). Legg dem (både
den private og den offentlige) inn i din
versjon av BinTre. For å unngå at det som utføres tar all tiden, lager vi
et lambda-uttrykk der det ikke gjøres noe arbeid:
public static void main(String[] args) { BinTre<Integer> tre = BinTre.random(100_000); // Tilfeldig tre 100_000 noder long tid = System.currentTimeMillis(); for (int i = 0; i < 1000; i++) tre.preorden(k -> {}); System.out.println("Tid: " + (System.currentTimeMillis() - tid)); } Programkode 5.1.10 d)
I Programkode 5.1.10 d) gjøres det et kall på metoden preorden. Men
vi har nå tre versjoner med samme navn. Hvis alle tre er lagt inn i BinTre-klassen,
må to av dem kommenteres vekk. Alternativt kan de hete
preorden (den rekursive), preorden2 og preorden3.
Tiden som Programkode 5.1.10 d) bruker, er avhengig av hva slags prosessor en har. Kjøring på en bestemt maskin gav disse resultatene for de forskjellige versjonene av preorden:
Programkode 5.1.10 a) ( rekursjon ) : 1,1 sek.
Programkode 5.1.10 b) ( iterasjon ) : 1,4 sek.
Programkode 5.1.10 c) ( iterasjon ) : 1,1 sek.
Den siste iterative versjonen er litt bedre enn den første, men er likevel ikke bedre enn den rekursive. Det er vanskelig å lage iterative metoder som er bedre enn rekursive siden rekursjon er innebygget i språket og kan benytte seg av spesielle maskininstruksjoner. Men det kan være at det er mulig å forbedre Programkode 5.1.10 c) noe ved å erstatte stakken med en tabell. Se Oppgave 6.
Iterativ inorden er også mulig
( postorden tas opp i
Oppgave 7 ).
Vi bruker treet i Figur 5.1.10 b) nedenfor som utgangspunkt.
Den første i inorden får vi ved å starte i roten og gå mot venstre så langt det går.
På tegningen er det H-noden. Deretter vet vi at hvis noden p
ikke er den siste i inorden, så er det to muligheter: 1) p
har et ikke-tomt høyre subtre. Da er den neste i
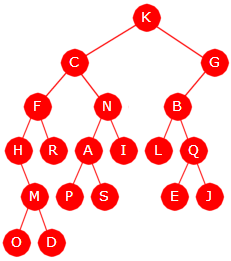 |
| Figur 5.1.10 b) : Et binærtre |
Eksempel: Hvis p er H-noden (den første i inorden), vil den neste i inorden være O-noden fordi den ligger lengst ned til venstre i H-nodens høyre subtre. Hvis p er O-noden er det M-noden som er den neste. Så kommer kommer D-noden og deretter F-noden. Fra både O-noden og D-noden må vi oppover for å komme til neste siden ingen av de to har høyre barn. Det er da vi bruker en stakk. På veien nedover legger vi på stakken de nodene vi passerer. Da kan vi etterpå «gå oppover» ved å ta noder fra stakken. Det gir flg. algoritme:
- En referanse p må starte i rotnoden (K-noden) og flyttes ned mot venstre så langt det går (til H-noden). De nodene vi passerer på veien (K-noden , C-noden og F-noden) legges på stakken. Dermed vil p vise på den første noden i inorden.
- En løkke settes i gang. Først utføres oppgaven på verdien til p (dvs. på H ). Deretter skal p flyttes til den neste i inorden. Da sjekkes først om p har et høyre barn. Hvis ja, flyttes p dit og videre mot venstre så langt det går hvis det er flere noder den veien. På veien legges de passerte nodene på stakken. Hvis nei, dvs. at p ikke har høyre barn, er den neste rett og slett den vi henter fra stakken. Osv.
public void inorden(Oppgave<? super T> oppgave) // iterativ inorden { if (tom()) return; // tomt tre Stakk<Node<T>> stakk = new TabellStakk<>(); Node<T> p = rot; // starter i roten og går til venstre for ( ; p.venstre != null; p = p.venstre) stakk.leggInn(p); while (true) { oppgave.utførOppgave(p.verdi); // oppgaven utføres if (p.høyre != null) // til venstre i høyre subtre { for (p = p.høyre; p.venstre != null; p = p.venstre) { stakk.leggInn(p); } } else if (!stakk.tom()) { p = stakk.taUt(); // p.høyre == null, henter fra stakken } else break; // stakken er tom - vi er ferdig } // while } Programkode 5.1.10 e)
Flg. kodebit kan brukes til å sammenligne rekursiv og iterativ inorden:
BinTre<Integer> tre = BinTre.random(100_000); // Tilfeldig tre 100_000 noder long t = System.currentTimeMillis(); for (int i = 0; i < 1000; i++) tre.inorden(k -> {}); System.out.println("Tid: " + (System.currentTimeMillis() - t)); Programkode 5.1.10 f)
I de iterative traverseringene må en kunne gå oppover (mot roten) i treet og til det brukes en stakk. En annen teknikk er å legge en ekstra referanse i hver node. Den skal da gå opp til sin forelder. Dette tas opp i Avsnitt 5.1.15.
Det er mulig traversere iterativt uten å bruke hverken stakk eller ekstra nodevariabler. Den mest elegante løsningen kalles Morris' algoritme. Se Avsnitt 5.1.17. En annen teknikk som ikke er så god, er å gå fra roten og nedover istedenfor å gå oppover. Se Oppgave 9.
Oppsummering av begrepet neste node i inorden:
- Hvis p har et ikke tomt høyre subtre, kommer vi til den neste i inorden ved å gå så langt som mulig på skrå nedover til venstre i det subtreet.
- Hvis ikke (og p ikke er sist i inorden) finner vi den neste ved å gå så langt som mulig på skrå oppover mot venstre og så en opp mot høyre. Alternativt: Den neste er den nærmeste noden i retning mot roten som er slik at p ligger i dens venstre subtre.
- Hvis p er siste node i inorden, så vil posisjonstallet på binærform bare ha 1-ere. Det betyr at hvis vi går fra p og kun på skrå oppover mot venstre, kommer vi til roten.
| 1. | Metoden preorden i Programkode 5.1.10 a)
har halerekursjon. Det siste rekursive kallet kan erstattes med en løkke siden
et rekursivt kall i siste programsetning kun har som effekt at eksekveringen av metodens
setninger starter, med endret parameterverdi, fra toppen igjen. Gjør denne endringen i metoden.
|
| 2. | Test at den iterative preorden-metoden fra Programkode 5.1.10 b)
virker som den skal ved å bruke den i testprogrammet i
Programkode 5.1.7 b). Gjør det
samme med metoden fra
Programkode 5.1.10 c). Hvis en skal ha flere
preorden-metoder i klassen BinTre, kan de f.eks. hete preorden1,
preorden2 og preorden3.
|
| 3. | Kjør Programkode 5.1.10 d) med
de forskjellige preorden-metodene
og se hva slags tidsforbruk du får.
|
| 4. | Metoden inorden i Programkode 5.1.7 d) har også halerekursjon. Siste setning har et rekursivt kall. Bytt ut det siste rekursive kallet med en løkke. Se også Oppgave 1. |
| 5. | Bruk både rekursiv og iterativ inorden i Programkode 5.1.10 d). Hva blir tidsforbruket? |
| 6. | I preorden i
Programkode 5.1.10 c)
brukes en instans av klassen TabellStakk. Gjør om slik at du implementerer
stakken direkte i koden ved hjelp av en tabell. Da vil metoden kunne bli nesten
like effektiv som den rekursive versjonen av preorden().
|
| 7. | Lag en iterativ versjon av postorden().
Husk at hvis aktuell node er høyre barn til sin forelder, så vil forelder være
neste i postorden, og hvis aktuell node er venstre barn vil den neste i
postorden være den første (i postorden) i forelderens høyre subtre.
Start med å gå til den første i postorden og legg de nodene som passeres
på stakken. Videre bruker du at forelder er den som ligger øverst på stakken.
|
| 8. | Lag iterative versjoner av omvendtPreorden(), omvendtInorden() og
omvendtPostorden(). Se Avsnitt 5.1.8.
|
| 9. | Det er mulig å lage en iterativ metode som traverserer i inorden uten hjelp av en stakk og ekstra
nodevariabler ved å gå nedover fra roten istedenfor oppover mot roten. Skal vi gå nedover er det
imidlertid nødvendig å vite nodeposisjonen til den vi skal til. Det kan vi gjøre ved hjelp av et heltall
k som er 1 når vi starter. Når vi går nedover legger vi en 0 bakerst
(k = 2*k eller k <<= 1) når vi går til venstre og en 1 bakerst
(k = 2*k + 1 eller k <<= 1; k |= 1;) når vi går til høyre. Når
vi skal oppover til rett node fjernes alle de bakerste 0-ene i k og deretter en 1-er.
For å finne tilhørende node må en søke nedover fra roten til den nodeposjonen ved hjelp av den
verdien k nå har. Ulempen med denne teknikken er at heltallet k kan få mange siffer hvis
treet har stor høyde. Den kan være av typen int, men da må treet ha en høyde på maksimum 30 siden ingen
nodeposjon da vil ha flere enn 31 siffer. Med typen long kan høyden være maksimalt på 62, men
da vil den bruke dobbelt så lang tid.
Forøvrig blir metoden av orden n log(n).
|
| 10. | Lag en iterativ metode som traverserer i preorden uten hjelp av en stakk og ekstra nodevariabler. Se Oppgave 9. |
![]() 5.1.11 Traversering med iterator
5.1.11 Traversering med iterator
Et binærtre bør kunne traverseres ved hjelp av en iterator, dvs.
være Iterable. Vi diskuterte iteratorer for beholdere
i Avsnitt 3.1.1.
Vi gir klassen BinTre<T>
flg. tillegg:
public class BinTre<T> implements Iterable<T>
Det betyr at BinTre-klassen må ha metoden
public Iterator<T> iterator()
Vi kan traversere i preorden, inorden,
postorden eller nivåorden. Klassen kan ha kun én metode med
navn iterator. Her velger vi inorden. I
øvingsoppgavene vil du bli bedt å lage iteratorer
som traverserer treet i preorden, i postorden og i nivåorden.
Den indre iterator-klassen kan f.eks. hete InordenIterator. En referanse
p flyttes i inorden etter hvert kall på metoden next(). Dermed
er det flere igjen så lenge p ikke er null. Siden vi flere ganger må oppover i treet er enklest
å bruke en stakk.
Vi bruker samme teknikk som i
Programkode 5.1.10 e).
I klassen under er en av metodene allerede kodet:
private class InordenIterator implements Iterator<T> { private Stakk<Node<T>> stakk; // hjelpestakk private Node<T> p = null; // hjelpevariabel // en privat hjelpemetoder skal inn her private InordenIterator() // konstruktør { // kode mangler } public T next() { // kode mangler } public boolean hasNext() { return p != null; } } Programkode 5.1.11 a)
Det er ofte nødvendig å finne den første noden i inorden i et subtre. Flg. metode finner den første i subtreet med q som rot og legger samtidig nodene som passeres inn på stakken:
private Node<T> først(Node<T> q) // en hjelpemetode { while (q.venstre != null) // starter i q { stakk.leggInn(q); // legger q på stakken q = q.venstre; // går videre mot venstre } return q; // q er lengst ned til venstre } Programkode 5.1.11 b)
Konstruktøren må sørge for at referansen p går til den første noden i inorden:
private InordenIterator() // konstruktør { if (tom()) return; // treet er tomt stakk = new TabellStakk<>(); // oppretter stakken p = først(rot); // bruker hjelpemetoden } Programkode 5.1.11 c)
Metoden next() skal returnere verdien til p og samtidig
flytte p til den neste noden:
public T next() { if (!hasNext()) throw new NoSuchElementException("Ingen verdier!"); T verdi = p.verdi; // tar vare på verdien if (p.høyre != null) p = først(p.høyre); // p har høyre subtre else if (stakk.tom()) p = null; // stakken er tom else p = stakk.taUt(); // tar fra stakken return verdi; // returnerer verdien } Programkode 5.1.11 d)
Det eneste som nå gjenstår er å kode metoden iterator i BinTre-klassen:
public Iterator<T> iterator() // skal ligge i class BinTre { return new InordenIterator(); } Programkode 5.1.11 e)
Eksempel:
InordenIterator
inneholder det som er diskutert i dette avsnittet. Hvis den, sammen med metoden iterator(), er lagt
inn i BinTre-klassen, vil flg. kode være kjørbar.
int[] posisjon = {1,2,3,4,5,6,7,8,9,10}; // posisjoner og String[] verdi = "ABCDEFGHIJ".split(""); // verdier i nivåorden BinTre<String> tre = new BinTre<>(posisjon, verdi); // konstruktør for (String s : tre) System.out.print(s + " "); // for-alle-løkke // Utskrift: H D I B J E A F C G Programkode 5.1.11 f)
For-alle-løkken i Programkode 5.1.11 f) bruker treets iterator implisitt.
Det er også mulig å bruke «for-alle-løkkene»
forEach og forEachRemaining. Da brukes også iteratoren implisitt.
Metoden forEach er default i grensesnittet Iterable
og forEachRemaining i Iterator. De har en Consumer som
argument og kan brukes slik:
tre.forEach(s -> System.out.print(s + " ")); tre.iterator().forEachRemaining(s -> System.out.print(s + " ")); Programkode 5.1.11 g)
Iteratoren kan også brukes direkte i koden. Se
Oppgave 2.
Fordelen med en iterator er at den «avgir» én og én verdi og vi
kan dermed selv bestemme hva som skal gjøres. Vi kan også stoppe itereringen hvis det er ønskelig. Det er også mulig å ha
flere iteratorer i parallell. En iterator er ikke fullt så effektiv
som en separat traverseringsmetode. Metodene hasNext() og next()
må kalles for hver verdi. Men iteratorteknikken
brukes likevel svært ofte siden den er så fleksibel. De fleste
Collection-klassene i java.util har en iterator.
Grensesnittet Iterator har også default-metoden remove().
Den er initielt utilgjengelig (den kaster en UnsupportedOperationException). Kravet er ellers
at den skal fjerne verdien som next() sist returnerte. I et vanlig binærtre
er det normalt bare bladnoder som kan fjernes. Dermed vil det ikke være aktuelt å kode remove() i klassen
BinTre. Oppgave 4.
Et problem som ikke er tatt opp ennå, er hva som kan skje hvis det forgår en endring i treet mens en iterator er i gang. Det tas opp i Oppgave 9.
| 1. | Legg klassen InordenIterator og
metoden iterator() inn i klassen BinTre. Pass
også på at BinTre blir Iterable. Sjekk så at
Programkode 5.1.11 f) virker. Sjekk deretter
at også Programkode 5.1.11 g) virker.
|
| 2. | Bruk en eksplisitt iterator i Programkode 5.1.11 f) - i en for-løkke eller i en while-løkke. |
| 3. | Bruk for-alle-løkken i Programkode 5.1.11 f) til å finne antallet verdier i treet. |
| 4. | Opprett en iterator: Iterator<String> i = tre.iterator(); Gjør et kall på
next() og så et kall på remove(). Hva skjer?
|
| 5. | Fordelen med en iterator er at den kan stoppes. Bruk en iterator til å avgjøre om treet i Programkode 5.1.11 f) inneholder F. Stopp iteratoren når den eventuelt er funnet. |
| 6. | Lag klassen OmvendtInordenIterator i BinTre
og la den ha omvendtIterator() som offentlig metode. Den skal returnere en
instans av klassen. Iteratoren skal
traversere i omvendt inorden, dvs. den siste i inorden kommer først, osv.
|
| 7. | Lag klassen PreordenIterator i BinTre
og la den ha preIterator() som offentlig metode. Den skal returnere en
instans av klassen. Iteratoren skal
traversere i preorden.
|
| 8. | Lag klassen PostordenIterator i BinTre
og la den ha postIterator() som offentlig metode. Den skal returnere en
instans av klassen. Iteratoren skal
traversere i postorden.
|
| 9. | Lag klassen NivåordenIterator i BinTre
og la den ha nivåIterator() som offentlig metode. Den skal returnere en
instans av klassen. Iteratoren skal
traversere i nivåorden.
|
| 10. | Gjør om klassen InordenIterator fra en instansklasse til en
klasseklasse (dvs. en statisk klasse). Da blir det ingen kobling til den ytre klassen.
Bruk f.eks. S som typeparameter alle aktuelle steder.
Konstruktøren må ha Node<S> p som parameter.
Metoden iterator() i BinTre må bruke
den nye konstruktøren med rot som parameter.
|
| 11. | Istedenfor å lage klassen InordenIterator, kan vi la metoden iterator()
returnere en instans av en anonym klasse. Gjør det!
|
| 12. | Det er vanlig å blokkere alle iteratorer som er i gang, hvis det gjøres en endring i treet.
Sett inn en privat instansvariabel int endringer i BinTre-klassen. Den økes med
én for hver endring (dvs. i metodene
leggInn,
oppdater og fjern).
Sett så inn en privat instansvariabel int iteratorendringer i
klassen InordenIterator og sett den lik endringer.
I metoden next() sjekkes det om disse er like. Hvis ikke, kastes unntaket
ConcurrentModificationException.
|
![]() 5.1.12 Splitt og hersk
5.1.12 Splitt og hersk
Binære trær har en struktur der det naturlig å bruke «splitt og hersk».
Det betyr å dele et problem i mindre deler, løse hver del
for seg og sette løsningene sammen til en løsning for hele problemet.
I Avsnitt 5.1.7 bygger
koden for preorden,
inorden og postorden på at rotnodens to subtrær
traverseres hver for seg - noe som gir en traversering av hele treet.
«Splitt og hersk» kan finne antallet noder i treet.
BinTre-klassen har allerede metoden antall(),
se Programkode 5.1.5 a).
Hvis klassen ikke hadde hatt det, kunne vi ha funnet antallet ved hjelp av flg.
«splitt og hersk»-idé: Finn antallet i rotens venstre
og så antallet i høyre subtre. Det totale antallet blir summen av disse pluss en
ekstra for rotnoden. Basistilfellet er et tomt tre (0 noder).
Dette kan oversettes til flg. enkle og elegante metode:
private static int antall(Node<?> p) // ? betyr vilkårlig type { if (p == null) return 0; // et tomt tre har 0 noder return 1 + antall(p.venstre) + antall(p.høyre); } public int antall() { return antall(rot); // kaller hjelpemetoden } Programkode 5.1.12 a)
Legg merke til at metoden arbeider i postorden.
Den må gjøre seg ferdig med hvert subtre før den «behandler» noden.
For å få enkel kode testes her parameteren etter kallet og ikke før slik som
f.eks. i Programkode 5.1.7 a).
Dette kan forbedres. Se Oppgave 2.
Vi kan finne høyden til et tre ved å bruke flg. «splitt og hersk»-idé: Høyden til hele treet er én mer enn høyden til det høyeste av rotnodens to subtrær. Basistilfellet er at treet er tomt og et tomt tre har høyde -1. Dette gir følgende enkle og elegante metode:
private static int høyde(Node<?> p) // ? betyr vilkårlig type { if (p == null) return -1; // et tomt tre har høyde -1 return 1 + Math.max(høyde(p.venstre), høyde(p.høyre)); } public int høyde() { return høyde(rot); // kaller hjelpemetoden } Programkode 5.1.12 b)
Koden i både antall() og
høyde() kan ses på som
en direkte oversettelse av en definisjon. Et alternativ er å traversere treet på vanlig måte, men i tillegg
bruke en parameter til å fortelle hvilket nivå en node er på. Da er det ikke nødvendig at den rekursive
metoden har en returverdi. Dette diskuteres mer nøye på slutten av avsnittet.
Det er ikke noen bestemt orden på verdiene i et generelt binærtre. Hvis vi skal avgjøre om en verdi ligger der, må vi lete gjennom hele treet. Men det er viktig at vi stopper så fort verdien er funnet. Hvis vi finner den søkte verdien i venstre subtre til en node, er det unødvendig å søke i det høyre subtreet. Dette kan kodes rekursivt ved hjelp av operatoren || :
private static <T> boolean inneholder(Node<T> p, T verdi) { if (p == null) return false; // kan ikke ligge i et tomt tre return verdi.equals(p.verdi) || inneholder(p.venstre,verdi) || inneholder(p.høyre,verdi); } public boolean inneholder(T verdi) { return inneholder(rot,verdi); // kaller den private metoden } Programkode 5.1.12 c)
Den rekursive metoden i Programkode 5.1.9 e) setter i
gang en preordentraversering. Men den returnerer (eller trekker seg tilbake) så snart
verdien er funnet fordi et logisk uttrykk med en ||-operator mellom to ledd
(to operander) er sann hvis første ledd er sann og da evalueres ikke andre ledd.
Hele treet blir gjennomsøkt hvis verdi ikke finnes.
Vi kan finne posisjonen til en verdi i et tre.
Barn til en node med posisjon k, har posisjoner 2k og
2k + 1. Flg. metode returnerer -1 hvis verdi ikke finnes
i treet og posisjonstallet til verdi hvis den finnes. Hvis det er flere
forekomster, stopper vi ved den første vi finner:
private static <T> int posisjon(Node<T> p, int k, T verdi) { if (p == null) return -1; // ligger ikke i et tomt tre if (verdi.equals(p.verdi)) return k; // verdi ligger i p int i = posisjon(p.venstre,2*k,verdi); // leter i venstre subtre if (i > 0) return i; // ligger i venstre subtre return posisjon(p.høyre,2*k+1,verdi); // leter i høyre subtre } public int posisjon(T verdi) { return posisjon(rot,1,verdi); // kaller den private metoden } Programkode 5.1.12 d)
Traversering med nivåparameter Det å finne høyden i et binærtre kan løses på en
annen måte enn den i Programkode 5.1.12 b).
Her er et forslag (med en «nybegynnerfeil»):
private static <T> void høyde(Node<T> p, int nivå, int maksnivå) { if (nivå > maksnivå) maksnivå = nivå; if (p.venstre != null) høyde(p.venstre, nivå + 1, maksnivå); if (p.høyre != null) høyde(p.høyre, nivå + 1, maksnivå); } public int høyde() { int maksnivå = -1; if (!tom()) høyde(rot, 0, maksnivå); // roten har nivå 0 return maksnivå; } Programkode 5.1.12 e)
Logikken i koden over er korrekt. For hvert rekursivt kall går vi ett nivå ned i treet og dermed kommer vi før eller
senere til det nederste nivået. Men en vil fort oppdage at dette gir høyde -1 for alle trær.
Metoder i Java har det
som heter verdioverføring. Argumentet maksnivå i den rekursive metoden verdioverføres.
Det betyr at det opprettes en ny og lokal variabel med samme navn og den får som verdi den verdien argumentet har.
Det betyr at enhver endring av maksnivå i metoden gjelder den lokale variabelen og blir ikke
overført til den variabelen som inngår som argument når metoden kalles. Hadde dette vært kodet i C++, så
ville det ha virket hvis argumentet ble deklaret slik: int& maksverdi. Da hadde vi fått det som heter
referanseoverføring og ikke verdioverføring. Men slik er det ikke i Java.
I Java må vi, for å få til en slik effekt, bruke en referansetype som argument. Et slikt argument blir også
verdioverført, men nå er verdien en referanse (eller adresse). Det som det refereres til (objektets innhold)
ligger imidlertid utenfor metoden. Hvis objektet har et innhold som kan endres, så kan det gjøres via referansen.
En tabell er en referansetype (navnet er en referanse til der tabellen ligger). Bruker vi tabellen
int[] maksnivå, holder det at den
har lengde 1 og dermed kun elementet maksnivå[0]. Det elementet kan endres. Koden blir slik:
private static void høyde(Node<?> p, int nivå, int[] maksnivå) { if (nivå > maksnivå[0]) maksnivå[0] = nivå; if (p.venstre != null) høyde(p.venstre, nivå + 1, maksnivå); if (p.høyre != null) høyde(p.høyre, nivå + 1, maksnivå); } public int høyde() { int[] maksnivå = {-1}; // tabellen har lengde 1 if (!tom()) høyde(rot, 0, maksnivå); // roten har nivå 0 return maksnivå[0]; // inneholder høyden } Programkode 5.1.12 f)
Det er noen som synes at teknikken over (en tabell med ett element) er litt kunstig. Men den virker og brukes ofte.
Et alternativ er en klasse med kun ett heltall som instansvariabel. I tilegg måtte klassen ha
(offentlige) metoder for å aksessere og endre variabelen. Java har ingen ferdig klasse for dette. Men vi kan lage en selv
(legges under hjelpeklasser):
public class IntObject { private int value; // kun denne som instansvariabel public IntObject(int value) { this.value = value; } public void add(int value) { this.value += value; } public void subtract(int value) { this.value -= value; } public void set(int value) { this.value = value; } public int get() { return value; } } Programkode 5.1.12 g)
Bruker vi en instans av denne klassen istedenfor en int-tabell med kun ett element (slik som i Programkode 5.1.12 f),
blir koden slik:
private static void høyde(Node<?> p, int nivå, IntObject o) { if (nivå > o.get()) o.set(nivå); if (p.venstre != null) høyde(p.venstre, nivå + 1, o); if (p.høyre != null) høyde(p.høyre, nivå + 1, o); } public int høyde() { IntObject o = new IntObject(-1); if (!tom()) høyde(rot, 0, o); return o.get(); } Programkode 5.1.12 h)
Treets diameter Vi har nå funnet treets høyde med to ulike rekursive teknikker. I den
første ble metodens returverdi utnyttet og i den andre inngikk argumenter. Vi avslutter dette avsnittet med en
metode som bruker begge teknikkene.
Diameteren til et binærtre er lik den største avstanden mellom to noder. For to noder
p og q som ligger på en og samme
gren, er det lett å finne avstanden. Det er antall kanter på veien mellom dem. Hvis ikke,
må de to ha en nærmeste felles forgjenger f, dvs. at de to ligger i hver sitt subtre
til f. I så fall er avstanden mellom p og
q er lik avstanden mellom p og f pluss
avstanden mellom q og f. Vi ka ha at p og q
er like, men da er avstanden 0.
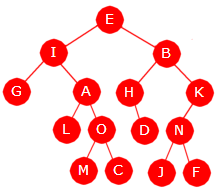 |
| Figur 5.1.12 a) |
Eksempel: I treet til venstre vil avstanden mellom I-noden og C-noden være 3 siden det er tre kanter på veien mellom dem. Ta vi isteden D-noden og J-noden, ser vi at de ikke ligger på en og samme gren. Da er det B-noden som er nærmeste felles forgjenger. Det betyr at avstanden mellom dem er 2 + 3 = 5.
Hva er treets diameter? La p være M- eller C-noden og la q
være J- eller F-noden. Da vil rotnoden (E-noden) være nærmeste felles forgjenger. Avstanden
mellom p og q blir da 4 + 4 = 8. Dette blir også treets diameter siden det ikke finnes noe annet par noder
med større avstand.
Det følger direkte av definisjonen at diameteren til et tre med kun én node er 0. Da passer det å si at
et tomt tre har diameter -1. Et tre med n noder kan maksimalt ha
n − 1 som diameter. Det gjelder f.eks. et tre som er ekstremt høyreskjevt, dvs.
et tre der ingen noder har venstre barn. Generelt gjelder at hvis p og q
er to noder med størst avstand, så må p eller q eller
både p og q, være bladnoder. Hvis p og
q ligger på en og samme gren, må den ene være roten og den andre nederst på grenen.
Hvis de ikke ligger på samme gren, må begge være bladnoder for hvis ikke, kan vi velge noder nedover fra dem og
få større avstand.
En tenkbar måte å finne diameteren på kunne være å finne avstanden mellom samtlige par av noder. Den største av de avstandene blir da diameter. Men det vil i beste fall gi en algoritme av kvadratisk orden. Vi må tenke annerledes.
Vi kan definere at en node er sin egen forgjenger. Dermed vil
alle par av noder ha en felles nærmeste forgjenger.
Det må finnes minst ett par p , q av
noder med størst mulig avstand. La f være deres felles nærmeste forgjenger.
La videre h1 og h2 være høyden til venstre og
høyre subtre til f (høyden til et tomt tre er -1). Da er avstanden mellom
p og f lik h1 + 1 siden
p må ligge nederst i subtreet. Hvis ikke, måtte vi kunne komme
enda lenger ned. Men det er umulig siden avstanden mellom p og
q er den største mulige. Tilsvarende blir avstanden mellom
q og f lik h2 + 1. Altså er avstanden
mellom p og q lik
h1 + h2 + 2. Det betyr at vi kan traversere
treet og for hver node finne subtrærnes høyde, osv.
Vi kombinerer teknikkene fra Programkode 5.1.12 b)
og Programkode 5.1.12 h):
private static int høyde(Node<?> p, IntObject o) { if (p == null) return -1; // et tomt tre har høyde -1 int h1 = høyde(p.venstre, o); // høyden til venstre subtre int h2 = høyde(p.høyre, o); // høyden til høyre subtre int avstand = h1 + h2 + 2; // avstanden mellom to noder if (avstand > o.get()) o.set(avstand); // sammenligner/oppdaterer return Math.max(h1, h2) + 1; // høyden til treet med p som rot } public int diameter() { IntObject o = new IntObject(-1); // lager et tallobjekt høyde(rot, o); // traverserer return o.get(); // returnerer diameter } Programkode 5.1.12 i)
Algoritmen over blir av orden n i alle tilfeller. Det er fordi vi går gjennom treet kun én gang
og alle operasjoner som utføres på en node er av konstant orden.
Hvis koden over ligger i klassen BinTre, kan vi teste dette på treet i
Figur 5.1.12 a):
String[] bokstav = "EIBGAHKLODNMCJF".split(""); int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29}; BinTre<String> tre = new BinTre<>(posisjon, bokstav); System.out.println(tre.diameter()); // Utskrift: 8 Programkode 5.1.12 j)
Dette virker også hvis vi har et ekstremt høyreskjevt tre. I flg. tre vil de 10 bokstavene fra A til J ligge på skrå nedover mot høyre. Diameter og høyde blir da det samme, dvs. 9:
String[] bokstav = "ABCDEFGHIJ".split(""); int[] posisjon = {1,3,7,15,31,63,127,255,511,1023}; BinTre<String> tre = new BinTre<>(posisjon, bokstav); System.out.println(tre.diameter()); // Utskrift: 9 Programkode 5.1.12 k)
Diameteren til et perfekt binærtre er det dobbelte av treets høyde:
int[] posisjoner = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}; String[] bokstaver = "ABCDEFGHIJKLMNO".split(""); BinTre<String> tre = new BinTre<>(posisjoner, bokstaver); System.out.println(tre.høyde() + " " + tre.diameter()); // Utskrift: 3 6 Programkode 5.1.12 l)
| 1. | Sjekk at metodene
antall,
høyde,
inneholder
og posisjon virker. Lag testprogram!
Klassen BinTre har en antall-metode fra før.
Da må den kommenteres vekk eller så bør metodene i
Programkode 5.1.12 a) skifte navn til
f.eks. antall2().
|
| 2. | I Programkode 5.1.12 a) sjekkes
parameteren p etter at metoden er kalt. Gjør om metoden slik at parameteren
sjekkes før metoden kalles.
|
| 3. | Fortsett fra Oppgave 2. Gjør om til kun ett rekursivt kall. Se Oppgave 1 i 5.1.10. |
| 4. | En antall-metode kan kodes på samme måte som høyde-metodene i
Programkode 5.1.12 f) og
Programkode 5.1.12 h). Nå skal nodene telles opp under
traverseringen. Lag metoden private static void antall(Node<?> p, IntObject o).
Lag så en offentlig metode som kaller den.
|
| 5. | Lag metoden public int antallBladnoder(). Den skal returnere antallet bladnoder. Bruk
en rekursiv hjelpemetode.
|
| 6. | Lag metoden public int antallBladnoder() uten rekursjon. Traverser f.eks. i preorden ved
hjelp av en stakk. Se f.eks. Programkode 5.1.10 c).
|
| 7. | Lag en iterativ versjon av metoden høyde().
|
| 8. | Metoden inneholder() virker ikke hvis treet
inneholder en null-verdi. Klassen BinTre tillater null-verdier.
Se leggInn().
Gjør metoden inneholder() slik at det også
er mulig å søke etter en null-verdi. Lag så en iterativ versjon av metoden.
|
| 9. | Metoden
public int posisjon(T verdi)
virker ikke hvis treet inneholder en null-verdi. Klassen BinTre tillater null-verdier.
Se leggInn(). Gjør om metoden
slik at det også er mulig å søke etter en null-verdi. Lag så en iterativ
versjon av metoden.
|
| 10. | Metoden public int makspos() skal returnere treets største nodeposisjon. Hvis treet
er tomt, skal -1 returneres. Hvilken node har den posisjonen? Bruk en rekursiv hjelpemetode. Hvis
pos er parameter, får vi 2*pos til venstre og
2*pos + 1 til høyre. Bruk klassen IntObject.
Se også Programkode 5.1.12 h).
|
| 11. | i) Hva er diameteren til et
perfekt binærtre
med n? Hva
med et komplett binærtre?
|
ii) Hva er den minste diameter et binærtre med n noder kan ha?
| |
iii) Vis at hvis p og q er to noder med størst avstand, så må minst en av dem ligge
på treets nederste nivå.
|
![]() 5.1.13 Tilfeldige trær
5.1.13 Tilfeldige trær
En metodes effektivitet bør normalt testes på trær av forskjellig form og størrelse.
Et tilfeldig (eng: random) binærtre med n noder kan rekursivt lages slik:
Det består av en rotnode, et venstre subtre med k noder med k
tilfeldig valgt fra intervallet [0,n> og et høyre subtre med
n − k − 1 noder. Basistilfeller: Et tomt tre
(0 noder) og et tre med én node.
private static <T> Node<T> random(int n, Random r) { if (n == 0) return null; // et tomt tre else if (n == 1) return new Node<>(null); // tre med kun en node int k = r.nextInt(n); // k velges tilfeldig fra [0,n> Node<T> venstre = random(k,r); // tilfeldig tre med k noder Node<T> høyre = random(n-k-1,r); // tilfeldig tre med n-k-1 noder return new Node<>(null,venstre,høyre); } public static <T> BinTre<T> random(int n) { if (n < 0) throw new IllegalArgumentException("Må ha n >= 0!"); BinTre<T> tre = new BinTre<>(); tre.antall = n; tre.rot = random(n,new Random()); // kaller den private metoden return tre; } Programkode 5.1.13 a)
Hvis random-metodene og
høyde()
er lagt inn i klassen BinTre, vil flg. programbit virke:
int n = 100000; BinTre<Object> tre = BinTre.random(n); // tre med n noder System.out.println("Treets høyde = " + tre.høyde()); Programkode 5.1.13 b)
Et binærtre med n noder kan ha en høyde fra ⌊log2(n)⌋ til n − 1. Med n = 100000 blir det fra 16 til 99999. Kjør Programkode 5.1.13 b) flere ganger. Hva slags verdier får du?
Metoden lager et tilfeldig binærtre. I Avsnitt 5.1.2 fant vi en formel for antallet (isomorft) forskjellige binære trær. Men metoden virker ikke slik at alle disse har samme sannsynlighet for å bli valgt. La f.eks. n = 3. Det er 5 forskjellige trær med 3 noder. Se Figur 5.1.2 c). Metoden starter med å velge et tilfeldig heltall fra 0 til 2, alle med sannsynlighet 1/3. Tallet 1 gir det midterste treet i Figur 5.1.2 c), dvs. en sannsynlighet på 1/3 for det treet. Hvis isteden 0 velges først, vil vi få et av de to første. Hvert av disse har derfor en sannsynlighet på 1/6. Sjekk dette ved å sette n = 3 i Programkode 5.1.13 b). Se Oppgave 1.
Hvis vi har verdier f.eks. i en tabell, vil det kunne være interessant å lage et tilfeldig binærtre med det som nodeverdier. I tillegg kan det være ønskelig at verdiene blir lagt slik i treet at en bestemt traversering gir samme rekkefølge som den verdiene hadde i tabellen.
Her skal vi lage det slik at preorden og tabellen gir samme rekkefølge. La tabellen hete a og la v være venstre endepunkt i et intervall med n verdier, dvs. intervallet a[v : v + n >. Da må verdien i posisjon v legges i rotnoden. Hvis det videre skal være k noder i venstre subtre, må verdiene i a[v + 1 : v + k > legges i venstre subtre og resten i høyre subtre:
private static <T> Node<T> prerandom(int v, int n, T[] a, Random r) { if (n == 0) return null; // et tomt tre else if (n == 1) return new Node<>(a[v]); // tre med kun en node int k = r.nextInt(n); // k velges tilfeldig fra [0,n> Node<T> venstre = prerandom(v + 1, k, a, r); Node<T> høyre = prerandom(v + k + 1, n - k - 1, a, r); return new Node<>(a[v], venstre, høyre); } public static <T> BinTre<T> prerandom(T[] a) { BinTre<T> tre = new BinTre<>(); tre.antall = a.length; tre.rot = prerandom(0, a.length ,a ,new Random()); return tre; } Programkode 5.1.13 c)
Flg. eksempel viser hvordan metoden kan brukes:
Integer[] a = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
BinTre<Integer> tre = BinTre.prerandom(a);
System.out.println(tre.høyde());
tre.preorden(new KonsollUtskrift<>());
Programkode 5.1.13 d)
Hvis Programkode 5.1.13 d) kjøres, vil høyden variere fra gang til gang, mens utskriften i preorden blir alltid i samme rekkefølge som tallene har i tabellen.
Det er også mulig å lage metodene inrandom, postrandom og nivårandom.
Da bygges det tilfeldige trær slik at verdiene i henholdsvis inorden, postorden
og nivåorden blir slik den er i tabellen. Se
Oppgave 4, 5, 6.
I Programkode 5.1.10 d) ble
tidsforbruket til tre forskjellige versjoner av metoden preorden undersøkt
ved at metodene ble kalt diverse ganger på et stort tre. Treet var imidlertid ikke noe
typisk binærtre. Siden det ble bygget opp ved hjelp av alle nodeposisjonene
fra 1 til 100000, ble treet et komplett binærtre. Det kan være interessant å sjekke
tidsforbruken på et mer tilfeldig binærtre, men fortsatt et binærtre med 100000 noder.
Nodeverdiene har ikke interesse her. Derfor passer det best å lage et tilfeldig tre
ved hjelp av random-metoden i
Programkode 5.1.13 a).
Bytt ut de to første programsetningene i
Programkode 5.1.10 d)
med flg. to setninger:
BinTre<Integer> tre = BinTre.random(100000); // tilfeldig binærtre System.out.println("Treets høyde: " + tre.høyde()); Programkode 5.1.13 e)
Hvis en nå kjører programmet, vil en se at det normalt blir et noe større tidsforbruk enn da det ble brukt et komplett tre.
| 1. | Bruk n = 3 i Programkode 5.1.13 b), lag en løkke som går en del ganger (f.eks. 100) og finn så gjennomsnittlig høyde. |
| 2. | Lag, hvis du ikke allerede har gjort det (se Oppgave 12 i Avsnitt 5.1.7), en metode som returnerer en tabell som inneholder treets nodeposisjoner i nivåorden. Lag så tilfeldige trær med 10 noder og sjekk hva slags nodeposisjoner trærne får. |
| 3. | Lag metoden public static <T> BinTre<T> . Den
skal generere et tilfeldig tre der antall noder er lik lengden til tabellen posisjoner.
Alle nodene skal ha null som nodeverdi. Tabellen posisjoner skal
etterpå inneholde treets nodeposisjoner i preorden.
|
| 4. | Lag metoden public static <T> BinTre<T> . Den skal
lage et tilfeldig binærtre der verdiene fra a kommer i inorden.
|
| 5. | Lag metoden public static <T> BinTre<T> . Den skal
lage et tilfeldig binærtre der verdiene fra a kommer i postorden.
|
| 6. | Lag metoden public static <T> BinTre<T> . Den skal
lage et tilfeldig binærtre der verdiene fra a kommer i nivåorden.
|
| 7. | Bytt ut de to første setningene i Programkode 5.1.10 d) med de to setningene i Programkode 5.1.13 e) og kjør programmet. Hvilken av de tre versjonene av preorden() er nå best? Hvor store trær tåler datamaskinen din. Prøv med et tre med 1 million noder. Hva med 10 millioner? Både de rekursive og iterative traverseringene er av lineær orden. Det betyr at hvis trestørrelsen øker med f.eks. en faktor på 10, vil tidsforbruket øke med samme faktor. |
![]() 5.1.14 Isomorfe trær
5.1.14 Isomorfe trær
Vi sier at to binære trær er isomorfe hvis de har samme form. Se
Avsnitt 5.1.2. Hvordan skal vi avgjøre
om to binære trær er isomorfe? Vi kan finne mengden av posisjonstall for hvert tre
(se Avsnitt 5.1.3) og så sjekke
om mengdene er like. Se Oppgave 1.
Det er imidlertid enklere å bruke en «splitt og hersk»-idé: To binære trær tre1 og tre2 er isomorfe hvis venstre subtre til tre1 er isomorft med venstre subtre til tre2 og høyre subtre til tre1 er isomorft med høyre subtre til tre2. Basistilfellene er at to tomme trær er isomorfe, og et tomt og et ikke-tomt tre er ikke isomorfe. Vi ser kun på trærnes form og ikke på verdiene. Dermed kan vi bruke ubestemt datatype (dvs. ? ). Dette kan kodes slik:
private static boolean isomorf(Node<?> p, Node<?> q) { if (p == null && q == null) return true; // to tomme trær if (p == null ^ q == null) return false; // tomt og ikke tomt return isomorf(p.venstre,q.venstre) && isomorf(p.høyre,q.høyre); } public boolean isomorf(BinTre<?> tre) { if (this == tre) return true; // ett og samme tre if (antall != tre.antall) return false; // må ha samme antall return isomorf(rot,tre.rot); // den private metoden } Programkode 5.1.14 a)
Legg merke til at vi bruker operatoren ^ (eksklusiv eller). Hvis α og β er to logiske utsagn, vil α ^ β være sann hvis og bare hvis α og β har innbyrdes forskjellige sannhetsverdier.
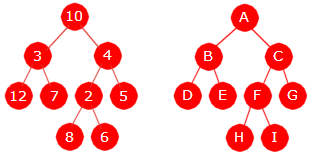 |
| Figur 5.1.14 a) : Trær med ulike verdier, men med samme form |
De to trærne i Figur 5.1.14 a) har forskjellige verdier, men har samme form. De
er isomorfe. Flg. eksempel viser hvordan isomorf-metoden kan brukes til å sammenligne dem.
I koden brukes BinTre-konstruktøren fra
Programkode 5.1.5 c):
int[] p = {1,2,3,4,5,6,7,12,13}; // nodeposisjoner for begge trær Integer[] tall = {10,3,4,12,7,2,5,8,6}; // venstre tre Character[] c = {'A','B','C','D','E','F','G','H','I'}; // høyre tre BinTre<Integer> tre1 = new BinTre<>(p,tall); // venstre tre BinTre<Character> tre2 = new BinTre<>(p,c); // høyre tre System.out.println(tre1.isomorf(tre2)); // utskrift: true Programkode 5.1.14 b)
I Programkode 5.1.14 b) har begge trærne samme posisjonstallmengde og skal derfor
per definisjon være isomorfe. Er koden korrekt, må det bli true som utskrift. La
fortsatt p være posisjonstabell for det venstre treet. Sett isteden opp en posisjontabell q
for det høyre treet. Da vil vi få false som utskrift hvis innholdet i q er
forskjellig fra p. Prøv det!
I Avsnitt 5.1.3 definerte vi at to binære trær
er like hvis de både er isomorfe og har samme innhold. Samme innhold betyr
like verdier i de samme posisjonene.
Basisklassen Object har metoden public boolean
equals(Object o) som vår klasse BinTre arver. Den gir at to trær er like
hvis de er identiske, dvs. hvis det er et og samme tre. Vi må derfor lage vår egen versjon
(eng: override) av equals hvis den skal sammenfalle med vår definisjon av
likhet:
private static boolean equals(Node<?> p, Node<?> q) { if (p == null && q == null) return true; // to tomme trær if (p == null ^ q == null) return false; // tomt og ikke tomt return p.verdi.equals(q.verdi) && equals(p.venstre, q.venstre) && equals(p.høyre, q.høyre); } public boolean equals(Object objekt) { if (this == objekt) return true; // samme objekt if (!(objekt instanceof BinTre)) return false; // feil type! @SuppressWarnings("unchecked") BinTre<T> tre = (BinTre<T>)objekt; // gjør om til BinTre if (antall != tre.antall) return false; // må ha samme antall return equals(rot,tre.rot); // kaller den private equals-metoden } Programkode 5.1.14 c)
Vi kan gjøre to trær like ved at det ene lages som en kopi av det andre.
Det kan gjøres ved en kopieringskonstruktør (eng: copy constructor).
Det er også mulig å la klassen være Cloneable og
implementere metoden clone. Men som Joshua Bloch sier
(han har laget store deler av java.util og skrevet boken
«Effective Java»): «Because of its many shortcomings, some expert
programmers simply choose never to override the clone-method and never to invoke
it except, perhaps, to copy arrays cheaply». Vi ser derfor ikke mer på metoden clone.
Flg. kopieringskonstruktør tar i mot en instans av BinTre og
bruker en rekursiv kopi-metode til å konstruere en kopi. Det
gjøres ved hjelp av flg. «splitt og hersk»-idé: Kopier først høyre subtre,
så venstre subtre og til slutt noden. Dette kan gjøres med flg. korte og elegante kode:
private static <T> Node<T> kopi(Node<T> p) { if (p == null) return null; // ingenting å kopiere return new Node<>(p.verdi,kopi(p.venstre),kopi(p.høyre)); } public BinTre(BinTre<T> tre) // kopieringskonstruktør { rot = kopi(tre.rot); antall = tre.antall; } Programkode 5.1.14 d)
Det å kopiere kan bety ulike ting. Vi har flg. begreper:
- referansekopi
- kopi (en ekte kopi (eller grunn kopi (eng: shallow copy))
- dyp kopi (eng: deep copy)
En variabel av en referansetype er
en referanse til et objekt (en instans av datatypen). En referansekopi er derfor en kopi
av referansen, mens en kopi er en (ekte) kopi av objektet. Kopieringskonstruktøren i
Programkode 5.1.14 d) lager
en kopi av parametertreet tre.
En kopi et helt nytt tre med egne noder helt separat fra nodene i tre,
men verdiene i nodene er referansekopiert. En dyp kopi er en kopi
der også nodeverdiene kopieres. Men nodeverdiene kan være referansetyper som igjen inneholder referansetyper.
Osv. Dette betyr at en «dyp kopi» er et komplisert begrep.
Spørsmålet blir da hvor mange nivåer nedover en skal kopiere.
En (vanlig eller ekte) kopi dekker normalt vårt kopibehov.
I java.util er det mange datastrukturer som kan kopieres ved hjelp av en konstruktør eller
ved hjelp av clone(). Da blir det kopier (og ikke dype kopier). Flg. kodebit viser hvordan vi kan lage
en kopi av en instans av klassen TreeSet:
int[] a = {4,2,6,5,1,3,7}; // en samling tall Set<Integer> A = new TreeSet<>(); // A er en TreeSet for (int k : a) A.add(k); // legger inn tallene Set<Integer> B = new TreeSet<>(A); // B blir en kopi av A A.add(8); // gjør et tillegg i A System.out.println(A + " " + B); // Utskrift: [1, 2, 3, 4, 5, 6, 7, 8] [1, 2, 3, 4, 5, 6, 7] Programkode 5.1.14 e)
Vi kan nå bruke den samme teknikken for våre binære trær:
int[] posisjon = {1,2,3,4,5,6,7,12,13}; // posisjoner String[] verdi = "ABCDEFGHI".split(""); // verdier BinTre<String> tre1 = new BinTre<>(posisjon, verdi); // konstruktør BinTre<String> tre2 = tre1; // tre2 en referansekopi av tre1 BinTre<String> tre3 = new BinTre<>(tre1); // tre3 er en (ekte) kopi av tre1 System.out.println(tre1.equals(tre2) + " " + tre1.equals(tre3)); // true true tre1.oppdater(13,"X"); // setter X i posisjon 13 i tre1 System.out.println(tre1.equals(tre2) + " " + tre1.equals(tre3)); // true false Programkode 5.1.14 f)
I koden over oppdateres tre1 med en X i posisjon 13. Fortsatt er tre1 og tre2 like siden de refererer til det samme treet. Men tre1 er ikke lenger lik tre3. De to er adskilte trær.
| 1. |
Lag public boolean isomorf(BinTre<?> tre) på den måten at
først lages det tabeller med nodeposisjoner for de to trærne. Se
Oppgave 11 og 12 i Avsnitt 5.1.7.
Deretter sammenlignes tabellene ved hjelp av metoden equals i klassen Arrays.
|
| 2. | Det er tillatt med null som nodeverdi i en node i et binærtre.
Men equals-metoden i
Programkode 5.1.14 c)
vil gi NullPointerException hvis en node har null som verdi.
Gjør om metoden slik at to nodeverdier anses som like hvis begge er null.
|
| 3. | Metoden equals i
Programkode 5.1.14 c)
er en overskriving (eng: override) av metoden som arves fra basisklassen Object.
Det er vanlig å lage en direkte equals-metode i tillegg. Da slipper man
typekonverteringen m.m. Lag public boolean equals(BinTre<T> tre). Hvem
av dem tror du da vil bli kalt i
Programkode 5.1.14 f)?
Når vil den arvede metoden bli brukt?
|
| 4. | Den rekursive kopieringsmetoden i
Programkode 5.1.14 d)
arbeider i postorden. Lag en kopieringsmetode
private static <T> void kopi(Node<T> p, Node<T> q)
som arbeider i preorden. Referansen p skal gå i kopitreet og referansen q
i treet som skal kopieres. I koden sjekkes det om q har et venstre barn,
hvis ja får p som sitt venstre barn en ny node med verdien i q sitt
venstre barn som verdi. Tilsvarende for høyre barn. Kopieringskonstruktøren må
da endres litt for å kunne benytte metoden.
|
| 5. | I enkelte programmeringsmiljøer får vi en melding (eng: warning) hvis den
arvede equals-metoden er overskrevet (eng: overridden) uten at den arvede
hashCode-metoden er overskrevet. Lag derfor public int hashCode()
for BinTre. La sum1 være summen av posisjonstallene og
sum2 summen av hashCode()-verdiene for verdiene i alle nodene.
La metoden returnere produktet av sum1 og sum2.
Sjekk at hashCode-metoden gir samme tall for to forskjellige trær som
equals-metoden sier er like. Gi et eksempel på to trær som equals-metoden
sier er ulike, men der hashCode-metoden laget slik som beskrevet over,
gir samme tall. Er dette en god hashCode-metode?
|
![]() 5.1.15 Trær med forelderreferanser
5.1.15 Trær med forelderreferanser
Hvis vi legger en forelderreferanse i hver node, kan vi gå oppover i treet når det er behov for det.
Minnebehovet vil da imidlertid øke siden det blir fire variabler i hver node mot før tre.
Fordelen er imidlertid at noen algoritmer blir enklere og mer effektive.
Klassen TreeMap
(og TreeSet )
i java.util bruker denne teknikken. Vi lager en egen klasse med navnet FBinTre
for denne typen binære trær. Bokstaven F står for forelder. Det som er nytt i forhold til et vanlig
binærtre, er markert med rødt:
public class FBinTre<T> implements Iterable<T> { private static final class Node<T> { private T verdi; private Node<T> venstre, høyre, forelder; // forelder private Node(T verdi, Node<T> v, Node<T> h, Node<T> f) { this.verdi = verdi; venstre = v; høyre = h; forelder = f; } private Node(T verdi, Node<T> f) { this(verdi,null,null,f); } } // class Node private Node<T> rot; // referanse til rotnoden private int antall; // antall noder i treet public FBinTre() // standardkonstruktør { rot = null; antall = 0; } public int antall() { return antall; } public boolean tom() { return antall == 0; } public Iterator<T> iterator() { return null; // kodes senere } } // class FBinTre Programkode 5.1.15 a)
Figur 5.1.15 a) nedenfor viser et binærtre der hver node, bortsett fra rotnoden, har en referanse opp til sin forelder (rotnodens forelder er null). Det fører som nevnt over, til at treets minnebehov øker med 33% i forhold til et vanlig binærtre.
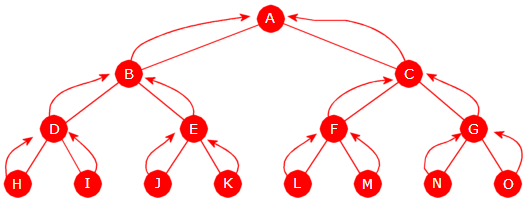 |
| Figur 5.1.15 a) : Forelderreferanse i hver node |
Denne nye nodestrukturen krever at leggInn-metoden må endres. Når en ny node legges inn i treet må dens forelderreferanse bli satt korrekt. Spesielt må rotnodens forelderreferanse settes til null. Dette gjør vi ved å hente Programkode 5.1.5 b), endre den programlinjen der noden opprettes til flg. kode:
p = new Node<>(verdi,q); // q settes som forelder til p
og så legge hele metoden nederst i den nye FBinTre-klassen.
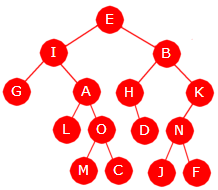 |
| Figur 5.1.15 b) : Et binærtre |
La p og q være to noder slik at q er den neste til p i inorden. Da gjelder også det omvendte, dvs. at p er den forrige til q. Med andre ord må p ligge lengst ned til høyre i q sitt venstre subtre. For å komme fra p til q går vi derfor motsatt vei, dvs. vi går på skrå oppover mot venstre så langt som mulig og deretter vil q være første node opp til høyre.
Eksempel: La p være C-noden i Figur 5.1.15 b). Da må q, dvs. den neste til p i inorden, være E-noden. Vi ser på tegningen at vi kommer fra C til E ved å gå på skrå oppover mot venstre så langt som mulig (dvs. til I ) og deretter videre opp til høyre til første node. La isteden p være D-noden. Da er det B-noden som er den neste og vi kommer dit på samme måte: først oppover mot venstre så langt som mulig (til H ) og videre rett opp til høyre.
Vi må ta hensyn til et par spesialtilfeller: Hvis p er den siste noden i inorden, kommer vi til roten og ikke lenger når vi går på skrå oppover mot venstre så langt vi kan. Derfra er det ikke mulig å gå opp til høyre. Dermed er traverseringen ferdig. Hvis p f.eks. er G-noden, er det ikke mulig å gå oppover mot venstre. Da finner vi den neste ved å gå rett opp til høyre.
Det er kun når p er et høyre barn til sin forelder at det er mulig å gå på skrå opp til venstre.
Vi lager to private hjelpemetoder. Metoden førsteInorden finner den første i inorden i det treet som har p som rot. Metoden nesteInorden finner den neste. Det er to muligheter: 1) Hvis p har et høyre barn, er den neste den første i inorden med hensyn på det høyre barnet og 2) hvis p ikke har et høyre barn, må vi oppover i treet slik som beskrevet over.
private static <T> Node<T> førsteInorden(Node<T> p) { while (p.venstre != null) p = p.venstre; return p; } private static <T> Node<T> nesteInorden(Node<T> p) { if (p.høyre != null) // p har høyre barn { return førsteInorden(p.høyre); } else // må gå oppover i treet { while (p.forelder != null && p.forelder.høyre == p) { p = p.forelder; } return p.forelder; } } Programkode 5.1.15 b)
Ved hjelp av de to metodene får vi denne enkle versjonen av en inorden-traversering:
public void inorden(Oppgave<? super T> oppgave) { if (rot == null) return; // tomt tre Node<T> p = førsteInorden(rot); // den aller første i inorden while (p != null) { oppgave.utførOppgave(p.verdi); p = nesteInorden(p); } } Programkode 5.1.15 c)
Flg. programbit bygger opp treet i Figur 5.1.15 b) og skriver ut verdiene i inorden:
int[] p = {1,2,4,5,10,11,22,23,3,6,13,7,14,28,29}; char[] c = "EIGALOMCBHDKNJF".toCharArray(); FBinTre<Character> tre = new FBinTre<>(); for (int i = 0; i < p.length; i++) tre.leggInn(p[i], c[i]); tre.inorden(new KonsollUtskrift<>()); // Utskrift: G I L A M O C E H D B J N F K Programkode 5.1.15 d)
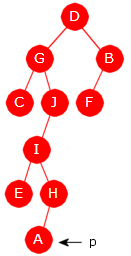 |
| Figur 5.1.15 c) |
Det er også mulig å gjøre en iterativ traversering i preorden ved hjelp av forelderreferansene. Huskereglen for preorden er: node, venstre, høyre. Det betyr at hvis vi har gjort oss ferdige med en node p, så står nodens venstre barn for tur, og hvis noden ikke har et venstre barn, er det høyre barns tur. Men hvis p er en bladnode, må vi oppover i treet for å finne den neste. Da må vi opp til første node f som har et høyre barn samtidig som vi (dvs. p) er i det venstre subtreet til f. Den neste i preorden er da det høyre barnet til f.
Eksempel: La p være A-noden i Figur 5.1.15 c) til venstre, dvs. en bladnode. Da er det B-noden som er den neste i preorden. For å komme dit må vi først gå oppover til D-noden. Vi må gå helt dit fordi alle nodene vi passerer underveis mangler enten et høyre barn eller så er ikke p i nodens venstre subtre: H og J mangler høyre barn og p er ikke i venstre subtre til I og G. Hvis det ikke finnes noen node oppover med en slik egenskap, betyr det at p er den siste i preorden.
public void preorden(Oppgave<? super T> oppgave) { if (rot == null) return; // tomt tre Node<T> p = rot; // roten er første i preorden while (true) { oppgave.utførOppgave(p.verdi); // oppgaven utføres if (p.venstre != null) p = p.venstre; else if (p.høyre != null) p = p.høyre; else { Node<T> f = p.forelder; // vi må oppover i treet while (f != null && (f.venstre != p || f.høyre == null)) { p = f; f = f.forelder; } if (f == null) return; // p var den siste else p = f.høyre; } } } Programkode 5.1.15 e)
Hvis inorden erstattes med preorden i Programkode 5.1.15 d), får du sjekket om dette virker. Det er også mulig å lage en traversering i postorden ved hjelp av forelderreferansene. Iterator-klasser for preorden, inorden og postorden er nå enkle å lage. Se oppgavene.
| 1. | Lag en iterativ versjon av public void postorden(Oppgave<? super T> oppgave)
ved å bruke forelderreferansene.
|
| 2. | Lag en iterativ versjon av public void omvendtInorden(Oppgave<? super T> oppgave)
ved å bruke forelderreferansene. Se Avsnitt 5.1.8.
|
| 3. | Lag en iterativ versjon av public void omvendtPreorden(Oppgave<? super T> oppgave)
ved å bruke forelderreferanser.
|
| 4. | Lag en iterativ versjon av public void omvendtPostorden(Oppgave<? super T> oppgave)
ved å bruke forelderreferanser.
|
| 5. | Klassen FBinTre er satt opp som
Iterable. Det betyr at den må ha metoden iterator(). Den er satt opp i klassen,
men mangler kode. Hent klassen InordenIterator,
legg den inn i FBinTre-klassen, ta vekk stakken og kod metodene ved hjelp av metodene i
Programkode 5.1.15 b). La så metoden
iterator() returnere en instans av klassen.
|
| 6. | La klassen ha en PreordenIterator og metoden preiterator(). Lag koden
ved hjelp av forelderreferanser.
|
| 7. | La klassen ha en PostordenIterator og metoden postiterator(). Lag koden
ved hjelp av forelderreferanser.
|
| 8. | La klassen ha en OmvendtInordenIterator og metoden omvendtiterator(). Lag koden
ved hjelp av forelderreferanser. Den skal traversere i omvendt inorden.
|
| 9. | Lag en iterativ versjon av metoden public int[] nodeposisjoner(). Den skal returnere en tabell som
inneholder treets nodeposisjoner i preorden. Lag koden
ved hjelp av forelderreferanser.
|
| 10. | Lag en iterativ versjon av metoden public Object[] tilTabell(). Den skal returnere en tabell som
inneholder treets verdier i preorden. Lag koden
ved hjelp av forelderreferanser.
|
| 11. | I Avsnitt 5.1.13 ble det laget flere metoder for å generere tilfeldige trær. Lag spesielle versjoner av de metodene for klassen FBinTre. Da må metodene generere trær der alle forelderreferansene er satt riktig. Lag så en programbit (se Programkode 5.1.13 e) der du sjekker om traversering ved hjelp av forelderreferanser er mer effektivt enn en rekursiv traversering eller en iterativ traversering ved hjelp av en stakk. |
![]() 5.1.16 Trær med tråder
5.1.16 Trær med tråder
Hvis en node p i et binærtre ikke er den siste i inorden og ikke har et høyre barn,
vil den neste i inorden være den nærmeste av nodene oppover mot roten som har p
i sitt venstre subtre. Det at p ikke har et høyre barn betyr at referansen
p.høyre er null. Hvis vi lar alle null-referanser av den typen isteden gå til den
neste i inorden, får vi flg. figur:
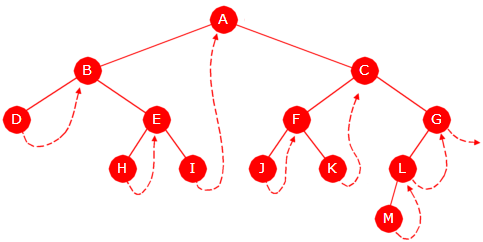 |
| Figur 5.1.16 a) : Binærtre med tråder |
På Figur 5.1.16 a) er det markert med stiplet pil det at en referanse som egentlig skal gå til null, isteden går til den neste i inorden. Dermed går en «tråd» gjennom treet. «Tråden» starter i den første i inorden (D-noden på figuren). Hvis en node p har et høyre barn, går «tråden» fra det barnet og på skrå nedover til venstre så langt det går. Ved å følge «tråden» får vi en traversering i inorden. Treet kalles et tredd tre (eng: threaded tree).
For å skille mellom tilfellene når en høyrereferanse går til et høyre barn og når den går til den neste i inorden, legges det inn en ekstra boolsk variabel i nodene. Den kan f.eks. hete harHøyreBarn. Når den er true går referansen til det høyre barnet og når den er false går den til den neste i inorden. Nodeklassen blir da slik:
private static final class Node<T> { private T verdi; private Node<T> venstre; private Node<T> høyre; private boolean harHøyreBarn; private Node(T verdi, Node<T> v, Node<T> h) { this.verdi = verdi; venstre = v; høyre = h; harHøyreBarn = false; } } Programkode 5.1.16 a)
Noden i Programkode 5.1.16 a) skal legges inn i en ny klasse med navn TBinTre (T for tråd). Gjør det ved å kopiere i skjelettet til FBinTre. Skift navn til TBinTre og bytt ut nodeklassen med den nye i Programkode 5.1.16 a). Resten kan være som det er.
Metoden leggInn må kodes slik at treet hele tiden holdes som et «tredd tre». Vi kan ta utgangspunkt i leggInn fra BinTre-klassen og så ta flg. hensyn:
- I letingen etter rett posisjon brukes p.harHøyreBarn og ikke p.høyre.
- En ny node blir alltid en bladnode og dermed skal harHøyreBarn være false.
- Hvis ny node p blir venstre barn til sin forelder q, settes p.høyre til q.
- Hvis ny node p blir høyre barn til sin forelder q, settes først harHøyreBarn i q til true og deretter p.høyre til det som var den neste i inorden for q, dvs. til q.høyre.
public void leggInn(int k, T verdi) { if (k < 1) throw new IllegalArgumentException("Posisjon k(" + k + ") < 1!"); Node<T> p = rot, q = null; // hjelpereferanse int n = Integer.highestOneBit(k >> 1); // n = 100...00 while (p != null && n > 0) { q = p; // q er forelder til p if ((n & k) == 0) p = p.venstre; // går til venstre else if (p.harHøyreBarn) p = p.høyre; // den boolske variabelen else break; // p har blitt null n >>= 1; // bitforskyver n } if (n > 0) throw new IllegalArgumentException("Posisjon k(" + k + ") mangler forelder!"); else if (p != null) throw new IllegalArgumentException("Posisjon k(" + k + ") finnes fra før!"); if (q == null) { rot = new Node<>(verdi, null, null); // tomt tre - ny rot } else if ((k & 1) == 0) // sjekker siste siffer i k { q.venstre = new Node<>(verdi, null, q); } else { q.harHøyreBarn = true; q.høyre = new Node<>(verdi, null, q.høyre); } antall++; // en ny verdi i treet } Programkode 5.1.16 b)
Hvis noden p ikke har høyre barn, kan vi hoppe rett til neste i inorden ved å følge «tråden». Det gir enkel og effektiv kode for en traversering. Kodingen blir også enklere hvis vi lager en hjelpemetode som finner den første i inorden med hensyn på p. Den kan lages helt lik den som vi laget i forrige avsnitt, men for oversiktens skyld setter vi den opp på nytt:
private static <T> Node<T> førsteInorden(Node<T> p) { while (p.venstre != null) p = p.venstre; return p; } public void inorden(Oppgave<? super T> oppgave) { Node<T> p = tom() ? null : førsteInorden(rot); while (p != null) { oppgave.utførOppgave(p.verdi); p = p.harHøyreBarn ? førsteInorden(p.høyre) : p.høyre; } } Programkode 5.1.16 c)
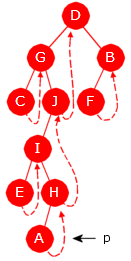 |
| Figur 5.1.16 b) |
«Tråden» i treet er laget for at en traversering i inorden skal kunne foregå på en enkel og effektiv måte. Men det er også mulig å bruke «tråden» til å gjøre en iterativ traversering i preorden. Husk at hvis p er en bladnode, er neste i preorden den nærmeste noden q i retning mot roten som har et høyre barn samtidig som p er i det venstre subtreet til q. Den neste i preorden er da det høyre barnet til q.
Figur 5.1.16 b) til venstre viser samme tre som i Figur 5.1.15 c), men nå med «tråder» inntegnet. La som eksempel p være A-noden. dvs. en bladnode. Da er det B-noden som er den neste i preorden. For å komme dit kan vi følge «trådene» oppover til vi kommer til den første noden som har et høyre barn, dvs. til D-noden. Vi må gå helt dit fordi nodene vi passerer underveis, mens vi følger «tråden» (H-noden og J-noden), mangler høyre barn. Den neste i preorden blir da dette høyre barnet. Hvis det ikke finnes noen node langs «tråden» med en slik egenskap, må p være den siste i preorden. Se F-noden.
public void preorden(Oppgave<? super T> oppgave) { for (Node<T> p = rot; p != null; ) // roten er første i preorden { oppgave.utførOppgave(p.verdi); // oppgaven utføres if (p.venstre != null) p = p.venstre; else if (p.harHøyreBarn) p = p.høyre; else { while (p != null && p.harHøyreBarn == false) { p = p.høyre; // går oppover langs tråden } if (p == null) return; // den siste er passert else p = p.høyre; } } } Programkode 5.1.16 d)
«Tråd»-teknikken kan også brukes til å lage iteratorer. Se oppgavene.
Hvis vi skal sjekke om traversering ved hjelp av «tråder» er effektivt, trenger vi store og tilfeldige trær av denne typen. I Avsnitt 5.1.13 laget vi metoder som generer tilfeldige trær. Vi kan ta utgangspunkt i dem, men gjøre de endringene som trengs for å få treet tredd.
Teknikken gikk ut på å lage en ny node med to tilfeldige trær venstre og høyre som subtrær/barn. Da vil den nye noden bli neste i inorden for den noden som er sist i inorden i treet venstre. Videre vil den nye noden få høyre som høyre barn og dermed må variabelen harHøyreBarn settes til true. Her kommer koden som lager et tilfeldig TBinTre-tre ved hjelp av en tabell med verdier slik at verdiene i inorden i treet blir den samme de har i tabellen:
private static <T> Node<T> inrandom(int v, int n, T[] a, Random r) { if (n == 0) return null; // et tomt tre else if (n == 1) return new Node<>(a[v],null,null); // bladnode int k = r.nextInt(n); // k velges tilfeldig fra [0,n> Node<T> venstre = inrandom(v, k, a, r); Node<T> høyre = inrandom(v + k + 1, n - k - 1, a, r); Node<T> rot = new Node<>(a[v + k], venstre, høyre); if (venstre != null) { Node<T> p = venstre; while (p.harHøyreBarn) p = p.høyre; // finner siste i inorden p.høyre = rot; // en tråd } if (høyre != null) rot.harHøyreBarn = true; return rot; } public static <T> TBinTre<T> inrandom(T[] a) { TBinTre<T> tre = new TBinTre<>(); tre.antall = a.length; tre.rot = inrandom(0, a.length, a, new Random()); return tre; } Programkode 5.1.16 e)
Flg. eksempel viser hvordan metoden inrandom(T[]) kan brukes:
Character[] c = {'A','B','C','D','E','F','G','H','I','J'};
TBinTre<Character> tre = TBinTre.inrandom(c);
tre.inorden(new KonsollUtskrift<>());
// Utskrift: A B C D E F G H I J
Programkode 5.1.16 e)
Figur 5.1.16 c) under viser et tre der det er lagt inn «tråder» i begge retninger. For å få til det kodemessig må nodene ha en ekstra boolsk variabel f.eks.med navn harVenstreBarn. I alle noder som ikke har venstre barn, skal p.venstre vise til den forrige i inorden. Dette krever at leggInn-metoden kodes om. Se oppgavene.
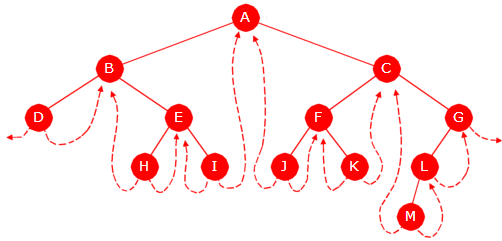 |
| Figur 5.1.16 c) : Binærtre med tråder i begge retninger |
| 1. | Opprett klassen TBinTre hos deg og legg inn metodene i dette avsnittet.
Sjekk at inorden-metoden i Programkode 5.1.16 c)
virker som den skal ved å erstate FBinTre med TBinTre i
Programkode 5.1.15 d). Test
så preorden i
Programkode 5.1.16 d).
|
| 2. | Lag en indre klasse InordenIterator i TBinTre-klassen og la metoden
iterator() returnere en instans av klassen. Bruk «tråd»-teknikken i koden.
|
| 3. | Metoden i Programkode 5.1.16 e) genererer et tilfeldig tredd tre. Lag metoder som genererer et tilfeldig tredd tre der 1) alle verdiene er null, 2) verdiene hentes fra en tabell slik at preorden i treet svarer til rekkefølgen i tabellen, 3) som 2) men i postorden og 4) som 2) men i nivåorden. Se Avsnitt 5.1.13. Lag en programbit (se Programkode 5.1.13 e) der du sjekker om traversering ved hjelp av «tråder» er mer effektivt enn en rekursiv traversering eller en iterativ traversering ved hjelp av en stakk. |
| 4. | Legg inn den boolske variabelen harVenstreBarn som privat variabel i nodeklassen
i klassen TBinTre. Sett den til false i konstruktøren. Gjør så de endringene som trengs
i leggInn-metoden slik at det blir en «tråd» i treet som går i omvendt inorden.
|
| 5. | Lag metoden public static void omvendtInorden(Oppgave<? super T> oppgave)
ved hjelp av «tråden» som går motsatt vei. Se Oppgave 4.
|
| 6. | Lag metoden public static void omvendtPreorden(Oppgave<? super T> oppgave)
ved hjelp av «tråden» som går motsatt vei. Se Oppgave 4.
|
| 7. | Lag metoden public static void postorden(Oppgave<? super T> oppgave)
ved hjelp av «trådene».
|
![]() 5.1.17 Morris' algoritme
5.1.17 Morris' algoritme
Vi har nå studert både rekursive og iterative traverseringer.
Allerede i 1968 kom
Donald Knuth
med flg. ønske: Finn den mest effektive iterative algoritmen som traverserer i
inorden der det hverken brukes en stakk eller ekstra hjelpevariabler i nodene.
Treet måtte også være uberørt i den forstand at treet etter traverseringen
skulle være nøyaktig som det var før. J.M.Morris kom med et forslag i 1979 og
hans løsning regnes fortsatt som den beste.
Morris' algoritme bruker delvis samme idé som i et tredd tre, men siden det ikke
trengs en ekstra boolsk variabel i nodene, vil ideen kunne brukes i et vanlig binærtre,
dvs. i klasssen BinTre.
Et tredd tre har permanente «tråder». Her skal det isteden brukes
midlertidige «tråder». Hvis en node ikke
har høyre barn, legges en midlertidig «tråd» fra noden til dens
neste i inorden. Når traverseringen har passert noden, fjernes «tråden»,
dvs. nodens høyre-referanse sette tilbake til null.
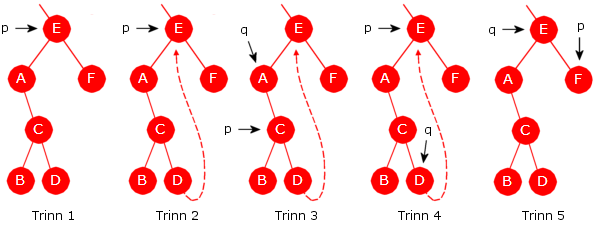 |
| Figur 5.1.17 a) : Fem trinn i Morris' algoritme |
Figur 5.1.17 a) viser fem stadier/trinn som et subtre gjennomgår i algoritmen. Vi kan tenke oss at dette er høyre subtre til en node som ligger oppe til venstre for noden E. Referansen p flyttes fra node til node og i Trinn 1 har p kommet til subtreets rotnode, dvs. til noden E.
Den første i inorden i subtreet ligger lengst ned på skrå til venstre, dvs noden A. Men før p flyttes til A, må vi passe på at vi kan komme tilbake til E. Det gjør vi ved å finne den forrige til E i inorden. Den ligger lengst ned på skrå til høyre i det venstre subtreet til E. Vi setter høyrereferansen der (dvs. i D) til det samme som p, dvs. til E. På tegningen er det markert ved en stiplet pil - se figurens Trinn 2. Dermed kan vi komme opp igjen til E når vi er ferdige i D.
Vi flytter så p til A og utfører oppgaven. Da A ikke har venstre barn, flytter vi p videre ned til høyre til C. Samtidig innfører vi en hjelpereferanse q som ligger et hakk bak p. Her betyr det at p blir det samme som q.høyre. Se figurens Trinn 3. Problemet med den siste flyttingen av p er at algoritmen ikke kan vite om høyre referanse i A går til et barn eller til den neste i inorden.
La oss først gå noen skritt videre. Anta at p er flyttet først til D-noden og så videre til E-noden. Da vil q stå på D-noden. Se figurens Trinn 4. Problemet dukker opp igjen. Hvordan kan vi vite om p nå står på et høyre barn til q eller på den neste til q i inorden? Hvis p er den neste i inorden skal stiplingen fjernes, dvs. høyre referanse i q skal settes tilbake til null.
Se på Trinn 4. Der vil det være mulig å gå fra p til q ved å først gå til p sitt venstre barn og så videre ned mot høyre. Hvis vi isteden ser på Trinn 3 der p ble flyttet fra A-noden til C-noden, vil det ikke være mulig å komme til q ved å først gå til p sitt venstre barn og så videre ned mot høyre. Denne forskjellen kan brukes til å avgjøre om høyre referanse i en node går til et barn eller til den neste i inorden.
Første hjelpemetode behandler et subtre (med p som rot). For hver node som passeres på vei nedover mot venstre, finner vi dens forgjenger i inorden og i den settes høyrereferanse (som er null fra før) til å referere til noden. Med andre ord trekeks det for hver slik node en «tråd» Metoden returnerer den som ligger lengst ned til venstre:
private static <T> Node<T> trekkTråderInorden(Node<T> p) { while (p.venstre != null) { Node<T> q = p.venstre; while (q.høyre != null) q = q.høyre; q.høyre = p; // q er forgjengeren til p p = p.venstre; } return p; } Programkode 5.1.17 a)
Neste hjelpemetode skal avgjøre om høyrereferanse i en node går til høyre barn eller til den neste i inorden. Anta at p lik q.høyre og at r er lik p.venstre. Metoden skal avgjøre om det er mulig å komme fra r til q ved å gå nedover mot høyre. I så fall returneres true.
private static <T> boolean fraTilInorden(Node<T> r, Node<T> q) { while (r != null && r != q) r = r.høyre; return r != null; } Programkode 5.1.17 b)
Dette setter vi sammen til en metode som traverserer treet i inorden:
public void inordenMorris(Oppgave<? super T> oppgave) { if (rot == null) return; for (Node<T> p = trekkTråderInorden(rot);;) { oppgave.utførOppgave(p.verdi); Node<T> q = p; if ((p = p.høyre) == null) return; if (p.venstre != null) { if (fraTilInorden(p.venstre,q)) q.høyre = null; // kutter tråden else p = trekkTråderInorden(p); } } } Programkode 5.1.17 c)
Det er også mulig å lage traverseringer i preorden og postorden ved hjelp av samme type idé som over. I preorden må vi oppover i treet fra bladnodene. Da kan høyrereferanse brukes til å etablere en tråd og venstrereferanse kan signalisere at det går en tråd fra noden. Som i inorden må tråden «kappes» når noden forlates. Se Oppgave 3.
| 1. | Lag et program som tester effektiviten til metoden inordenMorris. |
| 2. | Lag metoden public void omvendtInordenMorris(Oppgave<? super T> oppgave).
Den skal traversere treet i omvendt inorden. Metoden skal være iterativ, uten en stakk
eller ekstra variabler i nodene.
|
| 3. | Lag en iterativ metode som traverserer et binærtre i preorden uten at bruk av en stakk eller ekstra variabler i nodene. I preorden er det kun fra bladnoder at vi må oppover i treet for å finne den neste i rekkefølgen. I en bladnode kan en la venstre referanse gå til en fast hjelpenode for å markere at høyre referanse går til neste i preorden. Dette minner om et tredd tre der en ekstra variabel i noden ble brukt til samme formål. Når vi under traverseringen kommer til en node p som har både venstre og høyre barn, vil høyre barn være neste i preorden i forhold til den bladnoden som ligger lengst ned til høyre i p sitt venstre subtre. Før vi går videre må det derfor lages en «tråd» for å opprette den forbindelsen, og tråden må kappes når vi senere kommer til p sin høyre. Treet skal være nøyaktig som det var etter at traverseringen er ferdig. |
![]() 5.1.18 Binærtre som liste
5.1.18 Binærtre som liste
Grensesnittet Liste ble definert i
Delkapittel 3.2
og en liste ble betraktet som en nummerert rekkefølge av verdier - nummerert fra 0
og utover. De to mest vanlige måtene å lage en liste på er å bruke
en «dynamisk» tabell eller å bruke en referansekjede.
En «dynamisk» tabell gir normalt de mest effektive operasjonene.
En tabell har imidlertid den ulempen at når en ny verdi skal legges
inn i første del av tabellen, må mange verdier forskyves for å gi plass.
En tanke kunne derfor være å bruke et binærtre som intern datastruktur i
en listeklasse.
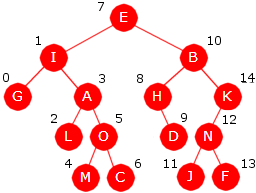
|
| Figur 5.1.18 a) : Inordennummerering |
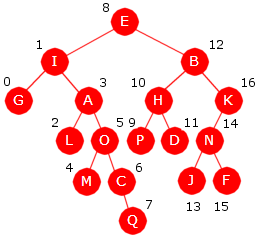
|
| Figur 5.1.18 b) : To nye verdier |
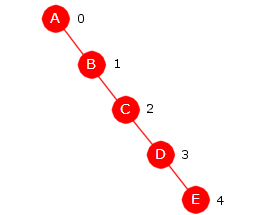
|
| Figur 5.1.18 c) : Et skjevt tre |
Treet i Figur 5.1.18 a) har 15 noder og de er nummerert i inorden. Dvs. den første i inorden er nr. 0, den neste i inorden nr. 1, osv. Kan dette brukes som en liste? La k være et nummer i intervallet [0 , n] der n er antallet noder i treet. En ny verdi legges i en bladnode. Hvor i treet må den opprettes for at den skal bli nr. k i inorden? Hvis k er 0, kan vi la noden som nå er nr. 0, få et venstre barn. Hvis k er lik n (dvs. lik 15 i figuren) kan vi la den siste noden (nr. 14 på figuren) få et et høyre barn.
Hvis 0 < k < n gjelder: Hvis nåværende node nr. k ikke har et venstre barn, skal den få et venstre barn med den nye verdien. Da blir den nr. k. Hvis nåværende node nr. k har et venstre barn, går vi til node nr. k - 1. Det er den noden som ligger lengst ned til høyre i det venstre subtreet til node nr. k. Denne noden skal få et høyre barn med den nye verdien. Dermed blir den nr. k i inorden.
Eksempel: P skal inn i treet i Figur 5.1.18 a) slik at den blir nr. 8 i inorden. Nåværende nr. 8 har ikke venstre barn. Vi kan legge P der. Q skal så inn slik at den blir nr. 7. Nåværende nr. 7 har et venstre barn. Da legger vi inn Q som høyre barn til nr. 6.
Et problem: Lister brukes ofte på den måten at nye verdier legges bak de som er der fra før. Oppskriften sier da at det skal opprettes en node som høyre barn til den som fra før var sist i inorden. Det vil gjøre treet ekstremt høyreskjevt, dvs. at ingen noder får venstre barn. Da blir treet egentlig en referansekjede og en innlegging bakerst får orden n.
Et binærtre med høyde av orden log2 (n) er godt balansert, dvs. ingen node ligger langt fra roten. Et ekstremt høyreskjevt tre er imidlertid så ubalansert som mulig. Nå finnes det teknikker for å fortløpende holde et tre balansert. Se Delkapittel 9. Vi venter imidlertid til senere med slike teknikker.
Det er lett å se på en tegning hvor en verdi må plasseres for at den skal få et bestemt nr. i inorden. Men hvordan løser vi det datateknisk? La hver node få en ekstra heltallsvariabel med navn vantall. Den skal inneholde.antallet noder i nodens venstre subtre. Klassen BinTreListe implementerer grensesnittet Liste og bruker et binærtre som intern datastruktur:
public class BinTreListe<T> // implements Liste<T> { private static final class Node<T> // nodeklasse for BinTreListe { private T verdi; // nodens verdi private Node<T> venstre, høyre; // nodens to barn private int vantall; // antall noder i venstre subtre private Node(T verdi) // konstruktør { this.verdi = verdi; venstre = høyre = null; vantall = 0; } } private Node<T> rot; // treets rot private int antall; // antallet verdier private Node<T> hentNode(int indeks) // posisjon indeks i inorden { return null; // foreløpig kode } public BinTreListe() // standardkonstruktør { rot = null; antall = 0; } public int antall() // antall verdier i treet { return antall; } public boolean tom() // er treet tomt? { return antall == 0; } public boolean leggInn(T verdi) // ny verdi bakerst { return false; // foreløpig kode } public void leggInn(int indeks, T verdi) // ny verdi på oppgitt plass { // kode mangler } } Programkode 5.1.18 a)
Grensesnittet
Liste inneholder
flere metoder enn de som er satt opp i vår klasse BinTreListe. Øverst i klassen er
derfor kravet implements Liste<T> midlertidig kommentert vekk. Hvis ikke vil
kompilatoren komme med feilmeldinger inntil alle metodene er klare..
Metoden leggInn(T verdi) skal legge verdi bakerst i listen, dvs.
sist i inorden. Det betyr at den siste noden i inorden må få et høyre barn.
Ingen av noden på veien dit vil få flere noder enn de har fra før i sitt venstre subtre. Dermed
skal ikke variabelen vantall oppdateres:
public boolean leggInn(T verdi) { if (rot == null) rot = new Node<>(verdi); else { Node<T> p = rot; while (p.høyre != null) p = p.høyre; p.høyre = new Node<>(verdi); } antall++; return true; } Programkode 5.1.18 b)
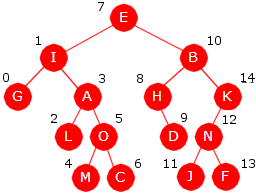
|
| Figur 5.1.18 d) : Et binærtre |
Vi må finne noden som har posisjon indeks i inorden. Se på treet i Figur 5.1.18 b) til venstre. I rotnoden må variabelen vantall ha verdien 7 siden det er 7 noder i det venstre subtreet. Med andre ord må alle noder med indekser mindre enn rot.vantall ligge i venstre subtre og de med indekser som er større, i høyre subtre. Skal vi f.eks. finnen noden med indeks 12, må vi derfor gå fra rotnoden og til B-noden. Ser vi isolert på subtreet med B-noden som rot, vil noden vi leter etter (N-noden) ha indeks 4 i det treet. Tallet 4 oppstår slik: 12 - (7 + 1) der 7 er antallet i venstre subtre til E-noden. Osv. Det betyr at indeks endres når vi går til høyre:
private Node<T> hentNode(int indeks) // posisjon indeks i inorden { Node<T> p = rot; // starter i roten while (true) { if (indeks < p.vantall) p = p.venstre; // går til venstre else if (indeks > p.vantall) { indeks -= (p.vantall + 1); // indeks endres p = p.høyre; // går til høyre } else return p; // noden er funnet } } Programkode 5.1.18 c)
Når en verdi skal inn på plass indeks i treet, bruker vi samme idé som i metoden hentNode(). I tillegg må variabelen vantall økes når vi går til venstre siden det venstre subtreet da får en ny node. En hjelpevariabel venstre holder rede på om vi går til venstre eller høyre. Den brueks til slutt for å avgjøre om det skal lages et venstre barn eller et høyre barn:
public void leggInn(int indeks, T verdi) { if (indeks < 0 || indeks > antall) throw new IndexOutOfBoundsException("Ulovlig indeks!"); Node<T> p = rot, q = null; // hjelpevariabler boolean venstre = true; // hjelpevariabel while (p != null) { q = p; // q skal være forelder til p if (indeks <= p.vantall) { p.vantall++; // ny node i venstre subtre venstre = true; p = p.venstre; } else { indeks -= (p.vantall + 1); venstre = false; p = p.høyre; } } p = new Node<>(verdi); if (q == null) rot = p; else if (venstre) q.venstre = p; else q.høyre = p; antall++; // ny node i treet } Programkode 5.1.18 d)
Det er enkelt å sjekke etterpå om en verdi kom på rett indeks i listen, dvs. på rett plass
i inorden i treet. Metoden public T hent(int indeks) som ligger i grensesnittet
Liste, gjør det. Den kan
enkelt kodes ved hjelp av metoden i Programkode 5.1.18 c):
public T hent(int indeks) { if (indeks < 0 || indeks >= antall) throw new IndexOutOfBoundsException("Ulovlig indeks!"); return hentNode(indeks).verdi; } Programkode 5.1.18 e)
Eksempel: Flg. kode bygger opp treet i Figur 5.1.18 a) og b):
BinTreListe<Character> liste = new BinTreListe<>(); int[] indeks = {0,0,2,0,2,4,6,2,4,7,9,4,6,11,13}; char[] verdi = "EIBGAHKLODNMCJF".toCharArray(); for (int i = 0; i < indeks.length; i++) liste.leggInn(indeks[i],verdi[i]); liste.leggInn(8,'P'); // P som ny nr. 8 liste.leggInn(7,'Q'); // Q som ny nr. 7 for (int i = 0; i < liste.antall(); i++) System.out.print(liste.hent(i) + " "); Programkode 5.1.18 f)
Hvor effektivt er det å bruke et binærtre til å implementere en liste? La n være antallet noder. Hvis treet ikke er skjevt, dvs høyden er av orden log2(n), vil alle metodene som bruker posisjoner også være av orden log2(n). De metodene der det søkes etter en bestemt verdi blir imidlertid av orden n. I slike tilfeller må treet traverseres i en eller annen rekkefølge for å finne verdien.
Konklusjon: Inntil videre er det ikke noe lurt å bruke et binærtre til å implementere en liste siden treet kan bli skjevt. Det kan overvinnes hvis vi rebalanserer treet når det måtte være nødvendig. Dette tas opp i Delkapittel 9 om Balanserte søketrær.
Det er flere metoder klassen må ha for at den skal implementere grensesnittet Liste. Se oppgavene. Vi avslutter her med en kort diskusjon om hvordan fjern-metoden kan lages. Etter at en verdi med et bestemt nr. i inorden er fjernet, skal den innbyrdes rekkefølgen mellom de øvrige verdiene være som før. Dette kan vi få til ved å dele det opp i to tilfeller. Anta at vi skal fjerne verdien som er nr. k og at treet har n noder. Da må 0 <= k < n:
- Hvis node nr. k i inorden ikke har venstre barn, fjernes verdien ved at referansen fra nodens forelder settes til å vise til nodens høyre subtre.
- Hvis noden har et venstre barn, erstatter vi verdien med verdien i nodens forgjenger i inorden (node nr. k - 1) og fjerner så denne noden.
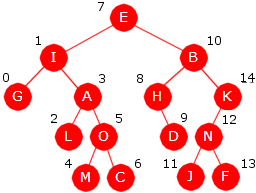
|
| Figur 5.1.18 e) : Et binærtre |
Eksempel: Hvis vi skal fjerne node nr. 8 (dvs. H-noden) i Figur 5.1.18 e), settes venstre referanse i foreldernoden (B-noden) til å gå til D-noden. Da vil innbyrdes rekkefølge (i inorden) bevares for resten av verdiene. Hvis vi skal fjerne node nr. 7 (E-noden) fjerner vi isteden node nr. 6 (C-noden) og C legges inn på plassen til E. Dermed forsvinner E. Det å fjerne forgjengeren til en node er mulig siden forgjengeren ikke har et høyre barn. Også her vil innbyrdes rekkefølge for resten av verdiene bevares. En må også huske å oppdatere variablen vantall i hver node som berøres og variablen antall i treet.
| 1. | Vis ved å tegne at Programkode 5.1.18 f) bygger opp treet i Figur 5.1.18 a) og b). |
| 2. | Ta utgangspunkt i treet i Figur 5.1.18 b) og utfør fortløpende flg. innlegginger på en tegning: R som nr. 0, S som nr. 18, T som nr. 2. Slett så nr. 10, deretter nr. 4 og igjen nr. 4. Hvordan ser treet ut nå? |
| 3. | Lag kode som bygger opp et tre som er isomorft med det i Figur 5.1.18 a) og med de sammen verdiene, men slik at de kommer sortert i inorden. |
| 4. | Legg klassen BinTreListe i Programkode 5.1.18 a) inn i ditt programsystem. Legg også inn de metodene som er kodet. |
| 5. | Legg inn de metodene fra grensesnittet
Liste
som mangler i BinTreListe. Gi dem foreløpig kode slik at kompilatoren blir fornøyd. Ta vekk kommentartegnet øverst slik
at det står public class BinTreListe<T> implements Liste<T>.
|
| 6. | Koden til public boolean innneholder(T verdi) fra
Programkode 5.1.12 c) kan brukes uforandret
i klassen BinTreListe. Gjør imidlertid de endringene som trengs for at null-verdier er
tillatt.
|
| 7. | Klassen InordenIterator kan brukes i
BinTreListe. Metoden iterator() skal returnere en instans av klassen.
|
| 8. | Lag metoden public T oppdater(int indeks, T verdi).
Den skal oppdatere verdien på plass indeks og returnere den
gamle verdien. Hvis indeks er ulovlig
skal det kastes et unntak. Bruk hentNode fra
Programkode 5.1.18 c) i kodingen.
|
| 9. | Lag metoden public T fjern(int indeks). Den skal fjerne
(og returnere) den verdien som er nr. indeks i inorden. Hvis
indeks er ulovlig skal det kastes et unntak. Se teksten over når det gjelder hvordan den
skal implementeres.
|
| 10. | Lag metoden public int indeksTil(T verdi). Hvis verdi
ligger i treet skal den returnere hvilket nr. i inorden. Hvis det er flere forkomster
skal det laveste nummeret returneres. Hvis verdi ikke ligger i treet returneres -1.
Lag både en rekursiv og en iterativ versjon.
|
| 11. | Lag metoden public boolean fjern(T verdi). Den skal fjerne
verdi fra listen. Hvis verdi forekommer flere ganger, skal den første av dem
fjernes. Metoden skal returnere true hvis fjerningen var vellykket og false ellers.
|
| 12. | Lag metoden public void nullstill(). Lag metoden ved hjelp av en postorden
traversering der verdier og referanser nulles.
|
| 13. | Lag metoden public String toString(). Hvis treet f.eks. inneholder verdiene A, B og C i inorden, skal metoden returnere strengen "[A, B, C]". |

|