![]() 1.7.1 Biter og bitsekvenser
1.7.1 Biter og bitsekvenser
Enheten bit har verdien 0 eller 1. På norsk betyr
ordet bit en liten del - f.eks. en sjokoladebit eller en bit i et puslespill.
Ordet bit brukt i databehandling har
en annen opprinnelse. Ordet er konstruert og består av de to
første og siste bokstav i «binary digit» (binært siffer).
Men også i databehandling kan en bit ses på som en liten del. Det er
den minste mulige enheten for lagring av dataverdier. Obs: Vi vil
konsekvent bruke biter (ikke bits) som flertall for bit.
| 0 | 1 | |
| 0-bit og 1-bit | ||
En bitsekvens (eng: bit string) er en ordnet sekvens med én eller flere (eller ingen) biter. Den kan gjerne ha en eller flere 0-biter i starten. I noen sammenhenger gir det også mening å snakke om en bitsekvens uten biter. Det kalles en tom sekvens. Eksempler:
1, 0, 101, 0101010, 00101000111, 100100101110101000
Hvor mange forskjellige bitsekvenser finnes det? En bitsekvens med nøyaktig n biter kan ha 0 eller 1 først, 0 eller 1 på neste plass, osv. Det betyr 2 · 2 · . . . · 2 = 2n muligheter. Med andre ord finnes det 2n forskjellige bitsekvenser med n biter. Hvor mange er det som har n eller færre biter? Hvis vi regner med den tomme bitsekvensen blir det:
For eksempel finnes det 25 = 32 forskjellige bitsekvenser med nøyaktig 5 biter og 26 – 1 = 63 med 5 eller færre biter.
(1.7.1.1) Det finnes 2n forskjellige bitsekvenser med n biter,
n ≥ 0.
(1.7.1.2) Det finnes 2n+1 – 1 forskjellige bitsekvenser
med n eller færre biter, n ≥ 0.
En int-tabell kan brukes til å representere en bitsekvens. Ta den siste bitsekvensen i oppramsinger over, dvs. 100100101110101000. Den kan representeres kodemessig slik:
int[] s = {1,0,0,1,0,0,1,0,1,1,1,0,1,0,1,0,0,0}; |
| Java-kode for int-tabell |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| Figur 1.7.1 a) : En bitsekvens med 18 biter tegnet som en tabell | |||||||||||||||||
Det er imidlertid sløsing med ressurser å bruke en int-tabell til å representere en bitsekvens. Hvert tabellelement er selv en int og har med sine 32 biter plass til mye mer enn bare verdiene 0 og 1. Noe bedre er det å bruke en variabel av typen String:
String s = "100100101110101000";
En String-variabel bruker en char-tabell som intern lagringsstruktur og hvert tegn i tegnstrengen er dermed en char og bruker 16 biter. Da sløser vi noe mindre med ressursene enn om vi bruker en int-tabell.
En tredje mulighet er å bruke en byte-tabell til å representere en bitsekvens, men også da sløser vi litt. Hvert element i tabellen er da en byte (8 biter):
byte[] s = {1,0,0,1,0,0,1,0,1,1,1,0,1,0,1,0,0,0};
Verdiene 1 og 0 kan tolkes som sann og usann (eng: true, false). Dermed kan vi også bruke en boolean-tabell til å representere en bitsekvens. F.eks. kan bitsekvensen 01100011 representeres slik:
boolean[] s = {false,true,true,false,false,false,true,true};
Nå er det imidlertid ikke noe å vinne ressursmessig på å bruke en boolean-tabell fremfor en byte-tabell. I Java bruker både boolean og byte 8 biter.
Det finnes langt mer effektive (effektive med hensyn på plass) måter å representere en bitsekvens på enn de måtene vi har sett på her. Det beste er å la den være representert ved hjelp av bitene i en int-variabel. Det skal vi se nærmere på i senere avsnitt.
| 1. | Hvor mange forskjellige bitsekvenser er det som har 2 eller færre biter. Skriv dem opp. |
| 2. | Hvor mange forskjellige bitsekvenser er det som har nøyaktig 3 biter. Skriv dem opp. |
| 3. | Hvor mange forskjellige bitsekvenser er det som har 10 eller færre biter? |
| 4. | Lag metoden public static boolean[] tilBoolean(String s). Bitsekvensen
representert ved strengen s skal gjøres om til en boolean-tabell. Hvis
s ikke er en bitsekvens (et eller flere tegn i s er forskjellig fra 0/1),
skal det kastes en IllegalArgumentException. |
| 5. | Klassen String inneholder instansmetoden getBytes().
Hva vil byte-tabellen b inneholde
hvis setningen byte[] b = "10011101".getBytes(); utføres? |
| 6. | Bitsekvensen 00100100101110101000 har 20 biter. Den kan representeres ved hjelp av to int-variabler. Den første skal inneholde en verdi som forteller hvor mange biter sekvensen har. Her blir det tallet 20. Den andre skal inneholde de 20 gitte bitene som de 20 bakerste bitene. Hvordan vil du få til det? Lag et program som gjør dette. La programmet ha en utskrift som viser at det hele ble riktig. |
![]() 1.7.2 Heltall og bitsekvenser
1.7.2 Heltall og bitsekvenser
En vilkårlig bitsekvens kan tolkes som et binært heltall og da kalles bitene
binære siffer. Hvis en bitsekvens har én eller flere 0-biter i starten, kalles
0-bitene frem til første 1-bit for ledende 0-biter eller ledende 0-er
(eng: leading zeros). Første 1-bit
(fra venstre) kalles tallets første og mest signifikante siffer. Ordet signifikant
betyr «å være av betydning», dvs. ledende 0-biter er ikke av betydning
når dette tolkes som et heltall. Bitene fra og med første 1-bit kalles de signifikante sifrene.
Vi får et spesialtilfelle hvis alle bitene i sekvensen er 0-biter. Da er det vanlig å si at alle bitene, bortsett fra den siste, er ledende 0-biter. Hele sekvensen blir da tolket som tallet 0. I det tilfellet kalles den siste 0-biten for tallets første og eneste signifikante siffer.
Eksempel: Gitt de to bitsekvensene 00110010 og 110010. Tolket som heltall er disse to like siden vi får den andre sekvensen ved å fjerne de ledende 0-ene i den første. I sekvensen 110010 er 1-biten lengst til venstre tallets mest signifikante siffer og 0-biten lengst til høyre tallets minst signifikante siffer. Navnene på disse begrepene høres rimelige ut. Hvis vi endrer på det minst signifikante sifferet vil tallets verdi bare forandre seg med 1. Men hvis vi endrer det mest signifikante sifferet (fra 1 til 0) vil tallets verdi endre seg svært mye.
Det er ofte aktuelt å konvertere fra binære til desimale siffer ( dvs. til 10-tallssystemet). Gitt sekvensen eller det binære tallet 110010. Det har 6 binære siffer og konverteres slik:
(1.7.2.1) 110010 = 1 · 25 + 1 · 24+ 0 · 23 + 0 · 22 + 1 · 21 + 0 · 20 = 32 + 16 + 2 = 50
Obs. Hvis tallformatene ikke fremgår av sammenhengen, er det vanlig å skrive 1100102 istedenfor 110010 og 5010 istedenfor 50 for å markere at det første er et binært tall (grunntall 2) og det andre et desimalt tall (grunntall 10).
Java har flere ferdige metoder for å konvertere en bitsekvens til et heltall på desimalform hvis bitsekvensen er gitt som en tegnstreng. Vi kan konvertere både til byte, short, int og long. I flg. eksempel konverteres det til int og byte:
String s = "110010"; int n = Integer.parseInt(s,2); byte b = Byte.parseByte(s,2); System.out.println(n + " " + b); // Utskrift: 50 50 Programkode 1.7.2 a)
Klassemetoden parseInt (fra klassene Integer og Byte) har to parametere - en tegnstreng og et grunntall (eng: radix). I Programkode 1.7.2 a) brukes 2 som grunntall. Dermed forventes det at tegnstrengen s kun har binære «siffer», dvs. kun inneholder tegnene '0' og '1'. Hvis det forekommer andre tegn kastes en NumberFormatException. Det er imidlertid tillatt med '–' helt først. Da blir s tolket som et negativt tall. Det kastes også et unntak hvis antallet binære siffer er så stort at det tilhørende heltallet blir for stort for den tilhørende datatypen (int, byte). Det hoppes over eventuelle ledende 0-er. Se flg. eksempel:
String s1 = "110010", s2 = "00110010", s3 = "–00110010"; int n1 = Integer.parseInt(s1,2); // konverterer 110010 int n2 = Integer.parseInt(s2,2); // konverterer 00110010 int n3 = Integer.parseInt(s3,2); // konverterer –00110010 System.out.println(n1 + " " + n2 + " " + n3); // Utskrift: 50 50 –50 Programkode 1.7.2 b)
Det finnes en enkel og effektiv algoritme for å konvertere fra binære til desimale siffer. Den kalles Horners regel. Gitt bitsekvensen 110010. Summen (potensrekken) i regnestykket (1.7.2.1) over kan regnes ut på en annen måte:
Dette blir klarere hvis vi tenker oss at 110010 er gitt som en tegnstreng s med tegnene (fra venstre) s0 , s1 , . . . , s5. Horners regel gir da denne omregningsformelen:
Dvs. vi starter med s0 , ganger så med 2 og legger til s1 , ganger så resultatet med 2 og legger til s2 , osv. Dette kan lett gjøres om til programkode:
public static int parseBitInt(String s) { int k = s.charAt(0) == '0' ? 0 : 1; // starter med s[0] for (int i = 1, n = s.length(); i < n; i++) { k *= 2; // ganger med 2 if (s.charAt(i) == '1') k += 1; // legger til s[i] } return k; } Programkode 1.7.2 c)
Programkode 1.7.2 c) gjør det samme som parseInt med grunntall 2 (se også Oppgave 2):
String s1 = "110010", s2 = "00110010"; int n1 = parseBitInt(s1); // konverterer 110010 int n2 = parseBitInt(s2); // konverterer 00110010 System.out.println(n1 + " " + n2); // Utskrift: 50 50 Programkode 1.7.2 d)
Det er også aktuelt å kunne gå den omvendte veien, dvs. konvertere fra et heltall på desimalform til en bitsekvens. Java har ferdige metoder for dette. Se flg. eksempel:
int n = 50; String s1 = Integer.toBinaryString(n); String s2 = Integer.toString(n,2); System.out.println(s1 + " " + s2); // Utskrift: 110010 110010 Programkode 1.7.2 e)
I metoden toBinaryString sier navnet hva som skjer. Metoden toString er mer generell. Hvis vi bruker 2 som grunntall (eng: radix) får vi konvertert heltallet til en bitsekvens.
OBS: toBinaryString bruker 2-komplement for negative tall, mens toString returnerer bitsekvensen til tallverdien med et minustegn foran:
int n = -50; // et negativt tall String s1 = Integer.toBinaryString(n); // bruker 2-komplement String s2 = Integer.toString(n,2); // setter minus-tegn først System.out.println(s1 + " " + s2); // Utskrift: 11111111111111111111111111001110 -110010 Programkode 1.7.2 f)
I Figur 1.7.2 a) under er den negative bitsekvensen –110010 tegnet som en tabell med fortegnet lengst til venstre:
| − | 1 | 1 | 0 | 0 | 1 | 0 |
| Figur 1.7.2 a) : Minustegn | ||||||
Metoden toString setter, som utskriften i Programkode 1.7.2 f) over viser, et minustegn aller først i tegnstrengen. Men toBinaryString bruker en annen teknikk. Det kalles 2-komplement. Det skal vi se nøyere på i Avsnitt 1.7.5.
Algoritmen for å konvertere et positivt heltall til en bitsekvens er ganske enkel. Gitt tallet n = 12345. Da vet vi at n % 10 gir oss det siste desimale sifferet i n (dvs. 5) fordi n % 10 gir oss resten når n heltallsdivideres med 10. Videre vil n/10 gi oss det antallet ganger 10 går opp i n. Her blir det 1234 som er det samme som å fjerne det siste sifferet i n. De binære sifrene finnes på samme måte, men da deler vi med 2 istedenfor med 10. Flg. regler gjelder når n er et ikke-negativt (dvs. n ≥ 0) heltall:
1. Divisjonen n % 2 (resten når n deles med 2) gir siste binære siffer i n.
2. Divisjonen n / 2 (antall ganger 2 går opp) fjerner siste binære siffer i n.
Dette kan vi bruke til å lage en konverteringsalgoritme. Det er imidlertid et lite problem. Algoritmen gir oss de binære sifrene i motsatt rekkefølge enn den vi ønsker. Det kan vi enten løse ved hjelp av rekursjon eller ved å mellomlagre sifrene og så snu rekkefølgen. Flg. eksempel viser den siste måten å gjøre det på:
public static String tilBinærStreng(int n) // n må være ikke-negativ { if (n < 0) throw new IllegalArgumentException("Parameter n(" + n + ") er negativ!"); if (n == 0) return "" + 0; StringBuilder b = new StringBuilder(); while (n > 0) { if (n % 2 == 1) b.append('1'); else b.append('0'); n /= 2; } return b.reverse().toString(); // må snu siffer-rekkefølgen } Programkode 1.7.2 g)
I while-løkken i Programkode 1.7.2 g) legges de binære sifrene (egentlig tegnene '0' og '1') fortløpende inn i en StringBuilder. Men de legges inn i omvendt rekkefølge av det som er ønskelig. Siste sifferet legges inn først, så det nest siste sifferet, osv. Men innholdet i en StringBuilder kan snus (reverseres). Ved å gjøre det får vi rett rekkefølge.
| 1. | Gjør om (med hoderegning) følgende bitsekvenser til heltall på desimal form: i) 101010, ii) 11111 og iii) 010101. Bruk både vanlig teknikk og Horners regel. |
| 2. | Metoden parseBitInt i Programkode 1.7.2 c) skal virke som metoden parseInt (med grunntall 2) i klassen Integer. Men den er ikke robust slik den nå er kodet. Utvid metoden slik at den kaster en NumberFormatException hvis s inneholder noe annet enn '0' og '1'. Første tegnet i s kan imidlertid være '-' og i så fall skal det tolkes som et negativt tall. Det skal heller ikke «renne over» (eng: overflow). Hvis s representerer et tall som er for stort for datatypen int skal det kastes en NumberFormatException. |
| 3. | Finn (ved å bruke papir og blyant) de binære sifrene til følgende heltall, dvs. konverter dem til bitsekvenser: i) 123, ii) 1234 og iii) 12345. |
| 4. | Lag en rekursiv versjon av tilBinærStreng-metoden i Programkode 1.7.2 g). Da kan sifrene legges inn i en StringBuilder i rett rekkefølge. Dermed behøver den ikke snus til slutt. Se Delkapittel 1.5 når det gjelder rekursjon. |
| 5. | Lag en versjon av tilBinærStreng-metoden i Programkode 1.7.2 g) som også behandler negative heltall. Da skal tegnstrengen som metoden returnerer starte med et minus-tegn, dvs. virke slik som toString-metoden i klassen Integer. |
![]() 1.7.3 Binæraritmetikk
1.7.3 Binæraritmetikk
To bitsekvenser kan adderes som heltall. Dette kan vi få til ved først å konvertere
sekvensene til heltall på desimalform (10-tallssystemet), så addere dem på vanlig måte
og til slutt gjøre om svaret til en bitsekvens. Men dette er en stor omvei.
Hvert siffer er 0 eller 1. En addisjon kan dermed utføres direkte
gjennom å addere hvert sifferpar (fra høyre mot venstre) ved å bruke flg. regler:
0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 (0 og 1 i mente)
Når vi bruker mente vil det kunne bli tre sifre. Da kan vi bruke flg. utvidelse av regelen over:
1 + 0 + 0 = 1 1 + 1 + 0 = 10 1 + 0 + 1 = 10 1 + 1 + 1 = 11 (1 og 1 i mente)
La flg. to bitsekvenser være gitt. Den første har 10 biter og den andre 8 biter:
1 0 1 0 1 1 0 0 1 1 1 1 0 1 0 1 1 0
I flg. regnestykke er mentene satt på over den første bitsekvensen:
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| + | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | ||
| = | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Figur 1.7.3 a) : Addisjon med binæraritmetikk | ||||||||||
Subtraksjon foregår på en tilsvarende måte. Her må vi kunne, som det heter, «låne» fra en nabo til venstre. Det gjør subtraksjon litt mer komplisert enn addisjon. I flg. regnestykke finner vi differansen mellom de samme to tallene som i Figur 1.7.3 a) over. Sifrene vi «låner» fra er overstreket. En overstreket 1-er blir en 0. «Lånene» er plassert over de neste sifrene:
| 1 | 2 | 2 | 2 | 1 | 2 | |||||
| 0 | 0 | 0 | 0 | 1 | 1 | |||||
| − | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | ||
| = | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | |
| Figur 1.7.3 b) : Subtraktsjon med binæraritmetikk | ||||||||||
| 1. | Utfør addisjonen i Figur 1.7.3 a) ved først å konvertere bitsekvensene til heltall på desimalform, så legge dem sammen og til slutt konvertere summen til en bitsekvens. Sjekk at du får samme resultat som i Figur 1.7.3 a). |
| 2. | Sjekk at svaret i Figur 1.7.3 b) stemmer ved å addere (bruk binæraritmetikk) svaret og den andre bitsekvensen. Da skal du få den første bitsekvensen. |
| 3. | La m = 11110000110 og n = 10101110110. Finn m + n og m – n ved binæraritmetikk slik som i Figur 1.7.3 a) og b). |
| 4. | La m = 100110011011 og n = 1111111111. Gjør som i Oppgave 3. |
![]() 1.7.4 Fast bitformat
1.7.4 Fast bitformat
Enkeltvariabler av typene byte, short, int eller long kan brukes til
å representere bitsekvenser på en svært effektiv måte.
| Datatype | Antall biter | Minste verdi | Største verdi |
| byte | 8 | −128 | 127 |
| short | 16 | −32.768 | 32.767 |
| int | 32 | −2.147.483.648 | 2.147.483.647 |
| long | 64 | −9.223.372.036.854.775.808 | 9.223.372.036.854.775.807 |
| Figur 1.7.4 a) : Oversikt over heltallstypene i Java | |||
|---|---|---|---|
En variabel av en av de fire heltallstypene kan betraktes både som en bitsekvens og som et heltall. Vi bruker her byte som eksempel:
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Figur 1.7.4 b) : Innholdet i en byte | |||||||
Datatypen byte har et fast bitformat på 8 biter. Figur 1.7.4 b) viser hva en slik variabel kan inneholde. Tolket som en bitsekvens er dette rett og slett sekvensen 00110010. Når innholdet av en byte settes opp på tabellform slik som i Figur 1.7.4 b), er det vanlig å posisjonere eller indeksere bitene fra høyre mot venstre. Biten lengst til venstre kalles fortsatt første bit og den lengst til høyre siste bit. Men nå har siste bit posisjon 0, nest siste bit posisjon 1, osv. Altså det omvendte av hva vi gjør for vanlige tabeller.
Hvis dette tolkes som et heltall, kalles det som før et binært tall og bitene kalles binære siffer. Vi skiller skarpt mellom to tilfeller:
- Hvis første bit er en 0-bit, representerer bitsekvensen et ikke-negativt heltall.
- Hvis første bit er en 1-bit representerer bitsekvensen et negativt heltall.
OBS. Et ikke-negativt tall er enten lik 0 eller er positivt (større enn 0).
Det er vanlig, når vi har fast bitformat, å kalle den første biten i bitsekvensen for en fortegnsbit. Innholdet i byte-variablen i i Figur 1.7.4 b) representerer dermed et ikke-negativt tall. Vi ser nærmere på negative heltall i Avsnitt 1.7.5.
Bitsekvensen i en byte-variabel er som en bitsekvens ikke annerledes enn de vi har sett på før. Det er bare lagringsformatet som er annerledes. Dermed gjelder fortsatt begrepene fra Definisjon 1.7.2. Det samme gjelder regelen for omregning til et tall med desimale siffer. Det eneste nye er at man, siden bitene nå er indeksert fra høyre mot venstre (se Figur 1.7.4 b), noen ganger velger å sette opp potensrekken med stigende eksponenter, dvs. slik for de signifikante sifrene 110010 i byte-tallet 00110010:
Legg merke til rekkefølgen i summen over. Den svarer til at vi går fra høyre mot venstre blant de signifikante sifrene i Figur 1.7.4 b). Hvis x er et signifikant binært siffer og står i posisjon k − se Figur 1.7.4 b) − så bidrar det med x · 2k i summen over.
Heltallstypen byte har på lik linje med de andre heltallstypene, sin egen omslagsklasse (eng: wrapper class). Den heter Byte. Den inneholder både instans- og klassemetoder, og enkelte klassekonstanter. Hvis en f.eks. ikke husker hva som er største og minste mulige verdi for datatypen byte − se Figur 1.7.4 a) − kan en benytte konstantene MAX_VALUE og MIN_VALUE i class Byte. For eksempel slik:
byte max = Byte.MAX_VALUE; // maksimal byte-verdi byte min = Byte.MIN_VALUE; // minimal byte-verdi System.out.println(max + " " + min); // Utskrift: 127 -128 Programkode 1.7.4 a)
Alt det som er tatt opp her for datatypen byte gjelder også for datatypene short, int og long. Den eneste forskjellen er at de har 16, 32 og 64 biter som fast bitformat.
| 1. | Omslagsklassene for short, int og long heter Short, Integer og Long. Gjør som i Programkode 1.7.4 a) for hver av disse datatypene. |
| 2. | I Avsnitt 1.7.2 ble noen av konverteringsmetodene (konvertering mellom tegnstreng og heltall) i omslagsklasssen Integer diskutert. Også omslagsklassene Byte, Short og Long har noen slike metoder. Sett deg inn i metodene. |
![]() 1.7.5 Negative heltall
1.7.5 Negative heltall
Vi bruker også her datatypen byte som eksempel når vi diskuterer negative tall. Det er lettere
å illustrere idéene ved hjelp av tegninger når datatypen bare har 8 biter. Men de reglene og prinsippene
vi kommer frem til vil også gjelde for datatypene short, int og long.
Ta som eksempel bitsekvensen 11010101. Den har åtte biter og kan dermed ses på som en byte. I figuren under er den satt opp som en tabell:
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Figur 1.7.5 a) : Et negativt tall | |||||||
Figur 1.7.5 a) viser en byte der bitsekvensen starter med en 1-bit og som tidligere nevnt, representerer det et negativt tall. Men hvilket tall? For å finne ut det tar vi først komplementet til byte-variablen, dvs. alle bitene får et verdiskifte. En 1-bit til 0-bit og en 0-bit til 1-bit:
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Figur 1.7.5 b) : Komplementet | |||||||
Neste skritt er å øke bitsekvensens verdi med 1, dvs. å addere 1 til det binære tallet gitt ved Figur 1.7.5 b). Her må vi bruke binæraritmetikk. Først legges 1 til siste siffer (bit). Da får vi enten 1 + 0 eller 1 + 1. I tilfellet 1 + 0 = 1 er vi ferdige. I tilfellet 1 + 1 = 2, blir det 0 og i tillegg 1 i «mente». Dvs. menten legges til det nest siste sifferet. Osv. For vårt eksempel i Figur 1.7.5 b) blir resultatet dette:
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Figur 1.7.5 c) : Verdien er økt med 1 | |||||||
Bitsekvensen i Figur 1.7.5 c) som representerer et positivt tall siden fortegnsbiten er 0, gjør vi om til et tall med desimale siffer på vanlig måte:
Dette betyr at det byte-tallet vi startet med, dvs. 11010101, har verdien –43.
Et eksempel til. Flg. tall (Figur 1.7.5 d) til venstre under) er negativt siden fortegnsbiten er 1, men resten av bitene er 0-er. Komplementet (Figur 1.7.5 e) til høyre under) vil dermed ha en 0-bit først og deretter bare 1-ere:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Vi må så ved hjelp binær aritmetikk legge til 1. Vi starter med siste siffer. Det gir 1 + 1 = 2, dvs. 0 og 1 i mente. Nest siste siffer er 1 og sammen med menten blir det 1 + 1 = 2. På nytt 0 og 1 i mente. Osv. til vi kommer til første siffer. Der blir 0 + 1 = 1:
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Figur 1.7.5 f) : Verdien er økt med 1 | |||||||
Men dette ser rart ut! Bitsekvensen i Figur 1.7.5 f) er akkurat den samme som den vi startet med i Figur 1.7.5 d). Men det er ok. Vi ser på det som en bitsekvens og konverterer den til et tall på desimal form på vanlig måte:
= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 128 = 128.
Dette betyr at det byte-tallet vi startet med, dvs. 10000000, har verdien –128 og det er det minste byte-tallet. Se tabellen i Figur 1.7.4 a).
Obs. Det er bare det negative byte-tallet 10000000 som er slik at tallets komplement pluss 1 gir en fortegnsbit på 1. For alle andre negative byte-tall (dvs. med fortegnsbit lik 1) vil tallets komplement pluss 1 gi noe som er positivt (dvs. 0 som fortegnsbit).
Et siste eksempel: Hva er verdien til det negative byte-tallet 11111111? Komplementet blir 00000000 og legger vi til 1 blir det 00000001. Det betyr at 11111111 er det samme som –1.
Regelen er den samme hvis en til et gitt ikke-negativt byte-tall ønsker å finne hva bitsekvensen til tallets minusverdi er. Da vil komplementet pluss 1 gi bitsekvensen. Eksempel: Hva er bitsekvensen til –100? Vi finner først bitsekvensen til 100 (f.eks. ved å bruke Formel 1.7.2.2 flere ganger). Den er lik 01100100. Komplementet er 10011011 og når vi legger til 1 blir det 10011100. Med andre ord er bitsekvensen til –100 lik 10011100.
Omslagsklassen Byte har ingen metoder for å finne bitsekvensen til tall. Men det har omslagsklassen Integer. Datatypen int har 32 biter. Regelen for negative tall er den samme for int-tall som for byte-tall med unntak av antall biter. Hva blir bitsekvensen til –100 i int-format? Bitsekvensen til 100 er 00 . . . 01100100 der prikkene står for 22 0-er. Et int-tall har alltid 32 biter. Komplementet blir 11 . . . 10011011 der prikkene nå står for 22 1-ere. Legger vi til 1 får vi at 11 . . . 10011100 er bitsekvensen til –100. Dette kan vi sjekke med å la en Java-metode finne bitsekvensen:
String s = Integer.toBinaryString(-100); System.out.println(s); // Utskrift: 11111111111111111111111110011100 Programkode 1.7.5 a)
Flg. tabell viser bitsekvensen til en del positive og negative byte-tall, dvs. heltall med et fast bitformat på 8 biter:
|
|
|||||||||
Figur 1.7.5 g) : Bitsekvensen til noen byte-tall |
||||||||||
| 1. | Bruk 8 biter som fast bitformat, dvs. en byte. Hva blir bitsekvensen til 50 og til –50? Hvilke tall er gitt ved 01100110, ved 11110000 og ved 10001111? |
| 2. | Anta at vi har fast bitformat og at du kjenner den siste biten i bitsekvensen. Kan du da raskt avgjøre om det er et oddetall eller et partall? |
| 3. | Metoden parseInt kan kun konvertere tegnstrenger med bitsekvenser som representerer ikke-negative tall eller eventuelt starter med tegnet '–'. Lag metoden public static int parseBitInt(String s). Tegnstrengen s skal inneholde en bitsekvens. Hvis s har flere enn 32 biter kasets et unntak. Hvis s har færre en 32 biter eller har en 0-bit først, returneres resultatet av parseInt (grunntall 2) anvendt på s. Hvis s har 32 biter med første bit lik 1, lages en ny tegnstreng t som inneholder komplementet til s. Metoden returnerer så –(n + 1) der n er resultatet av å anvende parseInt (grunntall 2) på t. Bruk toBinaryString på et negativt tall til å sjekke metoden din. |
![]() 1.7.6 Konvertering mellom bitformater
1.7.6 Konvertering mellom bitformater
Hvis vi har et tall i ett bitformat kan det være aktuelt å konvertere
(eng: cast) tallet (enten implisitt eller eksplisitt) til et annet bitformat med
flere eller færre biter. Eksempel:
byte b = 100; // b har 8 biter int n = b; // n har 32 biter String s = Integer.toString(b); System.out.println(n + " " + s); // Utskrift: 100 100 Programkode 1.7.6 a)
Setningen int n = b; inneholder to forskjellige bitformater.
Her vil kompilatoren foreta en implisitt konvertering fra byte
til int (dvs. fra 8 til 32 biter). De 8 bitene i b legges bakerst.
De 24 forreste bitene blir 0-biter hvis b er ikke-negativ og 1-biter hvis
b er negativ. I metodekallet Integer.toString(b) skjer også en implisitt
konvertering. Signaturen til metoden toString i class Integer sier at
parameteren skal være av typen int, men i metodekallet brukes byte-variablen
b. Her vil kompilatoren automatisk konvertere b til en intern int-verdi.
En eksplisitt konvertering betyr at vi i koden sier i fra hva vi ønsker:
byte b = 100; int n = (int)b; Programkode 1.7.6 b)
I setningen int n = (int)b; ber vi spesifikt om at b konverteres til
en int. Deretter vil inneholdet i den bli kopiert over i n.
Konverteringer fra én heltallstype til en annen med flere biter enn den første, foregår generelt på samme måte som fra byte til int. Bitene fra den første legges bakerst i den andre. Resten fylles med 0-er eller 1-ere avhengig av fortegnsbiten til det første tallet. Dette er helt farefrie operasjoner sidene tallenes verdi bevares. Det ikke nødvendig for oss å gjøre eksplisitte konverteringer i slike tilfeller. Det overlater vi til kompilatoren.
Det er også aktuelt å kunne konvertere motsatt vei, dvs. fra én heltallstype til en annen som har færre biter enn den første:
int n = 100; // n har 32 biter byte b = n; // Kompileringsfeil: possible loss of precision Programkode 1.7.6 c)
Setningen byte b = n; gir
«possible loss of precision».
Hvis n har mer enn 8 signifikante binære sifre, vil de foran de 8 siste
fjernes, dvs. verdien vil bli endret.
Det er imidlertid tillatt å gjøre en eksplisitt konvertering, men da må man vite hva man gjør:
int n = 100; // n har 32 biter byte b = (byte)n; // eksplisitt konvertering fra int til byte System.out.println(n + " " + b); // Utskrift: 100 100 Programkode 1.7.6 d)
I den eksplisitte konverteringen i setningen byte b = (byte)n; blir de 8 siste
bitene i int-variablen n lagt over i byte-variablen b.
I Programkode 1.7.6 d) gikk dette bra siden de signifikante bitene i
tallet 100 er 1100100. Dermed blir tallet representert som 01100100 i
byte-variablen.
Flg. eksempel viser at en eksplisitt konvertering kan føre til et uventet resultat hvis en ikke er klar over hva som egentlig foregår:
int n = 128; // n = 00000000000000000000000010000000 byte b = (byte)n; // b = 10000000 System.out.println(n + " " + b); // Utskrift: 128 -128 Programkode 1.7.6 e)
Representasjonen til 128 i 32 biters format er 24 0-biter fulgt av én 1-bit og så
7 0-biter. Den eksplisitte konverteringen i byte b = (byte)n; gjør at de første
24 bitene (uansett hva som måtte ligge der) fjernes og vi står igjen med de 8 siste
bitene, og det er disse som blir innholdet i byte-variablen. Men en 1-bit og 7
0-biter i 8 biters format er et negativt tall (1 som fortegnsbit) og
representerer tallet -128. Se Figur 1.7.5 g).
Mulighetene i Java når det gjelder Regel 1.7.6 a), er fra byte til short, int eller long, fra short til int eller long, fra int til long og fra char til int eller long. Motsatt vei, dvs. fra long til byte, short eller int, fra int til byte eller short og fra short til byte, dekkes av Regel 1.7.6 b):
Som nevnt over gjør kompilatoren mange ganger implisitte konverteringer. Spesielt skjer det i programsetninger av typen aritmetiske uttrykk og andre uttrykk med en blanding av datatyper (eng: mixed mode). Et aritmetisk uttrykk er en programsetning som består av variabler, konstanter og aritmetiske operatorer:
int n = 100; short s = 50; byte b = 10; System.out.println(n + s + b - 60); // Utskrift: 100 if (s < n) System.out.println(s + " < " + n); // Utskrift: 50 < 100 Programkode 1.7.6 f)
Uttrykket n + s + b − 60 i koden over er et aritmetisk utrykk. Det består av tre variabler, tallkonstanten 60, addisjonsoperatoren + og subtraksjonsoperatoren – . Så sant et uttrykk ikke inneholder datatypen long, vil kompilatoren konvertere alt til int før regneoperasjonene utføres, og resultatet blir lagret i int-format. Dette gjelder også selv om ingen av variablene er av typen int. Java er konstruert slik at alle regneoperasjoner skjer i 32-biters format. (Hvis uttrykket inneholder noe i long-format vil alt bli konvertert til det formatet før regneoperasjonene utføres og resulatet lagres i long-format.) Også i setningen s < n blir s først konvertert til int før sammenligningen utføres.
Resultatet av regneoperasjonene, dvs. verdien til det aritmetiske uttrykket, lagres som nevnt over i int-format selv om ingen av operandene er av typen int. Eksempel:
short s1 = 100, s2 = 50, s3 = 10; short resultat = s1 + s2 + s3; // possible loss of precision Programkode 1.7.6 g)
Kompilatoren gir feilmeldingen «possible loss of precision» siden regneoperasjonene i uttrykket s1 + s2 + s3 foregår i int-format og resultatet lagres i det samme formatet. Dermed er det ikke tillatt uten videre å legge resultatet inn i short-variablen resultat. Men vi kan selv gjøre en eksplisitt konvertering, men da kan, som tidligere diskutert, «rare» ting skje. Hvis summen er et tall som på binær form ikke får plass i en short, vil noe av tallet «kappes av» - se Regel 1.7.6 b). Med andre ord må en vite hva en gjør:
short s1 = 100, s2 = 50, s3 = 10; short resultat = (short)(s1 + s2 + s3); // konvertering til short System.out.println(resultat); // Utskrift: 160 Programkode 1.7.6 h)
Vi kan trekke flg. konklusjoner angående konverteringer:
- Det er helt farefritt å konvertere fra et «lite» bitformat til et som er «større». Det gjøres automatisk av kompilatoren en serie ganger uten at vi eksplisitt ber om det. Det er normalt ikke behov for at vi gjør det selv.
- Det forekommer aldri implisitt konvertering fra et «stort» bitformat til et som er «mindre». Kompilatoren hindrer det og gir feilmeldingen «possible loss of precision».
- Det er mulig å gjøre eksplisitt konvertering fra et «stort» bitformat til et som er «mindre». Men da må en være klar over hvordan konverteringen foregår og hvilke effekter den kan ha. Med andre gjør en da dette på «eget ansvar».
Datatypen char er til nå ikke tatt med i diskusjonen. Den har et 16-biters format, men er egentlig ingen heltallstype. Den kan likevel inngå både i aritmetiske uttrykk og i andre sammenhenger der det forventes en int eller long (dvs. implisitt konvertering):
char c = 'A'; int n = 'B'; char d = 67; int sum = c + d; for (char a = 'A'; a <= 'Z'; a++) System.out.print(a); System.out.println(", " + c + " " + n + " " + d + " " + sum); // Utskrift: ABCDEFGHIJKLMNOPQRSTUVWXYZ, A 66 C 132 Programkode 1.7.6 i)
Implisitt konvertering fra en heltallstype (byte, short, int, long)
til char forekommer ikke. I setningen
char d = 67;
i Programkode 1.7.6 i) kan det se ut som at det skjer en implisitt
konvertering fra int til char. Men her tolkes 67 som en
lovlig unicode-verdi. Også setningen
char d = 65535; er lovlig siden tallkonstanten
65535 er største mulige unicode-verdi. Men setningen
char d = 65536; er ulovlig.
char d = 65536; // Type mismatch: cannot convert from int to char
Hvis en ønsker å konvertere fra en heltallstype til char må det skje eksplisitt:
int k = 65; char c = k; // Type mismatch: cannot convert from int to char char d = (char)k; // lovlig - eksplisitt konvertering, d = 'A' char e = (char)65601; // lovlig - eksplisitt konvertering, e = 'A' Programkode 1.7.6 j)
Hvorfor blir e lik bokstaven 'A' i koden over? Bitkoden til tallet 65601 har flg. 17 signifikante binære siffer: 10000000001000001. Men datatypen char har kun 16 binære siffer. Konverteringen fjerner derfor det første sifferet. Da blir det igjen 0000000001000001 eller 1000001 hvis en kun tar med de signifikante sifrene. Men 1000001 er binærkoden til tallet 65 som igjen svarer til 'A'.
| 1. | Sett n lik 255 i Programkode 1.7.6 d). Finn ut på forhånd, dvs. før programmet kjøres, hva utskriften vil bli. |
| 2. | Gjør som i oppgave 1, men sett n lik det tallet som har først 23 0-biter, så en 1-bit og deretter 8 0-biter. Hvilket tall er det? |
| 3. | Gjør som i oppgave 1, men sett n lik -1. |
| 4. | Gjør som i oppgave 1, men sett n lik Integer.MIN_VALUE. |
| 5. | Gjør som i oppgave 1, men sett n lik 32768 og erstatt så datatypen byte med short. |
| 6. | Hvilke tall kan n settes lik i Programkode 1.7.6 d) for å få samme utskrift for n og b? |
| 7. | Ta med variabelen char c = 'A'; i
Programkode 1.7.6 f) og
ta så med c først i summen i println-setningen. Hva skjer?
Hva er bitsekvensen til
c (dvs. til 'A')? Hva blir verdien til d i
setningen char d = 65;? Hva er bitsekvensen
til 'B', 'C', 'a', 'b' og 'c'?
|
| 8. | La n = 128 være gitt i et fast bitformat. Konverter n til 8 biters format. Hvilket resultat gir det? Vis at resulatet er lik 128 modulo 256. Vis at uansett hviken n vi starter med vil resultatet etter konverteringen være likt n modulo 256. |
![]() 1.7.7 Heltallsdivisjon
1.7.7 Heltallsdivisjon
Når et heltall a skal deles med et positivt heltall d får vi en kvotient (eng: quotient)
og en rest (eng: remainder). Hvis resten er 0 sier vi at divisjonen går opp:
Her står q for kvotienten og r for resten. Det positive tallet d kalles divisor. Kvotienten blir også omtalt som «det antallet ganger d går opp i a ».
De matematiske operatorene div og mod blir definert ved hjelp av divisjonsalgoritmen:
(1.7.7.1) a div d = q a mod d = r
Eksempler: 12 div 3 = 4, 12 mod 3 = 0, 53 div 8 = 6, 53 mod 8 = 5
Legg merke til at divisjonsalgoritmen sier at resten r må oppfylle 0 ≤ r < d. Med andre ord er resten alltid ikke-negativ og mindre enn d. Dette må vi passe på når a er negativ.
Eksempel 1: –12 div 3 = –4 og –12 mod 3 = 0
fordi –12 = 3 · (–4) + 0
Eksempel 2: –53 div 8 = –7 og –53 mod 8 = 3
fordi –53 = 8 · (–7) + 3
De to divisjonsoperatorene / og % i Java virker nesten som div og mod, men ikke helt:
- Hvis a er ikke-negativ
eller d går opp i a, så er a / d det samme
som a div d og
a % d er det samme som a mod d. - Men hvis a er negativ og d ikke går opp i a, så
er a / d = (a div d ) + 1 og
a % d = (a mod d ) – d.
Denne forskjellen mellom Java-operatorene / og % og de matematiske operatorene div og mod kommer av man i Java har valgt å implementere / og % slik at en for negative a-er får a / d = –(–a / d ) og a % d = –(–a % d ).
Eksempel 3: –12 / 3 = –(12 / 3) = –4, –12 % 3 = –(12 % 3) = 0
Eksempel 4: –53 / 8 = –(53 / 8) = –6, –53 % 8 = –(53 % 8) = –5
Dette kan vi få bekreftet ved å kjøre en programbit med disse «regnestykkene»:
int k1 = -12 / 3, k2 = -12 % 3, k3 = -53 / 8, k4 = -53 % 8; System.out.println(k1 + " " + k2 + " " + k3 + " " + k4); // Utskrift: -4 0 -6 -5
Obs. Denne forskjellen mellom de matematiske operatorene div og mod og Java-operatorene / og % for negative tall er det viktig å kjenne til. Da unngår man uventede resulater når negative heltall inngår i «regnestykker». Se Oppgave 1.
| 1. | Hva blir 19 / 7, 19 % 7, –19 / 7, –19 % 7, –19 div 7 og –19 mod 7 ? |
| 2. | Lag metodene public static int div(int a, int d) ogpublic static int mod(int a, int d) i henhold til den matematiske definisjonen.
|
![]() 1.7.8 Bitforskyvninger
1.7.8 Bitforskyvninger
Vi går nå tilbake til det å betrakte en heltallsvariabel som en bitsekvens. Java har en serie
operatorer som kan brukes både til å manipulere enkeltbiter i en bitsekvens og til å manipulere
hele bitsekvenser. Disse operatorene kalles bitoperatorer (eng: bitwise operators). Flg.
operatorer kalles bitforskyvningsoperatorer:
Disse operatorene brukes vanligvis på variabler av datatypen int (og noen ganger på long), men kan brukes på alle heltallstyper (og på typen char). Også her gjelder hovedregelen at hvis vi har et blandet uttrykk (eng: mixed mode bitwise expression), dvs. et uttrykk der flere datatyper inngår, vil disse implisitt bli konvertert til int før operasjonene utføres, og resultatet lagres i int-format. (Hvis uttrykket inneholder en long vil alt bli gjort om til long.)
Bitforskyvning mot venstre Symbolet << betyr bitskifte eller bitforskyvning mot venstre (eng: leftwise bit shift). La n være av typen int. Gitt uttrykket n << k. Her lages det først en lokal kopi av n og i denne forskyves bitene k enheter mot venstre. De k bitene som opprinnelig lå lengst til venstre, forsvinner ut i «intet» og k 0-biter fylles på fra høyre. Legg merke til at n selv ikke endres. Se på flg. eksempel:
int n1 = 1; // n1 = 0 . . . . . 0000000001 = 1 int n2 = n1 << 4; // n2 = 0 . . . . . 0000010000 = 16 int m1 = -1; // m1 = 1 . . . . . 11111111111 = -1 int m2 = m1 << 1; // m2 = 1 . . . . . 11111111110 = -2 System.out.println(n1 + " " + n2 + " " + m1 + " " + m2); // Utskrift: 1 16 -1 -2 Programkode 1.7.8 a)
Symbolet <<= står for det samme som << , men nå er det en oppdateringsoperator. Dvs. n <<= k fører til at bitforskyvningen skjer i n selv. La 00110011 være de siste 8 bitene i n:
n = · · · 0 0 1 1 0 0 1 1 // de siste 8 bitene i n
n <<= 1; // bitforskyvning på 1 i n
n = · · · 0 1 1 0 0 1 1 0 // de siste 8 bitene i n
Figur 1.7.8 a)
Med Java-kode blir det slik:
int n = 51; // n = 0 . . . 00110011 System.out.print(n + " "); // Utskrift: 51 n <<= 1; // n = 0 . . . 01100110 System.out.println(n); // Utskrift: 102 Programkode 1.7.8 b)
Programkode 1.7.8 b) vil også virke hvis n får typen byte, short eller char. Se Oppgave 3. Det som da skjer er at n blir kopiert over i en lokal int-variabel, så utføres operasjonen på den og resultatet konverteres til det formatet n har og legges inn i n.
Bitforskyvning kan gi oss bestemte bitsekvenser. En sekvens med en 1-bit først og så 31 0-biter representerer den aller minste int-verdien, dvs. Integer.MIN_VALUE. Den kan konstrueres ved hjelp av bitforskyvning, dvs. en venstre bitforskyvning på 31 i tallet 1:
int n = Integer.MIN_VALUE; // n = 1000 . . . . . 0000 int m = 1 << 31; // m = 1000 . . . . . 0000 System.out.println(n + " " + m); // Utskrift: -2147483648 -2147483648 Programkode 1.7.8 c)
Et siste eksempel. Vi ønsker en bitsekvens der første halvpart av sekvensen består av 1-biter og andre halvpart av 0-biter. Da kan vi starte med tallet -1. Det er en bitsekvens der det bare er 1-biter. Deretter gjør vi en venstre bitforskyvning på 16:
int n = -1 << 16; String s = Integer.toBinaryString(n); System.out.println(s + " " + n); // Utskrift: 11111111111111110000000000000000 -65536 Programkode 1.7.8 d)
Obs. Legg merke til at en bitforskyvning på 1 mot venstre fører til at første bit i bitsekvensen forsvinner og en ny 0-bit kommer inn bakerst. Dette er det samme som å gange tallet med 2. Se Figur 1.7.8 a) og Programkode 1.7.8 b). Der ble resultatet 102 etter en bitforskyvning i tallet 51. Prinsippet er som i 10-tallssystemet. Tallet 1230 er 10 ganger så stort som 123. I 2-tallssystemet blir tallet 2 ganger så stort når det legges på en 0-bit bakerst. På samme måte vil en bitforskyvning på 2 gjøre tallet 4 ganger så stort, osv.
En må være litt oppmerksom når det gjelder bitforskyvning og multiplikasjon med 2. Hvis første og andre bit er ulike, vil en bitforskyvning gjøre at det «renner over» (eng: overflow). Det tallet vi skulle ha fått ved å gange med 2 blir for stort for bitformatet. I flg. eksempel lar vi n = 125 ha byte-format (8 biter). Det gir bitsekvensen 01111101. En venstre bitforskyvning i den på 1 gir 11111010. Med andre ord har fortegnet skiftet:
n = 0 1 1 1 1 1 0 1 = 125 // bitene i byte-tallet 125
n <<= 1; // bitforskyvning på 1 i n
n = 1 1 1 1 1 0 1 0 = -6 // dette blir bitene i byte-tallet -6
Figur 1.7.8 b)
Med Java-kode blir det slik:
byte n = 125; // n = 01111101 System.out.println(n); // Utskrift: 125 n <<= 1; // bitforskyvning i n System.out.println(n); // Utskrift: -6 Programkode 1.7.8 e)
Det å multiplisere 125 med 2 skulle egentlig ha gitt oss 250 og ikke −6. Men dette blir likevel riktig i såkalt modulo-aritmetikk. I 8 biters format kan det lagres 256 forskjellige tall. Resulatet av bitforskyvningen i 125, dvs. tallet −6, er lik 250 modulo 256. Slik vil det alltid være. Hvis vi starter med et vilkårlig heltall n i 8 biters format, vil resultatet etter en venstre bitforskyvning på 1 være likt 2·n modulo 256. Det blir på tilsvarende måte for de andre bitfomatene, dvs. formatene 16, 32 og 64. I 16 biters format handler det om modulo 216 = 65536, osv. Generelt gjelder at enten vi bruker n << 1 eller n·2 i koden vår blir resultatet alltid det samme. Tidligere het det at n << 1 ville gi noe mer effektiv kode, men det er antageligvis ikke sant lenger. Moderne optimaliserende kompilatorer vil gjenkjenne et utrykk av typen n·2 og erstatte det med n << 1.
Bitforskyvning mot høyre Operatorene >> , >>= , >>> og >>>= gjør alle bitforskyvninger mot høyre. En høyre forskyvning på k gjør at de k siste bitene i bitsekvensen forsvinner ut i «intet». Det som skiller >> fra >>> er hva som kommer inn fra venstre. Operatoren >> sender inn k biter av samme verdi som det som opprinnelig lå først. Den kalles derfor fortegnsbevarende (eng: signed right shift). Operatoren >>> sender alltid inn k 0-biter. Den kalles ikke-fortegnsbevarende (eng:unsigned right shift). Eksempel:
int n1 = 123; // n1 = 0 . . . . . 01111101 = 123 int n2 = n1 >> 1; // n2 = 0 . . . . . 00111110 = 61 int n3 = n1 >>> 1; // n2 = 0 . . . . . 00111110 = 61 int m1 = -1; // m1 = 1 . . . . . 11111111 = -1 int m2 = m1 >> 1; // m2 = 1 . . . . . 11111111 = -1 int m3 = m1 >>> 1; // m3 = 01 . . . . 11111111 = 2147483647 System.out.println(n2 + " " + n3 + " " + m2 + " " + m3); // Utskrift: 61 61 -1 2147483647 Programkode 1.7.8 f)
I tilfellet n1 = 123 har vi et positivt heltall, dvs. den første biten er 0. Da vil operatorene >> og >>> fungere likt. Operatoren >> skyver en 0-bit inn fra venstre siden det ligger en 0-bit først. Operatoren >>> skyver alltid inn en 0-bit. Men i tilfellet m1 = –1 blir det forskjellig. Der vil >> skyve inn en 1-bit fra venstre siden det ligger en 1-bit først (tallet er negativt), mens operatoren >>> vil som alltid skyve inn en 0-bit.
Hvis vi starter med et ikke-negativt tall n, vil n >> 1 svare til at den siste biten i bitsekvensen til n forsvinner. Men det er nøyaktig det samme som en heltallsdivisjon av n med 2. Med andre ord vil n >> 1 og n/2 gi samme resultat.
I Avsnitt 1.7.7 om heltallsdivisjon ble det vist at for negative tall var det en forskjell mellom Java-operatorene / og % og de matematiske operatorene div og mod. Men bitforskyvning mot høyre (dvs. >>) og operatoren div gjør det samme:
Dermed kan vi på grunnlag av det vi fant i Avsnitt 1.7.7 si at flg. gjelder i Java:
Se på flg. eksempel:
int n1 = -124/2, n2 = -124 >> 1; // -124 er negativt partall int k1 = -123/2, k2 = -123 >> 1; // -123 er negativt oddetall System.out.println(n1 + " " + n2 + " " + k1 + " " + k2); // Utskrift: -62 -62 -61 -62 Programkode 1.7.8 g)
Et heltall er et partall hvis siste bit er en 0-bit og et oddetall hvis siste bit er en 1-bit. En vanlig måte å avgjøre dette på er å sjekke verdien til n % 2. Men det finnes andre måter - se Oppgave 5. Men her må en være litt på vakt. Hvis n er ikke-negativ vil verdien til n % 2 være enten 0 eller 1, og det kan brukes til å avgjøre om n er et oddetall eller et partall:
int n = 123; if (n % 2 == 1) System.out.println(n + " er oddetall"); else System.out.println(n + " er partall"); // Utskrift: 123 er et oddetall Programkode 1.7.8 h)
Men hva skjer hvis vi skifter fortegn på n:
int n = -123; if (n % 2 == 1) System.out.println(n + " er oddetall"); else System.out.println(n + " er partall"); // Utskrift: -123 er et partall Programkode 1.7.8 i)
Den tabben vi har begått i Programkode 1.7.8 i) er å tro at n % 2 enten blir 1 eller 0. Det er lett å tro dette siden den matematiske operatoren mod er definert slik at n mod 2 er enten 0 eller 1. Men som diskutert i Avsnitt 1.7.7 er det en forskjell mellom de matematiske operatorene div og mod og Java-operatorene / og % for negative tall. Spesielt betyr det hvis n er negativ vil n % 2 være enten -1 eller 0. Det som imidlertid alltid stemmer er at n er et partall hvis og bare hvis n % 2 er lik 0. Derfor bør vi omkode testingen slik:
int n = -123; if (n % 2 != 0) System.out.println(n + " er oddetall"); else System.out.println(n + " er partall"); // Utskrift: -123 er et oddetall Programkode 1.7.8 j)
Operatorene >>= og >>>= er oppdateringsversjonene av >> og >>> . Det betyr at i uttrykkene n >>= k og n >>>= k vil bitforskyvningen skjer i n selv. La som eksempel n og m være to heltall med verdier lik henholdsvis 85 og –85:
n = 0 · · · 0 1 0 1 0 1 0 1 = 85 // bitene i n = 85
m = 1 · · · 1 0 1 0 1 0 1 1 = -85 // bitene i m = -85
n >>= 1; // bitforskyvning på 1 i n
m >>= 1; // bitforskyvning på 1 i m
n = 0 · · · 0 0 1 0 1 0 1 0 = 42 // bitene i n = 42
m = 1 · · · 1 1 0 1 0 1 0 1 = -43 // bitene i m = -43
m >>> = 1; // bitforskyvning på 1 i m
m = 0 1 · · 1 1 1 0 1 0 1 0 = 2147483626
Figur 1.7.8 c) : Bitforskyvningen skjer i n og m
Med Java-kode blir det slik:
int n = 85; // n = 0 . . . 01010101 int m = -85; // m = 1 . . . 10101011 System.out.println(n + " " + m); // Utskrift: 85 -85 n >>= 1; // n = 0 . . . 00101010 m >>= 1; // m = 1 . . . 11010101 System.out.println(n + " " + m); // Utskrift: 42 -43 m >>>= 1; // m = 01 . . . 1101010 System.out.println(m); // Utskrift: 2147483626 Programkode 1.7.8 k)
Legg merke til at den siste bitforskyvningen i Programkode 1.7.8 k) bruker operatoren >>>= . Tallet m var opprinnelig negativt (1 som fortegnsbit), men skiftoperatoren skyver inn en 0-bit fra venstre. Dermed blir resulatet et posistivt tall.
Advarsel: Oppdateringsoperatorene >>= og >>>= brukes vanligvis på int-variabler, men kan også brukes på variabler av typen byte, short, char og long. En må imidertid være spesielt oppmerksom hvis en bruker >>>= på byte, short eller char. La f.eks. n være en variabel av typen byte. Da vil n = –1 gjøre at n får 8 1-biter. Hvis vi så utfører setningen n >>>= 1, vil mange gjette på at n da vil få en 0-bit først og så 7 1-biter. Det svarer til tallet 127. Men se hve som skjer:
byte n = -1; // n = 11111111 n >>>= 1; // en bitforskyvning i n System.out.println(n); // Utskrift: -1 Programkode 1.7.8 l)
Vi får -1 som utskrift i Programkode 1.7.8 l) og ikke 127. Det kommer av at bak kulissene skjer bitforskyvningen i int-format og så konverteres resultatet tilbake til byte-format. Heltallet -1 i int-format består av 32 1-biter. Bitforskyvningen gjør at det blir en 0-bit først og så 31 1-biter. Når dette konverteres til byte-format tas bare de 8 siste bitene med. Det gir 8 1-biter og det er lik -1 i byte-format.
Også bitforskyvning mot høyre kan brukes til å generere bestemte bitsekvenser. Gitt at vi ønsker en bitsekvens der første halvpart av sekvensen består av 0-biter og andre halvpart av 1-biter. Da kan vi starte med tallet -1, dvs. en bitsekvens der det bare er 1-biter. Deretter gjør vi en høyre bitforskyvning (dvs. >>>) på 16:
int n = -1 >>> 16; String s = Integer.toBinaryString(n); System.out.println(s + " " + n); // Utskrift: 1111111111111111 65535 Programkode 1.7.8 m)
Utskriften i Programkode 1.7.8 m) gir kun 1111111111111111. Egentlig er det 16 0-er først, men metoden toBinaryString tar ikke med ledende 0-er.
| 1. | La n = 1. Hva blir n << 2 og n << 3? |
| 2. | La n = -1. Hva blir n << 2 og n << 3? |
| 3. | La n få typen byte istedenfor typen int i
Programkode 1.7.8 b).
Sjekk at programmet virker og gir samme utskrift.
La så n få typen short. Hva skjer? La til slutt
n få typen char. Hva skjer nå?
|
| 4. | La n = -128 i Programkode 1.7.8 e).
Hva blir utskriften?
Gi en forklaring på det som skjer! La deretter n = -127. Hva skjer da?
|
| 5. | En effektiv måte å finne den siste biten i et heltall på er å bruke bitoperatoren & sammen med tallet 1. Da blir resultatet 1 eller 0 avhengig av om siste bit er 1 eller 0. Lag kode der du sjekker dette. |
| 6. | Vis ved å analysere bitsekvensene at (1 << 31) >> 15 blir det samme som –1 << 16. |
| 7. | Hva blir (–1 << 16) + (–1 >>> 16)? |
| 8. | Sett opp tallet n = -100 i 8 biters format og finn resultatet av operasjonen n <<= 1? Vis at resulatet og n·2 er like modulo 256. |
![]() 1.7.9 Effektivisering av regneoperasjoner
1.7.9 Effektivisering av regneoperasjoner
Enkelte regneoperasjoner kan effektiviseres ved hjelp av bitforskyvninger.
Et heltall n blir doblet hvis det settes en ekstra 0-bit bakerst
i tallets binære representasjon. Hvis n er gitt som en int-variabel, settes
en ekstra 0-bit bakerst ved hjelp av en bitforskyvning mot venstre. Generelt gjelder
at det å multiplisere n med et heltall på formen 2k, er det
samme som å sette inn k 0-biter bakerst i tallet, og det får vi til ved
å gjøre k bitforskyvninger mot venstre:
n · 2 = 246810 = 1001101001002 (en ny 0 bakerst)
n · 64 = n · 26 = 7897610 = 100110100100000002 (seks nye 0-er bakerst)
Vi får 0-biter bakerst i et heltall ved å gjøre bitforskyvninger mot venstre:
int n = 1234; int k = n << 1; // k = 2468 int m = n << 6; // m = 78976 Programkode 1.7.9 a)
Hvis vi skal multiplisere n med et heltall som ikke er på formen 2k, kan vi dele opp tallet. Ta f.eks. tallet 10. Det kan skrives som 8 + 2. Dermed:
En vinner lite på å erstatte en multiplikasjon med bitforskyvninger og addisjoner. En moderne Java-kompilator vil sannsynligvis gjøre slike optimaliseringer for oss. Se Oppgave 3a) og 3b).
En divisjon er en langt mer komplisert operasjon enn en multiplikasjon. En heltallsdivisjon kan faktisk være så mye som 5 - 10 ganger mer tidkrevende enn en multiplikasjon. Se Oppgave 3d). Her finnes det imidlertid noen smarte effektiviseringstriks.
La n og d (d for divisor) være positive heltall. Uttrykket n / d er matematisk sett en brøk. La f.eks. d = 5. Brøken n / 5 kan skrives som n · (1/5). Dvs. å dele med 5 er det samme som å gange med 1/5. Når brøken n / 5 avrundes ned til nærmeste heltall får vi kvotienten q (se Avsnitt 1.7.7). La f.eks. n = 654. Da vil n / 5 = 130,8. Avrunding nedover gir kvotienten 130.
Hvis vi multipliserer n med en brøk på formen m / 2k istedenfor med brøken 1/5, får vi selvfølgelig et annet svar. Men hvis vi velger m og k slik at m / 2k er nær 1/5 i verdi, vil vi likevel få samme resultat etter en avrunding nedover. La f.eks. m = 205 og k = 10. Da blir m / 2k = 205 / 210 = 205/1024 = 0,2002. Dette er nær 1/5 = 0,2. La som over n = 654. Da vil (654 · 205) / 1024 = 130,92. Dette avrundes nedover til 130. Poenget med dette er at i Java kan en divisjon med 1024 = 210 utføres som en bitforskyvning, og dermed kan divisjonen 654/5 ersattes med en multiplikasjon og en bitforskyvning. Husk at i Java er verdien til uttrykket n / d lik kvotienten til den matematiske brøken n / d, dvs. antall ganger d går opp i n og det er igjen lik avrundingen av den matematiske brøken n / d nedover til nærmeste heltall.
(1.7.9.1) I Java har 654 / 5 og 654 * 205 >>> 10 samme verdi.
Den feilen vi gjør ved å erstatte brøken n / 5 med brøken (n · 205) / 1024 blir enda mindre for verdier av n mindre enn 654. Det betyr at etter avrunding nedover gir n / 5 samme resultat som (n · 205) / 1024 for alle verdier av n mellom 0 og 654. Men dette gjelder også verdier av n større enn 654. Et lite Java-program kan hjelpe oss her:
for (int n = 0; ; n++) { if ((n / 5) != (n * 205 >>> 10)) { System.out.println(n); break; } } Programkode 1.7.9 b)
Koden over gir 1024 som utskrift. Det betyr at i Java-kode har n / 5 og n * 205 >>> 10 samme verdi for alle ikke-negative heltall n mindre enn 1024. La n = 1023. Da blir 1023 /5 = 204,6, mens (1023 · 205) / 1024 = 204,7998. Men begge gir 204 etter avrunding nedover. Men hvis n = 1024, blir det galt. Vi har 1024/5 = 204,8, mens (1024 · 205) / 1024 = 205.
(1.7.9.2) I Java har n / 5 og n * 205 >>> 10 samme verdi for 0 ≤ n < 1024.
Vi kan få bedre resultater hvis vi erstatter 1/5 med brøken m / 2k der k er større enn 10. For hver k velger vi da m lik det minste mulige heltallet slik at m / 2k blir større enn 1/5. Det får vi til ved å la m være avrundingen av brøken 2k / 5 oppover til nærmeste heltall. På den måten vil m / 2k bli nærmere 1/5 jo større k velges. Men hvis k velges for stor, vil den tilhørende verdien m også bli stor. Dermed blir det fare for «oversvømmelse» (eng: overflow) i multiplikasjonen n · m, dvs. resulatet blir for stort for 32 biter.
Flg. program finner den optimale verdien på k for divisorer d som ikke er på formen 2k:
int d = 5, potens = 1; // divisor og potens for (int k = 1; k < 31; k++) // prøver k-verdier fra 1 til 31 { potens *= 2; // potens er lik 2 opphøyd i k int m = (potens / d) + 1; // avrunding oppover for (int n = 0; ; n++) { if ((n / d) != (n * m >>> k)) { System.out.println("k = " + k + " m = " + m + " n = " + n); break; } } } Programkode 1.7.9 c)
Vi tar med kun noen linjer fra utskriften til Programkode 1.7.9 c):
k = 16 m = 13108 n = 16384 k = 17 m = 26215 n = 43694 k = 18 m = 52429 n = 81920 k = 19 m = 104858 n = 40960 k = 20 m = 209716 n = 20480 k = 21 m = 419431 n = 10240
Dette forteller at k = 18 og m = 52429 gir best resultat:
(1.7.9.3) I Java har n / 5 og n * 52429 >>> 18 samme verdi for 0 ≤ n < 81920.
Programkode 1.7.9 b) kan brukes til å undersøke andre divisorer enn 5, dvs. alle divisorer som ikke er på formen 2k. Deler av flg. tabell er laget på den måten:
| Divisor d | n / d kan erstattes med | Intervall for n |
| 2 | n >> 1 | 0 ≤ n < 231 |
| 3 | n * 43691 >>> 17 | 0 ≤ n < 98304 |
| 4 | n >> 2 | 0 ≤ n < 231 |
| 5 | n * 52429 >>> 18 | 0 ≤ n < 81920 |
| 6 | (n >> 1) * 43691 >>> 17 | 0 ≤ n < 196608 |
| 7 | n * 74899 >>> 19 | 0 ≤ n < 57344 |
| 8 | n >> 3 | 0 ≤ n < 231 |
| 9 | n * 58255 >>> 19 | 0 ≤ n < 73728 |
| 9 | (n * 43691 >>> 17) * 43691 >>> 17 | 0 ≤ n < 98304 |
| 10 | (n >> 1) * 52429 >>> 18 | 0 ≤ n < 163840 |
| Tabell 1.7.9 : Divisjon kan erstattes med multiplikasjon og bitforskyvning | ||
|---|---|---|
5 er et primtall og kan ikke faktoriseres. Men det kan f.eks. 6 og 10. La n div d være kvotienten når n deles med d. Anta at divisor d kan faktoriseres, dvs. d = d1 · d2. Dermed:
Java-kode: n / d = (n / d1) / d2
Divisoren 6 kan skrives som 2 · 3 og divisoren 10 som 2 · 5. Det betyr at i Java-kode er f.eks. n / 10 = (n / 2) / 5. Hvis n er mindre enn 163840, vil n / 2 være mindre enn 81920. Dermed får vi det som står om 10 i Tabell 1.7.9:
(1.7.9.4) I Java: n / 10 er lik (n >> 1) * 52429 >>> 18 for 0 ≤ n < 163840.
De spesielle m-verdiene, f.eks.tallet 52429 i (1.7.9.4), blir ofte omtalt som «magiske tall». Det er jo nesten som trolldom at det er mulig å effektivisere heltallsdivisjon så mye på denne enkle måten. Ulempen er at det kun gjelder for en begrenset mengde av heltall n. I Oppgave 3e) og 3f) skal vi se nærmere på hvor stor effektivitetsgevinsten er.
Vi kan også erstatte en modulodivisjon med multiplikasjon og bitforskyvning. Generelt gjelder at n % d = n - (n / d) * d. Hvis f.eks. d = 10, kan vi bruke (1.7.9.4):
int n = 123456; // n < 163840 int r = n - ((n >> 1) * 52429 >>> 18) * 10; // r = n % 10 System.out.println(n + " % 10 = " + r); // Utskrift: 123456 % 10 = 6 Programkode 1.7.9 d)
Vi kan finne antallet desimale siffer i et ikke-negativt heltall ved fortløpende å dele med 10:
public static int antallDesimaleSiffer1(int n) { int antSiffer = 1; // antall desimale siffer for (; n >= 10; antSiffer++) n /= 10; return antSiffer; } Programkode 1.7.9 e)
Dette kan imidlertid effektiviseres mye ved å bruke den nye teknikken. Den gjelder for heltall mindre enn 163840 og spesielt for alle heltall med mindre enn 6 siffer. Se flg. metode:
public static int antallDesimaleSiffer2(int n) { int antSiffer = 1; // antall desimale siffer if (n >= 100000) { antSiffer = 6; // n har minst 6 siffer n /= 100000; // fjerner de 6 siste sifrene } for (; n >= 10; antSiffer++) n = (n >> 1) * 52429 >>> 18; return antSiffer; } Programkode 1.7.9 f)
Eksempel på bruk av metodene:
int n = 1234567890; int antall1 = antallDesimaleSiffer1(n); int antall2 = antallDesimaleSiffer2(n); System.out.println(antall1 + " " + antall2); // Utskrift: 10 10
Begge metodene vil selvfølgelig returnere 10 siden tallet 1234567890 har 10 siffer. Men den andre metoden vil nok i gjennomsnitt være 4-5 ganger så effektiv som den første.
Ulempen med teknikken over er at den kun gjelder for en begrenset mengde av n-verdier. F.eks. fant vi at med divisor 5 virket den kun for ikke-negative verdier av n mindre enn 81920. Årsaken er problemet med oversvømmelse i multiplikasjonen. Vi kan unngå det ved å bruke 64 biter, dvs. gjøre multiplikasjonen i long-format. Da vil k = 33 være den beste verdien. Det «magiske» tallet m velges som vanlig som det minste heltallet slik at m / 233 blir større enn 1/5, dvs. m lik kvotienten til (233 / 5) pluss 1. Det gir tallet 1717986919. Dermed gjelder flg. for alle 32-biters heltall (datatypen int):
(1.7.9.5) n / 5 er lik (int)(n * 1717986919L >>> 33) for alle ikke-negative n
På en 32 biters prosessor vil regneoperasjoner i long-format gå vesentlig saktere enn i int-format. Derfor vil (1.7.9.5) ikke gi så stor effektivitetsgevinst. Men på en 64 biters prosessor vil det være annereledes. Se Oppgave 3g).
Det er mulig å få utført en divisjon ved hjelp av multiplikasjoner, addisjoner og bitforskyvninger uten å gå utover int-formatet. Problemet med oversvømmelse i en multiplikasjon kan takles ved å starte med bitforskyvninger. Desimaltallet 0,2 (dvs. 1/5) kan settes opp som en binærbøk:
0,210 = 0,00110011001100110011001100110011 . . . . . 2
Målet vårt er å finne kvotienten q i heltallsdivisjonen n / 5, dvs. det samme som å avrunde n · 0,2 nedover. De binære sifrene 0011 repeteres fortløpende i binærbrøken til 0,2. Vi kan derfor bruke n · 0,0011 som første tilnærming til kvotienten. Nå er 0,0011 det samme som 1/8 + 1/16. Dermed blir q = (n >> 3) + (n >> 4) første tilnærming.
Vi har at 0,0011 / 16 = 0,00000011 siden divisjon med 16 svarer til å flytte komma 4 enheter mot venstre. Dermed blir 0,00110011 = 0,0011 + 0,0011 / 16. Som neste tilnærming bruker vi n · 0,00110011 = n · 0,0011 + n · 0,0011 / 16 = q + q / 16. Dvs. q = q + (q >> 16). Osv:
int n = 123456789; int q = (n >> 3) + (n >> 4); q = q + (q >> 4); // eller q += (q >> 4); q = q + (q >> 8); // eller q += (q >> 8); q = q + (q >> 16); // eller q += (q >> 16); Programkode 1.7.9 g)
Hvis n = 123456789, vil kvotienten i divisjonen n / 5 bli lik 24691357. Hvis vi kjører programbiten over vil q til slutt blir 24691355. Slik q er konstruert kan den aldri bli større enn kvotienten, men den kan, som vi ser, bli mindre. Tallet r gitt ved r = n - q * 5 blir en tilnærmimgsverdi til resten, dvs. til n mod 5. Det viser seg at r alltid blir mindre enn 25. La n div 5 være kvotienten. Da gjelder n div 5 = q + r div 5. Men r div 5 kan vi finne ved å multiplisere r med en brøk av typen m / 2k. Her vil m = 13 og k = 6 fungere siden r / 5 og r * 13 >> 6 gir samme svar for 0 ≤ r < 65. Dermed:
int r = n - q * 5;
q = q + (r * 13 >> 6);
Vi legger alt dette inn i en metode:
public static int div5(int n) // gjelder for alle n >= 0 { int q = (n >> 3) + (n >> 4); q += (q >> 4); q += (q >> 8); q += (q >> 16); int r = n - q * 5; return q + (r * 13 >> 6); } Programkode 1.7.9 h)
Programkode 1.7.9 h) kan effektiviseres noe. Se Oppgave 4. Poenget er at en divisjon med 5 kan utføres uten at divisjonsoperatoren / brukes. Spørsmålet er imidlertid hvor effektivt det blir. Det er mange operasjoner som utføres. Se Oppgave 3h).
Det finnes to bitskiftoperatorer som begge forskvyver bitene fra venstre mot høyre. Den første ( >> ) kalles fortegnsbevarende (eng: signed right shift) og den andre ( >>> ) ikke-fortegnsbevarende (eng: unsigned right shift). Eksempel:
int n = -1; int k1 = n >> 1; int k2 = n >>> 1; System.out.println(k1 + " " + k2); // Utskrift: -1 2147483647 Programkode 1.7.9 i)
I Programkode 1.7.9 i) er n = -1. Binærkoden til -1 består av 32 1-biter. Den fortegnsbevarende operatoren >> flytter alle bitene en enhet mot høyre. Dermed forsvinner den siste biten (den lengst til høyre). Men lengst til venstre kommer det inn en ny bit maken til den som opprinnelig lå der. Biten lengst til venstre kalles fortegnsbiten, dvs. 0 for ikke-negative tall og 1 for negative tall. Det betyr at operatoren >> bevarer fortegnet. Dermed blir k1 = n >> 1 det samme som n siden alle bitene i n er 1-biter. Den ikke-fortegnsbevarende operatoren >>> setter inn en 0-bit helt til venstre etter forskyvningen uansett hva som lå der fra før. Dermed blir k2 = n >>> 1 det tallet som 0 fortegnsbit og så 31 1-biter. Det er det største mulige int-tallet, dvs. 2147483647.
I dette avsnittet brukes noen ganger operatoren >> og noen ganger operatoren >>>. Der hvor tallet helt sikkert er positivt, kan vi like gjerne bruke >> som >>>. Men noen steder må >>> brukes. Multiplikasjonen n · m kan gi oversvømmelse. Hvis resultatet består av 31 eller færre signifikante biter, går det helt fint. Hvis det består 33 eller flere signifikante biter, går det galt. Men hvis det består av nøyaktig 32 signifikante biter, kan det likevel gå bra. Det blir negativt som int-tall, men vi kan se bort fra fortegnet. Eksempel:
int n = 32768; // n = 1000000000000000 16 biter int m = 65536; // m = 10000000000000000 17 biter int k = n * m; // vanlig tallregning: 32768 * 65536 = 2147483648 System.out.println(k); // Utskrift: -2147483648 System.out.println(k >> 1); // Utskrift: -1073741824 System.out.println(k >>> 1); // Utskrift: 1073741824 Programkode 1.7.9 j)
De fleste av idéene i Avsnitt 1.7.9 er hentet fra boken Henry S. Warren, Hacker's Delight. Se referanselisten på slutten i Avsnitt 1.7.20.
| 1. | Erstatt multiplikasjonene a) n*3, b) n*5, c) n*6, d) n*7 og e) n*100 med addisjon(er) (eller eventuelt en subtraksjon) og bitforskyvninger. |
| 2. | Utvid Tabell 1.7.9 med divisorene 11, 12, 13 og 14. Husk at 12 = 4*3 og 14 = 2*7. Bruk Programkode 1.7.9 b) for 11 og 13. |
| 3. |
Kjør flg. kode. Velg N slik at tidsforbruket blir ca. 1 sekund
(1000 millisekunder).
int n = 12345, N = 100000000, k = 0; long tid = System.currentTimeMillis(); for (int i = 0; i < N; i++) k = n; System.out.println(System.currentTimeMillis() - tid); |
| a) Bytt ut k = n med k = n*10 . Hva blir tidsforbruket? | |
| b) Bruk isteden k = (n << 3) + (n << 1) . Blir tidsforbruket annerledes? | |
| c) Sammenlign tidsforbruket for k = n / 64 og k = n >> 6 . | |
| d) Sammenlign tidsforbruket for k = n * 10 og k = n / 10 . | |
| e) Sammenlign tidsforbruket for k = n / 5 og k = n * 52429 >>> 18 . | |
| f) Sammenlign tidsforbruket for k = n / 10 og k = (n >> 1) * 52429 >>> 18 . | |
| g) Finn tidsforbruket for k = (int)(n * 1717986919L >>> 33) . | |
| h) Finn tidsforbruket for k = div5(n) der div5 er metoden i Programkode 1.7.9 f). | |
| 4. | Programkode 1.7.9 f) kan effektiviseres litt. Hvis setningen q += (q >> 16) fjernes vil r likevel ikke bli større enn 32787. Dermed kan r / 5 erstattes. Se (1.7.9.3). |
| 5. | Lag metodene div3 og div7. Bruk idéer tilsvarende de som ble brukt i koden for div5, dvs. i Programkode 1.7.9 f). |
| 6. | Lag metoden public static String toString(int n). Den skal returnere en tegnstreng som inneholder de desimale sifrene til heltallet n. Hvis n er negativ skal strengen ha tegnet '-' som første tegn. |
![]() 1.7.10 Operatorer på bitnivå
1.7.10 Operatorer på bitnivå
Java har flg. bitoperatorer som alle arbeider med int-verdier (eller eventuelt
med long-verdier). Det er mulig å lage uttrykk med disse operatorene der både
byte-, short-, char- og int-verdier inngår, men da blir
implisitt alle verdier av typer som er «mindre» enn int, først konvertert til
int-verdier. Resultatet blir en int-verdi. (Hvis det inngår en
long-verdi blir alt konvertert til long-verdier.)
Hvis vi tenker oss at operatorene anvendes på enkeltbiter, vil flg. regler gjelde:
Lå nå La k og n være to int-verdier (variabler eller konstanter).
Binær og. Vi finner k & n ved å bruke regel 1 over på hvert par av biter i k og n. I eksempelet i Figur 1.7.10 a) under er bare de 10 siste bitene tatt med:
| k = · · · | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| n = · · · | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| k & n = · · · | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| Figur 1.7.10 a) : Resultatet av binær og | ||||||||||
Binær eller. Vi finner k | n ved å bruke regel 2 over på hvert par av biter i k og n. I eksempelet i Figur 1.7.10 b) under er bare de 8 siste bitene tatt med:
| k = · · · | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| n = · · · | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| k | n = · · · | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| Figur 1.7.10 b) : Resultatet av binær eller | ||||||||||
Binær eksklusiv eller (xeller). Vi finner k ^ n ved å bruke regel 3 over på hvert par av biter i k og n. I eksempelet i Figur 1.7.10 c) under er bare de 8 siste bitene tatt med:
| k = · · · | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| n = · · · | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| k ^ n = · · · | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| Figur 1.7.10 c) : Resultatet av binær xeller | ||||||||||
Binær ikke. Vi finner ~n ved å bruke regel 4 over på hver bit i n. Uttrykket ~n kalles komplementet til n. I Figur 1.7.10 d) under er bare de 8 siste bitene tatt med:
| n = · · · | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| ~n = · · · | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| Figur 1.7.10 d) : Komplementet til n | ||||||||||
Operatorene &= , |= og ^= er oppdateringsoperatorer. De virker slik:
2. n |= k svarer til n = n | k
3. n ^= k svarer til n = n ^ k
Her følger noen eksempler på hvordan bitoperatorene kan brukes:
Eksempel 1. Gitt en bitsekvens i form av et heltall n. Anta at vi ønsker å avgjøre om biten på en bestemt plass i sekvensen er 0 eller 1. Det er vanlig å si at den bakerste posisjonen (den lengst til høyre) er posisjon 0, den nest bakerste er posisjon 1, osv. Se Avsnitt 1.7.4. Anta at vi ønsker å vite om biten i posisjon k er 0 eller 1. Vi starter med å gjøre en venstre bitforskyvning på k i tallet 1. Dermed får vi et tall (en bitsekvens) p der det står 1 i posisjon k og 0 på alle andre plasser. Deretter sjekker vi resultatet av operasjonen & mellom n og p. Hvis resultatet er 0 må det være en 0-bit på plass k i n. Hvis derimot resultatet er forskjellig fra 0, må det være en 1-bit der. Se på flg. kode:
int k = 5; int n = 123456789; // n = 00000111010110111100110100010101 int p = 1 << k; // p = 00000000000000000000000000100000 String s = (n & p) == 0 ? "0-bit" : "1-bit"; System.out.println(s + " på plass " + k); // Utskrift: 0-bit på plass 5 Programkode 1.7.10 a)
Eksempel 2. Vi kan ta Eksempel 1 et skritt videre. Vi kan få tak i alle de binære sifrene
i et heltall ved å finne ut om det er 0-bit eller 1-bit på hver plass. Da starter vi med
plass 31, dvs. lengst til venstre. Deretter flytter vi oss en posisjon om gangen mot høyre
ved hjelp bitforskyvning. Vi kan finne bitene ved hjelp av metoden
Integer.toBinaryString, men da får vi ikke de ledende 0-ene. Det gjør vi her:
int n = 123456789; for (int p = 1 << 31; p != 0; p >>>= 1) { System.out.print((n & p) == 0 ? 0 : 1); } // Utskrift: 00000111010110111100110100010101 Programkode 1.7.10 b)
Eksempel 3. Ved hjelp av bitoperatorer og bitforskyvning kan det konstrueres bestemte bitsekvenser. Gitt bitsekvensen 0101 . . . 010101, dvs. annenhver gang 0 og 1. Hvordan kan vi få konstruert den? Vi kan starte med tallet n = 1, Det har 01 bakerst. Så forskyver vi to mot venstre og får: 0100 bakerst. Deretter bruker vi | (eller) og får 0101 bakerst. Så forskyver vi 4 mot venstre, osv. Se flg. kode:
int n = 1; // n = 00000000000000000000000000000001 n = n | (n << 2); // n = 00000000000000000000000000000101 n = n | (n << 4); // n = 00000000000000000000000001010101 n = n | (n << 8); // n = 00000000000000000101010101010101 n = n | (n << 16); // n = 01010101010101010101010101010101 System.out.println(Integer.toBinaryString(n)); // Utskrift: 1010101010101010101010101010101 Programkode 1.7.10 c)
| 1. | Lag kode som setter de 16 første bitene i et vilkårlig int-tall n til 0 og som lar de 16 siste bitene være som de er. |
| 2. | Vis at -n = ~n + 1. |
| 3. | Hva blir ~0 ? Lag kode som skriver ut verdien til ~0. |
| 4. | Bruke idéen Programkode 1.7.10 b) til å finne antallet 1-biter i den binære representasjonen til et vilkårlig heltall n. |
| 5. | Lag Programkode 1.7.10 c) litt kortere ved å bruke operatoren |=. |
| 6. | Heltallet 5 har en binærrepresentasjon som ender på 0101. Lag Programkode 1.7.10 c) litt kortere ved å starte med n = 5. |
| 7. | Hvilket heltall representerer bitsekvensen 01010101? Finn det tallet og lag Programkode 1.7.10 c) litt kortere ved å starte med n lik det tallet. |
| 8. | Den enkleste måten å lage et heltall som har 0 og 1 annenhver gang er å bruke
heksadesimale siffer. Lag kode som viser at setningen int n = 0x55555555;
gjør at n får det innholdet. Se også Avsnitt 1.7.12.
|
![]() 1.7.11 Boolske tabeller
1.7.11 Boolske tabeller
Den boolske datatypen boolean kan kun ha de to verdiene true (sann)
og false (usann) og kan derfor brukes som et flagg (heist - ikke heist)
eller som en bryter (på - av).
En bit har også kun to verdier, dvs. 1 og 0. Dermed kan også den brukes som et flagg eller som en bryter. Men en bit kan ikke opptre helt alene. Den forekommer kun som en del av en bitsekvens på 8 (byte), 16 (short), 32 (int) eller 64 (long) biter. En slik bitsekvens kan betraktes som en bit-tabell:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| Figur 1.7.11 a) : En int-verdi kan betraktes som en bit-tabell med 32 biter | ||||||||||||||||
Legg merke til at når en int-verdi på 32 biter betraktes som en bit-tabell, er det vanlig å nummerere posisjonene fra høyre mot venstre. Posisjon 0 er lengst til høyre, posisjon 1 nest lengst til høyre, osv. Lengst til venstre har vi posisjon 31.
I Figur 1.7.11 a) er det kun 0-biter. Det svarer til heltallet 0. La k, 0 ≤ k ≤ 31, være en tabellposisjon. Flg. kode vil sette biten i posisjon k til 1 uavhengig av hva som er der fra før:
int n = 0; // en bit-tabell der alle bitene er 0 int k = 5; // k er en tabellposisjon n |= (1 << k); // gir en 1-bit i posisjon k System.out.println(n); // Utskrift: 32 Programkode 1.7.11 a)
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| Figur 1.7.11 b) : En 1-bit i posisjon k = 5 | ||||||||||||||||
Programkode 1.7.11 a) virker etter hensikten fordi bitforskyvningen 1 << k gir en bitsekvens med en 1-bit i posisjon k og 0-biter ellers. Operasjonen n | (1 << k) gir en sekvens som har en 1-bit i posisjon k. Det blir en 1-bit der uansett om det var en 0-bit eller en 1-bit i posisjon k i variablen n fra før. I alle de andre posisjonene får vi det som var i n.
Hvis en bit-tabell inneholder både 1-biter oh 0-biter, er det av interesse å kunne avgjøre om biten i en bestemt posisjon k er 0 eller 1.
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| Figur 1.7.11 c) : En bit-tabell med et tilfeldig innhold | ||||||||||||||||
Dette kan vi avgjøre på samme måte som i Eksempel 1 i Avsnitt 1.7.10, ved å bruke &-operatoren. Heltallet n under, som blir oppgitt med heksadesimale siffer, vil ha en bitsekvens eller bit-tabell som er lik den i Figur 1.7.11 c) over på de 8 første og de 8 siste bitene:
int n = 0x6E0000A5; int k = 28; // k er en tabellposisjon if ((n & (1 << k)) == 0) System.out.println("0-bit i posisjon " + k); else System.out.println("1-bit i posisjon " + k); // Utskrift: 0-bit i posisjon 28 Programkode 1.7.11 b)
Hvis en ønsker å gjøre om biten i posisjon k i et hetall n til en 0-bit uansett om det er en 0-bit eller en 1-bit der fra før, kan en bruke &-operatoren og en bitsekvens som har 0 i posisjon k og 1-biter alle andre steder:
int n = 96; // 1-bit i posisjon 5 og 6 int k = 5; // k er en tabellposisjon n &= ~(1 << k); // ~(1 << k) har 0-bit i posisjon k System.out.println(n); // Utskrift: 64 Programkode 1.7.11 c)
Det kan også være aktuelt å endre biten i posisjon k i et hetall n til den motsatte verdien, dvs. til 0 hvis det er en 1-bit der og til 1 hvis det er en 0-bit. Det kan vi gjøre ved hjelp eksklusiv eller, dvs. ved hjelp av ^-operatoren:
int n = 96; // 1-bit i posisjon 5 og 6 n ^= (1 << 5); // endrer biten i posisjon 5 n ^= (1 << 4); // endrer biten i posisjon 4 System.out.println(n); // Utskrift: 80 Programkode 1.7.11 d)
Flg. tabell gir en oversikt over mulige operasjoner på enkeltbiter i en bit-tabell:
| Programkode | Heltall n og posisjon k, 0 ≤ k ≤ 31 |
| n |= (1 << k) | Setter 1-bit i posisjon k i n |
| (n & (1 << k)) == 0 | Sann hvis 0-bit i posisjon k i n, usann ellers |
| (n & (1 << k)) != 0 | Sann hvis 1-bit i posisjon k i n, usann ellers |
| n &= ~(1 << k) | Setter 0-bit i posisjon k i n |
| n ^= (1 << k) | Setter motsatt bit i posisjon k i n |
| Tabell 1.7.11 Operasjoner i bit-tabell | |
|---|---|
Eksempel 1. Bit-tabeller kan brukes til å representere tallmengder. La A og B være gitt ved A = {1,3,5,6,7,9} og B = {2,4,5,6,7,8}. De kan representeres ved hjelp av int-variabler med biter satt til 1 i de posisjonene som elementene i mengde gir. Heltall som er negative eller større enn 31, kan imidlertid ikke inngå. Mengder med elementer fra og med 0 til 64 kan imidlertid representeres ved hjelp av long-variabler. Det er også mulig å bruke flere variabler for å representere én mengde. Dette gjøres i klassen BitSet. Se Avsnitt 1.7.17.
Snitt og union kan utføres ved hjelp av & og | hvis mengder representeres på denne måten:
int A = 0; // konstruerer A = {1,3,5,6,7,9} A |= (1 << 1); A |= (1 << 3); A |= (1 << 5); A |= (1 << 6); A |= (1 << 7); A |= (1 << 9); int B = 0; // konstruerer B = {2,4,5,6,7,8} B |= (1 << 2); B |= (1 << 4); B |= (1 << 5); B |= (1 << 6); B |= (1 << 7); B |= (1 << 8); int U = A | B; // U = A union B = {1,2,3,4,5,6,7,8,9} int S = A & B; // S = A snitt B = {5,6,7} for (int k = 0; k < 32; k++) if ((U & (1 << k)) != 0) System.out.print(k + " "); // Utskrift: 1 2 3 4 5 6 7 8 9 Programkode 1.7.11 e)
Eksempel 2. I Avsnitt 1.5.6 ble to boolske tabeller brukt i forbindelse med det å avgjøre om en permutasjon av tallene 0, 1, 2, . . . , n – 1 representerte en lovlig dronningplassering. Metoden lovligPlassering i Programkode 1.5.6 a) vil bli noe mer effektiv hvis vi bruker en bit-tabell istedenfor en boolsk tabell. Metoden kan kodes slik:
public static boolean lovligPlassering(int[] a) { int n = a.length; int diagonal = 0, bidiagonal = 0; // to bit-tabeller for (int i = 0; i < n; i++) { int s = 1 << (i + a[i]); if ((bidiagonal & s) != 0) return false; int d = 1 << (n - 1 + i - a[i]); if ((diagonal & d) != 0) return false; bidiagonal |= s; diagonal |= d; // setter en 1-biter } return true; } Programkode 1.7.11 f)
| 1. | Ta utgangspunkt i Programkode 1.7.11 e). Finn differensen mellom A og B, dvs. A – B. Finn også den eksklusive unionen (kalles også symmetrisk differens) mellom A og B. |
![]() 1.7.12 Oktale og heksadesimale tall
1.7.12 Oktale og heksadesimale tall
Vi har tidligere sett hvordan bitforskyvninger (Avsnitt 1.7.8) og
bitoperatorer (Avsnitt 1.7.10) kan brukes til å konstruere bestemte bitsekvenser
og da spesielt bitsekvenser med et repeterende mønster. Det finnes imidlertid
andre og enklere teknikker hvis vi ønsker å konstruere bitsekvenser som er mer uregelmessige.
Eksempel: Gitt flg. bitsekvens med 32 biter:
Problem: Hvordan skal vi få en int-variabel til å inneholde nøyaktig denne sekvensen?
Vi kan gruppere bitene i enheter på 4 og 4, og da vil hver enhet representere et heltall i 4 biters format. Hvis vi regner uten fortegn, vil det være tallene 0, 1, 2, . . . . , 13, 14 og 15. Dette er nettopp tallene i det heksadesimale tallsystemet. Forskjellen er at der har tallene 10, 11, 12, 13, 14 og 15 fått egen symboler, dvs. A, B, C, D, E og F:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| Figur 1.7.12 a) : De heksadesimale sifrene | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Vi grupperer bitene i bitsekvensen (1.7.12.1) slik:
Bruker vi tabellen i Figur 1.7.12 a) kan dette skrives slik:
OBS. I Java tolkes sifrene som heksadesimale hvis vi setter 0x foran tallet:
int n = 0xEBA58D63; // heksadesimale tall starter med 0x String s = Integer.toBinaryString(n); // bitsekvensen til n System.out.println(s + " " + n); // Utskrift: 11101011101001011000110101100011 -341471901 Programkode 1.7.12 a)
Vi har tidligere diskutert det å konstruere en bitsekvens på 32 biter der første halvdel
består av 0-biter og andre halvdel av 1-biter. Ved hjelp av bitforskyvning kunne den
f.eks. konstrueres slik: -1 >>> 16 eller ~(-1 << 16). Men dette
er også enkelt å få til ved hjelp av heksadesimale siffer siden F er lik 1111:
int m = 0xFFFF; // på heksadesimal form int n = -1 >>> 16; // høyre bitforskyvning int k = ~(-1 << 16); // venstre bitforskyvning og komplement System.out.print(m + " " + n + " " + k); // Utskrift: 65535 65535 65535 Programkode 1.7.12 b)
Vi kan også bruke oktale siffer. Vi ser igjen på bitsekvensen i (1.7.12.1). Nå grupperer vi bitene i enheter på 3 og 3. De første to bitene danner sin egen gruppe:
Hver enhet på 3 biter representerer et heltall i 3 biters format. Tabellen under viser sammenhengen mellom tre biter og et oktalt siffer:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | ||||||||
| Figur 1.7.12 b) : De oktale sifrene | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Vi bruker tabellen i Figur 1.7.12 b) til å ersatte hver 3 biters enhet med et oktalt siffer:
OBS. I Java forteller vi at et heltall er gitt med oktale siffer ved å sette 0 foran tallet:
int n = 035351306543; // oktale tall starter med 0 String s = Integer.toBinaryString(n); // bitsekvensen til n System.out.println(s + " " + n); // Utskrift: 11101011101001011000110101100011 -341471901 Programkode 1.7.12 c)
Advarsel: I Java (og i andre språk som C, C++ og C#) er det slik at hvis 0 er første siffer i en tallkonstant blir tallet tolket som et oktalt tall. Da er det kun tillatt med 0, 1, . . , 7 som siffer og en vil få kompileringsfeil hvis tallet inneholder 8 eller 9. Et problem med dette er at en kan komme i skade for å sette en 0 som første siffer uten at tallet er tenkt å være oktalt. I vanlig tallbehandling er det jo slik at en 0 fra eller til foran et tall ikke endrer tallets verdi, men her får en ekstra 0 store konsekvenser. En feil av den typen kan være vanskelig å oppdage i et stort program.
| 1. | Det største mulige int-tallet har en 0-bit først og deretter 31 1-biter. Lag dette tallet både ved hjelp av heksadesimale siffer og ved hjelp av oktale siffer. |
| 2. | Det minste mulige int-tallet (det største negative) har en 1-bit først og deretter 31 0-biter. Gjør som i Oppgave 1. |
| 3. | Lag en bitsekvens på 32 biter der første halvdel består av 1-biter og andre halvdel av 0-biter. Gjør det både ved hjelp av heksadesimale siffer og ved hjelp av oktale siffer. |
| 4. | Gjør som i Oppgave 3, men la bitsekvensen bestå av 0 og 1 annenhver gang. Det vil si 0101 . . . 010101 (32 biter). |
| 5. | Som Oppgave 3, men med bitsekevensen 11100101110111110101100011010001. |
| 6. | Som Oppgave 3, men med bitsekevensen 00010010001101000101011001111000. |
| 7. | Som Oppgave 3, men med bitsekevensen 11111110110111001011101010011000. |
![]() 1.7.13 Binæraritmetikk i parallell
1.7.13 Binæraritmetikk i parallell
Gitt at vi har fire par med heltall og at vi ønsker å addere tallene i hvert par, dvs. utføre
flg. fire addisjonsstykker:
50 37 18 125
+ 170 + 94 + 81 + 44
----- ----- ----- -----
= 220 = 131 = 99 = 169
Figur 1.7.13 a)
Alle addendene er mindre enn 256 og kan dermed skrives med maksimalt åtte binære siffer eller med to heksadesimale siffer:
5010 = 001100102 = 3216 3710 = 001001012 = 2516
1810 = 000100102 = 1216 12510 = 011111012 = 7d16
17010 = 101010102 = aa16 9410 = 010111102 = 5e16
8110 = 010100012 = 5116 4410 = 001011002 = 2c16
Figur 1.7.13 b)
Vi kan dele de 32 bitene i et int-tall i fire enheter med åtte biter i hver enhet. Da vil hver enhet ha plass til et ikke-negativt heltall mindre enn 256. Vi legger, ved å bruke heksadesimalt format, de fire addendene 50, 37, 18 og 125 inn i hver sin enhet i et heltall m og de fire addendene 170, 94, 81 og 44 i et annet heltall n:
int m = 0x3225127d; int n = 0xaa5e512c; int sum = m + n; Programkode 1.7.13 a)
Summen sum = m + n utføres som én operasjon, men vi kan betrakte det som fire operasjoner i parallell. De åtte siste bitene i m og de åtte siste bitene i n adderes ved vanlig binæraritmetikk og siden resultatet 169 er mindre enn 256 vil det få plass blant de åtte siste bitene i heltallet sum. Tilsvarende blir det med de tre andre enhetene på åtte biter. Figuren under viser resultatet:
m = 00110010 00100101 00010010 01111101
n = 10101010 01011110 01010001 00101100
----- -------- -------- -------- --------
m + n = 11011100 10000011 01100011 10101001
Figur 1.7.13 c)
Vi kan få tak i resulatene av de fire addisjonsstykkene ved å «plukke ut» åtte og åtte biter fra sum. Til det bruker vi den bitsekvensen som har åtte 1 biter bakerst (og resten 0 biter) som maske. Operasjonen & mellom sum og denne bitsekvensen maskerer vekk de 24 første bitene (dvs. de ersattes med 0 biter) og beholder de åtte siste bitene i sum som de er:
sum = 11011100 10000011 01100011 10101001
maske = 00000000 00000000 00000000 11111111
sum & maske = 00000000 00000000 00000000 10101001
Figur 1.7.13 d)
Vi får tak i de tre andre enhetene ved å gjøre en bitforskyvning på 8 mot høyre i sum og så bruke samme maske på nytt, så en bitforskyvning på 16 og til slutt en på 24:
int m = 0x3225127d; int n = 0xaa5e512c; int sum = m + n; int s1 = sum & 0xff; int s2 = (sum >>> 8) & 0xff; int s3 = (sum >>> 16) & 0xff; int s4 = sum >>> 24; System.out.println(s4 + " " + s3 + " " + s2 + " " + s1); // Utskrift: 220 131 99 169 Programkode 1.7.13 b)
Vi kan også bruke bitforskyvning og maskering til å finne summen av de enkelte delene av en bitsekvens. La flg tall/bitsekvens være gitt:
n = 10001111011010100010110001011101
Denne sekvensen kan vi se på som en serie av åtte enheter på hver fire biter:
n = 1000 1111 0110 1010 0010 1100 0101 1101 = 8f6a2c5d16
Hver enhet kan ses på som et firesifret binært eller som et ensifret heksadesimalt tall. På desimalform blir det tallene: 8, 15, 6, 10, 2, 12, 5 og 13. Målet er nå å finne summen av disse tallene. Vi ser med en gang at det er 71, men vi skal finne det ved hjelp av bitforskyvning og maskering. Vi bruker som maske den sekvensen som har fire 0 biter og fire 1 biter annenhver gang. Sammen med en bitforskyvning på fire vil det gi oss summen av to og to firebiters enheter:
n = 1000 1111 0110 1010 0010 1100 0101 1101
m = n >> 4 = 1111 1000 1111 0110 1010 0010 1100 0101
k = 0000 1111 0000 1111 0000 1111 0000 1111
n & k = 0000 1111 0000 1010 0000 1100 0000 1101
m & k = 0000 1000 0000 0110 0000 0010 0000 0101
(n & k) + (m & k) = 0001 1110 0001 0000 0000 1110 0001 0010
Figur 1.7.13 e)
La nå n = (n & k) + (m & k). Nå skal vi addere to og to
åttebiters enheter i n. Til det bruker vi
bitforskyvning på 8. Her trenger vi ingen maskering. Den største verdien en enhet på
fire biter kan ha er 15, dvs. 1111. Den største verdien som en åttebiters enhet
kan ha her er summen av to firebiters enheter, dvs. 15 + 15 = 30 = 11110. Summen av
to slike kan igjen aldri bli større enn 60 = 111110 og dermed
aldri mer enn 6 signifikante biter. Dvs. summen vil aldri gå inn i naboenheten.
n = 0001 1110 0001 0000 0000 1110 0001 0010
n >> 8 = 0000 0000 0001 1110 0001 0000 0000 1110
n + (n >> 8) = 0001 1110 0011 1100 0011 1100 0011 1100
Figur 1.7.13 f)
Siste del av jobben er å addere den først 16-biters enheten med den siste. Dette gir oss tilsammen flg. kode:
int n = 0x8f6a2c5d; // 8 15 6 10 2 12 5 13 n = (n & 0xf0f0f0f) + ((n >> 4) & 0xf0f0f0f); n += (n >> 8); n += (n >> 16); n &= 0x7f; // maskerer vekk de 25 første bitene System.out.println(n); // Utskrift: 71 Programkode 1.7.13 c)
| 1. | Velg andre regnestykker enn de i Figur 1.7.13 a) og sjekk at Programkode 1.7.13 b) gir rett svar. Addendene må alltid være slik at summen blir mindre enn 256. |
| 2. | Velg n i Programkode 1.7.13 c) slik at vi i) får ut summen av talllene fra 1 til 8 og ii) summen av tallene fra 8 til 15 som utskrift. |
![]() 1.7.14 Algoritmer på bitnivå
1.7.14 Algoritmer på bitnivå
I databehandling er det ofte behov for å kunne regne ut logaritmen til både desimaltall og
heltall. Javablioteket Math inneholder metoder som finner den naturlige
(grunntall e) og den Briggske logaritmen (grunntall 10) til desimaltall.
Metodene heter log og log10 og er definert for datatypen
double, men de kan også brukes på heltall (int):
int n = 12345; // n et heltall double x = Math.log(n); // den naturlige logaritmen til n double y = Math.log10(n); // den Briggske logaritmen til n System.out.println(x + " " + y); // Utskrift: 9.42100640177928 4.091491094267951 Programkode 1.7.14 a)
I algoritmeanalyse inngår ofte logaritmeregning med grunntall 2. Der er det også
vanlig å avrunde logaritmen oppover (eller nedover) til nærmeste heltall. Dette kan vi
få til ved hjelp av de metodene som allerede finnes i Java (metoden ceil avrunder
oppover og metoden floor nedover til næremste heltall):
int n = 12345; // n et heltall double x = Math.log(n)/Math.log(2); // x = log2(n) int k = (int)Math.ceil(x); // avrunder oppover til nærmeste heltall System.out.println(x + " " + k); // Utskrift: 13.591639216030146 14 Programkode 1.7.14 b)
Variablen k inneholder verdien til log2(n) avrundet oppover til nærmeste heltall. Hvis det kun er den verdien vi er interessert i og ikke den eksakte logaritmen, kan dette gjøres langt mer effektivt. Til ethvert positivt heltall n finnes det et positivt heltall k slik at 2k-1 ≤ n < 2k.
Eksempel: n = 12345 ligger mellom 213 og 214 siden 213 = 8192 og 214 = 16384.
Videre har vi at hvis 2k-1 ≤ n < 2k, så vil k - 1 ≤ log2(n) < k. Men vi har også at hvis n oppfyller dette, vil n ha nøyaktig k signifikante binære siffer i sin binære representasjon.
Eksempel: n = 1234510 = 110000001110012 har 14 binære siffer.
Konklusjon: Hvis 2k-1 < n < 2k, så vil log2(n) avrundet oppover til næremste heltall være lik k. Men antall signifikante binære siffer i n er også lik k. Hvis derimot n = 2k-1, så vil log2(n) bli heltallig, dvs. log2(n) = k − 1, mens n fortsatt har k binære siffer. Dette kan vi takle ved isteden å se på de binære sifrene i tallet n − 1. Hvis 2k-1 < n < 2k, så er antall signifikante binære siffer i n − 1 lik log2(n) avrundet oppover til nærmeste heltall. Hvis n = 2k-1, vil antallet binære siffer i n − 1 være lik k − 1 og det er igjen lik log2(n). Dermed:
Setning 1.7.14 a) La n være et positivt heltall. Da er log2(n) avrundet oppover til nærmste heltall ( dvs. ⌈log2(n)⌉ ) det samme som antall signifikante binære siffer i n − 1.
Eksempel 1: La n = 25 og dermed n − 1 = 24. Vi har 24 = 16 < 25 < 32 = 25. Det betyr at log2(n) ligger mellom 4 og 5 eller mer eksakt: log2(n) = 4.64 . . . Tallet n − 1 = 11000 har 5 signifikante binære siffer. Med andre ord er avrundingen oppover av log225 lik antall signifikante siffer i 25 − 1 = 24.
Eksempel 2: La nå n = 16 og dermed n − 1 = 15. Vi har n = 24 og dermed log2(n) = 4. Heltallet n − 1 = 15 = 1111 har 4 signifikante binære siffer. Nå er log216 = 4 heltallig og derfor blir en avrunding lik tallet selv. Dermed: Avrundingen oppover av log216 er lik antall signifikante siffer i 16 − 1 = 15.
Eksempel 3: Setning 1.7.14 a) stemmer også hvis n = 1 fordi log21 = 0 og 1 − 1 = 0 har ingen signifikant binære siffer. Se Avsnitt 1.7.2.
Setning 1.7.14 a) sier at istedenfor å regne ut en logaritme, kan vi telle binære siffer.
Dataypen int har 32 biter. Det betyr at antallet signifikante binære siffer
i et int-tall n er lik 32 minus antallet ledende 0-biter i n.
Nå har allerede Java en metode som finner antallet ledende 0-biter i et int-tall.
Den ligger i klassen Integer og heter
numberOfLeadingZeros.
Den kan for eksempel brukes slik:
int n = 54321; // n et heltall double x = Math.log(n)/Math.log(2); // x = log2(n) int k = (int)Math.ceil(x); // avrunder oppover til nærmeste heltall int m = 32 - Integer.numberOfLeadingZeros(n - 1); System.out.println(x + " " + k + " " + m); // Utskrift: 15.729222418074684 16 16 Programkode 1.7.14 c)
Vi kan finne avrundingen av log2(n) nedover til nærmeste heltall på en tilsvarende måte:
Setning 1.7.14 b) La n være et positivt heltall. Da er log2(n) avrundet nedover til nærmste heltall ( dvs. ⌊log2(n)⌋ ) én mindre enn antall signifikante binære siffer i n.
Eksempel på bruk av Setning 1.7.14 b):
int n = 54321; // n et heltall double x = Math.log(n)/Math.log(2); // x = log2(n) int k = (int)Math.floor(x); // avrunder nedover til nærmeste heltall int m = 31 - Integer.numberOfLeadingZeros(n); System.out.println(x + " " + k + " " + m); // Utskrift: 15.729222418074684 15 15 Programkode 1.7.14 d)
Antall ledende 0-biter Er det vanskelig å finne antallet ledende 0-biter i et int-tall, dvs. i et heltall som har 32 biter? For det første er antallet ledende 0-biter da det samme som 32 minus antallet signifikante siffer. Tallet 0 har 32 ledende 0-biter. Hvis n ikke er 0, kan vi skyve bitene i n en enhet mot høyre ved hjelp av operatoren >>>. Hvis det gir 0, har n kun ett signifikant siffer og dermed 31 ledende 0-biter. Hvis ikke, skyver vi bitene enda en gang. Hvis det det da blir 0, har n to signifikante siffer og dermed 30 ledende 0-biter. Osv. Dette kan kodes slik:
int n = 54321; // n et heltall int antall = 32; // n = 0 har 32 0-biter while (n != 0) { antall--; // en ledende 0-bit mindre n >>>= 1; // skyver bitene i n en mot høyre } System.out.println("Antall ledende 0-biter: " + antall); // Utskrift: Antall ledende 0-biter: 16 Programkode 1.7.14 e)
Algoritmen i Programkode 1.7.14 e) fungerer utmerket for små verdier av n, dvs. når n har få signifikante binære siffer. Da vil while-løkken stoppe tidlig. Men hvis n er stor eller er negativ, vil while-løkken måtte gå mange runder. Spesielt vil den måtte gå 32 runder hvis n er negativ siden et negativt tall har 1 som fortegnsbit og er dermed uten ledende 0-biter.
Vi kan imidlertid gjøre det mer effektivt ved hjelp av en «splitt-og-hersk»-idé, dvs. ved å bruke en halveringsteknikk. Gitt flg. heltall n:
(1.7.14.1) n = 000000000011010011101001101101101 (n = 6935405)
Hvis vi gjør en høyre bitforskyvning på 16 i n, dvs. n >>> 16, får vi flg. bitsekvens:
(1.7.14.2) n >>> 16 = 000000000000000000000000001101001
Vi ser at n >>> 16 ikke har blitt 0 (bare 0-biter). Det betyr at n selv må ha færre enn 16 ledende 0-biter. Hvis derimot n >>> 16 hadde blitt 0 (bare 0-biter), så måtte n selv ha minst 16 ledende 0-biter. Dette kan vi sette opp i flg. kode:
int n = 6935405; // n et heltall int antall = 0; // utgangspunkter er ingen ledende 0-biter if (n >>> 16 == 0) antall += 16; else n >>>= 16; Programkode 1.7.14 f)
Effekten av Programkode 1.7.14 f) blir at antall fortsatt er 0 siden n har færre enn 16 ledende 0-biter, mens n blir oppdatert til verdien i (1.7.14.2). I den nye n-verdien gjør vi en høyre bitforskyvning på 8 (n >>> 8) med 0 som resultat siden n nå har kun 7 signifikante binære siffer. Det betyr at den opprinnelige n-verdien (1.7.14.1) må ha minst 8 ledende 0-biter. Så forskyver vi med 4 og til slutt med 2. Dette gir oss flg. metode:
public static int antallLedendeNuller(int n) { if (n == 0) return 32; int antall = 0; if (n >>> 16 == 0) antall += 16; else n >>>= 16; if (n >>> 8 == 0) antall += 8; else n >>>= 8; if (n >>> 4 == 0) antall += 4; else n >>>= 4; if (n >>> 2 == 0) antall += 2; else n >>>= 2; if (n == 1) antall++; return antall; } Programkode 1.7.14 g)
Halveringsidéen kan kodes på mange måter. Se f.eks. boken Henry S. Warren, Hacker's Delight. Hvis metoden skal brukes mest på små tall, kunne vi ha omkodet litt slik at det ble noen færre operasjoner. Men det vil føre til flere operasjoner enn nå på store tall. Det er også mulig å la metoden ha en løkke istedenfor mange if-setninger. Se Oppgave 6 - 8.
Første 1-bit Med første 1-bit menes første 1-bit fra venstre. Hvis n er et negativt int-tall, vil første 1-bit være det samme som første bit siden negative tall har 1 som fortegnsbit. Men hvis tallet ikke er negativt, vil vi ikke uten videre kunne vite hvor første 1-bit ligger. Eksempel:
(1.7.14.3) n = 00000001000111001101010001100010 (n = 18666594)
Vi ser at første 1-bit ligger som nr. 8 fra venstre. Et behov som noen ganger dukker opp er at vi til en gitt n ønsker å finne et bitsekvens/heltall k som har kun én 1-bit (og resten 0-biter) og denne 1-biten skal stå på samme plass som den første 1-biten i n. Hvis vi bruker n-verdien i (1.7.14.3) som eksempel, skal den ønskede k-verdien se slik ut:
(1.7.14.4) k = 00000001000000000000000000000000 (k = 16777216 = 224 )
Verdien k i (1.7.14.4) kan vi finne hvis vi kjenner antall ledende 0-biter i n. Vi kan starte med bitsekvensen som har 1 først og deretter 31 0-biter. I den gjør vi en høyre bitforskyvning slik at vi får like mange ledende 0-biter som det n har. Alternativt kan vi gjøre en venstre bitforskyvning i tallet 1:
int n = 18666594; // n = 00000001000111001101010001100010 int m = Integer.numberOfLeadingZeros(n); int k1 = (1 << 31) >>> m; // k1 = 00000001000000000000000000000000 int k2 = 1 << (31 - m); // k2 = 00000001000000000000000000000000 System.out.println(m + " " + k1 + " " + k2); // Utskrift: 7 16777216 16777216 Programkode 1.7.14 h)
Som Programkode 1.7.14 h) viser kan vi bruke metoden
numberOfLeadingZeros (eller vår metode antallLedendeNuller)
til å finne den ønskede k-verdien. Men det er mulig å finne k-en på
en mer direkte måte. Vi finner først verdien n | n >> 1:
| (1.7.14.5) | n | = | 00000001000111001101010001100010 |
| (1.7.14.6) | n >> 1 | = | 00000000100011100110101000110001 |
| (1.7.14.7) | n | (n >> 1) | = | 00000001100111101111111001110011 |
I (1.7.14.7) er det samme antall ledende 0-biter som i n, men så kommer to 1-biter på rad. Vi lar nå n bli sekvensen i (1.7.14.7). Så gjør vi som over, men med en bitforskyvning på 2:
| (1.7.14.8) | n | = | 00000001100111101111111001110011 |
| (1.7.14.9) | n >> 2 | = | 00000000011001111011111110011100 |
| (1.7.14.10) | n | (n >> 2) | = | 00000001111111111111111111111111 |
I (1.7.14.10) er det samme antall ledende 0-biter som i n, men deretter er det bare 1-biter. Det var litt flaks. Teknikken gir imidlertid alltid fire 1-biter. Videre gjør vi en bitforskyvning på 4, så en på 8 og til slutt en på 16. Da er det garantert at vi alltid vil få samme antall ledende 0-biter som i den n-verdien vi opprinnelig startet med, og deretter bare 1-biter.
Siste skritt er å bli kvitt alle 1-bitene bortsett fra den første. Det får vi til ved å bruke eksklusiv eller mellom det vi har og det vi får ved å forskyve én mot høyre (bruk >>>):
| (1.7.14.11) | n | = | 00000001111111111111111111111111 |
| (1.7.14.12) | n >>> 1 | = | 00000000111111111111111111111111 |
| (1.7.14.13) | n ^ (n >>> 1) | = | 00000000100000000000000000000000 |
Dette kan settes sammen til flg. metode som virker for alle hele tall
(inklusive 0). Dette er også slik metoden
highestOneBit
i klassen Integer er kodet:
public static int førsteEnBit(int n) { n |= (n >> 1); n |= (n >> 2); n |= (n >> 4); n |= (n >> 8); n |= (n >> 16); return n ^ (n >>> 1); } Programkode 1.7.14 i)
Antall 1-biter Vi kan finne antall 1-biter i en bitsekvens ved traversere sekvensen og telle opp de 1-bitene vi finner. En metode for dette kan kodes slik:
public static int antallEnBiter(int n) { int antall = 0; for (; n != 0; n >>>= 1) // forskyver i n if ((n & 1) != 0) antall++; // sjekker siste bit return antall; } Programkode 1.7.14 j)
I flg. eksempel finner metoden antallet 1-biter samtidig som alle bitene skrives ut:
int n = 123456789; int antall = antallEnBiter(n); String biter = Integer.toBinaryString(n); System.out.println(biter + " " + antall); // Utskrift: 111010110111100110100010101 16 Programkode 1.7.14 k)
I Programkode 1.7.14 j) må hele bitsekvensen traverseres hver gang og det betyr 32 iterasjoner. Heldigvis finnes det også her noen smarte idéer som kan løse problemet vesentlig mer effektivt. Vi bruker flg. bitsekvens som eksempel:
(1.7.14.14) n = 00000111010110111100110100010101 (n = 123456789)
Hvis vi legger sammen bitene i (1.7.14.14) får vi 16 siden 0-bitene ikke gir bidrag i en slik sum. Problemet kan derfor snus til det å finne tverrsummen av de binære sifrene til n.
Først et kort sidesprang. Hvordan kan vi finne tverrsummen av de desimale sifrene til et heltall? La f.eks. n = 57. Hvis n har maksimalt to siffer gjelder flg. formel:
Med n = 57 får vi n div 10 = 5 og dermed 57 − 9 · 5 = 57 − 45 = 12 som tverrsum.
Hvis n har maksimalt tre siffer gjelder:
Eksempel: La n = 638. Da er (n div 10) = 63 og (n div 102) = 6. Dermed blir tverrsummen til 638 lik 638 − 9 · 63 − 9 · 6 = 638 − 567 − 54 = 17.
Hvis et heltall er gitt i et annet tallsystem (et annet grunntall enn 10), finnes det en tilsvarende formel for å berege en tverrsum. La f.eks. n være gitt med to binære siffer:
For å vise (1.7.14.17) kan vi sette n = ab der a og b er enten 0 eller 1. Da vil n div 2 = a, dvs. lik en bitforskyvning på 1 mot høyre i n. Verdien til tallet n = ab er lik 2 · a + b. Dermed blir n – (n div 2) = 2 · a + b – a = a + b.
En bitsekvens på 32 biter (et int-tall) kan betraktes som 16 tall der hvert tall har to binære siffer. Poenget nå er å bruke (1.7.14.17) på hvert av de 16 sifferparene. La som eksempel a, b, c, d, e, f, g og h være de 8 siste binære sifrene i n. Vi grupperer dette i to og to siffer:
(1.7.14.18) m = · · · · ab cd ef gh
Vi skal nå bruke formel (1.7.14.17) på hvert par av siffer, dvs. på ab, cd, ef og gh. Men da må vi først konstruere en bitsekvens m som ser slik ut:
(1.7.14.19) m = · · · · 0a 0c 0e 0g
Dette får vi til ved å bruke bitsforskyvning og maskering. La k være den bitsekvensen som har 0 og 1 annenhver gang. Husk at 5 som heksadesimalt siffer, er lik 0101 på binærform. Dermed blir k = 0x55555555. Hvis vi først gjør en bitforskyvning på 1 mot høyre i n og så maskerer vekk annenhver bit ved hjelp av k, får vi den ønskede bitsekvensen:
| (1.7.14.20) | n | = | · · · · ab cd ef gh |
| n >> 1 | = | · · · · xa bc de fg | |
| k | = | · · · · 01 01 01 01 | |
| (n >> 1) & k | = | · · · · 0a 0c 0e 0g |
Differensen n – ((n >> 1) & k) utført som en vanlig heltallsdifferens, vil gi oss 16 differenser, dvs. . . . ab – 0a , cd – 0g , ef – 0e og gh – 0g. Men binæraritmetikken og (1.7.14.17) gjør at disse 16 differensene vil gi antall 1-ere blant de to sifrene. Med andre ord vil ab – 0a bli 10 = 2 hvis både a og b er lik 1, bli 01 = 1 hvis bare en av dem er lik 1 og bli lik 00 = 0 hvis begge er 0.
Flg. eksempel viser hvordan dette virker på en konkret bitsekvens:
n = 00 00 01 11 01 01 10 11 11 00 11 01 00 01 01 01
n >> 1 = 00 00 00 11 10 10 11 01 11 10 01 10 10 00 10 10
k = 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01
(n >> 1) & k = 00 00 00 01 00 00 01 01 01 00 01 00 00 00 00 00
n - (n >> 1) & k = 00 00 01 10 01 01 01 10 10 00 10 01 00 01 01 01
Figur 1.7.14.21
La m være bitsekvensen n – ((n >> 1) & k). Hvert av de 16 bitparene eller tallene i m har som verdi antallet 1 biter i de tilsvarende bitparene i n. Neste skritt er derfor å addere disse 16 tallene. Men da kan vi bruke teknikken fra Avsnitt 1.7.13, dvs. binæraddisjon i parallell. Først adderes to og to av de 16 tallene som hver har to binære siffer. Det gir oss åtte tall som hver har fire binære siffer. Så adderes to og to av disse og vi får fire tall som hver har åtte binære siffer. Denne siste delen blir slik som i Programkode 1.7.13 c) bortsett fra at nå starter vi et nivå før, dvs. med 16 tall. Dette kan kodes slik:
public static int antallEnBiter(int n) { n -= (n >> 1) & 0x55555555; n = (n & 0x33333333) + ((n >> 2) & 0x33333333); n = (n & 0xf0f0f0f) + ((n >> 4) & 0xf0f0f0f); n += (n >> 8); n += (n >> 16); n &= 0x7f; return n; } Programkode 1.7.14 l)
OBS. Java har allerede en metode maken til den i Programkode 1.7.14 l). Den heter bitCount og ligger i klassen Integer.
| 1. | Kjør Programkode 1.7.14 c) med andre (positive) verdier på n. Velg spesielt noen n-verdier av typen n = 2 k. |
| 2. | Gjør som i Oppgave 1, men bruk Programkode 1.7.14 d). |
| 3. | Argumentér for at Setning 1.7.14 b) er riktig. |
| 4. |
Kjør Programkode 1.7.14 e) med andre verdier på n (posistive
og negative). Sjekk at det blir samme svar som det metoden
numberOfLeadingZeros fra klassen Integer gir.
|
| 5. | Lag en metode som bruker idéen i Programkode 1.7.14 e). Dvs. en metode med n som parameter og som returnerer antallet ledende 0-biter i n. |
| 6. | Gjør om Programkode 1.7.14 g) til å ha en løkke istedenfor flere likeartede if-setninger. |
| 7. | Gjør om Programkode 1.7.14 g) slik at det blir utført færre operasjoner i de tilfellene parameterverdien n er liten, dvs. har mange ledende 0-biter. |
| 8. |
Sjekk hvordan metoden numberOfLeadingZeros i klassen Integer er kodet.
|
| 9. | Gjør om Programkode 1.7.14 h) til å ha en løkke istedenfor fem likeartede setninger. |
![]() 1.7.15 Gray-koder
1.7.15 Gray-koder
Det finnes 2 n forskjellige bitsekvenser med lengde n. Disse kan settes opp
i mange forskjellige rekkefølger. Det mest vanlige er å sette dem opp i stigende rekkefølge med
hensyn på den leksikografiske ordningen. Hvis vi tolker hver sekvens som et ikke-negativt heltall
på binærform, svarer det til den vanlige ordningen med hensyn på tallstørrelse.
La for eksempel n = 3. De 8 bitsekvensene får da denne rekkefølgen:
I den leksikografiske rekkefølgen vi antall biter som er forandret fra en bitsekvens til den neste, variere. Fra 001 til 010 er to biter forandret, fra 010 til 011 er bare den siste biten forandret, mens det fra 011 til 100 er en forandring i alle tre bitene.
Spørsmål: Er det mulig å sette opp de 2 n bitsekvensene med lengde n i en rekkefølge slik at det kun er én bit som er forandret fra en bitsekvens til den neste i rekkefølgen?
Svaret på spørsmålet er ja. Det finnes mange rekkefølger som oppfyller ønsket. Antallet kan imidlertid reduseres hvis vi i tillegg krever at rekkefølgen skal starte med 0-sekvensen, dvs. med den sekvensen som bare har 0-biter. Det er også vanlig å kreve at rekkefølgen er syklisk. Hvis bitsekvensene hadde vært satt opp i en sirkel, ville den første være den som kommer etter den siste. Vi sier derfor at den er syklisk hvis forskjellen også mellom den siste og den første er bare i én bit.
La for eksempel n = 3. Se på flg. tre rekkefølger av de 8 bitsekvensene:
000 001 011 010 110 111 101 100
000 001 011 111 101 100 110 010
000 100 110 010 011 111 101 001
Figur 1.7.15 a)
Vi ser at alle tre tilfellene i Figur 1.7.15 a) oppfyller kravene, dvs. at rekkfølgen skal starte med 0-sekvensen og ha en forskjell i kun én bit fra en sekvens til den neste (inklusiv siste til første). Det finnes ytterligere 9 rekkefølger til for tilfellet n = 3. Se Oppgave 1.
En rekkefølge som oppfyller disse kravene kalles en Gray-kode. Navnet Gray kommer fra Frank Gray, Bell Labs som i 1953 fikk patentert en bestemt anvendelse av slike bitsekvenser. Men den typen koder var imidlertid i bruk lenge før ham.
Gray-koder kan lages på flere måter. Hvis vi f.eks. har en Gray-kode for en bestemt n, kan den brukes til å finne en Gray-kode for n + 1. Se på flg. eksempel der n = 2:
- Gitt Gray-kode for n = 2: 00 01 11 10
- Legg til den speilvendte koden: 00 01 11 10 10 11 01 00
- Legg på en ekstra 0-bit foran i første halvpart av bitsekvensene og en ekstra 1-bit foran i resten av dem: 000 001 011 010 110 111 101 100
Idéen over er generell. En Gray-kode for n og dens speilvending vil hver for seg oppfylle kravet om en forskjell i kun én bit fra en bitsekvens til den neste i rekkefølgen. Dette vil også gjelde hvis det settes en ekstra 0-bit eller en ekstra 1-bit først. Den siste i Gray-koden for n og den første i speilvendigen er like. Settes det en 0-bit foran i den ene og en 1-bit foran i den andre får vi to bitsekvenser på lengde n + 1 som er forskjellige kun i den første biten. Den første i Gray-koden for n og den siste i speilvendingen er også like. Setter vi på henholdsvis 0 og 1 som ekstra første bit skiller også de seg kun i den første biten. Når dette til slutt skjøtes sammen får vi en Gray-kode for n + 1.
Vi kan la hver bitsekvens være representert ved hjelp av en tegnstreng. Dermed kan en Gray-kode for n representeres ved hjelp av en String-tabell av lengde 2 n. Flg. metode, som bruker idéen over, returnerer en String-tabell som inneholder en Gray-kode for n. Hvis n = 0, sier vi at den tomme bitsekvensen er Gray-kode:
public static String[] gray(int n) { int m = 1 << n; // m lik 2 opphøyd i n String[] g = new String[m]; // tabell for gray-koden g[0] = ""; // den "tomme" koden for (int k = 1; k < m; k = 2*k + 1) // k = 1, 3, 7, 15, . . { int i = 0, j = k; while (i < j) // oppdaterer g[0:k] { g[j] = "1" + g[i]; j--; // setter 1 først g[i] = "0" + g[i]; i++; // setter 0 først } } return g; // returnerer tabellen med gray-koden } Programkode 1.7.15 a)
Programkode 1.7.15 a) kan brukes slik:
int n = 3; // Gray-kode for n = 3 String[] g = gray(n); for (String s : g) System.out.print(s + " "); // Utskrift: 000 001 011 010 110 111 101 100 Programkode 1.7.15 b)
Vi kan lage det slik at Gray-koden returneres som en int-tabell der hver bitsekvens er representert ved hjelp av bitene i en int-verdi. Det vil bli mer effektivt. Se Oppgave 3.
I Programkode 1.7.15 a) settes henholdsvis en 0-bit og en 1-bit som ekstra bit først. Men vi får også en Gray-kode hvis vi snur på idéen, dvs. hvis vi isteden setter henholdsvis en 0-bit og en 1-bit som ekstra bit bakerst. Da vil vi for tilfellet n = 3 ende opp med den tredje av de Gray-kodene som står i Figur 1.7.15 a). Se Oppgave 4.
Vi ser på nytt på flg. Gray-kode for tilfellet n = 3:
Vi kan se på hver bitsekvens på tre biter som en tabell indeksert fra 0 til 2. For hver av disse er det en endring kun på én plass fra en bitsekvens til den neste. Vi starter med 000. Sekvensen 001 får vi ved å endre 000 på plass eller indeks 2, dvs. den lengst til høyre. Videre kommer vi til 011 ved å endre 001 på plass 1, så fra 011 til 010 ved å endre biten på plass 2, så derfra til 110 ved å endre på plass 0, osv. Vi får denne tallfølgen for endringsindekser:
Bruker vi n = 4 i Programkode 1.7.15 b), får vi flg. utskrift:
1100 1101 1111 1110 1010 1011 1001 1000
Også her kan vi sette opp tallfølgen for endringsindekser. Den blir slik:
For det første, hvis vi skal oppgi en Gray-kode, kan vi isteden oppgi tallfølgen for endringsindekser. Den tar mindre plass enn selve Gray-koden. For det andre er det åpenbart noe systematisk med tallene i tallfølgen for endringsindekser. Det kan illustreres ved hjelp av følgende trestrukturer:
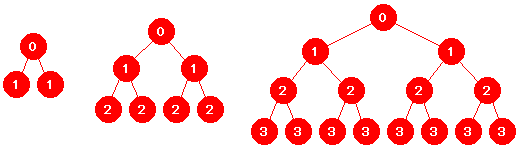 |
| Figur 1.7.15 b): Tre perfekte binære trær med 3, 7 og 15 noder |
I Figur 1.7.15 b) har hver node fått som verdi det nivået som noden befinner seg på. Rotnoden er på nivå 0, osv. Hvis vi i hvert tre skriver ut nodeverdiene i inorden (se Avsnitt 5.1.7 i Kapittel 5), får vi flg utskrifter:
2 1 2 0 2 1 2
3 2 3 1 3 2 3 0 3 2 3 1 3 2 3
Linje 2 og 3 er de tallfølgene vi har sett tidligere for endringsindekser for n = 3 og 4. Den første linjen er en tallfølge for tilfellet n = 2. Denne trestrukturen forteller at vi på en enkel måte kan få skrevet ut en Gray-koden ved hjelp av flg. rekursive metode:
public static void gray(int[] a, int k) { if (k < a.length - 1) gray(a,k+1); // et rekursivt kall a[k] ^= 1; // bytter verdi på plass k for (int i : a) System.out.print(i); // skriver ut bitsekvensen a System.out.print(' '); // et mellomrom if (k < a.length - 1) gray(a,k+1); // et rekursivt kall } Programkode 1.7.15 c)
I flg. eksempel brukes Programkode 1.7.15 c) til å skrive ut en Gray-kode for n = 3:
int[] a = {0,0,0}; // 0-sekvensen for n = 3 for (int i : a) System.out.print(i); // skriver ut 0-sekvensen System.out.print(' '); // et mellomrom gray(a,0); // kaller rekursiv metode // Utskrift: 000 001 011 010 110 111 101 100 Programkode 1.7.15 d)
Det finnes som nevnt mange Gray-koder. Vi får imidlertid en bestemt Gray-kode når vi bruker konstruksjonsteknikken beskrevet over. Dvs. den som tar utgangspunkt i en «tom» kode og så fortløpende speilvender og legger til 0- og 1-biter foran. Både Programkode 1.7.15 a) og Programkode 1.7.15 c) gir denne Gray-koden. På grunn av speilvendingene kalles dette den binærspeilvendte Gray-koden (eng: binary reflected Gray code).
Gitt at vi har den binærspeilvendte Gray-koden for en verdi n. La k være et heltall fra 0 til 2n. Er det da mulig å finne den bitsekvensen som er på plass k i rekkefølgen på en direkte måte?
| g | 0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| g | 0 | 1 | 3 | 2 | 6 | 7 | 5 | 4 | 12 | 13 | 15 | 14 | 10 | 11 | 9 | 8 |
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| k | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| Figur 1.7.15 c): Den binærspeilvendte Gray-koden for n = 4 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Første rad i Figur 1.7.15 c) inneholder den binærspeilvendte Gray-koden for n = 4 og neste rad hver bitsekvens tolket som et heltall. Den tredje inneholder indeksene eller posisjonene k til kodens bitsekvenser g og den siste raden indeksene på binærform (skrevet med fire binære siffer). Vi ser at hvis første binære siffer i k er 0, så er første siffer i tilhørende g også 0, og hvis første binære siffer i k er 1, så er første siffer i tilhørende g også 1. Videre, hvis første og andre siffer i k er like, så er andre siffer i tilhørende g lik 0, og hvis første og andre siffer i k er ulike, så er andre siffer i tilhørende g lik 1. Dette fortsetter: hvis andre og tredje siffer i k er like, så er tredje siffer i tilhørende g lik 0, og hvis andre og tredje siffer i k er ulike, så er tredje siffer i tilhørende g lik 1. Osv.
La x og y være to bit-variabler, dvs. x og y kan ha 0 eller 1 som verdier. Vi bruker her symbolet ^ for operatoren xeller (eksklusiv eller). Da gjelder
- x ^ y = y ^ x = 0 hvis x og y har like verdier
- x ^ y = y ^ x = 1 hvis x og y har ulike verdier
- x ^ 0 = 0 ^ x = x
- x ^ x = 0
La nå k ha fire binære siffer. La sifrene hete a, b, c og d. Da vil de fire sifrene i den tilhørende bitsekvensen g (i den binærspeilvendte Gray-koden) for n = 4 være gitt ved:
Hvis bitene i k er representert ved hjelp av int-tabell, kan idéen over kodes slik:
int[] k = {1,0,1,0}; // svarer til k = 10 int[] g = (int[])k.clone(); // g starter som en kopi av k for (int i = 1; i < g.length; i++) { g[i] = k[i-1] ^ k[i]; } Tabell.skriv(g); // Utskrift: 1 1 1 1 Programkode 1.7.15 e)
Vi ser at utskriften i Programkode 1.7.15 e) nettopp er bitsekvens nr. 10 i den binærspeilvendte Gray-koden.
Vi får imidlertid langt mer effektiv kode hvis bitene i k er representert ved bitene i en int-variabel. Da virker operatoren ^ på alle bitene på en gang. I tillegg kan vi bruke bitforskyvningsoperatoren >> (eller eventuelt >>>). Dette kan illustreres slik hvis vi tenker oss at k har kun fire biter og at de heter a, b, c og d :
| k | = | a | b | c | d |
| k >> 1 | = | 0 | a | b | c |
| k ^ (k >> 1) | = | a | a ^ b | b ^ c | c ^ d |
Dette kan kodes slik:
int k = 10; // k har bitene 00. . . 01010 int g = k ^ (k >> 1); System.out.println(g); // Utskrift: 15 Programkode 1.7.15 f)
Utskriften i Programkode 1.7.15 f) blir 15 og det er som forventet siden binærkoden til heltallet 15 er lik 1111.
Idéen i Programkode 1.7.15 f) kan brukes til å skrive ut alle bitsekvensene i Gray-koden fortløpende. Da får vi imidlertid utskriften som heltall og ikke som bitsekvenser. Men det kan vi løse ved å lage kode som skriver ut bitene i et heltall. Se Oppgave 5.
for (int k = 0; k < 16; k++) { int g = k ^ (k >> 1); // bitsekvens nr. k i Gray-koden System.out.print(g + " "); } // Utskrift: 0 1 3 2 6 7 5 4 12 13 15 14 10 11 9 8 Programkode 1.7.15 g)
Vi kan også gå motsatt vei. Hvis vi har gitt en bitsekvens i den binærspeilvendte Gray-koden for en betsemt n, så kan vi finne hvilket nummer i rekkefølgen den har. Vi bruker her n = 4 som eksempel. De fire bitene kan som før hete a, b, c og d. Poenget nå er å kunne komme fra a , a ^ b , b ^ c og c ^ d og over til a, b, c og d.
| g | = | a | a ^ b | b ^ c | c ^ d |
| g >> 1 | = | 0 | a | a ^ b | b ^ c |
| g ^ (g >> 1) | = | a | b | a ^ c | b ^ d |
Resultatet over fikk vi ved å bruke regnereglene for operatoren ^. Vi kan gjenta dette, men nå med det vi fikk som resultat over som g og med en forskyvning på 2 enheter:
| g | = | a | b | a ^ c | b ^ d |
| g >> 2 | = | 0 | 0 | a | b |
| g ^ (g >> 2) | = | a | b | c | d |
Dette kan tilsammen oversettes til flg. kode:
int g = 15; // bitsekvensen 1111 i Gray-koden g = g ^ (g >> 1); // eller g ^= g >> 1; g = g ^ (g >> 2); // eller g ^= g >> 2; System.out.println(g); // Utskrift: 10 Programkode 1.7.15 h)
En bitsekvens gitt ved hjelp av bitene i en int-variabel kan ha opptil 32 biter. For å takle det kan vi bare gå videre i Programkode 1.7.15 h), dvs. i tillegg bitforskyve 4, 8 og 16 enheter. Dette settes sammen til en metode som til en bitsekvens i den binærspeilvendte Gray-koden finner den neste i rekkefølgen. Det gjøres ved at vi først finner hvilket nummer bitsekvensen har i rekkefølgen, så økes det med 1 og så finner vi tilhørende bitsekvens til den verdien:
public static int nesteGray(int g) { g ^= g >>> 1; // finner hvor g ligger i rekkefølgen g ^= g >>> 2; g ^= g >>> 4; g ^= g >>> 8; g ^= g >>> 16; g++; // øker med 1 return g ^ (g >>> 1); // finner tilhørende bitsekevns } Programkode 1.7.15 i)
Vi vet (se trestrukturen i Figur 1.7.15 b) at for å komme til neste bitsekvens i rekkefølgen er det annen hver gang den siste biten som må endres, fjerde hver gang den nest siste biten, osv. Men når g representerer en vilkårlig bitsekvens er det faktisk nødvendig å gjøre så mye arbeid som det som gjøres i Programkode 1.7.15 i) for å sikre at rett bit endres. Obs. Det er litt mer komplisert å lage en nesteGray-metode hvis bitsekvensen er representert ved hjelp av tallene 0 og 1 i en int-tabell, men det er de samme idéene som brukes. Se Oppgave 6.
Metoden nesteGray i Programkode 1.7.15 i) kan brukes til å skrive ut én og én bitsekvens i rekkefølgen. Den første er 0-sekvensen representert ved g = 0. Men hva er den siste? Speilvendingsteknikken gjør at etter speilvendingen havner 0-sekvensen bakerst og så settes det på en 1-bit foran. Det blir dermed den bitsekvensen som har en 1-bit først og deretter 0-biter på de neste n – 1 plassene. Det er det samme som tallet 2n–1 eller lik 1 << (n – 1) om en vil. Dermed kan vi få alle bitsekvensene skrevet ut (som heltall) på denne måten:
int n = 4; // Gray-kode for n = 4 int g = 0; // 0000 er første bitsekvens int siste = 1 << (n - 1); // 1000 er siste bitsekvens while (g != siste) { System.out.print(g + " "); g = nesteGray(g); } System.out.println(siste); // Utskrift: 0 1 3 2 6 7 5 4 12 13 15 14 10 11 9 8 Programkode 1.7.15 j)
De 2n bitsekvensene med n biter kan tolkes som hjørnene i en n-dimensjonal kubus (terning). Til venstre Figur 1.7.15 d) under er det tegnet en terning. Hvis vi tenker oss at den ligger i et x,y,z-koordinatsystem, vil de tre bitene utgjøre de tre koordinatene. F.eks. vil 000 svare til origo og 100 det punktet som har 1, 0 og 0 som henholdsvis x-, y- og z-koordinat.
 |
| Figur 1.7.15 d): En terning (til venstre) med hjørner og kanter som en graf |
Koordinatene til to nabohjørner i en terning er forskjellige bare på én plass. Hjørnene og kantene kan ses på som nodene (hjørnene) og kantene i en graf. Til høyre i Figur 1.7.15 d) er dette tegnet som en plan graf (dvs. som en graf der ingen kanter skjærer hverandre). En lukket Hamilton-vei gjennom en graf er en vei som starter i en node, som passerer hver av de andre nodene én og bare én gang og som ender der den startet.
 |
| Figur 1.7.15 e) |
Beskrivelsen over gir at en Gray-kode for n er ekvivalent med en lukket Hamilton-vei i en n-dimensjonal terning med start i origo. I tilfellet n = 3, har vi Gray-koden 000, 001, 011, 010, 110, 111 101 og 100. Den svarer til den lukkede Hamilton-veien markert med røde piler i Figur 1.7.15 e) til venstre.
Det er nevnt over at det finnes 12 forskjellige Gray-koder for n = 3. Det betyr også at det finnes 12 forskjellige lukkede Hamilton-veier med start i 000. Vi ser at ut fra 000 er det tre muligheter. Det er til 100, 010 eller 001. Hver av disse tre mulighetene gir 4 Hamilton-veier. Se Oppgave 7.
| 1. | Det er 2 forskjellige Gray-koder for n = 2. Finn dem! Det er 12 forskjellige for n = 3. Tre av dem er satt opp i Figur 1.7.15 a). Finn flere! |
| 2. | Som nevnt er det 12 Gray-koder for n = 3. To er ekvivalente hvis vi får den andre fra den første ved at det i hver bitsekvens i den første gjøres samme type omstokking. De 12 utgjør to ekvivalensklasser. Finn en Gray-kode fra hver av de to klassene. |
| 3. | Gjør om Programkode 1.7.15 a) slik at Gray-koden returneres som en int-tabell der bitene i hvert tabellelement repepresentere tilhørende bitsekvens i Gray-koden. |
| 4. | Gjør om Programkode 1.7.15 a) slik at 0- og 1-biten isteden legges til bakerst i tegnstrengen. Hva slags Gray-kode vil Programkode 1.7.15 b) da skrive ut. |
| 5. | Utvid Programkode 1.7.15 g) slik at bitene skrives ut istedenfor tallverdiene. |
| 6. | Lag en nesteGray-metode (se Programkode 1.7.15 i)) der Gray-koden er en int-tabell. |
| 7. | Finn alle de lukkede Hamilton-veiene som starter i 000 i Figur 1.7.15 e). |
![]() 1.7.16 Sjakkbrett og dronninger
1.7.16 Sjakkbrett og dronninger
Her skal vi komme frem til den «ultimate» metoden for å finne antallet lovlige
dronningoppstillinger på et n × n − sjakkbrett.
Vi skal ikke bruke permutasjoner av tallene fra 0 til n − 1 til
å løse oppgaven, men isteden arbeide på bitnivå.
 |
| Figur 1.7.16 a) : 8 × 8 − sjakkbrett − dronninger i radene 0, 1, 2 og 3 |
I Figur 1.7.16 a) er det plassert dronninger i de fire øverste radene, dvs. radene 0, 1, 2 og 3. Ingen av disse slår hverandre. På de tre brettene i figuren er det satt på røde kryss i rad 4. Brettet lengst til venstre hør røde kryss i de posisjonene som beherskes av dronningene over ved at de kan slå bidiagonalt, dvs. på skrå ned mot venstre. Brettet på midten har røde kryss der det allerede står dronninger i de tilhørende kolonnene. Til slutt har brettet lengst til høyre røde kryss der dronningene over kan slå diagonalt, dvs. på skrå ned mot høyre.
Skal en dronning plasseres i rad 4 må posisjonene med røde kryss unngås. I Figur 1.7.16 a) er rad 4 tatt ut fra hvert av brettene og satt opp som egen tabell nederst. Kolonnene på brettene og indeksene i tabellene nederst er nummerert i motsatt rekkefølge enn det vanlige. Det er fordi tabellene skal representeres ved hjelp av heltall. I et heltall indekseres bitene fra høyre mot venstre. Den siste biten, dvs. den lengst til høyre, har indeks 0, osv. Et rødt kryss betyr at biten er 1 og en tom rute at biten er 0. Vi kan «legge sammen» de tre tabellene:
| Figur 1.7.16 b) : 6 røde kryss |
La de tre tabellene nederst i Figur 1.7.16 a) være representert ved heltallsvariablene b, k og d. Bokstaven b står for bidiagonal, k for kolonne og d for diagonal. Vi «legger sammen» de røde kryssene ved å bruke binær eller. Variabelen sum svarer til tabellen i Figur 1.7.16 b):
int b = 48; // 48 = 00110000 int k = 156; // 156 = 10011100 int d = 37; // 37 = 00100101 int sum = b | k | d; // 189 = 10111101
Variablene b, k og d representerer posisjonene i en rad på et n × n − brett. Det betyr spesielt at det kun er de n siste bitene som vi bruker og at de 32 − n første bitene alltid er 0-biter. Dermed vil også 32 − n første bitene i sum alltid være 0-biter.
Det er umulig å plassere en dronning på en rad hvis de n bitene i sum er 1-biter. (Som nevnt over er de 32 − n første bitene alltid 0-biter.) Med tanke på beskrivelsen over betyr det at hele raden har røde kryss. Vi kan lett lage et heltall der de n siste bitene er 1-biter og resten er 0-biter. Vi bruker navnet full på en variabel som har en slikt bitmønster:
int full = (1 << n) - 1; // de n siste bitene i full er 1-biter
Vi kan dermed avgjøre om det er mulig å plassere en dronning noe sted på en rad ved å sammenligne sum med full. Hvis de er ulike, er det minst én ledig plass.
Neste oppgave er å finne posisjonen p til en ledig plass hvis det ikke er fullt. Flg. kodebit gir oss et heltall p som har en 1-bit i en posisjon som er «ledig» og 0-biter ellers. Hvis det er flere ledige posisjoner i sum får vi den bakerste (lengst til høyre) av dem (se Oppgave xx):
int p = (sum + 1) & ~sum; // posisjonen til bakerste 0-bit i sum
Vi setter en dronning på raden ved å sette en 1-bit på den ledige plassen i variablene sum, b, k og d. Det svarer til å sette et rødt kryss i de tre tabellene nederst i Figur 1.7.16 a) og i tabellen i Figur 1.7.16 b) .
Deretter ser vi på neste rad. Vi finner hvilke posisjoner som er opptatt der ved 1) å gjøre
en bitforskyvning mot venstre av bitene i b siden dronningene kan slå bidiagonalt
og 2) en bitforskyvning mot høyre av bitene i d siden dronningene også kan slå diagonalt.
De kan også slå vertikalt langs en kolonne, men det er det tatt vare på i
variabelen k.
En dronning kan slå bidiagonalt kun innenfor brettet. Hvis en forskyvning i b
fører en 1-bit «utenfor» brettet, må 1-biten fjernes fra sum og det skjer ved
koden sum = full & (b | k | d).
Vi oppsummerer dette i den rekursive metoden antall. Den starter øverst på brettet og setter én dronning per rad så lenge det er mulig. Passerer vi den siste raden har vi funnet en lovlig oppstilling. Kommer vi til en full rad, trekker metoden seg tilbake fra raden og sjekker om det er mulig å sette en dronning et annet sted i raden over. Osv. Opptellingen av lovlige plasseringer skjer ved hjelp av returverdiene. Hvert rekursivt kall returnerer det antallet lovlige plasseringer som starter med de valgte dronningene på de r + 1 øverste radene.
public static int antall(int r, int b, int k, int d, int n) { if (r == n) return 1; // ny lovlig oppstilling int full = (1 << n) - 1; // n stykker 1-biter int sum = full & (b | k | d); // slår sammen b, k og d int antallLovlige = 0; // hjelpevariabel while (sum != full) // så lenge raden ikke er full { int p = (sum + 1) & ~sum; // posisjon til ledig plass sum |= p; // setter dronning på plassen antallLovlige += // går ned til neste rad antall(r + 1, (b | p) << 1, k | p, (d | p) >> 1, n); } return antallLovlige; } Programkode 1.7.16 a)
Legg Programkode 1.7.16 a) i klassen Dronning (se Avsnitt 1.3.16 og Avsnitt 1.5.6). Flg. eksempel viser hvordan metoden kan brukes til å finne antallet på et 8 × 8 − brett:
System.out.println(Dronning.antall(0,0,0,0,8)); // Utskrift: 92
Kan antall-metoden effektiviseres? Ideene kan nok på noen punkter kodes litt annerledes, men det vil føre til kun marginale forbedringer. Men arbeidsmengden kan imidlertid halveres ved hjelp av brettets symmetri. Se diskusjonen i tilknytning til Figur 1.3.16 b) i Avsnitt 1.3.16. Dermed holder det å sette dronninger i halvparten av øverste rad på brettet.
La p være en posisjon på øverste rad. La parameterne b , k og d ha en 1-bit i hhv. posisjon p + 1, p og p − 1. Et kall på antall-metoden med dette som parameterverdier og med r lik 1, vil gi oss antallet lovlige oppstillinger der det står en dronning i posisjon p på øverste rad. Hvis n er et partall, holder det å sette dronninger på halvparten av plassene og så doble resultatet. Hvis n er odde, må vi passe på å ta med de tilfellene der den øverste dronningen står på midten, kun én gang. Metoden legges i klassen Dronning med navn antallB for å skille den fra andre antall-metoder. B står for det at løsningsteknikken er basert på bitoperatorer:
public static int antallB(int n) { int b = 2, k = 1, d = 0; // startverdier for parametrene int antall = 0; while (k < (1 << n/2)) // går midtveis i øverste rad { antall += antall(1,b,k,d,n); // dronning på samme plass øverst d = k; k = b; b <<= 1; // endrer verdier på parametrene } return antall*2 + ((n & 1) == 0 ? 0 : antall(1,b,k,d,n)); } Programkode 1.7.16 b)
Flg. eksempel viser hvordan vi kan finne antallet forskjellige og lovlige dronningoppstillinger på et n × n − brett for n fra 12 til 18, ved å bruke metoden i Programkode 1.7.16 b):
for (int n = 12; n < 19; n++) { long tid = System.currentTimeMillis(); int antall = Dronning.antallB(n); tid = System.currentTimeMillis() - tid; System.out.printf("%2d%12d%10d\n",n,antall,tid); } // Utskrift: // 12 14200 16 // 13 73712 63 // 14 365596 375 // 15 2279184 2500 // 16 14772512 15703 // 17 95815104 114734 // 18 666090624 785625 Programkode 1.7.16 c)
Algoritmen er av orden n! og det fremgår også av utskriften i Programkode 1.7.16 c). Det aktuelle tidsforbruket er avhengig av hvor rask prosessor en har. I dette tilfellet er det en Pentium 4, 2.8 GHz med Windows XP, Java HotSpot og JDK 1.6.0_1. Men forholdet mellom tidsforbruket for to forskjellige verdier av n, er i hovedsak uavhenig av prosessorhastighet. Det ser ut til at tidsforbruket for neste verdi av n er omtrent det vi får ved å gange det for n med et tall litt mindre enn n/2. Tidsforbruket for n = 18 var 786 sekunder eller ca. 13 minutter. Dermed kan man spå at tidsforbruket for n = 19 vil bli 90 - 100 minutter.
Problemet med å finne antallet lovlige dronningoppstillinger er løst for alle verdier av n opp til og med 26. Tilfellet 26 ble løst i 2009 og svaret var 22317699616364044. Når en ser hvor mye tidsforbruket øker for hver n, kan en lure på hvordan det ble løst. Se Technische Univeristet Dresden.
Det en kan gjøre er å dele opp oppgaven og løse delene på forskjellige maskiner. Vi kaller det parallellprosessering. La oss ta n = 19 som eksempel. Metoden i Programkode 1.7.16 b) vil da kalle metoden i Programkode 1.7.16 a) 10 ganger. Det svarer til at vi setter dronninger kun på de 10 første plassene i øverste rad på brettet. Men disse 10 kallene kan gjøres hver for seg på 10 forskjellige datamaskiner. Tiden dette vil ta på hver av datamaskinene vil være litt mindre enn det det tar å kjøre Programkode 1.7.16 b) for n = 18. Med andre ord vil vi med 10 datamaskiner av samme type som nevnt over, kunne løse oppgaven for n = 19 innenfor rammen av 13 minutter.
Med tanke på n = 20 kan vi gå et skritt videre. Setter vi en dronning i posisjon 0 i øverste rad, er det mulig å sette dronninger fra og med posisjon 2 og til og med posisjon 19 i nest øverste rad − dvs. 18 muligheter. Setter vi en dronning i posisjon 1 i øverste rad, blir det 17 muligheter i nest øverste rad. Osv. Tilsammen (n − 1)(n − 1)/2 = 171 muligheter. Med andre ord kan dette løses som 171 deloppgaver og med like mange datamaskiner kan vi finne løsningen også for n = 20 innenfor rammen av 13 minutter.
Flg. eksempel viser hvordan vi finner antallet oppstillinger på et 20 × 20 − brett som har en dronning i posisjon 0 i øverste rad og en i posisjon 2 i nest øverste rad:
System.out.print(Dronning.antall(2,12,5,2,20)); // Svar: 26141384 Programkode 1.7.16 d)
De som løste dette for n = 26 brukte over et halv år. Se Technische Univeristet Dresden.
Unike løsninger To løsninger som er slik at den ene kan oppnås fra den andre ved speilinger og/eller rotasjoner, kalles ekvivalente. Løsninger som ikke er ekvivalente kalles unike. Se Avsnitt 1.3.16. Det er ikke kjent andre teknikker for å finne unike løsninger enn å teste de løsningene en finner når en leter etter alle løsningene. Programkode 1.7.16 a) gir oss ikke direkte de permutasjonene som representerer lovlige oppstillinger. Men vi kan få tak i dem ved å bruke en int-tabell som en tilleggsparameter.
Men først må vi ha en metode som gjør om tabellens posisjonsverdier til heltall fra 0 til n − 1. Et posisjontall er et heltall der det står en 1-bit i en bestemt posisjon og som har 0-biter på alle andre plasser. Et slikt heltall er alltid på formen 2k og det er verdien til k vi skal ha tak i. Til det bruker vi logaritmen med grunntall 2 siden flg. alltid er sant:
(1.7.16.1) log 2 (2k ) = k
Setning 1.7.14 b) sier at hvis x er et positivt heltall, vil log 2 (x) avrundet nedover til nærmeste heltall være én mindre enn antall signifikante binære siffer i x. Hvis x = 2k betyr det at log 2 (x) blir heltallig. Videre vil antallet signifikante binære siffer være det samme som 32 minus antallet ledende 0-er i binærrepresentasjonen til x. Flg. metode som legges i klassen Dronning, konverterer en heltallstabell a der hvert element er på formen 2k, til en tabell b der de tilsvarende elementene får verdien k:
public static int[] konverter(int[] a) { int[] b = new int[a.length]; for (int i = 0; i < b.length; i++) b[i] = 31 - Integer.numberOfLeadingZeros(a[i]); return b; } Programkode 1.7.16 e)
Flg. antall-metode tar utgangspunkt i Programkode 1.7.16 a), men med en int-tabell som tilleggsparameter. Den får, for hver rad på brettet, posisjonsverdien til en dronning. Når vi finner en lovlig oppstilling, blir int-tabell konvertert til en tabell med en permutasjon av tallene fra 0 til n − 1 som innhold. Videre bruker vi Programkode 1.3.16 j) til å sjekke om tabellen representerer en oppstilling som er den første i leksikografisk orden:
public static int antall(int r, int b, int k, int d, int n, int[] a) { if (r == n) { if (førstLeksikografisk(konverter(a))) return 1; } int full = (1 << n) - 1; // n stykker 1-biter int sum = full & (b | k | d); // slår sammen b, k og d int antallUnike = 0; // hjelpevariabel while (sum != full) // så lenge raden ikke er full { int p = (sum + 1) & ~sum; // posisjon til ledig plass sum |= p; // setter dronning på plassen a[r] = p; // legger posisjonen i a antallUnike += // går ned til neste rad antall(r + 1, (b | p) << 1, k | p, (d | p) >> 1, n, a); } return antallUnike; // de unike løsningene } Programkode 1.7.16 f)
Hvis Programkode 1.7.16 f) legges i klassen Dronning, vil flg. eksempel vise hvordan metoden kan brukes til å finne antallet unike oppstillinger på et 8 × 8 − brett:
System.out.println(Dronning.antall(0,0,0,0,8,new int[8])); // 12
Programkode 1.7.16 f) teller kun opp en løsning hvis den kommer først leksikografisk blant de ekvivalente løsningene. En som kommer først leksikografisk må ha en dronning i første halvdel av øverste rad. Hvis ikke kan vi speile løsningen vertikalt og få en som kommer foran leksikografisk. Videre er det ikke nødvendig, hvis n er odde, å se på løsninger der en dronning står midt på øverste rad. Se Oppgave 7 i Avsnitt 1.5.6. Dermed kan vi lage en antall-metode som bruker bare halvparten så mye tid. Vi kaller den antallUB for å skille den fra andre antall-metoder i klassen Dronning:
public static int antallUB(int n) // legges i klassen Dronning { int b = 2, k = 1, d = 0; // startverdier for parametre int antallUnike = 0; // hjelpevariabel int[] a = new int[n]; // hjelpetabell while (k < (1 << n/2)) // går midtveis i øverste rad { a[0] = k; // dronning i kolonne k antallUnike += antall(1,b,k,d,n,a); // dronning i kolonne k d = k; k = b; b <<= 1; // endrer parameterverdiene } return antallUnike; } Programkode 1.7.16 g)
Programkode 1.7.16 g) må nødvendigvis bruke noe mer tid enn Programkode 1.7.16 b). Se Oppgave 4. Det å sjekke om en løsning er den første i leksikografisk orden vil kreve en del arbeid. Det er nok mulig å få redusert det arbeidet ved å bruke bitoperatorer, men det spørs om det har noe poeng å gjøre det. Vi kan uansett ikke finne de unike løsningene raskere enn vi finner alle løsningene.
| 1. | Finn hvor mange lovige oppstillinger det er på et 20 × 20 − brett med en dronning i posisjon 0 på øverst rad og i posisjon 3 på nest øverste rad. Se Programkode 1.7.16 d). |
| 2. | Programkode 1.7.16 d) gir antallet lovlige oppstillinger på et 20 × 20 − brett med en dronning i posisjon 0 i øverste rad og en dronning i posisjon 2 i nest øverste rad. Speilingen gir at det er det samme antallet som har en dronning i posisjon 19 i øverste rad og en dronning i posisjon 17 i nest øverste rad. Lag kode som gir det som resultat. |
| 3. | Bruk Programkode 1.7.16 b) som start
for å lage metoden int[] antallRad0(int n). Den skal returnere en heltallstabell
med (n + 1)/2 elementer der elementet med indeks i skal være antallet
lovlige oppstillinger på et n × n − brett
med en dronning i posisjon i på øverste rad på brettet. Vil antallet lovlige oppstillinger
variere mye med hensyn på hvor en dronning står i øverste rad? Er det flest hvis dronningen
står på enden av raden eller er det flest hvis den står på midten?
|
| 4. | Lag et program maken til det i Programkode 1.7.16 c), men der metoden som finner unike løsninger (Programkode 1.7.16 g) inngår. Blir tidsforbruket mye større? |
| 5. | Gjør som i Oppgave 3, men la metoden returnere en tabell med n/2 elementer
der elementene er antallet unike løsninger. La metoden hete antallUnikeRad0.
|
![]() 1.7.17 class BitSet
1.7.17 class BitSet
I Avsnitt 1.7.11 så vi på hvordan et heltall (en int-variabel)
kunne brukes som en boolsk tabell. Det betyr at et heltall også kan brukes til å representere en
mengde av heltall. F.eks. kan mengden A = {4,5,6,7,8} være representert ved et heltall
der det er 1-biter i posisjonene 4, 5, 6, 7 og 8 og 0-biter ellers.
Tabell 1.7.11
viser de bitoperasjonene vi kan bruke for å aksessere og endre de enkelte bitene i et heltall.
Java-klassen BitSet benytter en slik teknikk, men bruker en variabel av typen long (eller egentlig en long-tabell). Den har fire set-metoder som kan brukes til å sette 0 eller 1 i en bestemt posisjon (eller bestemte posisjoner) i heltallet:
1. public void set(int indeks); // 1 i posisjon indeks 2. public void set(int fra, int til); // 1 i [fra:til> 3. public void set(int indeks, boolean verdi); // 1 eller 0 i indeks 4. public void set (int fra, int til, boolean verdi); // 1 eller 0 i [fra:til> Programkode 1.7.17 a)
Hvis vi skal opprette mengden {4,5,6,7,8}, kan vi bruke en av de to metodene
som setter verdier i et (halvåpent) intervall, f.eks. nr. 2 (men også
nr. 4 hvis verdi settes til true):
BitSet A = new BitSet(); // en tom mengde A.set(4,9); // {4, 5, 6, 7, 8} System.out.println("A = " + A); // bruker klassens toString-metode // Utskrift: A = {4, 5, 6, 7, 8} Programkode 1.7.17 b)
Mengden {4,5,6,7,8} har en sammenhengende rekke av heltall. Hvis den ikke har det, kan vi opprette den ved å sette 1-ere i de posisjonene som svarer til mengdens elementer. La f.eks. A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}, dvs. oddetallene som er mindre enn 20:
BitSet A = new BitSet(); // en tom mengde for (int i = 1; i < 20; i += 2) A.set(i); // A = {1, 3, . . , 19} System.out.println("A = " + A); // Utskrift: A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} Programkode 1.7.17 c)
Ved hjelp av metodene and og or kan vi finne snitt og union av to mengder:
BitSet A = new BitSet(); // A en tom mengde A.set(4,9); // A = {4, 5, 6, 7, 8} BitSet B = new BitSet(); // B en tom mengde B.set(6,11); // B = {6, 7, 8, 9, 10} A.and(B); // A = A snitt B System.out.println("A = " + A); // Utskrift: A = {6, 7, 8} Programkode 1.7.17 d)
Legg merke til at metoden and er en oppdateringsmetode. Dvs. at setningen A.and(B) gjør det samme som flg. mengdeformel: A = A ∩ B . Hvis en vil finne A ∩ B som en ny mengde uten at A eller B endres, kan en først lage en kopi av A og så bruke kopien i metoden and:
BitSet A = new BitSet(); // en tom mengde BitSet B = new BitSet(); // en tom mengde A.set(4,9); // A = {4, 5, 6, 7, 8} B.set(6,11); // B = {6, 7, 8, 9, 10} BitSet S = (BitSet)A.clone(); // S er en kopi av A S.and(B); // S er nå lik A snitt B System.out.println("A = " + A + " B = " + B + " S = " + S); // Utskrift: A = {4, 5, 6, 7, 8} B = {6, 7, 8, 9, 10} S = {6, 7, 8} Programkode 1.7.17 e)
Utskriften i Programkode 1.7.17 e) viser at både A og B har beholdt sine verdier. Hvis en isteden vil finne A U B, er det bare å bytte ut and med or i koden over.
Det er også mulig å finne differensen mellom A og B, dvs. A − B. La m og n være to heltall. Hvis det er en 1-bit i samme posisjon i begge, vil det bli en 0-bit i den posisjonen i heltallet gitt ved m & ~n. Hvis det derimot er en 1-bit i m i samme posisjon som det er en 0-bit i n, vil heltallet m & ~n få en 1-bit i den posisjonen. Med andre ord kan bitoperatorene & og ~ brukes til å lage mengdedifferens. Klassen BitSet bruker en slik teknikk i metoden andNot:
BitSet A = new BitSet(); // en tom mengde BitSet B = new BitSet(); // en tom mengde A.set(4,9); // A = {4, 5, 6, 7, 8} B.set(6,11); // B = {6, 7, 8, 9, 10} BitSet S = (BitSet)A.clone(); // S er en kopi av A S.andNot(B); // S er nå lik A - B System.out.println("A = " + A + " B = " + B + " S = " + S); // Utskrift: A = {4, 5, 6, 7, 8} B = {6, 7, 8, 9, 10} S = {4, 5} Programkode 1.7.17 f)
Under er det ramset opp en del andre metoder fra klassen BitSet:
public void clear(int indeks); // setter 0 i posisjon indeks public void clear(int fra, int til); // setter 0 i [fra:til> public void clear(); // setter 0 i alle posisjoner public boolean get(int indeks); // finner biten i posisjon indeks public BitSet get(int fra, int til); // lager en delmengde public boolean isEmpty(); // er mengden tom? public int cardinality(); // antall elementer i mengden public void xor(BitSet B); // eksklusiv union public boolean intersects(BitSet B); // disjunkte mengder? Programkode 1.7.17 g)
Metodene i Programkode 1.7.17 g) blir diskutert nærmere i øvingsoppgavene.
Som nevnt er «innmaten» i klassen BitSet en long-tabell. Hvis elementene i mengden er fra 0 til 63, får de plass i en enkelt long-verdi. Med andre ord holder det da at long-tabellen har kun ett element. Men det blir annerledes hvis vi har elementer som er større enn 63. Ta som eksempel mengden A = {1,64,126}:
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | ||
| 0 | 1 | 2 | 3 | · · · · · | 62 | 63 | 0 | 1 | 2 | 3 | · · · · · | 62 | 63 |
| 0 | 1 | 2 | 3 | · · · · · | 62 | 63 | 64 | 65 | 66 | 67 | · · · · · | 126 | 127 |
| Figur 1.7.17 a): To long-tall «skjøtet sammen» | |||||||||||||
Hvis mengden A = {1,64,126} skal lages som en BitSet, må long-tabellen ha to elementer. Hvert av dem har 64 biter og de to er «skjøtet sammen» slik som Figur 1.7.17 a) over viser. Da kan vi tenke oss en kontinuerlig posisjonering, dvs. at posisjonene 0 og 63 i det andre tallet blir posisjonene 64 og 127 i sammenskjøtingen. Med andre ord vil A = {1,64,126} som en BitSet bestå av en long-tabell med to elementer der det er en 1-bit i posisjon 1 i det første tallet og i posisjonene 1 og 62 i det andre tallet. Ellers er det 0-biter. Se Figur 1.7.17 a).
En BitSet er dynamisk, dvs. at hvis det ikke er plass til et nytt element, vil den interne long-tabellen bli «utvidet». Anta at vi har opprettet en BitSet A og at dens interne long-tabell a har n elementer (a.length = n). Hvis tallet k skal legges inn, må først resten r og kvotienten q med hensyn på 64 regnes ut, dvs. r = k mod 64 og q = k div 64. Hvis q er mindre enn n, er det plass til k. Da settes det en 1-bit i posisjon r i long-tallet a[q]. Hvis ikke må a «utvides» slik at den får lengde q + 1. Deretter settes det en 1-bit i posisjon r i a[q].
BitSet A = new BitSet(); System.out.println("A = " + A + " A.size = " + A.size()); A.set(1); A.set(64); A.set(126); System.out.println("A = " + A + " A.size = " + A.size()); A.set(1000); System.out.println("A = " + A + " A.size = " + A.size()); // Utskrift: // A = {} A.size = 64 // A = {1, 64, 126} A.size = 128 // A = {1, 64, 126, 1000} A.size = 1024 Programkode 1.7.17 h)
En BitSet A har metoden size(). Den returnerer ikke antallet elementer i mengden A. Det er det metoden cardinality() som gjør. Men size() returnerer «størrelsen» på A, dvs. den øverste grensen for hvilke tall det er plass til uten at den interne long-tabellen i A behøver å utvides. I Programkode 1.7.17 h) opprettes først A som en tom mengde, men den interne long-tabellen får likevel lengde lik 1. Dermed er «størrelsen» lik 64. Med andre ord kan alle heltall fra 0 til 63 legges inn. Dermed kan 1 settes inn. Men det er ikke plass til 64 og 126. Dermed utvides long-tabellen slik at den får lengde 2. «Størrelsen» på A blir derfor 64 · 2 = 128.
Når tallet 1000 skal legges inn (se Programkode 1.7.17 h), må long-tabellen på nytt «utvides». Vi har 1000 div 64 = 15. Derfor må tabellen «utvides» til lengde 15 + 1 = 16. Det gir en «størrelse» på 64 · 16 = 1024. Tallet 1000 legges inn ved at det settes en 1-bit i posisjon 1000 mod 64 = 40 i det siste elementet i tabellen.
| 1. | La mengden A bestå av heltallene fra 1 til 10. Lag en BitSet med samme innhold. Test resultatet ved å gjøre en utskrift. Se Programkode 1.7.17 b). |
| 2. | Lag en BitSet som inneholder 1,2,3,5,7,8,9. Dvs. tallene fra 1 til 9 bortsett fra 4 og 6. |
| 3. | Lag en BitSet som inneholder 1,2,4,8,16,32, . . . ,1024 |
| 4. | Hvis en på forhånd vet hvor store tall en BitSet skal inneholde, kan det
være lurt å bruke en konstruktør som på forhånd gjør den interne long-tabellen stor nok.
Hvis vi vet at alle tall som skal legges inn er mindre enn n, vil setningen
BitSet A = new BitSet(n); gjøre at det vil være plass til alle ikke-negative
heltall mindre enn n. Bruk denne teknikken i Oppgave 3 og i resten av oppgavene.
|
| 5. | Lag en BitSet A som inneholder de positive heltallene mindre enn 100 som er delelige med 6 (dvs. 6, 12, 18, . . . , 96). Lag så en BitSet B som inneholder de positive heltallene mindre enn 100 som er delelige med 9. Finn så snittet (metoden and) av A og B og sjekk at det blir lik de positive heltallene mindre enn 100 som er delelige med både 6 og 9. |
| 6. | Finn på forhånd de positive heltallene mindre enn 100 som er delelige med både 6 og 8. Bruk så teknikken i Oppgave 5 til å sjekke svaret ditt. |
| 7. | Finn de positive heltallene mindre enn 100 som er delelige med 6 eller med 9 (eller med begge). Hint: Finn unionen av de som er delelige med 6 og de som er delelige med 9. Bruk BitSet-metoden or. |
| 8. | Gjør som i Oppgave 7, men bruk tallene 6 og 8. |
| 9. | Finn de positive heltallene mindre enn 100 som er delelige med 6, men ikke med 9. |
| 10. | Gjør som i Oppgave 9, men bruk tallene 6 og 8. |
| 11. | Finn de positive heltallene mindre enn 100 som er delelige med både 6, 8 og 9. Hva er minste felles mutiplum for 6, 8 og 9? |
| 12. | Finn de positive heltallene mindre enn 100 som er delelige med enten 6 eller med 9, men ikke med både 6 og 9. |
| 13. | La A og B henholdsvis være de positive heltallene mindre enn 100 som er delelige med 6 og med 9. Vi har flg. formel for kardinalitet: |A U B| = |A| + |B| − |A ∩ B|. Sjekk at dette stemmer ved å bruke metodene or, and og cardinality(). |
| 14. | Finn primtallene som er mindre enn 1000! Det kan gjøres på flg. litt primitive måte: Lag først en BitSet A som inneholder heltallene fra og med 2 til og med 999. Lag så en int-tabell a som inneholder primtallene 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 og 31. Det er kun de som kan være faktorer siden kvadratroten til 1000 er lik 31,6. Fjern så alle tall fra A som er delelige med (men forskjellig fra) 2 (det er 4, 6, 8, . .). Fjern så alle som er delelige med (men forskjellig fra) 3. Osv. med alle tallene fra tabellen a. Bruk en dobbeltløkke. Tall fjernes fra A f.eks. ved hjelp av metoden clear. |
![]() 1.7.18 class BigInteger
1.7.18 class BigInteger
Standardtypene i Java (se Figur 1.7.4 a)
vil ikke kunne brukes hvis vi ønsker å operere med svært store heltall. Selv datatypen long,
som tillater heltall med opptil 19 desimale siffer (maks. 9.223.372.036.854.775.807), vil da ikke kunne brukes.
En mulig idé kunne være å la hvert siffer i tallet utgjøre et tegn i en tegnstreng. Da kunne long-tallet 9.223.372.036.854.775.807 representeres slik:
String a = "9223372036854775807";
Vi skal kunne regne med slike tall. Anta at tallet skal adderes med et annet stort tall. For enkelhets skyld tar vi et med like mange siffer, f.eks. "6.810.297.513.886.047.219":
String b = "6810297513886047219";
Disse to tallene kan adderes ved å bruke den vanlige regneregelen. Vi legger først sammen de to siste sifrene. Det blir 7 + 9 = 16. Med andre ord 6 og 1 i mente. Så adderer vi de to nest siste sifrene og tar med eventuell mente. Det gir oss 0 + 1 + 1 = 2, dvs. 2 og 0 i mente. Osv. Dette kan lett oversettes til Java-kode:
String a = "9223372036854775807"; // første tall String b = "6810297513886047219"; // andre tall StringBuilder sum = new StringBuilder(); // summen int mente = 0; // mente for (int i = a.length() - 1 ; i >= 0; i--) // for-løkke { int s = a.charAt(i) + b.charAt(i) - 96 + mente; // adderer sum.append(s < 10 ? s : s - 10); // finner sifret mente = s < 10 ? 0 : 1; // finner menten } if (mente > 0) sum.append(1); // den siste menten System.out.println(sum.reverse()); // Utskrift: 16033669550740823026 Programkode 1.7.18 a)
I Programkode 1.7.18 a) er hvert siffer egentlig et tegn. Når to tegn (typen char) adderes er det ascii-verdiene som inngår. Ascii-verdien til '0' er 48. Det betyr at ascii-verdien for hvert siffertegn er 48 mer enn tegnets verdi som desimalt siffer. I summen s blir derfor 2 · 48 = 96 trukket fra. Normalt vil ikke to tall ha like mange siffer. Hvis de to tallene a og b har ulik lengde, må det gjøres noen små endringer i koden. Se Oppgave 2.
Java-klassen BigInteger som ligger under java.math, tillater at et
heltall oppgis som en tegnstreng. Addisjonen i
Programkode 1.7.18 a) kan
derfor utføres på denne måten (obs: det må være med import java.math.*; øverst):
BigInteger a = new BigInteger("9223372036854775807"); BigInteger b = new BigInteger("6810297513886047219"); BigInteger sum = a.add(b); System.out.println(sum); // Utskrift: 16033669550740823026 Programkode 1.7.18 b)
Klassen BigInteger har alle de vanlige operasjonene for heltallsregning,
f.eks. addisjon, subtraksjon, multiplikasjon, heltallsdivisjon, modulo og mange flere.
En oppgave i faget Diskret matematikk er å finne antallet 0-er bakerst i
tallet 100! (utropstegnet ! står for fakultet ), dvs. tallet
100 · 99 · 98 ·
· · 3 · 2 · 1.
Dette blir et svært stort tall med hele 158 desimale siffer. Poenget er at man skal analysere
seg frem til hvor mange 0-er det er bakerst uten å regne ut tallet. Men ved hjelp av klassen
BigInteger kan vi finne tallet og få det skrevet ut (se også
Oppgave 3).
Tallet 100! blir stort, men de enkelte faktorene er ikke store. Metoden
multiply krever at begge faktorene er av typen BigInteger. Da
er det enklest å bruke den statiske metoden valueOf som direkte gjør om
et vanlig heltall til en BigInteger:
BigInteger produkt = BigInteger.ONE; // tallet 1 for (int i = 2; i <= 100; i++) // for-løkke fra 2 til 100 { BigInteger faktor = BigInteger.valueOf(i); // fra int til BigInteger produkt = produkt.multiply(faktor); // multipliserer } System.out.println(produkt); Programkode 1.7.18 c)
Utskriften (fordelt på to linjer) blir:
9332621544394415268169923885626670049071596826438162146859296389521759999322991
5608941463976156518286253697920827223758251185210916864000000000000000000000000
Hvis en allerede har et heltall på binærform og vil gjøre det til en BigInteger,
kan en dele det opp i åtte og åtte biter (byter) og legge disse fortløpende i en byte-tabell. Da skal
den mest signifikante byten legges i posisjon 0, osv. Gitt tallet n = 1001 00110011 10101010.
De først fire bitene er de mest signifikante og utgjør tallet 9, deretter kommer 51 og 170.
Hvis vi lager flg. kode, vil vi imidlertid få syntaksfeil:
byte[] b = {9,51,170}; // cannot convert from int to byte
Poenget er at 10101010 som bitsekvens representerer tallet 170, men byte-tall kan kun være fra -128 til 127. Men i byte-formatets to-komplement står 10101010 for -86:
byte[] b = {9,51,-86}; // ok kode
Bitsekvensen 10010011001110101010 står generelt for tallet 603050. Vi signaliserer om vi skal ha fortegn (-603050) eller ikke ved å bruke 1 eller -1 som parameter:
byte[] b = {9,51,-86}; // 10010011001110101010 BigInteger x = new BigInteger(1,b); // 1 betyr uten fortegn BigInteger y = new BigInteger(-1,b); // -1 betyr med fortegn System.out.println(x + " " + y); // Utskrift: 603050 -603050 Programkode 1.7.18 d)
Hva blir desimalformatet for det tallet (uten fortegn) som består av en sekvens på 100 1-ere? Da trenger vi 13 byter. Den første vil inneholde 1111 (eller egentlig 00001111) = 15 og de 12 andre av 11111111 = -1 (obs. 12 · 8 = 96):
byte[] b = {15,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}; BigInteger x = new BigInteger(1,b); // 1 betyr uten fortegn System.out.println(x); // Utskrift: 1267650600228229401496703205375 Programkode 1.7.18 e)
I Programkode 1.7.18 d) bestemte vi ved hjelp av en parameter om et heltall, gitt ved en byte-tabell, skulle være uten eller med fortegn (1 eller -1). Det er også mulig å la parameterverdien være 0, men da må byte-tabellen enten være tom eller kun inneholde 0-byter. I så fall registreres tallet som 0. Det er også mulig å bruke fortegn når tallet oppgis ved hjelp av en tegnstreng:
BigInteger x = new BigInteger(0,new byte[0]); BigInteger y = new BigInteger("-123456789"); System.out.println(x + " " + y); // Utskrift: 0 -123456789 Programkode 1.7.18 f)
Internt i klassen BigInteger blir et heltall lagret i en int-tabell mag på
binærformat uten to-komplement. Navnet mag er en forkortelse for magnitude. I tillegg
er det en konstant signum (fortegn) som blir satt til 1, 0 eller -1 avhengig av om
tallet skal være positivt, 0 eller negativt.
Ethvert heltall, uansett hvor stort, kan skrives på binærformat. Når dette så skal
lagres i en int-tabell, blir de binære sifrene (fra høyre mot venstre) delt i grupper
på 32 sifre. Hver slik gruppe kan ses på som et int-tall. Her brukes ikke to-komplement.
Det betyr f.eks. at 32 stykker 1-ere står for tallet 232 − 1
= 4294967295 og ikke for tallet -1. Hvert enkelt element i int-tabellen kan
derfor ses på som et «siffer» i tallsystemet med 232 som grunntall. Det mest
signifikante sifferet plasseres lengst til venstre i tabellen, dvs. i posisjon 0. Osv.
Vi ser på nytt på de to tallene vi startet med. Det var tallene 9.223.372.036.854.775.807, som er det største mulige long-tallet, og 6.810.297.513.886.047.219. Det første består av 63 1-ere (31 + 32) og en int-tabell for dette blir lik:
int[] a = {2147483647,-1};
Men tallet 6.810.297.513.886.047.219 er det litt verre med. Det er generelt en forholdsvis komplisert oppgave å konvertere et heltall på desimalform (f.eks. gitt som en tegnstreng) til dens representasjon som en int-tabell. Men her blir det:
int[] b = {1585645953,-1578673165};
Det andre tallet i b er -1578673165. Hva blir det uten to-komplement? Det er lik svaret på regnestykket 232 − 1578673165 = 4294967296 − 1578673165 = 2716294131. Alternativt kan vi først konvertere tallet til et long-tall og deretter «nulle» de 32 første bitene:
System.out.println(-1578673165L & 0xffffffffL); // Utskrift: 2716294131
De to elementene i tabellen b er sifre i tallsystemet som har 232
= 1L << 32 som grunntall. Dermed blir det dette tallet:
long k = (-1578673165 & 0xffffffffL) + 1585645953 * (1L << 32); System.out.println(k); // Utskrift: 6810297513886047219
To int-tabeller adderes ved at tallene midlertidig konverteres til long-tall. Siden det mest signifikante «sifferet» ligger i posisjon 0, må vi starte addisjonen lengst til høyre i tabellene. Koden blirforholdsvis enkel når tabellene er like lange:
int[] a = {2147483647,-1}; int[] b = {1585645953,-1578673165}; int[] c = new int[a.length]; long m = 0xffffffffL; // maskerer vekk de 32 første sifrene long sum = 0, mente = 0; for (int i = a.length - 1; i >= 0; i--) { sum = (a[i] & m) + (b[i] & m) + mente; mente = sum >> 32; c[j] = (int)(sum & m); } if (mente > 0) { int[] d = c; c = new int[d.length + 1]; System.arraycopy(d,0,c,1,d.length); c[0] = 1; } System.out.print(Arrays.toString(c) + " "); StringBuilder s = new StringBuilder(); for (int k : c) s.append(Integer.toBinaryString(k)); BigInteger x = new BigInteger(s.toString(),2); System.out.println(x); // Utskrift: [-561837695, -1578673166] 16033669550740823026 Programkode 1.7.18 g)
Ideen i Programkode 1.7.18 g) kan enkelt utvides til å kunne addere to int-tabeller med vilkårlig størrelse på hver av dem. Se Oppgave 4.
Klassen BigInteger er såkalt sammenlignbar med seg selv, dvs. at den
implementerer grensesnittet Comparable<BigInteger>. Med andre
ord har den metoden compareTo.
BigInteger a = new BigInteger("1234567890ABCDEF",16); // heksadesimalt BigInteger b = new BigInteger("123456712345671234567",8); // oktalt int comp = a.compareTo(b); // sammenligner a og b System.out.println(comp); // Utskrift: -1 (dvs. a er mindre enn b) Programkode 1.7.18 h)
En BigInteger kan ses på som en bitsekvens. Da kan
vi f.eks. bruke metoden or:
BigInteger a = new BigInteger("10110010100101111001",2); // binært BigInteger b = new BigInteger("10010111000011001101",2); // binært System.out.println(a.toString(2)); System.out.println(b.toString(2)); BigInteger c = a.or(b); System.out.println(c.toString(2)); // Utskrift: // 10110010100101111001 // 10010111000011001101 // 10110111100111111101 Programkode 1.7.18 i)
Det er også mulig å be om store primtall. Da kan vi velge om det skal være 100% sikkert at det vi får er et primtall, eller vi kan oppgi en usikkerhet.
| 1. | Tallene 9223372036854775807 og 6148914691236517205 i Programkode 1.7.18 a) kan representeres som long-tall. Hva blir summen av dem som long-tall? Lag kode! |
| 2. | Lag en metode public static String add(String a, String b) som legger sammen to heltall representert som tegnstrenger. Summen skal returneres som en tegnstreng. Bruk samme idé som i Programkode 1.7.18 a). Ta hensyn til at a og b skal kunne ha forskjellige lengder. |
| 3. | Finn antallet 0-er bakerst i tallet 100! uten å regne det ut. |
| 4. | Lag metoden public static int[] add(int[] a, int[] b). Den skal
legge sammen (addere) de to int-tabellene a og b og returnere resultatet.
Ta hensyn til at a og b skal kunne ha forskjellige lengder og at
resultattabellen kan være lengre enn både a og b. |
![]() 1.7.19 Primtall
1.7.19 Primtall
Et heltall større enn 1 kalles et primtall
(eng: a prime) hvis det ikke har andre positive divisorer enn 1 og tallet selv. Det betyr at 2 er første primtall. Deretter kommer
3, 5, 7, 11, 13, osv. Hvis et heltall større enn 1 ikke er et primtall, kalles det
et sammensatt tall (eng: composite number).
Vi har 4 = 2·2 . Dermed er 4 det første sammensatte heltallet. Deretter kommer 6, 8, 9, 10, 12, osv.
Obs: Tallet 1 er hverken et primtall eller et sammensatt tall.
Det største kjente primtallet (mars 2013) er Mersenne-tallet 2n − 1 med n = 57.885.161. Tallet har 17.425.170 desimale siffer. Men det finnes ikke et største primtall. Det er uendelig mange av dem - noe som var kjent allerede hos de «gamle grekerne» (Euclid 323–283 f.Kr). Det vises slik: Anta at det er endelig mange. Hvis vi ganger sammen disse og legger til 1, får vi et tall n som må være sammensatt. Minst ett av de endelig mange primtallene (kall det p) må da være divisor i n. Det betyr at p er divisor i både n og n − 1 og dermed i n − (n − 1) = 1. Umulig. Altså er det uendelig mange primtall.
Primtall har stor betydning i informasjonsteknologi - spesielt i forbindelse med kryptering. Hvis en vet at et gitt heltall n er produktet av to store primtall (dvs. et semiprimtall), er det en svært krevende oppgave å finne de to primtallene. RSA-teknikken for kryptering er basert på dette. Da trengs primtall med 2-300 desimale siffer.
Hvis et positivt heltall n er sammensatt, må det finnes positive heltall a og b slik at n = a·b. Hvis a og b er like, er n et kvadrattall. Hvis ikke, må det minste av dem være mindre enn kvadratroten til n. La f.eks. a være det minste. Hvis a ikke er primtall, så må det finnes et primtall som går opp i a og dermed i n. Med andre ord holder det å sjekke om et primtall fra 2 til √n er divisor i n for å avgjøre om n er et primtall eller ikke.
La n = 113. Da er √1013 = 10,6. Dermed holder det å sjekke om 2, 3, 5 eller 7 går opp i 113. Vi ser fort at det gjør ingen av dem. Dermed er 113 et primtall. Hvis n = 119, så holder det også å sjekke om 2, 3, 5 eller 7 går opp siden √119 = 10,9. Der ser vi at hverken 2, 3 eller 5 går opp, men 7 går opp siden 119 = 7·17. Med andre ord er 119 ikke et primtall.
Det holder som nevnt å sjekke om et primtall fra 2 til √n er divisor i n. Men hvis n er stor, vil vi normalt ikke ha tilgang til de primtallene. Da kunne vi isteden prøve med alle tall fra 2 til √n, men det gir svært mye ekstra arbeid. Dessuten er en divisjon relativt sett en kostbar operasjon. Den koster langt mer enn f.eks. en multiplikasjon. Vi snur derfor på problemet. Vi setter opp alle tallene fra 2 til n og så «fjerner» vi forløpende alle de sammensatte tallene. Da vil vi stå igjen med primtallene. Denne teknikken kalles Erathostenes sil (eng: sieve).
I Tabell 1.7.19 a) under står alle tallene fra 2 til 120.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| Tabell 1.7.19 a) - Tallene fra 2 til 120 | |||||||||||||||||||
Først «fjerner» vi alle multipler av 2, dvs. 2·2 = 4, 3·2 = 6, 4·2 = 8, 5·2 = 10, osv. Med andre ord «fjerner» vi alle partall større enn 2. I Tabell 1.7.19 b) under markeres det ved at de har fått grønn bakgrunn:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| Tabell 1.7.19 b) - Alle multipler av 2 er markert med grønn bakgrunn | |||||||||||||||||||
Så «fjerner» vi alle multipler av 3, dvs. 2·3 = 6, 3·3 = 9, 4·3 = 12, 5·3 = 15, osv. Vi ser at annenhvert multippel er et partall og de er jo allerede «fjernet». I de tilfellene beholder vi grønnfargen. Det gir oss Tabell 1.7.19 c) (de nye som er fjernet har lys brun bakgrunn):
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| Tabell 1.7.19 c) - Alle multipler av 2 og 3 er markert med grønn eller lys brun bakgrunn | |||||||||||||||||||
Så «fjerner» vi på samme måte alle multipler av 5:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| Tabell 1.7.19 c) - Multipler av 2, 3 og 5 er markert med grønn, lys brun eller blå bakgrunn | |||||||||||||||||||
Til slutt «fjerner» vi alle multipler av 7. Nå det er gjort, er vi ferdige. Vi har jo at √120 er mindre enn 11 og dermed holder det med å fjerne multipler av primtallene 2, 3, 5 og 7:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| Tabell 1.7.19 c) - Multipler av 2, 3, 5 og 7 er markert med grønn, lys brun, blå eller gul bakgrunn | |||||||||||||||||||
Primtallene fra 2 til 120 er de som har hvit bakgrunn. Med andre ord tallene 2, 3, 5, 7, 11, 13, 17, 19, 23, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113. Tilsammen 30 stykker.
Vi kan bruke en boolsk tabell med dimensjon n + 1 istedenfor en heltallstabell. Da er det indeksene til og med n som representerer heltallene:
boolean[] sammensatt = new boolean[n + 1];
Med n = 20 får vi tabellen under. De to første indeksene (0 og 1) er ikke tatt med siden de
ikke kan være primtall. I en boolsk tabell er alle elementene i utgangspunktet
satt til usann (false). Siden tabellen heter sammensatt kan det tolkes som at når vi starter
representerer alle indeksene ikke sammensatte tall (dvs. primtall).
| X | X | |||||||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| En boolsk tabell med navn sammensatt | ||||||||||||||||||||
Vi skal «fjerne» alle multipler av primtall og da holder det med å se på alle primtall k ≤ √n. Men
k ≤ √n er det samme som k2 ≤ n. Indeks k har første primtall, dvs. 2,
som startverdi. Deretter vil k være et primtall hvis sammensatt[k] er usann. Det er 2k som er første
multippel av k. Neste multippel får vi ved å legge til k, osv. Det gir flg. kode:
public static int antallPrimtall(int n) // antall primtall <= n { boolean[] sammensatt = new boolean[n+1]; // boolsk tabell for (int k = 2; k*k <= n; k++) // k starter med 2 { if (!sammensatt[k]) // k er et primtall for (int i = 2*k; i <= n; i += k) // øker med k sammensatt[i] = true; // i er et multippel av k } int antall = 0; for (int k = 2; k <= n; k++) // teller opp primtallene if (!sammensatt[k]) antall++; return antall; } Programkode 1.7.19 a)
Flg. programbit finner antall primtall mindre enn eller lik 120. Vi har allerde funnet ut at det er 30 stykker. Sjekk at vi får det samme svaret her. Se også Oppgave 1.
System.out.println(antallPrimtall(120)); // Utskrift: 30 Programkode 1.7.19 b)
Er dette effektivt? Vi kan prøve med n = 1.000.000.000 (1 milliard). Hvor lang tid tar det hos deg? Kanskje noen sekunder? På en 64-biters maskin med Intel Core i7, 2.50 GHz, Java 1.7.0_17 og Windows 7 tok det 12 sekunder.
long tid = System.currentTimeMillis(); int antall = antallPrimtall(1_000_000_000); tid = System.currentTimeMillis() - tid; System.out.println("Antall: " + antall + " Tid: " + tid); Programkode 1.7.19 c)
Kan Programkode 1.7.19 a) effektiviseres?
I den ytterste for-løkken inngår sammenligningen k*k <= n.
La m være avrundigen av √n ned til nærmeste
heltall. Da kunne vi isteden bruke sammenligningen k <= m. Men det gir nok ingen målbar effekt.
Med n = 1.000.000.000 vil ikke den ytterste løkken gå mer enn 31.622 ganger.
Se Oppgave 2.
I den innerste for-løkken derimot er det gode muligheter for effektiviseringer. For det første
vet vi at det ikke er noen partall større enn 2 som er primtall. Derfor kan vi la være å
fjerne dem. Men da må vi passe å unngå dem i opptellingen i den siste for-løkken. Dermed
kan den ytterste for-løkken starte med k = 3. Den innerste for-løkken startet med
i = 2*k. Vi kan faktisk isteden starte med
i = k*k. Alle odde multipler p*k med p mindre enn k, er allerede
«fjernet». Det kommer av at hvis p er et primtall eller har en primtallsdivisor,
så har jo de multiplene allerede blitt «fjernet». Det skjedde før vi kom til k.
Et primtall k større enn 2 er odde og dermed er også k*k odde. Deretter vil kun annenhvert
multippel av k være odde. Derfor kan vi bruke i += 2*k som oppdatering.
Tilsammen vil dette nær doble effektiviteten:
public static int antallPrimtall(int n) // ny versjon { if (n < 2) return 0; // ingen primtall mindre enn 2 boolean[] sammensatt = new boolean[n+1]; // boolsk tabell for (int k = 3; k*k <= n; k += 2) // k starter med 3, øker med 2 { if (!sammensatt[k]) // k er nå et primtall for (int i = k*k; i <= n; i += 2*k) // øker i med 2k sammensatt[i] = true; // i er et multippel av k } int antall = 1; // 2 er primtall for (int k = 3; k <= n; k += 2) // hopper over partallene if (!sammensatt[k]) antall++; // teller opp primtallene return antall; } Programkode 1.7.19 d)
Programkode 1.7.19 d) kan forbedres noe - ikke tiden, men
plassbehovet. Den boolske tabellen bruker en byte per element. Hvis vi isteden bruker de
enkelte bitene, trenger vi kun 1/8-del av plassen.
En instans av klassen BitSet (se Avsnitt 1.7.17)
kan tolkes som en logisk tabell.
Ved hjelp av set og get kan vi arbeide på samme måte som
i en tabell. Metoden cardinality gir antallet elementer som er satt til true (1).
Se Oppgave 4.
En svakhet ved teknikken er at mange sammensatte tall blir fjernet flere ganger. Ta f.eks. 3·5·7 = 105. Det blir fjernet tre ganger. Det finnes teknikker som fjerner sammensatte tall færre ganger, men de er ikke så enkle å kode. Se f.eks. Sieve of Sundaram og Sieve of Atkin.
Et annet viktig problem er å kunne avgjøre om et gitt heltall n er et primtall eller ikke. Hvis tallet
er svært stort, vil det være altfor kostbart å bruke f.eks. Erathostenes sil. Den for tiden mest effektive metoden
heter Miller-Rabins primtallstest.
Den har imidlertid den ulempen at den i sjeldne tilfeller sier at et tall er et primtall uten at det er det.
Denne metoden er implementert i klassen BigInteger (se Avsnitt 1.7.18).
Men da må en oppgi en sannsynlighet og så vil testen si med den sannsynligheten om tallet er primtall.
Se flg. eksempel:
BigInteger n = new BigInteger("999999937"); // er dette et primtall? System.out.println(n.isProbablePrime(10)); // Utskrift: true Programkode 1.7.19 e)
Parameterverdien 10 i metoden isProbablePrime er ikke sannsynligheten. Tallet inngår
i uttrykket 1 − 1/210 = 0,9990234375. Med andre ord betyr det at hvis metoden returnerer
true, er det minst 99,9% sannsynlig at det er et primtall. Velger man et større tall enn 10 vil
en få økt sannsynligheten. Metoden isProbablePrime brukte kort tid i dette eksemplet. Tallet
hadde bare 9 siffer. Men det blir verre når en skal analysere tall med 2-300 siffer.
AKS-metoden (Agrawal, Kayal og Saxena) er nyere (fra 2002) enn Miller-Rabins primtallstest. Den er ikke fullt så effektiv, men har den fordelen at den avgjør alltid med 100% sikkerhet om et tall er et primtall eller ikke. En vanlig brukt teknikk er først å finne primtall ved hjelp av Miller-Rabins primtallstest og deretter teste dem ved AKS-metoden.
| 1. | Kjør programbiten i Programkode 1.7.19 b). Prøv med andre verdier enn 120. Vi har at 2 er første primtall. Hva skjer hvis vi bruker en av verdiene 2, 1, 0 eller et negativt tall som inputverdi?. Blir resultatene da som forventet? |
| 2. | Kjør programbiten i Programkode 1.7.19 c). Legg så
inn kode i starten av metoden antallPrimtall som finner
m, dvs. avrundingen av √n ned til nærmeste heltall. Bruk så sammenligningen
k <= m istedenfor k*k <= n i den ytterste for-løkken. Vil dette redusere
tidsforbruket? |
| 3. | Lag metoden public static int[] primtall(int n). Den skal
returnere en tabell som inneholder primtallene mindre enn eller lik n. Hvis
n er mindre enn 2, skal en tom tabell (lengde lik 0) returneres. |
| 4. | Bruk en BitSet som en logisk tabell i metoden antallPrimtall. Metodene
set og get erstatter vanlige tabellaksesser. Metoden cardinality
gir antallet «sanne» i tabellen. Når en BitSet opprettes blir alle
elementene satt til false. |
| 5. | Lag metoden public static int maksprimtall(int n). Den skal returnere det største primtallet
som er mindre enn eller lik n. Bruk metoden til å finne største primtall som er mindre enn
1.000.000.000 (1 milliard). |
| 6. | Bruk metoden isProblablePrime fra klassen BigInteger til å finne
største primtall som er mindre enn 1.000.000.000 (1 milliard). |
Kommer!
- Torbjörn Granlund og Peter L. Montgomery, Division by Invariant Integers using Multiplication, ACM PLDI 1994
- Henry S. Warren, Hacker's Delight, Addison-Wesley 2003
- Løsning av dronningproblemet for n = 26

|