 |
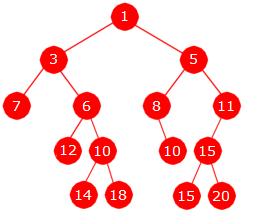
| Figur 5.3.1 a) : Et minimumstre |
Hvis vi i Figur 5.3.1 a) går fra roten og ned til en bladnode, kommer verdiene i sortert stigende rekkefølge. Hvis vi f.eks. går ned til den bladnoden som ligger lengst ned til høyre, får vi verdiene 1, 5, 11, 15 og 20. Hvis vi isteden starter i en bladnode og går oppover til roten, kommer verdiene i sortert avtagende rekkefølge. Med start i bladnoden med verdi 18 blir det 18, 10, 6, 3 og 1.
Observasjonene over kan brukes til å lage følgende definisjon:
I Definisjon 5.3.1 a) inngår indre noder og deres barn. Dette kunne imidlertid
ha vært definert omvendt.
Dvs. at et binærtre er et minimumstre hvis verdien i hver node (bortsett fra rotnoden) er
større enn eller lik verdien i nodens forelder.
Treet i Figur 5.3.1 a) oppfyller disse kravene og er dermed et minimumstre. Legg merke til
at definisjonen sier eller lik. Med andre ord er det tillatt at en node og dens
barn har samme verdi.
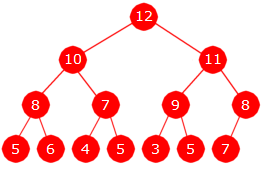 |
| Figur 5.3.1 b) : Et komplett maksimumstre |
Et maksimumstre definerers på en tilsvarende måte som et minimumstre:
Hvis treet er tomt eller har bare én node, sier vi at det er både et minimumstre og et maksimumstre. Dermed vil ethvert subtre i et minimumstre selv være et minimumstre, og ethvert subtre i et maksimumstre vil selv være et maksimumstre.
Definisjonene av minimumstre, maksimumstre og gren i et binærtre gir at:
- Minimumstre:
- Et binærtre er et minimumstre hvis og bare hvis hver gren er sortert stigende.
- I et minimumstre er rotnodeverdien mindre enn eller lik alle de andre verdiene.
- Ethvert subtre i et minimumstre er selv et minimumstre.
- Hvis treet har minst to verdier ligger nest minste verdi i et av rotnodens barn.
- Maksimumstre:
- Et binærtre er et maksimumstre hvis og bare hvis hver gren er sortert avtagende.
- I et maksimumstre er rotnodeverdien større enn eller lik alle de andre verdiene.
- Ethvert subtre i et maksimumstre er selv et maksimumstre.
- Hvis treet har minst to verdier ligger nest største verdi i et av rotnodens barn.
Hvis vi har et BinTre, dvs. en instans av klassen
BinTre fra Delkapittel 5.1,
kan vi sjekke om treet er
et minimumstre ved å bruke flg. metode (som legges inn i class BinTre):
public boolean erMintre(Comparator<? super T> c) // legges i BinTre { if (rot == null) return true; // et tomt tre er et minimumstre else return erMintre(rot,c); // kaller den private hjelpemetoden } private static <T> boolean erMintre(Node<T> p, Comparator<? super T> c) { if (p.venstre != null) { if (c.compare(p.venstre.verdi,p.verdi) < 0) return false; if (!erMintre(p.venstre,c)) return false; } if (p.høyre != null) { if (c.compare(p.høyre.verdi,p.verdi) < 0) return false; if (!erMintre(p.høyre,c)) return false; } return true; } Programkode 5.3.1 a)
Eksempel: Flg. kodebit lager treet fra
Figur 5.3.1 a)
og bruker metoden erMintre til å sjekke om det er et minimumstre:
int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29}; Integer[] verdi = {1,3,5,7,6,8,11,12,10,10,15,14,18,15,20}; BinTre<Integer> tre = new BinTre<>(posisjon, verdi); // Bruker en konstruktør Comparator<Integer> c = Comparator.naturalOrder(); System.out.println(tre.erMintre(c)); // Utskrift: true // en node med verdi 19 legges som høyre barn til noden med verdi 20 tre.leggInn(59,19); System.out.println(tre.erMintre(c)); // Utskrift: false Programkode 5.3.1 b)
| 1. | En gren i et binærtre starter i roten og ender i en bladnode. Dermed har treet
like mange grener som treet har bladnoder. Skriv ut (på papir) innholdet i alle grenene i
minimumstreet i Figur 5.3.1 a).
Skriv grenene fra venstre mot høyre. Sjekk at alle grenene er sortert stigende.
|
| 2. | Skriv ut (på papir) innholdet i alle grenene i maksimumstreet i Figur 5.3.1 b). Skriv grenene fra venstre mot høyre. Sjekk at alle grenene er sortert avtagende. |
| 3. | Den grenen i et minimumstre som starter i roten og som for hver node går videre ned til
det «minste» barnet, kalles minimumsgrenen. Hvis barna har like
verdier, definerer vi at minimumsgrenen går gjennom det venstre barnet. Hvis noden har bare ett barn, går grenen
til det barnet. Hvilke verdier
har minimumsgrenen i Figur 5.3.1 a)?
|
| 4. | Den grenen i et maksimumstre som starter i roten og som for hver node går videre ned til
det «største» barnet, kalles maksimumsgrenen. Hvis barna har like
verdier, definerer vi at maksimumsgrenen går gjennom det venstre barnet. Hvis noden
har bare ett barn, går grenen til det barnet. Hvilke verdier
har maksimumsgrenen i Figur 5.3.1 b)?
|
| 5. | Legg inn de to erMintre-metodene fra
Programkode 5.3.1 a)
i klassen BinTre og lag så et program som kjører
Programkode 5.3.1 b).
|
| 6. | Lag to erMakstre-metoder (en offentlig metode og en privat rekursiv metode)
på samme måte som de to erMintre-metodene
i Programkode 5.3.1 a).
|
| 7. | Lag en iterativ erMintre-metode. Legg den i klassen BinTre.
Da må treet traverseres og for hver node
sammenlignes verdiene i noden og nodens barn (hvis den har barn). Traverseringen avbrytes
hvis en sammenligning viser at treet ikke kan være et minimumstre. Bruk f.eks.
en nivåordentraversering slik som i
Programkode 5.1.6 a).
|
| 8. | Lag public String minimumsGrenen(Comparator<? super T> c). Den skal
returnere minimumsgrenen i et minimumstre som en tegnstreng. Hvis en bruker metoden på treet i
Figur 5.3.1 a) skal den inneholde:
[1, 3, 6, 10, 14]. Legg metoden i klassen BinTre.
|
| 9. | Lag metoden public String[] grener(). Den skal returnere en tabell med tegnstrenger -
en tegnstreng for hver gren. Legg metoden i klassen BinTre.
Hvis en bruker metoden på treet i
Figur 5.3.1 a) og skriver ut
en tegnstreng per linje, skal det bli:
|
![]() 5.3.2 Binære heaper
5.3.2 Binære heaper
I Webster's Dictionary står «a group of things lying one on
another» som første betydning av ordet heap. Det kan kanskje
sammenlignes med det norske ordet haug. Det er noen som har forsøkt å innføre
navnet haug på begrepet heap i databehandling, men har ikke lyktes
spesielt godt med det. Ordet heap er nok for godt innarbeidet. I databehandling
brukes navnet heap både om et område i maskinens minne (det som brukes til
dynamisk minneallokering)
og om en spesiell datastruktur.
Det er det siste vi skal se på.
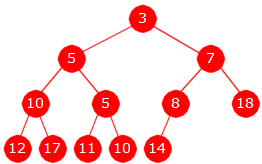 |
| Figur 5.3.2 a) : En minimumsheap |
Figur 5.3.2 a) til venstre viser et binærtre med 12 noder. Vi ser at hver gren er sortert stigende og dermed er det et minimumstre. Treet er komplett siden alle nivåer, bortsett fra det siste, er fulle av noder og det siste nivået (med 5 verdier), er fylt opp fra venstre. Med andre ord en minimumsheap. Når verdier skal legges inn og tas ut, må det skje på en slik måte at treet bevares som en minimumsheap, dvs. at både minimumsegenskapen og komplettheten bevares.
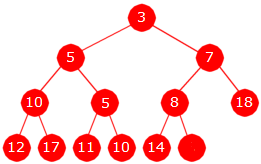
Innlegging i en minimumsheap Hvis en verdi skal legges, må nødvendigvis treet få en ekstra node og for å bevare komplettheten må den legges på bunnen (nederste nivå rett til høyre for den siste). Hvis det nederste nivået er fullt, må den isteden legges som første node (lengst til venstre) på et nytt nivå. Siden den nye noden alltid blir en bladnode, blir den siste node på en ny gren. Tar vi utgangspunkt i treet i Figur 5.3.2 a) over til venstre, vil den nye noden gi grenen 3, 7, 8, «blank». Se Figur 5.3.2 b) under til venstre.
 |
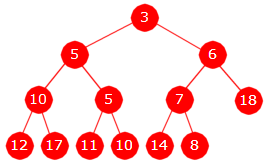 | |
| Figur 5.3.2 b) : En ny node på bunnen | Figur 5.3.2 c) : Verdien 6 er lagt inn |
For å bevare minimumsegenskapen må den nye verdien legges inn på rett sortert plass i grenen 3, 7, 8, «blank». Hvis ny verdi er større enn eller lik 8, kan den legges rett inn i den «blanke» noden. Hvis ikke må én og én verdi i grenen «trekkes» nedover inntil vi kommer til rett sortert plass. I verste fall må alle i grenen «trekkes» nedover. Det inntreffer hvis den nye verdien er mindre enn rotverdien, dvs. mindre enn 3 i vårt eksempel. La isteden 6 være ny verdi. Da blir resultatet slik som Figur 5.3.2 c) over til høyre viser. Det at verdien settes inn på rett sortert plass i grenen gjør at treet fortsatt er en minimumsheap.
Figur 5.3.2 d) og Figur 5.3.2 e) under viser resultatet etter at verdien 10 er lagt inn og så etter at verdien 12 er lagt inn:
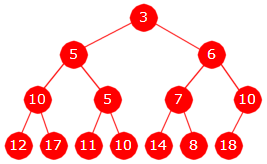 |
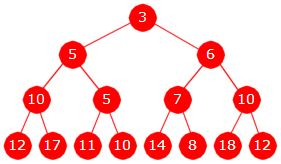 | |
| Figur 5.3.2 d) : Verdien 10 er lagt inn | Figur 5.3.2 e) : Verdien 12 er lagt inn |
Hvis en verdi skal legges inn i treet i Figur 5.3.2 e), vil treet få en nytt nivå siden nederste nivå er fullt. Den nye noden legges lengst til venstre på det nye nivået. Se Oppgave 1.
Uttak fra en minimumsheap Den minste verdien (som ligger i rotnoden) skal tas ut. Men rotnoden skal ikke fjernes. Isteden fjerner vi den siste noden (den lengst til høyre på nederste rad). Vi tar vare på verdien siden den skal inn på et annet sted i treet. I Figur 5.3.2 e) over inneholder den verdien 12. Figur 5.3.2 f) under til venstre viser første skritt:
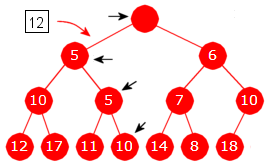 |
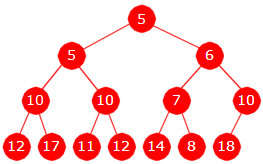 | |
| Figur 5.3.2 f) : Minste verdi (3) er tatt ut | Figur 5.3.2 g) : Verdien 12 er lagt inn |
Verdien 12 skal inn på rett sortert plass i minimumsgrenen, dvs. grenen fra rotnoden og for hver node videre til nodens «minste» barn (barnet med minst verdi). Har en node to «like» barn, velges det venstre. I Figur 5.3.2 f) er nodene i minimumsgrenen markert med små piler. Verdiene i grenen «trekkes» oppover inntil korrekt plass for 12 blir «ledig» og 12 kan settes inn der. Figur 5.3.2 g) over til høyre viser resultatet.
Ved neste uttak av minst verdi (5) «blankes» først rotnoden, den siste noden (den lengst til høyre på nederste rad) fjernes og dens verdi (18) legges inn på sortert plass i minimumsgrenen (rotnoden, 6, 7 og 8). Da blir resultatet som i Figur 5.3.2 h) under til venstre. Tar vi ut den minste enda en gang er det verdien 8 som skal inn på rett sortert plass i minimumsgrenen med Figur 5.3.2 i) under til høyre som resultat:
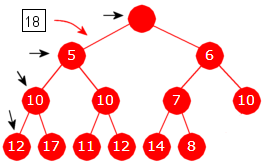 |
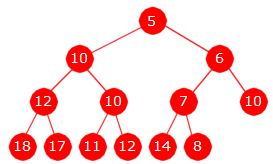 | |
| Figur 5.3.2 h) : Minste verdi (5) er tatt ut | Figur 5.3.2 i) : Minste verdi (5) er tatt ut |
Effektivitet Hvor effektivt er det å legge inn og ta ut fra en minimumsheap? En ny verdi skal
legges på rett sortert plass i den grenen som går ned til den nye noden i bunnen av treet. Men den
grenen vil få, hvis det er n noder på forhånd, en lengde
lik ⌊log2 (n + 1)⌋. I verste fall skal den nye
verdien legges øverst i grenen (i rotnoden) og innleggingen blir dermed av logaritmisk orden.
Men i gjennomsnitt blir det annerledes. En minimumsheap er et komplett tre og i et slikt tre
vil i gjennomsnitt ca. 2/3-deler (egentlig 1 − ½ log 2) av verdiene
ligge på de to nederste radene. Se Avsnitt 5.3.9.
Hvis treet er perfekt ligger i gjennomsnitt andelen på 3/4.
Alle grenene er sortert. Dermed vil verdiene på de to nederste radene utgjøre nær 2/3-deler
av de største verdiene. En ny verdi har derfor i gjennomsnitt stor sannsynlighet for å havne nær
en av de to nederste radene. Det viser seg at det i gjennomsnitt trengs kun litt over to
sammenligninger for å finne den rette plassen siden sammenligningene starter
fra bunnen. Innleggingen blir derfor i gjennomsnitt av konstant orden.
Det å ta ut den minste verdien vil være av logaritmisk orden både i gjennomsnitt og i det verste tilfellet. Når den minste, dvs. rotverdien, tas ut, fjernes den siste noden og dens verdi settes inn på rett sortert plass i minimumsgrenen. Denne verdien må relativt sett være stor siden den lå på bunnen av treet, og den vil derfor med stor sannsynlighet havne langt ned i minimumsgrenen. I verste tilfellet helt nederst. Det betyr at det i gjennomsnitt trengs nær like mange sammenligninger som grenen har lengde (som er lik ⌊log2 (n + 1)⌋) for å finne rett plass i grenen siden sammenligningene starter ovenifra.
| Effektivitet (orden) i en minimumsheap | |||
| Metode | Gjennomsnittlig | Beste tilfellet | Verste tilfellet |
| leggInn | konstant | konstant | logaritmisk |
| taUt | logartimisk | konstant | logaritmisk |
| 1. | Legg inn 2 i minimumsheapen i Figur 5.3.2 e). Tegn heapen. Legg så inn 4. Tegn heapen. |
| 2. | Legg verdiene 5, 8, 3, 7, 10, 2, 9, 6, 4 og 1 fortløpende inn i en på forhånd tom minimumsheap. Tegn heapen når alle er lagt inn. Skriv opp verdiene i minimumsgrenen. Ta så ut minste verdi. Tegn heapen. Skriv opp verdiene i minimumsgrenen i heapen du nå har. Fjern så ut den minste på nytt. Tegn heapen. |
| 3. | En ny verdi legges inn i en minimumsheap ved at det først opprettes en ny node i bunnen av treet. Noden blir da siste node på en gren i treet. Deretter trekkes verdier nedover i grenen inntil vi finner den rett sorterte plassen for den nye verdien. Minst arbeid blir det hvis den ny verdien kan legges nederst i grenen og mest arbeid hvis den nye verdien må legges øverst i grenen, dvs. i rotnoden. Gitt at vi skal legge verdiene/tallenen fra 1 til 10 inn i en på forhånd tom minimumsheap. Arbeidsmengden med å bygge opp heapen er avhengig av i hvilken rekkefølge verdiene legges inn. Hvilken rekkefølge vil sammenlagt gi minst arbeidsmengde og hvilken vil gi størst? Tegn de to heapene som gav henholdsvis minst og størst arbeidsmengde. |
| 4. | Som i Oppgave 2, men bruk verdiene 6, 4, 8, 5, 6, 9, 3, 8, 5, 3, 6 og 9. |
| 5. | Som i Oppgave 2, men bruk verdiene 5, 9, 4, 10, 15, 11, 3, 2, 12, 1, 13, 14, 6, 8 og 7. |
| 6. | Innlegging og uttak foregår på en tilsvarende måte i en maksmumsheap. Hvis en ny verdi skal legges inn, opprettes først en ny (og tom) node på bunnen av heapen. Deretter settes verdien inn på rett sortert plass i den tilhørende grenen. Men nå skal grenen være sortert avtagende. Den største verdien tas ut fra roten, den siste noden fjernes og dens verdi settes inn på rett sortert plass i maksimumsgrenen. Sett verdiene fra Oppgave 5 fortløpende inn i en maksimumsheap. Ta så ut den største to ganger. |
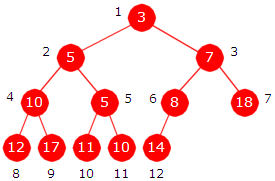 |
| Figur 5.3.3 a) : Heap med nodeposisjoner |
En minimumsheap kan (som et turneringstre) representeres ved hjelp av en tabell. Indekser svarer til nodeposisjoner. I algoritmene for å legge inn en verdi og å ta ut den minste verdien i en minimumsheap (se Avsnitt 5.3.2) var det nødvendig å kunne gå i begge retninge i treet, og det gjør vi ved hjelp av indeksene.
Treet fra Figur 5.3.3 a) er i figuren under lagt inn i en tabell med 20 posisjoner. Det første tabellelementet er ikke i bruk siden det ikke er noen node som har posisjon 0.
| 3 | 5 | 7 | 10 | 5 | 8 | 18 | 12 | 17 | 11 | 10 | 14 | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Tabell 5.3.3 a) : Heapen fra Figur 5.3.3 a) som en tabell | |||||||||||||||||||
Den generiske klassen HeapPrioritetsKø skal implementere
grensesnittet PrioritetsKø. Den skal videre
bruke en minimumsheap implementert ved hjelp av en tabell som intern datastruktur. Videre trengs en komparator for sammenligninger
og en antallvariabel for å holde orden på antallet verdier i tabellen.
Obs: Første element (indeks 0) i tabellen er ikke en del
av den ordinære heapen. Det betyr at variablen antall
nå blir posisjonen til den siste verdien i tabellen (og ikke som tidligere posisjonen til første ledige plass).
import java.util.*; public class HeapPrioritetsKø<T> implements PrioritetsKø<T> { private T[] heap; // heaptabellen private int antall; // antall verdier i køen private Comparator<? super T> comp; // for sammenligninger // konstruktører skal inn her public int antall() { return antall; } public boolean tom() { return antall == 0; } // leggInn, kikk, taUt, toString og nullstill skal inn her } // HeapPrioritetsKø Programkode 5.3.3 a)
Som vanlig for denne typen klasser, lager vi to konstruktører. Begge har en komparator som parameter. Den første har også en kapasitet, dvs. en tabellstørrelse, som parameter. Den andre bruker en standardstørrelse som startkapasitet – her er den satt til 8:
@SuppressWarnings("unchecked") public HeapPrioritetsKø(int kapasitet, Comparator<? super T> c) { if (kapasitet < 0) throw new IllegalArgumentException("Negativ kapasitet!"); heap = (T[])new Object[kapasitet + 1]; // indeks 0 brukes ikke antall = 0; comp = c; } public HeapPrioritetsKø(Comparator<? super T> c) { this(8,c); // bruker 8 som startkapasitet } Programkode 5.3.3 b)
Det kan også være gustig å ha et par konstruksjonsmetoder, dvs. statiske metoder
som returnerer en instans av klassen. Konstruksjonsmetodene forventer at datatypen T
er sammenlignbar, dvs. T implementerer Comparable<T> eller er
en subtype av en slik type:
public static <T extends Comparable<? super T>> HeapPrioritetsKø<T> naturligOrden(int kapasitet) { // bruker en komparator for datatypens naturlige orden return new HeapPrioritetsKø<>(kapasitet,Comparator.naturalOrder()); } public static <T extends Comparable<? super T>> HeapPrioritetsKø<T> naturligOrden() { return naturligOrden(8); } Programkode 5.3.3 c)
Metodene antall() og tom() er allerede kodet i
Programkode 5.3.3 a).
Metoden kikk() skal returnere
den største verdien og den ligger i posisjon 1 i tabellen. Metoden nullstill() skal
«nulle» eventuelle tabellverdier som måtte ligge igjen i tabellen og sette antall til 0.
public T kikk() { if (tom()) throw new NoSuchElementException("Køen er tom!"); return heap[1]; } public void nullstill() { for (int i = 0; i <= antall; i++) heap[i] = null; antall = 0; } Programkode 5.3.3 d)
Innlegging
Det må først opprettes
en tom node på første ledige plass på bunnen av treet. Når heapen er representert
ved hjelp av en tabell betyr det første ledige plass (bakerst) i tabellen.
Denne noden blir nederste node på en gren. Så «trekkes» verdier nedover langs
denne grenen inntil vi finner den rett sorterte plassen for den nye verdien.
Se Avsnitt 5.3.2.
Hvis en node har posisjon k, vil forelderen ha posisjon k/2. Det betyr at en verdi i forelderen «trekkes» ned til noden ved hjelp av koden:
heap[k] = heap[k/2];
Dette gjentas så lenge som forelderverdien heap[k/2] er større enn den nye verdien.
Øverste posisjon er 1. Hvis den nye verdien er mindre enn den minste i treet,
skal den plasseres i posisjon 1. Derfor må vi stoppe når vi
kommer opp til posisjon 1:
while (k > 1 && comp.compare(heap[k/2],verdi) > 0) { heap[k] = heap[k/2]; // trekker verdien i heap[k/2] nedover k /= 2; // k går opp til forelderen }
Det første tabellelementet, dvs. heap[0], er ikke i bruk. Men det kan brukes
som posisjon for en vaktpost eller stoppverdi. Hvis vi kopierer inn den nye verdien i
heap[0] vil den fungere som vaktpost. Dermed trenger vi ikke sammenligningen
k > 1. Dette kan kodes slik:
heap[0] = verdi; // stoppverdi for while-løkken while (comp.compare(heap[k/2],verdi) > 0) { heap[k] = heap[k/2]; // trekker verdien i heap[k/2] nedover k /= 2; // k går opp til forelderen }
Hele leggInn-metoden kan derfor kodes slik:
public void leggInn(T verdi) { Objects.requireNonNull(verdi, "verdi er null!"); // øker antaller først og "dobler" tabellen hvis den er full if (++antall == heap.length) heap = Arrays.copyOf(heap, 2*antall); int k = antall; // første ledige plass i tabellen heap[0] = verdi; // stoppverdi for while-løkken while (comp.compare(verdi, heap[k/2]) < 0) { heap[k] = heap[k/2]; // trekker verdien i heap[k/2] nedover k /= 2; // k går opp til forelderen } heap[0] = null; // fjerner referansen heap[k] = verdi; // verdi skal ligge i posisjon k } Programkode 5.3.3 e)
I Avsnitt 5.3.2 innlegging og uttak illustrert med tegninger. Hvis en vil teste seg selv (ved å lage tegninger), kan en få en «fasit» ved ved å bruke flg. metode. Den skriver innholdet av heapen i nivåorden:
public String toString() { StringBuilder s = new StringBuilder(); s.append('['); if (antall > 0) s.append(heap[1]); // roten er i posisjon 1 for (int i = 2; i <= antall; ++i) // går gjennom tabellen { s.append(',').append(' ').append(heap[i]); } s.append(']'); return s.toString(); } Programkode 5.3.3 f)
Under HeapPrioritetsKø ligger de metodene som vi har diskutert til nå.
Hvis du flytter klassen over til deg selv, vil du kunne sjekke at leggInn-metoden bygger opp heapen/treet slik som
beskrevet i Avsnitt 5.3.2. Heapen i
Figur 5.3.2 a) lages ved å legge inn i nivåorden.
En utskrift av heapen kan så gjøres etter innlegging av henholdsvis 6, 10 og 12. Det kan så sammenlignes med figurene:
int[] a = {3,5,7,10,5,8,18,12,17,11,10,14}; // verdiene i Figur 5.3.2 a) PrioritetsKø<Integer> kø = HeapPrioritetsKø.naturligOrden(); for (int k : a) kø.leggInn(k); kø.leggInn(6); System.out.println(kø); // legger inn 6 kø.leggInn(10); System.out.println(kø); // legger inn 10 kø.leggInn(12); System.out.println(kø); // legger inn 12 // Utskrift: // [3, 5, 6, 10, 5, 7, 18, 12, 17, 11, 10, 14, 8] se Figur 5.3.2 c) // [3, 5, 6, 10, 5, 7, 10, 12, 17, 11, 10, 14, 8, 18] se Figur 5.3.2 d) // [3, 5, 6, 10, 5, 7, 10, 12, 17, 11, 10, 14, 8, 18, 12] se Figur 5.3.2 e) Programkode 5.3.3 g)
Teknikken for taUt() er beskrevet i Avsnitt 5.3.2. Der skal
rotnoden «blankes», den siste noden skal fjernes og dens verdi skal inn på rett sortert plass i minimumsgrenen.
Da må vi kunne gå nedover langs grenen. Figuren under viser to heaper:
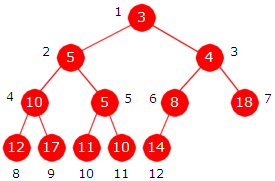 |
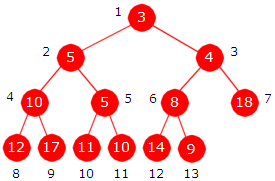 |
| Figur 5.3.3 b): To komplette binærtrær | |
I treet til venstre er det kun den indre noden med posjon 6 som har ett barn.
Alle de andre indre nodene (posisjoner fra 1 til 5) har to barn. Generelt gjelder at en node med posisjon
k har to barn hvis og bare hvis 2*k < antall. I treet til venstre
er antall lik 12. I treet til høyre
har noden med posisjon 6 to barn. Det passer siden antall der er 13 og
2*6 < 13. En node med posisjon k har kun ett barn (dvs. et venstre barn) hvis og bare hvis 2*k = antall.
Dette kan vi bruke til å lage en metode som finner minimumsgrenen:
public String minimumsGrenen() // skal legges i klassen HeapPrioritetsKø
{
StringBuilder s = new StringBuilder();
s.append('[');
if (antall > 0) s.append(heap[1]); // treet er ikke tomt
int k = 1;
while (2*k < antall) // forsetter så lenge k har to barn
{
k *= 2; // går til venstre barn ved å doble k
if (comp.compare(heap[k+1], heap[k]) < 0) k++; // er høyre barn minst?
s.append(',').append(' ').append(heap[k]); // det minste barnet
}
if (2*k == antall) // har treet et enebarn?
{
s.append(',').append(' ').append(heap[2*k]);
}
s.append(']');
return s.toString();
}
Programkode 5.3.3 h)
Flg. kode skriver ut minimumsgrenen i heapen til venstre i Figur 5.3.3 b):
int[] a = {3,5,4,10,5,8,18,12,17,11,10,14}; HeapPrioritetsKø<Integer> kø = HeapPrioritetsKø.naturligOrden(); for (int k : a) kø.leggInn(k); System.out.println(kø.minimumsGrenen()); // Utskrift: [3, 4, 8, 14] Programkode 5.3.3 i)
I taUt-metoden skal den siste noden fjernes og dens verdi skal inn på rett sortert plass i
minimumsgrenen. Men den verdien vil, siden den lå nederst, med stor sannsynlighet også havne nederst
eller nesten nederst i minimumsgrenen. Derfor vil det være mest effektivt å forskyve alle verdiene
oppover én enhet først. Til det kan vi bruke kode av samme type som i metoden
minimumsGrenen. Da sparer vi den sammenligningen vi
ellers måte ha hatt for å avgjøre hvor verdien skal settes inn.
Isteden kan vi starte fra bunnen for å finne rett sortert plass. Det gjøres på nøyaktig samme måte
som i metoden leggInn. I koden under brukes noen steder
k << 1 istedenfor 2*k, osv.
public T taUt() // skal legges i klassen HeapPrioritetsKø
{
if (tom()) throw new NoSuchElementException("Køen er tom!");
T min = heap[1]; // den minste ligger øverst
T verdi = heap[antall]; // skal omplasseres
heap[antall] = null; // for resirkulasjon
antall--; // en verdi mindre i køen
int k = 1; // nodeposisjon
while ((k << 1) < antall) // så lenge k har to barn
{
k <<= 1; // til venstre ved å doble k
// hvis høyre barn k + 1 er minst, setter vi k dit, dvs. k++
if (comp.compare(heap[k + 1], heap[k]) < 0) k++;
heap[k >>> 1] = heap[k]; // forskyver oppover
}
if (2*k == antall) // har k et barn?
{
k *= 2; // går til venstre barn
heap[k/2] = heap[k]; // forskyver oppover
}
heap[0] = verdi; // blir vaktpost
while (comp.compare(verdi, heap[k/2]) < 0)
{
heap[k] = heap[k/2]; // trekker verdien nedover
k /= 2; // k går opp til forelderen
}
heap[k] = verdi; // verdi skal ligge i posisjon k
heap[0] = null; // fjerner referansen
return min; // returnerer minste verdi
}
Programkode 5.3.3 j)
I taut-metoden går den første while-løkken så lenge som k har to barn (
2*k < antall). Uttrykket 2*k kan i verste fall
(en svært stor heap) føre til «oversvømmelse». Vi kunne isteden ha brukt
k < antall/2. Se Oppgave 5.
If-setningen etter den første while-løkken kunne vært unngått ved hjelp av en passende test inne i
løkken. Se Oppgave 6. Hele koden kunne vært kortere med
innsetting av verdi på vei nedover. Se Oppgave 7.
Diskusjonen i Avsnitt 5.3.2 gir flg. effektivitet
for de tre metodene leggInn,
kikk og
taUt:
| Metode: | leggInn | kikk | taUt |
| Orden i det verste tilfellet: | logaritmisk | konstant | logaritmisk |
| Gjennomsnittlig orden: | konstant | konstant | logaritmisk |
| Tabell 5.3.3 : Ordenen til de tre metodene | |||
|---|---|---|---|
En metode som ikke brukes så ofte i en prioritetskø, men som likevel kan være nyttig å ha, er
taUt(T verdi).
Metoden taUt()
tar ut den minste verdien. Men taUt(T verdi) skal kunne ta ut hvilken som helst verdi
i køen. Vi må først finne verdien. Anta at den ligger i posisjon k.
Hvis k er den siste (dvs. k = antall), fjernes den på direkten. Hvis ikke,
må vi se på det subtreet som har noden
k som rot. Vi «blanker» roten og flytter alle verdiene
i subtreets minimumsgren én posisjon oppover. Da blir det frigjort en plass nederst. Treets siste verdi
settes inn på rett sortert plass i den grenen (sett på som gren i hele treet).
Se Oppgave 9.
Vi kan sjekke leggInn og
taUt() ved å legge inn tilfeldige verdier
og så ta dem ut. Da skal de komme i sortert rekkefølge:
int n = 10; // velg n >= 0 int[] a = Tabell.randPerm(n); // en permutasjon av tallene fra 1 til n PrioritetsKø<Integer> kø = HeapPrioritetsKø.naturligOrden(); for (int k: a) kø.leggInn(k); // ett og ett tall inn i køen while (!kø.tom()) { System.out.print(kø.taUt() + " "); // tar ut fra køen } // Utskrift: 1 2 3 4 5 6 7 8 9 10 Programkode 5.3.3 k)
| 1. | Klassen HeapPrioritetsKø inneholder alle
metoden som hra blitt diskutert så langt.
Flere av oppgavene i Avsnitt 5.3.2 går ut på å
bygge opp minimumsheaper ved å bruke regelen for innlegging. En kan få en
«fasit» ved å gjøre som i Programkode 5.3.3 g).
Tegn treet som 7, 6, 5, 4, 3, 2, 1 gir. Bruk så de samme tallene i
Programkode 5.3.3 g).
|
| 2. | Programkode 5.3.3 i) skriver ut minimumsgrenen i treet til venstre i Figur 5.3.3 b). Hvis 9 legges sist i tabellen, får vi treet til høyre i Figur 5.3.3 b). Sjekk at metoden gir korrekt minimumsgren. Bruk andre verdier og sjekk at det hver gang blir korrekt minimumsgren. |
| 3. | Sjekk at Programkode 5.3.3 k) virker. Sjekk at verdiene kommer sortert også for andre verdier av n (fra 0 og oppover). |
| 4. | Sjekk din forståelse av uttaksregelen ved først å tegne en minimumsheap og så lage kode som bygger den samme heapen. Deretter kan du parallelt ta ut på tegningen og i koden. F.eks. vil tabellen {3,5,4,10,5,8,18,12,17,11,10,14,9} gi treet til høyre i Figur 5.3.3 b). Ta ut den minste på figuren og lag så kode som tar ut. Sammenlign ved å skrive ut treet. Gjenta dette flere ganger. Da får treet én verdi mindre for hver gang. |
| 5. | Sammenligningen 2*k < antall er ikke identisk med
k < antall/2 siden det inngår en heltallsdivisjon i den siste. Gjør
de endringene som trengs i metodene minimumsGrenen og
taUt slik at den første while-løkken
bruker sammenligningen k < antall/2.
|
| 6. | Ved å bruke 2*k <= antall og en ekstra sammenligning
inne i løkken, kan if-setningen etter første while-løkke fjernes. Gjør dette i taUt-metoden.
|
| 7. | Gjør om koden i taUt() slik at verdi settes inn på vei nedover.
|
| 8. | Lag metoden public String[] grener() i klassen
HeapPrioritetsKø.
Den skal returnere en tegnstrengtabell - en streng for hver gren - fra venstre
mot høyre.
|
| 9. | Lag metoden public boolean taUt(T verdi) i klassen
HeapPrioritetsKø.
|
| 10. | Lag en iterator i klassen
HeapPrioritetsKø. Den
skal gå gjennom heapen i nivåorden.
|
![]() 5.3.4 Prioritetskø i java.util
5.3.4 Prioritetskø i java.util
Javabiblioteket java.util har klassen
PriorityQueue.
Den er kodet på samme måte som vår klasse HeapPrioritetsKø, dvs. ved hjelp av en tabellbasert minimumsheap.
I oversikten under er de fleste av dens metoder satt opp:
public class PriorityQueue<T> extends AbstractQueue<T> { public int size(); // public int antall() public boolean isEmpty(); // public boolean tom() public void clear(); // public void nullstill() public boolean add(T e); // public boolean leggInn(T e) public boolean offer(T e); // public boolean leggInn(T e) public T element(); // public T kikk() public T peek(); // public T kikk() public T remove(); // public T taUt() public T poll(); // public T taUt() public boolean remove(Object o); // public boolean taUt(T verdi) public String toString(); // public String toString() public Iterator<T> iterator(); // + flere } Programkode 5.3.4 a)
De to metodene add og offer oppfører seg helt likt. Faktisk inneholder
add kun et kall på offer. Både element og peek
returnerer den første i køen (den minste verdien). Forskjellen er at element kaster et unntak
hvis køen er tom, mens peek i det tilfellet returnerer null. Både remove og poll
tar ut (og returnerer) den første i køen (den minste verdien). Forskjellen er at remove kaster et unntak
hvis køen er tom, mens poll returnerer null. Metoden toString
returnerer en tegnstreng med køens verdier i nivåorden. Det samme gjør iteratoren, dvs. gir oss verdiene
i nivåorden.
Metoden boolean remove(Object o) fjerner o fra køen. Hvis det er flere
eksemplarer av o, blir kun ett av dem fjernet.
| 1. | Sjekk hvilke andre metoder som klassen
PriorityQueue har. |
| 2. | Metoden element kaster et unntak
hvis køen er tom, mens peek i det tilfellet returnerer null. Lag kode som sjekker at
det stemmer |
| 3. | Metoden remove kaster et unntak
hvis køen er tom, mens poll i det tilfellet returnerer null. Lag kode som sjekker at
det stemmer |
![]() 5.3.5 Minimumsheap med noder
5.3.5 Minimumsheap med noder
I Avsnitt 5.3.3 ble minimumsheapen, dvs. et komplett minimumstre, implementert ved hjelp
av en tabell. Det er den mest optimale teknikken. Men det er også mulig å implementere et slikt tre ved hjelp av dynamiske noder.
En slik løsning har hverken bedre effektivitet eller mindre plassbehov. Men det kan være lærerikt rent kodeteknisk
å lage en slik implementasjon.
Vi kan bruke samme datastruktur som i et binært søketre der nodene har forelderreferanse. Se Avsnitt 5.2.11. Vi setter opp starten på klassen. Det å fullføre gis som oppgaver:
import java.util.*; public class BinTrePrioritetsKø<T> implements PrioritetsKø<T> { private static final class Node<T> // en indre nodeklasse { // En nodeklasse med forelderreferanse } // class Node private Node<T> rot; // referanse til rotnoden private int antall; // antall noder private final Comparator<? super T> comp; // komparator // Konstrukører og konstrusjonsmetoder skal inn her // Metodene leggInn, kikk, taUt, taUt(T) og toString skal inn her } // slutt på class BinTrePrioritetsKø Programkode 5.3.5 a)
| 1. |
BinTrePrioritetsKø inneholder
et skjelett av klassen. Konstruktør, konstruksjons-metoder og
antall, tom og nullstill er ferdigkodet. Flytt dette over til deg selv.
|
| 2. |
Ved innleggeing skal det opprettes en ny (blad)node i posisjon antall + 1. Verdien skal inn på rett
sortert plass i den tilhørende grenen. Det er det mulig å få til på veien nedover. Bruk samme teknikk som
i leggInn-metoden i et
vanlig binærtre.
|
| 3. |
Metoden kikk() skal så sant køen ikke er tom, returnere (uten å fjerne) den minste verdien. Det er
enkelt å få til siden den minste verdien ligger i roten.
|
| 4. |
Metoden toString() skal returnere en tegnstreng som inneholder køens verdier i nivåorden.
|
| 5. |
Metoden taUt() skal ta ut den minste verdien. Da må først den siste noden
(den med posisjon antall) fjernes. Dens verdi skal så inn på rett sortert plass i
minimumsgrenen.
|
| 6. |
Metoden taUt(T verdi) skal ta ut verdi fra køen hvis den finnes der. Det
løses på en tilsvarende måte som i Avsnitt 5.3.3.
|
| 7. |
Opprett en tabell med f.eks. 1 million tilfeldige tall. Legg dem fortløpende inn i en
BinTrePrioritetsKø. Ta så alle ut igjen. Mål tidsforbruket. Sammenlign med
HeapPrioritetsKø og med PriorityQueue i java.util.
|
![]() 5.3.6 Heapsortering
5.3.6 Heapsortering
En tabell kan sorteres ved at den først gjøres om til en
maksimumsheap og så gjøres den om til en
sortert tabell. En slik algoritme kalles
heapsortering.
Når verdiene allerede ligger i en tabell, må også tabellelementet med indeks lik 0 være med. Det betyr at når tabellen skal «tolkes» som et komplett binærtre, må roten ha posisjon 0:
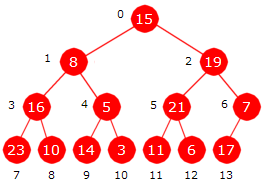 |
| 15 | 8 | 19 | 16 | 5 | 21 | 7 | 23 | 10 | 14 | 3 | 11 | 6 | 17 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Figur 5.3.6 a) : Et komplett binærtre og en (usortert) tabell. | |||||||||||||
Når rotnoden har posisjon 0, må vi bruke en annen regel enn før når det gjelder forelder og barn. Hvis en node nå har posisjon k, så vil venstre barn ha posisjon 2k + 1, høyre barn posisjon 2k + 2 og forelder posisjon (k − 1)/2. Sjekk treet og tabellen i Figur 5.3.6 a) og se at det stemmer. Dermed får en verdi samme indeks i tabellen som den har posisjon i treet.
Treet i Figur 5.3.6 a) er i utgangspunktet ingen maksimumsheap. For at den skal være det må alle grenene være sortert avtagende. Første del av heapsortering går ut på å gjøre om treet til en maksimumsheap.
Vi starter med verdien i posisjon 1, dvs. tallet 8. Men det ligger allerede riktig i forhold til forelderverdien. Tallet i posisjon 2 (dvs. tallet 19) er større enn forelderverdien. Dermed må de bytte plass. Med andre ord blir 19 ny rotnodeverdi. Tallet 16 i posisjon 3 er større enn forelderverdien 8. De to må bytte plass, dvs. posisjon 1 vil da inneholde 16 og posisjon 3 vil inneholde 8. Går vi så videre til posisjon 4 (tallet 5), ser vi at den ligger riktig. Treet i figuren under viser dette så langt:
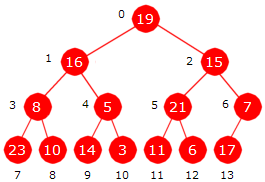 |
| Figur 5.3.6 b) : Posisjonene 1 til 4 er behandlet |
I Figur 5.3.6 b) over forstetter vi med verdien 21 i posisjon 5. Den er større enn verdiene i både forelder og besteforelder. Den skal derfor inn i posisjon 0 og de to andre (verdiene 19 og 15) trekkes nedover. Verdien 7 i posisjon 6 ligger riktig i forhold til forelderverdi. Verdien 23 i posisjon 7 er større enn rotnodeverdien. Den skal dit og de på veien oppover må forskyves nedover. Osv. til vi får flg. maksimumsheap:
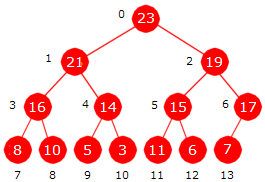 |
| Figur 5.3.6 c) : En maksimumsheap |
Beskrivelsen over gir flg. kode for å gjøre om en tabell til en maksimumsheap:
public static void lagMaksimumsheap(int[] a) // fra tabell til maksimumsheap { for (int i = 1; i < a.length; i++) // starter i posisjon 1 { int k = i; // k er en hjelpevariabel int verdi = a[i]; // verdi er en hjelpevariabel int forelder = (k - 1)/2; // forelder til k while (k > 0 && verdi > a[forelder]) // sammenligner med forelder { a[k] = a[forelder]; // trekker ned fra forelder k = forelder; // oppdaterer k forelder = (k - 1)/2; // oppdaterer forelder } a[k] = verdi; // rett sortert plass for verdi } } Programkode 5.3.6 a)
I algoritmen legges én og én verdi inn i en maksimumsheap. Vi vet at det å legge en tilfeldig verdi inn
i en minimumsheap er i gjennomsnitt av konstant orden. Det blir også slik for en maksimumsheap.
Sammenligningen verdi > a[forelder] i while-løkken blir i gjennomsnitt utført litt over to ganger (ca. 2,3).
Dermed blir algoritmen for å bygge opp heapen av lineær orden (av orden n der n er
tabellens lengde).
Flg. eksempel kan brukes til å sjekke om Programkode 5.3.6 a) gir samme resultat som i diskusjonen over. Den endte med Figur 5.3.6 d):
int[] a = {15,8,19,16,5,21,7,23,10,14,3,11,6,17}; // utgangstabellen lagMaksimumsheap(a); // lager maksimumsheapen System.out.println(Arrays.toString(a)); // utskrift i nivåorden // Utskrift: [23,21,19,16,14,15,17,8,10,5,3,11,6,7] Programkode 5.3.6 b)
Neste skritt i heapsortering er å gjøre om maksimumsheapen til en sortert tabell. Vi tar utgangspunkt i flg. maksimumsheap satt opp både som et tre og som en tabell:
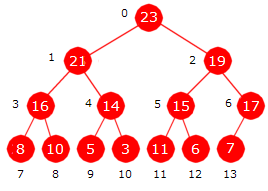 |
| 23 | 21 | 19 | 16 | 14 | 15 | 17 | 8 | 10 | 5 | 3 | 11 | 6 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Figur 5.3.6 d) : Maksimumsheap som tre og tabell | |||||||||||||
Siste verdi (7 i posisjon 13) tas vekk. Største verdi (rotnodeverdien 23) flyttes til posisjon 13. Så settes 7 inn på rett sortert plass i maksimumsgrenen. Det får vi til ved å flytte alle verdiene i grenen en enhet oppover og så legge 7 nederst (i posisjon 8). Det gir flg. resultat:
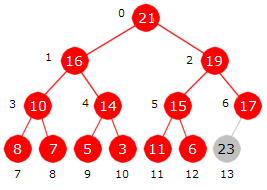 |
| 21 | 16 | 19 | 10 | 14 | 15 | 17 | 8 | 7 | 5 | 3 | 11 | 6 | 23 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Figur 5.3.6 e) : Den største ligger nederst/bakerst | |||||||||||||
I Figur 5.3.6 e) har den største verdien havnet bakerst og antallet i maksimumsheapen har blitt én mindre. Den delen som ikke hører til maksimumsheapen er markert med grått.
Dette gjentas. Siste verdi (6 i posisjon 12) tas vekk. 21 flyttes til posisjon 12 og 6 settes inn på rett sortert plass i maksimumsgrenen. Den vil nå ha verdiene 19, 17 og 6:
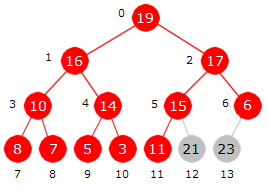 |
| 19 | 16 | 17 | 10 | 14 | 15 | 6 | 8 | 7 | 5 | 3 | 11 | 21 | 23 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Figur 5.3.6 f) : De to største ligger nederst/bakerst | |||||||||||||
Idéen over kan kodes på en tilsvarende måte som metoden
taUt for en minimumsheap. Forskjellen
er at vi nå har en maksimumsheap og en annen regel for posisjonene til forelder og barn.
La n være posisjonen til den siste noden i et komplett binærtre der rotnoden har posisjon 0.
La k være en vilkårlig nodeposisjon. Da har k to barn
hvis 2*k + 1 < n og ett (venstre) barn hvis 2*k + 1 = n.
Ta Figur 5.3.6 f) som eksempel.
Tar vi med de to grå nodene er 13 siste posisjon i treet. Node 5 har to barn siden
2*5 + 1 < 13, mens node 6 har kun et venstre barn siden 2*6 + 1 = 13.
La n være posisjonen til siste node i maksimumsheapen. Dit
skal den største verdien flyttes. Da forsvinner en node og dermed
blir n − 1 siste posisjon i den delen hvor en verdi skal settes inn på
rett sortert plass i maksimumsgrenen. Hvis 2*k + 1 < n - 1
(som er ekvivalent med 2*(k + 1) < n og med k < (n - 1)/2),
vil dermed k ha to barn.
public static void sorterMaksimumsheap(int[] a) { for (int n = a.length - 1; n > 0; n--) // n er posisjonen til siste node { int verdi = a[n]; // den bakerste i maksimumsheapen a[n] = a[0]; // den største flyttes bakerst int k = 0; // en nodeposisjon int m = (n - 1)/2; // stoppverdi while (k < m) // så lenge k har to barn { int barn = 2*k + 1; // venstre barn til k if (a[barn + 1] > a[barn]) barn++; // finner maksimumsgrenen a[k] = a[barn]; // forskyver oppover k = barn; // flytter k nedover } if (2*(k + 1) == n) // k har kun et venstre barn { k = 2*k + 1; // k går til venstre barn a[(k - 1)/2] = a[k]; // forskyver oppover } int forelder = (k - 1)/2; // forelder til k while (k > 0 && verdi > a[forelder]) // sammenligner med forelder { a[k] = a[forelder]; // trekker ned fra forelder k = forelder; // oppdaterer k forelder = (k - 1)/2; // oppdaterer forelder } a[k] = verdi; // rett sortert plass for verdi } } Programkode 5.3.6 c)
Den verdien som skal inn på rett sortert plass i maksimumsgrenen, lå opprinnelig nederst i en annen gren. Dermed er det stor sannsynlighet for at den må legges nederst eller nesten nederst i grenen. Derfor er det mest effektivt først å flytte alle verdiene i grenen oppover. Til det trengs ingen sammenligninger. Deretter leter vi nedenifra etter rett sortert plass. Alternativt kan vi lete etter rett sortert plass når vi går fra roten og nedover langs grenen og stoppe når vi har kommet til rett sted. Da får vi kortere kode. Se Oppgave 5.
De to metodene lagMaksimumsheap og
sorterMaksimumsheap vil tilsammen sortere
en heltallstabell a. Men det er mer naturlig å lage en egen sorteringsmetode med
f.eks. navn heapsortering. Den lages ved å skjøte sammen kodene for
de to metodene. Se Oppgave 6. Metoden
blir av orden n log(n) siden første del er av orden n og den
andre delen av n log(n). Den er i gjennomsnitt mindre effektiv enn f.eks.
kvikksortering,
men har den fordelen at den er av orden n log(n)
i alle tilfeller, mens kvikksortering er av kvadratisk orden i de verste tilfellene.
Metoden introsortering
som bl.a. inngår i standardbiblioteket til C++, er en kombinasjon
av kvikk- og heapsortering.
| 1. | Sjekk at metoden lagMaksimumsheap
virker som den skal hvis tabellen a har ingen verdier (er tom), har kun én verdi og kun
to verdier.
|
| 2. | I while-løkken i metoden lagMaksimumsheap
inngår sammenligningen k > 0. Den trengs for å hindre at vi går ut av tabellen i de
tilfellene verdi skal inn som ny rotverdi. Her kunne vi først sjekke om verdi
er større enn a[0]. I så fall trekker vi alle verdiene i grenen nedover og setter
verdi inn i a[0]. Hvis ikke, vil det som ligger i a[0]
fungere som vaktpost. Dette vil ikke effektivisere koden siden verdi
i gjennomsnitt vil havne på en av de 2 - 3 nederste plassene i grenen. Men en kan gjøre det som kodetrening.
|
| 3. | La a inneholde en permutasjon av tallene fra 1 til n.
Metoden lagMaksimumsheap
gir samme heap for forskjellige permutasjoner. Hvor mange ulike maksimumsheaper
blir det for n = 1, 2, 3, 4 og 5? Hva hvis n = 10? Lag kode som teller
opp antallet for en gitt n. Lag en metode som gir antallet rent matematisk.
|
| 4. | La n være siste posisjon i en maksimumsheap. Dit skal den største
verdien (rotverdien) flyttes og verdien som lå der skal omplasseres. I det nye
treet blir da n − 1 siste posisjon. Sjekk at 2*k + 1 < n - 1
(eller 2*(k + 1) < n) er ekvivalent med k < (n - 1)/2. Del
det i de to tilfellene n oddetall og n partall.
|
| 5. | I sorterMaksimumsheap flyttes
alle verdiene i maksimumsgrenen én enhet oppover og så starter letingen etter rett sortert plass
nedenifra. Det er mest effektivt siden verdien normalt skal inn nederst eller nesten nederst.
Koden kan imidlertid gjøres kortere hvis vi leter etter rett sortert plass på veien nedover
i maksimumsgrenen. Lag kode som gjør det.
|
| 6. | Lag metoden public static void heapsortering(int[] a). Den lages ved at en «klipper ut»
kode fra metoden lagMaksimumsheap og
kode fra sorterMaksimumsheap og
«limer det sammen» inn i heapsortering.
Sjekk at sorteringen blir riktig ved hjelp av en programbit der det genereres
tilfeldige tabeller som sorteres og der det så sjekkes at tabellen ble sortert. Metoden
i erSortertStigende
avgjør om en heltallstabell er sortert. Lag også tidsmålinger der heapsortering sammenlignes
med andre sorteringsteknikker. Sjekk også om det blir endringer i effektiviteten hvis du i den
delen av koden som sorterer en maksimumsheap, bruker ideen fa Oppgave 5.
|
| 7. | Lag public static <T> void heapsortering(T[] a, Comparator<? super T> c).
Den skal benytte en komparator i sorteringen. |
![]() 5.3.7 Heapifisering
5.3.7 Heapifisering
Treet i Figur 5.3.7 a) under er nesten en maksimumsheap, men ikke helt. Vi ser at det
venstre subtreet til rotnoden er isolert sett en maksimumsheap. Det samme gjelder det høyre subtreet.
Men treet som helhet er ikke en maksimumsheap siden 12 i rotnoden er feilplassert.
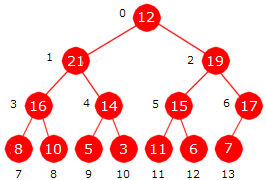 |
| Figur 5.3.7 a) : Rotnodeverdien ligger feil |
Vi kan gjøre om treet i Figur 5.3.7 a) til å bli en maksimumsheap ved å flytte rotnodeverdien 12 til rett sortert plass i maksimumsgrenen, dvs. i grenen som inneholder nodene med posisjoner 0, 1, 3 og 8. Denne prosessen kalles å heapifisere (eng: to heapify) treet.
Det er også mulig å heapifisere et subtre. I Figur 5.3.7 b) under konsentrerer vi oss om subtreet som har noden med posisjon 1 som rotnode, dvs. treet som er «ringet inn». Det treet har to subtrær som begge er maksimumsheaper.
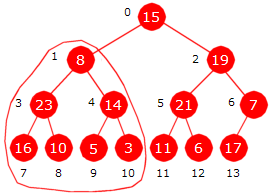 |
| Figur 5.3.7 b) : Venstre subtre er «ringet inn» |
Det «innringede» treet heapifiseres ved at 8 legges på rett sortert plass i maksimumsgrenen, dvs. i grenen som består av nodene med posisjoner 1, 3 og 7. Da får vi dette treet:
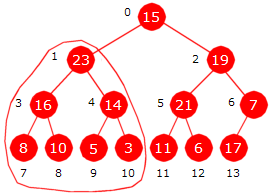 |
| Figur 5.3.7 c) : Venstre subtre er heapifisert |
Metoden public static void heapifiser(int[] a, int k, int n)
skal heapifisere et subtre. Hovedtreet ligger i tabellen a der parameter n forteller hvor mange
elementer i a som hører til hovedtreet. Parameter k er posisjonen til roten i det subtreet som skal
heapifiseres.
Også i metoden sorterMaksimumsheap skulle en verdi settes inn på rett sortert plass
i en maksimumsgren. Der valgte vi å skyve alle elementene oppover først og så lete etter rett sortert plass nedenifra. Det var mest effektivt der
siden verdien med stor sannsynlighet hørte hjemme enten enderst eller nesten nederst. Her blir det litt annerledes siden vi skal
kunne heapifisere subtrær. De kan ligge langt nede i hovedtreet og dermed ha liten høyde. Da blir det like effektivt å lete etter
rett sortert plass på veien nedover langs maksimumsgrenen. Da bruker vi at hvis k < n/2, så vil noden k ha minst ett barn.
Husk også at hvis barn er venstre barn til en node k, så vil barn + 1 være høyre barn hvis k har
et høyre barn.
public static void heapifiser(int[] a, int k, int n) { int verdi = a[k]; // skal omplasseres int halvveis = n / 2; // hjelpevariabel while (k < halvveis) // så lenge k har minst ett barn { int barn = 2 * k + 1; // venstre barn til k if (barn + 1 < n // har barn et søsken? && a[barn + 1] > a[barn]) barn++; // høyre barn er størst if (verdi >= a[barn]) break; // verdi skal på plass k a[k] = a[barn]; // forskyver oppover k = barn; // k går ned } a[k] = verdi; // rett sortert plass for verdi } Programkode 5.3.7 a)
Ta utgangspunkt i treet i Figur 5.3.7 b). Det subtreet som har noden med posisjon 6 som rot, utgjør ikke en maksimumsheap. Subtreet har kun ett barn, men det er ok. Vi heapifiserer subtreet. Når det er gjort heapifiserer vi subtreet med node nr 2 som rotnode. Det vil være mulig siden dets venstre subtre allerede er en maksimumsheap. Slik kan vi fortsette med trærne der røttene har posisjoner 1 og 0. Da blir hele treet heapifisert:
int[] a = {15,8,19,23,14,21,7,16,10,5,3,11,6,17}; // Figur 5.3.7 b) int n = a.length; // antall noder i hovedtreet heapifiser(a, 6, n); // noden med posisjon 6 er rotnode heapifiser(a, 2, n); // noden med posisjon 2 er rotnode heapifiser(a, 1, n); // noden med posisjon 1 er rotnode heapifiser(a, 0, n); // noden med posisjon 0 er rotnode System.out.println(Arrays.toString(a)); // Utskrift: [23, 16, 21, 15, 14, 19, 17, 8, 10, 5, 3, 11, 6, 7] Programkode 5.3.7 b)
Det som gjøres i Programkode 5.3.7 b) kan systematiseres. Anta at vi har et vilkårlig komplett binærtre
(gitt som en heltallstabell). Anta at det er n noder. Da vil siste node ha posisjon n − 1 og dens
forelder posisjon (n - 1 - 1)/2 = (n - 2)/2. Da starter vi prosessen med å sette
k = (n - 2)/2. I Figur 5.3.7 b) svarer det
til at k er 6. Så heapifiserer vi subtrærne fortløpende, dvs. ved å redusere k ved hjelp av k--.
Til sammen blir dette en alternativ algoritme for metoden lagMaksimumsheap:
public static void lagMaksimumsheap(int[] a) // alternativ versjon { int n = a.length; for (int k = (n - 2)/2; k >= 0; k--) heapifiser(a, k, n); } Programkode 5.3.7 c)
Denne nye versjonen av lagMaksimumsheap er faktisk mer effektiv enn den gamle versjonen i
Programkode 5.3.6 a). Dette tar vi opp nærmere i
Avsnitt 5.3.8.
Metoden heapifiser kan også brukes til en ny
versjon av metoden sorterMaksimumsheap:
public static void sorterMaksimumsheap(int[] a) { for (int n = a.length - 1; n > 0; n--) { Tabell.bytt(a, 0, n); // en hjelpemetode heapifiser(a, 0, n); } } Programkode 5.3.7 d)
Denne versjonen av sorterMaksimumsheap er nok marginalt mindre effektiv enn den gamle.
| 1. | Lag en versjon av heapsortering der første del, dvs. det å lage en maksimumsheap,
benytter ideen i Programkode 5.3.7 c). Den
andre delen, dvs. det å sortere en maksimumsheap, skal fortsatt bruke den «gamle»
ideen fra Programkode 5.3.6 c). Den
«nye» ideen fra Programkode 5.3.7 d)
gir ingen fordeler her.
|
![]() 5.3.8 Algoritmeanalyse1
5.3.8 Algoritmeanalyse1
Heapsortering består av to deler - først gjøres tabellen om til en maksimumsheap
og så gjøres den om til en sortert tabell. Den siste delen er av orden
n log(n) både i gjennomsnitt og i det verste tilfellet. Det kommer av at
når den siste verdien i det aktuelle treet tas ut og settes inn i maksimumsgrenen, vil den med stor
sannsynlighet havne nederst eller nesten nederst. Da grenens lengde er logaritmisk
blir det tilsammen en algoritme av orden n log(n).
Den første delen, dvs. omgjøringen av tabellen til en maksimumsheap, har vi laget i to versjoner. Påstanden er at den andre versjonen (Programkode 5.3.7 c) er litt bedre enn den første (Programkode 5.3.6 a). Vi ser fort at de er likeverdige i det beste tilfellet, dvs. når tabellen a er sortert avtagende.
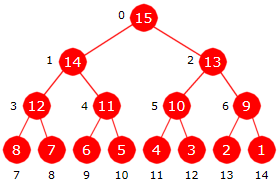 |
| Figur 5.3.8 a) : Treet er sortert avtagende |
I Programkode 5.3.6 a) vil sammenligningen
verdi > a[forelder] utføres en og bare en gang for hver i siden den er sann med en gang.
Det betyr tilsammen 14 sammenligninger for treet i Figur 5.3.8 a) og generelt n − 1 sammenligninger
når treet har n verdier.
Programkode 5.3.7 c) bygger på
Programkode 5.3.7 a). Der
vil det fra og med
posisjon 6 bli utført to sammenligninger med tabellverdier. Der finner
a[barn + 1] > a[barn] «største» barn og
verdi >= a[barn] rett plass. Det betyr 2·7 = 14 sammenligninger.
Generelt blir det også her n − 1 sammenligninger når treet har n verdier.
Det verste tilfellet får vi når tabellen a er sortert stigende:
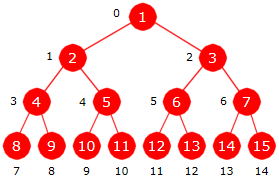 |
| Figur 5.3.8 b) : Treet er sortert stigende |
For å forenkle analysen noe velger vi her kun å se på perfekte trær. Antall noder n i et perfekt tre
er gitt ved n = 2k − 1. Treet i Figur 5.3.8 b) er perfekt. Der er
n = 15 og dermed k = 4. Sammenligningen verdi > a[forelder] i
Programkode 5.3.6 a) blir utført én gang for
de 2 verdiene på nivå 1, to ganger for de 4 verdiene på nivå 2, 3 ganger for de 8 verdiene på nivå 3, osv.
Nivå k − 1 er siste nivå. Dermed får vi flg. sum for antall sammenligninger:
1·21 + 2·22 + 3·23 + . . . + (k − 1)·2k - 1
= (k − 2)·2k + 2 (se 1.9.1.9)
Når n = 2k − 1, blir 2k = n + 1 og k = log2(n + 1). Dermed blir summen over lik:
Formel 5.3.8.a: (n + 1) log2(n + 1) − 2n
Velger vi f.eks. n = 15, blir summen 16 log2(16) − 16·4 − 2·15 = 64 − 30 = 34.
Analysen viser at algoritmen i Programkode 5.3.6 a) er av orden n log n i dette tilfellet. De andre operasjonene (indekssammenligninger, tabellaksesser, tilordninger og aritmetiske operasjoner) ser vi bort fra. Tabellverdisammenligningen er dominerende operasjon.
I Programkode 5.3.7 a) ser vi på:
a[barn + 1] > a[barn] og på: verdi >= a[barn]. I et perfekt tre
vil alle barn ha en søsken. Dermed vil begge sammenligningene bli utført i hver runde i
while-løkken. Vi starter på nest nederste nivå (nivå k - 2).
I treet i Figur 5.3.8 b) blir det nivå 2 siden
k der er 4. Når treet er sortert stigende vil de to sammenligningene bli utført én gang for
de 2k-2 nodene på nivå k - 2, to ganger for de 2k-3 nodene på nivå
k - 3, osv. Til slutt blir det k - 1 ganger for rotnoden (nivå 0). Det gir flg. sum for
antall sammenligninger:
2 [1·2k-2 + 2·2k-3 + 3·2k-4 + . . . + (k − 2)·21 + (k − 1)·20 ]
I Figur 5.3.8 b) blir det 2 [1·22 + 2·21 + 3·20 ] = 2 [4 + 4 + 3 ] = 22. Den generelle summen over kan gjøres om til flg. enkle uttrykk (se Oppgave 1):
Formel 5.3.8.b: 2 [n − log2(n + 1)]
Det betyr at lagMaksimumsheap
i Programkode 5.3.7 c) er av orden n i det verste tilfellet.
En analyse av gjennomsnittlig effektivitet for de to versjonene av lagMaksimumsheap
er svært mye vanskeligere enn for det beste og det verste tilfellet. Vi kan imidlertid lage tilfeldige tabeller
og «telle opp» antall ganger sammenligningene utføres. Metoden
opptelling1 tar seg av «opptellingen» for algoritmen i
Programkode 5.3.6 a):
public static int opptelling1(int[] a) { int antall = 0; for (int i = 1; i < a.length; i++) { int k = i, verdi = a[i]; while (k > 0) { antall++; // sammenligningen vil bli utført if (verdi > a[(k - 1)/2]) { a[k] = a[(k - 1)/2]; k = (k - 1)/2; } else break; } a[k] = verdi; } return antall; } Programkode 5.3.8 a)
Vi kan teste korrektheten til Formel 5.3.8 a) ved
å bruke opptelling1 på en tabell som er sortert stigende:
int n = 31; int[] a = new int[n]; for (int i = 0; i < n; i++) a[i] = i + 1; // a = {1,2,3, . . . , n} System.out.println(opptelling1(a)); // Utskrift: 98 Programkode 5.3.8 b)
Setter vi n = 31 inn i formelen (n + 1) log2(n + 1) − 2n får vi 32·5 − 62 = 98.
En opptellingsmetode for Programkode 5.3.7 c) må lages i to trinn.
Metoden delopptelling teller opp tabellverdisammenligningene i
Programkode 5.3.7 a):
public static int delopptelling(int[] a, int k, int n) { int antall = 0; // til opptellingen int verdi = a[k]; // skal omplasseres int halvveis = n / 2; // hjelpevariabel while (k < halvveis) // så lenge k har minst ett barn { int barn = 2 * k + 1; // venstre barn til k if (barn + 1 < n) // har barn et søsken? { antall++; // en sammenligning if (a[barn + 1] > a[barn]) barn++; // høyre barn er størst } antall++; // en sammenligning if (verdi >= a[barn]) break; // verdi skal på plass k a[k] = a[barn]; // forskyver oppover k = barn; // k går ned } a[k] = verdi; // rett sortert plass for verdi return antall; } Programkode 5.3.8 c)
Metoden opptelling2 under teller opp for algoritmen i
Programkode 5.3.7 c) ved at metoden
delopptelling kalles gjentatte ganger:
public static int opptelling2(int[] a) { int antall = 0, n = a.length; for (int k = (n - 2)/2; k >= 0; k--) antall += delopptelling(a, k, n); return antall; } Programkode 5.3.8 d)
Nå kan vi sammenligne effektiviteten til de to versjonene av lagMaksimumsheap i det verste tilfellet ved en liten utvidelse
Programkode 5.3.8 b):
int n = 31; int[] a = new int[n]; for (int i = 0; i < n; i++) a[i] = i + 1; // a = {1,2,3, . . . , n} int[] b = a.clone(); // b er en kopi av a System.out.println(opptelling1(a)); // Utskrift: 98 System.out.println(opptelling2(b)); // Utskrift: 52 Programkode 5.3.8 e)
Setter vi n = 31 inn i formelen 2 [n − log2(n + 1)] får vi 2·(31 − 5) = 52.
Vi kan studere den gjennomsnittlige effektiviteten for de to versjonene av lagMaksimumsheap
ved å generere tilfeldige heltallstabeller og så sammenligne resultatene slik som i
Programkode 5.3.8 e). Da vil vi se at begge er av orden n
og at den andre versjonen er best. Finn ut hvor mye bedre! Se oppgavene nedenfor.
| 1. | Vis at 2 [1·2k-2 + 2·2k-3 + 3·2k-4 + . . . + (k − 2)·21 + (k − 1)·20 ] = 2 [n − log2(n + 1)] |
| 2. | Kjør Programkode 5.3.8 e) med n = 63, 127 og 255. Sjekk at resultatene stemmer med formlene 5.3.8.a og 5.3.8.b. |
| 3. | La n være stor og lag tabeller som inneholder tilfeldige permutasjoner av tallene fra 1 til n i Programkode 5.3.8 e). Hvordan blir forholdet mellom de to «opptellingene»? |
| 4. | Hvis en bruker n = 15 i Programkode 5.3.8 e),
vil utskriften bli 22 for metoden opptelling2. Finn andre permutasjoner av tallene fra 1 til 15
som også gir 22 for opptelling2.
|
| 5. | Hvis en bruker n = 15 i Programkode 5.3.8 e) og
lar tallene fra 1 til 15 være sortert avtagende, vil utskriften bli 14 for metoden opptelling2.
Finn andre permutasjoner av tallene fra 1 til 15 som også gir 14 for opptelling2.
Hvor mange forskjellige finnes det?
|
| 6. | Hvis vi har en permutasjon av tallene fra 1 til 15 i Programkode 5.3.8 e),
vil opptelling2 gi enten 14, 16, 18, 20 eller 22.
Finn permutasjoner som gir henholdsvis 16, 18 og 20.
|
| 7. | I de to versjonene av lagMaksimumsheap
(Programkode 5.3.6 a) og
Programkode 5.3.7 c) inngår også andre operasjoner enn
tabellverdisammenligninger. Disse operasjonene tar også tid. Lag noen svært store tilfeldige tabeller og
mål tiden disse to versjonene bruker.
|
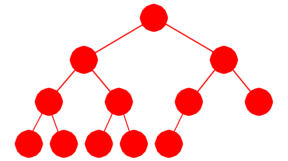 |
| Figur 5.3.9 a) : Et komplett tre med høyde 3 |
Avsnitt 5.3.2
at i slike trær vil i gjennomsnitt ca. 2/3-deler
(eller 1 − ½ log 2) av nodene ligge på de to nederste radene.
Et spørsmål er hva det er gjennomsnitt over. Her skal vi se på gjennomsnittet for komplette trær med
samme høyde. I Figur 5.3.9 a) har vi et komplett tre med høyde 3 og med 12 noder
der 9 av dem ligger på de to nederste radene. For dette treet blir dermed andelen 9/12 = 0,75.
Dette treet er et av de åtte mulige komplette trærne med høyde 3. Hvis det er kun én node på
nederste rad, blir andelen 5/8. Med to noder på nederste rad blir det 6/9. Osv. til en andel på
12/15 hvis det er åtte noder nederst. Tar vi gjennomsnittet av disse åtte mulighetene får vi:
(1/8)(5/8 + 6/9 + 7/10 + 8/11 + 9/12 + 10/13 + 11/14 + 12/15) = 0,728
Vi ser nå generelt på komplette trær med en fast høyde h ≥ 1.
La n = 2h. Slike trær vil ha fra 1 til n noder
på nederste nivå og alltid ha n/2 noder på nest nederste nivå.
Hvis treet har k noder på nederste nivå, vil det da være
k + n/2 noder på de to nederste nivåene og
k + n − 1 noder i hele treet.
Dermed blir andelen lik (k + n/2) / (k + n − 1).
Vi finner gjennomsnittet
ved å summere fra 1 til og med n og så til slutt dele summen med n.
Målet er å finne en formel for denne summen, men før vi gjør det kan vil lage en metode som regner det ut for oss. Dermed får vi gjennomsnittlig andel for en gitt høyde:
public static double g(int h) // g for gjennomsnitt { int n = 1 << h; double sum = 0.0; for (int k = 1; k <= n; k++) sum += (k + n/2.0) / (k + n - 1); return sum / n; }
Ved hjelp av metoden over kan vi lage flg. skjema:
høyde | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
gjennomsnitt | 1,0 | 0,81 | 0,728 | 0,6898 | 0,6714 | 0,6540 | 0,6534269 |
Vi ser at dette faktisk nærmer seg 1 − ½ log 2 = 0,6534264 . . . når høyden blir stor. Her kan en jo lure på hvorfor logaritmen kommer inn. Hvis du er interessert, finner du svaret her.

|