Oppgave 1

  Formel (*):

  C(5) = 1*14 + 1*5 + 2*2 + 5*1 + 14*1 = 42
  C(6) = 1*42 + 1*14 + 2*5 + 5*2 + 14*1 + 42*1 = 132


  Formel (**):

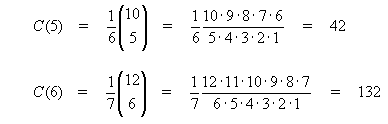
Oppgave 2

Det er 14 forskjellige binære trær med 4 noder

Oppgave 3

Gitt n noder. Det er kun én mulig plassering av rotnoden. For hver node videre er det to mulige plasseringer for et barn - venstre eller høyre. Dermed 1·2·2 · · ·2 = 2^n-1 forskjellige binære trær der ingen node har to barn.

Oppgave 4

Et fullt tre må ha et odde antall noder. Anta at vi har n noder. Det går en kant til hver node bortsett fra til rotnoden. Med andre ord er det n − 1 kanter. Det er kun fra indre noder det går kanter ut (eller ned) og for hver indre node går det to kanter. Siden det er kun n − 1 kanter, må n − 1 være et partall og dermed n et oddetall

Tar vi et vilkårlig fullt tre, må både venstre og høyre subtre være fulle trær. Et eller begge kan være et tre med kun én node. Et tre med én node er et fullt tre. La n være på formen 2k + 1. La videre F(n) være antallet forskjellige fulle trær med n noder. Da kan et venstre subtre ha F(1), F(3), . . . , F(2k-1) noder. Tilsvarende for høyre subtre. Dermed får vi flg. differensligning for F(n):

  F(n) = F(2k+1) = F(1) · F(2k-1) + F(3) · F(2k-3) + . . . + F(2k-1) · F(1)

La 2m + 1 være et vilkårlig oddetall og definer G(m) = F(2m+1) for m = 0, 1, 2, . . . . Da vil differensligningen kunne skrives slik:

  F(2k+1) = G(k) = G(0) · G(k-1) + G(1) · G(k-2) + . . . + G(k-1) · G(0)

Men differensligningen for G er nå den samme som for C. Det betyr at G og C har samme formel. Dermed:

  F(2k+1) = C(k)

Vi kunne ha funnet denne formelen på en raskere måte: Hvis vi har et binærtre med k noder og så legger til det manglende barnet på alle indre noder og to barn på alle bladnoder, får vi et fullt tre med 2k + 1 noder. Omvendt, hvis vi starter med et fullt tre med 2k + 1 noder og så tar vekk alle bladnodene, får vi et tre med k noder.

Formelen gir f.eks. at F(7) = F(2·3 + 1) = C(3) = 5. Det er med andre ord fem forskjellige fulle trær med 7 noder. Disse ser slik ut:

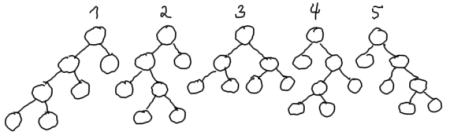Det er 5 forskjellige fulle trær med 7 noder

Oppgave 5 a)

  public static long catalan(int n)
  {
    if (n == 0 || n == 1) return 1;
    long c = 0;
    for (int i = 0; i < n; i++)
      c += catalan(i)*catalan(n-i-1);
    return c;
  }

Metoden over blir særdeles ineffektiv fordi det samme Catalan-tallet blir regnet ut på nytt en hel serie ganger. Dette er et eksempel der en direkte oversettelse fra en rekursiv definisjon til en rekursiv algoritme bærer helt galt av sted!!!

Oppgave 5 b)

  public static long catalan(int n)
  {
    if (n == 0 || n == 1)
      return 1;
    long[] c = new long[n+1];
    c[0] = 1;
    c[1] = 1;
    for (int k = 2; k <= n; k++)
    {
      for (int i = 0; i < k; i++)
        c[k] += c[i] * c[k - i - 1];
    }
    return c[n];
  }

Oppgave 5 c)

  public static long catalan(int n)
  {
    if (n == 0 || n == 1)
      return 1;
    long c = 2 * n, m = c;
    for (int k = 2; k < n; k++)
    {
      m--;
      c = (c * m) / k;
    }
    return c / n;
  }

Oppgave 6

La B(n) være antallet forskjellige måter vi kan sette parenteser når n + 1 tall skal ganges sammen. La f.eks. n = 5, dvs. vi har tallene a, b, c, d, e og f. Da kan vi starte med 5 flg. utrykk:

  a(bcdef)   (ab)(cdef)   (abc)(def)   (abcd)(ef)   (abcde)f

Vi ser at dette svarer til rekursjonsligningen

  B(5) = B(0)*B(4) + B(1)*B(3) + B(2)*B(2) + B(3)*B(1) + B(4)*B(0)

eller generelt

  B(n) = B(0)*B(n-1) + B(1)*B(n-2) + . . . . .  + B(n-1)*B(0)

Dette er den samme rekursjonsligningen som gjelder for Catalan-tallene. Her er det rimelig å si at både B(0) og B(1) er lik 1. Dette er det samme som for C(0) og C(1). Dermed er B(n) = C(n) for alle n >= 0.

Test: Formelen sier at B(3) = 5. Stemmer det? Ja, fordi vi kan sette parantesene slik:

  a(b(cd)),  a((bc)d),  (ab)(cd),  (a(bc))d,  ((ab)c)d

Legg merke til at vi i hvert av de 5 tilfellene bruker nøyaktig 4 parenteser (2 venstre og 2 høyre).