Oppgave 2

  int[] p = {1,2,3,5,6,7,10,11,12,13,21,24,25,42,43};
  String v = "DIHLOBAENGKMJFC";

  BinTre<String> tre1 = new BinTre<>();

  for (int i = 0; i < p.length; i++)
    tre1.leggInn(p[i],v.substring(i,i+1));


  int[] q = {1,2,3,5,6,7,10,11,12,13,21,24,25,42,43};
  char[] u = "EIBGAHKLODNMCJF".toCharArray();

  BinTre<Character> tre2 = new BinTre<>();

  for (int i = 0; i < q.length; i++)
    tre2.leggInn(q[i],u[i]);

Oppgave 3

  int[] p = {1,2,3,4,5,6,7,9,11,12,13,14,18,19,24,25,38,39};
  char[] v = "OGBKRELIANHJDPCQMF".toCharArray();

  BinTre<Character> tre1 = new BinTre<>();

  for (int i = 0; i < p.length; i++)
    tre1.leggInn(p[i],v[i]);


  int[] q = {1,2,3,5,6,7,10,11,13,15,23,26,30,31,52,53};
  Integer[] u = {10,3,7,13,2,1,5,15,19,10,10,8,5,6,9,11};

  BinTre<Integer> tre2 = new BinTre<>(q,u);

Oppgave 4

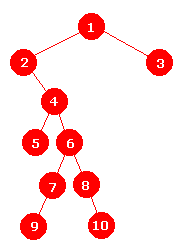int[] p = {1,2,3,5,10,11,22,23,44,47}; Integer[] v = {1,2,3,4,5,6,7,8,9,10}; BinTre<Integer> tre = new BinTre<>(p,v);

Oppgave 5

  BinTre<Integer> tre = new BinTre<>();

  int n = 15;
  for (int i = 1; i <= n; i++) tre.leggInn(i,i);

Oppgave 6

  // Kan lages på denne noe tungvinte måten:

  int[] p = {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384};
  Integer[] v = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};

  BinTre<Integer> tre1 = new BinTre<>(p,v);


  // Dette er en enklere og mer generell måte:

  BinTre<Integer> tre2 = new BinTre<>();

  int n = 15, k = 1;
  for (int i = 1; i <= n; i++)
  {
    tre2.leggInn(k,i);
    k *= 2;
  }

Oppgave 7

  // Kan lages på denne måten:

  int[] p = {1,2,3,4,7,8,15,16,31,32,63,64,127,128,255};
  Integer[] v = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};

  BinTre<Integer> tre1 = new BinTre<>(p,v);


  // Dette er en mer generell måte:

  BinTre<Integer> tre2 = new BinTre<>();

  tre2.leggInn(1,1);    // lager rotnoden

  int n = 7, k = 2;

  for (int i = 1; i <= n; i++)
  {
    tre2.leggInn(k,2*i);
    tre2.leggInn(2*k-1,2*i+1);
    k *= 2;
  }

Oppgave 8

  public int nodetype(int posisjon)
  {
    if (posisjon < 1) throw new IllegalArgumentException("Må ha posisjon > 0!");

    Node<T> p = finnNode(posisjon);

    if (p == null)
      return -1; // posisjon er utenfor treet
    else if (p.venstre != null || p.høyre != null)
      return 0; // posisjon er en indre node
    else return 1;  // posisjon er en bladnode
  }

Oppgave 9

  public T fjern(int posisjon)
  {
    if (posisjon < 1) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") < 1!");

    Node<T> p = rot, q = null;               // hjelpepekere
    int filter = Integer.highestOneBit(posisjon >> 1);   // binært siffer

    while (p != null && filter > 0)
    {
      q = p;
      p = (filter & posisjon) == 0 ? p.venstre : p.høyre;
      filter >>= 1;
    }

    if (p == null) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") er utenfor treet!");

    if (p.venstre != null || p.høyre != null) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") er ingen bladnode!");

    if (p == rot) rot = null;
    else if (p == q.venstre) q.venstre = null;
    else q.høyre = null;

    antall--;  // 
    return p.verdi;
  }

Oppgave 10

  BinTre<Integer> tre = new BinTre<>();

  int posisjon = 1;

  for (int i = 1; i <= 31; i++)
  {
    tre.leggInn(posisjon,i);
    posisjon <<= 1;  // dobler posisjon
  }

Oppgave 11

  public BinTre(long[] p, T[] v) // konstruktør
  {
    if (p.length > v.length) throw new
      IllegalArgumentException("Tabell v har for få verdier");

    for (int i = 0; i < p.length; i++) leggInn(p[i],v[i]);
  }

  public BinTre(BigInteger[] p, T[] v) // konstruktør
  {
    if (p.length > v.length) throw new
      IllegalArgumentException("Tabell v har for få verdier");

    for (int i = 0; i < p.length; i++) leggInn(p[i],v[i]);
  }

  public void leggInn(long posisjon, T verdi)
  {
    if (posisjon < 1) throw new
      IllegalArgumentException("Posisjon (" + posisjon + ") < 1!");

    Node<T> p = rot, q = null;               // nodereferanser

    long filter = Long.highestOneBit(posisjon >> 1);     // filter = 100...00

    while (p != null && filter > 0)
    {
      q = p;
      p = (filter & posisjon) == 0 ? p.venstre : p.høyre;
      filter >>= 1;  // bitforskyver filter
    }

    if (filter > 0) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") mangler forelder!");
    else if (p != null) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") finnes fra før!");

    p = new Node<>(verdi);  // ny node

    if (q == null) rot = p;   // tomt tre - ny rot
    else if ((posisjon & 1) == 0)    // sjekker siste siffer i posisjon
      q.venstre = p;
    else
      q.høyre = p;

    antall++;  // en ny verdi i treet
  }

  public void leggInn(BigInteger posisjon, T verdi)
  {
    if (posisjon.compareTo(BigInteger.ONE) < 0) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") < 1!");

    Node<T> p = rot, q = null;               // hjelpevariabler
    int i = 1;                               // hjelpevariabel

    String s = posisjon.toString(2);                // posisjon's binære siffer

    while (p != null && i < s.length())
    {
      q = p;
      p = s.charAt(i) == '0' ? p.venstre : p.høyre;
      i++;
    }

    if (i < s.length()) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") mangler forelder!");
    else if (p != null) throw new
      IllegalArgumentException("Posisjon(" + posisjon + ") finnes fra før!");

    p = new Node<>(verdi);

    if (q == null) rot = p; // tomt tre - ny rot
    else // sjekker siste binærsiffer i posisjon
    if (s.charAt(i-1) == '0') q.venstre = p;
    else q.høyre = p;

    antall++;  // en ny verdi i treet
  }

  private Node<T> finnNode(long k)    // finner noden i posisjon k
  {
    if (k < 1) return null;  // null hvis k ikke er i treet

    Node<T> p = rot;                         // hjelpepeker
    long n = Long.highestOneBit(k >> 1);   // n = 100...00

    for (; p != null && n > 0; n >>= 1)
      p = (k & n) == 0 ? p.venstre : p.høyre;

    return p;   // p blir null hvis k ikke er i treet
  }

  private Node<T> finnNode(BigInteger k)    // finner noden i posisjon k
  {
    if (k.compareTo(BigInteger.ONE) < 0) return null; // k ikke er i treet

    Node<T> p = rot, q = null;               // hjelpevariabler
    int i = 1;                               // hjelpevariabel

    String s = k.toString(2);                // k's binære siffer

    while (p != null && i < s.length())
    {
      q = p;
      p = s.charAt(i) == '0' ? p.venstre : p.høyre;
      i++;
    }

    return p;   // p blir null hvis k ikke er i treet
  }

  public boolean finnes(long k)
  {
    return finnNode(k) != null;
  }

  public boolean finnes(BigInteger k)
  {
    return finnNode(k) != null;
  }

  public T hent(long k)
  {
    Node<T> p = finnNode(k);

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ukjent!");

    return p.verdi;
  }

  public T hent(BigInteger k)
  {
    Node<T> p = finnNode(k);

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ukjent!");

    return p.verdi;
  }

  public T oppdater(long k, T nyverdi)
  {
    Node<T> p = finnNode(k);

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ukjent!");

    T gammelverdi = p.verdi;
    p.verdi = nyverdi;
    return gammelverdi;
  }

  public T oppdater(BigInteger k, T nyverdi)
  {
    Node<T> p = finnNode(k);

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ukjent!");

    T gammelverdi = p.verdi;
    p.verdi = nyverdi;
    return gammelverdi;
  }

  public T fjern(long k)
  {
    if (k < 1) throw new
      IllegalArgumentException("Posisjon k(" + k + ") < 1!");

    Node<T> p = rot, q = null;               // hjelpepekere
    long n = Long.highestOneBit(k >> 1);   // binært siffer

    while (p != null && n > 0)
    {
      q = p;
      p = (n & k) == 0 ? p.venstre : p.høyre;
      n >>= 1;
    }

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er utenfor treet!");

    if (p.venstre != null || p.høyre != null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ingen bladnode!");

    if (p == rot) rot = null;
    else if (p == q.venstre) q.venstre = null;
    else q.høyre = null;

    antall--;

    return p.verdi;
  }

  public T fjern(BigInteger k)
  {
    if (k.compareTo(BigInteger.ONE) < 0) throw new
      IllegalArgumentException("Posisjonstallet k(" + k + ") < 1!");

    Node<T> p = rot, q = null;               // hjelpevariabler
    int i = 1;                               // hjelpevariabel

    String s = k.toString(2);                // k's binære siffer

    while (p != null && i < s.length())
    {
      q = p;
      p = s.charAt(i) == '0' ? p.venstre : p.høyre;
      i++;
    }

    if (p == null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er utenfor treet!");

    if (p.venstre != null || p.høyre != null) throw new
      IllegalArgumentException("Posisjon k(" + k + ") er ingen bladnode!");

    if (p == rot) rot = null;
    else if (p == q.venstre) q.venstre = null;
    else q.høyre = null;

    antall--;

    return p.verdi;
  }

Oppgave 12

  BinTre<Integer> tre = new BinTre<>();

  long k = 1;

  for (int i = 1; i <= 63; i++)
  {
    tre.leggInn(k,i);
    k <<= 1;  // dobler k
  }

Oppgave 13

  BinTre<Integer> tre = new BinTre<>();

  BigInteger k = BigInteger.ONE;
  BigInteger to = new BigInteger("2");

  for (int i = 1; i <= 64; i++)
  {
    tre.leggInn(k,i);
    k = k.multiply(to);
  }

Oppgave 14

Vi må lete etter en verdi som kan ligge hvor som helst i treet. Da må vi gjøre en såkalt travesering av treet, dvs. vi må gå gjennom alle nodene i en eller annen rekkefølge. Teknikker for dette tas opp i neste avsnitt.