![]() 1.2.1 Tabellintervaller
1.2.1 Tabellintervaller
I Delkapittel 1.1 laget vi flere versjoner av metoden maks, dvs.
metoden som finner posisjonen til den største verdien i en tabell. Nå skal vi
gjøre metoden litt mer fleksibel ved at den skal kunne finne posisjonen til den
største i et tabellintervall. Vi lar metoden få flg. signatur
(en metodes signatur består av dens navn og parameterliste):
public static int maks(int[] a, int fra, int til) // metodens signatur Programkode 1.2.1 a)
Halvåpent intervall: Parametrene fra og til er grensene
for det halvåpne tabellintervallet
a[fra:til>.
Det består av elementene i a fra og med fra og til
(men ikke med) til:
a[fra:til> // halvåpent tabellintervall
I Figur 1.2.1 a) under er a[fra:til> markert med grått.
Som vi ser er elementet i posisjon fra med i intervallet, mens det i posisjon til
er ikke med:
| 0 | 1 | 2 | · | · | fra | · | · | · | · | · | til |
· | · | · | 15 | 16 |
| Figur 1.2.1 a): Tabellintervallet a[fra:til> består av de grå tabellelementene | ||||||||||||||||
Det må stilles bestemte krav til fra og til for at intervallet
a[fra:til> skal ha mening:
- Posisjonen/indeksen
frakan ikke være negativ siden 0 er første lovlige indeks. - Posisjonen
tilkan ikke være større enna.length, dvs. tabellens lengde. Tabellen i
Figur 1.2.1 a) har lengde 17. Lovlig verdi fortilvil der være 17 eller mindre. - Posisjonen
frakan ikke være større enntil, dvs vi kan ikke hafratil høyre fortil. - Vi kaller
a[fra:til>et lovlig (halvåpent) tabellintervall hvis 1, 2 og 3 er oppfylt. Vi sier at det ertomt(men lovlig) hvisfra=til. På samme måte som i mengdelære der den tomme mengden har mening, kan det gi mening å ha et tomt intervall.
 |
| Intervallgrensene må sjekkes |
Det gir imidlertid ikke mening å ha et tomt tabellintervall for den maks-metoden som er
satt opp i Programkode 1.2.1 a).
Posisjonen til den største blant ingen verdier har ikke mening. Metoden må
derfor starte med å sjekke at parameterverdiene fra og til
representerer et lovlig og ikke-tomt tabellintervall. Det kan f.eks. gjøres slik:
if (fra < 0 || til > a.length || fra >= til) throw new IllegalArgumentException("Illegalt intervall!");
Vi velger å kaste en IllegalArgumentException hvis
fra eller til (eller begge) har ulovlige (eller illegale) verdier.
Obs: Vi kaller vanligvis inputverdiene til en metode for parametre, men det er også
vanlig å kalle dem argumenter. Derfor heter unntaket IllegalArgumentException.
Vi tar utgangspunkt i Programkode 1.1.4
og gjør de endringene som må
til for at letingen etter den største verdien kun skjer i tabellintervallet
a[fra:til> og ikke i hele tabellen a:
public static int maks(int[] a, int fra, int til) { if (fra < 0 || til > a.length || fra >= til) { throw new IllegalArgumentException("Illegalt intervall!"); } int m = fra; // indeks til største verdi i a[fra:til> int maksverdi = a[fra]; // største verdi i a[fra:til> for (int i = fra + 1; i < til; i++) { if (a[i] > maksverdi) { m = i; // indeks til største verdi oppdateres maksverdi = a[m]; // største verdi oppdateres } } return m; // posisjonen til største verdi i a[fra:til> } Programkode 1.2.1 b)
Det er strengt tatt ikke nødvendig å ha en egen maks-metode for
det å finne den største i en hel tabell. Det holder om vi bruker metoden
over med fra = 0 og til = a.length som parameterverdier.
Men det er likevel praktisk å ha en slik maks-metode, og den kan lett kodes
ved hjelp av metoden i Programkode 1.2.1 b):
public static int maks(int[] a) // bruker hele tabellen { return maks(a,0,a.length); // kaller metoden over } Programkode 1.2.1 c)
Lukket intervall: I noen situasjoner er det mest naturlig at
en tabellmetode arbeider i et lukket tabellintervall. La
v og h betegne intervallets venstre og høyre endepunkt.
Et lukket tabellintervall betegnes med a[v:h] og består
av elementene i a fra og med indeks v til og med indeks h.
a[v:h] // lukket tabellintervall
I Figur 1.2.1 b) nedenfor er a[v:h] markert med grått.
Vi ser at elementene i begge ender, dvs. både a[v] og a[h],
hører til intervallet:
| 0 | 1 | 2 | · | · | · | · | · | v | · | · | · | · | h | · | 15 | 16 |
| Figur 1.2.1 b): Tabellintervallet a[v:h] består av de grå tabellelementene | ||||||||||||||||
Det må stilles krav til intervallendepunktene v og h for at
a[v:h] skal bli et lovlig intervall:
- Venstre endepunkt
vkan ikke være negativt. - Høyre endepunkt
hkan ikke være større enn eller lika.length. - Vi må ha at
h>=v− 1. - Hvis kravene 1, 2 og 3 er oppfylt, kaller vi
a[v:h] et lovlig (lukket) tabellintervall. Vi får et spesialtilfelle hvish=v− 1, dvs. hvishligger rett til venstre forv. Da era[v:h] et tomt (men lovlig) tabellintervall. Hvisv=hinneholdera[v:h] nøyaktig én verdi.
Legg merke til at det lukkede intervallet a[v:h] blir lik det
halvåpne intervallet a[v : h + 1>, og at det halvåpne
intervallet a[fra:til> blir lik det lukkede
intervallet a[fra : til − 1].
Huskeregel 1.2.1: En tabellmetode som skal arbeide med et
halvåpent tabellintervall, skal ha parameternavnene fra og til i sin signatur:
. . . . metode1(int[] a, int fra, int til, . .) // a[fra:til>
Hvis den skal arbeide med et lukket tabellintervall, skal den ha parameternavnene
v (v står for venstre) og
h (h står for høyre) i sin signatur:
. . . . metode2(int[] a, int v, int h, . .) // a[v:h]
Eksempel: Klassen Arrays
i biblioteket (Java: package) java.util har
mange metoder som arbeider med tabellintervaller. Et eksempel er metoden
copyOfRange.
Den har flg. signatur:
public static int[] copyOfRange(int[] a, int from, int to)
Her brukes from og to slik som vi bruker fra
og til. Metoden lager en kopi av det halvåpne intervallet
a[from:to>. I java.util brukes også fromIndex
og toIndex om det samme.
Eksempel: Flg. kode viser hvordan copyOfRange-metoden kan brukes:
char[] c = {'A','B','C','D','E','F','G','H','I','J'}; // 10 bokstaver char[] d = Arrays.copyOfRange(c,4,8); // en kopi av c[4:8> for (char k : d) System.out.print(k + " "); // kopien d skrives ut // Utskrift: E F G H Programkode 1.2.1 d)
| 1. | Lag to min-metoder (metoder som finner posisjonen til
den minste verdien) tilsvarende de to maks-metodene i
Programkode 1.2.1 b)
og 1.2.1 c). Legg dem i samleklassen Tabell. Se
Avsnitt 1.2.2.
|
| 2. | Lag en maks-metode med samme signatur som den i
Programkode 1.2.1 b),
men som bruker idéen fra
Programkode 1.1.5. |
| 3. | Hva skjer hvis siste parameter (to) i copyOfRange i
Programkode 1.2.1 d)
er større en lengden på tabellen c? |
| 4. | Finn hvilke metoder i class Arrays
som arbeider med tabellintervaller (from/to eller fromIndex/toIndex). |
| 5. | I Java 1.5 ble det innført en ny type for-løkke - en såkalt for-alle-løkke. Se
Programkode 1.2.1 d). Den må du lære deg hvis du ikke allerede kan den.
Se f.eks. Vedlegg E. |
![]() 1.2.2 En samleklasse for tabellmetoder
1.2.2 En samleklasse for tabellmetoder
Algoritmer som arbeider med tabeller kan kalles
tabellalgoritmer eller tabellmetoder. Java tillater
ikke frittstående metoder - en metode må ligge i en klasse. I
Delkapittel 1.1
la vi metodene inn i class Program. Nå skal vi
flytte dem over i en samleklasse med navn Tabell.
Java har allerede en slik samleklasse. Det er
Arrays
i java.util. Vår samleklasse Tabell vil komme til å inneholde
metoder av samme slag som dem i Arrays og andre typer
tabellmetoder.
Metodene våre er satt til å være statiske (eng: static).
Det betyr at de blir klassemetoder med hensyn på
den klassen de ligger i. En klasse kan også ha statiske variabler og
de kalles klassevariabler. En klassemetode kan kun benytte
klassens klassevariabler (og ikke klassens instansvariabler). En statisk metode
kan og skal normalt kalles direkte ved hjelp av klassenavnet
(dvs. klassenavn punktum metodenavn) og
ikke via en instans av klassen. Hvis en klassemetode skal benytte en
annen klassemetode i den samme klassen, er det ikke nødvendig
å referere til klassen.
I Vedlegg C om Samleklasser ser vi mer på dette.
Programmeringsregel:
En metode som kan utføre oppgaven sin ved hjelp av den informasjonen den får gjennom sine
parameterverdier (og ikke noe annet), kan og skal settes opp (deklareres) som statisk. Den er «seg selv nok».
Vi starter nå oppbyggingen av samleklassen Tabell. Den skal kun
inneholde klassemetoder (statiske metoder). Derfor skal det ikke
lages instanser av den. Det ordner vi ved å ha en privat standardkonstruktør som eneste
konstruktør.
Metodene som skal inn i class Tabell, kan vi kopiere fra
Delkapittel 1.1
og fra Avsnitt 1.2.1. De
vil være hjelpemetoder for senere bruk og Tabell kan dermed kalles
en hjelpeklasse. Opprett derfor package med navn
hjelpeklasser og legg Tabell der. Bruker du f.eks. NetBeans
eller Eclipse kan du oppgi dette pakkenavnet når Tabell opprettes. Da blir
pakken hjelpeklasser automatisk opprettet hvis du ikke har den fra før:
package hjelpeklasser; import java.util.*; public class Tabell // Samleklasse for tabellmetoder { private Tabell() {} // privat standardkonstruktør - hindrer instansiering // Metoden bytt(int[] a, int i, int j) Programkode 1.1.8 d) // Metoden randPerm(int n) Programkode 1.1.8 e) // Metoden randPerm(int[] a) Programkode 1.1.8 f) // Metoden maks(int[] a, int fra, int til) Programkode 1.2.1 b) // Metoden maks(int[] a) Programkode 1.2.1 c) // min-metodene - se Oppgave 1 i Avsnitt 1.2.1 } Programkode 1.2.2 a)
Hvis vi prøver oss med flg. kode
Tabell tabell = new Tabell();
i et program, kommer det en syntaksfeil. F.eks. kommer det The constructor Tabell()
is not visible i Eclipse og Tabell() has private access in Tabell i NetBeans.
I klassen Program som vi laget i Delkapittel 1.1,
kan vi fjerne alt
og isteden la den inneholde flg. testprogram. Klassen Program og dens
main-metode kan brukes til kodetesting også senere. Da er det bare å bytte
ut koden med ny kode.
import hjelpeklasser.*; public class Program { public static void main(String ... args) // hovedprogram { int[] a = Tabell.randPerm(20); // en tilfeldig tabell for (int k : a) System.out.print(k + " "); // skriver ut a int m = Tabell.maks(a); // finner posisjonen til største verdi System.out.println("\nStørste verdi ligger på plass " + m); } // main } // class Program Programkode 1.2.2 b)
| 1. | Bygg opp class Tabell slik som beskrevet i
Programkode 1.2.2 a). |
| 2. | Kjør programmet i Programkode 1.2.2 b). |
| 3. | Lag metoden public static void bytt(char[] c, int i, int j). Den skal
bytte om innholdet i posisjon i og j i char-tabellen c.
Legg metoden i samleklassen
Tabell. |
| 4. | Lag metoden public static void skriv(int[] a, int fra, int til).
Den skal skrive ut tallene i intervallet a[fra:til> til
konsollet - alle på én linje og et mellomrom mellom hvert tall. Ikke mellomrom og ikke linjeskift etter siste verdi.
Lag så metoden public static void skriv(int[] a). Den skal
skrive ut hele tabellen - alle på én linje, en blank mellom hvert tall. Ikke mellomrom og ikke linjeskift etter siste verdi.
Legg begge metodene i samleklassen Tabell. |
| 5. | Lag to skrivln-metoder. De skal ha samme signatur og
fungere på samme måte som de to skriv-metodene
i Oppgave 4 , men utskriften skal avsluttes med
et linjeskift. Legg begge metodene i samleklassen
Tabell. |
| 6. | Som i Oppgave 4 og 5, men med en tabell c av typen char[]. |
| 7. | Lag metoden public static int[] naturligeTall(int n). Den skal returnere
en heltallstabell som inneholder tallene 1, 2, . . . , n. Hvis n er mindre
enn 1 skal det kastes et unntak. Lag også den mer generelle metoden
public static int[] heleTall(int fra, int til). Den skal returnere
en heltallstabell som inneholder tallene fra og med fra og til, men ikke med,
tallet til. For eksempel skal kallet heleTall(1,6) gi tabellen
{1, 2, 3, 4, 5}. Hvis fra er større enn til kastes et unntak.
Hvis fra er lik til returneres en tom tabell.
Legg metodene i samleklassen Tabell.
|
![]() 1.2.3 Feil og unntak
1.2.3 Feil og unntak
Programkode 1.2.1 b)
starter med en parameterverditest.
Hvis noe er galt kastes en IllegalArgumentException med
teksten Illegalt intervall.
La flg. tabell a være gitt:
| 9 | 7 | 10 | 8 | 2 | 6 | 14 | 4 | 19 | 12 | 5 | 3 | 13 | 20 | 1 | 18 | 17 | 11 | 15 | 16 |
| 0 | 1 | 2 | · | · | · | · | · | · | · | 10 | · | · | · | · | · | · | · | 18 | 19 |
| Figur 1.2.3 a) : En tabell med 20 tilfeldige verdier | |||||||||||||||||||
Anta at vi skal finne den største verdien i første halvpart av tabellen, dvs. i a[0:10>.
Vi ser at det er tallet 19 som ligger i posisjon 8. I flg. kall har imidlertid
fra og til blitt forbyttet:
int m = Tabell.maks(a,10,0); // 0 og 10 har blitt forbyttet
Under eksekvering vil det kastes et unntak med en feilmelding i form av en utskrift av kjørestakken (stack trace). Formen på utskriften vil variere noe avhengig av hvilket utviklingsmiljø en bruker. I Eclipse kommer f.eks. dette:
Exception in thread "main"
java.lang.IllegalArgumentException: Illegalt intervall!
at hjelpeklasser.Tabell.maks(Tabell.java:11)
at algdat.Program.main(Program.java:21)
Først kommer en melding om hvilken programtråd (thread) unntaket kastes fra. Dernest hva slags unntak
(unntaksklasse) det er og den feilmeldingen vi selv har lagt inn (dvs. Illegalt intervall!). Så i hvilken
metode (her maks()) og programlinje (11) i klassen Tabell dette har skjedd.
Til slutt hvilken metode (her main()) og programlinje (21) i klassen
Program feilen har forplantet seg til. I et større program kan vi få mange flere linjer i en slik
utskrift siden vi der gjerne har et omfattende hierarki av metodekall.
Det som mangler er mer detaljert informasjon om hva som forårsaket feilen. Spesielt hadde det vært gunstig å få vite hvilke parametere det gjelder og hvilke verdier de har når unntaket kastes. Dette gjør ikke Java for oss, men vi kan få det til hvis vi lager våre egne tester.
Testen i Programkode 1.2.1 b)
undersøker først
om fra er negativ. Dette er det strengt tatt ikke nødvendig for oss å gjøre.
Java gjør det uansett. Hvis fra
er negativ, sørger Java for at tabelloperasjonen a[fra] kaster
en ArrayIndexOutOfBoundsException. Men da får vi kun
vite i hvilken programlinje feilen har oppstått. Hvis vi
ønsker flere detaljer enn det, må vi lage testen selv. Vi kan f.eks.
lage den slik:
if (fra < 0) throw new ArrayIndexOutOfBoundsException ("fra(" + fra + ") er negativ!");
Dette forteller for det første at det er en ArrayIndexOutOfBoundsException
og det sier mer enn det å få en IllegalArgumentException.
For det andre inneholder feilmeldingen den eksakte verdien til parameteren fra
i det øyeblikket unntaket kastes.
Det vil ofte være nødvendig å teste lovligheten til et tabellintervall. Vi kan derfor lage en egen metode for det formålet og samtidig passe på at den gir konkrete og detaljerte feilmeldinger. Vi bør da for det første velge unntaksklasser med navn som indikerer feiltypen. For det andre bør vi oppgi de eksakte verdiene til de parametrene som har gale verdier.
Følgende metode tester om
det halvåpne tabellintervallet a[fra:til> er lovlig.
Legg den i samleklassen Tabell:
public static void fratilKontroll(int tablengde, int fra, int til) { if (fra < 0) // fra er negativ throw new ArrayIndexOutOfBoundsException ("fra(" + fra + ") er negativ!"); if (til > tablengde) // til er utenfor tabellen throw new ArrayIndexOutOfBoundsException ("til(" + til + ") > tablengde(" + tablengde + ")"); if (fra > til) // fra er større enn til throw new IllegalArgumentException ("fra(" + fra + ") > til(" + til + ") - illegalt intervall!"); } Programkode 1.2.3 a)
OBS Klassen Arrays
i java.util har en tilsvarende metode. Den heter rangeCheck(), men er ikke offentlig og kan dermed ikke
brukes av oss. Gå inn i kildekoden til
Arrays
og se hvordan metoden er kodet og hva slags feilmeldinger den gir. Se også Oppgave 2.
Den første programsetningen i
Programkode 1.2.1 b), dvs. setningen:
if (fra < 0 || til > a.length || fra >= til) throw new IllegalArgumentException("Illegalt intervall!");
kan nå delvis erstattes med et kall på metoden fratilKontroll:
fratilKontroll(a.length,fra,til); Programkode 1.2.3 b)
Men det er et lite problem. Metoden fratilKontroll slipper gjennom et tomt
tabellintervall, dvs. et tabellintervall der fra = til.
Et tomt intervall har ingen verdier og dermed finnes det heller
ingen største verdi. I det tilfellet vil det passe å kaste en NoSuchElementException. Denne
unntaksklassen er definert i java.util, mens de andre unntaksklassene vi
har brukt til nå, er alle definert i java.lang. Flg. test fanger opp et tomt
tabellintervall:
if (fra == til) throw new NoSuchElementException ("fra(" + fra + ") = til(" + til + ") - tomt tabellintervall!"); Programkode 1.2.3 c)
Det betyr at vi får det samme testresultat hvis første programsetning i
Programkode 1.2.1 b)
erstattes med både metodekallet i
Programkode 1.2.3 b)
og i tillegg med programsetningen i
Programkode 1.2.3 c).
Se Oppgave 3.
 |
| Bedre føre var enn etter snar. |
null, vil det under programkjøring bli kastet
en NullPointerException hvis a er null. Det kommer imidlertid ingen melding
om at det nettopp var a som var null. Hvis det i vår kode også inngår andre ting som
kan forårsake en NullPointerException, er det ikke alltid lett å vite årsaken til
feilmeldingen. Det er derfor i mange tilfeller også lurt å lage egne pekertester slik
at feilmeldingene klart og tydelig forteller hvilken variabel (peker) det var som var null.
Se Oppgave 4.
Flg. metode (som skal legges i klassen Tabell ) sjekker om et lukket tabellinetrvall er lovlig:
public static void vhKontroll(int tablengde, int v, int h) { if (v < 0) throw new ArrayIndexOutOfBoundsException("v(" + v + ") < 0"); if (h >= tablengde) throw new ArrayIndexOutOfBoundsException ("h(" + h + ") >= tablengde(" + tablengde + ")"); if (v > h + 1) throw new IllegalArgumentException ("v = " + v + ", h = " + h); } Programkode 1.2.3 d)
Java har en hel serie ferdige unntaksklasser. Vi bør velge unntaksklasser med navn som passer for den typen feilsituasjon vi skal rapportere. Her er noen eksempler:
NullPointerException, IllegalArgumentException, IllegalStateException,
ArrayIndexOutOfBoundsException, StringIndexOutOfBoundsException,
IndexOutOfBoundsException, NoSuchElementException
InvalidParameterException, NumberFormatException
Alle disse klassene er subklasser av
RuntimeException.
Det er vanligvis en svakhet eller en feil i programkoden som er
årsaken til et unntak av denne typen.
De skal derfor normalt ikke fanges opp i
en try − catch. Det er bedre at programmet avsluttes slik at
feilen kan bli identifisert og rettet opp. Du finner
mer om feilhåndtering og unntaksklasser i Vedlegg D.
| 1. | Legg metodene Programkode 1.2.3 a) og
1.2.3 d),
inn i samleklassen Tabell. |
| 2. | Sett deg inn i (se kildekoden) metoden rangeCheck() i
Arrays.
|
| 3. | Gjør om maks-metoden i
Programkode 1.2.1 b),
som du nå skal ha lagt inn i class Tabell, slik at
parameterverditesten blir erstattet med
Programkode 1.2.3 b)
og c).
Lag så et testprogram der maks-metoden inngår
(bruk main i class Program), men med
parameterverdier som du vet vil føre til at unntak kastes.
Velg verdier slik at du får frem alle de mulige
feilmeldingstypene.
|
| 4. | Gå videre fra Oppgave 3. Dvs. lag også kode som tester parameteren a og som gir en fornuftig feilmelding hvis a er null. |
| 5. | I Oppgave 5, 6 og 7 i Avsnitt 1.2.2 skulle det lages metoder som
arbeidet i et halvåpent intervall. Bruk metoden fratilKontroll() til å sjekke
at intervallene er lovlige.
|
| 6. | Lag metoden public static void snu(int[] a, int v, int h). Metoden
skal snu rekkefølgen på verdiene i intervallet a[v:h]. Hvis
intervallet f.eks. inneholder verdiene 4, 2, 13, 7, skal intervallet etter et
kall på metodene inneholde 7, 13, 2, 4. Bruk metoden vhKontroll() til å sjekke
lovligheten av intervallet. Lag også en metode som snur en hel tabell. Legg metodene
i samleklassen Tabell.
|
| 7. | Gjør som i Oppgave 6, men med en char-tabell. Lag først, hvis du ikke har gjort det tidligere,
en bytt-metode som bytter om to elementer i en char-tabell.
|
| 8. | Sett deg mer inn i bruk av unntak (exceptions).
Se f.eks. Vedlegg D.
|
![]() 1.2.4 Den nest største verdien i en tabell
1.2.4 Den nest største verdien i en tabell
I Delkapittel 1.1 tok vi opp ulike aspekter rundt det å finne posisjonen
til den største verdien i en tabell. Kan vi finne den nest største verdien
på samme måte? Det kan vi, men det er også mulig å løse oppgaven ved hjelp av
nye og bedre teknikker.
Først må vi presisere hva vi skal mene med den nest største verdien. Hvis alle verdiene er forskjellige, er det klart hva som er nest størst. Men hva hvis den største verdien forekommer flere ganger? Er da størst og nest størst verdi det samme? Eller skal nest størst bety den største blant de verdiene som er forskjellige fra den største? Her må vi gjøre et valg og vi bestemmer at:
Definisjon 1.2.4 Gitt en samling verdier (f.eks. en tabell). Hvis den
største verdien forekommer flere ganger, sier vi at nest størst og størst
er det samme.
En annen måte å si det på er: Etter at verdiene er sortert i voksende rekkefølge, er største verdi den som ligger sist, og nest største verdi den som ligger nest sist. Men vi ønsker selvfølgelig å kunne finne den største og den nest største uten å måtte sortere først.
Anta at vi skal finne den største og den nest største verdien i flg. tabell a:
| 9 | 7 | 10 | 8 | 2 | 6 | 14 | 4 | 19 | 12 | 5 | 3 | 13 | 20 | 1 | 18 | 17 | 11 | 15 | 16 |
| 0 | 1 | 2 | · | · | · | · | · | · | · | · | · | · | m | · | · | · | · | 18 | 19 |
| Figur 1.2.4 a): Tabellens største verdi 20 ligger i posisjon m = 13 | |||||||||||||||||||
Vi bruker først maks-metoden til å finne posisjonen til den største
verdien. Vi ser at største verdi (tallet 20) ligger i posisjon m = 13 (markert med grått):
int m = maks(a); // i forhold til Figur 1.2.4 a) er nå m lik 13
Den nest største finner vi som den største blant resten av verdiene. Men resten består av
to tabellintervaller. Dermed kan vi bruke maks-metoden til å finne
den største i hvert intervall, og den største av de to er den nest største for
hele tabellen. Her ser vi nytten av å ha en maks-metode som arbeider
i et tabellintervall:
int mv = maks(a, 0, m); // leter i a[0:m> int mh = maks(a, m + 1, a.length); // leter i a[m + 1:a.length>
Her må en se opp for to spesialtilfeller:
- Hvis m = 0, dvs. den største verdien ligger lengst til venstre i tabellen a, så er intervallet til venstre for m tomt. Da søker vi videre kun på høyre side av m.
- Hvis m =
a.length– 1, dvs. den største verdien ligger lengst til høyre, så er intervallet til høyre for m tomt. Da søker vi videre kun til venstre for m.
Flg. metode tar hensyn til disse to spesialtilfellene. Den returnerer en tabell som
inneholder posisjonene til største og nest største verdi.
Metoden heter nestMaks() og skal legges i samleklassen Tabell:
public static int[] nestMaks(int[] a) // legges i class Tabell { int n = a.length; // tabellens lengde if (n < 2) throw // må ha minst to verdier! new java.util.NoSuchElementException("a.length(" + n + ") < 2!"); int m = maks(a); // m er posisjonen til tabellens største verdi int nm; // nm skal inneholde posisjonen til nest største verdi if (m == 0) // den største ligger først { nm = maks(a, 1, n); // leter i a[1:n> } else if (m == n - 1) // den største ligger bakerst { nm = maks(a, 0, n - 1); // leter i a[0:n-1> } else { int mv = maks(a, 0, m); // leter i a[0:m> int mh = maks(a, m + 1, n); // leter i a[m+1:n> nm = a[mh] > a[mv] ? mh : mv; // hvem er størst? } return new int[] {m,nm}; // m i posisjon 0 , nm i posisjon 1 } // nestMaks Programkode 1.2.4 a)
Flg. kodebit viser hvordan metoden kan brukes:
int[] a = Tabell.randPerm(20); // tilfeldig permutasjon av 1 . . 20 int[] b = Tabell.nestMaks(a); // metoden returnerer en tabell int m = b[0], nm = b[1]; // m for maks, nm for nestmaks Tabell.skrivln(a); // se Oppgave 5 i Avsnitt 1.2.2 System.out.print("Størst(" + a[m] + ") har posisjon " + m); System.out.println(", nest størst(" + a[nm] + ") har posisjon " + nm); // Eksempel på en utskrift: // 12 16 15 6 10 8 9 2 14 19 5 18 20 13 3 7 11 1 4 17 // Størst(20) har posisjon 12, nest størst(19) har posisjon 9 Programkode 1.2.4 b)
Vi kan korte ned en del på koden i
Programkode 1.2.4 a) hvis vi
bytter om to verdier. Se på tabellen i
Figur 1.2.4 a). Der kan vi kan bytte
om slik at den største verdien (tallet 20) havner forrest i tabellen.
Flg. kode gir oss tabellen i Figur 1.2.4 b) under:
bytt(a, 0, m); // den største legges forrest
| 20 | 7 | 10 | 8 | 2 | 6 | 14 | 4 | 19 | 12 | 5 | 3 | 13 | 9 | 1 | 18 | 17 | 11 | 15 | 16 |
| 0 | 1 | 2 | · | · | · | · | · | · | · | · | · | · | 13 | · | · | · | · | 18 | 19 |
| Figur 1.2.4 b): Verdiene i posisjon 0 og 13 har byttet plass - den største er nå forrest. | |||||||||||||||||||
Vi finner så den nest største ved å lete i tabellen fra og med posisjon 1.
Du vil bli bedt om å lage fullstendig kode for dette i
Oppgave 2.
Hvor effektiv blir nestMaks-metoden?
La n være antallet elementer tabellen. Vi vet at maks-metoden
alltid utfører et antall sammenligninger som er én mindre enn antallet i tabellen (eller
i tabellintervallet). Tilsammen blir det her 2n - 3 sammenligninger.
I tillegg er det én sammenligning der vi sjekker tabellens lengde.
Metoden er med andre ord av orden n. Er dette det optimale eller kan
vi lage noe som er bedre? Svaret kommer i de neste avsnittene!
| 1. | Legg nestMaks-metoden fra
Programkode 1.2.4 a) i samleklassen
Tabell. Legg så
Programkode 1.2.4 b)
inn i main-metoden
i klassen Program og sjekk at du får rett svar. Obs. Du får andre svar enn det
som eksempelutskriften i Programkode 1.2.4 b)
viser siden metoden
randPerm gir nye permutasjoner hver gang den kalles. |
| 2. | Lag en versjon av nestmaks-metoden der du bytter om
slik at den største kommer forrest. Dermed kan letingen etter den
nest største starte i posisjon 1. Pass på og bytt tilbake før metoden
avslutter slik at tabellen kommer tilbake i sin originale tilstand.
Obs. Det blir et spesialtilfelle her når den nest største verdien ligger forrest
i tabellen. Pass på at det tilfellet behandles rett. |
| 3. | Som i Oppgave 2, men bytt om slik at den største havner bakerst.
Obs. Det blir et spesialtilfelle her når den nest største verdien ligger bakerst
i tabellen. Pass på at det tilfellet behandles rett. |
| 4. | Idéen i Oppgave 3 kan utvides til å bli en sorteringsalgoritme.
Finn først den største og bytt om slik at den kommer bakerst. Finn så den
største i det intervallet som ikke har med den siste og bytt om slik at den
kommer nest bakerst. Finn så den største i intervallet som ikke har med de to
siste og bytt om slik at den kommer på tredje bakerst. Osv.
Lag metoden public static void sortering(int[] a) med dette som idé.
|
| 5. | Hvis du har en min-metode (se
Oppgave 1 i Avsnitt 1.2.1)
kan du gjøre som i Oppgave 4, men motsatt vei. Finn den minste og bytt
om slik at den kommer først. Finn så den minste i det intervallet som starter
i posisjon 1 og bytt om slik at den kommer nest først (i posisjon 1), osv.
|
![]() 1.2.5 En ny idé for nestMaks-metoden
1.2.5 En ny idé for nestMaks-metoden
Vi prøver flg. idé: La hjelpevariabler maksverdi og nestmaksverdi
holde på største og nest største verdi, og la hjelpevariabler m og nm holde på
posisjonene. Det betyr at vi må avgjøre, for hver ny verdi vi ser på, om den er
en ny størst verdi eller en ny nest størst verdi. Hvis det er en ny størst verdi,
vil den tidligere største bli ny nest størst verdi:
public static int[] nestMaks(int[] a) // ny versjon { int n = a.length; // tabellens lengde if (n < 2) throw // må ha minst to verdier new java.util.NoSuchElementException("a.length(" + n + ") < 2!"); int m = 0; // m er posisjonen til største verdi int nm = 1; // nm er posisjonen til nest største verdi // bytter om m og nm hvis a[1] er større enn a[0] if (a[1] > a[0]) { m = 1; nm = 0; } int maksverdi = a[m]; // største verdi int nestmaksverdi = a[nm]; // nest største verdi for (int i = 2; i < n; i++) { if (a[i] > nestmaksverdi) { if (a[i] > maksverdi) { nm = m; nestmaksverdi = maksverdi; // ny nest størst m = i; maksverdi = a[m]; // ny størst } else { nm = i; nestmaksverdi = a[nm]; // ny nest størst } } } // for return new int[] {m,nm}; // n i posisjon 0, nm i posisjon 1 } // nestMaks Programkode 1.2.5 a)
Metoden har bare én for-løkke og det betyr at den går gjennom
tabellen a bare én gang. I
Programkode 1.2.4 a) derimot
går algoritmen først gjennom tabellen én gang for å finne den største verdien og
så én gang til for å finne den nest største. Det bør bety at
Programkode 1.2.5 a) er mer effektiv. Men vi trenger noen
nye effektivitetsbegreper før vi kan si det med sikkerhet. Se neste avsnitt.
Det er mulig å gjøre implementasjonen i Programkode 1.2.5 a) litt
mer effektiv ved å bruke en vaktpost. Se
Avsnitt 1.1.5 og Oppgave 2
nedenfor.
| 1. | Legg nestMaks-metoden fra Programkode 1.2.5 a)
inn i samleklassen
Tabell, dvs. til erstatning for den som du kanskje har der fra før. Lag kode
som sjekker at den virker som den skal. Se f.eks.
Programkode 1.2.4 b). |
| 2. | Bruk den største mulige int-verdien som
vaktpost og legg den bakerst i tabellen. Da kan vi ta vekk testen
i < n i for-løkken i Programkode 1.2.5 a).
Gjør dette! Se hvordan det er gjort i Avsnitt 1.1.5. |
| 3. | Lag en nestMin-metode med samme idé som i
Programkode 1.2.5 a). |
| 4. | Lag metoden public static int[] tredjeMaks(int[] a). Den skal returnere
en tabell som inneholder posisjonene til de tre største verdiene. Bruk en idé tilsvarende den
i Programkode 1.2.5 a). |
![]() 1.2.6 Effektivitet - gjennomsnittlig og det verste tilfellet
1.2.6 Effektivitet - gjennomsnittlig og det verste tilfellet
Når det gjelder effektivitet skal vi skille mellom følgende tre tilfeller:
- Den
gjennomsnittligeeffektiviteten (eng: average case) - Effektiviteten i det mest
ugunstigeellerverstetilfellet (eng: worst case) - Effektiviteten i det
bestetilfellet (eng: best case)
Det har tidligere blitt sagt (Avsnitt 1.1.3) at antallet ganger den
dominerende operasjonen i en algoritme utføres, er en målestokk for
dens effektivitet. La a være en tabell med n verdier.
Med gjennomsnittlig effektivitet skal vi mene det gjennomsnittlige antallet
ganger den dominerende operasjonen (her en sammenligning) utføres.
Vi forenkler normalt situasjonen ved å si at de n verdiene som
tabellen a inneholder, rett og slett er tallene fra 1 til n.
Gjennomsnittet tas derfor over de n! forskjellige tabellene vi
får ved å permutere tallene fra 1 til n på alle mulige måter.
I mange algoritmer vil antallet ganger den dominerende operasjonen utføres, variere med hensyn på hvordan verdiene i tabellen er fordelt. Det tilfellet (eller de tilfellene) der den dominerende operasjonen utføres aller flest ganger, kalles det meste ugunstige eller verste tilfellet. Omvendt vil det tilfellet (eller de tilfellene) der den dominerende operasjonen utføres færrest mulig ganger, kalles det beste tilfellet.
Når vi løser oppgaver er det i mange tilfeller viktig at vi velger en algoritme med god gjennomsnittlig effektivitet, mens det i andre tilfeller kan være viktig å velge en algoritme som ikke nødvendigvis er blant de beste gjennomsnittlig, men som ikke er dårlig i det verste tilfellet. Det at algoritmen er god i det beste tilfellet er vanligvis av mindre interesse. Spørsmål som dette vil vi ta opp når vi utvikler nye algoritmer.
Anta at vi har en tabell som inneholder en eller annen permutasjon av tallene
fra 1 til n. I nestMaks-metoden fra
Programkode 1.2.4 a)
ble det utført 2n - 3 sammenligninger uansett
hva slags innhold tabellen måtte ha. Det betyr at der er det ingen forskjell på
den gjennomsnittlige effektiviteten og effektiviteten i det mest ugunstige
og i det beste tilfellet.
Men for nestMaks-versjonen i
Programkode 1.2.5 a) er det
annerledes. Hva er det verste tilfellet der, dvs. når utføres det flest mulig
sammenligninger? Tabellen i Figur 1.2.6 a) under inneholder
tallene fra 1 til n (= 20) i sortert rekkefølge:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0 | 1 | 2 | · | · | · | · | · | · | · | · | · | · | · | · | · | · | · | 18 | 19 |
| Figur 1.2.6 a): Tabellen inneholder tallene fra 1 til 20 i sortert rekkefølge. | |||||||||||||||||||
Sammenligningen a[i] > nestmaksverdi i for-løkken
i Programkode 1.2.5 a)
blir utført hver gang - dvs. n − 2 ganger. Men sidene tallene er sortert vil
hver ny verdi være større enn den største foran, og dermed større enn den nest største.
Siden a[i] > nestmaksverdi da blir sann hver gang, vil også
neste sammenligning a[i] > maksverdi bli utført hver gang.
Med andre ord 2(n - 2) = 2n − 4 sammenligninger i for-løkken.
I tillegg er det én sammenligning for å avgjøre om den største av a[0] og a[1].
Totalt 2n − 3 sammenligninger. Det betyr at i det verste tilfellet har
Programkode 1.2.4 a) og
Programkode 1.2.5 a)
samme effektivitet.
| 1. | Sjekk at versjonen av nestMaks-metoden i
Programkode 1.2.5 a)
utfører nøyaktig 2n − 3 sammenligninger når tabellen er sortert. |
| 2. | For hvilke tabeller bruker metoden færrest mulig sammenligninger? |
| 3. | Er det noen forskjell på gjennomsnittlig effektivitet, effektiviteten i
det mest ugunstige tilfellet og effektiviteten i det beste tilfellet for
maks-metoden,
dvs. for den metoden som finner posisjonen til den største
verdien i en tabell? |
![]() 1.2.7 Analyse av gjennomsnittlig effektivitet
1.2.7 Analyse av gjennomsnittlig effektivitet
La som før a være en heltallstabell som inneholder en tilfeldig permutasjon
av tallene fra 1 til n. I for-løkken i
Programkode 1.2.5 a)
blir sammenligningen
a[i] > nestmaksverdi alltid utført n − 2 ganger.
Spørsmålet er nå hvor mange ganger sammenligningen er sann. For hvis
den er sann blir også a[i] > maksverdi
utført. Vi vet at a[i] > nestmaksverdi blir sann
hver gang det kommer en verdi som er større enn den nest største av de foran.
Dette minner sterkt om den problemstillingen vi analyserte i
Avsnitt 1.1.6.
Vi må nå finne det gjennomsnittlige antallet tall som
er større enn det nest største av tallene foran. Vi ser på flg. fire eksempler der
hver tabell inneholder en permutasjon av tallene fra 1 til 10:
Tabell 1: 4, 6, 3, 5, 8, 1, 9, 2, 10, 7
Tabell 2: 7, 5, 1, 6, 8, 4, 3, 10, 2, 9
Tabell 3: 10, 3, 8, 2 6, 9, 1, 5, 4, 7
Tabell 4: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
De tallene som er større enn det nest største av tallene foran, er uthevet.
Opptellingen av slike tall starter hele tiden fra og med det tredje
tallet. For disse fire tilfellene får vi 4, 4, 2 og 8 slike tall. Det
gir et gjennomsnitt på 4,5. Men det er
jo hele 10! = 3.628.800 forskjellige permutasjoner av tallene fra 1 til 10. Det
er derfor helt umulig på grunnlag av disse fire å vite hva gjennomsnittet
for alle de 3.628.800 forskjellige blir.
Vi skal imidlertid klare å regne det ut for hånd i noen enkle tilfeller. Det er
hvis vi har 3 eller 4 forskjellige verdier. Husk at opptellingen går fra og med
det tredje tallet fordi et tall kan være større enn det nest største foran
kun når det er minst to tall foran.
|
1 2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 1 4 2 3 1 4 3 2 2 1 3 4 2 1 4 3 2 3 1 4 2 3 4 1 2 4 1 3 2 4 3 1 3 1 2 4 3 1 4 2 3 2 1 4 3 2 4 1 3 4 1 2 3 4 2 1 4 1 2 3 4 1 3 2 4 2 1 3 4 2 3 1 4 3 1 2 4 3 2 1 |
2 2 2 1 2 1 2 2 1 1 1 1 2 1 1 1 0 0 2 1 1 1 0 0 |
Hvis vi har tallene 1, 2 og 3 får vi de 6 permutasjonene:
1,2,3 1,3,2 2,1,3 2,3,1 3,1,2 3,2,1
Vi får 1, 1, 1, 0, 1 og 0 for antallet ganger det er et tall som er større enn det nest største av tallene foran. Gjennomsnittet blir 4/6 = 2/3.
I første kolonne til venstre har vi de 24 permutasjonene av tallene 1, 2, 3 og 4, og i andre kolonne antallet tall som er større enn det nest største av alle tallene foran. Gjennomsnittet blir 28/24 = 7/6. Her observerer vi at 7/6 = 2/3 + 2/4.
Setning 1.2.7 a) I en tabell med n > 2 forskjellige tall er i gjennomsnitt
2/3 + 2/4 + . . . . + 2/n av dem større enn det nest største av tallene foran.
Det er åpenbart det samme om vi bruker n forskjellige tall eller tallene fra
1 til n. Dermed har vi vist at påstanden i Setning 1.2.7 a)
stemmer for n = 3 og 4. Det å vise at den stemmer for alle n krever et induksjonsbevis.
Se
Avsnitt 1.2.15.
Konklusjon: Hn
(se Avsnitt 1.1.6) er definert ved Hn =
1 + 1/2 + 1/3 + . . . + 1/n . Dermed blir
2/3 + 2/4 + . . . . + 2/n = 2Hn - 3. Husk at for
store n er Hn tilnærmet lik log(n) + 0,577.
Det gjennomsnittlige antallet sammenligninger som utføres i
Programkode 1.2.5 a),
gitt at alle verdiene i tabellen er forskjellige,
finner vi slik:
- Alltid én sammenligning for å avgjøre hvem som er størst av
a[0] oga[1]. - Da
for-løkken starter medilik 2 utføresa[i] >nestmaksverdin − 2 ganger. - Sammenligningen
a[i] >maksverdiutføres nåra[i] >nestmaksverdier sann, og det skjer gjennomsnittlig 2Hn − 3 = 2(log(n) + 0,577) − 3 = 2log(n) − 1,846 ganger. - Til sammen: 1 + n − 2 + 2
log(n) − 1,846 = n + 2log(n) − 2,846 for n forskjellige verdier.
Vi oppsummerer resultatene i flg. oversikt der n er antall verdier i tabellen:
| Algoritme | Gjennomsnittlig | Det verste tilfellet | Det beste tilfellet |
Programkode 1.2.4 a) | 2n − 3 | 2n − 3 | 2n − 3 |
Programkode 1.2.5 a) | n + 2 log(n) − 2,846 |
2n − 3 | n − 1 |
Programkode 1.2.4 a) og
1.2.5 a)
er like i det verste tilfellet,
men i gjennomsnitt er den andre bedre. Hvis n = 100.000 vil den første
utføre 199.997 og den andre bare 100.020 sammenligninger. Selv om de har ulik
effektivitet er likevel begge av orden n, både gjennomsnittlig og i det verste tilfellet.
Men kan vi gjøre det enda bedre?
| 1. | Sjekk at påstanden i Setning 1.2.7 a) stemmer for
n = 5 ved å se på alle de 120 permutasjonene av tallene fra 1 til 5. Se også
Oppgave 1 i Avsnitt 1.1.6. |
| 2. | Lag metoden int antallNestMaks(int[] a). Den skal telle opp og returnere
det antallet ganger a[i] > nestmaksverdi er sann i
Programkode 1.2.5 a).
Kjør metoden på tabeller med tilfeldige permutasjoner og sammenlign med den teoretiske verdien.
|
| 3. | Hvorfor n − 1 sammenligninger i det beste tilfellet. Se også
Oppgave 2
i Avsnitt 1.2.6. |
![]() 1.2.8 En turnering
1.2.8 En turnering
Når det gjelder å finne den nest største verdien er
Programkode 1.2.5 a)
god nok for alle praktiske formål.
Den har imidlertid - i hvert fall teoretisk sett - en ulempe. Den er ikke
effektiv i de ugunstige tilfellene. Vi skal derfor utvikle enda en algoritme som i hvert fall
i teorien bøter på det problemet. Det vil samtidig gi oss en fin mulighet til
å introdusere binære trær - en av de viktigste datastrukturene i vårt fag.
Når en i idrett eller i spill ønsker å avgjøre hvem som er
best, lager man en turnering (eng: tournament). Det er to hovedtyper
- serie
(eng: round robin)
og cup. En cup-turnering er
en utslagsturnering (eng: knockout).
Deltagerne møtes to og to i første runde, vinnerne
går videre til neste runde, osv. inntil to stykker når
finalen. Den som vinner finalen er best.
Det er mulig å bruke en utslagsturnering både til å finne største og nest største verdi i en samling tall. Vi bestemmer at når to tall «møtes» er det alltid det største som vinner. Det betyr egentlig at alt er forutsigbart. Hvis de samme to tallene «møtes» flere ganger, er det alltid samme vinner. Slik er det jo normalt ikke innen idrett og spill. Men enten det er forutsigbart eller ikke, er det vinner av finalen som er best. Men hvem er egentlig nest best? I vanlige turneringer kan to deltagere som på forhånd anses å være de to beste, på grunn av en «uheldig» trekning, møte hverandre tidlig i turneringen. Bare en av dem kan gå videre. Dermed vil noen si at den tapende finalisten ikke nødvendigvis er nest best. I vår turnering behøver ikke det tallet som taper finalen være nest størst. Men det er klart at den nest største må befinne seg blant de tallene som ble «slått ut» av vinneren.
Eksempel: Gitt tallene 9, 21, 5, 25, 27, 23, 26, 28, 17, 15, 19, 18,
16, 20, 14, 10. Til sammen 16 tall. Vi setter opp turneringen slik at 9 og 21
møtes, 5 og 25 møtes, 23 og 27, osv. Vinneren i hvert møte (det største
tallet) går videre til neste runde. Turneringstreet (eng: tournament tree)
er tegnet nedenfor. I nederste rad står alle tallene eller deltagerne, i neste rad
vinnerne av første runde, osv. På toppen har vi vinneren, dvs. det største
tallet. Når vi som her har 16 deltagere, kalles også første runde for
en åttendelsfinale. Neste runde blir da kvartfinale, så semifinale og til slutt
finale.
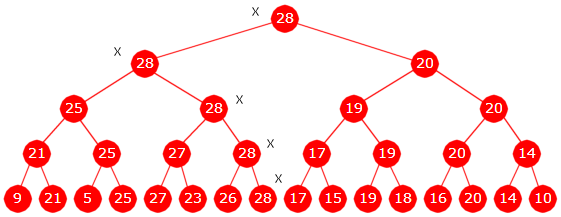 |
| Figur 1.2.8 a): Et turneringstre for 9, 21, 5, 25, 27, 23, 26, 28, 17, 15, 19, 18, 16, 20, 14, 10 |
Finalevinneren (28) kan følges bakover til første runde. Det gir oss tallene som vinneren har slått ut. På tegningen er vinnerens vei gjennom turneringen markert med et kryss (X).
Den tapende finalisten 20 ikke er nest størst. Men den nest største er blant dem som 28 har «slått ut». For hvis den nest største ikke er slått ut av vinneren, må den være slått ut av en annen verdi. Denne må da være større enn den nest største - en selvmotsigelse! På figuren ser vi at vinneren har slått ut 20, 25, 27 og 26. Dermed er det bare å finne den største blant disse (det er selvfølgelig 27), og til det trengs bare tre sammenligninger.
Et lite problem: Når to tall «møtes» vinner det største tallet. Men hva hvis de to tallene er like? Blir det da uavgjort? I en utslagsturnering må vi ha en vinner i hvert møte. I vår tall-turnering spiller det ingen rolle hvilket tall som vinner og går videre hvis tallene er like. Vi bestemmer likevel at i tilfelle likhet er det alltid det første (venstre) tallet som vinner.
| 1. | Et «møte» er det samme som en sammenligning. Hvor mange
sammenligninger trengs for å gjennomføre en turnering med 16 deltagere slik som
i Figur 1.2.8 a)?
Hva med 8 deltagere? Hva med 2k deltagere der
k er et positivt heltall. |
| 2. | Tegn et turneringstre slik som i Figur 1.2.8 a)
for tilfellene: a) 3, 15, 8, 11, 13, 9, 10, 5 og b)
10, 17, 13, 16, 17, 8, 12, 15, 9, 15, 16, 15, 10, 13, 14, 17. |
| 3. | Bruk de samme 16 verdiene som i
Figur 1.2.8 a).
Lag en turnering for å finne minst verdi. |
Treet i
Figur 1.2.8 a)
kalles et turneringstre. Dette er ikke
et tre av den typen vi finner ute i naturen, men det har struktur og
egenskaper som minner om et botanisk tre. Vi skal derfor bruke begreper som rot,
 |
| Et eiketre |
Turneringstreet kalles et binærtre (eng: binary tree) siden det
ved hver forgrening går ut to grener. Rundingene i treet kalles noder
(eng: node). Den øverste noden kalles rotnoden eller ofte bare roten
(eng: root). Hver node hører til et nivå (eng: level) eller en generasjon.
Rotnoden er på nivå 0 (første generasjon), de to nodene under er på nivå 1
(andre generasjon), osv. Nodene på den nederste raden i
Figur 1.2.8 a) er dermed på nivå 4.
Vi ser at det fra
hver node, unntatt fra nodene på nederste rad, går en kant (en strek) ned
til to noder på raden nedenfor. De to kalles barn (eng: children)
til den første noden. Omvendt går det en kant oppover fra alle noder unntatt
fra rotnoden. Vi sier at den noden kanten går opp til er nodens forelder
(eng: parent).
Avstanden mellom en vilkårlig node og rotnoden er antall kanter på veien
mellom de to nodene. Treets høyde (eng: height) er den største avstanden
i treet. Eller: Høyden er lik nivået til den eller de
nodene som har det største (laveste) nivået. Treet i
Figur 1.2.8 a)
har derfor høyde 4.
I Figur 1.2.8 a)
er alle nederst «barnløse».
En barnløs node kalles et blad eller en bladnode (eng: leaf node).
Hvis det ikke er en bladnode er det en indre node (eng: inner node).
To barn/noder med samme forelder kalles søsken (eng: sibling).
Figur 1.2.8 a)
viser at de som møter hverandre i turneringen blir søsken i
turneringstreet. Vi skiller mellom hvem som er hvem i et søskenpar – den venstre
kalles venstre barn og den andre høyre barn (eng: left or right child).
Hvis en node kun har ett barn, så er det enten et venstre
eller et høyre barn.
I vårt turneringstre har hver node enten to eller ingen barn. Et binærtre er egentlig en mer generell struktur enn et turneringstre. I et generelt binærtre kan en node ha enten to, ett eller ingen barn. Vi skal studere generelle binærtrær senere.
| 1. | Finn antall noder i Figur 1.2.8 a)?
Hvor mange er bladnoder? Hvor mange er indre noder? |
| 2. | Hvor mange noder er det på nivå k (k = 0, 1, 2, . . )
i et turneringstre av den typen som
Figur 1.2.8 a) viser? |
| 3. | Anta at antall deltagere n i en turnering er på formen n = 2k, dvs. n = 1, 2, 4, 8, osv. Finn svarene på flg. spørsmål uttrykt ved n: Hvor mange noder får turneringstreet? Hvilken høyde får treet? Hvor mange er bladnoder og hvor mange er indre noder? Hvor mange sammenligninger utføres i turneringen? |
![]() 1.2.10 Generelle turneringer
1.2.10 Generelle turneringer
Utgangspunktet for turneringstreet i Figur 1.2.8 a)
var 16 tall/deltagere.
Vi vet fra idrett og spill at i en utslagsturnering er det vanligvis
2, 4, 8, 16, 32 osv. deltagere. Dette er antall på formen 2k
der k er et positivt heltall. Poenget er at antall deltagere skal kunne
halveres for hver runde. Men hva hvis antallet deltagere ikke
er på formen 2k ?
Anta at det er n deltagere. I idrett og spill brukes såkalt «walk over». Det betyr at noen av deltagerne går rett til andre runde. Men fra og med andre runde må antallet være på formen 2k. Dette får vi til ved å la turneringstreet inneholde nøyaktig 2n − 1 noder. Treet tegnes slik: Sett opp én node øverst (nivå 0), så 2 noder på nivå 1, så 4 noder på nivå 2, osv. For hvert nytt nivå nedover tegner vi nodene én og én fra venstre mot høyre. I det øyeblikket vi til sammen har tegnet 2n − 1 noder, stopper vi. Da behøver ikke det siste nivået i treet inneholde så mange noder som det er plass til.
Eksempel: Vi har de 13 tallene: 7, 5, 21, 15, 27, 23, 13, 31, 8, 9,
18, 14, 3. Treet skal derfor ha 2·13 − 1 = 26 − 1 = 25 noder. Treet må ha høyde 4.
Det holder ikke med høyde 3 siden det maksimalt kan være 15 noder i et binærtre
med høyde 3. Vi trenger imidlertid bare 10 noder på siste rad for at antall noder
skal bli 25 til sammen. Det gir oss turneringstreet i Figur 1.2.10 a) nedenfor. Legg
merke til at det er nøyaktig 13 bladnoder.
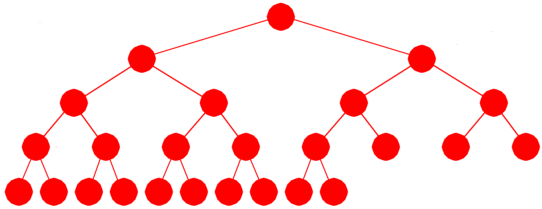 |
| Figur 1.2.10 a): Et turneringstre med plass til 13 deltagere |
Et turneringstre for n deltagere vil ha 2n − 1 noder, derav
n bladnoder og n − 1 indre noder. De n deltagerne/tallene
skal legges inn i bladnodene. Vi fyller ut bladnodene med tall fra venstre mot høyre,
først de på nest nederste rad og deretter de på nederste rad.
I Figur 1.2.10 b) nedenfor er de tre første av de gitte tallene
(dvs. 7, 5, 21) lagt inn på
nest nederste rad og de 10 øvrige (dvs. 15, 27, 23, 13, 31, 8, 9, 18, 14 og 3)
på nederste rad. De deltagerne/tallene som har blitt lagt inn på nest nederste rad
(dvs. 7, 5, 21) får «walk over» i første (innledende) runde. Legg merke til at det
er kun bladnodene som har fått verdier. De indre nodene vil få verdier i løpet av
turneringen.
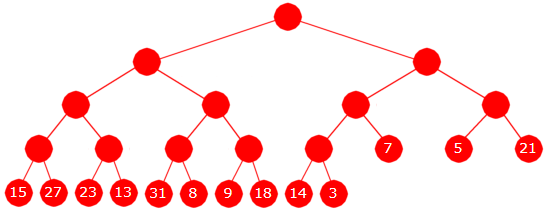 |
| Figur 1.2.10 b): Tallene 7, 5, 21, 15, 27, 23, 13, 31, 8, 9, 18, 14 og 3 er lagt inn i treet. |
Figur 1.2.10 c) nedenfor viser det ferdige turneringstreet.
Vinneren 31 ligger øverst. Kryssene (X) viser vinnerens vei gjennom turneringen.
Den nest største er som vanlig den største blant de vinnerne har slått ut, dvs.
det største av tallene 21, 27, 18 og 8. Med andre ord 27 - som forventet.
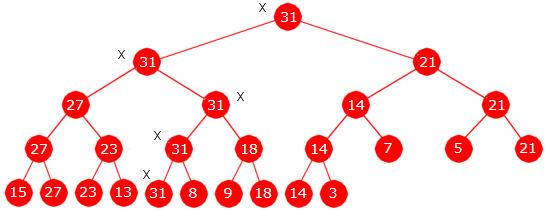 |
| Figur 1.2.10 c): Turneringen er gjennomført og resulatene er lagt inn i treet. |
| 1. | Tegn et turneringstre, slik som i Figur 1.2.10 c),
skriv opp de som vinneren har slått ut og finn den nest største verdien for flg. tre samlinger
av tall:a) 10, 17, 13, 16, 17, 8, 12, 15, 9, 15 b) 5, 11, 7, 13, 2, 9, 10, 8, 3, 14, 6, 12 og c) 5, 11, 7, 13, 2, 9, 10, 8, 3, 14, 6, 12, 9, 13, 4, 7, 13, 1, 14 . |
![]() 1.2.11 Perfekte, komplette og fulle trær
1.2.11 Perfekte, komplette og fulle trær
Et binærtre er perfekt (eng: a perfect binary tree) hvis
alle nivåene i treet inneholder så mange noder som det er plass til.
Det er plass til 1 node på nivå 0, 2 noder på nivå 1,
4 noder på nivå 2, 8 på nivå 3, osv. Generelt er det plass til 2k
noder på nivå k. Høyden er lik nivået til treets siste (nederste)
nivå. Et perfekt tre med høyde h inneholder dermed 1 + 2 + 4 + 8 + . . . +
2h = 2h+1 − 1 noder.
Turneringstreet i Figur 1.2.8 a)
er et perfekt binærtre med høyde 4 og har
dermed ha 24+1 − 1 = 25 − 1 = 32 − 1 = 31 noder.
Definisjon 1.2.11 a)
Et binærtre kalles perfekt (eng: a perfect binary tree) hvis
alle nivåene i treet inneholder så mange noder som det er plass til.
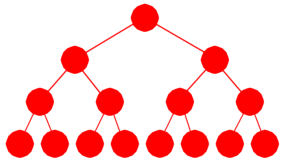 |
| Figur 1.2.11.a : Et perfekt binærtre med 15 noder |
Et binærtre er komplett (eng: a complete binary tree) hvis
hvert nivå, unntatt det siste (nederste) nivået, inneholder så mange noder som det er plass
til. På siste nivå kan det være færre enn det er plass til, men
det må ligge tett med noder fra venstre. F.eks. er alle turneringstrær
komplette. Hvis vi tar vekk noden lengst
til høyre på nederste rad/nivå i Figur 1.2.10 c)
(noden med tallet 3),
blir treet fortsatt komplett, men ikke lenger et turneringstre. Omvendt blir
et komplett binærtre et turneringstre hvis antall noder på nederste nivå er
et partall. Vi skal se mer på komplette trær senere, bl.a i forbindeles med
en prioritetskø.
Definisjon 1.2.11 b)
Et binærtre kalles komplett (eng: a complete binary tree) hvis
hvert nivå, unntatt det siste (nederste) nivået, inneholder så mange noder som det er plass
til. På siste nivå kan det være færre enn det er plass til, men
det må ligge tett med noder fra venstre.
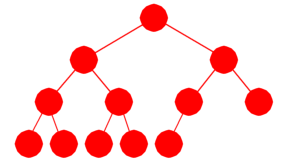 |
| Figur 1.2.11.b : Et komplett binærtre med 12 noder |
La et komplett binærtre ha høyde h. Da kan treet ha alt fra 1 til 2h noder på nederste nivå. Dermed vil det totale antallet noder ligge i intervallet [2h, 2h+1 – 1]. Det betyr spesielt at hvis et komplett binærtre har n noder, vil høyden h være gitt ved h = ⌈log2(n+1)⌉ – 1 .
Setning 1.2.11
Et komplett binærtre med n noder har høyde
h = ⌈log2(n+1)⌉ – 1 =
⌊log2(n)⌋
Eksempel: Treet i Figur 1.2.10 c)
er komplett og har høyde 4. Et komplett tre med høyde 4
kan ha fra og med 24 = 16 til og med
25 - 1 = 31 noder. Treet i Figur 1.2.10 c)
har 25 noder. Videre får vi at høyden
h er lik ⌈log226⌉ – 1 = ⌈4.7⌉ – 1 = 5 – 1 = 4.
Et binærtre er fullt (eng: a full binary tree) hvis hver node
har enten to eller ingen barn. Et turneringstre er både komplett
og fullt. Også det omvendte er sant: Et komplett og fullt binærtre er et
turneringstre. Vi skal senere se flere andre eksempler på fulle binærtrær,
f.eks.
alle Huffmantrær. Se Oppgave 1 og 3.
Definisjon 1.2.11 c)
Et binærtre kalles fullt (eng: a full binary tree) hvis hver node
har enten to eller ingen barn.
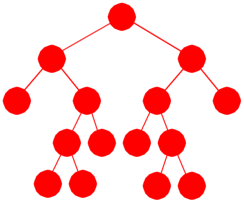 |
| Figur 1.2.11.c : Et fullt binærtre |
Turneringstrær har enda en interessant egenskap. Et binærtre
kalles et maksimumstre (eng: a max tree) hvis verdien i hver
node er større enn eller lik verdiene til nodens eventuelle barn.
Eller omvendt: Enhver node, unntatt bladnoden, har en verdi som er mindre
enn eller lik verdien i nodens forelder. I et turneringstre inneholder hver
indre node den største av de to verdiene i nodens to barn
og oppfyller dermed kravet til å være
et maksimumstre. Hvis vi i et maksimumstre starter i en bladnode
og går oppover mot rotnoden, kommer verdiene i sortert rekkefølge, dvs.
sortert stigende. Se Figur 1.2.8 a)
og Figur 1.2.10 c).
Definisjon 1.2.11 d)
Et binærtre kalles et maksimumstre (eng: a max tree) hvis hver node,
bortsett fra rotnoden, har en verdi som er mindre enn eller lik
verdien i nodens forelder.
Vi tar også med et fjerde begrep, dvs. begrepet heap. Det vil senere få betydning i
forbindelse med priortetskøer.
Definisjon 1.2.11 e)
Et binærtre kalles en maksimumsheap (eng: a max heap) hvis det er et komplett maksimumstre.
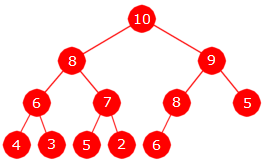 |
| Figur 1.2.11.d : En maksimumsheap |
Begrepene perfekt, komplett og fullt for binære trær blir ikke alltid definert på samme måte i litteraturen. Her er det definert slik som hos det amerikanske National Institute of Standards and Technology.
 |
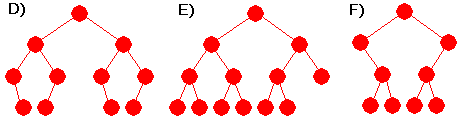 |
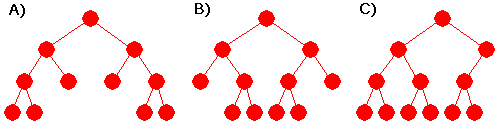
| 1. | Svar på flg. spørsmål for hvert av trærne A, B, C, D, E og F over: a) Er treet komplett? b) Er treet perfekt? c) Er treet fullt? d) Hva er treets høyde? e) Hvor mange bladnoder har treet? f) Er det et turneringstre? |
| 2. | Tegn et perfekt binærtre med høyde 3. Tegn et komplett binærtre med 10 noder. Tegn et komplett binærtre med 20 noder. |
| 3. | Tegn et fullt binærtre med 5 noder? Hvor mange slike finnes det? Hvor mange fulle binærtrær med 7 noder finnes det? Vis at antallet noder i et fullt binærtre alltid er et odde tall. |
| 4. | Vis at ⌈log2(n+1)⌉ - 1 = ⌊log2(n)⌋
for n >= 1
Se forøvrig Setning 1.2.11.
|
![]() 1.2.12 Turneringsanalyse
1.2.12 Turneringsanalyse
Når vi har n deltagere får turneringstreet 2n – 1 noder og treet
får like mange bladnoder som deltagere. Et «møte» i turneringen er det samme
som en sammenligning, og hver node som ikke er en bladnode, er resultatet av
et «møte». Med andre ord trengs det tilsammen 2n – 1 – n
= n – 1 sammenligninger for å gjennomføre turneringen og dermed blir det
n – 1 sammenligninger for å finne den største verdien.
Den nest største verdien befinner seg blant dem som vinneren har slått ut. Hvor mange
tall er det? Figur 1.2.10 c)
viser at vinneren 31 slo ut fire andre deltagere/tall.
Men hvis vinneren hadde hørt til de deltagerne som fikk «walk over» i første runde,
ville den bare ha slått ut 3 andre. Men uansett vil vinneren aldri møte eller slå
ut flere enn det er runder i turneringen, og antall runder er det samme som
treets høyde.
La log2(n) stå for logaritmen til n med grunntall 2.
Et turneringstre med n deltagere vil være komplett og ha 2n – 1 noder.
La h være treets høyde. Da gir Setning 1.2.11 at
h =
⌈log2(2n–1+1)⌉ – 1 = ⌈log2(2n)⌉ – 1
= ⌈log2(2) + log2(n)⌉ – 1 = ⌈1 + log2(n)⌉ – 1
= ⌈log2(n)⌉.
Setning 1.2.12
I en turnering med n deltagere vil antall runder (og dermed
turneringstreets høyde) bli lik ⌈log2(n)⌉
Eksempel: I Figur 1.2.10 c)
er det 13 deltagere. Formelen gir da h = ⌈log213⌉ =
⌈3.7⌉ = 4 .
Java: Metoden double Math.log(double x) finner den naturlige
logaritmen (grunntall e) til x, og metoden double Math.ceil(double x)
avrunder tallet x oppover til nærmeste heltall. Navnet ceil er
en forkortelse for ceiling, dvs. tak. Høyden h gitt ved
h = ⌈log2 n⌉ kan derfor uttrykkes slik:
int n = 13; int h = (int)Math.ceil(Math.log(n)/Math.log(2)); System.out.println(h); // Utskrift: 4 Programkode 1.2.12 a)
Men det kan gjøres mer effektivt. Vi vet at hvis 2k-1 < n <=
2k , så er log2 (n) et desimaltall i intervallet
<k–1 , k] og dermed at ⌈log2 (n)⌉ = k.
Hvis 2k-1 <= n < 2k, så vil n
ha nøyaktig k signifikante siffer i sin binærkode. Java har en metode som
forteller hvor mange ledende 0-biter et heltall n har i sin binærkode, det er
metoden numberOfLeadingZeros. Vi får antall signifikante binære siffer
ved å ta differansen mellom 32 og antallet ledende 0-biter. Hvis n =
2k, vil n ha k + 1 signifikante binære siffer.
Vi får imidlertid rett svar hvis vi isteden bruker antallet ledende 0-biter
i tallet n – 1 :
int n = 13; int h = 32 - Integer.numberOfLeadingZeros(n - 1); System.out.println(h); // Utskrift: 4 Programkode 1.2.12 b)
Konklusjon: Ved å bruke en utslagsturnering vil vi trenge n − 1
sammenligninger for å bygge opp turneringstreet og maksimalt
⌈log2(n)⌉ − 1 sammenligninger for å finne den største blant de
som vinneren har slått ut (en i hver runde). Dermed vil vi kunne klare oss
med n + ⌈log2(n)⌉ − 2 sammenligninger for å finne den nest
største verdien. Dette er bedre enn algoritmen fra
Programkode 1.2.5 a)
der vi trengte n + 2 log(n) − 2,846 i gjennomsnitt og 2n − 3
i det verste tilfellet. Til tross for forskjeller, er likevel alle
algoritmene i tabellen under av orden n:
| Algoritme: Nest størst verdi | Gjennomsnittlig antall sammenligninger | Verste tilfellet | Beste tilfellet | |
| Versjon | Generell n | n = 100000 | n = 100000 | n = 100000 |
Programkode 1.2.4 a) |
2n − 3 | 199997 | 199997 | 199997 |
Programkode 1.2.5 a) |
n + 2 log(n) − 2.846 | 100020 | 199997 | 99999 |
Programkode 1.2.13 a) |
n + ⌈log2(n)⌉ − 2 | 100015 | 100015 | 100015 |
| Tabell 1.2.12: Sammenligning av tre algoritmer for å finne den neste største verdien i en tabell | ||||
|---|---|---|---|---|
Tabell 1.2.12 viser at hvis f.eks. n = 100000, vil turneringen, uansett
hvordan verdiene er fordelt i tabellen, alltid klare seg med 100015 sammenligninger.
Programkode 1.2.5 a)
derimot trenger 100020 i gjennomsnitt, 199997 i det verste og
99999 i det beste tilfellet. En turnering bruker teoretisk sett færre sammenligninger
enn Programkode 1.2.5 a).
Men når vi i neste avsnitt skal implementere
turneringsalgoritmen, vil vi oppleve at koden likevel blir mindre effektiv (bruker lenger
tid i datamaskinen) enn Programkode 1.2.5 a).
| 1. | Turneringstreet i Figur 1.2.10 c)
hadde 13 deltagere som utgangspunkt. Da var det 3 deltagere som fikk
«walk over». Hvor mange deltagere vil få «walk over» hvis turneringen
har a) 14, b) 15 og c) 16 deltagere? Kan du finne
en formel for hvor mange deltagere som får «walk over» hvis antallet deltagere
i turneringen er n?
|
| 2. | Lag et program som sjekker at Programkode 1.2.12 a)
og 1.2.12 b)
gir samme svar for alle positive verdier av n. Lag f.eks. en
for-løkke som går fra n = 1 og et stykke utover.
|
![]() 1.2.13 Hvordan implementere en turnering
1.2.13 Hvordan implementere en turnering
Det er faktisk lettere enn en tror å implementere en turnering. Vi gir hver node i treet et nummer.
Rotnoden blir nr 1, rotnodens to barn nr 2 og 3, de på neste rad nr 4, 5,
6 og 7, osv. På hver rad/nivå gir vi nodene nummer fortløpende fra venstre
mot høyre. Dette kalles å nummerere nodene i nivåorden. På treet under
har nodene i treet i Figur 1.2.10 c)
blitt nummerert på denne måten:
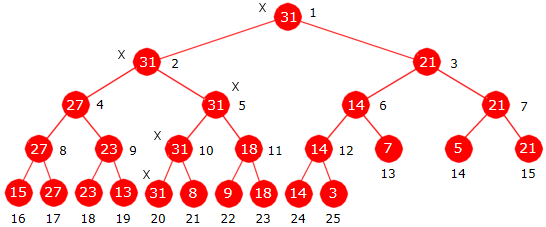 |
| Figur 1.2.13 a): Et turneringstre der nodene har fått nummer i nivåorden |
Ved hjelp av nummereringen kan vi lett bevege oss fra barn til forelder eller omvendt.
Vi ser at hvis k er nummeret til en node, så er k/2 nummeret til
forelderen. Dette gjelder for alle unntatt rotnoden. Med k/2 mener vi
heltallsdivisjon. Omvendt vil 2k og 2k + 1 gi numrene til de
to barna til node nr. k. Dette gjelder de nodene som har barn. Eksempel: Node
nr 11 har node nr 5 (5 = 11/2) som forelder og nodene med nr 22 (22 = 2·11) og
nr 23 (23 = 2·11 + 1) som barn. Figur 1.2.13 a) inneholder et tre der
det hver node har fått et nummer. Sjekk at at det stemmer!
Setning 1.2.13 For en node med k som nodenummer, vil
2k være nummeret til et venstre barn
og 2k + 1 nummeret til et høyre barn. Hvis noden har en
forelder (dvs. k > 1), vil k / 2 (heltallsdivisjon) være forelderens
nodenummer.
Turneringstreet i Figur 1.2.13 a)
kan bygges opp ved hjelp av
en tabell. Hvis det er n deltagere lager vi en tabell med lengde 2n.
Vi trenger bare 2n − 1 plasser. Det første tabellelementet
(indeks 0) vil derfor ikke bli brukt. De 13 deltagerne i turneringen
(tallene 7, 5, 21, 15, 27, 23, 13, 31, 8, 9, 18, 14 og 3) legges
bakerst i tabellen. Dermed får vi tabellen i Figur 1.2.13 b) nedenfor.
Vi ser at indeksen for hver av deltagerne stemmer overens med de tilsvarende
nodenumrene treet i Figur 1.2.13 a):
| X | 7 | 5 | 21 | 15 | 27 | 23 | 13 | 31 | 8 | 9 | 18 | 14 | 3 | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Figur 1.2.13 b): De 13 deltagerne er lagt inn bakerst i tabellen. | |||||||||||||||||||||||||
Turneringen settes i gang ved at to og to deltagere/tall møter hverandre.
Først møtes de to bakerste, dvs. tallene 14 og 3 med indeks 24 og 25. I treet i
Figur 1.2.13 a)
ser vi at vinneren 14 har flyttet opp til foreldernoden og
den har 12 som nodenummer. I tabellen finner vi dette nummeret med å halvere
indeksen, dvs. 24/2 = 12. Vi legger derfor tallet 14 inn på posisjon 12 i
tabellen. Deretter møtes tallene 9 og 18, og vinneren 18 flytter til posisjon
11 i tabellen. Osv. Når de fem møtene/kampene i turneringens første eller
innledende runde er ferdig, får vi det som vises i Figur 1.2.13 c):
| X | 27 | 23 | 31 | 18 | 14 | 7 | 5 | 21 | 15 | 27 | 23 | 13 | 31 | 8 | 9 | 18 | 14 | 3 | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Figur 1.2.13 c): Første eller innledende runde (5 «kamper») i turneringen er gjennomført. | |||||||||||||||||||||||||
Når vi fullfører resten av rundene i ender vi opp med tabellen
i Figur 1.2.13 d). Vi ser at vinneren, dvs. det største tallet, ligger
i posisjon/indeks 1:
| X | 31 | 31 | 21 | 27 | 31 | 14 | 21 | 27 | 23 | 31 | 18 | 14 | 7 | 5 | 21 | 15 | 27 | 23 | 13 | 31 | 8 | 9 | 18 | 14 | 3 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Figur 1.2.13 d): Turneringen er ferdig og vinneren ligger i posisjon/indeks 1. | |||||||||||||||||||||||||
Neste skritt er å finne den nest største. Vi vet at det er den største av de
som vinneren har slått ut. Vi ser lettest hva som må gjøres hvis vi tar
utgangspunkt i turneringstreet fra
Figur 1.2.13 a).
Vi kan starte med å sette k lik nodenr. 2, dvs. rotnodens venstre barn.
Videre går vi hele tiden nedover i treet ved å doble k. Hvis maksverdien
ikke ligger i node k øker vi k med 1. Det tallet som maksverdien har
slått ut ligger hele tiden i søskennoden til node k. Oppgaven løses derfor
ved å finne den største blant disse søskennodene.
Som beskrevet ovenfor må vi først lage en ny tabell med plass til det dobbelte av
antall deltagere, og så legge deltagerne bakerst i den nye tabellen -
se Figur 1.2.13 b).
Det betyr at vi må kopiere innholdet av
en tabell over i en annen tabell. Metoden arraycopy fra klassen System
i biblioteket java.lang er laget spesielt for dette formålet:
public static int[] nestMaks(int[] a) // en turnering { int n = a.length; // for å forenkle notasjonen if (n < 2) // må ha minst to verdier! throw new IllegalArgumentException("a.length(" + n + ") < 2!"); int[] b = new int[2*n]; // turneringstreet System.arraycopy(a,0,b,n,n); // legger a bakerst i b for (int k = 2*n-2; k > 1; k -= 2) // lager turneringstreet b[k/2] = Math.max(b[k],b[k+1]); int maksverdi = b[1], nestmaksverdi = Integer.MIN_VALUE; for (int m = 2*n - 1, k = 2; k < m; k *= 2) { int tempverdi = b[k+1]; // ok hvis maksverdi er b[k] if (maksverdi != b[k]) { tempverdi = b[k]; k++; } if (tempverdi > nestmaksverdi) nestmaksverdi = tempverdi; } return new int[] {maksverdi,nestmaksverdi}; // størst og nest størst } // nestMaks Programkode 1.2.13 a)
Turneringsalgoritmen er teoretisk sett litt bedre enn den i
Programkode 1.2.5 a),
spesielt i det verste tilfellet.
Men testkjøringer viser at Programkode 1.2.13 a)
likevel bruker langt mer tid enn
Programkode 1.2.5 a).
Grunnen er at i tillegg til sammenligningene, inngår mange
tabelloperasjoner, metodekall og aritmetiske operasjoner for å lage turneringstreet.
Selv om noen vil si at det å utvikle turneringsalgoritmen var «mye skrik og
lite ull» siden den ikke bruker kortere tid i datamaskinen enn de andre
nestMaks-algoritmene, så er likevel det vi har lært om binære trær
særdeles viktig. Binære trær er en av våre viktigste datastrukturer og vi vil
komme tilbake til dem mange ganger.
| 1. | Sjekk at Programkode 1.2.13 a)
virker. Obs: metoden returnerer størst og nest størst verdi og ikke indeksene.
Legg inn en setning som skriver ut tabellen b
etter ut turneringen er gjennomført. Dermed kan en se resultatet av turneringen.
|
| 2. | La Programkode 1.2.13 a) returnere |
| 3. | Metoden public static void kopier(int[] a, int i, int[] b, int j, int ant)
skal virke som arraycopy() fra class System. Lag den!
|
| 4. | Gitt tabeller int[] a og int[] b med
a.length <= b.length. Lag kode, vha.
arraycopy() eller vha. kopier()
fra Oppgave 3, slik at 1) a kopieres
inn først i b, 2) a kopieres inn bakerst i b
og 3) a kopieres inn på midten av b (gitt at lengdeforskjellen er et partall).
|
![]() 1.2.14 Andre problemstillinger
1.2.14 Andre problemstillinger
Det finnes flere problemstillinger av samme type.
Det kan f.eks. være å finne: 1) både den minste og den største verdien,
2) den k-te minste verdien og 3) medianen.
Den minste og den største
Vi kan først finne den minste, og deretter den
største av de øvrige. Til det trengs til sammen 2n - 3
sammenligninger. Men det kan gjøres enda bedre ved å bruke en turneringsteknikk.
Vi sammenligner første og siste verdi, så andre og nest siste, osv.
Hvis den første i det paret vi sammenligner er størst (er vinner) av de to, lar vi dem
bytte plass. Dette fører til høyre halvdel av tabellen vil inneholde
«vinnere» og venstre halvdel «tapere». Tabellens minste blir den minste av
taperne og tabellens største den største av vinnerne. Dette krever kun ⌈3n/2⌉ - 2
sammenligninger, men en serie ombyttinger som ekstra kostnad. Se også Oppgave 1.
Den k-te minste verdien i en tabell
En annen viktig problemstilling er å finne den k-te minste verdien i en tabell.
Dvs. den verdien som havner i posisjon k hvis vi sorterer tabellen.
Hvis k = 0, betyr det den minste verdien, hvis k = 1, den nest
minste verdien, osv. Men poenget er å finne den uten å måtte sortere først.
Vi har algoritmer for å finne den største og den nest største verdien og
de kan med små endringer brukes til å finne den minste og
den nest minste. Det er selvfølgelig mulig å videreutvikle disse
til det å finne den k-te minste verdien, men det vil generelt ikke gi oss
effektive algoritmer. Vi ser litt på dette i oppgavene nedenfor. I et senere
kapittel skal vi finne en effektiv algoritme for dette problemet.
Medianen
Gitt n verdier. Hvis n er odde, er medianen den midterste verdien og
hvis n er et partall er medianen gjennomsnittet av de to midterste verdiene.
Dvs. lik den n/2-te minste verdien eller gjennomsnittet av den (n-1)/2-te
minste verdien og den n/2-te minste verdien. Det er utviklet helt egne algoritmer for
dette problemet.
| 1. | Lag en metode int[] minmaks(int[] a) som returnerer både
den minste og den største verdien i tabellen a. Gjør som beskrevet over.
|
| 2. | Lag en metode static int kVerdi(int[] a, int k) som
finner og returnerer posisjonen til den k-te minste verdien i a.
Prøv både idéen i Programkode 1.2.4 a)
og idéen i
Programkode 1.2.5 a).
|
![]() 1.2.15 Antallet tall som er større enn det nest største foran
1.2.15 Antallet tall som er større enn det nest største foran
I Avsnitt 1.2.7 står flg. påstand:
Påstand: Av n (n ≥ 2) forskjellige tall i rekkefølge, er det gjennomsnittlig 2Hn − 3 av dem som er større enn det nest største av tallene foran i rekkefølgen.
Påstanden kan reformuleres til at summen, over alle de n! permutasjonene, av antallet tall som er større enn det nest største av de foran, er lik n! · (2Hn − 3). Det spiller ingen rolle om vi opererer med n forskjellige tall eller tallene fra 1 til n.
1) Påstanden er sann for n = 2. Antallet tall som er større enn det nest største
av de foran, er da lik 0 siden vi har kun to tall. Men også
2H2 − 3 er 0.
I Avsnitt 1.2.7
tellet vi opp antallene og fant at påstanden også
var sann for n = 3 og 4.
2) Induksjonshypotesen: Anta at påstanden er sann for n.
Vi skal vise at påstanden er sann for n + 1. I en permutasjon er det et bestemt antall tall som er større enn det nest største av tallene foran. La N(n + 1, k), k = 1, . . , n + 1 være summen av disse antallene for de n! permutasjonene av tallene fra 1 til n + 1 der k står bakerst.
Anta først at k < n. Da gir induksjonshypotesen at N(n + 1, k) = n! · (2Hn − 3) siden et tall mindre enn n bakerst ikke er større enn det nest største av de foran (som jo er n).
Hvis k = n får vi ett ekstra tall som er større enn det nest største av tallene foran. Når n står bakerst må jo det nest største av de foran være mindre enn n. Induksjonshypotesen gir dermed at N(n + 1, n) = n! · (2Hn − 3) + n!
Det blir på samme måte hvis k = n + 1. Da blir det også ett ekstra tall som er større enn det nest største foran. Induksjonshypotesen gir at N(n + 1, n + 1) = n! · (2Hn − 3) + n!
Summerer vi dette for k lik 1 til n + 1 blir det:
1.2.15 (n − 1) · n! · (2Hn − 3) + 2 · [ n! · (2Hn − 3) + n! ]
En utregning av 1.2.15 gir (n + 1)! · (2Hn + 1 − 3). Vi får gjennnomsnittsverdien 2Hn + 1 − 3 ved å dele på (n + 1)! Dette viser at påstanden er sann for n + 1. Ved hjelp av induksjonsprinsippet kan vi dermed si at påstanden er sann for alle n ≥ 2.
| 1. | Vis at en utregning av 1.2.15 gir (n + 1)! · (2Hn + 1 − 3). |

|