![]() 1.3.1 Permutasjoner
1.3.1 Permutasjoner
En samling verdier kan settes opp i en rekkefølge. Hver slik rekkefølge utgjør
en permutasjon
av verdiene. En samling på n ulike verdier kan permuteres på
n! (n fakultet) ulike måter. Det betyr at antallet
forskjellige permutasjoner vokser svært fort når n vokser:
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
10! = 3.628.800
20! = 2.432.902.008.176.640.000
I Avsnitt 1.1.8 så vi på teknikker for å lage
tilfeldige permutasjoner av tallene fra 1 til n. De er nyttige
i forbindelse med testing av algoritmer. Men det vil også være situasjoner der det er ønskelig å få tilgang
til alle permutasjonene. Vi skal her se på en teknikk som genererer samtlige permutasjoner i
leksikografisk (eng: lexicographic) rekkefølge.
Definisjon 1.3.1 Gitt to permutasjoner p og q av tallene fra 1 til n
q = q0 q1 q2 . . . qn−1
Eksempel 1.3.1: Gitt flg. to permutasjoner p og q av tallene fra 1 til 10:
p = 3 1 4 9 5 2 6 8 7 10 q = 3 1 4 9 7 10 8 6 5 2
De fire første tallene er like i p og q. Det femte tallet i p (dvs. 5) er mindre enn
det femte i q (dvs. 7). Dermed er p mindre enn q leksikografisk. Spesielt får vi
at 1 2 3 4 5 6 7 8 9 10 er leksikografisk sett den første (minste) og at 10 9 8 7 6 5 4 3 2 1 er den
siste (største) blant permutasjonene av tallene fra 1 til 10.
Spørsmål: Hvis en permutasjon er gitt, hva blir da den neste leksikografisk sett? Vi ser
først på noen enkle tilfeller og deretter på et som er mer generelt. Vi starter med flg. permutasjon av tallene fra 1 til 10:
| 3 | 1 | 4 | 9 | 7 | 10 | 8 | 5 | 2 | 6 |
| Figur 1: Siste tall er større enn nest siste | |||||||||
Hvis det siste tallet er større enn det nest siste (tallene 6 og 2 i Figur 1 over), får
vi den neste i leksikografisk rekkefølge ved å bytte om de to. Med andre
ord denne permutasjonen:
| 3 | 1 | 4 | 9 | 7 | 10 | 8 | 5 | 6 | 2 |
| Figur 2: Vi ser på de tre siste tallene | |||||||||
I Figur 2 er nå det siste tallet mindre enn det nest siste. Da nytter det ikke å bytte om dem.
Vi må isteden trekke inn de tre siste tallene. De kan permuteres i leksikografisk rekkefølge på flg. seks måter:
2 5 6 , 2 6 5 , 5 2 6 , 5 6 2 , 6 2 5 og 6 5 2. Her ser vi at det er
6 2 5 som kommer etter 5 6 2. Dermed blir dette neste permutasjon:
| 3 | 1 | 4 | 9 | 7 | 10 | 8 | 6 | 2 | 5 |
| Figur 3: Siste tall er større enn nest siste | |||||||||
I Figur 3 har vi igjen den situasjonen at det siste tallet er større enn det nest siste. Dermed
får vi neste permutasjon ved å bytte om de to:
| 3 | 1 | 4 | 9 | 7 | 10 | 8 | 6 | 5 | 2 |
| x | |||||||||
| Figur 4: Et mer generelt tilfelle | |||||||||
Figur 4 viser et mer generelt tilfelle. Der er de fem siste tallene
sortert avtagende. Generelt gjør vi slik for å finne den neste:
Start bakerst og gå mot venstre så lenge som det er sortert.
Dvs. vi skal stoppe på første tall som bryter sorteringen. I Figur 4 er det tallet 7 (markert med en x).
Neste skritt er: Bytt dette tallet med det minste av de til høyre som
er større. I Figur 4 er tallet 8 det minste av de til høyre for 7
som er større enn 7. Snu så alle tallene til høyre for posisjon x. Dermed blir
flg. permutasjon den som leksikografisk kommer etter den i Figur 4:
| 3 | 1 | 4 | 9 | 8 | 2 | 5 | 6 | 7 | 10 |
| Figur 5: Neste permutasjon | |||||||||
Beskrivelsen over sier at to tall skal bytte plass. Vi har tidligere laget metoden
bytt()
for det. Den må du ha i samleklassen Tabell.
Det er også nødvendig å kunne
snu rekkefølgen på et intervall av verdier. Det er noe som det også vil være behov for
andre steder. Vi lager derfor hjelpemetoder. De må legges i samleklassen Tabell:
public static void snu(int[] a, int v, int h) // snur intervallet a[v:h] { while (v < h) bytt(a, v++, h--); } public static void snu(int[] a, int v) // snur fra og med v og ut tabellen { snu(a, v, a.length - 1); } public static void snu(int[] a) // snur hele tabellen { snu(a, 0, a.length - 1); } Programkode 1.3.1 a)
Beskrivelsen i tilknytning til Figur 4
og Figur 5
over kan oversettes til følgende metode. Den skal ligge i samleklassen Tabell:
public static boolean nestePermutasjon(int[] a) { int i = a.length - 2; // i starter nest bakerst while (i >= 0 && a[i] > a[i + 1]) i--; // går mot venstre if (i < 0) return false; // a = {n, n-1, . . . , 2, 1} int j = a.length - 1; // j starter bakerst while (a[j] < a[i]) j--; // stopper når a[j] > a[i] bytt(a,i,j); snu(a,i + 1); // bytter og snur return true; // en ny permutasjon } Programkode 1.3.1 b)
Algoritmen i Programkode 1.3.3 b) er ineffektiv hvis n er stor.
Fordelen er imidlertid at vi får generert én og én permutasjon. Vi ser på andre og mer effektive teknikker i
Avsnitt 1.5.5.
Flg. eksempel viser hvordan metoden nestePermutasjon kan brukes:
int[] a = {3,1,4,9,7,10,8,6,5,2}; // permutasjon av tallene fra 1 til 10 Tabell.nestePermutasjon(a); // lager neste permutasjon System.out.println(Arrays.toString(a)); // [3, 1, 4, 9, 8, 2, 5, 6, 7, 10] Programkode 1.3.1 c)
En anvendelse
Setning 1.1.6 a)
i Avsnitt 1.1.6
sier at i en tilfeldig permutasjon av tallene fra 1 til n, vil det
gjennomsnittlig være 1/2 + 1/3 + . . + 1/n = Hn − 1
av dem som er større enn det største av tallene foran.
Oppgave 1 i det avsnittet gikk
ut på å verifisere dette for n = 5. Vi har at 1/2 + . . + 1/5 =
154/120. Hvis vi for hver av de 5! = 120 permutasjonene teller opp de tallene i permutasjonen som er større enn
det største av de foran, skal vi sammenlagt få 154. Dette kan sjekkes ved å la metoden
nestePermutasjon generere alle permutasjonene og
så la metoden
antallMaks telle opp.
Se også Oppgave 4.
int[] a = {1,2,3,4,5}; // første permutasjon int sum = 0; // hjelpevariabel do { sum += antallMaks(a); } // se Programkode 1.1.9 a) while (Tabell.nestePermutasjon(a)); // lager neste permutasjon System.out.println(sum); // Utskrift: 154 Programkode 1.3.1 d)
| 1. | Legg metodene fra Programkode 1.3.1 a)
og Programkode 1.3.1 b) i samleklassen Tabell. |
| 2. | Gitt flg. permutasjoner av tallene fra 1 til 6: a) 2 3 6 1 4 5,
b) 2 3 6 1 5 4,c) 2 3 1 6 5 4,
d) 2 3 6 5 4 1 og e) 2 6 5 4 3 1. Finn, for hver av dem, den neste i
leksikografisk rekkefølge. Bruk så metoden
nestePermutasjon som fasit. |
| 3. | Skriv opp de 10 første permutasjonene som
kommer etter 3 1 4 9 7 10 8 6 5 2 leksikografisk. Bruk metoden
nestePermutasjon
som fasit. |
| 4. | Lag kode som først skriver ut de 6 permutasjonene (én per linje) av tallene 1,2,3. Gjenta dette med de 24 permutasjonene av 1,2,3,4. |
| 5. | Kjør Programkode 1.3.1 d). Gjenta kjøringen
med n = 6. Da skal resultatet bli 1044. Sjekk
at det er lik (1/2 + 1/3 + . . + 1/6)·6! Gjenta med n = 7. |
![]() 1.3.2 Inversjoner og sortering
1.3.2 Inversjoner og sortering
Gitt flg. permutasjon av tallene fra 1 til 10:
1 2 4 3 6 7 9 5 8 10
Vi ser øyeblikkelig at tallene ikke er sortert. F.eks. er tallparene (4,3) og (6,5)
i utakt. Et annet navn på det å være i utakt er en inversjon.
Det gir oss flg. definisjon:
Definisjon 1.3.2 a) Inversjoner
x , y)
av tall fra rekkefølgen der x ligger til venstre for
y, kalles en inversjon hvis x og
y er i utakt, dvs. hvis tallet x er større enn tallet y.
Spørsmål: Hvor mange inversjoner er det i
permutasjonen 1 2 4 3 6 7 9 5 8 10 ? Dette
kan vi finne ut slik: Gå for hvert tall x, videre mot høyre og se om
det kommer et (eller flere) tall y som er mindre enn x. Det gir flg. inversjoner:
(4 , 3), (6 , 5), (7 , 5), (9 , 5) og (9 , 8).
Med andre ord fem inversjoner.
Vi kan bruke idéen over til å lage en metode som teller opp inversjonene
(en mer effektiv teknikk tas opp i Avsnitt 1.3.12). Den
skal ligge i samleklassen Tabell:
public static int inversjoner(int[] a) { int antall = 0; // antall inversjoner for (int i = 0; i < a.length - 1; i++) { for (int j = i + 1; j < a.length; j++) { if (a[i] > a[j]) antall++; // en inversjon siden i < j } } return antall; } Programkode 1.3.2 a)
Flg. eksempel viser hvordan metoden kan brukes:
int[] a = {1,2,4,3,6,7,9,5,8,10}; System.out.println(Tabell.inversjoner(a)); // Utskrift: 5 Programkode 1.3.2 b)
Nå ser vi generelt på permutasjoner av tallene fra 1 til n. Hvis en permutasjon er sortert stigende, vil
det være null inversjoner. Også det omvendte gjelder. Hvis en permutasjon av tallene fra 1 til n ikke inneholder
noen inversjoner, så er tallene sortert stigende. Dette gir oss flg. generelle definisjon:
Definisjon 1.3.2 b) Sortering
Det er heldigvis enklere å avgjøre om en rekkefølge av verdier er sortert enn å bruke definisjonen over. Det holder
å sjekke naboverdier. Den er sortert hvis ingen par (x , y) av
naboverdier utgjør en inversjon. Hvis verdiene ligger i en tabell, får vi flg. enkle metode:
public static boolean erSortert(int[] a) // legges i samleklassen Tabell { for (int i = 1; i < a.length; i++) // starter med i = 1 if (a[i-1] > a[i]) return false; // en inversjon return true; } Programkode 1.3.2 c)
Legg merke til at metoden erSortert() er av orden n. Det er det beste vi kan oppnå for den oppgaven.
Flg. eksempel viser hvordan den kan brukes:
int[] a = {}, b = {5}, c = {1,2,4,3,6,7,9,5,8,10}; // heltallstabeller int[] d = {1,2,3,4,5,6,7,8,9,10}; // heltallstabell boolean x = Tabell.erSortert(a), y = Tabell.erSortert(b); boolean z = Tabell.erSortert(c), u = Tabell.erSortert(d); System.out.println(x + " " + y + " " + z + " " + u); // Utskrift: true true false true Programkode 1.3.2 d)
Legg merke til at vi får true både for en tom tabell og for en med kun ett element. Det er slik det skal
være. Det er vanlig å si at en rekkefølge med ingen verdier eller én verdi, er sortert.
Antall inversjoner kan brukes til å si noe om hvor sortert eller eventuelt hvor usortert en permutasjon
av tallene fra 1 til n er. Hvis det ikke er noen
inversjoner, så er den sortert (stigende). Men når er det flest mulig inversjoner? Det er når permutasjonen er sortert
motsatt vei, dvs. avtagende.
Med n = 10 får vi 10 9 8 7 6 5 4 3 2 1. Det er 9 par med 10 først, dvs. (10,9), (10,8), . . , (10,1), så 8 par med
9 først, osv. Alle de 45 parene utgjør da inversjoner. Generelt blir det
n(n − 1)/2 stykker hvis tallene fra 1 til n er sortert avtagende.
Men hvor mange inversjoner er det i gjennomsnitt i en permutasjon av tallene fra 1 til n ?
Ytterpunktene er 0 og n(n − 1)/2. Det er mange tilfeller der et
gjennomsnitt ikke er midt mellom ytterpunktene, men her er det slik. Hvis vi tar en vilkårlig permutasjon, vil den ha
k inversjoner. I den omvendte permutasjonen vil alle ikke inversjoner bli inversjoner og omvendt. Det betyr
at den omvendte permutasjonen har n(n − 1)/2 − k
inversjoner og dermed n(n − 1)/4 som gjennomsnitt for de to.
Slik blir det for enhver permutasjon. Dermed blir gjennomsnittet over alle permutasjonene lik
n(n − 1)/4.
Observasjon 1.3.2 Antall inversjoner
n kan det være ingen inversjoner. Da er den sortert stigende.
Det kan være maksimalt n(n − 1)/2 stykker. Da er den
sortert avtagende. I gjennomsnitt er det n(n − 1)/4 inversjoner.
En anvendelse: Hvis en skal tippe resultatet i en konkurranse med mange deltagere, kan en si at den som
kommer «nærmest» det korrekte, har det beste tipset. Men hva er «nærmest»? Det kan f.eks. være
færrest inversjoner i tippingen. Mer om det i Avsnitt 1.3.12.
| 1. | Hvor mange inversjoner har premutasjonen 3 5 4 7 6 8 1 2 9 10 ? |
| 2. | Finn en permutasjon av tallene fra 1 til 10 med 22 inversjoner og en som har 23 stykker. |
![]() 1.3.3 Boblesortering
1.3.3 Boblesortering
Gitt at vi har en tabell a som inneholder en permutasjon av tallene fra 1 til n.
Den vil (hvis den ikke er sortert stigende) inneholde et antall
inversjoner.
I flg. metode sammenlignes to og to naboverdier og de bytter plass hvis de danner en inversjon.
Til slutt returneres antallet ombyttinger. Hvis vi tenker oss at tabellen står vertikalt, vil
store verdier «bobles» oppover (bobler som i en vannkjele som koker). Derav navnet.
Metoden bytt(), som inngår i koden, har vi laget tidligere.
public static int boble(int[] a) // legges i samleklassen Tabell { int antall = 0; // antall ombyttinger i tabellen for (int i = 1; i < a.length; i++) // starter med i = 1 { if (a[i - 1] > a[i]) // sammenligner to naboverdier { bytt(a, i - 1, i); // bytter om to naboverdier antall++; // teller opp ombyttingene } } return antall; // returnerer } Programkode 1.3.3 a)
Hvis Programkode 1.3.3 a) (og metoden bytt())
ligger i samleklassen Tabell, vil flg. kodebit kunne kjøres:
int[] a = {5, 9, 6, 10, 2, 7, 3, 8, 4, 1}; // en heltallstabell System.out.println(Arrays.toString(a)); // skriver ut tabellen int antInv = Tabell.inversjoner(a); //Programkode1.3.2 a) System.out.println("Inversjoner: " + antInv); // skriver ut int antOmb = Tabell.boble(a); // ombyttinger antInv = Tabell.inversjoner(a); //Programkode1.3.2 a) System.out.println(Arrays.toString(a)); // skriver ut tabellen System.out.print("Ombyttinger: " + antOmb + " "); // ombyttinger System.out.println("Inversjoner: " + antInv); // inversjoner // Utskrift: // [5, 9, 6, 10, 2, 7, 3, 8, 4, 1] // Inversjoner: 29 // [5, 6, 9, 2, 7, 3, 8, 4, 1, 10] // Ombyttinger: 7 Inversjoner: 22 Programkode 1.3.3 b)
Utskriften over viser at tabellen a i utgangspunktet
har 29 inversjoner. I metoden boble() blir det utført 7 ombyttinger og siden hver ombytting
fjerner en inversjon, vil tabellen etterpå ha 29 - 7 = 22 inversjoner. Tabellen a er fortsatt langt
fra å være sortert, men det går den rette veien. Vi ser også at den største verdien (dvs. 10) har kommet bakerst.
Slik vil det alltid bli. Hvis den største ikke hadde kommet bakerst, ville den hatt en nabo til høyre for seg som var
mindre. Men det er umulig. De to ville i så fall ha byttet plass i løpet av boble-prosessen.
I flg. kode starter vi med samme tabell (permutasjon)
som i Programkode 1.3.3 b). Men nå
kaller vi boble() flere ganger. Poenget er å få redusert antallet
inversjoner ytterligere:
int[] a = {5, 9, 6, 10, 2, 7, 3, 8, 4, 1}; for (int i = 1; i < a.length; i++) { int antall = Tabell.boble(a); // antall ombyttinger System.out.println(i + ". " + Arrays.toString(a) + " " + antall); } // Utskrift: 1. [5, 6, 9, 2, 7, 3, 8, 4, 1, 10] 7 2. [5, 6, 2, 7, 3, 8, 4, 1, 9, 10] 6 2. [5, 2, 6, 3, 7, 4, 1, 8, 9, 10] 4 4. [2, 5, 3, 6, 4, 1, 7, 8, 9, 10] 4 5. [2, 3, 5, 4, 1, 6, 7, 8, 9, 10] 3 6. [2, 3, 4, 1, 5, 6, 7, 8, 9, 10] 2 7. [2, 3, 1, 4, 5, 6, 7, 8, 9, 10] 1 8. [2, 1, 3, 4, 5, 6, 7, 8, 9, 10] 1 9. [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 1 Programkode 1.3.3 c)
Det å gå gjennom tabellen kalles en gjennomgang (eng: pass).
I koden over det det 9 stykker.
Utskriften viser at det startet med 7 ombyttinger, så 6, osv. Tilsammen 7 + 6 + 4 + 4 + 3 + 2 + 1 + 1 + 1
og det blir som forventet 29. Den siste utskriften viser at det er sortert. Denne teknikken kalles
boblesortering (eng: bubble sort).
Vi kunne ha kodet den slik:
public static void boblesortering(int[] a) { for (int i = 1; i < a.length; i++) boble(a); } Programkode 1.3.3 d)
Dette vil virke, men er unødvendig ineffektivt. F.eks. vil
boble() gå gjennom hele tabellen hver gang.
Men det er nødvendig kun første gang. Da kommer den største verdien bakerst. Neste gang kan vi stoppe én før. Det vil
føre til at den nest største verdien komme nest bakerst, osv. I flg. versjon gjøres sammenligningene direkte i koden og
kun bytt() brukes som hjelpemetode. Dette
kalles standardversjonen av boblesortering:
public static void boblesortering(int[] a) // hører til klassen Tabell { for (int n = a.length; n > 1; n--) // n reduseres med 1 hver gang { for (int i = 1; i < n; i++) // går fra 1 til n { if (a[i - 1] > a[i]) bytt(a, i - 1, i); // sammenligner/bytter } } } Programkode 1.3.3 e)
Algoritmeanalyse: La a inneholde en permutasjon av tallene fra 1 til n.
Vi må finne ut hvor mange sammenligninger av typen a[i - 1] > a[i] som
utføres og så hvor mange kall på bytt() (dvs. ombyttinger) det er.
I første gjennomgang blir det n − 1 sammenligninger. Så
reduseres n. Det betyr at i neste gjennomgang blir det n − 2 stykker, osv. til 1 i siste. Summen
blir (den aritmetiske rekken 1 + 2 + . . . + n − 1) lik n(n − 1)/2. Dette
er helt uavhengig av hva tabellen inneholder. Med andre er denne versjonen av boblesortering
av kvadratisk orden. I algoritmeanalyse skiller
vi normalt mellom hvilken orden en metode har i det verste tilfellet og i gjennomsnitt. Noen ganger ser vi også på
det beste tilfellet. Men her blir det kvadratisk orden i alle tilfellene siden det alltid blir n(n − 1)/2
sammenligninger.
Det utføres nøyaktig like mange ombyttinger som det er inversjoner. Det betyr at i det beste tilfellet (sortert stigende)
blir det ingen ombyttinger. I det verste tilfellet (sortert avtagende) blir det n(n − 1)/2
og i gjennomsnitt n(n − 1)/4 stykker.
Se Avsnitt 1.3.2.
Programkode 1.3.3 c) viser hva som skjer med permutasjonen
5, 9, 6, 10, 2, 7, 3, 8, 4, 1 når boble() kalles gjentatte ganger.
Det blir flest ombyttinger i første gjennomgang (7 stykker). Men hvor mange det blir i gjennomsnitt i hver gjennomgang?
Vi starter med den første. Hvis det er sortert stigende, blir det ingen ombyttinger.
I boble() blir en «stor» verdi, ved hjelp av
ombyttinger, flyttet mot høyre. Men hvis det så kommer en verdi som er enda større, blir det ingen ombytting.
Da er det isteden den som flyttes videre mot høyre. Med andre ord blir det ingen ombytting når det kommer en verdi som er
større enn verdiene foran (til venstre for den). I Avsnitt 1.1.6
fant vi at med n forskjellige verdier, vil i gjennomsnitt Hn − 1 av dem være
større enn de foran. Det maksimale antallet er n − 1. Trekker vi fra de tilfellene det
ikke blir ombyttinger, får vi n − Hn som gjennomsnitt. Med n = 10 blir det 7,07.
Det kan videre vises
at i gjennomgang nr. k der k går fra 1 til n − 1, blir det i
gjennomsnitt utført n + k (Hk − Hn − 1)
ombyttinger. Etter alle gjennomgangene vil alle inversjoner ha blitt fjernet. Med
n forskjellige verdier er det i gjennomsnitt
n(n − 1)/4 inversjoner. Dermed:
| Formel 1.3.3 a) | 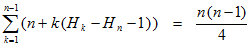 |
Mulige forbedringer: Tall etter siste ombytting i en gjennomgang vil ligge på rett plass og være sortert.
Ta 4, 3, 1, 2, 7, 5, 6, 8, 9, 10 som eksempel. Her vil først 4 og 3 bytte plass, så 4 og 1 og så 4 og 2. Deretter
7 og 5 og så 7 og 6. Men ingen etter det. Det gir dette: 3, 1, 2, 4, 5, 6, 7, 8, 9, 10. Dvs. sortert fra og med 4.
Dette oppdages i neste gjennomgang. Vi gjør flg. endringer i
Programkode 1.3.3 e):
public static void boblesortering(int[] a) { for (int n = a.length; n > 1; ) // n er intervallgrense { int byttindeks = 0; // hjelpevariabel for (int i = 1; i < n; i++) // går fra 1 til n { if (a[i - 1] > a[i]) // sammenligner { bytt(a, i - 1, i); // bytter byttindeks = i; // høyre indeks i ombyttingen } } n = byttindeks; // ny intervallgrense } } Programkode 1.3.3 f)
Ulempen med koden over er at det er introdusert en ekstra kostnad knyttet til en ombytting (dvs. en oppdatering av
byttindeks). Det kan hende den delvis oppveier fordelen med færre gjennomganger.
Se Oppgave 2. Men
en fordel er at hvis tabellen er sortert, vil algoritmen stoppe etter første gjennomgang. Dermed får den lineær orden
(orden n) i dette tilfellet. Men den har fortsatt kvadratisk orden (orden n²) både
i gjennomsnitt og i det verste tilfellet.
Hvor mange gjennomganger trengs i gjennomsnitt? La tabellen inneholde en permutasjon
av tallene fra 1 til n. Hvis den er sortert stigende, trengs ingen gjennomgang (bortsett fra den som avgjør
at den er sortert). Hvis den er sortert avtagende, blir det n − 1 gjennomganger. I gjennomsnitt er det mer
komplisert. Formelen a(k,n) =
k!kn-k (se [S & F])
gir antall som blir sortert etter maks k − 1 gjennomganger. Vi får f.eks.
a(1,10) = 1, a(2,10) = 512 og a(3,10) = 13122. Dermed 512 - 1 = 511 permutasjoner
der det trengs nøyaktig én gjennomgang. Videre 13122 - 512 = 12610 der det trengs nøyaktig to gjennomganger. Det er flest av
de som blir sortert etter nøyaktig 7 gjennomganger, dvs. 851 760 stykker.
F.eks. er 1, 2, 4, 5, 6, 7, 8, 9, 10, 3 en av dem. Sjekk det! Tabellen under viser hele fordelingen:
| 1 | 511 | 12610 | 85182 | 276696 | 558120 | 795600 | 851760 | 685440 | 362880 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Figur 1.3.3 b) : Fordeling av permutasjoner | |||||||||
Tallene over gir 6,5 som gjennomsnitt. Dvs. det trengs i gjennomsnitt 6,5 gjennomganger av en tabell med 10
forskjellige verdier for at den skal bli sortert vha. denne teknikken. For store n blir gjennomsnittet
tilnærmet lik n − √(Π·n/2).
Se [S & F].
Med n = 100 blir det 87,5. Men det er ikke så mye vi sparer siden gjennomgangene på slutten er langt mindre kostbare enn
i begynnelsen. Intervallet som som undersøkes blir kortere for hver gjennomgang. Vi kan bruke testkjøringer til å avgjøre om vi tjener på dette. Se
Oppgave 2.
Oppsummering - boblesortering:
Navn:I en «loddrett» tabell, vil ombyttinger føre til at store verdier flytter seg oppover og den største havner øverst. Navnetbobleer hentet fra det som skjer når vannet i en vannkjele koker. Da går det bobler oppover fra bunnen av kjelen.Effektivitet:Den «forbedrede» versjonen av boblesortering (Programkode1.3.3 f ) er (mhp. sammenligninger) av lineær orden (ordenn) i det beste (en sortert tabell) og av kvadratisk orden (ordenn²) i gjennomsnitt og i det verste tilfellet.Ombyttinger:Antallet vil variere fra 0 (en sortert tabell) tiln(n− 1)/2 (sortert motsatt vei). I gjennomsnitt blir detn(n− 1)/4 ombyttinger.Konklusjon:Av de mest kjente sorteringsmetodene erboblesorteringden som er minst effektiv. Den brukes normalt ikke. I hvert fall ikke på store tabeller.
| 1. | Sjekk at Programkode 1.3.3 f) virker.
Lag en serie permutasjoner (bruk randPerm)
av tallene fra 1 til 10. Skriv ut resultatet.
|
| 2. | Sammenlign Programkode 1.3.3 e)
og f). Kall dem boblesortering1 og boblesortering2.
Lag så store tilfeldige permutasjoner at den ene bruker noen sekunder. Ta en kopi før du sorterer. Hvor lang tid vil den andre bruke (på kopien).
|
| 3. | Lag en versjon der gjennomgangene går motsatt vei (fra høyre mot venstre). |
| 4. | Lag kode som generer innholdet i tabellen i Figur 1.3.3 b).
Både vha. formelen k!kn-k og ved å generere alle mulige
permutasjoner og så telle opp.
|
| 5. | I gjennomgang k (k = 1 til n − 1) i
Programkode 1.3.3 e)
blir det i gjennomsnitt utført
n + k (Hk − Hn − 1)
ombyttinger. Se Formel 1.3.3 a).
Med n = 10 og k = 1, blir det lik 7,07. La fortsatt
n være 10. Hva blir det for k = 2 og 3?
Lag kode som regner (og skriver) det ut for hver k. Summér alle verdiene og sjekk at summen blir lik
n(k − 1)/4.
|
![]() 1.3.4 Utvalgssortering
1.3.4 Utvalgssortering
Det er enkelt å finne den minste (eller den største) verdien i en tabell.
Utvalgssortering (eng: selection sort) går ut på å gjøre det gjentatte ganger.
Gitt flg. (usorterte) tabell:
| 15 | 8 | 21 | 16 | 5 | 19 | 7 | 23 | 10 | 14 | 3 | 11 | 6 | 17 | 4 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.4 a) : Gitt en (usortert) tabell. | ||||||||||||||
Første oppgave er å finne den minste verdien. Vi ser at den (tallet 3) ligger i posisjon 10. Den byttes med verdien i posisjon 0 slik at den minste verdien kommer først i tabellen:
| 3 | 8 | 21 | 16 | 5 | 19 | 7 | 23 | 10 | 14 | 15 | 11 | 6 | 17 | 4 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.4 b) : Den minste ligger først | ||||||||||||||
Vi gjør dette en gang til. Men nå finner vi den minste i resten av tabellen, dvs. i den delen av tabellen som starter i posisjon 1. Da får vi tallet 4 i posisjon 14. Den byttes med verdien i posisjon 1 slik at den nest minste verdien kommer nest først i tabellen:
| 3 | 4 | 21 | 16 | 5 | 19 | 7 | 23 | 10 | 14 | 15 | 11 | 6 | 17 | 8 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.4 c) : De to minste ligger på rett plass | ||||||||||||||
Da er det bare å fortsette. Den minste verdien fra og med posisjon 2 og utover er tallet 5 som har posisjon 4. En ombytting gir dette resultatet:
| 3 | 4 | 5 | 16 | 21 | 19 | 7 | 23 | 10 | 14 | 15 | 11 | 6 | 17 | 8 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.4 d) : De tre minste ligger på rett plass | ||||||||||||||
Tabellens første del (den «grå» delen) er sortert og resten (den «hvite» delen)
er usortert. For hver runde «velger» vi ut den minste i den «hvite» delen. Den byttes
med den første i den «hvite» delen. Det fortsetter til tabellen er sortert.
Navnet utvalgssortering kommer av
at vi forløpende «velger» den minste av de resterende. Vi kunne ha gjort det motsatte. Dvs. vi kunne
fortløpende ha valgt den største verdien og så plassert den bakerst. Se
Oppgave 2.
Vi kan kode utvalgssortering direkte eller med hjelpemetoder. I
Oppgave 1
i Avsnitt 1.2.1 ble du bedt om å lage en metode som finner posisjonen til minste
verdi i et tabellintervall. Bruker vi den, får vi flg. korte kode for utvalgssortering:
public static void utvalgssortering(int[] a) { for (int i = 0; i < a.length - 1; i++) bytt(a, i, min(a, i, a.length)); // to hjelpemetoder } Programkode 1.3.4 a)
I Oppgave 5 blir du bedt om å kode
utvalgssortering uten bruk av hjelpemetoder.
Programkode 1.3.4 a) sorterer stigende. Hvis vi ønsker
å sortere avtagende, kan vi lage en separat algoritme.
Se Oppgave 8. Men
det vil imidlertid være dumt om vi alltid måtte lage to versjoner av hver sorteringsmetode
- en stigende og en avtagende. Senere, når vi skal lage generiske sorteringsmetoder, vil vi lage kun
én versjon av hver metode. Ordningen kan da styres ved hjelp parameterverdier.
Men hvis en tabell allerede er sortert, er det lite arbeid som skal til
for å få den sortert omvendt vei. Vi kan «snu» tabellen, dvs. rotere den om midten
slik at første verdi kommer sist og siste verdi først, osv.
Programkode 1.3.1 a)
inneholder en slik metode. Hvis alle aktuelle metoder ligger i samleklassen Tabell,
vil flg. kode være kjørbar:
int[] a = {7,5,9,2,10,4,1,8,6,3}; // en usortert heltallstabell Tabell.utvalgssortering(a); // stigende sortering Tabell.snu(a); // tabellen snus Tabell.skriv(a); // 10 9 8 7 6 5 4 3 2 1 Programkode 1.3.4 b)
Effektivitet: Hvor effektiv er utvalgssortering? La n være antall verdier.
Det trengs n − 1 sammenligninger for å finne den minste verdien. Deretter leter vi etter den
minste blant resten. Til det trengs n − 2 sammenligninger. Osv.
Til sammen blir det:
n – 1 + n – 2 + · · · · + 3 + 2 + 1 = n(n – 1)/2
Resultatet n(n – 1)/2 er summen av en aritmetisk rekke. Hvis f.eks. n = 1000, blir det totalt 499.500 sammenligninger. Antallet kan også skrives som n2/2 – n/2, dvs. et kvadratisk uttrykk i n. Algoritmen er derfor av kvadratisk orden eller av orden n2. Det betyr at hvis vi dobler antall verdier, vil antall sammenligninger bli fire ganger så stort. Legg merke til at utvalgssortering er av kvadratisk orden i alle tilfeller - også om tabellen allerede er sortert.
Utvalgssortering er ineffektiv – i hvert fall hvis det
er mange verdier. Se Oppgave 4.
En fordel er imidlertid at algoritmen har en klar idé og har enkel kode.
Vi forstår umiddelbart at den gir korrekt resultat. Den har også få
ombyttinger. Dette er faktisk den sorteringsmetoden som har færrest ombyttinger, dvs.
n − 1 stykker i alle tilfeller. Dette er gunstig sammenlignet f.eks. med
boblesortering som i gjennomsnitt har
n(n − 1)/4 ombyttinger.
Oppsummering - utvalgssortering:
Navn:Algoritmen kallesutvalgssorteringfordi det fortløpende «velges ut» en verdi som så blir plassert på rett sortert plass. I den vanlige versjonen av utvalgssortering blir fortløpende den minste blant de usorterte «valgt ut» og så plassert først blant dem.Effektivitet:Det trengsn − 1sammenligninger for å finne den minste, sån − 2stykker for å finne den nest minste (den minste av de øvrige), osv. Til sammen blir detn(n− 1)/2 =n2/2 − n/2sammenligninger og det uansett fordelingen av verdiene. Det betyr at algoritmen har kvadratisk orden i alle tilfeller (verst, gjennomsnittlig og best).Ombyttinger:Det gjøres én ombytting i hver iterasjon og dermedn − 1til sammen. Dette kan reduseres noe. SeOppgave 11.Konklusjon:Utvalgssortering er som alle sorteringsalgoritmer av kvadratisk orden, ikke egnet til å sortere store tabeller. Den er imidlertid bedre ennboblesortering. SeOppgave 4. I noen situasjoner kan det være ekstra kostbart å bytte om verdier (gjelder ikke i Java). I slike tilfeller kan denne algoritmen brukes for tabeller av moderat størrelse. Dette er den algoritmen som har færrest ombyttinger.
| 1. | I Figur 1.3.4 d) er det gjort tre iterasjoner.
Hva blir det etter i) 5 og ii) 7
iterasjoner. |
| 2. | Start med tabellen i Figur 1.3.4 a). Utfør
tre iterasjoner der du isteden finner den største av de usorterte og bytter om slik at den kommer bakerst
av de usorterte.
|
| 3. | Legg metoden i
Programkode 1.3.4 a) inn i
samleklassen Tabell. Pass på at du da allerede har metodene bytt()
og min() der. Se også
Oppgave 1
i Avsnitt 1.2.1. Sjekk så at
Programkode 1.3.4 b)
virker.
|
| 4. | Kjør programbiten fra Oppgave 2
i Avsnitt 1.3.3, men bruk isteden utvalgssortering. Er den bedre enn boblesortering?
|
| 5. | utvalgssortering i
Programkode 1.3.4 a) bruker
to hjelpemetoder. Det er mest vanlig å kode den uten hjelpemetoder. Søk
på internett. Bruk «selection sort» som søkeord.
Lag så din egen versjon (uten hjelpemetoder)!
Hvor lang tid bruker den for en tilfeldig tabell med 100000 verdier? Er den bedre enn den fra
Programkode 1.3.4 a)?
|
| 6. | I løsningsforslaget til Oppgave 5 over gjøres en «ekte» ombytting ved
hjelp av flg. kode: int temp = a[i]; a[i] = a[m]; a[m] = temp;
Det er slik hjelpemetoden bytt() er kodet.
Her er det imidlertid mulig å forenkle noe siden vi vet at
a[m] og minverdi er like.
Gjør de endringene som trengs. Hvor mange operasjoner sparer du inn? |
| 7. | Lag en versjon av utvalgssortering
der den omvendte idéen brukes. Dvs. størst legges bakerst, nest størst nest bakerst, osv. |
| 8. | Lag en versjon av utvalgssortering som sorterer avtagende. |
| 9. | Lag metoden public static void utvalgssortering(int[] a, int fra, int til).
Den skal sortere intervallet a[fra:til>. Pass på at du tester lovligheten til
intervallet! |
| 10. | En sorteringsalgoritme kalles stabil hvis like verdier
har samme innbyrdes rekkefølge etter sorteringen som de hadde før.
Er utvalgssortering stabil? |
| 11. | Ta utgangspunkt i den versjonen av utvalgssortering som står i
Programkode 1.3.4 a).
Men gjør ingen ombytting
i det tilfellet samme verdi vil bli byttet med seg selv. Det vil påføre algoritmen en ekstra kostnad
siden det må gjøres en sammenligning hver gang, men spare arbeidet med unødvendige ombyttinger.
Finn ut, ved å bruke tilfeldige permutsajoner, hvor mange
ganger det skjer at en verdi ville ha blitt byttet med seg selv. Spesielt hvis tabellen allerede
er sortert, byttes en verdi med seg i hver iterasjon.
Kanskje du klarer å finne en formel for det gjennomsnittlige antall ganger en verdi vil bli byttet
med seg selv? Vil det lønne seg å ha denne ekstra testen? |
![]() 1.3.5 Søking
1.3.5 Søking
Usortert tabell Det å finne en verdi i en samling verdier er en av de mest grunnleggende oppgavene
i databehandling. Her skal vi se på det tilfellet at verdiene ligger i en tabell.
Hvis tabellen er usortert, er det ingen annen måte å gjøre det på enn å se på én og
én verdi. Da vil vi, hvis tabellen inneholder den vi leter etter, før eller senere finne den.
Hvis vi har sett på alle verdiene uten å finne den, kan vi konkludere med at den ikke er der.
Flg. metode returnerer posisjonen til søkeverdien hvis den ligger i tabellen, og returnerer –1 hvis den ikke er der. Hvis det er flere forekomster av søkeverdien, returneres posisjonen til den første av dem (fra venstre). Tabellen og søkeverdien inngår som parametere:
public static int usortertsøk(int[] a, int verdi) // tabell og søkeverdi { for (int i = 0; i < a.length; i++) // går gjennom tabellen if (verdi == a[i]) return i; // verdi funnet - har indeks i return -1; // verdi ikke funnet } Programkode 1.3.5 a)
Koden kan optimaliseres. Sammenligningen i < a.length i for-løkken kan
(som vi har sett tidligere) fjernes hvis vi bruker
søkeverdien som vaktpost. Det vil nok kun gi marginal effekt, men kan være en morsom øvelse i kodeteknikk.
Se Oppgave 1.
Det finnes ingen mer effektiv teknikk enn den i Programkode 1.3.5 a)
for å søke i en usortert tabell. La n være tabellengden. Hvis verdien
ikke er der, vil
if (verdi == a[i]) utføres n ganger.
Men hva hvis den er der? Vi antar at alle verdiene er forskjellige og
har samme sannsynlighet for å bli etterspurt.
Hvis verdi ligger først, trengs én
sammenligning, to hvis den ligger nest først, osv. Tilsammen
1 + 2 + · · · + n = n(n + 1)/2 stykker og dermed
blir det n(n + 1)/2n = (n + 1)/2 som gjennomsnitt. Søkemetoden er derfor
av orden n.
Sortert tabell
Hvis tabellen er sortert (f.eks. stigende), kan vi forbedre søkealgoritmen. Den mest
optimale teknikken kalles binærsøk. Den ser vi nærmere på i
Avsnitt 1.3.6. Her skal vi isteden
innføre en liten forbedring av idéen i
Programkode 1.3.5 a) over.
Det gir oss muligheten til å innføre begrepet innsettingspunkt.
Vi kan slik som i Programkde 1.3.5 a),
se på én og én tabellverdi og returnere
posisjonen så fort vi finner den vi leter etter. Hvis ikke, kan vi, siden tabellen er sortert, avbryte
letingen så fort vi kommer til en verdi som er for stor. Ta som eksempel
at vi leter etter 31 i flg. tabell:
| 3 | 8 | 10 | 12 | 14 | 16 | 21 | 24 | 27 | 30 | 32 | 33 | 34 | 37 | 40 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.5 a) : Et sortert tabell med 15 verdier | ||||||||||||||
Her stopper vi på 32. Vi kunne nå returnere –1 som et signal
om at vi ikke fant 31. Men her er det mulig å slå «to fluer i en smekk».
En negativ returverdi kan signalisere at verdien ikke er der. Men det vil også
være fordelaktig å kunne rapportere hvilken posisjon/indeks verdien
ville ha hatt dersom den hadde ligget der, dvs. verdiens
innsettingspunkt. Det er der den måtte ha blitt satt inn
for å få bevart sorteringen. Her er det posisjon eller indeks 10.
Definisjon 1.3.5 - Innsettingspunkt En verdi som ikke ligger i
en (stigende) sortert tabell, ville hvis den hadde ligget der, hatt
en bestemt posisjon p. Denne posisjonen kalles verdiens
innsettingspunkt (eng: insertion point).
Gitt en verdi som ikke er i tabellen. Hvis den er mindre enn den minste,
dvs. mindre enn den som ligger lengst til venstre, blir dens
innsettingspunktet p lik 0. Dermed kan vi ikke
bruke –p som returverdi siden –0 og 0 er det samme. Returverdien skal
alltid være negativ for verdier som ikke ligger i
tabellen. Vi returnerer isteden –(p + 1). Den blir
alltid negativ (også når p er 0). La videre
k = –(p + 1). Da vil
p = –(k + 1). Med andre ord kan vi, hvis søkeverdien ikke ligger i
tabellen, beregne innsettingspunktet ved hjelp av returverdien.
Flg. metode, som vi kaller lineærsøk fordi vi ser på én og én tabellverdi,
gjør som beskrevet over. Her vil tabellens siste (og dermed største) verdi fungere som
en vaktpost. En verdi som er større enn den, vil ha p = a.length som
innsettingspunkt. For alle andre søkeverdier vil den bli en stoppverdi.
Legg metoden i samleklassen Tabell.
public static int lineærsøk(int[] a, int verdi) // legges i class Tabell { if (a.length == 0 || verdi > a[a.length-1]) return -(a.length + 1); // verdi er større enn den største int i = 0; for( ; a[i] < verdi; i++); // siste verdi er vaktpost return verdi == a[i] ? i : -(i + 1); // sjekker innholdet i a[i] } Programkode 1.3.5 b)
Flg. eksempel viser hvordan metoden lineærsøk kan brukes:
int[] a = {3,8,10,12,14,16,21,24,27,30,32,33,34,37,40}; // Figur 1.3.5 a)
System.out.println(Tabell.lineærsøk(a,32)); // utskrift: 10
System.out.println(Tabell.lineærsøk(a,31)); // utskrift: -11
Programkode 1.3.5 c)
I Programkode 1.3.5 c) returnerer metoden 10 når det søkes etter
32. Det stemmer siden 32 har indeks/posisjon 10. Returverdien
blir –11 når det søkes etter 31. En negativ returverdi forteller at den
søkte verdien ikke ligger i tabellen. Tallet 31 hører hjemme mellom 30 og 32.
Innsettingspunktet blir derfor lik posisjonen til 32, dvs. 10. Men vi kan beregne
oss frem til det ved hjelp av returverdien. Generelt gjelder at hvis k er
en negativ returverdi, blir innsettingspunktet lik –(k + 1). I eksemplet:
–(–11 + 1) = 10. Se også Oppgave 2.
Med tanke på effektivitet er lineærsøk
litt bedre enn usortertsøk for verdier
som ikke ligger i tabellen. Den går i gjennomsnitt kun halvveis gjennom tabellen for å komme til første
verdi som er for stor. Det er andre teknikker som er vesentlig mer effektive, men
lineærsøk er likevel viktig. Den er god nok for små tabeller. Men det er selve
idéen som er viktig siden den også vil virke for datastrukturer som kan «leses» kun én vei (f.eks.
en pekerkjede).
Det er også mulig å forbedre lineærsøk,
f.eks. ved å gjøre en serie «hopp» under søkingen. La
tabellen a inneholde 100 verdier. Da kan vi f.eks. se på hver 10-ende verdi. Når
vi passerer stedet der søkeverdien hører hjemme, vet vi at den vil måtte befinne seg blant de 10 siste
vi hoppet over. Dermed kan vi lete etter søkeverdien blant dem.
Bruker vi en «hopplengde» lik kvadratroten av tabellens lengde, vil algoritmen
bli av orden kvadratrot. Da kalles algoritmen for kvadratrotsøk.
Se Oppgave 5.
Metoden lineærsøk Programkode 1.3.5 b)
er lite fleksibel. Det burde være mulig å kunne søke i et intervall og ikke kun i en hel tabell. Den
gitte metoden blir da et spesialtilfelle av public static int lineærsøk(int[] a, int fra, int til, int verdi).
Se Oppgave 4.
| 1. | Bruk en «vaktpost» (den søkte verdien) i
Programkode 1.3.5 a). Ta vare på den
siste verdien og legg isteden «vaktposten» der.
Pass på spesialtilfellet at det er den siste verdien vi søker etter.
|
| 2. | Sjekk at metoden lineærsøk
gir korrekt returverdi hvis det søkes etter en verdi som er mindre enn den minste i tabellen.
Hva skjer hvis tabellen er tom, dvs. a.length = 0? La a
være tabellen i Figur 1.3.5 a).
Hva blir returverdiene fra lineærsøk hvis vi søker etter 2, 15, 16, 40 og 41?
|
| 3. | Hvis verdi forekommer flere ganger i tabellen a,
vil posisjonen til den første av dem (fra venstre) bli returnert. Lag en versjon av
lineærsøk der det er posisjonen til den siste av dem som returneres. Gjør
det f.eks. ved å lete motsatt vei, dvs. fra høyre mot venstre. |
| 4. | Lag metoden public static int lineærsøk(int[] a, int fra, int til, int verdi).
Den skal søke i intervallet a[fra:til>. Sjekk først at intervallet er lovlig.
|
| 5. | I lineærsøk
sammenlignes én og én tabellverdi med verdi. Algoritmen stopper på
verdi hvis den finnes og på den første som er større hvis den ikke finnes.
Dette kan forbedres hvis vi «hopper» bortover i tabellen.
La oss si at tabellen a har 100 verdier. Da kan vi f.eks. se på hver 10-ende verdi
inntil vi har kommet langt nok (eller eventuelt havnet utenfor tabellen). Den søkte verdien
må da, hvis den er i tabellen, ligge blant de 10 siste verdiene vi hoppet over.
|
a) I metoden public static int lineærsøk(int[] a, int k, int verdi)
skal a og verdi være som i vanlig lineærsøk.
Parameter k (et positivt heltall) er «hopplengden». I beskrivelsen over var
k lik 10. Metoden skal returnere nøyaktig det samme som vanlig lineærsøk, også i
det tilfellet den søkte verdien ikke finnes. | |
b) Test metoden fra a) med ulike verdier på k (k = 1
gir vanlig lineærsøk). | |
c) Hvis «hopplengden» k settes lik heltallsdelen av kvadratroten til tabellens lengde,
får vi den beste utnyttelsen av metodens idé. Hvilken orden vil metoden da få? Bruk det til å lage
metoden public static int kvadratrotsøk(int[] a, int verdi).
| |
| 6. | Hvis vi ikke vet nøyaktig hvilken verdi vi søker etter, men kun vet at den befinner seg mellom
fraverdi og tilverdi, så er det aktuelt å få
tak i alle disse verdiene, dvs. alle verdier fra tabellen som et større enn eller lik fraverdi
og som er mindre enn tilverdi. Dette kalles et intervallsøk siden vi søker etter
de som befinner seg innenfor et intervall. Lag metoden
public static int[] lineærIntervallsøk (int[] a, int fraverdi, int tilverdi). Den skal gjøre som
beskrevet over og returnere en tabell som inneholder de aktuelle verdiene og eventuelt en tom tabell hvis det ikke
finnes noen slike verdier. Her er et eksempel på hvordan den kan brukes:
int[] a = {3,8,10,12,14,16,21,24,27,30,32,33,34,37,40}; int[] b = Tabell.lineærIntervallsøk(a, 10, 20); System.out.println(Arrays.toString(b)); // [10, 12, 14, 16] |
 |
| Keiser Augustus |
splitt og hersk (eng: divide
and conquer). Det har romersk opprinnelse og på latin: divide et
impera. Det går ut på å gjøre motstanderne innbyrdes uenige for så
å overvinne dem enkeltvis. Den idéen kan vi bruke. Hvis et problem skal løses, kan det ofte lønne
seg å dele problemet i to eller flere mindre problemer, løse hver av dem for seg
og så sette dette sammen til en løsning for hele problemet. Idéen er at det er enklere
å løse en del av et problem enn å løse hele problemet.
Vi prøver flg. idé: Det går raskere å søke i halvparten
enn i hele tabellen. Vi kan hoppe inn midt i en tabell.
Hvis verdien ikke er der, vil sorteringen avgjøre på hvilken side vi skal lete
videre. Da får vi halvert søkeområdet. Idéen kalles binærsøk. Den omtales
ofte som en splitt og hersk-idé, men et bedre navn er forminsk og
hersk (eng: decrease and conquer).
Vi skal generelt søke etter en verdi i et lukket intervall a[v:h] der v står for
venstre og h for høyre endepunkt. I tillegg har vi midten
m = (v + h)/2. Vi kan tenke på én av to måter:
- Verdien ligger enten på midten eller på
en av sidene
a[v:m–1]ellera[m+1:h]. Søkeområdet blir dermed delt i tre - ett element og to lukkede delintervaller. - Alternativt kan vi nøye oss med å dele søkeområdet i to deler. Dvs. vi avgjør
om den søkte verdien ligger i
a[v:m]eller ia[m+1:h].
Vi starter med 1. måte. Flg. tabellintervall a[v:h] med 15 verdier er gitt.
Anta at vi skal finne verdien 30.
Fra starten av er hele søkeområdet markert med grå bakgrunn:
| 3 | 8 | 10 | 14 | 14 | 16 | 21 | 24 | 27 | 30 | 32 | 33 | 34 | 37 | 40 |
| v | m | h | ||||||||||||
| Figur 1.3.6 a) : Et sortert tabellintervall med 15 verdier | ||||||||||||||
Midten er gitt ved m = (v + h)/2.
Figuren viser at a[m] er lik 24. Vår søkeverdi 30 er større.
Den må da, hvis den er der, ligge til høyre for m.
Vi setter v = m + 1 og fortsetter:
| 3 | 8 | 10 | 14 | 14 | 16 | 21 | 24 | 27 | 30 | 32 | 33 | 34 | 37 | 40 |
| v | m | h | ||||||||||||
| Figur 1.3.6 b) : Søkeområdet (den grå delen) er halvert | ||||||||||||||
På nytt er m = (v + h)/2. Søkeverdien 30 er heller ikke nå lik
a[m] (dvs. 33), men derimot mindre. Dermed må den ligge til
venstre for m. Nå settes h = m – 1:
| 3 | 8 | 10 | 14 | 14 | 16 | 21 | 24 | 27 | 30 | 32 | 33 | 34 | 37 | 40 |
| v | m | h | ||||||||||||
| Figur 1.3.6 c) : Søkeverdien 30 ligger midt i søkeområdet | ||||||||||||||
Nå ser vi at søkeverdien 30 er lik a[m]. Vi kan avslutte søkingen og returnere posisjonen.
Vi får flg. algoritme:
- Start med tabellintervallet
a[v:h]og søkeverdienverdi. - Finn midten
m = (v + h)/2. - Hvis
verdi == a[m], er vi ferdige! - Hvis
verdi > a[m], settesv = m + 1og hvis ikke, settesh = m – 1. - Hvis
v <= h, gå til 2. Hvisv > h, era[v:h]tom ogverdier ikke i tabellen.
Med v > h blir intervallet a[v:h] tomt. Det betyr at verdi
ikke er i tabellen. Men da blir v innsettingspunktet
(se Definisjon 1.3.5) til verdi. Flg. metode har
fra - til parametere siden det er det normale. Men inne i metoden gjøres det om til v
og h:
public static int binærsøk(int[] a, int fra, int til, int verdi) { Tabell.fratilKontroll(a.length,fra,til); // se Programkode 1.2.3 a) int v = fra, h = til - 1; // v og h er intervallets endepunkter while (v <= h) // fortsetter så lenge som a[v:h] ikke er tom { int m = (v + h)/2; // heltallsdivisjon - finner midten int midtverdi = a[m]; // hjelpevariabel for midtverdien if (verdi == midtverdi) return m; // funnet else if (verdi > midtverdi) v = m + 1; // verdi i a[m+1:h] else h = m - 1; // verdi i a[v:m-1] } return -(v + 1); // ikke funnet, v er relativt innsettingspunkt } public static int binærsøk(int[] a, int verdi) // søker i hele a { return binærsøk(a,0,a.length,verdi); // bruker metoden over } Programkode 1.3.6 a)
Obs. Hvis verdi ligger utenfor intervallet a[v:h], vil
metoden gi et innsettingspunkt relativt til intervallet a[v:h].
Se Oppgave 2.
Inne i while-løkken i Programkode 1.3.6 a) har vi først:
verdi == midtverdi. Er det lurest? Kunne vi isteden starte med:
verdi > midtverdi ? Når flere tester skal utføres,
er det ofte at rekkefølgen har betydning:
Viktig programmeringsregel: Hvis man i en valgsituasjon har mer enn
to utfall, skal man alltid teste i rekkefølge etter synkende sannsynlighet.
Dvs. først teste på det som har størst sannsynlighet for å inntreffe, dernest
det som har nest størst sannsynlighet, osv.
I mange situasjoner med flere utfall, kan det være vanskelig å vite hvilken
sannsynlighet de forskjellige utfallene har. I while-løkken i
Programkode 1.3.6 a)
er det imidlertid enkelt.
Det er tre muligheter eller utfall: 1) den søkte verdien ligger på midten,
2) den ligger til høyre for midten eller 3) den ligger til venstre for midten. Det
er bare én verdi på midten, men normalt mange på hver side.
Det betyr at det er langt mer sannsynlig at den søkte verdien ligger på en av
sidene enn at den ligger på midten. Hvis a[v:h] inneholder
et odde antall verdier,
vil høyre og venstre side av midten ha nøyaktig like mange verdier. Men hvis
a[v:h] har et like antall verdier, vil det til høyre for
midten m = (v + h)/2 være én mer enn til venstre.
Vi burde derfor få en mer effektiv implementasjon av binærsøk hvis vi endrer på
rekkefølgen av sammenligningene. Endringene i forhold til
Programkode 1.3.6 a)
er med uthevet rødt:
// 2. versjon av binærsøk - returverdier som for Programkode 1.3.6 a) public static int binærsøk(int[] a, int fra, int til, int verdi) { Tabell.fratilKontroll(a.length,fra,til); // se Programkode 1.2.3 a) int v = fra, h = til - 1; // v og h er intervallets endepunkter while (v <= h) // fortsetter så lenge som a[v:h] ikke er tom { int m = (v + h)/2; // heltallsdivisjon - finner midten int midtverdi = a[m]; // hjelpevariabel for midtverdien if (verdi > midtverdi) v = m + 1; // verdi i a[m+1:h] else if (verdi < midtverdi) h = m - 1; // verdi i a[v:m-1] else return m; // funnet } return -(v + 1); // ikke funnet, v er relativt innsettingspunkt } Programkode 1.3.6 b)
Sammenligningene i while-løkken i Programkode 1.3.6 a)
starter med verdi == midtverdi. Men det vil sjelden gi sann. Det er
langt mer sannynlig at verdi ligger på én av sidene.
Det betyr at det nesten alltid må utføres enda en sammenligning. Dvs. i gjennomsnitt
ca. 2 av dem i hver iterasjon.
I Programkode 1.3.6 b) starter
det med verdi > midtverdi. Det er sant ca. annenhver gang.
Dermed blir det i gjennomsnitt omtrent 1,5 sammenligninger i hver iterasjon.
En forbedring på 25 prosent! Vi ser nærmere på dette i Avsnitt 1.3.7.
Den tredje versjonen av binærsøk tar utgangspunkt i
alternativ 2.
Søkeområdet deles kun i de to delene a[v:m] og a[m+1:h].
Dermed er det nok å utføre én sammenligning i hver runde. Det må imidlertid
sjekkes helt til slutt om den verdien som algoritmen stopper på, er den søkte
verdien eller ikke. Koden blir slik:
// 3. versjon av binærsøk - returverdier som for Programkode 1.3.6 a) public static int binærsøk(int[] a, int fra, int til, int verdi) { Tabell.fratilKontroll(a.length,fra,til); // se Programkode 1.2.3 a) int v = fra, h = til - 1; // v og h er intervallets endepunkter while (v < h) // obs. må ha v < h her og ikke v <= h { int m = (v + h)/2; // heltallsdivisjon - finner midten if (verdi > a[m]) v = m + 1; // verdi må ligge i a[m+1:h] else h = m; // verdi må ligge i a[v:m] } if (h < v || verdi < a[v]) return -(v + 1); // ikke funnet else if (verdi == a[v]) return v; // funnet else return -(v + 2); // ikke funnet } Programkode 1.3.6 c)
Denne 3. versjonen av binærsøk har, i tillegg til å være litt mer effektiv enn de to andre, også
en fordel når tabellintervallet har like verdier. Anta at verdi forekommer to eller flere
ganger. Da vil vi ikke kunne vite hvem av dem som versjon 1 (eller versjon 2) finner.
Men med 3. versjon av binærsøk er det annerledes. Gitt flg. tabell:
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 19 | 19 | 19 | 22 | 23 | 25 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.6 d) : Et sortert intervall der verdien 19 forekommer fire ganger | ||||||||||||||
Vi skal finne 19. While-løkken i
Programkode 1.3.6 c)
starter med intervallet a[0:14]. Vi får m = (0 + 14)/2 = 7 og a[7] = 17.
Dermed v = m + 1 = 8 siden 19 er større enn 17.
Nytt søkeområde blir a[8:14]:
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 19 | 19 | 19 | 22 | 23 | 25 |
| 8 | 11 | 14 | ||||||||||||
| Figur 1.3.6 e) : Søkeområdet (grå bakgrunn) har blitt halvert | ||||||||||||||
Midten i søkeområdet (grå bakgrunn) er nå lik (8 + 14)/2 = 11 og a[11] = 19.
Men 19 er ikke større enn 19. Dermed
settes h = 11. Nytt søkeområde blir a[8:11]:
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 19 | 19 | 19 | 22 | 23 | 25 |
| 8 | 9 | 11 | ||||||||||||
| Figur 1.3.6 f) : Søkeområdet (grå bakgrunn) har blitt halvert igjen | ||||||||||||||
Nå består søkeområdet av de fire forekomstene av 19, men algoritmen fortsetter likevel inntil søkeområdet
består av kun én verdi, dvs. til v er lik h. Først blir området lik
a[8:9] siden midten er (8 + 11)/2 = 9. Til slutt blir søkeområdet lik a[8:8]:
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 19 | 19 | 19 | 22 | 23 | 25 |
| 8 | 9 | |||||||||||||
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 19 | 19 | 19 | 22 | 23 | 25 |
| 8 | ||||||||||||||
| Figur 1.3.6 g) : while-løkken stppper når v er lik h | ||||||||||||||
Vi ser at v (her = 8) stopper på den første av de fire forekomstene av 19.
Det er ikke tilfeldig! Det er kun setningen if (verdi > a[m]) v = m + 1;
som «flytter» på
v. Det betyr at når while-løkken stopper, er enten v uforandret eller så er verdien
rett til venstre for v mindre enn verdi. Dermed må a[v]
inneholde første forekomst fra venstre av verdi.
Hvis a ikke inneholder søkeverdien, vil v (med ett unntak)
stoppe på innsettingspunktet
(se Definisjon 1.3.5).
Med en søkeverdi som er større enn alle, vil v stoppe på
siste indeks. Men innsettingspunktet er én videre til høyre. Eksempel: Vi skal finne 26
i Figur 1.3.6 d).
Det gir flg. sekvens av intervaller: a[0:14], a[8:14],
a[12:14] og a[14:14].
Men det er 15 som er innsettingspunkt. Derfor må metoden returnere
–(v + 2) i dette tilfellet.
Konklusjon: Det finnes mange søkealgoritmer for sorterte tabeller. En kan, ved å gjøre noen forutsetninger, finne formler for tilnærmet gjennomsnittlig antall sammenligninger. F.eks. at alle verdiene er forskjellige. Det gir oss algoritmenes orden:
| Søkealgoritme | Det gjennomsnittlige antallet sammenligninger | |||||
| Navn | Formel | n = 10 | n = 100 | n = 10.000 | n = 1.000.000 | Orden |
| Lineærsøk | (n + 1)/2 + 2 | 7,5 | 52,5 | ≈ 5 000 | ≈ 500 000 | n |
| Kvadratrotsøk | √n + 2 | 5,2 | 12 | 102 | 1002 | √n |
| Binærsøk, 1. versjon | 2 · log2(n+1) - 3 | 4,8 | 10,3 | 23,6 | 37 | log2(n) |
| Binærsøk, 2. versjon | 1,5 · log2(n+1) - 1 | 4,8 | 9,0 | 18,9 | 29 | log2(n) |
| Binærsøk, 3. versjon | log2(n) + 1 | 4,4 | 7,7 | 14,3 | 21 | log2(n) |
| Tabell 1.3.6 : Formler for gjennomsnittlig antall sammenligninger i søkealgoritmer. Verdiene for n = 10 er regnet ut eksakt, uten bruk av tilnærmingsformlene. |
||||||
|---|---|---|---|---|---|---|
Det liten forskjell når det er få verdier.
Lineærsøk ser litt dårligere ut for n = 10, men er
minst like god fordi den har færre omkostninger
knyttet til hver sammenligning. Men når n blir stor,
ser vi at binærsøk er overlegent best.
Alle de tre binærsøk-versjonene er svært effektive. En ekstra fordel med 3. versjon er
at hvis søkeverdien forekommer flere ganger, vil den alltid returnere
indeksen til den første av dem fra venstre. Det kan være en nyttig.
Derfor er det 3. versjon vi kommer til å bruke senerer (den legges i samleklassen Tabell).
De som har laget klassebiblioteket java.util har valgt 2. versjon. Se kildekoden til
int binarySearch(int[] a, int key) i
i klassen Arrays.
| 1. | Lag kode som sjekker at alle de tre versjonene av binærsøk gir rett
resultat. |
| 2. | Hvis verdi ikke er i a[v:h], vil binærsøk
gi innsettingspunktet relativt til [v:h]. Men det behøver ikke
være korrekt for tabellen som helhet. Bruk tabellen i
Figur 1.3.6 d).
Hva får vi som returverdi når 1. versjon
kalles med fra = 0,
til = 10 og verdi = 26?
|
| 3. | Gitt at søkeverdien har duplikater. Bruker vi 1. eller 2. versjon
av binærsøk, vet vi ikke hvem av dem som den returnerte indeksen
hører til. Gitt verdiene: 1, 3, 4, 4, 5, 7, 7, 7, 7, 8, 9, 10, 10, 12, 15, 15, 15. Bruk
1. versjon. Søk etter i) 4, ii) 7, iii) 10 og iv) 15.
Hvilken av verdiene hører den returnerte indeksen til? Obs. Det er det samme om det er 1. eller
2. versjon. De gir alltid de samme returverdi. |
| 4. | 3. versjon av binærsøk returnerer alltid indeksen til den første av
dem hvis søkeverdien det søkes forekommer flere ganger. Sjekk at det
stemmer for tallene i Oppgave 3. |
| 5. | Indeks m = (v + h)/2 gir korrekt midtpunkt blir når intervallet har et odde antall verdier.
Er det et partall, vil m bli posisjonen rett til venstre for den egentlige midten. La
isteden m = (v + h + 1)/2. Vis at m fortsatt er det korrekte midtpunktet for
et odde antall verdier, men er posisjonen rett til høyre for den egentlige midten når antallet
er et partall. |
| 6. | Lag en 4. versjon av binærsøk. Den skal som 3. versjon dele
intervallet i to deler i hver runde, men den skal returnere posisjonen til den siste av dem
hvis verdien det søkes etter forekommer flere ganger. Hint: Oppgave 5 kan være til hjelp. |
| 7. | Se Oppgave 6 i
Avsnitt 1.3.5. Lag en metode
med samme parameterliste og som gjør det samme, men bruk binærsøk-teknikk.
Kall den nå binærIntervallsøk.
|
![]() 1.3.7 Matematisk analyse av binærsøk
1.3.7 Matematisk analyse av binærsøk
Tabell 1.3.6
har formler for gjennomsnittlig antall sammenligninger i de tre versjonene av binærsøk. Vi
kan finne dem ved hjelp av beslutningstrær (eng: decision tree). Gitt flg. tabell:
| 2 | 5 | 6 | 9 | 10 | 12 | 15 | 17 | 19 | 22 | 25 | 30 | 31 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 1.3.7 a) : En sortert tabell med 13 verdier | ||||||||||||
Vi ser på 1. versjon
av binærsøk. I Figur 1.3.7 a) over vil
v = 0 og h = 12. I while-løkken settes m = (v + h)/2 =
(0 + 12)/2 = 6 og midtverdien a[6] = 15. Hvis den er lik søkeverdien,
avslutter vi etter kun én sammenligning. Hvis ikke, avgjør vi hvilken side av midten vi skal inn på.
Til det trengs én sammenligning til. I neste runde går vi inn på midten av en av sidene, dvs. til
m = (0 + 5)/2 = 2 eller m = (7 + 12)/2 = 9 med tilhørende
verdier lik 6 eller 22. Hvis det er en av disse to vi søker etter, kan vi avslutte
etter å ha gjort tilsammen 3 sammenligninger.
Hvis ikke må vi halvere igjen og kommer til m = 0, 4, 7 eller 11. Osv.
beslutningstre med like mange noder som tabellen
har verdier. Midtverdien a[6] = 15 legges i rotnoden, midtverdiene på hver side
(a[2] = 6 og a[9] = 22) legges i de to nodene
på nivået under, osv.
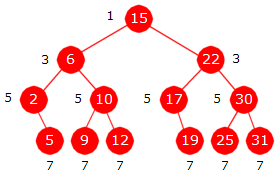 |
| Figur 1.3.7 b) : Et beslutningstre |
ordnet.
For hver node gjelder at dens verdi ligger mellom verdiene i dens to
subtrær. Et ordnet binærtre eller binært søketre som det kalles, er en viktig
datastruktur og vi vil arbeide med slike trær i flere kapitler utover.
I Figur 1.3.7 b) er det et heltall ved hver node. Det angir
hvor mange sammenligninger som skal til i while-løkken i
1. versjon
av binærsøk for å finne nodens verdi. Hvis vi søker rotverdien
(nivå 0) holder det med 1 sammenligning. Hvis det er en av de to verdiene i neste
rad (nivå 1) holder det med 3 sammenligninger, for de fire i neste rad (nivå 2)
5 sammenligninger, osv. Med andre ord trengs det 2k + 1
stykker for å finne en verdi som ligger på nivå k i beslutningstreet.
Anta at alle de 13 verdiene har samme sannsynlighet for å bli etterspurt og at den vi leter etter finnes i tabellen. Det gjennomsnittlige antallet sammenligninger blir da
Treet i Figur 1.3.7 b) mangler to noder på nederste rad for å kunne være
perfekt. Med andre ord må vi ha en tabell med 15 verdier for å få 8 noder
på nederste rad.
Et beslutningstre blir derfor perfekt hvis tabellen har en lengde på 1, 3, 7, 15, 31, 63, osv, eller
generelt en lengde på 2k – 1 med k > 0. Formen på et
beslutningstre er kun bestemt av antall verdier i tabellen.
Som et nytt eksempel tar vi en tabell med lengde 25 - 1 = 31:
| 5 | 7 | 10 | 11 | 12 | 15 | 18 | 19 | 20 | 25 | 26 | 29 | 31 | 33 | 36 | 42 | 43 | 48 | 49 | 52 | 53 | 55 | 58 | 62 | 65 | 66 | 68 | 69 | 70 | 75 | 77 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Figur 1.3.7 c) : En sortert tabell med 31 verdier | ||||||||||||||||||||||||||||||
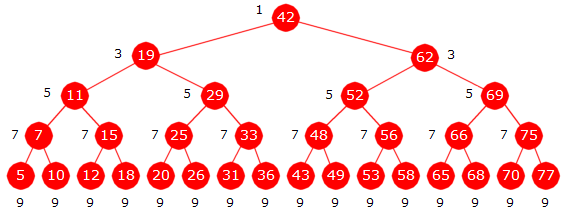 |
| Figur 1.3.7 d) : Et beslutningstre for 31 verdier basert på Programkode 1.3.6 a) |
Midtverdien a[15] = 42 havner i rotnoden (nivå 0), midtverdiene på hver side
(a[7] = 19 og a[23] = 62) havner i rotnodens to barn (venstre
og høyre barn) på nivå 1, osv. Ved siden av hver node står antall
sammenligninger som trengs i while-løkken i
Programkode 1.3.6 a) for å finne
verdien i noden. Vi antar at alle verdiene er forskjellige og har like stor sannsynlighet
for å bli etterspurt. Det gjennomsnittlige
antallet sammenligninger blir da:
Summen kan også skrives ved hjelp av potenser:
La antall verdier være n = 2k − 1 istedenfor 31 (dvs. k = 5) og la Ak være summen
Summen av denne potensrekken (se Formel G.1.12 i
Vedlegg G.1 ) blir:
Eksempel: k = 5 gir A5 = (2 · 5 – 3) · 25 + 3 = 7 · 32 + 3 = 227. Det passer med tegningen.
Når n = 2k – 1 blir 2k = n + 1 og k = log2(n+1), og gjennomsnittet for de n verdiene:
For store n (1/n liten) blir dette tilnærmet lik 2 · log2(n+1) – 3. Hvis n ikke er lik 2k – 1, vil formelen gi (for n stor) en god tilnærming for det gjennomsnittlige antallet sammenligninger.
Treet i Figur 1.3.7 d)
viser at det mest ugunstige tilfellet
(søkeverdien ligger nederst) trengs 2 · log2(32) − 1 = 9
eller generelt 2 · log2(n+1) − 1 sammenligninger.
Hvis søkeverdien ikke finnes,
går algoritmen til bunns i treet og et hakk videre. Dvs. 2 · log2(32) = 10 eller
generelt 2 · log2(n+1) sammenligninger.
Konklusjon: I 1. versjon
av binærsøk
trengs kun én sammenligning i det mest gunstige tilfellet (verdien ligger midt i tabellen),
2 · log2(n+1) – 3 i gjennomsnitt,
2 · log2(n+1) − 1 i det mest ugunstige tilfellet og
2 · log2(n+1) stykker for å avgjøre at en verdi ikke finnes.
Den er av orden log2(n+1)
(logaritmisk orden) både i gjennomsnitt og i de mest ugunstige tilfellene.
I 2. versjon
av binærsøk ble sammenligningenes rekkefølge endret i forhold til 1. versjon:
if (verdi > midtverdi) v = m + 1; // verdi må ligge i a[m+1:h] else if (verdi < midtverdi) h = m - 1; // verdi må ligge i a[v:m-1] else return m; // funnet
Endringen gir faktisk en forbedring. Se på
Figur 1.3.7 c).
Nå trengs to sammenligninger for å finne midtverdien 42, dvs. én
for å avgjøre at vi ikke skal til høyre og én til for å avgjøre at vi ikke skal til venstre.
Vi trenger 3 stykker for å finne 62, dvs. én sammenligning
for å avgjøre at 62 er til høyre for 42 og så to til for å avgjøre at vi verken skal til høyre
eller til venstre for 62. Vi må imidlertid ha 4 stykker for å finne 19. Vi trenger
to for å avgjøre at 19 ligger til venstre for 42 og så to til for å avgjøre at vi verken skal
til høyre eller venstre for 19. Osv. I Figur 1.3.7 e) under står det
ved siden av hver node antallet sammenligninger i while-løkken i
2. versjon
av binærsøk for å finne den verdien:
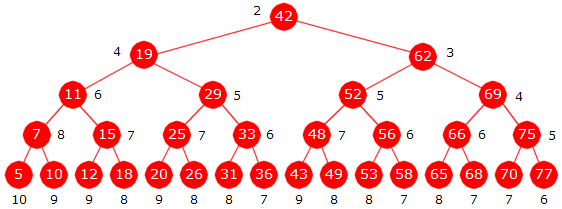 |
| Figur 1.3.7 e) : Et beslutningstre for 31 verdier basert på Programkode 1.3.6 b |
Vi summerer tallene og deler med 31.
Gjenomsnittlig antall sammenligninger blir 209/31 = 6,7.
Treet i Figur 1.3.7 d) gav resultatet 7,3.
Dermed har vi fått en liten forbedring.
La antall verdier være på formen n = 2k – 1
og la Ak være det sammenlagte antallet sammenligninger.
Kan vi finne en formel for Ak?
Det er lett å finne et gjennomsnitt for hver rad i treet i Figur 1.3.7 e).
Ta f.eks. 4. rad (nivå 3). Der er summen av tallene ved første og siste node lik
8 + 5 = 13. Den samme summen får vi for andre og nest siste node, dvs. 7 + 6 = 13. Osv.
Gjennomsnittet for nodene på raden blir dermed 13/2 = 6,5. På samme måte ser vi
at rad 5 har et gjennomsnitt på 8 og rad 3 et gjennomsnitt på 5. Dermed får vi:
Med k = 5 blir siste ledd (1,5 · 5 + 0,5) · 24
= 8 · 24.
Ak blir (se Avsnitt 1.3.16):
Eksempel: Hvis k = 5 blir A5 = (1,2 · 5 - 1) · 25 + 1
= 6,5 · 32 + 1 = 209. Dette stemmer med treet i
Figur 1.3.7 e).
Obs: Ak kan finnes på flere måter. Se Avsnitt 1.3.16.
Når n = 2k − 1 blir k = log2(n + 1). Gjennomsnittet for de n verdiene blir:
For store n (dvs. når 1/n er liten) blir dette tilnærmet lik 1,5 · log2(n + 1) – 1. Hvis n ikke er på formen 2k - 1, gir likevel formelen en god tilnærmingsverdi.
Det trengs 1,5 · log2(n + 1) sammenligninger i gjennomsnitt for å avgjøre at en verdi ikke er der. Det kreves flest hvis verdien er lik tabellens minste verdi, dvs. 2 · log2(n + 1) stykker.
Konklusjon:
I 2. versjon
av binærsøk
trengs to sammenligninger i det mest gunstige
tilfellet (søkeverdien ligger på midten av tabellen),
1,5 · log2(n + 1) – 1 sammenligninger i gjennomsnitt,
2 · log2(n + 1) i det mest ugunstige tilfellet og
gjennomsnittlig 1,5 · log2(n + 1) stykker for å avgjøre at en verdi ikke finnes.
Det betyr at 1. og 2. versjon er av samme orden, men 2. versjon
er i gjennomsnitt 25% mer effektiv enn 1. versjon.
I 3. versjon
av binærsøk er analysen mye enklere. Anta at tabellen har en lengde n
på formen 2k, dvs. n = 2, 4, 8, 16, 32, 64, osv.
I denne versjonen ser while-løkken slik ut:
while (v < h) { int m = (v + h)/2; if (verdi > a[m]) v = m + 1; else h = m; }
Hvis antall verdier i tabellintervallet a[v:h] er på formen 2k vil divisjonen m = (v + h)/2 gjøre at intervallene a[v:m] og a[m+1:h] blir eksakt like store, begge med 2k–1 verdier. Dvs. at for hver sammenligning if (verdi > a[m]) i while-løkken blir søkeområdet a[v:h] nøyaktig halvert.
Vi ser på et eksempel med bare 8 verdier. Gangen i algoritmen kan illustreres på flg. måte:
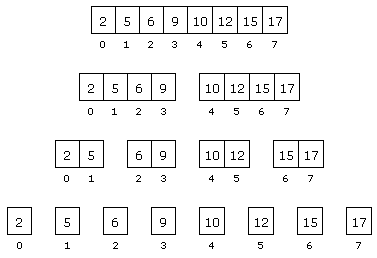 |
| Figur 1.3.7 f) : Tabellintervallene halveres hver gang |
While-løkken går så lenge som v < h.
Vi starter med 8 = 23 verdier og kommer til v = h etter 3 iterasjoner.
Generelt, hvis vi starter med n = 2k verdier, trengs k
iterasjoner. I tilegg trengs en sammenligning
(se Programkode 1.3.6 c )
for å avgjøre om verdien ligger på denne plassen.
Til sammen k + 1 sammenligninger. Men vi kan, siden
n = 2k, sette k = log2(n). Dermed
blir det log2(n) + 1 sammenligninger enten den verdien ligger i tabellen eller ikke.
Hvis n ikke er på formen 2k, så må det finnes en k slik at
2k < n < 2k+1. Dermed vil det gjennomsnittlige
antallet sammenligninger ligge mellom log2(n) og log2(n) + 2.
Konklusjon:
Alle de tre versjonene av binærsøk er av logaritmisk orden. Den 3. versjonen
er noe bedre (33%) enn 2. versjon, og 2. versjon er noe bedre (25%) enn
1. versjon. Dermed er det 3. versjon som bør inngå i vårt arsenal av søkemetoder for
sorterte tabeller, dvs. ligge i samleklassen Tabell.
| 1. | Gitt tallene 3, 5, 6, 9, 10, 13, 14, 15, 18, 19, 20, 21.a) Tegn det beslutningstreet som
1. versjon
av binærsøk gir.b) Bruk igjen
1. versjon.
Sett opp ved hver node det antallet sammenligninger som trengs for å finne nodeverdien. Finn
gjennomsnittet.c) Gjør det samme som i punkt b), men ta nå
utgangspunkt i 2. versjon
av binærsøk.
|
| 2. | Som Oppgave 1, men med
5, 11, 13, 17, 18, 19, 20, 25, 26, 29, 30, 31, 32, 35, 36.
|
| 3. | Som Oppgave 1:
2, 4, 5, 8, 13, 14, 15, 18, 19, 22, 23, 24, 28, 29, 33, 35, 36, 37.
|
| 4. | Sjekk at formelen Ak = (1,5 · k – 1) · 2k + 1
stemmer for k = 1, 2, 3, 4 og 5. Trær med færre nivåer enn det i
Figur 1.3.7 e)
lages ved fortløpende å fjerne nederste rad.
|
| 5. | Sjekk at formelen 1,5 · log2(n+1) - 1
for 2. versjon
gir god tilnærming for gjennomsnittet også når tabellens
lengde n ikke er på formen 2k – 1. Lag et testprogram!
For en gitt n, la en tabell inneholde tallene fra 1 til n i sortert rekkefølge. Bruk så
metoden til å søke etter hvert tall fra 1 til n. Tell opp antall
sammenligninger som utføres hver gang, legg sammen disse og finn gjennomsnittet.
Sammenlign med formelverdien.
|
![]() 1.3.8 Ordnet innsetting, innsettings- og shellsortering
1.3.8 Ordnet innsetting, innsettings- og shellsortering
Hvis en tabell skal holdes sortert, kan vi ikke legge inn nye verdier på vilkårlige
plasser. De må legges inn på rett sortert plass. Hvis en verdi ikke er der
fra før, har den et veldefinert
innsettingspunkt.
Hvis verdien allerede er der, kan den settes inn foran, bak eller eventuelt mellom
dem som er der fra før. Det må også være plass i tabellen til en ny eller nye verdier.
I flg. eksempel har tabellen plass til 15 verdier, men det er foreløpig lagt inn kun 10 stykker.
| 3 | 5 | 6 | 10 | 10 | 11 | 13 | 14 | 16 | 20 | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.8 a) : 10 verdier i sortert rekkefølge - plass til 15 verdier | ||||||||||||||
Hvis vi skal legge inn en ny verdi i tabellen over, må vi først forvisse oss om at det er plass.
Dernest må vi finne hvor den skal ligge, forskyve verdier mot høyre for å få plass
og så legge den inn. For å finne plassen kan vi bruke en søkemetode, f.eks. binærsøk
fra Avsnitt 1.3.6. Alt dette gjøres i flg. kodebit
(metoden skrivln() er fra Oppgave 4 og 5 i
Avsnitt 1.2.2 ):
int[] a = {3,5,6,10,10,11,13,14,16,20,0,0,0,0,0}; // en tabell
int antall = 10; // antall verdier
if (antall >= a.length) throw new IllegalStateException("Tabellen er full");
int nyverdi = 10; // ny verdi
int k = Tabell.binærsøk(a, 0, antall, nyverdi); // søker i a[0:antall>
if (k < 0) k = -(k + 1); // innsettingspunkt
for (int i = antall; i > k; i--) a[i] = a[i-1]; // forskyver
a[k] = nyverdi; // legger inn
antall++; // øker antallet
Tabell.skrivln(a, 0, antall); // Se Oppgave 4 og 5 i Avsnitt 1.2.2
Programkode 1.3.8 a)
Programsetningen: if (k < 0) k = -(k + 1); sørger for at k
blir innsettingspunktet i det tilfellet nyverdi ikke finnes fra før. Her er den lik 10 og
siden den finnes fra før, vil k være positiv. Den eksakte verdien til k er avhengig av
hvilken versjon av binærsøk() som brukes. Er det 3. versjon, vil k = 3.
Se Oppgave 1.
Hvis det ikke er plass i tabellen, kastes et unntak. Et alternativ er
å «utvide» tabellen. Det betyr at det opprettes en ny og større tabell og så kopieres
innholdet av den gamle over i den nye. Det kan f.eks. gjøres slik (se
Oppgave 2):
if (antall >= a.length) a = Arrays.copyOf(a,2*a.length); // dobbelt størrelse Programkode 1.3.8 b)
I koden over brukes metoden copyOf() fra klassen
Arrays.
Se Oppgave 3.
Innsettingssortering (eng: insertion sort) er en sorteringsteknikk
som gjentar det samme som i
Programkode 1.3.8 a).
Vi tenker oss nå at tabellen i
Figur 1.3.8 a)
også har verdier på de fem siste plassene, men at de er usortert når vi ser på hele tabellen:
| 3 | 5 | 6 | 10 | 10 | 11 | 13 | 14 | 16 | 20 | 12 | 4 | 7 | 2 | 15 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.3.8 b) : 10 verdier sortert (hvit del) - 5 verdier usortert (grå del) | ||||||||||||||
I innsettingssortering er tabellen todelt. Første del inneholder sorterte og andre del (med grå bakgrunn) usorterte verdier. Fortsettelsen går ut på at den første verdien i den usorterte delen settes inn på rett plass i den sorterte delen. Vi legger den (her 12) midlertidig til side i en hjelpevariabel. Dermed får den «hvite» delen en ledig plass (indeks 10):
|
|
||||||||||||||||||||||||||||||||
| Figur 1.3.8 c) : Første usorterte verdi (dvs. 12) er flyttet til en hjelpevariabel | |||||||||||||||||||||||||||||||||
Neste skritt er å finne hvor verdien 12 skal inn. Én og én verdi forskyves mot høyre inntil vi finner rett plass. Først flyttes 20 én mot høyre, så 16, osv. inntil indeks 6 der 12 skal inn:
|
|
|
||||||||||||||||||||||||||||||||
| Figur 1.3.8 d) : Tallet 12 er nå på rett sortert plass | |||||||||||||||||||||||||||||||||
Dette fortsetter: Den første av de usorterte (dvs. 4) legges til side og dens plass blir ledig:
|
|
||||||||||||||||||||||||||||||||
| Figur 1.3.8 e) : Første usorterte verdi (dvs. 4) er flyttet til en hjelpevariabel | |||||||||||||||||||||||||||||||||
Så forskyves én og én verdi. Vi ser at rett plass er nest først (indeks 1). Dermed:
|
|
|
||||||||||||||||||||||||||||||||
| Figur 1.3.8 f) : Tallet 4 har kommet på rett sortert plass | |||||||||||||||||||||||||||||||||
Vi er ferdige når hele tabellen har blitt «hvit». I utgangspunktet er hele tabellen usortert. Men vi kan se på det første elementet som sortert. Det betyr at når innsettingssorteringen starter, utgjør første element den «hvite» delen og resten den «grå» delen.
I Programkode 1.3.8 a)
inngår binærsøk, men det er
mest vanlig å sammenligne og forskyve én og én verdi ved hjelp av en indeks j.
Den må sjekkes i tilfellet verdi skal legges helt først:
public static void innsettingssortering(int[] a) { for (int i = 1; i < a.length; i++) // starter med i = 1 { int verdi = a[i], j = i - 1; // verdi er et tabellelemnet, j er en indeks for (; j >= 0 && verdi < a[j]; j--) a[j+1] = a[j]; // sammenligner og flytter a[j + 1] = verdi; // j + 1 er rett sortert plass } } Programkode 1.3.8 c)
Flg. eksempel viser hvordan metoden kan brukes:
int[] a = {13,11,10,20,15,5,3,2,14,10,12,6,7,4,16}; Tabell.innsettingssortering(a); System.out.println(Arrays.toString(a)); // Utskrift: [2, 3, 4, 5, 6, 7, 10, 10, 11, 12, 13, 14, 15, 16, 20] Programkode 1.3.8 d)
Algoritmeanalyse:
Vi skal finne ut hvor mange ganger sammenligningen verdi < a[j] utføres i
en tabell med n verdier der alle er forskjellige.
Anta at de i første verdiene er sortert, dvs. a[0],
a[1], · · · a[.
Tallet i - 1]verdi skal inn på rett plass blant dem.
Det er i + 1 forskjellige muligheter: foran a[0], mellom a[0] og
a[1], mellom a[1] og a[2], osv. eller etter
a[.
Alle er like sannsynlige siden verdiene er forskjellige.
i - 1]
Vi trenger én sammenligning for å avgjøre om verdi skal bak
a[,
to for å avgjøre om den skal mellom a[i – 1]
og a[i – 2], osv.
Til slutt trengs i - 1]i stykker både for å avgjøre
om verdi skal mellom a[0] og a[1] eller
foran a[0]. Sum: 1 + 2 + · · · + i + i
= i(i+1)/2 + i. Gjennomsnittet får vi ved å dele med
i + 1, dvs. lik i/2 + 1 - 1/(i + 1)
Vi summerer fra 1 til n - 1 og får det gjennomsnittlige antallet ganger
verdi < a[j] utføres:
n(n − 1)/4 + n − Hn
= n(n + 3)/4 − Hn
Det verste tilfellet er en sortert avtagende tabell. Da er verdi < a[j]
sann for hver j. Dermed
i sammenligninger i indre løkke, og totalt
1 + 2 + · · · + i =
n (n − 1)/2
sammenligninger. Det beste tilfellet er når tabellen
er sortert stigende. Da er verdi < a[j] aldri sann og antallet
blir 1 + 1 + · · · + 1 = n − 1.
n(n + 3)/4 − Hn.
Det verste: n(n − 1)/2 og
det beste: n − 1. Dermed av kvadratisk orden
både i gjennomsnitt og i det verste tilfellet.
Det er tre algoritmer av kvadratisk orden som vanligvis diskuteres i et fag som «Algoritmer og datastrukturer». Flg. tabell viser deres effektivtet med tanke på sammenligninger:
| Sorteringsalgoritme | Antall sammenligninger | ||
| Navn | Gjennomsnittlig | Verste tilfelle | Beste tilfelle |
| Boblesortering | n(n – 1)/2 | n(n – 1)/2 | n – 1 |
| Utvalgssortering | n(n – 1)/2 | n(n – 1)/2 | n(n – 1)/2 |
| Innsettingssortering | n(n + 3)/4 − Hn | n(n – 1)/2 | n – 1 |
| Figur 1.3.8 f) : Sorteringsalgoritmer av kvadratisk orden | |||
|---|---|---|---|
Det er antall sammenligninger det legges mest vekt på i algoritmeanalyse. Men også antall ombyttinger
er av interesse. Nå er det egentlig ingen ombyttinger i innsettingssortering slik den er satt opp
i Programkode 1.3.8 c)
- kun tilordninger. F.eks. a[j+1] = a[j]. Men det er fullt mulig å kode metoden ved å
bruke ombyttinger. Men en ombytting er litt mer kostbar enn en enkel tilordning.
Ta utgangspunkt i tabellen i
Figur 1.3.8 b). Der skal den første
i den «grå» delen (tallet 12) inn på rett plass i den «hvite» delen. Det får vi til
ved å bytte om 12 og 20, så bytte om 12 og 16, så 12 og 14 og til slutt 12 og 13. Da vil 12 komme mellom
11 og 13. Bruker vi
bytt-metoden fra
samleklassen Tabell, vil flg. kode virke:
public static void innsettingssortering(int[] a) { for (int i = 1; i < a.length; i++) // starter med i = 1 { int temp = a[i]; // hjelpevariabel for (int j = i - 1; j >= 0 && temp < a[j]; j--) Tabell.bytt(a, j, j + 1); } } Programkode 1.3.8 e)
Hvis de i første verdiene er sortert, kreves ingen ombytting hvis a[i]
ligger riktig, én ombytting hvis a[i] skal foran a[i - 1],
osv. til i ombyttinger hvis a[i] hører hjemme lengst til venstre.
Dermed tilsammen
1 + 2 + · · · + i = i(i + 1)/2
stykker. Gjennomsnittet får vi ved å dele på (i + 1)
og det blir i/2. Summerer vi dette fra 1 til n - 1
får vi at gjennomsnittlig antall ombyttinger er: n(n - 1)/4.
Oppsummering - innsettingssortering:
Navn:Det kallesinnsettingssorteringfordi tabellen underveis er todelt. Venstre del er sortert. Én og én verdi fra høyre del settes inn på rett sortert plass i venstre del. Ved start består venstre del av det første elementet og høyre del av resten. Når algoritmen slutter, består venstre del av hele tabellen (og høyre del er tom).Effektivitet:Det kan vises (sealgoritmeanalyse) at det i gjennomsnitt (hvis alle verdiene er forskjellige) utføresn(n + 3)/4 − Hnsammenligninger. Det betyr at den er av kvadratisk orden i gjennomsnitt. Hvis tabellen allerede er sortert, utføres det n − 1 sammenligninger. Dermed er den av lineær orden i det beste tilfellet.Ombyttinger:Det er ingen ombyttinger slik som innsettingssortering er kodet iProgramkode1.3.8 c). Det er isteden forskyvninger (tilordninger) som er litt mindre kostbare, og av dem er det i gjennomsnitt n(n − 1)/4 stykker.Konklusjon:Av de tre av kvadratisk orden som vi har sett på, er innsettingssortering best. Vi skal se på algoritmer av orden n log(n) og de er langt bedre for store tabeller. Men innsettingssortering er best hvis tabellen er liten eller stor, men delvis sortert. Det erkvikksorteringsom er best av de «avanserte». Den arbeider på intervaller og når de har blitt små nok, er det der vanlig å skifte over til innsettingssortering.
Mulige forbedringer En enkel forbedringsidé er å ta to verdier om gangen fra den
høyre delen. Først settes den største av dem inn på rett sortert plass i venstre del. Deretter kan letingen etter
plassen til den minste fortsette derfra. Dermed blir det færre sammenligninger. I gjennomsnitt vil den minste av de
to havne i 1/3-dels avstand fra starten av venstre del og den andre i
2/3-dels avstand. Det gir ca. n²/6 sammenligninger i gjennomsnitt mot ca. n²/4 stykker for
vanlig innsettingssortering. Dvs. ca. 30% mer effektiv. Se
Oppgave 11 - 13.
Shellsortering En annen mulig (og vesentlig) forbedring har som idé
at tabellen fortløpende deles opp i mindre og mindre grupper av verdier og de sorteres hver for seg ved hjelp av
innsettingssortering. Det kalles
shellsortering etter Donald Shell.
Ta utgangspunkt i flg. tabell:
| 8 | 14 | 16 | 19 | 17 | 9 | 3 | 4 | 1 | 15 | 5 | 18 | 13 | 11 | 12 | 2 | 6 | 20 | 7 | 10 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Figur 1.3.8 g) : En (usortert) tabell a med 20 verdier. | |||||||||||||||||||
Vi deler opp i 10 grupper à to verdier. Første gruppe består av a[0]
og a[10], andre gruppe av a[1]
og a[11], tredje gruppe a[2]
og a[12], osv. til a[9]
og a[19] som tiende gruppe. Hver gruppe sorteres for seg. Med kun to verdier kan det gjøres
ved at de to verdiene bytter plass hvis de er i utakt. Det betyr f.eks. at a[0] = 8
må bytte plass med a[10] = 5. Osv.
| 5 | 14 | 13 | 11 | 12 | 2 | 3 | 4 | 1 | 10 | 8 | 18 | 16 | 19 | 17 | 9 | 6 | 20 | 7 | 15 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Figur 1.3.8 h) : I 6 av de 10 parene har verdiene skiftet plass | |||||||||||||||||||
Nå deler vi opp i 4 grupper à fem verdier. Første gruppe skal bestå av a[0],
a[4], a[8], a[12] og a[16],
dvs. av verdiene 5, 12, 1, 16 og 6. For lesbarhetens skyld får de (se figuren under) grå bakgrunn.
Andre gruppe: a[1],
a[5], a[9], a[13] og a[17],
dvs. verdiene 14, 2, 10, 19 og 20. Osv. Disse 4 gruppene skal sorteres hver for seg ved hjelp av
innsettingssortering.
| 5 | 14 | 13 | 11 | 12 | 2 | 3 | 4 | 1 | 10 | 8 | 18 | 16 | 19 | 17 | 9 | 6 | 20 | 7 | 15 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Figur 1.3.8 i) : Verdiene i første gruppe har fått grå bakgrunn | |||||||||||||||||||
Innsettingssortering brukes normalt på en hel tabell eller på
et intervall. Men her har vi ingen av delene. Men verdiene har en fast avstand
eller gap. Den er forskjellen mellom indeksene for to naboverdier.
Mellom a[0] og a[4] er det 4 - 0 = 4, mellom
a[4] og a[8] lik 8 - 4 = 4. Osv. Vanligvis økes (eller
reduseres) en indeks med 1, men her blir det 4. Ta utgangspunkt i
Programkode 1.3.8 c), bruk
4 istedenfor 1, i += 4 istedenfor i++ og
j -= 4 istedenfor j--.
Flg. kode vil sortere første gruppe
(a[0],
a[4], a[8], a[12], a[16])
i Figur 1.3.8 i):
int[] a = {5,14,13,11,12,2,3,4,1,10,8,18,16,19,17,9,6,20,7,15}; for (int i = 4; i < a.length; i += 4) // avstanden/gapet er nå 4 og ikke 1 { int temp = a[i], j = i - 4; for (; j >= 0 && temp < a[j]; j -= 4) a[j + 4] = a[j]; a[j + 4] = temp; }
Hvis denne koden kjøres, vil tabellen a få samme innhold som i figuren under:
| 1 | 14 | 13 | 11 | 5 | 2 | 3 | 4 | 6 | 10 | 8 | 18 | 12 | 19 | 17 | 9 | 16 | 20 | 7 | 15 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Figur 1.3.8 j) : De fem verdiene i første gruppe (grå bakgrunn) er sortert | |||||||||||||||||||
Det trengs kun én endring i koden over for at alle de fire
gruppene skal bli sortert. Endringen er i++ i den ytterste for-løkken istedenfor i += 4.
Det starter med i = 4. Med i++ blir i neste gang lik 5.
Da sammenlignes a[5] og a[1] og de bytter plass hvis de er i «utakt».
Så blir i = 6 og a[6] og a[2] sammenlignes. Osv. Det betyr at de to
første verdiene i hver gruppe behandles først, så de tre første verdiene i hver gruppe, osv. Vi kan lage en metode for
dette der avstanden eller gapet ikke er 4, men er generelt lik k:
public static void shell(int[] a, int k) { for (int i = k; i < a.length; i++) { int temp = a[i], j = i - k; for ( ; j >= 0 && temp < a[j]; j -= k) a[j + k] = a[j]; a[j + k] = temp; } } Programkode 1.3.8 f)
Ved hjelp av metoden shell() kan vi sortere en tabell
fullstendig. Vi starter med tabellen i
Figur 1.3.8 g). Så bruker vi først avstand/gap
lik 10, så lik 4 og til slutt lik 1:
int[] a = {8,14,16,19,17,9,3,4,1,15,5,18,13,11,12,2,6,20,7,10}; int[] gap = {1,4,10}; for (int i = gap.length - 1; i >= 0; i--) { shell(a,gap[i]); // først 10, så 4 og 1 til slutt System.out.println(Arrays.toString(a)); // skriver ut } // [5, 14, 13, 11, 12, 2, 3, 4, 1, 10, 8, 18, 16, 19, 17, 9, 6, 20, 7, 15] // [1, 2, 3, 4, 5, 10, 7, 9, 6, 14, 8, 11, 12, 19, 13, 15, 16, 20, 17, 18] // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20] Programkode 1.3.8 g)
Den som er observant vil se at i siste runde (1 som gap) utføres full innsettingssortering.
Men hva er da poenget? Det er en masse arbeid i rundene foran og så full innsettingssortering til slutt.
Men poenget er at i siste runde er tabellen delvis sortert. Det ser vi på den nest siste utskriften
i Programkode 1.3.8 g). I slike tilfeller er vanlig innsettingssortering
den beste av alle sorteringsalgoritmer. I starten (gapet er 10) foregår det på
små grupper (eller intervaller med store gap). I slike tilfeller er også innsettingssortering best. Med andre ord
er dette (dvs. shellsortering) en systematisk utnyttelse av de beste sidene ved innsettingssortering.
I figurene over og i Programkode 1.3.8 g)
ble det brukt først 10, så 4 og til slutt 1.
Hvorfor akkurat disse tallene? For det første må vi ha 1 til slutt for å sikre at tabellen blir sortert. Som nevnt
svarer det til vanlig innsettingssortering og dermed vil tabellen bli sortert uansett hva som måtte å hendt på forhånd.
Både 10 og 4 går opp i tabellengden 20, men det er ikke noe krav. Vi kunne f.eks. ha valgt 9 først. Da får vi
9 grupper med verdier der de to første får 3 verdier og de seks siste 2 verdier. F.eks. vil første gruppe
da bestå av a[0],
a[9] og a[18], mens a[8] og
a[17] utgjør siste gruppe.
Generelt: La n være lengden på tabellen og k et tall
mellom 0 og n. La r være resten og q
kvotienten når n deles med k.
Et gap på k vil da gi k grupper
med q + 1 verdier i de r første gruppene og q
verdier i de øvrige. Hvis r = 0 (k går opp i
n), vil alle gruppene ha q verdier.
Men hvilke tall skal vi velge hvis tabellen er stor? Det er bygget opp en hel vitenskap rundt dette. Valget er avgjørende for effektiviteten. For store tabeller viser teori og eksperimenter at å bruke 1, 4, 10, 23, 57, 132, 301, 701, · · · er nær optimalt. Dette minner litt om en geometrisk følge. Husk at en følge er geometrisk hvis forholdet (kvotienten) mellom et tall i følgen og det foregående tallet, er konstant. Her får vi flg. kvotienter:
4,00 2,50 2,30 2,48 2,32 2,28 2,33
Kvotientene (bortsett fra den første) svinger mellom 2,2 og 2,5. Dvs. ingen geometrisk følge, men kvotientene er ikke langt unna å være lik en konstant. Hvis vi ønsker oss slike tall som er større enn 701, har det blitt foreslått at vi da bør velge tall som er ca. 2,25 ganger større enn det forrige. F.eks. er 2,25 · 701 = 1577,25. Med avrunding nedover blir det 1577.
Vi skal nå sammenligne effektiviteten til innsettings- og shellsortering.
Tilfeldige tabeller med f.eks. 200.000 verdier (eller færre på din maskin)
vil gjøre at innsettingssortering ikke bruker alt for lang tid. Vi kan, som nevnt over, finne flere
gap-verdier. Tilsammen blir det:
1, 4, 10, 23, 57, 132, 301, 701, 1577, 3548, 7984, 17965, 40423, 90952, 204642. Hvis metodene
innsettingssortering(),
shell() og
erSortert() er lagt i samleklassen
Tabell, vil flg. kode være kjørbar:
int[] gap = {1,4,10,23,57,132,301,701,1577,3548,7984,17965,40423,90952,204642}; int[] a = Tabell.randPerm(200_000); // en tilfeldig tabell System.out.println(Tabell.erSortert(a)); // sjekker tabellen long tid = System.currentTimeMillis(); // starter klokken Tabell.innsettingssortering(a); // sorterer //for (int i = gap.length - 1; i >= 0; i--) Tabell.shell(a,gap[i]); System.out.println(System.currentTimeMillis() - tid); // tiden System.out.println(Tabell.erSortert(a)); // sjekker sorteringen Programkode 1.3.8 h)
Hvis du kjører programmet over, vil du se hvor lang tid (millisekunder) innsettingssortering bruker på din
maskin. Kjør programmet et par-tre ganger for å få forskjellige tabeller. De to andre utskriftene
(true/false) er kun for å sjekke at tabellen faktisk blir sortert. Flytt så kommentartegnet
// fra for-løkken over til kallet på innsettingssortering. Hva
blir resultatet nå? Bruk også Arrays.sort(a); dvs. Java's sorteringsmetode. Hvor
lang tid bruker den?
Oppsummering - shellsortering:
Navn:Kallesshellsorteringtil ære for «oppdageren» Donald Shell. Den ble kjent i 1959 og vakte stor interesse siden man på den tiden ikke kjente til generelle metoder med en (gjennomsnittlig) orden vesentlig bedre ennn².Effektivitet:Det er kjent at den er av kvadrastisk (n²) orden i det verste og av ordennlog(n) i det beste tilfellet. Men metoden er sterkt avhengig av sekvensen av gap-verdier og det er ikke kjent hvilken orden den har i gjennomsnitt.Konklusjon:Metoden brukes ikke lenger i praksis siden det nå finnes bedre metoder - f.eks. kvikksortering. Men den er interessant siden den på en systematisk måte utnytter de beste sidene ved innsettingssortering.
| 1. | Sørg for at du har en versjon av binærsøk
(se Avsnitt 1.3.6)
og skrivln()
(se Oppgave 4 og 5 i Avsnitt 1.2.2)
tilgjengelig i din hjelpeklasse Tabell. Kjør
Programkode 1.3.8 a) flere ganger.
Bruk som nyverdi både verdier som er i tabellen og som ikke er der fra før.
|
| 2. | Bytt ut den setningen i Programkode 1.3.8 a)
som kaster et unntak hvis tabellen er full, med setningen i
Programkode 1.3.8 b). Fjern så de fem siste
0-ene i tabellen a slik at den er full fra starten av. Gjør så som i Oppgave 1.
Fjern så alle verdiene i a slik at den blir tom
(int[] a = {};) og sett antall til 0. Kjør programmet! Hva skjer? Hvordan kan problemet
løses?
|
| 3. | Sett deg inn i metodene copyOf() og copyOfRange()
fra klassen Arrays. De
brukes både til å «utvide» en tabell og til å lage en kopi av hele eller en del av en tabell.
|
| 4. | Setningen for (int i = antall; i > k; i--) a[i] = a[i-1];
i Programkode 1.3.8 a) forskyver
verdier i tabellen. Dette kan også gjøres ved hjelp av metoden arraycopy()
i klassen System.
Gjør det!
|
| 5. | Se på innsettings- og utvalgssortering.
Se Figur 1.3.8 g).
Hvor mange sammenligninger brukes i gjennomsnitt i hver av dem hvis det er 1000 verdier?
|
| 6. | Lag kode som viser tidsforbruket til innsettings- og utvalgssortering. Den første har bare halvparten så mange sammenligninger, men har flere ombyttinger (eller tilordninger). |
| 7. | Lag en versjon av innsettingssortering som sorterer i tabellintervallet
a[fra:til>. Legg den i samleklassen Tabell. |
| 8. | En sorteringsmetode kalles stabil hvis like verdier
har samme innbyrdes rekkefølge etter som før sorteringen.
Sjekk at innsettingssortering er stabil. |
| 9. | Bruk en «vaktpost»-teknikk i
Programkode 1.3.8 c).
Den innerste for-løkken inneholder sammenligningen j >= 0.
Hvis verdi er mindre enn a[0], skal den inn på plass 0.
Hvis ikke, vil a[0] fungere som en stoppverdi. Da trengs ikke sammenligningen
j >= 0.
|
| 10. | Lag en versjon av innsettingssortering der binærsøk finner rett plass
og arraycopy flytter på verdiene. Se f.eks.
Programkode 1.3.8 a).
Blir den raskere?
|
| 11. | Lag en versjon av innsettingssortering der to og to verdier settes inn på rett sortert plass. Den største av de to settes inn først og letingen etter plassen til den andre kan starte fra der den største ble satt inn. Husk at tabellens lengde er et partall eller et oddetall. Blir den raskere. Gjør tidsmålinger. |
| 12. | Idéen fra Oppgave 11 kan forbedres. Bruk k verdier
der k >= 1. Sortér de k første verdiene vha
vanlig innsettingssortering (se Oppgave 7). Sortér de neste k verdiene på samme måte,
flett dem sammen med de k første verdiene. Sortér så de neste k verdiene,
flett dem sammen med de som nå er sortert. Osv. Gjør forbedringen.
|
| 13. | Lag en metode der metoden fra Oppgave 13 kalles med k lik
heltallsverdien til kvadratroten til tabellens størrelse n. Da får vi en sorteringsmetode
av orden n3/2. Lag testkjøringer der du måler tidsforbruket for denne versjonen
og sammenlign det med tidsforbruket for versjonen i
Programkode 1.3.8 c).
|
| 14. |
Ta utgangspunkt i Programkode 1.3.8 c). Gjør om metoden
slik at den returnerer antallet ganger sammenligningen temp < a[j] utføres. Bruk
nestePermutasjon til å generere alle
permutasjoner av tallene fra 1 til n. Legg sammen og finn det totale antallet sammenligninger.
Lag så en metode som til et positivt heltall n returnerer verdien til formelen
[n(n + 3)/4 − Hn]·n!
Det å sjekke at det tilsammen blir det antallet sammenligninger som formelen sier, kan ikke gjøres for
store verdier av n siden antallet permutasjoner blir så enormt stort, men det går i hvert fall
an for n-verdier opp til 10.
|
| 15. |
En ulempe med slik det er gjort i Programkode 1.3.8 h),
er at tabellen med gap-verdier må være laget på forhånd. Hvis tabellen har lengde n, kan
vi som et alternativ starte med gap-verdi g = n/2 og så fortløpende
halvere gapverdien til vi kommer til 1. Gjør dette i
Programkode 1.3.8 h). Hva blir da tidsforbruket sammenlignet
med den du fikk med tabellen av gap-verdier.
|
| 16. |
I Programkode 1.3.8 h) brukes tilfeldige tabeller med
400.000 verdier. Bruk isteden 20.000.000 (20 millioner) verdier. Da må gap-tabellen utvides. Hver ny verdi
skal være 2,25 ganger så stor som den forrige. Finn slike verdier (start med 701). Stopp når du har
kommet til ca. 10 millioner. La g være double og bruk g = 2.25*g
og for hver ny g bruker du:
(int)Math.floor(g).
Hva blir nå tidsforbruket. Sammenlign med teknikken fra Oppgave 15. Sammenlig også med
Arrays.sort(a).
|
| 17. |
Tidsforbruket med teknikken (gap-verdiene) fra Oppgave 16 er ned mot halvparten av det i Oppgave 15. Ulempen
er at tabellverdiene må regnes ut først. En alternativ mulighet er, hvis n er tabellengde,
å bruke heltallsverdien til g = n/2.25 som første gap. Så
heltallsverdien til g = g/2.25 som neste gap, osv. Men vi må sørge for
at 1 blir siste gap-verdi. Det kan vi f.eks. få til ved å bruke g = g/2.25
så lenge som g > 5.0, og så til slutt bruke 1 som gap-verdi. Gjør dette og sammenlign
tidsforbruket med det i Oppgave 15 og 16.
|
![]() 1.3.9 Partisjonering og kvikksortering
1.3.9 Partisjonering og kvikksortering
Å partisjonere en tabell betyr å omorganisere og ordne den i deler
etter bestemte kriterier.
Eksempel 1.3.9 a): Flg. tabell inneholder kun tallene 0 og 1:
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Vi ønsker å «partisjonere» den slik at alle 0-ene kommer i første halvdel og dermed alle 1-erne i andre halvdel. Målet er å gjøre det med minst mulig innsats.
Eksempel 1.3.9 b): Flg. tabell inneholder 20 tall i området fra 1 til 25:
| 8 | 3 | 15 | 13 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 8 | 20 | 16 | 5 | 21 | 11 | 14 |
Ønske: Todelt tabell der venstre del inneholder alle mindre enn 10, høyre del resten og ingen krav til fordelingen innen de to delene. Målet er å få det gjort med minst mulig innsats.
Eksempel 1.3.9 c): Flg. tabell inneholder kun bokstavene R, H og B:
| H | B | R | B | H | H | R | B | R | H | B | R | H | R | R | B | H | B | H | R |
Ønske: Tredelt tabell der R-ene kommer først, så H-ene og til slutt B-ene. Det å gjøre dette på en mest mulig effektiv måte, kalles «Det hollandske flaggproblemet» (eng: The Dutch National Flag Problem). Her står bokstavene R, H og B for flaggfargene rød, hvit og blå.
Todelt partisjonering Målet er å finne en algoritme som omorganiserer
en tabell slik at alle verdier som er mindre enn en skilleverdi kommer
først. Vi bruker Eksempel 1.3.9 b)
som utgangspunkt.
Tabellen kan, men behøver ikke, inneholde selve skilleverdien. La f.eks. 10 være skilleverdi.
To indekser v og h starter i hver sin ende av tabellen:
| 8 | 3 | 15 | 13 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 8 | 20 | 16 | 5 | 21 | 11 | 14 |
| v | h |
Det starter ved at v flyttes mot høyre så lenge som
tilhørende tabellverdi er mindre enn 10. Da vil v
stoppe ved 15. Så flyttes h mot venstre så lenge som tilhørende
tabellverdi er større enn eller lik 10. Da vil h stoppe ved 5.
De verdiene som v og h har passert får hvit bakgrunn:
| 8 | 3 | 15 | 13 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 8 | 20 | 16 | 5 | 21 | 11 | 14 |
| v | h |
Tabellen er nå (og vil inntil videre være) tredelt. Venstre del
(hvit bakgrunn) har verdier som er mindre enn 10 og høyre del
(også hvit bakgrunn) verdier som er større enn (eller lik) 10.
Den midterste delen (grå bakgrunn) inneholder de «ukjente» verdiene,
dvs. de som ennå ikke er undersøkt. Indeksene v og h
skal hele tiden ligge i hver sin ende av den «ukjente» delen.
I tabellen over har indeksen v stoppet
på en verdi (15) som er større enn 10 og h på en verdi (5) som er mindre enn
10. Hvis de to bytter plass, vil 5 høre til den venstre «hvite» delen
og 15 til de som er større enn (eller lik) 10. Men da må også v og
h flyttes videre:
| 8 | 3 | 5 | 13 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 8 | 20 | 16 | 15 | 21 | 11 | 14 |
| v | h |
Nå står allerede v på en verdi (13) som er større enn 10 og må stå der.
Men h må flyttes videre mot venstre til første verdi
som er mindre enn (eller lik) 10:
| 8 | 3 | 5 | 13 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 8 | 20 | 16 | 15 | 21 | 11 | 14 |
| v | h |
Verdiene til v og h (13 og 8) bytter plass, v
og h flyttes én posisjon:
| 8 | 3 | 5 | 8 | 1 | 9 | 20 | 3 | 18 | 2 | 6 | 25 | 14 | 13 | 20 | 16 | 15 | 21 | 11 | 14 |
| v | h |
Vi fortsetter
til den «ukjente» (grå) delen er tom. Da vil v høre til den første av de
som er større enn (eller lik) 10 og h til den siste av
de som er mindre enn 10:
| 8 | 3 | 5 | 8 | 1 | 9 | 6 | 3 | 2 | 18 | 20 | 25 | 14 | 13 | 20 | 16 | 15 | 21 | 11 | 14 |
| h | v |
Legg merke til at det i tabellen over ikke er noen spesiell rekkefølge på tallene i venstre del (de mindre enn 10) og heller ingen spesiell rekkfølge på de i høyre del.
Spesialtilfeller: Hvis alle er mindre enn skilleverdi, vil v havne
utenfor når den flyttes mot høyre. Omvendt vil h
havne utenfor til venstre hvis ingen er mindre enn skilleverdi.
Flg. metode (som legges i klassen Tabell) deler intervallet a[v:h]
ved hjelp av idéene over:
private static int parter0(int[] a, int v, int h, int skilleverdi)
{
while (true) // stopper når v > h
{
while (v <= h && a[v] < skilleverdi) v++; // h er stoppverdi for v
while (v <= h && a[h] >= skilleverdi) h--; // v er stoppverdi for h
if (v < h) bytt(a,v++,h--); // bytter om a[v] og a[h]
else return v; // a[v] er nåden første som ikke er mindre enn skilleverdi
}
} Programkode 1.3.9 a)
De to while-løkkene over inneholder v <= h.
Hvis alle verdiene i
a[v:h] er mindre enn skilleverdi,
vil v stoppe på h + 1. Omvendt vil
h stoppe på v − 1 hvis ingen
av dem er mindre enn skilleverdi.
Hvis vi ikke har noen av disse tilfellene, vil
første ombytting gjøre at a[v] er mindre enn og a[h] større enn eller lik
skilleverdi. De to blir da
stoppverdier eller vaktposter. Dermed kan vi fjerne v <= h i resten av algoritmen.
Se Oppgave 8.
Metoden parter0()
er privat. En offentlig metode bør (slik som metodene i java.util) bruke
halvåpent intervall, dvs. fra
og til. Se Oppgave 1.
Eksempel 1.3.1 d): Eksempel 1.3.9 a)
og b) kan løses ved hjelp av en offentlig versjon av
Programkode 1.3.9 a) fra
samleklassen Tabell (der det brukes fra
og til). Se Oppgave 1.
int[] a = {0,0,1,0,0,1,0,1,1,0,0,1,1,1,0,1,0,1,1,0};
int[] b = {8,3,15,13,1,9,20,3,18,2,6,25,14,8,20,16,5,21,11,14};
Tabell.parter(a, 0, a.length, 1); // bruker 1 som skilleverdi
Tabell.parter(b, 0, b.length, 10); // bruker 10 som skilleverdi
System.out.println(Arrays.toString(a));
System.out.println(Arrays.toString(b));
// Utskrift:
// [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
// [8, 3, 5, 8, 1, 9, 6, 3, 2, 18, 20, 25, 14, 13, 20, 16, 15, 21, 11, 14]
Programkode 1.3.9 b)
Eksempel 1.3.9 e): Tabellen i
Eksempel 1.3.9 b)
ble brukt til å utlede algoritmen for partisjonering, men den inneholdt ikke selve skilleverdien.
Tabellen i Figur 1.3.9 g) nedenfor inneholder tallene fra 1 til 20.
Den skal partisjoneres med 11 som skilleverdi. Her kan en som en øvelse på papir og med penn
(se Oppgave 2)
finne hvilket resultat algoritmen vil gi. Fasit får en så ved å kjøre
Programkode 1.3.9 c) under. Se også Oppgave 1.
Se spesielt på hvor skilleverdien havner. Den behøver
ikke havne på skillet mellom de to delene:
| 13 | 2 | 8 | 10 | 16 | 9 | 15 | 4 | 18 | 14 | 12 | 11 | 7 | 5 | 3 | 6 | 17 | 1 | 20 | 19 |
| Figur 1.3.9 g) : Tabellen inneholder en permutasjon av tallene fra 1 til 20 | |||||||||||||||||||
int[] a = {13,2,8,10,16,9,15,4,18,14,12,11,7,5,3,6,17,1,20,19};
int pos = Tabell.parter(a, 11); // bruker 11 som skilleverdi
System.out.println(pos + " " + Arrays.toString(a));
Programkode 1.3.9 c)
Effektivitet: Hvor effektiv er
parter0()?
Skilleverdien sammenlignes med alle verdiene. Hvis det er n av dem, blir det
derfor minst n sammenligninger (og maksimalt n + 1 stykker). Se
Oppgave 5. Men hva med ombyttinger?
For å gjøre analysen enklere antar vi at tabellen
inneholder en permutasjon av tallene fra 1 til n og at et av dem, f.eks. tallet s,
brukes som skilleverdi. Etter partisjoneringen vil de
som er mindre enn s (tall fra 1 til s − 1) havne først, dvs. på de
s − 1 første plassene. Det betyr at alle som ikke er mindre enn s
blant de s − 1 første i den opprinnelige tabellen, vil bli flyttet ved ombyttinger.
Det gir flg. setning:
Setning 1.3.9 a) La tabellen inneholde en vilkårlig permutasjon av tallene fra
1 til n og la s være et av dem. Da vil antallet tall blant de s − 1 første
som ikke er mindre enn s (dvs. større enn eller lik s), være det samme som antallet
ombyttinger med s som skilleverdi i partisjoneringsalgoritmen.
Tabellen i Figur 1.3.9 g)
inneholder en permutasjon av tallene fra 1 til 20. La s = 11 være skilleverdi. Blant de
s − 1 = 10 første tallene er det fire (17, 20, 11 og 15) som ikke er mindre enn s.
Dermed fire ombyttinger. Vi kan snu dette på hodet. Antallet ombyttinger
blir også lik antallet tall blant de n − s + 1 siste som er mindre enn
s. Flg. metode finner antallet:
public static int antallOmbyttinger(int[] a, int s)
{
int antall = 0, m = s - 1;
for (int i = 0; i < m; i++) if (a[i] > m) antall++;
return antall;
}
Programkode 1.3.9 d)
Hvor mange ombyttinger er det i gjennomsnitt i partisjoneringsalgoritmen? Under bestemte forutsetninger
kan antallet beregnes eksakt. Vi har flg. setning
(se Avsnitt 1.3.16):
Setning 1.3.9 b) Det gjennomsnittlige antallet ombyttinger i
algoritmen for partisjonering, der gjennomsnittet
tas over alle permutasjoner av tallene fra 1 til n og over alle skilleverdier s
fra 1 til n, er eksakt lik (n2 − 1)/6n.
Vi kan telle opp ved hjelp av metoden
Programkode 1.3.9 d). I flg. kode
telles ombyttingene i alle permutasjonene av tallene fra 1 til 10 og med hvert av tallene som skilleverdi:
int[] a = {1,2,3,4,5,6,7,8,9,10};
boolean flere = true;
int antall = 0;
while (flere)
{
for (int s = 1; s <= a.length; s++) antall += antallOmbyttinger(a, s);
flere = Tabell.nestePermutasjon(a);
}
System.out.println(antall); // Utskrift: 59875200
Programkode 1.3.9 e)
Det totale antallet ble 59 875 200 =
27·35·52·7·11. Gjennomsnittet finner vi ved først å dele med
10 = 2·5 siden det er 10 skilleverdier for hver permutasjon. Deretter deler vi med antall permutasjoner
som er 10! = 3 628 800 = 28·34·52·7. Forkorting
gir 33/20 som gjennomsnitt. Men det er eksakt lik (n2 - 1)/6n = (102 - 1)/60
= 99/60 = 33/20. Se også Oppgave 6.
I Eksempel 1.3.9 e) inngikk
skilleverdien 11 i tabellen. Etter partisjoneringen havnet den litt til høyre for skillet mellom
de to delene. Et mål kan være å få en skilleverdi, som hører til tabellen, til å havne nøyaktig
på skillet mellom de to delene. Da er den på rett sortert plass:
Definisjon 1.3.9 c): En verdi
i en tabell står på rett sortert plass hvis alle elementene til venstre for den
er mindre enn eller lik og alle elementene til høyre for den
er større enn eller lik.
I tabellen i Eksempel 1.3.9 e)
har tallet 11, som ble brukt som skilleverdi, en bestemt indeks m. I flg. tabell er indeksene
v, m og h markert:
| 13 | 2 | 8 | 10 | 16 | 9 | 15 | 4 | 18 | 14 | 12 | 11 | 7 | 5 | 3 | 6 | 17 | 1 | 20 | 19 |
| v | m | h | |||||||||||||||||
| Figur 1.3.9 h) : Skilleverdien 11 har indeks lik m. | |||||||||||||||||||
Verdiene på indeks m og h (dvs. 11 og 19) bytter plass og indeks h flyttes én mot venstre:
| 13 | 2 | 8 | 10 | 16 | 9 | 15 | 4 | 18 | 14 | 12 | 19 | 7 | 5 | 3 | 6 | 17 | 1 | 20 | 11 |
| v | h | ||||||||||||||||||
Figur 1.3.9 i) : 11 ligger bakerst og
intervallet a[v:h] har fått grå bakgrunn. | |||||||||||||||||||
En partisjonering av intervallet a[v:h] − den grå delen i
Figur 1.3.9 i) over − med bakerste verdi (11) som skilleverdi,
gir flg. oppdeling der indeks k angir skillet:
| 1 | 2 | 8 | 10 | 6 | 9 | 3 | 4 | 5 | 7 | 12 | 19 | 14 | 18 | 15 | 16 | 17 | 13 | 20 | 11 |
| v | k | h | |||||||||||||||||
Figur 1.3.9 j) : k er indeks til første verdi i a[v:h] som er større enn eller lik skilleverdi 11 | |||||||||||||||||||
Tallet 11 som opprinnelig hadde indeks m i
Figur 1.3.9 h), ble først flyttet bakerst. Den vil
komme på rett sortert plass hvis den byttes med verdien (tallet 12) på indeks/plass k:
| 1 | 2 | 8 | 10 | 6 | 9 | 3 | 4 | 5 | 7 | 11 | 19 | 14 | 18 | 15 | 16 | 17 | 13 | 20 | 12 |
| Figur 1.3.9 k) : 11 er på rett sortert plass - de til venstre er mindre og de til høyre er større | |||||||||||||||||||
En vilkårlig tabellverdi, f.eks. a[indeks], kan være
skilleverdi i parter0(). To ombyttinger
(en før og en etter) får den inn på rett sortert plass (flg. metode hører til klassen Tabell):
private static int sParter0(int[] a, int v, int h, int indeks) { bytt(a, indeks, h); // skilleverdi a[indeks] flyttes bakerst int pos = parter0(a, v, h - 1, a[h]); // partisjonerer a[v:h - 1] bytt(a, pos, h); // bytter for å få skilleverdien på rett plass return pos; // returnerer posisjonen til skilleverdien } Programkode 1.3.9 f)
Det er ingen ekstra sammenligninger i sParter0(). Hvis intervallet a[v:h]
har n verdier, blir det n − 1 stykker i parter0() siden kallet skjer på
a[v:h-1]. Det blir to ekstra ombyttinger. Det kan vises at hvis sParter0()
brukes på en permutasjon
av tallene fra 1 til n og med en tilfeldig indeks, vil gjennomsnittlig
antall ombyttinger bli eksakt 2 + (n − 2)/6 = (n + 10)/6.
Hvis vi har offentlige versjoner av sParter0()
(se Oppgave 9) vil flg. kode gjøre som i
Fig. 1.3.9 h) − k). Legg
merke til at tabelleverdien 11 også ligger på plass/indeks 11:
int[] a = {13,2,8,10,16,9,15,4,18,14,12,11,7,5,3,6,17,1,20,19}; int k = Tabell.sParter(a, 11); // verdi 11 ligger på indeks 11 System.out.println(k + " " + Arrays.toString(a)); // Utskrift: // 10 [1, 2, 8, 10, 6, 9, 3, 4, 5, 7, 11, 19, 14, 18, 15, 16, 17, 13, 20, 12] Programkode 1.3.9 g)
Utskriften fra Programkode 1.3.9 g) viser at 11 er på
rett sortert plass. Alle
verdiene til venstre for 11 er mindre og alle de til høyre er større.
Kvikksortering er en systematisk anvendelse av
sParter0().
Først velges en tabellverdi som skilleverdi. Et kall på sParter0()
får den inn på rett sortert plass k. Dette gjentas på hver side av
k. Osv. Det beste er en skilleverdi som gjør de to sidene noenlunde
like i størrelse. Men med en ukjent tabell er det ingen annen mulighet enn
å velge vilkårlig. F.eks. den første, den midterste eller den siste. En bedre strategi er å ta den
«midterste» av de tre. Se Oppgave 13.
Her velger vi den på midten av a[v:h] (m = (v + h)/2) som
skilleverdi:
Vi bruker på nytt tabellen fra
Figur 1.3.9 h) som utgangspunkt, men denne
gangen bruker vi verdien på midten, dvs. a[m] der m = (v + h)/2, som
skilleverdi:
| 13 | 2 | 8 | 10 | 16 | 9 | 15 | 4 | 18 | 14 | 12 | 11 | 7 | 5 | 3 | 6 | 17 | 1 | 20 | 19 |
| v | m | h | |||||||||||||||||
| Figur 1.3.9 l) : Midtverdien a[m] der m = (v + h)/2 er skilleverdi | |||||||||||||||||||
Metodekallet sParter0(a,v,h,(v + h)/2)
vil gjøre at tabellen blir slik:
| 13 | 2 | 8 | 10 | 1 | 9 | 6 | 4 | 3 | 5 | 12 | 11 | 7 | 14 | 18 | 15 | 17 | 16 | 20 | 19 |
| v | k | h | |||||||||||||||||
| Figur 1.3.9 m) : Tallene i a[v:k − 1] er mindre enn 14 og de i a[ k + 1:h] større enn 14 | |||||||||||||||||||
De «grå» delene a[v:k−1]
og a[k+1:h] er
separate deler. Hvis a[v:k−1]
partisjoneres mhp. midtverdien (6), vil dens verdier fortsatt
ligge til venstre for 14. Hvis a[k+1:h] partisjoneres
mhp. dens midtverdi (17) blir det tilsvarende. Gjør vi begge deler, får vi flg. resultat:
| 5 | 2 | 3 | 4 | 1 | 6 | 7 | 10 | 8 | 13 | 12 | 11 | 9 | 14 | 16 | 15 | 17 | 18 | 20 | 19 |
| Figur 1.3.9 n) : Tallene 6, 14 og 17 ligger alle nå på rett sortert plass | |||||||||||||||||||
Dette fortsetter ved
at sParter0() kalles på hver av de fire «grå» delene. Osv.
Hvis et intervall (en «grå» del) er tomt eller har kun ett element, stopper vi siden det
er sortert.
private static void kvikksortering0(int[] a, int v, int h) // en privat metode { if (v >= h) return; // a[v:h] er tomt eller har maks ett element int k = sParter0(a, v, h, (v + h)/2); // bruker midtverdien kvikksortering0(a, v, k - 1); // sorterer intervallet a[v:k-1] kvikksortering0(a, k + 1, h); // sorterer intervallet a[k+1:h] } public static void kvikksortering(int[] a, int fra, int til) // a[fra:til> { fratilKontroll(a.length, fra, til); // sjekker når metoden er offentlig kvikksortering0(a, fra, til - 1); // v = fra, h = til - 1 } public static void kvikksortering(int[] a) // sorterer hele tabellen { kvikksortering0(a, 0, a.length - 1); } Programkode 1.3.9 h)
Kvikksortering kaller seg selv to ganger. Det kalles rekursjon.
Mer om det i Avsnitt 1.5.7.
Metodekallene stopper når vi får v >= h, og det vil før eller senere skje siden
kallene utføres på intervaller som er kortere enn a[v:h].
Det ene kan i verste fall være tomt. Det andre er dermed bare én kortere enn a[v:h]. Det
gjør at metoden i verste fall blir av kvadratisk orden. Men i gjennomsnitt
vil lengden til intervallene a[v:k−1] og a[k+1:h] ikke skille seg så mye.
Det gjør at kvikksortering i gjennomsnitt er av orden n log2(n).
Mer om dette senere.
Hvis metodene i Programkode 1.3.9 h)
ligger i samleklassen Tabell, vil flg. være kjørbart:
int[] a = Tabell.randPerm(20); // en tilfeldig permutasjon
Tabell.kvikksortering(a); // sorterer
System.out.println(Arrays.toString(a)); // skriver ut
Programkode 1.3.9 i)
Oppsummering - kvikksortering:
Navn:Kvikksortering (eng: quick sort) ble «oppfunnet» allerede i 1959 av briten Tony Hoare og er kjent som den beste (mest effektive) generelle sorteringsteknikken. Ijava.utiler det en optimalisert versjon (a dual-pivot quicksort) som brukes for standardtypene (byte,short,int,long,float,double,char). Men for generiske typer brukes (ijava.util) imidlertidflettesortering(eng: merge sort).Idé og effektivitet:Den kan ses på som en anvendelse av partisjonering, dvs. å dele en tabell (eller et tabellintervall) i to deler mhp. en skilleverdi (eng: pivot). Et enkelt valg av skilleverdi kan være den første eller siste verdien. Men det vil føre til at den får orden n² hvis tabellen allerede er sortert. Da er det bedre å velge den midterste. Men i optimaliserte versjoner gjøres valget på en «lurere» måte. Men uansett vil det være mulig (men ikke enkelt) å konstruere en tabell som gjør at den får orden n². Men i gjennomsnitt er den garantert av orden n log(n). SeOppgave17. En mulig optimaliseringsteknikk er å skifte tilinnsettingssorteringfor små intervaller (lengde mindre enn 47 brukes ijava.util). Den er en «på plass»-algoritme (eng: in place), dvs. at den ikke trenger noen hjelpetabell.Ulemper:Den optimaliserte versjonen vil, som nevnt over, kunne være av kvadratisk orden i (svært) spesielle tilfeller. Hvis en trenger en teknikk som alltid er n log(n), må en velge noe annet - f.eks.heapsorteringsom alltid er av orden n log(n), men som ikke er fullt så god som kvikksortering i gjennomsnitt. Et mulig valg er å kombinere de to slik det er gjort iintrosort. En (liten) ulempe er at den ikke er stabil, dvs. like verdier får ikke nødvendigvis samme innbyrdes rekkefølge etter sorteringen som de hadde før.Konklusjon:Dette vil normalt være førstevalget når en trenger en sorteringsalgoritme.
Vi kan også bruke partisjonering til å finne den m-te minste verdien i en (usortert) tabell, dvs. den verdien som ville ha kommet på plass nr m hvis vi hadde sortert tabellen. F.eks. er den 0-te minste verdien det samme som den minste og den 1-te minste verdien det samme som den andre eller nest minste verdien.
Kvikksøk bruker idéen i kvikksortering.
En partisjonering med midtverdien som skilleverdi, vil
gjøre at den havner på rett sortert plass (indeks k). Hvis det er lik
indeks m, er vi ferdige. Hvis ikke må vi lete videre på venstre side
hvis m < k og på høyre side hvis m > k. Flg. metode
flytter om på på verdiene i tabellen a slik at den m-te verdien til slutt havner på
indeks m. Hvis tabellen a har lengde n, vil kvikksøk får orden n
siden sParter0() kalles kun én gang i hver iterasjon. I
Oppgave 14 blir du bedt om å teste metoden.
public static int kvikksøk(int[] a, int m)
{
if (m < 0 || m >= a.length)
throw new IllegalArgumentException("m(" + m + ") er ulovlig!");
int v = 0, h = a.length - 1; // intervallgrenser
while (true)
{
int k = sParter0(a,v,h,(v + h)/2); // se Programkode 1.3.9 f)
if (m < k) h = k - 1;
else if (m > k) v = k + 1;
else return k;
}
} Programkode 1.3.9 j)
Medianen til en samling verdier er den som ville ha havnet på midten etter en sortering.
Hvis antallet er odde, er dette veldefinert. Hvis ikke, defineres medianen som gjennomsnittet
av de to verdiene på hver side av «midten». Vi kan bruke kvikksøk() til å finne
medianen:
public static double median(int[] a)
{
if (a.length == 0) throw new NoSuchElementException("Tom tabell!");
int k = kvikksøk(a, a.length/2);
return (a.length & 1) == 0 ? (a[k-1] + a[k])/2.0 : a[k];
}
Programkode 1.3.9 k)
| 1. | I parter0() testes ikke
a[v:h]. En privat metode er laget for bruk i andre
metoder. Lag en offentlig versjon med navn parter der
a[fra:til> er intervallet. Test den vha. metoden
fraTilKontroll().
Lag også en versjon som bruker hele tabellen.
|
| 2. |
Gjennomfør Eksempel 1.3.9 e)
med «papir og penn».
Setning 1.3.9 a)
vil på forhånd si hvor mange ombyttinger det blir.
Legg parter0() i klassen
Tabell (og løs Oppgave 1 hvis du ikke har gjort det).
Programkode 1.3.9 c)
gir en fasit. (Du får en fasit etter hver iterasjon hvis du midlertidig legger inn en utskriftssetning
etter hver ombytting).
|
| 3. | Gjør som i Oppgave 2 med tabellen 7,10,3,4,1,6,8,2,9,5. Først
7 og så 5 som skilleverdi.
|
| 4. | Gitt tabellen 11,2,17,1,9,8,12,14,15,3,19,18,7,10,16,20,13,4,6,5. Gjør som
Oppgave 2. Bruk først 6
som skilleverdi, så 10 og til slutt 15.
|
| 5. | Sjekk at hvis parter0() kalles
på et intervall med lengde n, vil antall sammenligninger med skilleverdi
være n eller n + 1.
|
| 6. |
Sjekk at resultatet i Programkode 1.3.9 e)
også stemmer for 8 og 9.
|
| 7. |
Gitt en vilkårlig tabell med tallene fra 1 til 30.
Del den i tre - 1. del tallene fra 1 til 10, 2. del de fra 11 til 20 og
3. del resten. Hint: Bruk parter() to ganger. Se Oppgave 1.
|
| 8. |
La Programkode 1.3.9 a)
starte med to while-løkker med v <= h. Så en
while (true)-løkke der det først sjekkes om v < h. Hvis nei,
returneres v. Hvis ja, byttes
verdiene. Da blir a[v] og a[h] stoppverdier og
vi kan fortsette med to while-løkker uten v <= h.
|
| 9. | Den private metoden sParter0() tester ikke
a[v:h]. En privat metode er laget for bruk i andre
metoder. Lag to offentlige versjoner med navn sParter, den ene med
a[fra:til> og den andre hele tabellen. Indeksen må ligge
innenfor intervallet (eller tabellen). Derfor må intervallet være lovlig og inneholde minst én verdi.
|
| 10. | Kjør Programkode 1.3.9 g).
Bruk også andre indekser enn 11. Bruker du f.eks. indeks 3, vil a[3] = 10
og med indeks 0 vil a[0] = 13 komme på rett sortert plass.
|
| 11. | Legg metodene i Programkode 1.3.9 h)
i samleklassen Tabell.
Kjør Programkode 1.3.9 i)
flere ganger. Sjekk at det blir sortert. Sjekk spesielt en tabell med lengde 1 og lengde 0.
|
| 12. |
Sjekk tidsforbruket til
kvikksortering() sammenlignet med
innsettingssortering().
Sammenlign også med metoden sort() i klassen
Arrays.
I kvikksortering0() kan en stoppe hvis
f.eks. h - v < 20. Bruk innsettingssortering til slutt. Øker effektiviteten?
|
| 13. |
Gjør om kvikksortering0()
slik at den «midterste» av den første, den på midten og den siste verdien i
tabellintervallet a[v:h] brukes som skilleverdi.
|
| 14. |
Lag kode som tester
kvikksøk(). Lag så kode som tester
median(). Pass på at du bruker
tabeller med oddetallslengde og med partallslengde. Vær oppmerksom på at tabellen endrer seg når
en av disse metodene brukes.
|
| 15. | Prøv flg. idé for parter0():
La v og h være som før. Hvis a[v] < skilleverdi,
økes v med 1. Hvis ikke byttes a[v] og a[h] og h
reduseres med 1. Igjen sammenlignes a[v] og skilleverdi osv.
så lenge som v <= h. Til slutt returneres v.
Hvor mange ombyttinger og sammenligninger er det i denne algoritmen. |
| 16. | Prøv flg. idé for parter0():
La v og h være som før.
Legg a[v] i en variabel verdi og sett indeks k
lik v. Da er a[k] «ledig». Så v++. Hvis
a[v] < skilleverdi, flyttes a[v]
til indeks k. Da blir indeks v ledig. Verdien a[k+1] flyttes til indeks
v. Det gjør indeks k + 1 «ledig». Så k++.
Så v++ uansett om a[v] < skilleverdi eller ikke.
Dette går så lenge som v <= h.
Til slutt må verdi legges på indeks k. Metoden må returnere
k + 1 hvis a[k] er mindre enn skilleverdi og
k ellers. Hvor effektivt blir dette?
|
| 17. | Med n forskjellige tall vil vår versjon
i gjennomsnitt utføre 2(n + 1)Hn − (11/3)n − 1/6
sammenligninger med og (1/3)(n + 1)Hn + (5/9)n − 11/18
ombyttinger av tabellverdier. Hvis du er interessert, finner du et bevis
Avsnitt 1.3.16.
Vi kan også lage kode som tester dette. Legg inn flg. kode i samleklassen Tabell:
public static int teller = 0; private static boolean comp(int x, int y) { teller++; // øker for hver sammenligning return x < y; }
Alle sammenligninger der tabellverdier inngår, gjøres i metoden
Lag så tilfeldige permutasjoner av tallene fra 1 til 1000. Bruk
I |
 |
| Hollands flagg |
Eksempel 1.3.9 c)
har en tabell som kun inneholder bokstavene R, H og B.
Oppgaven er å få den omorganisert slik at først kommer R-ene, så
H-ene og til slutt B-ene. Oppgaven har (av E. W. Dijkstra)
fått navnet «The Dutch National Flag Problem».
Bokstavene stå for fargene i det hollandske flagget
(rød, hvit og blå). Målet er, med minst mulig «arbeid», å få tabellen «lik» flagget, dvs. det «røde»
først, så det «hvite» og det «blå» til slutt.
Tabellen fra Eksempel 1.3.9 c)
så slik ut:
| H | B | R | B | H | H | R | B | R | H | B | R | H | R | R | B | H | B | H | R |
Vi ønsker (med minst mulig «arbeid») at den skal bli slik:
| R | R | R | R | R | R | R | H | H | H | H | H | H | H | B | B | B | B | B | B |
Et mulighet å bruke vanlig partisjonering to ganger. Først separeres R-ene fra resten av bokstavene og legges først. Så deles resten av tabellen opp i H-er og B-er. For eksempel slik:
public static void omorganiser(char[] c)
{
int v = 0, h = c.length-1;
while (v <= h) if (c[v] == 'R') v++; else Tabell.bytt(c,v,h--);
h = c.length-1; // nå ligger R-ene først
while (v <= h) if (c[v] == 'H') v++; else Tabell.bytt(c,v,h--);
}
Programkode 1.3.10 a)
La c ha n verdier som er R,
H eller B. Dermed blir det 3n
mulige tabeller med i gjennomsnitt 1/3 R-er, 1/3 H-er
og 1/3 B-er. I første while-løkke i
Programkode 1.3.10 a)
blir det alltid n sammenligninger. I andre like mange som det
er H-er og B-er, dvs. i gjennomsnitt 2n/3 stykker.
Til sammen 5n/3 sammenligninger i gjennomsnitt.
I første while-løkke blir det én ombytting hver gang c[v]
er ulik R. Dvs. i gjennomsnitt 2n/3 ganger.
I den andre løkken blir det en hver gang c[v]
er ulik H, dvs. n/3 ganger. Sammenlagt
n ombyttinger i gjennomsnitt.
Det er ikke mulig med færre sammenligninger i
gjennomsnitt enn i Programkode 1.3.10 a). Hver
verdi må undersøkes minst én gang. Da trengs én sammenligning
for å avgjøre om den er en R. Hvis ikke,
én til for å avgjøre om det er en H eller B.
I gjennomsnitt (1 · 1/3 + 2 · 2/3)n = 5n/3
stykker. Men det er mulig å gjøe det med færre
ombyttinger.
Vi kan gjøre som i Avsnitt 1.3.9, men nå
ha tabellen firedelt.
Først R-er, så den «ukjente» delen, så H-er og til slutt B-er.
Figuren viser hvordan det kan se ut etter noen iterasjoner:
| R | R | R | R | ? | ? | ? | ? | ? | ? | ? | ? | H | H | H | H | H | B | B | B |
| v | h | k | |||||||||||||||||
Indeksene v og h står først og sist i den «ukjente» delen og k sist i H-delen (h = k hvis ingen H-er). Vi har tre muligheter for c[h]. Hvis den er lik R, bytter vi c[h] og c[v]. Da blir den én R mer og v må økes med 1. Hvis c[h] er lik H flytter vi h en mot venstre. Hvis c[h] er lik B, bytter vi c[h] og c[k] og reduserer både h og k med 1. Algoritmen går så lenge som v <= h:
public static void omorganiser(char[] c) // ny versjon
{
int v = 0, h = c.length-1, k = h; // v forrest, h og k bakerst
while (v <= h)
{
if (c[h] == 'R') Tabell.bytt(c,v++,h);
else if (c[h] == 'H') h--;
else Tabell.bytt(c,h--,k--);
}
} Programkode 1.3.10 b)
Det er ikke vanskelig å se at det utføres nøyaktig 5n/3 sammenligninger
i gjennomsnitt i
Programkode 1.3.10 b). I hver iterasjon vil det bli én ombytting
hvis c[h] er lik R, ingen hvis den er lik H og én
hvis den er lik B. Det gir 2n/3 ombyttinger i gjennomsnitt. Med
andre ord er dette en del bedre enn i
Programkode 1.3.10 a).
Det er mulig med noen færre ombyttinger. Hvis c[h]
er lik R eller H samtidig som v er lik h, er
ombyttingen unødvendig.
Den kan fjernes ved å la while-løkken gå så lenge som v < h og så
behandle v lik h spesielt.
Det er også unødvendig å bytte om hvis c[h] er lik B og h
er lik k. En test på om h er lik k vil imidlertid koste mer enn
vi tjener inn. Men
Programkode 1.3.10 b)
kan endres slik at det gjennomsnittlig antall ombyttinger blir
(se Oppgave 3):
(*) 2n/3 - 4/3 + (2/3)n
Det finnes 3n forskjellige n-permutasjoner med repetisjon som inneholder R, H eller B. Her definerer vi, med tanke på leksikografisk ordning, at R kommer foran H som igjen kommer foran B. Flg. metode gir den neste n-permutasjonen med repetisjon:
public static boolean nestePermutasjon(char[] c)
{
int n = c.length, i = n - 1; // i starter bakerst i c
while (i >= 0 && c[i] == 'B') i--;
if (i < 0) return false; // tabellen c har kun B-er
c[i] = (c[i] == 'R' ? 'H' : 'B');
for (int j = i+1; j < n; j++) c[j] = 'R';
return true; // c inneholder en ny permutasjon
}
Programkode 1.3.10 c)
Hvis vi starter med RRR, vil neste bli RRH, så RRB, så RHR, osv. Flg. kodebit gir alle:
char[] c = "RRR".toCharArray();
boolean flere = true;
while (flere)
{
Tabell.skrivln(c);
flere = nestePermutasjon(c);
}
Programkode 1.3.10 d)
Vi kan finne det gjennomsnittlige antallet ombyttinger som utføres i
Programkode 1.3.10 b)
ved å bruke Programkode 1.3.10 d) til
å generere alle mulige n-permutasjoner (med repetisjon). Vi må imidlertid
lage en omorganiser-metode der ombyttingene telles opp:
public static int antallOmorganiser(char[] c)
{
int v = 0, h = c.length-1, k = h; // v forrest, h og k bakerst
int antall = 0; // antall ombyttinger
while (v <= h)
{
if (c[h] == 'R') { Tabell.bytt(c,v++,h); antall++; }
else if (c[h] == 'H') h--;
else { Tabell.bytt(c,h--,k--); antall++; }
}
return antall;
}
Programkode 1.3.10 e)
Vi kan generere alle permutasjoner og så la metoden over telle opp.
Gjennomsnittlig antall ombyttinger i
Programkode 1.3.10 b) var 2n/3. Hvis n = 3 får vi totalt
27 permutasjoner og dermed 27*2*3/3 = 54 ombyttinger tilsammen. Flg.
programbit bør derfor gi 54 som utskrift:
char[] c = "RRR".toCharArray(), d = new char[c.length];
boolean flere = true; int antall = 0; // antall ombyttinger
while (flere)
{
System.arraycopy(c,0,d,0,c.length); // kopierer c over i d
antall += antallOmorganiser(d); // omorganiserer d
flere = nestePermutasjon(c); // ny permutasjon
}
System.out.println(antall); // Utskrift: 54
Programkode 1.3.10 f)
Vi kan gå fra R, H og B til tre vilkårlige tegn
ved hjelp av parameterverdier. Se Oppgave 2.
| 1. | Gjennomsnittlig antall ombyttinger som metoden i
Programkode 1.3.10 b) gjør for de
3n forskjellige n-permutasjonene, er 2n/3.
Hva blir det totale antallet ombyttinger for alle
permutasjonene hvis n = 4, 5 og 6?
Test med Programkode 1.3.10 f).
| ||
| 2. | Lag generaliserte versjoner av
Programkode 1.3.10 b),
1.3.10 c) og
1.3.10 e)
der de tre aktuelle tegnene oppgis som parameterverdier.
Bruk dem i 1.3.10 f).
| ||
| 3. | En ombytting er unødvendig hvis c[h]
er lik R eller H samtidig som v er lik h.
Det er også unødvendig å bytte om hvis c[h] er lik B samtidig
som h er lik k. Lag en ny versjon av
antallOmorganiser
uten disse ombyttingene. Hvis den brukes i
Programkode 1.3.10 f),
blir svaret lik formelen i (*)
ganget med 3n. Sjekk det for noen verdier av n.
| ||
| 4. | Bruk idéen fra Programkode 1.3.10 b)
til å lage en
parter-metode med
to skilleverdier s1 og s2 der s1 <= s2.
Første del skal inneholde de som er mindre enn s1, andre del de som er
mindre enn s2 (men ikke mindre enn s1) og siste del
av de som ikke er mindre enn s2. | ||
| 5. |
Mauritius har flaggfargene rød, blå, gul og grønn. Vi bruker
|
![]() 1.3.11 Fletting og flettesortering
1.3.11 Fletting og flettesortering
Å flette (eng: merge) betyr å forene. F.eks. å tvinne sammen flere enheter til en felles enhet.
Vi kan flette hår eller vi kan flette kvister til en kurv. Hvis en vei med to felter i samme retning snevres
inn til kun ett felt, er det mest «rettferdig» at trafikken «flettes sammen».
I databehandling er det aktuelt å flette to eller flere sekvensielle enheter (f.eks. tegnstrenger, tabeller, lister eller filer) til en felles enhet av samme type. En enkel form for fletting av to enheter er at annenhver verdi kommer fra den ene og annenhver fra den andre. Hvis det er ulikt antall, må vi ha en regel for de som er «til overs». De kan f.eks. legges inn bakerst:
public static int[] enkelFletting(int[] a, int[] b) { int[] c = new int[a.length + b.length]; // en tabell av rett størrelse int i = 0, j = 0, k = 0; // løkkevariabler while (i < a.length && j < b.length) { c[k++] = a[i++]; // først en verdi fra a c[k++] = b[j++]; // så en verdi fra b } // vi må ta med resten while (i < a.length) c[k++] = a[i++]; while (j < b.length) c[k++] = b[j++]; return c; } Programkode 1.3.11 a)
Hvis a og b er like lange, vil ingen av de to siste while-løkkene utføres. Med ulike lengder vil kun den som hører til den lengste, utføres. Flg. eksempel viser hvordan den virker:
int[] a = {1,3,5,7,9,11}, b = {2,4,6,8,10}; // to heltallstabeller int[] c = enkelFletting(a, b); System.out.println(Arrays.toString(c)); // Utskrift: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] Programkode 1.3.11 b)
Det blir på samme måte for andre typer strukturer, f.eks. to tegnstrenger. Det som vil være forskjellig er hvordan en henter ut en og en verdi fra de to strukturene og hvordan man setter inn annenhver gang fra de to. Se Oppgave 1b).
Sortert fletting Anta at vi har to sekvensielle datastrukturer, f.eks. to tabeller, som begge er sortert.
En viktig oppgave er da å kunne flette dem sammen til en datastruktur som er sortert. Da blir det normalt feil
bruke regelen om «annenhver verdi». Vi må gjøre det på en annen måte.
Se på flg. eksempel med to heltallstabeller:
| a |
|
b |
|
||||||||||||||||||||||||||||||||||
| c |
|
||||||||||||||||||||||||||||||||||
| Figur 1.3.11 a) : To sorterte tabeller a og b skal flettes sammen i c | |||||||||||||||||||||||||||||||||||
I Figur 1.3.11 a) har vi to sorterte tabeller a og b med
henholdsvis 7 og 10 verdier. De skal flettes sammen og legges i en tredje tabell c slik at c blir sortert.
Den har plass til de 7 + 10 = 17 verdiene.
Første posisjon (posisjon 0) i a, b og c er markert med henholdsvis
i, j og k.
Algoritme: Sammenlign a[i]
og b[j]. Hvis a[i] er mindre enn eller lik b[j],
kopieres den over i posisjon k i c og både i og k økes med 1.
Hvis ikke, dvs. hvis b[j] er minst, kopieres
den over i posisjon k i c og både j og k økes med 1.
Etter fem «runder» får vi:
| a |
|
b |
|
||||||||||||||||||||||||||||||||||
| c |
|
||||||||||||||||||||||||||||||||||
| Figur 1.3.11 b) : Fem verdier er flettet sammen. | |||||||||||||||||||||||||||||||||||
Det er ofte aktuelt å kunne flette sammen to sorterte tabellintervaller, f.eks. de to halvåpne intervallene
a[0:m> og b[0:n>. Flg. metode gjør dette
og returnerer antallet. Tabellen c må være
stor nok, dvs. ha plass til minst
m + n verdier. Metoden legges i samleklassen Tabell:
public static int flett(int[] a, int m, int[] b, int n, int[] c) { int i = 0, j = 0, k = 0; while (i < m && j < n) c[k++] = a[i] <= b[j] ? a[i++] : b[j++]; while (i < m) c[k++] = a[i++]; // tar med resten av a while (j < n) c[k++] = b[j++]; // tar med resten av b return k; // antallet verdier som er lagt inn i c } Programkode 1.3.11 c)
I Programkode 1.3.11 c) blir a[i] <= b[j]
utført m + n – 1 ganger hvis
tallene i a og b er slik at a[i] <= b[j] blir
sann/usann annenhver gang.
F.eks. hvis a = { 1, 3, 5, 7, 9 }
og b = { 2, 4, 6, 8, 10 }.
Hvis siste verdi i a er mindre enn første i b, vil
a[i] <= b[j] bli utført m ganger, og hvis omvendt,
n ganger. Normalt et sted
mellom min( m , n ) og m + n – 1.
Det betyr at algoritmen har orden m + n i gjennomsnitt.
Flg. metode fletter sammen to hele tabeller ved hjelp av
flett():
public static int flett(int[] a, int[] b, int[] c) // legges i samleklassen Tabell { return flett(a, a.length, b, b.length, c); } Programkode 1.3.11 d)
Flg. eksempel viser hvordan dette kan brukes:
int[] a = {1,3,4,6,9,9,11}, b = {2,3,5,6,7,8,9,10,12,14}; // sorterte tabeller int[] c = new int[a.length + b.length]; // nå er c stor nok Tabell.flett(a,b,c); // fletter sammen Tabell.skriv(c); // Utskrift: 1 2 3 3 4 5 6 6 7 8 9 9 9 10 11 12 14 Programkode 1.3.11 e)
Fletting er en viktig teknikk. F.eks. er fletting den essensielle delen
i flettesortering (eng: merge sort). Idéen er at en tabell kan sorteres
ved at dens to halvdeler sorteres hver for seg og at de så flettes sammen.
Dette gjentas rekursivt for hver av de to delene. I flettesortering er det
sorterte nabointervaller som flettes sammen. Se på flg. eksempel:
| a |
|
||||||||||||||||||||||||||||||||||||||
| Figur 1.3.11 c) : Nabointervallene a[fra:m> og a[m:til> skal flettes sammen. | |||||||||||||||||||||||||||||||||||||||
Intervallene a[fra:m> (hvit del med tall) og a[m:til> (den grå delen) skal flettes sammen. Først kopieres a[fra:m> over
i b. Den må minst ha plass til n verdier der n = m – fra:
| a |
|
||||||||||||||||||||||||||||||||||||||
| b |
|
||||||||||||||||||||||||||
| Figur 1.3.11 d) : Intervallet a[fra:m> er kopiert over i b[0:n>. | |||||||||||||||||||||||||||
Neste skritt er å flette sammen b[0:n> og a[m:til>. Legg spesielt merke til
at hvis vi i flettingen blir ferdig med verdiene i b[0:n> først, trenger vi ikke gjøre noe
med det som ligger igjen bakerst i a[m:til>. De ligger der de skal ligge:
| a |
|
||||||||||||||||||||||||||||||||||||||
| b |
|
||||||||||||||||||||||||||
| Figur 1.3.11 e) : Intervallet a[fra:til> er nå sortert. | |||||||||||||||||||||||||||
Flg. private hjelpemetode fletter b[0:n> og a[m:til> over
i a[fra:til>:
private static void flett(int[] a, int[] b, int fra, int m, int til) { int n = m - fra; // antall elementer i a[fra:m> System.arraycopy(a,fra,b,0,n); // kopierer a[fra:m> over i b[0:n> int i = 0, j = m, k = fra; // løkkevariabler og indekser while (i < n && j < til) // fletter b[0:n> og a[m:til> og { // legger resultatet i a[fra:til> a[k++] = b[i] <= a[j] ? b[i++] : a[j++]; } while (i < n) a[k++] = b[i++]; // tar med resten av b[0:n> } Programkode 1.3.11 f)
Flg. rekursive (og private) metode benytter flett-metoden i Programkode 1.3.11 f):
private static void flettesortering(int[] a, int[] b, int fra, int til) { if (til - fra <= 1) return; // a[fra:til> har maks ett element int m = (fra + til)/2; // midt mellom fra og til flettesortering(a,b,fra,m); // sorterer a[fra:m> flettesortering(a,b,m,til); // sorterer a[m:til> if (a[m-1] > a[m]) flett(a,b,fra,m,til); // fletter a[fra:m> og a[m:til> } Programkode 1.3.11 g)
I koden over deles a[fra:til> på midten og metoden kalles (rekursjon) først på
a[fra:m> og så på a[m:til>.
Etterpå vil de være sortert og kan flettes sammen. Legg merke til setningen:
if (a[m-1] > a[m]). Intervallet a[fra:til> er allerede
sortert hvis den siste i a[fra:m> er mindre enn eller lik den første i a[m:til>.
Midtdelingen gjør at dette blir av orden n log2(n) og dermed en effektiv metode.
Flg. offentlige metode sorterer en hel tabell:
public static void flettesortering(int[] a) { int[] b = Arrays.copyOf(a, a.length/2); // en hjelpetabell for flettingen flettesortering(a,b,0,a.length); // kaller metoden over } Programkode 1.3.11 h)
Hvis metodene over er lagt i samleklassen Tabell, vil flg. kodebit være kjørbar:
int[] a = Tabell.randPerm(15); Tabell.flettesortering(a); Tabell.skriv(a); // Utskrift: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Programkode 1.3.11 i)
Union
La a[0:m> være sortert med ulike verdier. Tilsvarende for b[0:n>.
De kan da ses på som to mengder. Vi finner
«unionen» ved å flette dem sammen. En verdi som ligger i begge to
tas med kun én gang. Flg. metode legger «unionen» i tabellen c
og returnerer antallet:
public static int union(int[] a, int m, int[] b, int n, int[] c) { int i = 0, j = 0, k = 0; // indekser for a, b og c while (i < m && j < n) { if (a[i] < b[j]) c[k++] = a[i++]; // tar med a[i] else if (a[i] == b[j]) // a[i] og b[j] er like { c[k++] = a[i++]; j++; // tar med a[i], men ikke b[j] } else c[k++] = b[j++]; // tar med b[j] } while (i < m) c[k++] = a[i++]; // tar med resten av a[0:m> while (j < n) c[k++] = b[j++]; // tar med resten av b[0:n> return k; // antall verdier i unionen } Programkode 1.3.11 j)
Metoden union() returnerer antallet. Det er mindre enn m +
n hvis a og b har felles verdier. Flg. metode finner
«unionen» av hele tabeller:
public static int union(int[] a, int[] b, int[] c) { return union(a, a.length, b, b.length, c); } Programkode 1.3.11 k)
Hvis metodene over er lagt i samleklassen Tabell, vil flg. kodebit være kjørbar:
int[] a = {1,3,4,6,9,11,13}; // ingen like verdier int[] b = {2,3,5,6,7,8,9,10,11,12}; // ingen like verdier int[] c = new int[a.length + b.length]; // c er nå stor nok System.out.println(Arrays.toString(Arrays.copyOf(c, union(a, b, c)))); // Utskrift: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13] Programkode 1.3.11 l)
Snittet av to mengder er det de har felles.
Vi kan finne snittet ved å bruke en fletteteknikk:
public static int snitt(int[] a, int m, int[] b, int n, int[] c) { int i = 0, j = 0, k = 0; // indekser for a, b og c while (i < m && j < n) { if (a[i] < b[j]) i++; // hopper over a[i] else if (a[i] == b[j]) // a[i] og b[j] er like { c[k++] = a[i++]; j++; // tar med a[i], men ikke b[j] } else j++; // hopper over b[j] } return k; // antall i snittet } public static int snitt(int[] a, int[] b, int[] c) // hele tabeller { return snitt(a, a.length, b, b.length, c); } Programkode 1.3.11 m)
Hvis metodene over er lagt i samleklassen Tabell, vil flg. kodebit være kjørbar:
int[] a = {1,3,4,6,9,11,13}; // ingen like verdier int[] b = {2,3,5,6,7,8,9,10,11,12}; // ingen like verdier int[] c = new int[Math.min(a.length,b.length)]; // c er nå stor nok System.out.println(Arrays.toString(Arrays.copyOf(c, snitt(a, b, c)))); // Utskrift: [3, 6, 9, 11] Programkode 1.3.11 n)
I oppgavene nedenfor blir du bedt om, ved hjelp av fletteteknikk, å lage metoder for
differens,
xunion (eksklusiv union eller symmetrisk differens) og inklusjon.
| 1. | a) Bruk arraycopy() til slutt
i enkelFletting() istedenfor for-løkker. |
b) Lag metoden public static String enkelFletting(String a, String b). Den skal returnere
en tegnstreng der annethvert tegn kommer fra a og annethvert fra b. | |
| 2. | a) Figur 1.3.11 b) viser resultatet
av flettealgoritmen etter at 5 verdier er kopiert over i c. Tegn resultatet
etter at henholdsbvis 7, 9 og 11 verdier er kopiert over. |
b) La a inneholde tallene 1, 2, 3 og b tallene 4, 5, 6, 7, 8.
Hvor mange ganger vil sammenligningen a[i] <= b[j]
i Programkode 1.3.11 c)
bli utført hvis metoden anvendes på a
og b? Hva hvis a og b isteden inneholder 1, 3, 5, 7 og 2, 4, 6, 8? | |
| 3. | Test effektiviteten til
Programkode 1.3.11 h).
Lag tilfeldige tabeller (bruk randPerm) og ta tiden.
Velg så store tabeller at det tar ca. 1 sekund.
Sammenlign med kvikksortering() og med metoden sort() i klassen
Arrays.
|
| 4. | Vi sier at a[0:m> er tomt hvis m = 0
og ulovlig hvis m < 0 eller m > a.length. Tilsvarende for b[0:n>. Hva vil skje i
metodene
flett(),
union() og
snitt()
hvis både a[0:m>
og b[0:n>, eller eventuelt bare en av dem, er tomme? Hva hvis en eller begge
er ulovlige? |
| 5. | Lag metoden public static int forskjellige(int[] a) der
a er sortert, men kan ha like verdier.
Den skal omorganisere a slik at de forskjellige verdiene kommer sortert
først og duplikatene sortert bakerst, og returnere antallet forskjellige
verdier. |
| 6. | Medianen til en samling heltall er den verdien som havner på midten
når samlingen sorteres. Gitt to sorterte heltallstabeller a og b.
Finn en teknikk av logaritmisk orden som finner medianen for a og b.
Hint: Finn midtverdiene i a og b, sammenlign, osv.
|
Fra nå av skal vi anta at hverken
a[0:m> eller b[0:n> har like verdier og
i tillegg at begge er sortert stigende. Videre sier vi at a[0:m> er tom hvis m = 0
og ulovlig hvis m < 0. Tilsvarende for b[0:n>. Legg alle
metodene i samleklassen Tabell.
| |
| 7. | Lag public static boolean erLik(int[] a, int m, int[] b, int n).
Den skal avgjøre om a[0:m> og b[0:n> er like, dvs. har
nøyaktig samme innhold. Her kan det være lurt å bruke at de er ulike hvis de inneholder
forskjellige antall verdier. Lag også en versjon som arbeider med hele tabeller.
|
| 8. | Lag public static int differens(int[] a, int m, int[] b, int n, int[] c).
Den skal legge, i sortert rekkefølge, de verdiene som er i a[0:m>, men som
ikke er i b[0:n>, over i c. Dette svarer til begrepet mengdedifferens
fra mengdelæren. Metoden skal returnere antallet verdier som er lagt i c.
Bruk idéen fra flett-metoden.
Lag også en versjon som arbeider med hele tabeller.
|
| 9. | Lag public static boolean inklusjon(int[] a, int m, int[] b, int n).
Den skal avgjøre om b[0:n> er inneholdt i a[0:m>. Dette svarer til
begrepet inklusjon (dvs. være en delmengde) fra mengdelæren. Metoden skal returnere true eller false.
Bruk idéen fra flett-metoden.
Lag også en versjon som arbeider med hele tabeller.
|
| 10. | Lag public static int xunion(int[] a, int m, int[] b, int n, int[] c).
Den skal legge, i sortert rekkefølge, de verdiene som er i a[0:m> eller i
b[0:n>, men som ikke er i begge, over i c. Dette svarer til begrepet
eksklusiv union (eller symmetrisk differens) fra mengdelæren. Den skal returnere antallet verdier
som er lagt i c. Bruk idéen fra flett-metoden.
Lag også en versjon som arbeider
med hele tabeller. |
![]() 1.3.12 Inversjoner
1.3.12 Inversjoner
La a være en tabell med sorterbare verdier (f.eks. heltall).
Definisjon 1.3.2 a)
sier at et par av verdier danner en inversjon hvis de er i utakt, dvs. hvis den
første av dem er større enn den andre. I
Avsnitt 1.3.2 fant vi at en permutasjon av
heltallene fra 1 til n kunne inneholde fra 0 til n(n − 1)/2
inversjoner. Ingen inversjoner betyr at permutasjonen er sortert stigende og n(n − 1)/2
stykker at den er sortert motsatt vei, dvs. avtagende.
En anvendelse: Per og Kari skal tippe resultatet i en konkurranse.
Konkurransen har A, B, C, D og E som deltagere. Kari tipper
at D blir nr. 1, B nr. 2, E nr. 3, A nr. 4 og C nr. 5.
Per tipper at B blir nr. 1, A nr. 2, D nr. 3, E nr. 4 og C nr. 5.
Konkurransen endte imidlertid med at D vant, A ble nr. 2, C nr. 3, B nr. 4 og E sist. Hverken Per eller Kari tippet rett. Men hvem var best? Spørsmålet kan ikke besvares før det er bestemt en regel for hvordan tipperesultater skal rangeres. F.eks. har Kari tippet vinneren riktig. Da kan man si at Kari har det beste tipperesultatet hvis det er viktigst å tippe rett vinner. Men her skal vi bruke en regel der det er like viktig med rett på alle plasser. Dermed: «det resultatet som har færrest inversjoner er best».
| Kari tipper | Per tipper | Resulatet |
| 1. D | 1. B | 1. D |
| 2. B | 2. A | 2. A |
| 3. E | 3. D | 3. C |
| 4. A | 4. E | 4. B |
| 5. C | 5. C | 5. E |
I forhold til det riktige resulatet gir tipset til Kari permutasjonen 1, 4, 5, 2, 3 siden hun har tippet D riktig på 1. plass, B (som ble nr. 4) på 2.plass, E (som ble nr. 5) på 3. plass, osv. Tilsvarende gir tipset til Per permutasjonen 4, 2, 1, 5, 3. Tipset til Kari har 4 inversjoner og det til Per 5 stykker. Kari har færrest inversjoner og har dermed det beste tipset.
Programkode 1.3.2 a)
inneholder en enkel n2 metode for å finne antallet inversjoner i en tabell.
Men ved å bruke en fletteteknikk (se Avsnitt 1.3.11)
er det mulig å lage en metode av orden n log(n).
Observasjon
La x og y (der x ligger til venstre for y) høre
til en rekkefølge med sorterbare verdier. Hvis vi deler rekkefølgen i to (f.eks. på
midten), vil en eventuell
inversjon
(x, y) enten 1) ha både x og y
i den venstre delen, 2) ha både x og y i den høyre delen eller 3) ha
x i den venstre delen og y i den høyre delen.
Figur 1.3.12 a) under inneholder en tabell med 20 tall som er delt i to
(hvit og grå):
| 4 | 3 | 17 | 10 | 6 | 20 | 1 | 11 | 15 | 8 | 18 | 9 | 2 | 7 | 19 | 13 | 5 | 14 | 16 | 12 |
| Figur 1.3.12 a) : Venstre del er «hvit» og høyre del «grå» | |||||||||||||||||||
I tabellen over er f.eks. (4,3), (4,1) og (17,10) inversjoner av den første
typen, dvs. av typen (x, y) der begge verdiene ligger i venstre del (den «hvit» delen).
Inversjonene (18,9), (9,2) og (9,7) har begge verdiene i høyre del (den «grå» delen).
Mens (4,2), (20,18) og (11,9) er av den tredje typen: første verdi i venstre del
og andre verdi i høyre del. Tabellen har tilsammen 80 inversjoner og det er flest av den tredje typen. Se
Oppgave 1.
Ved hjelp av observasjonen kan vi sette opp flg. oppskrift for en algoritme:
- Del tabellen i to deler - venstre og høyre del.
- Finn antall inversjoner (x, y) i venstre del.
- Finn antall inversjoner (x, y) i høyre del.
- Finn antall inversjoner (x, y) der x ligger i venstre del og y i høyre del.
- Summen av disse antallene er antallet inversjoner i hele tabellen.
Vi setter opp tallene fra Figur 1.3.12 a)
på nytt, men med hver av de to halvdelene sortert:
| 1 | 3 | 4 | 6 | 8 | 10 | 11 | 15 | 17 | 20 | 2 | 5 | 7 | 9 | 12 | 13 | 14 | 16 | 18 | 19 |
| Figur 1.3.12 b) : De to halvdelene er sortert hver for seg | |||||||||||||||||||
Dette endrer ikke antallet inversjoner av den tredje typen, dvs. inversjoner (x, y) der x ligger i venstre og y i høyre del. Det spiller ingen rolle hvor x og y ligger så lenge de er på hver sin side. Det gjør det raskere å finne antallet. De ni tallene tallene i venstre del fra 3 og utover danner en inversjon med tallet 2. De syv tallene i venstre del fra 6 og utover danner en inversjon med 5. Osv. På denne måten finner vi fort at det er 40 stykker av den tredje typen.
En algoritme: La tabellen hete a og hjelpetabellen b. Vi starter
med å kopiere den venstre delen av a over i hjelpetabellen b (slik som i
flettesortering):
| a |
|
||||||||||||||||||||||||||||||||||||||||
| b |
|
||||||||||||||||||||
| Figur 1.3.12 c) : Venstre del av a er kopiert over i b. | |||||||||||||||||||||
Vi starter med å sammenligne b[i] og a[j]
(tallene 1 og 2). Siden b[i] er minst, flyttes den til posisjon k
i a. Deretter økes både i og k med 1:
| a |
|
||||||||||||||||||||||||||||||||||||||||
| b |
|
||||||||||||||||||||
| Figur 1.3.12 d) : Tallet 1 er flyttet fra b til a | |||||||||||||||||||||
Vi sammenligner igjen b[i] og a[j]
(tallene 3 og 2). Det gir en inversjon da b[i] er størst.
Men alle tallene til høyre for 3 i tabellen b
er større enn 3. Det gir like mange inversjoner som antallet verdier i b fra og med
posisjon i og ut tabellen. Det er ni stykker. Den minste av de to,
dvs. a[j], flyttes til posisjon k i a.
Deretter økes både j og k med 1:
| a |
|
||||||||||||||||||||||||||||||||||||||||
| b |
|
||||||||||||||||||||
| Figur 1.3.12 e) : 2 er flyttet fra «grå» til «hvit» del | |||||||||||||||||||||
Vi fortsetter med å sammenligne b[i] og a[j]
(tallene 3 og 5). Siden b[i] er minst flyttes den til posisjon k
i a. Deretter økes både i og k med 1.
Osv. Neste gang vi får en inversjon er når
6 og 5 sammenlignes. Det gir tilsammen syv inversjoner siden det er syv tall i tabellen b
fra og med 6 og utover. Osv. På denne måten finner vi alle inversjoner (x, y) der x ligger
i den venstre og y i den høyre delen av a ved kun én gjennomgang.
Metoden inv nedenfor tar utgangspunkt i tabellintervallet a[fra:til>
og tar som gitt at de to delene a[fra:m> og a[m:til> av
a[fra:til> er sortert hver for seg.
Deretter gjøres det slik som beskrevet i
Figur 1.3.12 c) - d):
private static int inv(int[] a, int[] b, int fra, int m, int til) { int n = m - fra; // antall elementer i a[fra:m> System.arraycopy(a,fra,b,0,n); // kopierer a[fra:m> over i b[0:n> int i = 0, j = m, k = fra; // indekser int antall = 0; // antall inversjoner while (i < n && j < til) // går gjennom tabellene { if (b[i] > a[j]) antall += (n - i); // nye inversjoner a[k++] = b[i] < a[j] ? b[i++] : a[j++]; // kopierer } while (i < n) a[k++] = b[i++]; // tar med resten av b[0:n> return antall; // antall inversjoner } Programkode 1.3.12 a)
Nå har vi det som trengs for å følge oppskriften:
private static int inversjoner(int[] a, int[] b, int fra, int til) { if (til - fra <= 1) return 0; // maks ett element - 0 inversjoner int m = (fra + til)/2; // deler a[fra:til> på midten return inversjoner(a, b, fra, m) // inversjoner av første type + inversjoner(a, b, m, til) // inversjoner av andre type + inv(a, b, fra , m, til); // inversjoner av tredje type } public static int inversjoner(int[] a) { int[] b = new int[a.length/2]; // hjelpetabell return inversjoner(a, b, 0, a.length); // kaller metoden over } Programkode 1.3.12 b)
Metoden i inversjoner()
i Avsnitt 1.3.2
har samme navn som den vi nettopp har laget. Det er den nye som vi ønsker å teste i flg. kodebit:
int[] a = {4,3,17,10,6,20,1,11,15,8,18,9,2,7,19,13,5,14,16,12}; System.out.println(inversjoner(a)); // Utskrift: 80 Programkode 1.3.12 c)
Det finnes n! (n fakultet) forskjellige permutasjoner av
tallene fra 1 til n og en permutasjon vil kunne inneholde fra
0 til n(n – 1)/2 inversjoner.
La k være et mulig antall inversjoner og la
I(n,k) være antallet permutasjoner av de n! mulige som inneholder nøyaktig k inversjoner.
La n = 3. Det er 3! = 6 permutasjoner av tallene fra 1 til 3. Det er
(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2) og (3,2,1). Der har (1,2,3) ingen
inversjoner, både (1,3,2) og (2,1,3) én inversjon, både (2,3,1) og (3,1,2) to inversjoner
og (3,2,1) tre inversjoner.
Dermed får vi:
I(3,0) = 1, I(3,1) = 2, I(3,2) = 2, I(3,3) = 1
Gitt permutasjonen (3,5,2,1,4) av tallene fra 1 til 5. Snur vi den får vi permutasjonen
(4,1,2,5,3). I den første har vi paret (5,2) som er en inversjon, men i den omvendte permutasjonen
går det over til å bli paret (2,5) som ikke er en permutasjon. Omvendt er paret (2,4) ikke en
inversjon i den første permutasjonen, men (4,2) blir en inversjon i den andre. Det betyr generelt
at hvis en permutasjon har k inversjoner, vil den omvendte permutasjonen ha m – k
inversjoner der m = n(n – 1)/2. Det gir oss en symmetriegenskap
for I(n,k). Flg. differensligninger gjelder for I(n,k):
(1.3.12.0) I(n,0) = 1 , n > 1
(1.3.12.1) I(n,k) = I(n,k-1) + I(n-1,k) ,
0 < k < n
(1.3.12.2) I(n,k) = I(n,k-1) + I(n-1,k)
− I(n-1,k-n) ,
1 < n ≤ k ≤ n(n – 1)/4
(1.3.12.3) I(n,k) = I(n,m - k) ,
n > 1 , 0 ≤ k ≤ (n - 1)/2
Flg. tabell viser I(n,k) for små verdier av n og k:
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||
| 2 | 1 | 1 | |||||||||||||||||
| 3 | 1 | 2 | 2 | 1 | |||||||||||||||
| 4 | 1 | 3 | 5 | 6 | 5 | 3 | 1 | ||||||||||||
| 5 | 1 | 4 | 9 | 15 | 20 | 22 | 20 | 15 | 9 | 4 | 1 | ||||||||
| 6 | 1 | 5 | 14 | 29 | 49 | 71 | 90 | 101 | 101 | 90 | 71 | 49 | 29 | 14 | |||||
| 7 | 1 | 6 | 20 | 49 | 98 | 169 | 259 | 359 | 455 | 531 | 573 | 573 | 531 | 455 | |||||
| 8 | 1 | 7 | 27 | 76 | 174 | 343 | 602 | 961 | 1415 | 1940 | 2493 | 3017 | 3450 | 3736 | |||||
| Figur 1.3.12 f) : En I(n,k)-tabell for noen verdier av n og k | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Finn hvor mange inversjoner det er av de tre typene i tabellen i
Figur 1.3.12 a).
I Figur 1.3.12 b)
er de to delene av tabellen sortert hver for seg. Sjekk at antallet inversjoner av den tredje typen er
det samme i de to tabellene.
|
| 2. | Metoden inversjoner() i
Programkode 1.3.2 a)
er av orden n2, mens den i
Programkode 1.3.12 b)
er av orden n log(n). Sjekk at begge alltid gir samme svar. Sammenlign
også tidsforbruket de to har for store permutasjoner (dvs. n stor).
|
![]() 1.3.13 Forskyvninger og rotasjoner
1.3.13 Forskyvninger og rotasjoner
Gitt flg. heltallstabell:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Figur 1.3.13 a) : En heltallstabell med 20 verdier | |||||||||||||||||||
Tabellforskyvninger. En forskyvning (eng: array shift) på f.eks. 3 enheter mot høyre i
tabellen over, vil føre til at de tre siste verdiene forsvinner:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||
| Figur 1.3.13 b) : Tabellinnholdet er forskjøvet tre enheter mot høyre | |||||||||||||||||||
I Figur 1.3.13 b) har ikke de tre første rutene noe innhold. Men
de hører til tabellen og må derfor ha et innhold. Vi kunne f.eks. tenke oss at verdiene er 0.
Men det er kanskje mer naturlig å kreve at de skal inneholde den verdien som opprinnelig lå først. Dvs. slik:
| 1 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Figur 1.3.13 c) : Det er fylt på fra venstre med verdien som opprinnelig lå først | |||||||||||||||||||
Dette svarer til
bitskyvning av bitene
i et heltall. Der er det to typer bitforskyving mot høyre: >> og
>>>. Operatoren >> kalles en fortegnsbevarende shiftoperator.
Det betyr at det fylles på fra venstre med den biten som opprinnnelig lå lengst til venstre. Mens
>>> fyller alltid på 0-biter. Setningen: int k = -1; gjør at
k får 32 1-biter. Setningen: k >>= 3; forskyver bitene i k tre
enheter mot høyre. Men siden den første biten er 1, fylles det på med 1-biter. Det betyr at k
fortsatt er lik −1. Se Oppgave 1.
Det er ingen operator for tabellforskyving. Men vi kan lage en metode som gjør det:
public static void rightshift(int[] a, int d)
Programkode 1.3.13 a)
I metoden rightshift() må parameter d
være ikke-negativ. Den angir hvor mange enheter det skal forskyves. Hvis den er større enn eller lik
tabellens lengde, gjør vi omtrent som for bitshiftoperatorene i Java. Hvis k er
av typen int (dvs. 32 biter) og d er et positivt heltall, vil
setningen: k >> d ha samme effekt som: k >> (d & 31).
Det er derfor kun de 5 siste bitene i d som regnes med. Dette gjelder også for en
negative d. F.eks. vil: 0x80000000 >> -1 bli det samme som -1 siden
(-1 & 31) = 31. Bitforskyves tallet som starter med 1 og har 31 0-er,
31 enheter mot høyre, får vi et tall med 32 1-ere (dvs. -1). Fortegnet til d har ikke
retningsbetydning. Den er kun bestemt av hvilken shiftoperator som brukes.
Se Oppgave 2.
public static void rightshift(int[] a, int d)
{
if (d < 0) throw new IllegalArgumentException("Negativ parameter!");
if (a.length <= 1) return; // a har maksimalt ett element
d %= a.length; // d < a.length
for (int i = a.length - 1; i >= d; i--) a[i] = a[i - d]; // forskyver
for (int i = 1; i < d; i++) a[i] = a[0]; // kopierer inn a[0]
}
Programkode 1.3.13 b)
Flg. eksempel viser hvordan rightshift() kan brukes:
int[] a = new int[32];
for (int i = 16; i < 32; i++) a[i] = 1; // 16 0-er, 16 1-ere
for (int verdi : a) System.out.print(verdi); // utskrift av a
rightshift(a,10); // shift høyre
System.out.println(); // linjeskift
for (int verdi : a) System.out.print(verdi); // utskrift av a
// 00000000000000001111111111111111
// 00000000000000000000000000111111
Programkode 1.3.13 c)
Metoden leftshift() kan lages tilsvarende. Sjekk så at hvis tabellen kun har 0-er og 1-ere, vil
rightshift() og leftshift() virke som shiftoperatorene >>
og <<. Se Oppgave 3.
Rotasjoner Tabellen under inneholder de 16 bokstavene fra A til P.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Figur 1.3.13 d): En tabell med bokstavene fra A til P | |||||||||||||||
 |
| Figur 1.3.13 e) |
Figur 1.3.13 e)
til venstre. Vi kan tenke på dette som et «lykkehjul». Indeksene holdes fast, mens
«hjulet» kan snurre både med og mot klokken. En rotasjon på f.eks. 8 enheter får vi ved å rotere hjulet med klokken slik at bokstaven A kommer ned til indeks 8. En rotasjon på f.eks. −5 enheter får vi ved å rotere hjulet 5 enheter mot klokken slik at A kommer til indeks 11. Dette kunne vi også ha fått til ved å rotere 11 enheter med klokken. Det kommer av at en rotasjon på k enheter mot klokken er det samme som en rotasjon på 16 − k enheter med klokken der 16 er tabellens lengde.
Dette kan enkelt kodes ved hjelp av idéen fra
rightshift(). Men vi må passe
på å ta vare på de elementene som skyves ut av tabellen. De må kopieres inn i den
andre enden:
public static void rotasjon(char[] a, int d) // 1. versjon
{
int n = a.length; if (n < 2) return; // tomt eller en verdi
if ((d %= n) < 0) d += n; // motsatt vei?
char[] b = Arrays.copyOfRange(a, n - d, n); // hjelpetabell
for (int i = n - 1; i >= d; i--) a[i] = a[i - d]; // forskyver
System.arraycopy(b, 0, a, 0, d); // kopierer
}
Programkode 1.3.13 d)
I Figur 1.3.13 d) og i
metoden over, inngår en char-tabell. I
Oppgave 4 ser vi på int-tabeller.
Flg. eksempel viser hvordan metoden virker for en char-tabell:
char[] c = "ABCDEFGHIJKLMNOP".toCharArray();
rotasjon(c,-5);
System.out.println(Arrays.toString(c));
// Utskrift: [F, G, H, I, J, K, L, M, N, O, P, A, B, C, D, E]
Programkode 1.3.13 e)
Programkode 1.3.13 d) er effektiv nok hvis
tabellen skal roteres få enheter. Men med mange enheter mot høyre (med klokken)
eller få enheter mot venstre (mot klokken), er den mindre effektiv. F.eks. utføres en rotasjon på
én enhet mot venstre som en rotasjon på a.length − 1 enheter mot høyre.
Da må hjelpetabellen ha samme lengde og dermed svært mye kopiering. Det er imidlertid mulig
å lage kode der hjelpetabellen maksimalt blir halvparten av a.length.
Se Oppgave 5. Men målet er å lage en
rotasjonsmetode som ikke bruker en hjelpetabell.
Anta at vi skal rotere tabellen under (med 16 verdier) 10 enheter mot høyre:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Figur 1.3.13 f): En tabell med bokstavene fra A til P | |||||||||||||||
Vi starter med å snu rekkefølgen på elementene i tabellen. Det gir oss flg. resultat:
| P | O | N | M | L | K | J | I | H | G | F | E | D | C | B | A |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Figur 1.3.13 g): Rekkefølgen er snudd | |||||||||||||||
Så snur vi rekkefølgen på de 10 første og deretter på de 16 - 10 = 6 siste:
| G | H | I | J | K | L | M | N | O | P | A | B | C | D | E | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Figur 1.3.13 h): Tabellen er rotert 10 enheter mot høyre | |||||||||||||||
Hokus pokus og simsalabim. Tabellen har blitt rotert 10 enheter mot høyre. For å innse at dette alltid gir korrekt resultat er det enklest å tenke motsatt vei. Anta derfor at vi starter med resultatet, dvs. med at tabellen er blitt rotert 10 enheter mot høyre. De 6 siste elementene er da de som opprinnelig lå først. Snur vi disse kommer de som de 6 siste i en snudd tabell. Snur vi de 10 første kommer disse som de 10 første i en snudd tabell. Hvis vi så avslutter med å snu tabellen, vil vi dermed få den opprinnelige tabellen. Denne argumentasjonen gjelder generelt, dvs. ved rotasjon på et bestemt antall enheter i en vilkårlig tabell.
Vi snur en tabell eller et tabellinetvall ved hjelp av en serie ombyttinger. Da
kan det være praktisk med en egen ombyttingsmetode. Kanskje du allerede har en
metode (i samleklassen Tabell) som bytter om elementer i
en char-tabell? Hvis ikke, er det enkelt å lage en:
public static void bytt(char[] a, int i, int j)
{
char temp = a[i]; a[i] = a[j]; a[j] = temp;
}
Programkode 1.3.13 f)
Følgende rotasjonsmetode bruker idéen over:
public static void rotasjon(char[] a, int d) // 2. versjon
{
int n = a.length;
if (n < 2) return; // tomt eller en verdi
if ((d %= n) < 0) d += n; // motsatt vei?
for (int v = 0, h = n - 1; v < h; Tabell.bytt(a, v++, h--)); // snur a[a:n>
for (int v = 0, h = d - 1; v < h; Tabell.bytt(a, v++, h--)); // snur a[0:d>
for (int v = d, h = n - 1; v < h; Tabell.bytt(a, v++, h--)); // snur a[d:n>
}
Programkode 1.3.13 g)
Med tanke på effektivitet ser vi på tabellaksesser.
I bytt er det
fire av dem. Vi snur en tabell (eller intervall) ved å bytte
inntil vi kommer til midten. Hvis et intervall har lengde k, blir
det dermed 4·(k/2) tabellaksesser. For en tabell med lengde n, blir det
tilsammen tilnærmet lik 4n tabellaksesser i
Programkode 1.3.13 g).
Dette er litt dårligere enn gjennomsnittet
for metoden i Programkode 1.3.13 d), men
det brukes ingen hjelpetabell og det er fordelaktig.
 |
| Figur 1.3.13 j) : «Sirkeltabell» |
 |
| Figur 1.3.13 k) : «Sirkeltabell» |
Det finnes flere måter å rotere en tabell uten bruk av hjelpetabell. Flg. idé gir ingen forbedring i effektiviteten i forhold til de to versjonene vi allerede har sett på, men har interessante egenskaper. Ta utgangspunkt i tabellen til venstre. Den er satt opp i sirkelform. Anta at den skal roteres 3 enheter mot høyre (med klokken):
Det kan gjøres ved flg. skritt: Først tar vi vare på det som ligger på indeks 0, dvs. A. Så flytter vi N på indeks 13 til indeks 0 (dvs. 3 enheter med klokken). Så K på indeks 10 til indeks 13, så H på indeks 7 til indeks 10, så E på indeks 4 til indeks 7 og så B på indeks 1 til indeks 4. Neste skritt er å flytte det som ligger 3 enheter mot klokken fra 1. Vi ser på figuren at det er O på indeks 14. Men 3 enheter mot klokken fra 1 er 1 − 3 = −2. Hvis en indeks på denne måten blir negativ, legger vi til 16, dvs. −2 + 16 = 14. Figuren rett til venstre viser det som har skjedd så langt.
Vi fortsetter med å flytte L på indeks 11 til indeks 14, osv. På denne måten får vi indeksene til tabellen i rekkefølgen: 0, 13, 10, 7, 4, 1, 14, 11, 8, 5, 2, 15 12, 9, 6, 3. Til slutt med vi legge inn A som vi tok vare på, på indeks 3.
Bruker vi i som indeks, vil oppdateringen av i bli slik:
i -= enheter;
if (i < 0) i += 16;
Det er enkelt å lage kode som gjør det som vises i
Figur 1.3.13 k) og fortsettelsen av det:
char[] c = "ABCDEFGHIJKLMNOP".toCharArray(); int d = 3; char temp = c[0]; // tar vare på verdien i indeks 0 for (int i = -d, j = 0; i != 0; i -= d) // stopper i 0 { if (i < 0) i += 16; // sjekker fortegnet til indeks i c[j] = c[i]; // kopierer j = i; // oppdaterer indeks j } c[d] = temp; // legger tilbake verdien System.out.println(Arrays.toString(c)); // Utskrift: [N, O, P, A, B, C, D, E, F, G, H, I, J, K, L, M] Programkode 1.3.13 h)
 |
| Figur 1.3.13 l) : «Sirkeltabell» |
 |
| Figur 1.3.13 m) : «Sirkeltabell» |
Eksemplet over viser at en tabell med 16 verdier kan roteres 3 enheter med
klokken ved å flytte én og én verdi. Men vil dette virke generelt?
Vi gjentar dette, men nå med 4 enheter istedenfor 3. Start med
Figur 1.3.13 j).
Som sist legges verdien i indeks 0 (bokstaven A) tilside.
Deretter flytter vi M i indeks 0 - 4 = 12 til indeks 0. Så bokstaven I
i indeks 12 - 4 = 8 til indeks 12 og så bokstaven E
i indeks 8 - 4 = 4 til indeks 8. Neste skritt skulle da ha vært å flytte bokstaven M
i indeks 4 - 4 = 0 til indeks 4, men det blir galt. Bokstaven M
har jo allerede blitt flyttet og skal ligge i indeks 0. Se
Figur 1.3.13 l) til venstre. Bokstaven A skal isteden
inn på indeks 4 for å få korrekt rotasjon. Men dette fører til at kun fire av tabellens
16 verdier har blitt flyttet dit de skal.
Vi kan få fullført dette ved å starte på nytt, men denne gangen på indeks 1.
Dvs. verdien i indeks 1 (bokstaven B) legges tilside. Så flyttes
bokstaven N i indeks 1 - 4 = 13 til indeks 1, så bokstaven J
i indeks 13 - 4 = 9 til indeks 13, osv. til at bokstaven B som ble lagt til side,
legges inn på indeks 1. Dette gir Figur 1.3.13 m) til venstre.
For å få flyttet alle bokstavene dit de skal, må dette gjøres to ganger til. Det som står igjen er å flytte de fire som starter med indeks 2 og til slutt de fire som starter med indeks 3. Hver runde som er gjennomført, kalles en sykel. Det betyr at med tabellengde 16 og rotasjon på 3 enheter ble det kun én sykel, men fire sykler når det er 4 enheter.
Det viser seg at antall sykler i en slik rotasjonsteknikk er det samme som største felles divisor
for tabellens lengde (her 16) og rotasjonslengden (her 3 og 4). Største felles divisor for 16 og 3 er
1, mens største felles divisor for 16 og 4 er 4.
Se Avsnitt 1.3.16.
public static int gcd(int a, int b) // Euklids algoritme
{
return b == 0 ? a : gcd(b, a % b);
}
public static void rotasjon(char[] c, int d) // 3. versjon
{
int n = c.length; if (n < 2) return; // ingen rotasjon
if ((d %= n) < 0) d += n; // motsatt vei?
int s = gcd(n, d); // største felles divisor
for (int k = 0; k < s; k++) // antall sykler
{
char verdi = c[k]; // hjelpevariabel
for (int i = k - d, j = k; i != k; i -= d) // løkke
{
if (i < 0) i += n; // sjekker fortegnet til i
c[j] = c[i]; j = i; // kopierer og oppdaterer j
}
c[k + d] = verdi; // legger tilbake verdien
}
} Programkode 1.3.13 i)
Effektivitet La n = c.length. Anta vi skal rotere
0 ≤ d < n enheter.
- I 1. versjon blir det 2(n + d) tabellaksesser
- I 2. versjon blir det 4n tabellaksesser
- I 3. versjon blir det 2n tabellaksesser
Hvis d er liten i forhold til n, vil 1. versjon være mest effektiv. Men den har ulempen at det inngår en hjelpetabell. 3. versjon har færrest tabellaksesser, men der er det en del mer arbeid knyttet til hver aksess.
| 1. | Sjekk at >> bevarer fortegn. Det betyr at k >> 1
er positiv hvis k er positiv og negativ hvis k er negativ.
Sjekk at >>> er annerledes. Dvs. k >>> 1
blir positiv hvis k er negativ.
|
| 2. | Sjekk at k >> d alltid er lik k >> (d & 31)
uansett hva slags verdier k og d har. Bruk f.eks.
System.out.println(k >> d) og
System.out.println(k >> (d & 31)). Bruk både små og store,
posistive og negative verdier på k og d.
|
| 3. | Lag kode for public static void leftshift(int[] a, int d).
Den skal forskyve bitene d enheter mot venstre. Fra høyre skal det komme inn 0-er.
|
| 4. | Gjør om Programkode 1.3.13 d)
slik at tabellen b aldri er større enn (a.length + 1)/2. Hint:
Hvis d er større enn (a.length + 1)/2, kan en isteden forskyve motsatt vei. |
| 5. | Lag en versjon av Programkode 1.3.13 g)
der det brukes en int-tabell. |
| 6. | Programkode 1.3.13 h) virker når
tabellen skal roteres 3 enheter. Det påstas senere at denne koden også vil fungere hvis antall
enheter og tabellens lengde 16 er relativt primiske. Sjekk at dette stemmer ved velge antall
enheter lik 1, 5, 7, 9, 11, 13 og 15.
|
| 7. | La antallet enheter være 6 i
Programkode 1.3.13 h).
Største felles divisor for 6 og 16 er 2. Sjekk at det da bare er annenhver bokstav som har blitt
rotert 6 enheter.
|
![]() 1.3.14 Anvendelser: En tallmengde
1.3.14 Anvendelser: En tallmengde
I mengder har vi begreper som element og inklusjon
og operasjoner som snitt og union. Her skal vi
bruke teknikker fra søking, sortering og fletting til å lage klassen Tallmengde
med heltall som elementer og en sortert tabell som datastruktur.
Java har allerede klassen
BitSet
for heltallsmengder (se
Avsnitt 1.7.17).
Der brukes en smartere teknikk, men den tillater
ikke negative heltall. Vår klasse kan ha både positive og negative
heltall og kan lett endres til mengder av elementer som kan ordnes
(f.eks. tall, tegn og tegnstrenger). Klassen er konstant (eng: immutable). Dvs. at en mengde ikke kan endres
når den først er opprettet.
Legg flg. klasse på filen Tallmengde.java under mappen hjelpeklasser:
public final class Tallmengde // legges på filen Tallmengde.java { private final int[] a; // en heltallstabell // public Tallmengde() // standardkonstruktør // public Tallmengde(int[] b) // lager en mengde av b // public Tallmengde(Tallmengde B) // kopieringskonstruktør // public Tallmengde(int element) // mengde med ett element // private Tallmengde(int[] b, int n) // privat hjelpekonstruktør // public Tallmengde union(Tallmengde B) // returnerer unionen // public Tallmengde snitt(Tallmengde B) // returnerer snittet // public Tallmengde differens(Tallmengde B) // differensen // public Tallmengde xunion(Tallmengde B) // returnerer xunionen // public boolean erElement(int element) // er det element i mengden? // public boolean inklusjon(Tallmengde B) // er B delmengde? public boolean tom() { return a.length == 0; } // er mengden tom? public int antall() { return a.length; } // antallet i mengden // public boolean equals(Object o) // like mengder? // public String toString() // for utskrift // public int[] tilTabell() // mengden som tabell } Programkode 1.3.14 a)
Klassen Tallmengde har én instansvariabel - en heltallstabell
a som skal inneholde
mengdens elementer. Den skal være sortert og ikke ha like verdier.
Programkode 1.3.14 a) over viser de konstruktørene og
metodene klassen skal ha. De er, bortsett fra tom() og antall(),
midlertidig kommentert vekk. En konstruktør
(eng: constructor) har samme navn som klassen. Det er egentlig
ikke en metode, men blir av og til omtalt som det. Objekter, dvs. instanser av en klasse, lages
ved hjelp av konstruktører.
Alle klasser blir automatisk utstyrt med en standardkonstruktør (eng: default constructor).
Den kalles også den parameterløse konstruktøren. Den kan brukes slik:
Tallmengde A = new Tallmengde();
Dette gir oss et objekt A der instansvariabelen a er satt til null. Dette kunne tolkes som en tom tallmengde. Men vi bestemmer imidlertid at en tallmengde er tom kun hvis den interne tabellen a er tom. For å få til det må vi selv programmere standardkonstruktøren:
public Tallmengde() // standardkonstruktør { a = new int[0]; // en tom tabell } Programkode 1.3.14 b)
Den normale måten å opprette en mengde på vil være ved hjelp av en tabell. F.eks. slik:
Tallmengde A = new Tallmengde(new int[] {1,3,5,2,4,6,1});
Dette svarer til en av de andre konstruktørene i
Tallmengde. Den må lages
litt robust siden parametertabellen kan være null, kan være usortert og ha like verdier (duplikater).
public Tallmengde (int[] b) { if (b == null) throw new IllegalArgumentException("Tabellen er null!"); Tabell.innsettingssortering(b); // sorterer for sikkerhets skyld int antall = b.length == 0 ? 0 : 1; // for å få med det første elementet for (int i = 1; i < b.length; i++) // sammenligner { if (b[i-1] < b[i]) b[antall++] = b[i]; } a = Arrays.copyOf(b, antall); // a er nå korrekt } Programkode 1.3.14 c)
I koden over blir tabellen b alltid sortert og da ved hjelp av innsettingssortering. Den
brukes fordi det nok her vil handle om små tabeller og fordi den er effektiv hvis b
allerede er sortert. Men den kan byttes ut f.eks. med kvikksortering.
I for-løkken blir eventuelle like verdier (duplikater) fjernet. Vi burde kanskje teste på det først. Se
Oppgave 1.
Vi trenger en toString-metode for å kunne sjekke at dette blir ok. Vi ønsker at utskriften
skal ha mengdeform, dvs. hvis mengden har elementene 1, 2 og 3, skal utskriften bli {1,2,3}:
public String toString() // for utskrift { StringJoiner s = new StringJoiner(",","{","}"); for (int element : a) s.add(Integer.toString(element)); return s.toString(); } Programkode 1.3.14 d)
Det som nå er laget kan testes ved hjelp av flg. kodebit:
Tallmengde A = new Tallmengde(new int[] {1,3,5,2,4,6,1}); Tallmengde B = new Tallmengde(new int[] {}); System.out.println("A = " + A + " B = " + B); // Utskrift: A = {1,2,3,4,5,6} B = {} Programkode 1.3.14 e)
En kopieringskonstruktør (eng: copy constructor) lager en kopi av et objekt som allerede finnes. Hvis tallmengden B allerede eksisterer, lages A som en kopi av B på denne måten:
Tallmengde A = new Tallmengde(B); // A blir en kopi av B
Kopieringskonstruktøren for class Tallmengde lages slik:
public Tallmengde(Tallmengde B) // en kopi av mengden B { a = B.a.clone(); // kopierer tabellen i B } Programkode 1.3.14 f)
Konstruktøren i Programkode 1.3.14 c)
lager en tallmengde ved hjelp av
elementene i en tabell. Hvis vi var helt sikre på at parametertabellen var sortert
stigende og uten duplikater, kunne vi lage konstruktøren mer effektiv. Flg. private
konstruktør forutsetter at de n første elementene i parametertabellen b
er sortert og er forskjellige. Disse n verdiene blir da elementene i den tallmengden
som konstruktøren lager:
private Tallmengde(int[] b, int n)
{
a = Arrays.copyOf(b, n); // de n første verdiene i b
}
Programkode 1.3.14 g)
Metodene union og snitt i Tallmengde kan lages ved hjelp av
union- og snitt-metodene
fra Programkode 1.3.11
k) og
m)
og den private konstruktøren fra Programkode 1.3.14 g):
public Tallmengde union(Tallmengde B) // returnerer unionen { int[] c = new int[antall() + B.antall()]; // en stor nok tabell int n = Tabell.union(a, B.a, c); // unionen return new Tallmengde(c,n); // privat konstruktør } public Tallmengde snitt(Tallmengde B) // returnerer snittet { int[] c = new int[Math.max(antall(),B.antall())]; // en stor nok tabell int n = Tabell.snitt(a, B.a, c); // snittet return new Tallmengde(c,n); // privat konstruktør } Programkode 1.3.14 h)
Flg. eksempel viser hvordan metodene kan brukes:
Tallmengde A = new Tallmengde(new int[] {1,3,5,7,9}); // A = {1,3,5,7,9} Tallmengde B = new Tallmengde(new int[] {5,2,6,2,4,3,5}); // B = {2,3,4,5,6} Tallmengde C = A.union(B); // C = {1,2,3,4,5,6,7,9} Tallmengde D = A.snitt(B); // D = {3,5} System.out.println("A = " + A + " B = " + B + " C = " + C + " D = " + D); // Utskrift: // A = {1,3,5,7,9} B = {2,3,4,5,6} C = {1,2,3,4,5,6,7,9} D = {3,5} Programkode 1.3.14 i)
Resten av metodene som er satt opp i
Programkode 1.3.14 a) tas
som øvingsoppgaver.
| 1. | Konstruktøren i
Programkode 1.3.14 c)
fjerner eventuelle like verdier. Det normale er nok at parametertabellen b ikke
har like verdier. Derfor vil det gjennomsnittlig bli mer effektivt hvis vi sjekker først om det er
duplikater. Gjør det i konstruktøren!
|
| 2. | Lag konstruktøren Tallmengde(int element). Den skal
lage en mengde som består av det ene elementet element. |
| 3. | Lag metoden tilTabell. Den skal returnere en kopi
av klassens interne tabell.
|
| 4. | Lag metoden equals i Tallmengde. Vi må først undersøke
om mengden blir sammenlignet med seg selv, dvs. om parameteren o er lik this.
Hvis ja, returneres true. Så må o konverteres.
Hvis o ikke er en instans av Tallmengde, returneres false.
Til slutt sjekkes det om tabellene er like.
|
| 5. | Lag metoden erElement i Tallmengde. Den skal
returnere true hvis parameteren element er element i mengden, og
returnere false ellers. Bruk binærsøk! |
| 6. | Lag metoden differens i Tallmengde. Se hvordan
union og snitt er laget! Benytt differens-metoden
fra Oppgave 8 i Avsnitt 1.3.11.
Husk at antallet i differensen A – B er
mindre enn eller lik antallet i A. |
| 7. | Lag metoden inklusjon i Tallmengde.
Benytt inklusjon-metoden fra Oppgave 9
i Avsnitt 1.3.11. |
| 8. | Vi kan lage inklusjon ved hjelp av
equals og snitt. Mengden
B vil være inkludert i A hvis A snitt B er lik B.
Lag en versjon av inklusjon som bruker denne idéen. |
| 9. | Lag metoden xunion i Tallmengde. Se hvordan
Benytt xunion-metoden fra Oppgave 10
i Avsnitt 1.3.11. |
| 10. | Metoden xunion kan lages ved hjelp av metodene union
og differens. Vi har at
A xunion B er lik (A – B) union (B – A).
Lag en versjon av xunion som bruker denne idéen. |
| 11. | Metoden union, snitt og differens. Vi har at
A xunion B er lik
(A union B) – (A snitt B). Lag en versjon av xunion
som bruker denne idéen. |
| 12. | Hvis en ønsker å lage en mengde som inneholder ett element i tillegg til en eksisterende mengde,
kan det gjøres ved å lage en mengde med ett element og så ta unionen. Lag isteden
metoden: public Tallmengde union(int element).
Den skal gjøre det samme. Lag den så direkte som mulig! F.eks. ved først å søke etter verdien. Hvis den
ikke er der, har vi innsettingspunktet. Bruk så den private konstruktøren til å lage en Tallmengde
med plass til ett element mer. Flytt så på verdiene og sett inn det nye elementet.
|
| 13. | Hvis en ønsker å lage en mengde som vi får ved å fjerne et element fra en eksisterende mengde,
kan det gjøres ved å lage en mengde med ett element og så ta differensen. Lag isteden
metoden: public Tallmengde differens(int element).
Den skal gjøre det samme. Lag den så direkte som mulig!
|
| 14. | Lag et program der du tester alle metodene i Tallmengde.
|
Et vanlig sjakkbrett har 8 × 8 ruter. En dronning kan slå vertikalt, horisontalt og på skrå.
Problem: Er
det mulig å stille opp dronninger på 8 forskjellige ruter på brettet
slik at ingen av dem slår hverandre?
 |
| Figur 1.3.15 a) : En oppstilling |
| Figur 1.3.15 b) : En permutasjon |
 |
| Figur 1.3.15 c) : En ny oppstilling |
Figur 1.3.15 a) til venstre viser et 8 × 8 brett.
Bokstaven D brukes som symbol for en dronning.
Vi ser fort at hver av de 8 radene og hver av de 8 kolonnene inneholder nøyaktig én dronning.
En diagonal går nedover mot høyre (eller oppover mot venstre). Ingen av de
15 diagonalene har mer enn én dronning. En bidiagonal går nedover mot venstre
(eller oppover mot høyre). Heller ingen av de 15 bidiagonalene inneholder
mer enn én dronning. Dette betyr at i dronningoppstillingen på
dette brettet er det ingen dronninger som slår hverandre. Vi kaller
det derfor en lovlig dronningoppstilling.
I Figur 1.3.15 a) er både radene og kolonnene
indeksert fra 0 til 7. Posisjonen til en rute er gitt ved tallparet
( r , k ) der r er rad- og k
kolonneindeks. Ramser vi opp posisjonene radvis, ovenfra og nedover, til de
rutene som inneholder dronninger, får vi (0,3), (1,5), (2,0), (3,4),
(4,1), (5,7), (6,2) og (7,6). Ser vi på første tall i hvert par som en indeks,
gir de andre tallene permutasjonen i Figur 1.3.15 b).
Tabellen i Figur 1.3.15 b) har en permutasjon
av tallene fra 0 til 7. Vi kan gå motsatt vei.
En vilkårlig permutasjon av tallene fra 0 til 7, for eksempel 5, 2, 6, 3, 1, 4, 0, 7,
kan tolkes som en oppstilling der hver rad og kolonne inneholder nøyaktig
én dronning. For hvert tall i permutasjonen brukes tallets posisjon/indeks i permutasjonen
som radindeks og tallet
selv som kolonneindeks. Det gir rutene (0,5), (1,2), (2,6), (3,3), (4,1), (5,4),
(6,0) og (7,7). I Figur 1.3.15 c) står det en D
i hver av disse rutene.
Det er 8! = 40320 permutasjoner av tallene fra 0 til 7.
Det er selvfølgelig ikke alle som gir en lovlig oppstilling. Vi fant at
den i Figur 1.3.15 a) er lovlig. Men den i
Figur 1.3.15 c) er ulovlig. Starter vi i øverste rad og går nedover
ser vi at ingen av de fire første dronningene slår hverandre. Men den femte, den i
rute (4,1), blir slått av dronningen i (0,5). På Figur 1.3.15 c)
er diagonalen og bidiagonalen som dronningen i rute (0,5) behersker, markert med
små røde prikker. Dronningen i rute (4,1) ligger på bidiagonalen.
Vi ser også at dronningene i rute (6,0) og (7,7) står ulovlig. Begge kan
begge slås av den i rute (3,3).
Vi har generelt at enhver lovlig dronningoppstilling representerer en permutasjon av
tallene fra 0 til 7, men at det motsatte ikke er sant. For å avgjøre om en permutasjon
representerer en lovlig en holder det å sjekke diagonalene og bidiagonalene.
utasjon av tallene fra 0 til 7. I Figur 1.3.15 c) består
diagonalen gjennom rute (0,5) av rutene (0,5), (1,6) og (2,7). Differensen mellom radindeks
og kolonneindeks er lik –5 for alle disse rutene. Bidiagonalen gjennom
rute (0,5) består av rutene (0,5), (1,4), (2,3), (3,2), (4,1) og (5,0). For disse er
summen av radindeks og kolonneindeks lik 5. Disse observasjonen gir oss flg. setning:
Setning 1.3.15 a) - Diagonal og bidiagonal To ruter (a , b)
og (c , d) ligger
på samme diagonal hvis og
bare hvis a – b = c – d. To ruter (a , b) og (c , d) ligger
på samme bidiagonal
hvis og bare hvis a + b = c + d.
Anta at en permutasjon p er gitt og at dronningene er plassert på brettet i henhold
til den. For hver dronning må vi sjekke om det er en dronning høyere opp på brettet
(til venstre i p) som slår «vår» dronning på skrå. Til dette trengs to
for-løkker - en yttre og en indre. Den yttre går nedover brettet (mot høyre i p)
og den indre oppover brettet (til venstre i p) for å sjekke
diagonalen og bidiagonalen (se Setning 1.3.15 a).
Dette kan kodes slik:
public static boolean lovligOppstilling(int[] p) // p er en permutasjon { for (int r = 1; r < p.length; r++) // r rad, p[r] kolonne { int diff = r - p[r], sum = r + p[r]; // differens og sum for (int i = r - 1; i >= 0; i--) // radene oppover fra r { if (sum == i + p[i] || diff == i - p[i]) { return false; // dronningen på (i,p[i]) slår dronningen på (r,p[r]) } } } return true; // vi har en lovlig oppstilling } Programkode 1.3.15 a)
Ved hjelp av metodene
nestePermutasjon() og
lovligOppstilling() kan finne alle lovlige
dronningoppstillinger på et 8 × 8 brett:
int[] p = {0,1,2,3,4,5,6,7}; // første permutasjon int antall = 0; // hjelpevariabel do { if (lovligOppstilling(p)) antall++; // sjekker permutasjonen } while (Tabell.nestePermutasjon(p)); // lager neste permutasjon System.out.println(antall); // Utskrift: 92 Programkode 1.3.15 b)
Programkode 1.3.15 b) er ikke spesielt effektiv. For det første finnes det
langt bedre teknikker for å lage permutasjoner enn den i
nestePermutasjon().
Hvis en permutasjon er «ulovlig», er det normalt heller ikke nødvendig å prøve den neste.
Vi kan hoppe over mange før vi tester en ny en. Mer effektive
teknikker (rekursjon i
Avsnitt 1.5.6 og
bitoperatorer
i Avsnitt 1.7.16) tas opp andre steder.
Her skal vi se på måter å redusere antallet permutasjoner som sjekkes.
I Programkode 1.3.15 b) starter vi med 0, 1, 2, 3, 4, 5, 6, 7.
Metoden lovligOppstilling()
oppdager med en gang at det ikke kan stå en dronning i rute (1,1) når det allerede
står en i (0,0). Vi kan dermed hoppe over de 6! = 720 permutasjonene som starter med 0, 1.
Den første som starter med 0, 2 finner vi ved å snu rekkefølgen på tallene som kommer etter første
posisjon der det ikke kan stå en dronning, dvs. ved å snu 2, 3, 4, 5, 6, 7. Det gir
0, 1, 7, 6, 5, 4, 3, 2. Dette er den siste permutasjonen som
starter med 0, 1. Et nytt kall på metoden nestePermutasjon()
vil gi den
første som ikke starter med 0, 1, dvs. 0, 2, 1, 3, 4, 5, 6, 7.
Dette gjelder generelt. Vi lager en ny versjon av metoden lovligOppstilling() og nå
med int som returtype. Hvis permutasjonen representerer en «lovlig»
oppstilling skal 0 returneres. Hvis ikke skal posisjonen til den
første dronningen som står «ulovlig», returneres:
public static int lovligOppstilling(int[] p) // p er en permutasjon { for (int r = 1; r < p.length; r++) // r rad, p[r] kolonne { int diff = r - p[r], sum = r + p[r]; // differens og sum for (int i = r - 1; i >= 0; i--) // radene oppover fra r if (sum == i + p[i] || diff == i - p[i]) return r; // ulovlig } return 0; // lovlig oppstilling } Programkode 1.3.15 c)
Metoden over gir oss posisjonen til den
første dronningen som er «feilplassert». Da snur vi tallene i permutasjonen
etter denne posisjonen (se Programkode 1.3.1 a ).
Vi kommer her til å lage mange forskjellige metoder i tilknytning til
«Dronningproblemet». Da er det gunstig å samle dem i en egen klasse, dvs. klassen Dronning.
Metoden i Programkode 1.3.15 c)
hører hjemme der. I tillegg lager vi en egen antall-metode som bruker teknikken beskrevet over:
public class Dronning { // Legg metoden fra Programkode 1.3.15 c) inn her! public static int antallLovlige(int n) { int[] p = new int[n]; for (int i = 0; i < n; i++) p[i] = i; // 0, 1, 2, . . . , n-1 int antall = 0; while (true) { int r = lovligOppstilling(p); // Programkode 1.3.15 c) if (r == 0) antall++; else Tabell.snu(p,r + 1); //Programkode1.3.1 a if (Tabell.nestePermutasjon(p) == false) //Programkode 1.3.1 b)return antall; } } } // Dronning Programkode 1.3.15 d)
Metoden antallLovlige() i Dronning teller opp de «lovlige»
på en vesentlig mer effektiv måte. Den er god nok til å finne antallet også for større brett enn
8 × 8. F.eks. kan vi finne svarene for brett opp til og med 14 × 14 brett uten at det går så mange sekunder.
Men som nevnt skal vi lage enda mer effektive løsninger i
Avsnitt 1.5.6 og
i Avsnitt 1.7.16.
Flg. kode finner antallet «lovlige» dronningoppstillinger for n × n brett for n lik 8 til 14:
for (int n = 2; n < 15; n++) System.out.print(Dronning.antallLovlige(n) + " "); // Utskrift: 0 0 2 10 4 40 92 352 724 2680 14200 73712 365596 Programkode 1.3.15 e)
Halvering Det er mulig på enkel måte å halvere antallet
permutasjoner som må undersøkes. Gitt de to permutasjonene 0, 4, 7, 5, 2, 6, 1, 3
og 7, 3, 0, 2, 5, 1, 6, 4. Flg. to sjakkbrett viser hvilke dronningoppstillinger
som de to representerer:
 |
| Figur 1.3.15 d) : En oppstilling (venstre) og dens vertikale speiling (høyre) |
Brettet til venstre i Figur 1.3.15 d) viser oppstillingen som
hører til permutasjonen 0, 4, 7, 5, 2, 6, 1, 3 og brettet til høyre den som hører
til 7, 3, 0, 2, 5, 1, 6, 4. Begge er «lovlige»
oppstillinger. Det spesielle er imidlertid at den til høyre er en speiling
om den vertikale midtlinjen på brettet av den til venstre. Dette gjelder generelt: Hvis
en permutasjon som starter med 0, 1, 2 eller 3 gir en «lovlig» oppstilling,
så får vi en ny en hvis den første
speiles vertikalt. Det betyr at vi kan nøye oss med å se på de permutasjonene som starter med
0, 1, 2 eller 3, og så gange det antallet vi finner med 2.
Med et generelt n × n - brett må vi imidlertid være litt mer nøye. Argumentasjonen over gjelder hvis n er et partall. Men hvis n er et oddetall, får brettet en kolonne på midten. En vertikal speiling av en oppstilling med øverste dronning på midten, vil fortsatt ha øverste dronning på midten. Men hvis den nest øverste dronningen på en «lovlig» oppstilling står til venstre for midten, vil den komme til til høyre for midten etter en slik speiling. Dermed kan vi nøye oss med i dette tilfellet å se på de permutasjonene der nest øverste dronning står til venstre for midten og så gange antallet «lovlig» oppstillinger vi finner med 2.
Flg. nye versjon av metoden
antallLovlige() bruker idéen fra diskusjonen over:
public static int antallLovlige(int n) // ny versjon { int[] p = new int[n]; // plass til n tall for (int i = 0; i < n; i++) p[i] = i; // 0, 1, 2, . . . , n-1 int antall = 0, m = n / 2; // m er midt på brettet boolean odd = (n & 1) != 0; // n odd eller lik while (p[0] < m || (odd && p[0] == m && p[1] < m)) { int r = lovligOppstilling(p); // sjekker if (r == 0) antall++; // en til som er lovlig else Tabell.snu(p,r + 1); Tabell.nestePermutasjon(p); // ny permutasjon } return antall * 2; // tar med speilingene } Programkode 1.3.15 f)
Denne nye versjonen av antallLovlige() er
omtrent dobbelt så rask. Se Oppgave 6.
Ekvivalensklasser
Figur 1.3.17 b)
viser at hvis en «lovlig» oppstilling
(permutasjonen 0, 4, 7, 5, 2, 6, 1, 3) speiles om brettets vertikale midtlinje, får
vi en ny «lovlig» oppstilling (7, 3, 0, 2, 5, 1, 6, 4).
Men vi kan også speile horisontalt (om den horisontale midtlinjen), diagonalt og bidiagonalt.
Videre kan vi rotere om brettes sentrum − 90°, 180° eller 270°. Hvis
vi starter med
0, 4, 7, 5, 2, 6, 1, 3, får vi dermed flg. «lovlige» oppstillinger:
0, 4, 7, 5, 2, 6, 1, 3 Utgangspermutasjon
7, 1, 3, 0, 6, 4, 2, 5 Rotasjon 90°
4, 6, 1, 5, 2, 0, 3, 7 Rotasjon 180°
2, 5, 3, 1, 7, 4, 6, 0 Rotasjon 270°
7, 3, 0, 2, 5, 1, 6, 4 Vertikal speiling
3, 1, 6, 2, 5, 7, 4, 0 Horisontal speiling
0, 6, 4, 7, 1, 3, 5, 2 Diagonal speiling
5, 2, 4, 6, 0, 3, 1, 7 Bidiagonal speiling
Figur 1.3.15 e) : Rotasjoner og speilinger
Figur 1.3.15 e) viser at én «lovlig» oppstilling
kan gi opptil syv nye ved å utføre rotasjoner og speilinger. De åtte
kalles permutasjonstransformasjoner eller bare transformasjoner.
 |
| Figur 1.3.15 f) : En oversikt over permutasjonstransformasjoner |
I tabellen over betyr 0, 90, 180 og 270 rotasjoner og V, H, D og B henholdsvis vertikal, horisontal, diagonal og bidiagonal speiling. Tar vi raden for 90° rotasjon og kolonnen for vertikal speiling (V), sier tabellen at det å rotere 90° og så speile vertikalt, er det samme som kun å speile diagonalt (D). Tabellen viser resultatet av alle mulige sammensetninger av to transformasjoner. F.eks. vil en horisontal speiling etterfulgt av en diagonal speiling gi samme resultat som en 90° rotasjon. Legg merke til at tabellen ikke er symmetrisk om hoveddiagonalen. Det betyr at det å bytte rekkefølgen på to transformasjoner kan gi et annet resultat. Som nevnt over blir en horisontal og så en diagonal speiling, det samme som en rotasjon på 90°. Men motsatt vei, dvs. en diagonal og så en horisontal speiling blir det samme som en rotasjon på 270°.
La p og q være to permutasjoner. Vi sier at p er relatert til q
hvis vi kan få q ved å anvende en av de åtte transformasjonene på p. Dette blir
en ekvivalensrelasjon. Den er åpenbart refleksiv siden vi kan få p ved å rotere p
en vinkel på 0° (identitetstransformasjonen). La q være relatert til p, dvs. det finnes
en transformasjon T slik at T(p) = q. Da finnes det også
en transformasjon S slik at S(q) = p. Hvis T er en speiling, vil
S = T fungere, og hvis T er en rotasjon, velger vi en rotasjon S
slik at det tilsammen blir 360 grader. Det betyr at relasjonen er symmetrisk. La så p
være relatert til q og q relatert til r. Det betyr at det finnes
transformasjoner T og S slik at T(p) = q og
S(q) = r. Men tabellen i Figur 1.3.15 f) viser at uansett hva
T og S er, så kan sammensetingen S º T erstattes av en enkelt transformasjon.
Det betyr at p og r er relatert. Med andre ord er relasjonen transitiv.
Relasjonen definert ovenfor er en ekvivalensrelasjon på mengden av permutasjoner. Det betyr at permutasjonene kan deles opp i ekvivalensklasser.
Definisjon 1.3.15 a) – Ekvivalens To
«lovlige» oppstillinger er ekvivalente hvis de hører til samme ekvivalensklasse,
dvs. hvis vi kan få den ene fra den andre ved en rotasjon eller speiling.
Vi fant at et 8 × 8 – brett har 92 forskjellige løsninger. Spørsmålet er nå hvor mange forskjellige ekvivalensklasser det er for disse 92 løsningene?
Vi har sett at ekvivalensklassen til 0, 4, 7, 5, 2, 6, 1, 3 inneholder 8 ulike
permutasjoner. Da kunne man lett tro at vi finner antallet ekvivalensklasser
ved å dele 92 med 8. Men det regnestykket går ikke opp. Det viser seg at
det er 12 ekvivalensklasser. Det er 11 som alle inneholder 8 permutasjoner
og en som inneholder 4. Det gir 11 · 8 + 4 = 92.
Permutasjonen 2, 4, 1, 7, 0, 6, 3, 5 representerer en «lovlig» oppstilling.
Men dens ekvivalensklasse inneholder bare 4 permutasjoner. Vi får samme permutasjon enten
vi speiler permutasjonen 2, 4, 1, 7, 0, 6, 3, 5 vertikalt eller horisontalt.
Se Oppgave 8.
Noen av transformasjonene har enkel kode. Vertikal speiling er kanskje
den enkleste. Hvis vi på et 8 × 8 – brett
har en dronning i en rute med r og k som rad- og kolonneindeks,
vil den ved en vertikal speiling havne på samme rad,
men med kolonneindeks lik 7 – k. F.eks. vil en dronning i rute (0,2) speiles til
(0,5) der 5 = 7 – 2. På et n × n – brett
vil rute (r , k) speiles til
rute (r , n – 1 – k).
De andre transformasjonene er litt mer kompliserte å lage, men med litt
prøving og feiling finner en fort hvordan de må lages. Flg. metoder legges i
klassen Dronning:
public static int[] rotasjon90(int[] p) // rotasjon 90 grader { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[p[i]] = n - 1 - i; return q; } public static int[] rotasjon180(int[] p) // rotasjon 180 grader { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[n - 1 - i] = n - 1 - p[i]; return q; } public static int[] rotasjon270(int[] p) // rotasjon 270 grader { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[n - 1 - p[i]] = i; return q; } public static int[] vertikal(int[] p) // vertikal speiling { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[i] = n - 1 - p[i]; return q; }
public static int[] horisontal(int[] p) // horisontal speiling { int n = p.length; int[] q = new int[n]; for (int i = 0, j = n - 1; i < n;) q[i++] = p[j--]; return q; } public static int[] diagonal(int[] p) // diagonal speiling { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[p[i]] = i; return q; } public static int[] bidiagonal(int[] p) // bidiagonal speiling { int n = p.length; int[] q = new int[n]; for (int i = 0; i < n; i++) q[n - 1 - p[i]] = n - 1 - i; return q; } Programkode 1.3.15 g)
Flg. eksempel viser hvordan rotasjons- og speilingsmetodene kan brukes:
int[] p = {0,4,7,5,2,6,1,3};
String p90 = Arrays.toString(Dronning.rotasjon90(p));
String pD = Arrays.toString(Dronning.diagonal(p));
System.out.println(p90 + " " + pD);
// Utskrift: [7, 1, 3, 0, 6, 4, 2, 5] [0, 6, 4, 7, 1, 3, 5, 2]
Programkode 1.3.15 h)
Metoden antallLovlige()
finner alle «lovlige» oppstillinger på et
n × n – brett. Målet nå er å finne de som er «ekte» forskjellige, dvs.
antall ekvivalensklasser. Permutasjonene genereres i leksikografisk rekkefølge. Av de
ekvivalente kommer derfor den «minste» først.
Dermed kan vi for hver permutasjon avgjøre om det er den første av de som er ekvivalente
eller ikke. For hver permutasjon p utfører vi de syv
transformasjonene og hvis en av dem gir en som kommer før p
leksikografisk, må vi ha fått den tidligere. Dermed kan vi la være å telle opp
p siden en som er ekvivalent allerede er registert.
Vi trenger en metode som avgjør om en permutasjon p er lik eller kommer foran en
permutasjon q leksikografisk.
Flg. metode returnerer true hvis det er tilfellet
og false ellers. Metoden skal ligge i klassen Dronning:
public static boolean foran(int[] p, int[] q)
{
for (int i = 0; i < p.length; i++)
{
if (p[i] < q[i]) return true; // p kommer foran q
else if (p[i] > q[i]) return false; // q kommer foran p
}
return true; // p og q er like
}
Programkode 1.3.15 i)
Vi trenger i tillegg en metode som avgjør om en permutasjon p er først av de permutasjonene som den er ekvivalent med:
public static boolean førstLeksikografisk(int[] p)
{
return
foran(p,rotasjon90(p)) // roterer 90 grader
&& foran(p,rotasjon180(p)) // roterer 180 grader
&& foran(p,rotasjon270(p)) // roterer 270 grader
&& foran(p,vertikal(p)) // speiler vertikalt
&& foran(p,horisontal(p)) // speiler horisontalt>
&& foran(p,diagonal(p)) // speiler diagonalt
&& foran(p,bidiagonal(p)); // speiler bidiagonalt
}
Programkode 1.3.15 j)
En metode som finner antallet unike «lovlige» oppstillinger på
et n × n – brett kan lages ved hjelp av
en liten endring i metoden
antallLovlige() :
public static int antallEkvivalensklasser(int n)
{
int[] p = new int[n]; // plass til n tall
for (int i = 0; i < n; i++) p[i] = i; // 0, 1, 2, . . . , n-1
int antall = 0, m = n / 2; // m er midt på brettet
boolean odd = (n & 1) != 0; // n odd eller lik
while (p[0] < m || (odd && p[0] == m && p[1] < m))
{
int r = lovligOppstilling(p); // sjekker permutasjonen
if (r == 0)
{
if (førstLeksikografisk(p)) antall++; // telles med
}
else Tabell.snu(p,r + 1);
Tabell.nestePermutasjon(p); // ny permutasjon
}
return antall;
}
Programkode 1.3.15 k)
Flg. eksempel viser hvordan metoden antallEkvivalensklasser() kan brukes:
for (int n = 2; n < 15; n++) System.out.print(Dronning.antallEkvivalensklasser(n) + " "); // Utskrift: 0 0 1 2 1 6 12 46 92 341 1787 9233 45752 Programkode 1.3.15 l)
Utskriften over viser at tilfellet n = 8 gir 12 som resultat.
Konklusjon Teknikkene i dette avsnittet finner korrekte løsninger, men kan
som nevnt effektiviseres. Dette tas opp i Avsnitt 1.5.6
der det brukes rekursjon
og i Avsnitt 1.7.16 der det brukes både
rekursjon og bitoperatorer.
| 1. | Søk på internett etter informasjon om dronningproblemet. Bruk f.eks. eight queens som
søkeord. Antallet lovlige dronningoppstillinger er kjent for brett opp til størrelse
25 × 25. Les på internett om hvordan man løste dette for et 25 × 25 – brett.
|
| 2. | På et 3 × 3 – brett er det ingen lovlige oppstillinger. Sjekk at det stemmer! |
| 3. | På et 4 × 4 – brett er det kun to lovlige oppstillinger. Finn dem! |
| 4. | Hvilke av flg. permutasjoner utgjør lovlige dronningoppstillinger
på et 6 × 6 – brett: i) 1, 3, 0, 2, 4, 5 ii) 1, 3, 5, 0, 2, 4 iii) 3, 0, 4, 1, 5, 2 |
| 5. | Hvilke av flg. permutasjoner utgjør lovlige dronningoppstillinger
på et 8 × 8 – brett: i) 1, 3, 0, 6, 4, 2, 5, 7 ii) 2, 0, 6, 4, 7, 1, 3, 5 iii) 3, 0, 2, 5, 1, 6, 4, 7 iv) 5, 7, 1, 3, 0, 6, 4, 2 |
| 6. | Flytt klassen Dronning over til deg.
Legg så inn den versjonen av lovligOppstilling() som står i
Programkode 1.3.15 c).
Lag så et program med
Programkode1.3.15 e) og
ta tiden det bruker. Bruk deretter den versjonen av lovligOppstilling() som står i
Programkode 1.3.15 f).
Ta tiden. Går det fortere?
|
| 7. | Lag en metoden public static int[] førsteLovlige(int n)
i klassen Dronning.
Den skal returere den første permutasjonen
(i leksikografisk
rekkefølge) som representerer en «lovlig» dronningoppstilling
på et n × n − brett. Finn så disse permutasjonene for
n fra 4 til 14.
|
| 8. | Permutasjonen p = 0, 2, 4, 1, 3 utgjør en lovlig dronningoppstilling på et 5 × 5 – brett. Finn f.eks. ved hjelp av tegninger hvilke permutasjoner vi får når p roteres på de tre måtene og speiles på de fire måtene. Hva blir det hvis p isteden er lik 1, 4, 2, 0, 3? |
| 9. | La p = 2, 4, 1, 7, 0, 6, 3, 5 dvs. et 8 × 8 – brett. Gjør som i
Oppgave 8.
|
| 10. | Tabellen i Figur 1.3.15 f)
viser resultatet av å sette sammen to og to transformasjoner. Det påstås f.eks.
at en horisontal speiling etterfulgt av en diagonal speiling er det samme som en
rotasjon på 90 grader og at hvis rekkefølgen byttes blir det lik en rotasjon på 270 grader.
Tegn et brett med en oppstilling og sjekk at disse påstandene stemmer.
|
| 11. | Legg alle transformasjonsmetodene fra
Programkode 1.3.15 g)
inn i klassen Dronning.
Kjør så Programkode 1.3.15 h).
Tegn et 8 × 8 – brett og sjekk at det som kommer som utskrift er korrekt.
Gjør det samme med noen av de andre transformasjonene.
|
| 12. | Lag kode som skriver ut de 12 unike løsningene for et 8 × 8 – brett, dvs. en
permutasjon fra hver av de 12 ekvivalensklassene. Hver av dem skal være den som kommer
først leksikografisk.
|
- Binærsøk - antall sammenligninger er i pdf-format.
- Partisjonering - antall ombyttinger er i pdf-format.
- Rotasjonssykler er i pdf-format.
- Kvikksortering er i pdf-format.


|
