Oppgave 1

Oppgave 2

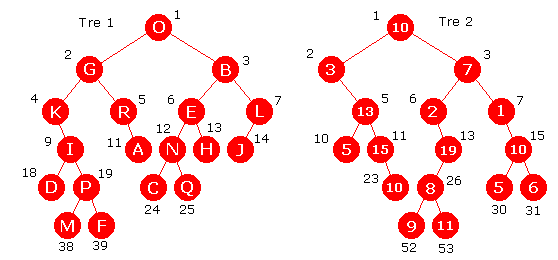
Tre 1 har 39 som største posisjonstall og de signifikante sifferne er (noe en kan lese rett fra treet ved å følge veien fra rotnoden og ned til noden med posisjonstall 39) 100111. Antallet signifikante siffer er 6 og høyden til Tre 1 er 5. Tallet 53 i Tre 2 har de signifikante sifferne 110101, dvs. 6 stykker. Tre 2 har høyde 5.

Oppgave 3 og 4

Oppgave 5

Hvis treet skal ha en node med posisjon 12 må det også ha en node med posisjon 6 siden det er foreldernoden. Men det er ikke satt opp noen node med posisjon 6. Med andre ord utgjør ikke disse tallene nodeposisjonene til et binærtre.

Oppgave 6

I et såkalt ekstremt høyreskjevt tre er alle posisjonstallene odde. I et slikt tre har ingen noder venstre barn. Dette er de eneste trærne av denne typen siden et venstre barn alltid har en partall som posisjonstall.

Oppgave 7

1) {1,2,4}, 2) {1,2,5}, 3) {1,2,3}, 4) {1,3,6}, 5) {1,3,7}

Oppgave 8

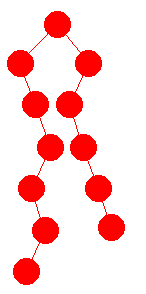Hvis et tre har en node med posisjon 90, må det også inneholde noder med posjonstall 90/2 = 45, 45/2 = 22, 22/2 = 11, 11/2 = 5, 5/2 = 2 og 2/2 = 1. Hvis det i tillegg har en node med posisjon 55, må det ha noder med posisjon 55/2 = 27, 27/2 = 13, 13/2 = 6 og 6/2 = 3. Det minste mulige treet er tegnet til venstre. Oppgave 9 P(T) og P(S) er like som tallmengder. Det betyr at de representerer posisjonstallene til to trær med samme form.

Oppgave 10

  public static boolean girBinærtre(int[] a)
  {
    if (a.length == 0) return true;  // et tomt tre

    Arrays.sort(a);
    if (a[0] != 1) return false;  // må ha 1 først

    for (int i = 1; i < a.length; i++)
      if (a[i-1] == a[i]) return false;  // duplikater

    for (int i = 1; i < a.length; i++)
    {
      int j = i - 1;
      int forelder = a[i]/2;
      for (; j >= 0; j--) if (forelder == a[j]) break;
      if (j < 0) return false;  // forelder mangler
    }

    return true;
  }

Oppgave 11

Hvis tabellen a inneholder tallet k, så må utvidelsen også inneholde k/2, (k/2)/2, osv. Hvis f.eks. k = 90, må utvidelsen inneholde 45, 22, 11, 5, 2 og 1.

  public static int[] utvid(int[] a)
  {
    Arrays.sort(a);
    boolean[] finnes = new boolean[a[a.length-1]+1];
    int antall = 0;
    for (int i = 0; i < a.length; i++)
    {
      int k = a[i];
      while (k > 0)
      {
        if (!finnes[k])
        {
          finnes[k] = true;
          antall++;
        }
        else break;
        k /= 2;
      }
    }

    int[] b = new int[antall];
    for (int i = 0, j = 0; i < finnes.length; i++)
      if (finnes[i]) b[j++] = i;

    return b;
  }

Metoden kan brukes slik:

  public static void main(String[] args) throws IOException
  {
    int[] a = {55,90};
    int[] b = utvid(a);

    System.out.println(Arrays.toString(b));

    // Utskrift: [1, 2, 3, 5, 6, 11, 13, 22, 27, 45, 55, 90]

  }

Oppgave 12

  public static boolean girFulltBinærtre(int[] a)
  {
    if (!girBinærtre(a)) return false;
    if ((a.length & 1) == 0) return false;  // a.length må være odd

    for (int i = 1; i < a.length; i += 2)
    {
      if (a[i] + 1 != a[i+1]) return false;
      else if (a[i]/2 != a[i+1]/2) return false;
    }

    return true;
  }

Oppgave 13

  public static boolean girIsomorfeTrær(int[] a, int[] b)
  {
    if (!Arrays.equals(a,b)) return false;
    return girBinærtre(a);
  }

Oppgave 14

Metoden preSorter sorterer nodeposisjonene i preorden. Begrepet preorden i et binærtre tas opp i et senere avsnitt.

  public static void preSorter(int[] a)
  {
   for (int i = 1; i < a.length; i++)  // a[0] er første verdi
    {
      int temp = a[i];
      String s = Integer.toBinaryString(temp);

      // verdier flyttes inntil rett sortert plass i a[fra:i> er funnet
      int j = i-1;
      for (; j >= 0 && s.compareTo(Integer.toBinaryString(a[j])) < 0; j--)
        a[j+1] = a[j];

      a[j+1] = temp;  // verdien settes inn på rett sortert plass
    }
  }