Oppgave 1

Det første treet:

Preorden: D I L A K F C E H O N M J G B
Inorden: I A F K C L E D M N J O G H B
Postorden: F C K A E L I M J N G O B H D

Det andre treet:

Preorden: E I G A L O M C B H D K N J F
Inorden: G I L A M O C E H D B J N F K
Postorden: G L M C O A I D H J F N K B E

Oppgave 2

Det første treet:

Preorden: O G K I D P M F R A B E N C Q H L J
Inorden: K D I M P F G R A O C N Q E H B J L
Postorden: D M F P I K A R G C Q N H E J L B O

Det andre treet:

Preorden: 10 3 13 5 15 10 7 2 19 8 9 11 1 10 5 6
Inorden: 3 5 13 15 10 10 2 9 8 11 19 7 1 5 10 6
Postorden: 5 10 15 13 3 9 11 8 19 2 5 6 10 1 7 10

Oppgave 3

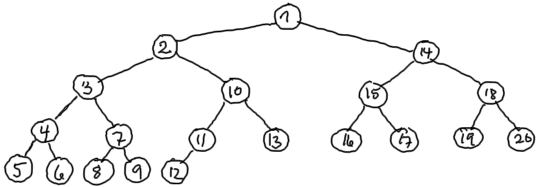Preorden

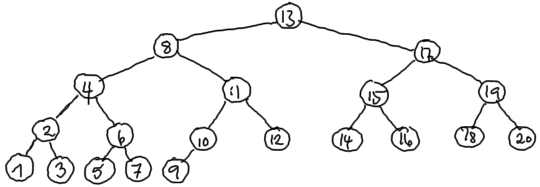Inorden

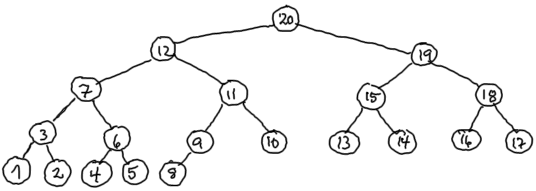Postorden

Oppgave 4

For bladnoder er første, andre og tredje passering av konturkurven det samme. Dermed kommer bladnodene i samme rekkefølge både i preorden, inorden og postorden.

Oppgave 5

  BinTre<Character> tre = new BinTre<>();   // et tomt tre

  String v = "HBKADIOCFJMEGLN";  // verdiene i nivåorden
  int[] p = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29};

  for (int i = 0; i < p.length; i++)
    tre.leggInn(p[i],v.charAt(i));  // autoboksing fra char til Character

  tre.inorden(new KonsollUtskrift<>());  // skriver ut

  // Utskrift: A B C D E F G H I J K L M N O

Oppgave 6

  BinTre<Character> tre = new BinTre<>();   // et tomt tre

  String v = "ABICDJLEFKMGHNO";  // verdiene i nivåorden
  int[] p = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29};

  for (int i = 0; i < p.length; i++)
    tre.leggInn(p[i],v.charAt(i));  // autoboksing fra char til Character

  tre.preorden(new KonsollUtskrift<>());  // skriver ut

  // Utskrift: A B C D E F G H I J K L M N O

Oppgave 7

  private static <T> void postorden(Node<T> p, Oppgave<? super T> oppgave)
  {
    if (p.venstre != null) postorden(p.venstre,oppgave);
    if (p.høyre != null) postorden(p.høyre,oppgave);
    oppgave.utførOppgave(p.verdi);
  }

  public void postorden(Oppgave<? super T> oppgave)
  {
    if (rot != null) postorden(rot,oppgave);
  }

Oppgave 8

  public void nullstill()
  {
    if (!tom()) nullstill(rot);  // nullstiller
    rot = null; antall = 0;      // treet er nå tomt
  }

  private void nullstill(Node<T> p)
  {
    if (p.venstre != null)
    {
      nullstill(p.venstre);      // venstre subtre
      p.venstre = null;          // nuller peker
    }
    if (p.høyre != null)
    {
      nullstill(p.høyre);        // høyre subtre
      p.høyre = null;            // nuller peker
    }
    p.verdi = null;              // nuller verdien
  }

Oppgave 9

  BinTre<Character> tre = new BinTre<>();   // et tomt tre

  String v = "OGNAFIMBEHLCDJK";  // verdiene i nivåorden
  int[] p = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29};

  for (int i = 0; i < p.length; i++)
    tre.leggInn(p[i],v.charAt(i));  // autoboksing fra char til Character

  tre.postorden(new KonsollUtskrift<>());  // skriver ut

  // Utskrift: A B C D E F G H I J K L M N O

Oppgave 10

  private static <T> void toString(Node<T> p, StringBuilder s)
  {
    if (p.venstre != null)
    {
      toString(p.venstre, s);
      s.append(',').append(' ');
    }

    s.append(p.verdi);

    if (p.høyre != null)
    {
      s.append(',').append(' ');
      toString(p.høyre, s);
    }
  }

  public String toString()
  {
    StringBuilder s = new StringBuilder();
    s.append('[');
    if (!tom()) toString(rot, s);
    s.append(']');
    return s.toString();
  } 

Oppgave 11

  public String toPreString()
  {
    StringJoiner s = new StringJoiner(", ", "[", "]");
    if (!tom()) preorden(x -> s.add(x.toString()));
    return s.toString();
  }

  public String toPostString()
  {
    StringJoiner s = new StringJoiner(", ", "[", "]");
    if (!tom()) postorden(x -> s.add(x.toString()));
    return s.toString();
  }

  public String toNivåString()
  {
    StringJoiner s = new StringJoiner(", ", "[", "]");
    if (!tom()) nivåorden(x -> s.add(x.toString()));
    return s.toString();
  }

Oppgave 12

Hvis treet har en høyde på minst 31, vil det bli nodeposisjoner som er for store for å kunne være positive tall i datatypen int. Da vil der være minst én node som har avstand 31 fra roten og det betyr at dens nodeposisjon har 32 binære siffer der første siffer er 1. Men det er et negativt tall. Vi kunne imidlertid se bort fra fortegn, men da går det galt hvis treet har en høyde på minst 32.

  public int[] posisjonerPreorden()
  {
    List<Integer> liste = new ArrayList<>();
    if (rot != null) posisjonerPreorden(rot, 1, liste);
    int[] pos = new int[antall];
    int i = 0; for (Integer k : liste) pos[i++] = k;
    return pos;
  }

  private static void
  posisjonerPreorden(Node<?> p, int k, List<Integer> liste)
  {
    liste.add(k);
    if (p.venstre != null) posisjonerPreorden(p.venstre, 2*k, liste);
    if (p.høyre != null) posisjonerPreorden(p.høyre, 2*k + 1, liste);
  }

Oppgave 13

 public int[] posisjonerNivåorden()
  {
    Kø<Node<?>> kø = new TabellKø<>();
    kø.leggInn(rot);

    Kø<Integer> pos = new TabellKø<>();
    pos.leggInn(1);

    int[] posisjon = new int[antall];
    int i = 0;

    while (!kø.tom())
    {
      Node<?> p = kø.taUt();
      int k = pos.taUt();
      posisjon[i++] = k;

      if (p.venstre != null)
      {
        kø.leggInn(p.venstre);
        pos.leggInn(2*k);
      }

      if (p.høyre != null)
      {
        kø.leggInn(p.høyre);
        pos.leggInn(2*k + 1);
      }
    }
    return posisjon;
  }

Oppgave 14

  Liste<Character> liste = new TabellListe<>(tre.antall());
  tre.preorden(c -> liste.leggInn(c));
  System.out.println(liste);

Oppgave 15

  StringBuilder s = new StringBuilder("[");
  tre.preorden(c -> s.append(c).append(',').append(' '));
  int n = s.length();
  if (n > 1) s.replace(n - 2, n, "]"); else s.append(']');
  String verdier = s.toString();
  System.out.println(verdier);

Oppgave 16

  StringJoiner s = new StringJoiner(", ","[","]");
  tre.preorden(c -> s.add(c.toString()));
  String verdier = s.toString();
  System.out.println(verdier);

Oppgave 17

  public T sistInorden()
  {
    if (tom()) throw new NoSuchElementException("Treet er tomt!");

    Node<T> p = rot;
    while (p.høyre != null) p = p.høyre;

    return p.verdi;
  }

Oppgave 18

  public T sistPreorden()
  {
    if (tom()) throw new NoSuchElementException("Treet er tomt!");

    Node<T> p = rot;
    while (true)
    {
      if (p.høyre != null) p = p.høyre;
      else if (p.venstre != null) p = p.venstre;
      else return p.verdi;
    }
  }

Oppgave 19

  public void preorden(ObjIntConsumer<? super T> oppgave)
  {
    if (tom()) return;

    Node<T> p = rot;    // starter i roten
    int k = 1;          // rotens posisjon

    while (true)
    {
      oppgave.accept(p.verdi,k);

      if (p.venstre != null)
      {
        p = p.venstre;
        k <<= 1;        // 2*k
      }
      else if (p.høyre != null)
      {
        p = p.høyre;
        k <<= 1; k++;   // 2*k + 1
      }
      else
      {
        // current node har posisjon k
        // vi starter i roten og går ned til k

        int n = Integer.highestOneBit(k >> 1);

        p = rot;             // p brukes nå som hjelpepeker
        int  l = 1;          // hjelpeposisjon som følger p

        int m = -1;          // posisjonen til den neste
        Node<T> q = null;    // den neste til k

        while (n > 0)        // inntil vi kommer til k
        {
          if ((k & n) == 0)  // vi skal til venstre
          {
            if (p.høyre != null)
            {
              q = p.høyre;   // kandidat for å være den neste
              m = 2*l + 1;   // posisjonen til kandidaten
            }
            p = p.venstre;   // hjelpepeker går til venstre
            l <<= 1;         // hjelpeposisjon går til venstre
          }
          else
          {
            p = p.høyre;     // hjelpepeker går til høyre
            l <<= 1; l++;    // hjelpeposisjon går til høyre
          }

          n >>= 1;           // flytter til neste binære siffer
        }

        if (m == -1) break;  // k var den siste i preorden

        p = q;               // flytter p til den neste
        k = m;               // flytter k til den neste
      }
    }
  }
  

Metoden kan f.eks. brukes slik:

  int[] p = {1,2,3,4,5,6,7,8,9,10};               // nodeposisjoner
  char[] v = "ABCDEFGHIJ".toCharArray();          // nodeverdier

  BinTre<Character> tre = new BinTre<>();         // et tomt binærtre
  for (int i = 0; i < p.length; i++) tre.leggInn(p[i],v[i]);

  tre.preorden((c,k) -> System.out.print("(" + c + ',' + k + ") "));
 

Oppgave 20

Løsningsforslag mangler!

Oppgave 21

Løsningsforslag mangler!

Oppgave 22

I NetBeans får du meldingen «refrence to preorden is ambiguous». Eclipse sier omtrent det samme. Hvis den ene (likegyldig hvem av dem) er kommentert vekk, vil det ikke komme feilmelding og kodebiten kan kjøres.

Oppgave 24

  Liste<Character> cliste = new TabellListe<>();
  Liste<Integer> iliste = new TabellListe<>();

  tre.preorden((c,i) -> {cliste.leggInn(c); iliste.leggInn(i);});

  System.out.println(cliste);
  System.out.println(iliste);

Oppgave 25

  char bokstav = 'G';
  tre.preorden((c,i) -> {if (c == bokstav) System.out.println(i);});

  int k = 13;
  tre.preorden((c,i) -> {if (k == i) System.out.println(c);});

Oppgave 26

  char[] c = {(char)0};   // minste mulige tegn
  int[] a = {-1};

  tre.preorden((d,k) -> { if (d > c[0]) { c[0] = d; a[0] = k; } } );

  if (!tre.tom())
    System.out.println("Størst verdi " + c[0] + " har posisjon " + a[0]);

Oppgave 27

  int[] a = {0};

  tre.preorden((d, k) -> { if (k > a[0]) a[0] = k; } );

  int høyde = tre.tom() ? -1 : 31 - Integer.numberOfLeadingZeros(a[0]);

  System.out.println(høyde);

Oppgave 28

  public void preorden(BiConsumer<? super T, Integer> oppgave)
  {
    if (!tom()) preorden(rot, 1, oppgave);  // roten har posisjon 1
  }

  private static <T> void postorden(Node<T> p, Oppgave<? super T> oppgave)
  {
    if (p.venstre != null) postorden(p.venstre,oppgave);
    if (p.høyre != null) postorden(p.høyre,oppgave);
    oppgave.utførOppgave(p.verdi);
  }

Feilmeldingen sier at det er en tvetydighet (eng: ambiguous). Setningen virker for begge tilfellene.

Oppgave 30

  int[] posisjon = {1,2,3,4,5,6,7,10,11,13,14,22,23,28,29};     // posisjoner og
  String[] verdi = "EIBGAHKLODNMCJF".split("");                 // verdier i nivåorden
  BinTre<String> tre = new BinTre<>(posisjon, verdi);           // en konstruktør

  String[] preorden = new String[tre.antall()];                 // String-tabell
  int[] i = {0};                                                // en teller
  tre.preorden(x -> preorden[i[0]++] = x);                      // traverserer
  System.out.println(Arrays.toString(preorden));                // skriver tabellen

  String[] inorden = new String[tre.antall()];                  // String-tabell
  int[] j = {0};                                                // en teller
  tre.inorden(x -> inorden[j[0]++] = x);                        // traverserer
  System.out.println(Arrays.toString(inorden));                 // skriver tabellen

  BinTre<String> tre2 = BinTre.trePreorden(preorden, inorden);  // bygger opp treet

  tre.nivåorden(Oppgave.konsollutskrift());                     // nivåorden i tre
  System.out.println();                                         // linjeskift
  tre2.nivåorden(Oppgave.konsollutskrift());                    // nivåorden i tre2

Oppgave 31

  private static <T> Node<T> trePostorden(T[] postorden, int rot, T[] inorden, int v, int h)
  {
    if (v > h) return null;  // tomt intervall -> tomt tre

    int k = v; T verdi = postorden[rot];
    while (!verdi.equals(inorden[k])) k++;  // finner verdi i inorden[v:h]

    Node<T> høyre   = trePostorden(postorden, rot - 1, inorden, k + 1, h);
    Node<T> venstre = trePostorden(postorden, rot - 1 - (h - k), inorden, v, k - 1);

    return new Node<>(verdi, venstre, høyre);
  }

  public static <T> BinTre<T> trePostorden(T[] postorden, T[] inorden)
  {
    BinTre<T> tre = new BinTre<>();
    tre.rot = trePostorden(postorden, postorden.length - 1, inorden, 0, inorden.length - 1);
    tre.antall = postorden.length;
    return tre;
  }