![]() 1.5.1 Hva er en rekursiv metode?
1.5.1 Hva er en rekursiv metode?
Når en metode brukes i et program sier vi at metoden kalles eller at det gjøres
et metodekall. En rekursiv metode er en metode som kaller seg selv.
Det betyr at metodens kode inneholder et eller flere kall på den samme metoden.
Eksempel 1: Vi har den samme idéen, men i en litt annen form, i matematikk.
Flg. uttrykk kalles enten en differensligning eller en rekurensligning
(eng: recurrence relation):
(1.5.1.1) an = 2 an−1 + 3 an−2 , n ≥ 2 a0 = 1 , a1 = 2
I ligning (1.5.1.1) står an for det generelle leddet i en tallfølge. Leddet an er definert rekursivt, dvs. ved hjelp av de to leddene an−1 og an−2 . Verdiene til de to første leddene er oppgitt. Dermed kan vi regne ut de andre leddene. F.eks. vil a2 = 2 a1 + 3 a0 = 2·2 + 3·1 = 7.
Vi kan, ved hjelp av ligning (1.5.1.1), lage en rekursiv metode som gir oss verdien til an :
public static int a(int n) // n må være et ikke-negativt tall { if (n == 0) return 1; // a0 = 1 else if (n == 1) return 2; // a1 = 2 else return 2*a(n-1) + 3*a(n-2); // to rekursive kall } Programkode 1.5.1 a)
Programkode 1.5.1 a) er nærmest en «avskrift» av ligning (1.5.1.1). Metoden med det korte navnet a er en rekursiv metode siden den kalles to ganger i siste programsetning. I begge kallene er imidlertid parameterverdien annerledes (mindre) enn det den opprinnelig var. Det betyr at før eller senere vil parameterverdien bli 1 eller 0 og da returnerer metoden verdien 2 eller 1 uten flere nye metodekall. Obs: Hvis metoden kalles med en negativ parameterverdi, vil vi få en «uendelig» mange kall.
Flg. eksempel viser hvordan Programkode 1.5.1 a) kan brukes til å finne f.eks. a10 :
System.out.println(a(10)); // Uskrift: 44287
Metoden Programkode 1.5.1 a) virker, men det viser seg at den er særdeles ineffektiv. En forklaring på det kommer senere. Mange problemer kan løses på en naturlig måte ved hjelp av rekursjon. Ofte blir koden både enkel, kort og elegant. Men hvis en ikke er klar over hva rekursjon handler om, kan man risikere at metoden som lages blir ineffektiv og i verste fall føre til en «uendelig» mange kall. Det er forøvrig kjent at ethvert problem som kan løses rekursivt, også kan løses iterativt, dvs. uten bruk av rekursjon. Hvis en rekursiv metode blir ineffektiv, bør man derfor lage en iterativ løsning. F.eks. kan metoden i Programkode 1.5.1 a) lett lages iterativ. Se Oppgave 1.
Dette skal først og fremst være en praktisk innføring i hvordan man lager rekursive metoder. Derfor vil det flere steder bli laget rekursive løsninger på problemer der en iterativ løsning både kan være enklere, mer naturlig og mer effektiv. Hensikten er å lære hvordan rekursiv programmering rent teknisk foregår og hva som må til for at løsningen skal virke.
Eksempel 2: Tverrsummen til et heltall er lik summen av tallets sifre. La
f.eks. n = 72416. Da er tverrsum(n) = tverrsum(72416)
= 7 + 2 + 4 + 1 + 6 = 20. Men dette kan også defineres rekursivt:
tverrsum(72416) = tverrsum(7241) + 6. Dvs. tverrsummen er
lik tverrsummen til tallet vi får ved å ta vekk siste siffer pluss siste siffer.
Hvis tallet har bare ett siffer, er tverrsummen lik tallet selv. Vi vet også
at når 72416 deles med 10, dvs. 72416 / 10, blir kvotienten lik 7241 og at siste
siffer 6 i 72416 er lik 72416 % 10. Dette gjør oss i stand til å lage flg. rekursive metode:
public static int tverrsum(int n) // n må være >= 0 { if (n < 10) return n; // kun ett siffer else return tverrsum(n / 10) + (n % 10); // metoden kalles } Programkode 1.5.1 b)
Flg. programeksempel viser hvordan metoden virker:
System.out.println(tverrsum(0)); // Utskrift: 0 System.out.println(tverrsum(72416)); // Utskrift: 20 System.out.println(tverrsum(2147483647)); // Utskrift: 46
Tverrsummen (eng: digit sum) vil normalt ha flere siffer. Dermed kan en finne tverrsummen til tverrsummen, osv. inntil en står igjen med et tall med kun ett siffer. Dette tallet kalles den gjentatte (eller minste) tverrsummen (eng: digital root). Ta tallet 956847 som eksempel. Det har 39 som tverrsum. Tverrsummen til 39 er 12 og 12 har 3 som tverrsum. Dette kan brukes til å avsløre noen typer regnefeil når en «håndregner» med store heltall. Se Oppgave 3 - 5.
Eksempel 3: Gitt to ikke-negative heltall a og b der ikke begge er 0. Det største
heltallet som går opp i både a og b, kalles største felles divisor. Hvis
a og b ikke er for store, går det raskt å finne største felles divisor
ved prøving og feiling eller ved f.eks. å faktorisere tallene. Men heldigvis finnes
det en enkel og effektiv algoritme og den kan brukes for alle tall. Algoritmen var kjent
for den greske matematikeren Euklid. Han levde for over 2000 år siden
(ca. 325 f.Kr. – ca. 265 f.Kr.) og algoritmen har fått navnet Euklids algoritme.
 |
| Euklid 325 f.Kr. – 265 f.Kr. |
La r være resten vi får når a deles med b (b ≠ 0). Da kan det vises (vi tar det imidlertid som gitt) at b og r har samme største felles divisor som a og b. La f.eks. a = 480 og b = 126. Da blir r = 102. Det betyr at 126 og 102 har samme største felles divisor som 480 og 126. Vi får spesialtilfeller hvis a = 0 eller b = 0. Hvis bare den ene er 0, vil største felles divisor for de to bli lik den andre. F.eks. er største felles divisor 10 og 0 lik 10 fordi 10 går opp i både 10 og 0. Hvis begge er 0, har ikke problemet løsning.
public static int euklid(int a, int b) { if (b == 0) return a; int r = a % b; // r er resten return euklid(b,r); // rekursivt kall } Programkode 1.5.1 c)
I koden over returneres a hvis b = 0. Hvis a ikke er 0, blir det korrekt. Men a blir returnert også hvis begge er 0. Det er ikke korrekt. Metoden burde derfor sjekke dette på forhånd og eventuelt kaste et unntak hvis begge er 0. Det rekursive kallet benytter at største felles divisor for a og b er det samme som største felles divisor for b og r. Det er ikke nødvendig at b er mindre enn a når metoden kalles. Hvis a er minst av de to, vil r bli lik a. Dermed bytter a og b plass i det rekursive kallet. Metoden kan brukes på flg. måte:
int a = 480, b = 126; System.out.println(euklid(a,b)); // Utskrift: 6
Det er like enkelt å implementere Euklids algoritme iterativt som rekursivt. Da brukes en for-løkke med tre hjelpevariabler. Se Oppgave 6.
Eksempel 4: Summen av tallene fra 1 til n er gitt ved formelen n(n+1)/2. Men vi kan også summere tallene fortløpende vha. en for-løkke. Men kan det gjøres rekursivt? Ja, vi kan tenke slik: Anta at vi kjenner summen av de n – 1 første tallene. Da finner vi hele summen ved å legge til n. Summen av ett tall er lik tallet selv. Dette kan oversettes til flg. metode:
public static int sum(int n) // summen av tallene fra 1 til n { if (n == 1) return 1; // summen av 1 er lik 1 return sum(n - 1) + n; // summen av de n – 1 første + n } Programkode 1.5.1 d)
Metoden sum kan brukes slik:
System.out.println(sum(100)); // Utskrift>: 5050
Vi kan bruke samme idé i en litt annen situasjon. Anta at vi skal finne summen av de n første verdiene i en tabell, dvs. summen a[0] + a[1] + a[2] + a[3] + . . . + a[n–1]. Det kan vi løse rekursivt ved å tenke på samme måte som sist: Anta at vi kjenner summen av de n – 1 første verdiene i tabellen. Da finner vi hele summen ved å legge til verdien a[n–1]. Spesielt kan vi si at summen av én tabellverdi er tabellverdien selv:
public static int sum(int[] a, int n) // summen av de n første { if (n == 1) return a[0]; // summen er verdien selv return sum(a,n-1) + a[n-1]; // summen av de n-1 første + a[n-1] } Programkode 1.5.1 e)
Også metoden sum over kan brukes til å finne summen av tallene fra 1 til 100. Legg merke til at tabellens lengde må inngå som parameterverdi:
int[] a = Tabell.randPerm(100); // en permutasjon av tallene fra 1 til 100 System.out.println(sum(a,a.length)); // Utskrift: 5050 Programkode 1.5.1 f)
Eksempel 5: I Avsnitt 1.3.6 om binærsøk ble begrepet «splitt og hersk» innført (eller egentlig «forminsk og hersk»). Dette er en idé som nærmest er rekursiv i sin natur. Hvis et problem kan deles opp i mindre delproblemer av nøyaktig samme type, så kan vi løse problemet ved å lage en metode som kaller seg selv for hvert delproblem og så bruke løsningene av delproblemene til å løse hele problemet.
Kan vi finne summen av verdiene i en tabell ved hjelp av «splitt og hersk»? Ja, vi kan dele tabellen i to deler, summere verdiene i hver del for seg og så addere de to delsummene for å få hele summen. Hvis en tabell (eller et tabellintervall) består av bare én verdi er summen lik denne verdien. Dette kan vi oversette til flg. metode:
public static int sum(int[] a, int v, int h) // intervallet a[v:h] { if (v == h) return a[v]; // summen av én verdi er verdien selv int m = (v + h)/2; // finner midten return sum(a,v,m) + sum(a,m+1,h); // summen av de to halvdelene } Programkode 1.5.1 g)
Denne metoden kan også brukes til å finne summen av tallene fra 1 til 100.
Legg merke til at startintervallet for kallet på metoden i
Programkode 1.5.1 g)
må settes til a[0:a.length – 1]:
int[] a = Tabell.randPerm(100); // en permutasjon av tallene fra 1 til 100 System.out.println(sum(a,0,a.length-1)); // Utskrift: 5050
 |
| Carl Friedrich Gauss |
Det er en anekdote knyttet til den store tyske matematikeren Carl Friedrich Gauss
(1777 – 1855) når det gjelder å finne summen av tallene fra 1 til 100. En dag
på skolen da Gauss var 7 år, ville læreren gi elevene en oppgave som han regnet
med ville holde dem okkupert en god stund. Oppgaven var nettopp det å summere
tallene fra 1 til 100. Men lille Gauss kom frem til læreren nesten med en gang og viste
frem det korrrekte svaret. Gauss hadde observert at istedenfor å legge sammen
fortløpende, kunne han først legge sammen 1 og 100, så 2 og 99, osv. Hver slik sum hadde
101 som svar. Dermed ble hele summen lik 50 ganger 101 lik 5050.
Eksempel 6:
Det n-te Fibonacci-tallet fib(n)
er definert som summen av de to foregående Fibonacci-tallene, dvs. fib(n) =
fib(n-1) + fib(n-2). Vanligvis sies det at første eller
det 0-te Fibonacci-tallet er 0 og at det neste er 1, dvs. fib(0) = 0 og
fib(1) = 1. Ved hjelp av dette kan vi finne alle Fibonacci-tall.
De 10 første er: 0, 1, 1, 2, 3, 5, 8, 13, 21 og 34. Definisjonen gjør det også lett å lage
en rekursiv metode som gir oss det n-te Fibonacci-tallet:
public static int fib(int n) // det n-te Fibonacci-tallet { if (n <= 1) return n; // fib(0) = 0, fib(1) = 1 else return fib(n-1) + fib(n-2); // summen av de to foregående } Programkode 1.5.1 h)
Fib-metoden og 1.5.1 a) er av samme type og er svært ineffektive. De er (skrekk)eksempler på når rekursjon absolutt ikke skal brukes. Metoden gir (i prinsippet) ethvert Fibonacci-tall. Men hvis n er stor, vil den nærmest gå inn i «evig» løkke. Se neste avsnitt.
Flg. eksempel viser hvordan fib-metoden i Programkode 1.5.1 h) kan brukes:
System.out.println(fib(10)); // Utskrift: 55 System.out.println(fib(20)); // Utskrift: 6765
| 1. | Lag en iterativ versjon av metoden a i Programkode 1.5.1 a). |
| 2. | Løs ligning (1.5.1.1), dvs. finn en formel for an . |
| 3. | Programkode 1.5.1 b) er rekursiv. Lag en iterativ løsning. |
| 4. | Gjentatt tverrsum til et tall n får vi ved å ta tverrsummen til n, så tverrsummen
av dette, osv. til vi står igjen med et tall med kun ett siffer. Vi bruker navnet sifferrot
på dette istedenfor gjentatt tverrsum. Det svarer til det engelske navnet digital root. Ta tallet
956847 som eksempel:
tverrsum(956847) = 39, tverrsum(39) = 12 og
tverrsum(12) = 3. Dermed blir sifferrot(956847) = 3.
Lag metoden public static int sifferrot(int n). Den skal returnere sifferroten til n.
|
| 5. | a) En regel sier at et heltall er delelig med 9 hvis og bare hvis tallets tverrsum er delelig med 9. Hvorfor er det sant? |
b) En regel sier at hvis a ganget med b
gir c som svar, vil sifferroten til produktet av sifferrøttene til a og b
være lik sifferroten til c. Hvorfor er det sant? (Det samme er sant for en
sum av to hele tall.) Lag et program som velger store heltall og
sjekker at dette stemmer ved å bruke metoden sifferrot() fra Oppgave 4.
| |
| 6. | a) Bruk euklid-metoden i Eksempel 3 til å finne største felles divisor for 1529 og 14036. |
| b) Lag en iterativ versjon av Euklids algoritme. | |
| c) Hvor effektiv er Euklids algoritme? Hva er dens orden? | |
| 7. | Lag en rekursiv metode som finner summen av kvadrattallene fra 1 til n, dvs. finner summen 12 + 22 + 32 + . . . + n2. Kjenner du noen formel for den samme summen? |
| 8. | Summen av heltallene fra 1 til n er et spesialtilfelle av det å finne summen av heltallene fra k til n der k <= n. Lag en metode public static int sum(int k, int n) som finner denne summen, og gjør det ved å bruke «splitt og hersk». |
| 9. | Lag en rekursiv metode som returnerer posisjonen til den største blant de n første verdiene i en heltallstabell. Kan du få det til ved en «splitt og hersk»-teknikk? |
| 10. | Lag en rekursiv metode som finner n! (dvs. n fakultet) når n er parameterverdi. |
| 11. | Bruk Programkode 1.5.1 h) til å finne Fibonacci-tall nr. 20, 30, 40 og 50. Hva skjer? |
| 12. | Lag en ikke-rekursiv metode som finner det n-te Fibonacci-tallet. Bruk long som datatype istedenfor int. Bruk metoden til å finne Fibonacci-tall nr. 50. |
| 13. | Lag en rekursiv Fibonacci-metode som har kun ett rekursivt kall. |
| 14. | B(n,k) er binomialkoeffisienten «n over k», dvs. brøken med n! i teller og k! · (n-k)! i nevner. Den er definert for 0 ≤ k ≤ n. Husk at per definisjon er 0! = 1. |
a) Vi har B(n,k)
= B(n − 1,k − 1) +
B(n − 1,k). Lag en rekursiv metode
public static int B(int n, int k) som bruker dette til å finne
binomialkoeffisienten. Det kan tas som gitt at n og k har
lovlige verdier. Husk at for bestemte verdier av k vil
B(n,k) kunne bestemmes (og returneres) uten nye kall på metoden.
| |
b) Lag metoden public static int binomial(int n, int k).
Det kastes et unntak hvis n og/eller k er ulovlige.
Det kjent at B(n,k) = B(n,n − k).
Hvis k > n/2, skal k erstattes med n − k.
Til slutt brukes metoden fra punkt a.
| |
| c) Lag en versjon av metoden binomial (se punkt b) der det brukes forløpende ganging og deling. Vi finner f.eks. «9 over 4» ved å starte med 9, så dele med 1, gange med 8, dele med 2, gange med 7, dele med 3, gange med 6 og til slutt dele med 4. |
![]() 1.5.2 Hva skjer når en rekursiv metode kjøres?
1.5.2 Hva skjer når en rekursiv metode kjøres?
Når en metode kalles, legges data knyttet til kallet på programstakken.
På engelsk har dette begrepet mange navn, f.eks.
call stack,
execution stack, control stack,
run-time stack
eller machine stack. Det som legges på programstakken ved et metodekall,
skal vi her kalle et aktivitetslag (eng: activation layer,
activation record eller
stack frame). Det består av kopier av parameterverdiene,
lokale hjelpevariabler og adresser/pekere. Når kallet er fullført, blir plassen på stakken frigjort og programkontrollen
går til første programsetning etter der metoden ble kalt.
I Java er det et kall på main-metoden
som starter et program. Derfor vil dataene knyttet til main allltid ligge nederst på
programstakken. Når det i main skjer et metodekall, vil verdiene knyttet til metodekallet bli
lagt på programmstakken på toppen av de verdiene som allerede ligger der. Når et
metodekall er ferdig utført blir stakkplassen frigjort.
I Eksempel 2 i Avsnitt 1.5.1 laget vi en metode som fant tverrsummen til et heltall:
public static int tverrsum(int n) // n må være >= 0 { if (n < 10) return n; // kun ett siffer else return tverrsum(n / 10) + (n % 10); // metoden kalles } Programkode 1.5.2 a)
Vi kan nå bruke denne metoden i flg. enkle program:
public static void main(String... args) { int sum = tverrsum(7295); } Programkode 1.5.2 b)
Når Programkode 1.5.2 b) kjøres, vil programstakken få aktivitetslaget
til main på bunnen. Videre inneholder main et kall på tverrsum(7295).
Det gir et nytt aktivitetslag. Men metoden er rekursiv. Den inneholder kallet
tverrsum(n / 10) og siden n = 7295 blir det tverrsum(729). Det
kallet må returnere før addisjonen med 5 (dvs. 7295 % 10) kan gjennomføres. Kallet
tverrsum(729) gir et nytt aktivitetslag på stakken. Osv.
| Programstakken | |
| Aktivitetslag 4 | tverrsum(7) |
| Aktivitetslag 3 | tverrsum(72) |
| Aktivitetslag 2 | tverrsum(729) |
| Aktivitetslag 1 | tverrsum(7295) |
| Aktivitetslag 0 | main() |
For hvert kall får n ett siffer mindre. Til slutt blir n = 7 som gir det øverste aktivitetslaget. I metoden sjekkes det først om n er mindre enn 10 (kun ett siffer) og det vil være tilfellet når n = 7. Dermed returnerer metoden verdien 7 uten flere rekursive kall. Det betyr at det foregående kallet tverrsum(72) kan gjøre seg ferdig og returnere verdien 7 + 2 = 9. Osv.
Vi kan få en god illustrasjon av dette hvis vi legger inn to utskriftssetninger. Den første som første programsetning i metoden. Den andre skal være siste programsetning før metoden returnerer, men for å få til det må vi endre litt på koden:
public static int tverrsum(int n) { System.out.println("tverrsum(" + n + ") starter!"); int sum = (n < 10) ? n : tverrsum(n / 10) + (n % 10); System.out.println("tverrsum(" + n + ") er ferdig!"); return sum; } Programkode 1.5.2 c)
Den nye versjonen av tverrsum i Programkode 1.5.2 c) gir utskriften nedenfor:
public static void main(String... args) { System.out.println("main() starter!"); int sum = tverrsum(7295); System.out.println("main() er ferdig!"); } Programkode 1.5.2 d)
main() starter! tverrsum(7295) starter! tverrsum(729) starter! tverrsum(72) starter! tverrsum(7) starter! tverrsum(7) er ferdig! tverrsum(72) er ferdig! tverrsum(729) er ferdig! tverrsum(7295) er ferdig! main() er ferdig!
Utskriften over viser at programstakken får fem aktivitetslag og at metodekallene deretter gjør seg ferdige (og forsvinner fra stakken) i motsatt rekkefølge.
I Eksempel 6
laget vi en rekursiv
fib-metode. Med to rekursive kall er den mer
komplisert. Anta at vi kaller fib med 5 som parameterverdi.
Da legges aktivitetslaget til fib(5) på programstakken. Koden inneholder
de to kallene fib(4) og fib(3). Først kalles fib(4) og
det gir et nytt aktivitetslag på programstakken. Når fib(4) er ferdig utført
vil programkontrollen returnere til der kallet skjedde. Så utføres neste kall,
dvs. fib(3). Når det er ferdig, adderes resultatene av de to kallene
og summen returneres. Dermed er kallet fib(5) ferdig. Osv.
Stakken vokser, synker, vokser osv. inntil alt
er ferdig. Først legges main() på stakken. Så fib(5),
fib(4), osv. til fib(1). Men fib(1)
kan gjøre seg ferdig uten flere rekursive kall.
Laget fjernes og programkontrollen går dit
fib(1) ble kalt. Der gjenstår kallet fib(0). Osv.
Det som foregår når fib-metoden utføres, kan illustreres ved hjelp
av et binærtre. De forskjellige parameterverdiene kan ses på som nodeverdier. Hvert
kall deler seg opp i to nye kall. Dermed blir det et binærtre. Vi kan også få dette
illustrert ved å legge inn ekstra utskriftssetninger i koden til fib-metoden:
public static int fib(int n) // med utskriftssetninger { System.out.println("fib(" + n + ") starter!"); int fib = n > 1 ? fib(n-1) + fib(n-2) : n; System.out.println("fib(" + n + ") er ferdig!"); return fib; // metoden er ferdig } Programkode 1.5.2 e)
Hvis vi kjører et program som inneholder kallet fib(5) og der versjonen
av fib-metoden fra Programkode 1.5.2 e) brukes, får vi
følgende utskrift. Tallene til venstre er satt på etterpå:
1 fib(5) starter!
|
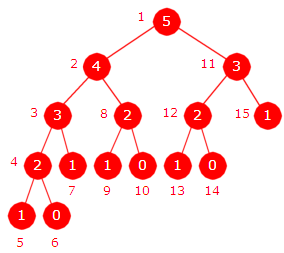  | |
| Figur 1.5.2 c) - En utskrift av Fibonacci-kall og to binærtrær som viser rekkefølgen på kallene | ||
Binærtreet i figuren over kalles et rekursjonstre.
Verdiene i nodene er parameterverdiene
i kallene på fib-metoden. I tillegg er nodene nummerert fra 1 til 15.
I det øverste treet gir nummereringen den rekkefølgen som kallene på fib-metoden
starter. I et binærtre har den rekkefølgen navnet preorden.
Hvis vi ser på utskriften (de røde tallene lengst til venstre) i figuren over, vil vi se at det er samsvar mellom
denne rekkefølgen i treet og rekkefølgen på de setningene som inneholder ordet
«starter». De tilhørende parameterverdiene har rekkefølgen 5, 4, 3, 2,
1, 0, 1, 2, 1, 0, 3, 2, 1, 0, 1.
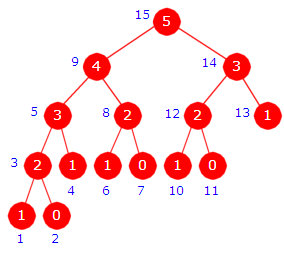
I det nederste treet gir nummereringen den rekkefølgen som kallene på fib-metoden
gjør seg ferdige. I et binærtre har den rekkefølgen navnet postorden.
Vi ser av utskriften (de blå tallene lengst til venstre) i figuren over at det er samsvar mellom
denne rekkefølgen i treet og rekkefølgen på de setningene som inneholder ordene
«er ferdig». De tilhørende parameterverdiene har rekkefølgen 1, 0, 2, 1, 3,
1, 0, 2, 4, 1, 0, 2, 1, 3, 5.
Antallet aktivitetslag som til enhver tid ligger på programstakken under
eksekveringen av en rekursiv metode, kalles rekursjonens dybde. Det
største antallet lag kalles den maksimale rekursjonsdybden. For
fib-metoden vil rekursjonstreet gi oss informasjon om rekursjonens dybde.
Figur 1.5.2 c)
viser at når fib-metoden utføres, vil den maksimale rekursjonsdybden bli 5
siden treet har 5 nivåer.
OBS: I et binærtre kan vi nummerere eller ramse opp nodene på mange måter. En slik
oppramsing kalles en rekkefølge. Både preorden og postorden er viktige
rekkefølger i binære trær. Inorden og nivåorden er to andre rekkefølger.
Dette og mye mer vil bli diskutert detaljert i
Kapittel 5 om Binære trær.
Vi ser at den rekursive fib-metoden er særdeles ineffektiv. Den kalles på nytt og på nytt
med samme parameterverdi. Det betyr at samme Fibonacci-tall regnes ut på nytt
og på nytt. Hvis en skal løse en oppgave ved å bruke rekursjon, må en passe på at de
rekursive kallene ikke utfører samme oppgave flere ganger. Hvis vi ser på
utskriften eller på trærne i
Figur 1.5.2 c), ser vi f.eks. at kallet fib(0)
utføres tre ganger, fib(1) hele fem ganger, fib(2) tre ganger, fib(3)
to ganger og hver av fib(4) og fib(5) kun én gang.
I Oppgavene
6, 7 og 8 skal vi se nærmere på hvor mange rekursive kall som blir
utført når den rekursive fib-metoden brukes til å finne et bestemt Fibonacci-tall.
For eksempel vil den rekursive fib-metoden bli kalt hele 40.730.022.147 ganger
for å finne fib(50).
Den rekursive metoden i Programkode 1.5.1 a) er
av nøyaktig samme type som fib-metoden og oppfører seg på samme måte. Også der blir
et og samme ledd i tallfølgen regnet ut mange ganger. Hvis man bruker den til å finne
et ledd an der n er stor, vil metoden komme til
å bruke ekstremt lang tid.
| 1. | Kjør Programkode 1.5.2 d) med et tall som har flere siffer enn 7295, dvs. flere enn 4 siffer. Sjekk så utskriften. |
| 2. | Legg inn utskriftssetninger i den rekursive euklid-metoden i
Programkode 1.5.1 c). Gjør omtrent som i
tverrsum-metoden i
Programkode 1.5.2 c). Kjør
så euklid-metoden med et passelig valg av parameterverdier og se hva
utskriften blir.
|
| 3. | Regn ut for hånd og skriv opp de 16 første Fibonacci-tallene, dvs.
fib(0), . . . . , fib(15).
|
| 4. | Lag et program som skriver ut de 52 første Fibonacci-tallene,
fib(0), . . . . , fib(51). Bruk en iterativ teknikk. Se
Oppgave 12 i Avsnitt 1.5.1.
|
| 5. | La sn = fib(0) + fib(1) + . . . . + fib(n−1).
Det vil si la sn være summen av de n første Fibonacci-tallene.
Finn en formel for sn .
|
| 6. | Figur 1.5.2 c)
viser hva som skjer når fib(5) utføres. Hver gang
fib-metoden kalles blir kallet lagt på programstakken. I denne prosessen blir
metoden tilsammen kalt like mange ganger som rekursjonstreet får noder. Hvor mange
noder har treet i Figur 1.5.2 c)?
Tegn det rekursjonstreet du får når fib(6) utføres. Hvor mange noder får treet?
|
| 7. | La n være et ikke-negativt heltall og la An være antallet noder
i rekursjonstreet til kallet fib(n). Vis at An
= An − 1 + An − 2 + 1
for n > 1. Hva blir A0 og A1?
Finn en formel for An . Hvor mange ganger vil fib-metoden bli
kalt hvis kallet fib(50) utføres?
|
| 8. | Lag et program som teller opp hvor mange ganger den rekursive fib-metoden
kalles. Metoden er satt opp som statisk. Da kan opptellingen gjøres enkelt hvis den klassen
som inneholder metoden, får en statisk heltallsvariabel. La så første setning i metoden
øke denne med 1. Hvis heltallsvariabelen er satt til 0 før metoden kalles, vil den
etterpå inneholde antallet kall. Bruk dette til å sjekke, for noen få (og små) verdier,
at formelen som er oppgitt som fasit i Oppgave 7, stemmer.
|
![]() 1.5.3 Krav til rekursive metoder
1.5.3 Krav til rekursive metoder
Det er to krav som må være oppfylt for at en rekursiv metode skal virke etter
hensikten:
basistilfelle (eller en basissituasjon).
Hvis en rekursiv metode oppfyller disse to kravene, skal den teoretisk sett virke.
Men det vil være situasjoner der metoden likevel feiler. Hvis metoden f.eks.
gjør svært mange rekursive kall før det oppstår et basistilfelle, vil
rekursjonsdybden kunne bli så stor at det ikke lenger er plass til programstakken
innenfor tilgjengelig minne. Da kastes en StackOverflowError.
Vi må også her se på metodens orden, dvs. antallet operasjoner eller metodekall som
utføres i forhold til oppgavens størrelse. Hvis metoden har en «dårlig» orden vil
den være helt uegnet til å løse «store» problemer.
Eksempel 1: Den rekursive metoden tverrsum i
Programkode 1.5.1 b)
finner tverrsummen til et ikke-negativt heltall n.
Krav 1 er oppfylt siden det rekursive metodekallet inneholder n/10 som
parameterverdi. Antall siffer i kvotienten n/10 er én mindre enn antallet i
n. Dermed har vi fått et enklere tilfelle. Det regnes heller ikke ut noe som
allerede er regnet ut. Basistilfellene er de heltallene som bare har ett siffer.
For hvert nytt kall vil antallet siffer bli redusert med én. Dermed vil
dette helt sikkert stoppe på et basistilfelle. Krav 2 er oppfylt.
Den maksimale rekursjonsdybden er lik antall siffer i n. Hvis
n er av typen int, vil det maksimalt bli 10. Det totale antall kall på
metoden blir også lik antall siffer i n. Dette er derfor en helt akseptabel måte
å finne sifrene på. Men en for-løkke hadde nok vært bedre.
Eksempel 2: Den rekursive metoden euklid i
Programkode 1.5.1 c)
finner største felles divisor for to ikke-negative
heltall a og b forutsatt at ikke begge er lik 0.
Det rekursive kallet har a som første parameterverdi og resten r vi får når
a deles med b som andre parameterverdi. Det betyr at den andre parameterverdien
blir mindre for hvert kall. Basistilfellet, som er b lik 0, vil derfor alltid nås.
Dermed er både krav 1 og krav 2 oppfylt. Metoden har bare ett rekursivt kall. Da vil
maksimal rekursjonsdybde og det totale antallet kall bli det samme. I
Oppgave 6 i
Avsnitt 1.5.1 fant vi at metoden er, hvis b er mindre enn eller lik a
når den kalles første gang, av orden log10(b). Det betyr at den er
effektiv.
Eksempel 3: Den rekursive metoden sum i
Programkode 1.5.1 d)
finner summen av tallene fra 1 til n. Krav 1 er
oppfylt siden det rekursive metodekallet inneholder et enklere
tilfelle ved at parmeterverdien er én mindre enn den var. Det regnes heller ikke ut noe som
allerede er regnet ut. Basistilfellet får vi når parameterverdien har blitt 1 og det
tilfellet vil helt sikkert inntreffe. Krav 2 er dermed oppfylt.
Vi ser fort at den maksimale rekursjonsdybden til sum-metoden blir lik størrelsen til parameterverdien
n. Hvis n er stor, vil programstakken få for mange aktivitetslag.
Dvs. en StackOverflowError. Hvor stor plass som er avsatt til programstakken,
varierer litt. Men flg. program fører til StackOverflowError på undertegnedes maskin.
Hvis flg. program ikke gir StackOverflowError hos deg, kan du bare øke verdien på
parameteren n:
public static void main(String... args) { int n = 20000; System.out.println(sum(n)); // metoden fra Programkode 1.5.1 g) } // Feilmelding: // Exception in thread "main" java.lang.StackOverflowError Programkode 1.5.3 a)
Metoden sum(n) kan derfor ikke brukes for store n-verdier. Det totale antall kall på
metoden blir også lik n. Metoden er derfor av orden n. Det er ikke spesielt
ineffektivt. Enhver metode som skal finne summen av tallene fra fra 1 til n
ved å summere et og et tall, vil være av orden n. Men en metode som bruker
en for-løkke istedenfor rekursjon vil være bedre. Det beste er selvfølgelig å bruke
en formel for denne summen.
Eksempel 4: Vi kan finne summen av tallene fra 1 til n som et spesialtilfelle av det å finne summen av tallene fra k til n ved hjelp av en splitt-og-hersk teknikk. Vi deler tallene i to grupper, summerer tallene i hver gruppe og adderer de to summene. Dette kan kodes slik (se Oppgave 8 i Avsnitt 1.5.1):
public static int sum(int k, int n) // summen av tallene fra k til n { if (k == n) return k; // summen av ett tall int m = (k + n)/2; // det midterste tallet return sum(k,m) + sum(m+1,n); } Programkode 1.5.3 b)
Metoden kan brukes til å finne summen av tallene fra 1 til n:
int n = 100; System.out.println(sum(1,n)); // Utskrift: 5050
Avstanden mellom første og andre parameter blir halvert for hvert rekursivt kall. Det betyr
at de to før eller senere må bli like. Antall halveringer som skal til er av orden
log2(n - k). Det betyr at hvis vi bruker metoden til å finne
summen av tallene fra 1 til n, vil maksimal rekursjonsdybde bli av orden
log2(n). Dermed vil StackOverflowError aldri inntreffe.
Det totale antallet rekursive kall er lik 2(n − k) + 1. Hvis metoden brukes til å finne summen av tallene fra 1 til n, blir det 2n − 1 kall. Metoden er med andre ord av orden n. Men også her gjelder sluttkommentaren i Eksempel 3. Det er bedre å bruke en for-løkke enn rekursjon, og det absolutt beste er å bruke en formel for summen.
Eksempel 5: Den rekursive fib-metoden fra
Programkode 1.5.1 g)
oppfyller kravene 1 og 2. I de to rekursive kallene
har parameterverdiene blitt henholdsvis én og to mindre. Derfor vil et av basistilfellene
n = 0 eller n = 1 oppstå. Maksimal rekursjonsdybde er lik størrelsen
på parameterverdien n. Fibonacci-tallene blir ganske fort svært store og spesielt
blir de for store for datatypen int. Allerede Fibonacci-tall nr. 50, som er lik
12.586.269.025, er for stort for datatypen. Det betyr at StackOverflowError aldri blir
et problem her. Problemet er imidlertid det store antallet kall som utføres for å finne
et Fibonacci-tall. I Oppgave 7 i Avsnitt 1.5.2
fant vi at metoden er
av orden fib(n) siden det totalt utføres 2·fib(n + 1) − 1
kall. F.eks. trengs det 40.730.022.147 metodekall for å finne Fibonacci-tall nr. 50. Det
betyr at metoden er ekstremt ineffektiv. Heldigvis er det enkelt å lage en iterativ
metode for dette. Se Oppgave 12 i
Avsnitt 1.5.1. Den er av orden n.
| 1. | Sjekk at sum-metoden i Programkode 1.5.1 e) oppfyller krav 1 og 2. Hva blir maksimal rekutsjonsdybde og hva blir det totale antallet kall? |
| 2. | Sjekk at sum-metoden i
Programkode 1.5.1 f) oppfyller krav 1 og 2.
Hva blir maksimal rekutsjonsdybde og hva blir det totale antallet kall?
|
| 3. | Tegn rekursjonstreet til kallet sum(1,8) der sum er metoden i
Programkode 1.5.3 b).
|
![]() 1.5.4 Rekursiv binærsøk
1.5.4 Rekursiv binærsøk
I Avsnitt 1.3.6 ble binærsøk
kalt en «splitt og hersk»-metode («forminsk og hersk»).
Den burde derfor kunne egne seg for rekursjon. Tabellen
deles på midten og metoden kalles rekursivt på den av de to delene
som det eventuelt må søkes videre i. Søket starter i
a[v:h]:
public static int binærsøk(int[] a, int v, int h, int verdi) { if (v < 0 || h >= a.length) throw new IllegalArgumentException("Ulovlig intervall"); if (h < v) return -(v + 1); // tomt intervall - ikke funnet int m = (v + h)/2; // finner midten int midtverdi = a[m]; // midtverdien if (verdi > midtverdi) return binærsøk(a,m+1,h,verdi); else if (verdi < midtverdi) return binærsøk(a,v,m-1,verdi); else return m; // funnet } public static int binærsøk(int[] a, int verdi) // leter i hele a { return binærsøk(a,0,a.length-1,verdi); } Programkode 1.5.4 a)
Vi må sjekke om de to kravene er oppfylt. For det første vil det rekursive kallet skje på enten den delen som ligger til høyre for midten eller den som ligger til venstre for midten, og i hvert tilfelle er det en enklere situasjon enn den vi hadde (dvs. et halvparten så stort intervall). Videre har vi to basistilfeller. Det ene er at den søkte verdien er lik midtverdien og det andre at vi ender opp med et tomt intervall. Et av de to basistilfellene vil alltid inntreffe.
Obs. Det har ingen hensikt å lage en rekursiv versjon av binærsøk. Den rekursive versjonen i Programkode 1.5.4 a) er ikke enklere å programmere enn den vanlige versjonen. Faktisk blir den også marginalt mindre effektiv siden det normalt er mer kostbart med metodekall enn med en løkke slik som i den vanlige versjonen. Programkode 1.5.4 a) er tatt med kun for å illustrere hvordan vi programmerer rekursivt. Vi skal imidlertid senere se på eksempler der rekursjon gir kort og elegant kode og hvor rekursjon også gir den mest effektive løsningen.
| 1. | Lag en rekursiv versjon av binærsøk fra
Programkode 1.3.6 c), dvs.
3. versjon.
|
| 2. | Lag en rekursiv versjon av lineærsøk fra
Programkode 1.3.5 b).
En kan tenke slik: Hvis den søkte verdien ikke ligger i posisjon i kaller vi metoden på
neste (dvs. i + 1) posisjon. Oppgaven er kun gitt for at en skal få trening i å lage
rekursive metoder. Ellers er dette en problemstillig der rekursjon ikke egner seg. Den iterative
løsningen er absolutt best.
|
![]() 1.5.5 Permutasjoner
1.5.5 Permutasjoner
I Avsnitt 1.3.1
diskuterte vi permutasjoner av tallene fra 1 til n. Blant annet
ble det laget en metode som genererte permutasjoner i stigende leksikografisk rekkefølge.
Det ble også utviklet en iterator som brukte denne metoden. Her skal vi se på hvordan rekursjon
kan brukes til å generere permutasjoner. Da kan vi bruke flg. rekursive idé:
- La etter tur (ved hjelp av ombytting) hvert av tallene fra 1 til n stå først.
- For hvert slikt valg permuteres resten av tallene på alle mulige måter.
- Den første ombyttingen reverseres slik at tabellen blir slik den var.
Tallene som skal permuteres ligger i en tabell a. La k være en tabellindeks. Da tenker vi oss som det generelle tilfellet, at innholdet i intervallet a[0 : k > skal ligge i ro, mens resten av tabellen skal permuteres. Som start må tabellen inneholde en eller annen permutasjon av tallene fra 1 til n. Vi kan f.eks. velge 1 , 2 , 3 , . . . n . Den rekursive metoden vil generelt operere på delintervallet fra og med indeks k og ut tabellen, dvs. på a[k : a.length >. Basistilfellet er når k blir lik a.length − 1 og det vil oppstå siden k øker med 1 for hvert kall:
public static void perm(int[] a, int k) // permuterer a[k:a.length> { if (k == a.length-1) Tabell.skrivln(a); // en ny permutasjon else for (int i = k; i < a.length; i++) { Tabell.bytt(a,k,i); // bytter om a[k] og a[i] perm(a,k+1); // permuterer a[k+1:a.length> Tabell.bytt(a,k,i); // bytter tilbake } } // perm Programkode 1.5.5 a)
Eksempel 1 Flg. programbit skriver ut de 24 permutasjonene av tallene 1 , 2 , 3 , 4 :
int[] a = {1,2,3,4}; perm(a,0); Programkode 1.5.5 b)
Programkode 1.5.5 a) genererer ikke permutasjonene i leksikografisk orden. Det er det mulig å få til hvis en lager en litt annerledes versjon av koden. Metoden kan også effektiviseres en del. I tillegg finnes andre rekursive teknikker for å lage permutasjoner. Se Oppgavene 2 - 6.
Programkode 1.5.5 a)
permuterer tallene og skriver
dem til konsollet. Det kan være aktuelt å gjøre andre ting −
f.eks. skrive dem til en fil, telle dem opp eller
«utføre en arbeidsoppgave» på dem. Vi lager et generisk funksjonsgrensesnitt
(se også Programkode 5.1.6 c):
@FunctionalInterface public interface Oppgave<T> // legges på Oppgave.java under hjelpeklasser { void utførOppgave(T t); // en abstrakt metode } Programkode 1.5.5 c)
Metoden i Programkode 1.5.5 a)
må endres litt for at den skal lage permutasjoner av verdiene i en T-tabell og
videre kunne utføre en oppgave på dem.
Skal dette virke må samleklassen Tabell inneholde en generisk bytt-metode.
Se Oppgave 5 i Avsnitt 1.4.3 :
public static <T> void perm(T[] a, int k, Oppgave<T[]> o) { if (k == a.length-1) o.utførOppgave(a); // en ny permutasjon else for (int i = k; i < a.length; i++) { Tabell.bytt(a,k,i); // bytter om a[k] og a[i] perm(a,k+1,o); // permuterer a[k+1:a.length> Tabell.bytt(a,k,i); // bytter tilbake } } // perm Programkode 1.5.5 d)
Det er bare små endringer i Programkode 1.5.5 d) i forhold til
Programkode 1.5.5 a). Metoden har en generisk
typeparameter T og en generisk arbeidsoppgave som vanlig parameter.
I selve koden er skrivln-setningen byttet ut med metoden utførOppgave.
Eksempel 2 Den generiske perm-metoden kan sammen med et lambda-uttrykk
skrive ut permutasjonene av tallene fra 1 til 4. Nå må vi imidlertid bruke en Integer-tabell.
Skal flg. kode virke må du
ha en skrivln-metode i klassen Tabell.
Se Oppgave 5 i Avsnitt 1.4.3 :
Integer[] a = {1,2,3,4}; // Integer-tabell
perm(a,0, p -> Tabell.skrivln(p)); // et lambda-uttrykk som argument
Programkode 1.5.5 e)
Eksempel 3 Hvis vi isteden ønsker å skrive ut de 6 permutasjonene av
de tre bokstavene A,
B og C, kan det gjøres uten å endre i perm-metoden:
Character[] a = {'A','B','C'}; // Character-tabell
perm(a,0, p -> Tabell.skrivln(p)); // et lambda-uttrykk som argument
Programkode 1.5.5 f)
Eksempel 4
En oppgave kan være å telle opp permutasjoner som oppfyller et bestemt krav.
Her skal vi imidlertid telle alle. Det har ingen hensikt
siden antallet er kjent − n verdier gir n!
permutasjoner. Men poenget her er å vise hvordan et lambda-uttrykk også kan benytte en ekstern variabel.
Her en heltallstabell med kun ett element. Det brukes til opptellingen:
String[] s = {"Per","Kari","Ola"}; // tre verdier
int[] antall = {0}; // tabell med ett element
perm(s,0, p -> antall[0]++); // et lambda-uttrykk som argument
System.out.println(antall[0]); // Utskrift: 6
Programkode 1.5.5 g)
Eksempel 5
I Eksempel 2 og 3 gikk utskriften til konsollet. Med en PrintWriter kan vi styre utskriften dit vi vil.
Først til konsollet ved hjelp av System.out:
public static void main(String... args) throws IOException { Integer[] a = {1,2,3,4}; // fire verdier PrintWriter ut = new PrintWriter(System.out); // System.out -> konsollet perm(a,0,p -> ut.println(Arrays.toString(a))); // toString fra Arrays ut.close(); // lukker } Programkode 1.5.5 h)
Hvis vi skal ha utskriften til en fil, f.eks. ut.txt, bruker vi det som argument:
public static void main(String... args) throws IOException { Integer[] a = {1,2,3,4}; // fire verdier PrintWriter ut = new PrintWriter("ut.txt"); // til navngitt fil perm(a,0,p -> ut.println(Arrays.toString(a))); // toString fra Arrays ut.close(); // lukker } Programkode 1.5.5 i)
| 1. | I Programkode 1.5.5 b) starter tabellen a med verdiene 1, 2, 3 og 4. Sjekk at vi får alle de 24 permutasjonene også om a starter med en annen permutasjon. Da vil imidlertid permutasjonene komme i en annen rekkefølge. |
| 2. | Programkode 1.5.5 a) kan effektiviseres noe. Verdien til k kan testes før det rekursive kallet istedenfor i første setning i metoden. Det vil mer enn halvere antallet metodekall. Første ombytting i for-løkken er unødvendig siden vi da har k lik i. Vi gjør isteden et metodekall først og starter for-løkken med i lik k + 1. Det vil redusere antallet kall på bytt-metoden med ca. 40%. Gjør disse endringene. |
| 3. | Gå gjennom utskriften fra I Programkode 1.5.5 b). Der vil en se at permutasjonene ikke kommer i leksikografisk rekkefølge. Sjekk at det stemmer. Lag en rekursiv perm-metode der permutasjonene kommer i leksikografisk rekkefølge. |
| 4. | Snu idéen i Programkode 1.5.5 a) på hodet: La alle verdiene etter tur stå bakerst og permutér resten (de foran) på alle mulige måter. Lag en metode som gjør dette! |
| 5. | Flg. enkle metode ble laget av B.Heap i 1963. Sjekk at den virker: |
| 6. | Hvis vi har en permutasjon av tallene fra 1 til n − 1, får vi permutasjoner av tallenen fra 1 til n ved å plassere n på alle mulige steder i permutasjonen. Hvis vi f.eks. har 1,2,3 , kan vi sette 4 på 4 mulige steder og få 1,2,3,4 , 1,2,4,3 , 1,4,2,3 og 4,1,2,3. Lag en metode som bruker denne idéen. Den vil kunne bli mer enn dobbelt så effektiv som perm-metoden i Programkode 1.5.5 a) . |
| 7. | Johnson-Trotters algoritme regnes som en av de raskeste permutasjonsmetodene. Søk på internett etter informasjon om den algoritmen og lag den så i Java. |
| 8. | Finn ut hvilken av metodene som er mest effektiv ved å måle tidsbruken.
Pass på å kommentere vekk utskriftssetningen før målingen utføres. Det kan f.eks. gjøres
slik i Programkode 1.5.5 a) :
if (k == a.length-1); // Tabell.skrivln(a);
|
| 9. | Lag et lambda-uttrykk og bruk det sammen med den generiske perm-metoden slik at kun de permutasjonene av tallene fra 1 til n der n står bakerst blir skrevet ut. |
![]() 1.5.6 Sjakkbrett og dronninger
1.5.6 Sjakkbrett og dronninger
I Avsnitt 1.3.15
så vi problemet med
å sette dronninger på et n × n sjakkbrett.
Problemet ble omdefinert til å handle om permutasjoner av tallene fra 0 til
n − 1. Det betyr at idéen i den rekursive perm-metoden
i Programkode 1.5.5 a) også bør kunne
brukes til å finne antallet lovlige dronningoppstillinger på et
n × n sjakkbrett. Vi så i
Avsnitt 1.3.15 at det ikke var nødvendig
å undersøke alle permuasjonene.
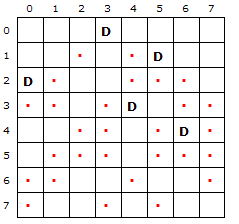 |
| Figur 1.5.6 a) : Fem dronninger |
I Figur 1.5.5 a) til venstre er det plassert fem dronninger i de fem øverste radene i henholdsvis kolonne 3 , 5 , 0 , 4 og 6. Dette svarer til de fem første tallene i en permutsjon av tallene fra 0 til 7. For hver dronning er det markert med prikker hvilke diagonaler (på skrå nedover mot høyre) og bidiagonaler (på skrå nedover mot venstre) som beherskes. Det å sette en dronning i neste rad − rad 5 − i en ledig kolonne svarer til å hente et av tallene som mangler for å få en full permutasjon. Det betyr 1 , 2 eller 7. Men alle tre hører til ruter som har en prikk. Dermed er det ikke mulig å sette noen dronning i rad 5. Vi må gå tilbake til rad 4 og prøve en annen dronningplassering der.
Idéen heter tilbaketrekning (eng: backtracking). Vi sette dronninger nedover i hver rad så lenge det går. Kommer vi til en rad der det ikke kan stå en dronning trekker vi oss tilbake til foregående rad og prøver ut en annen dronningplassering der. Osv. Problemet med to dronninger i samme kolonne oppstår ikke så lenge vi opererer med posisjoner som hører til tallene i en permutasjon. Men når en dronning plasseres må tilhørende diagonal og bidiagonal markeres som opptatt. Markeringene fjernes ved en tilbaketrekning.
Et n × n brett har 2·n − 1 diagonaler og 2·n − 1 bidiagonaler. Vi bruker boolske tabeller som parametere til å markere ruter som er «opptatt» − se Setning 1.3.15 a). Som parameternavn bruker vi r for radnummer, b for bidiagonal og d for diagonal:
public static int antall(int[] a, int r, boolean[] b, boolean[] d) { if (r == a.length) return 1; // lovlig oppstilling int antallLovlige = 0; // hjelpevariabel for (int i = r; i < a.length; i++) // fra r og ut a { int sum = r + a[i], diff = r - a[i] + a.length - 1; if (b[sum] != true && d[diff] != true) // sjekker om ledig { Tabell.bytt(a,i,r); // bytter a[i] og a[r] b[sum] = d[diff] = true; // markerer opptatt antallLovlige += antall(a,r+1,b,d); // går til neste rad b[sum] = d[diff] = false; // markerer ledig Tabell.bytt(a,r,i); // bytter tilbake } } return antallLovlige; } Programkode 1.5.6 a)
Programkode 1.5.6 a) bruker samme idé som perm-metoden i Programkode 1.5.5 a) for å generere permutasjoner. Her returnerer imidlertid metoden for hvert rekursivt kall hvor mange lovlige oppstillinger som har dronninger på de samme plassene i de r øverste radene. Det er også mulig å gjøre opptellingen på andre måter. En kan bruke en int-tabell med kun ett element som parameter. For hver ny oppstilling økes elementet med 1. Se Oppgave 5.
I Avsnitt 1.3.15 ble det foreslått å legge alle metodene laget for dronningproblemet i en egen klasse med navn Dronning. Legg derfor også Programkode 1.5.6 a) i denne klassen.
Følgende metode benytter metoden i Programkode 1.5.6 a) til å finne antallet lovlige dronningoppstillinger på et n × n − brett. Hvis du har studert Avsnitt 1.3.15 vil du kanskje allerede ha en antall-metode med brettets dimensjon n som eneste parameter i Dronning-klassen. Flg. metode har derfor fått navnet antallR der bokstaven R skal markere at vi her bruker rekursjon som en del av løsningen:
public static int antallR(int n) { int[] a = Tabell.naturligeTall(n); // a = {0,1,2, . . , n - 1} return antall(a,0,new boolean[2*n-1],new boolean[2*n-1]); } Programkode 1.5.6 b)
Hvis vi speiler en dronningoppstilling om en loddrett midtlinje, får vi en dronningsoppstilling til. Dermed holder det å undersøke de permutasjonene som svarer til at det står en dronning i første halvdel av øverste rad på brettet. Denne tankegangen ble nøye diskutert i tilknytning til Figur 1.3.15 d) i Avsnitt 1.3.15. Vi kan benytte samme idé som i Programkode 1.3.15 f) , men der ble det første elementet i permutasjonen testet unødvendig mange ganger. Her skal vi velge en annen strategi. Den går ut på at vi plasserer en dronning på en bestemt plass i første del av øverste rad før metoden i Programkode 1.5.6 a) kalles. Vi kan f.eks. sette en i posisjon 3 på et 8 × 8 − brett:
int[] a = {3,0,1,2,4,5,6,7}; // dronning i kolonne 3 og rad 0 int n = a.length; // hjelpevariabel boolean[] b = new boolean[2*n-1]; // bidiagonaler boolean[] d = new boolean[2*n-1]; // diagonaler b[3] = true; // markerer i bidiagonalen d[-3 + n - 1] = true; // markerer i diagonalen System.out.println(Dronning.antall(a,1,b,d)); // Utskrift: 18 Programkode 1.5.6 c)
I Programkode 1.5.6 c) har tabellen a tallet 3 som første element. Det svarer til at det er satt en dronning i kolonne 3 i øverste rad, dvs. rad 0. Den rekursive antall-metoden i Programkode 1.5.6 a) kalles med med 1 som radnummer. Det betyr at metoden jobber seg gjennnom alle permutasjoner av elementene i a bortsett fra det første som ligger i ro. Dermed får vi returnert 18 som er antallet lovlige dronningplasseringer på et 8 × 8 − brett med en dronning i posisjon 3 i øverste rad.
Ideen fra Programkode 1.5.6 c) kan gjentas. Vi finner antallet for hver dronning i første halvdel av øverste rad og det totale antallet blir det dobbelte av dette:
public static int antallR(int n) // ny versjon { int[] a = Tabell.naturligeTall(n); // a = {0,1, . . , n - 1} boolean[] b = new boolean[2*n-1]; // bidiagonaler boolean[] d = new boolean[2*n-1]; // diagonaler int antallLovlige = 0; // hjelpevariabel for (int i = 0; i < n/2; i++) // går til midten av rad 0 { b[i] = d[n - 1 - i] = true; // markerer en dronning antallLovlige += antall(a,1,b,d); // kaller metoden b[i] = d[n - 1 - i] = false; // opphever markering Tabell.bytt(a,0,i+1); // flytter dronning i rad 0 } antallLovlige *= 2; // dobler antallet if (n % 2 != 0) // er n et oddetall? { b[n/2] = d[n/2] = true; // dronning på midten antallLovlige += antall(a,1,b,d); // kaller metoden } return antallLovlige; // det totale antallet } Programkode 1.5.6 d)
Flg. eksempel viser hvor lang tid det tar å løse dronningproblemet for forskjellige versjoner av n ved å bruke den nye versjonen i Programkode 1.5.6 d). Her er det brukt en Pentium 4, 2.8 GHz med Windows XP, Java HotSpot og JDK 1.6.0_1:
for (int n = 8; n < 17; n++) { long tid = System.currentTimeMillis(); int antall = Dronning.antallR(n); tid = System.currentTimeMillis() - tid; System.out.printf("%2d%12d%10d\n",n,antall,tid); } // Utskrift: // 8 92 0 // 9 352 0 // 10 724 0 // 11 2680 16 // 12 14200 31 // 13 73712 203 // 14 365596 1172 // 15 2279184 8219 // 16 14772512 49500 Programkode 1.5.6 e)
Det er nok mulig å gjøre noen små effektivitetsforbedringer i Programkode 1.5.6 a). Blant annet kunne vi erstatte de to boolske tabellene med to int-verdier og bruke 0- og 1-verdier på bitene som usann og sann. Men hvis vi først skal jobbe på bitnivå og bruke bitoperatorer, er det bedre å lage en algoritme som utnytter dette på en smartere måte. Det vil gi en vesentlig mer effektiv metode. Vi skal se mer på det i Avsnitt 1.7.16.
Programkode 1.5.6 a) finner alle løsningene. Hvis vi ønsker å finne de unike løsningene, må vi gjøre en liten endring. Der hvor en løsning telles opp sjekkes det først om det det er den første av de ekvivalente løsningene eller ikke. Se Programkode 1.3.15 j). Vi ser nærmere på dette i Oppgave 7 og 8.
| 1. | Opprett class Dronning hvis du ikke allerede har gjort det. Legg Programkode 1.5.6 a) og Programkode 1.5.6 b) i klassen. Lag så et program som inneholder den for-løkken som er satt opp i Programkode 1.5.6 e). Notér deg hvilke tider du får. Poenget er å sjekke tidsforbruket til den versjonen av metoden antallR som står i Programkode 1.5.6 b). |
| 2. | Legg den nye versjonen av metoden antallR fra Programkode 1.5.6 d) inn i klassen Dronning. Den gamle versjonen fjernes eller omdøpes. Kjør så det programmet du laget i Oppgave 1 på nytt. Da bør resultatet være at tidsforbruket omtrent halveres. |
| 3. | I Avsnitt 1.3.15 (Programkode 1.3.15 b) ble det laget en metode som fant dronningoppstillinger ved å generere permutasjoner iterativt i leksikografisk rekkefølge. Legg metoden i klassen Dronning og kjør programmet fra Oppgave 1 og 2 der denne antallmetoden brukes. Hvordan er tidsforbruket for den? |
| 4. | Kodebiten i Programkode 1.5.6 c) gir 18 som utskrift. Det betyr at det er 18 dronningoppstillinger på et 8 × 8 − brett som har en dronning i kolonne 3 i øverste rad. Finn, ved å endre koden, hvor mange oppstillinger det er med dronning i kolonne 2, i kolonne 1 og i kolonne 0 i øverste rad. |
| 5. | Gjør om Programkode 1.5.6 a) og Programkode 1.5.6 d) slik at opptellingen skjer ved at en int-tabell inngår som parameter. Tabellen skal ha kun ett element og det elementet økes med 1 for hver ny oppstilling. Blir det mer effektivt enn det var? |
| 6. | Lag en Integer-versjon (Intger[] a istedenfor int[] a)
av i Programkode 1.5.6 a) med
Oppgave<Integer[]> o som parameter.
Lag så en Integer-tabell som en startpermutasjon og bruk en instans av
klassen Opptelling i Programkode 1.5.5 h)
til å finne antallet lovlige dronningoppstillinger.
|
| 7. | I Avsnitt 1.3.15 så vi på unike løsninger av dronningproblemet. Hver løsning hører til en ekvivalensklasse. Vis at hvis n er et oddetall vil aldri en løsning som har en dronning på midten av øverste rad være den første i leksikografisk rekkefølge blant de som hører til ekvivalensklassen. Vis det ved hjelp av speilinger og/eller rotasjoner. |
| 8. | Lag metodene antallU (U for unik) og antallRU. Den første metoden skal være som Programkode 1.5.6 a), men returnere antallet unike løsninger. Det gjøres ved å teste om løsningen som er funnet kommer først i den leksikografiske ordningen. Se metoden i Programkode 1.3.15 j). Lag så antallRU på samme måte som Programkode 1.5.6 d), men ta hensyn til det som står i Oppgave 7 over. Legg metodene i klassen Dronning. Bruk så metoden antallRU i et testprogram slik som i Oppgavene 1, 2 og 3. Bruker metoden mye lenger tid for å finne de unike løsningene istedenfor alle løsningene? |
![]() 1.5.7 Kvikksortering
1.5.7 Kvikksortering
Flere av de mest kjente sorteringsmetodene implementeres vanligvis ved hjelp av
rekursjon, f.eks. kvikksortering. Den så vi på i
Avsnitt 1.3.9
og der laget vi denne implementasjonen:
private static void kvikksortering0(int[] a, int v, int h) { if (v >= h) return; // tomt eller maks ett element int k = sParter0(a,v,h,(v + h)/2); // se Programkode 1.3.9 f) kvikksortering0(a,v,k-1); kvikksortering0(a,k+1,h); } Programkode 1.5.7 a)
Idéen er å velge midtelementet i a[v:h] og så sette det på rett sortert plass i a[v:h] ved partisjonering. Metoden sParter0 gjør det og returnerer posisjonen k. Da vil v ≤ k ≤ h. Det betyr at både a[v:k−1] og a[k+1:h] er kortere enn a[v:h]. En av dem eller begge kan være tomme. Dette betyr at metoden oppfyller krav 1, dvs. at de rekursive kallene skjer på enklere tilfeller enn det det var opprinnelig. Her menes enklere i betydningen mindre tabellintervaller. Basistilfellene blir at v = h eller at v > h, dvs. at a[v:h] består av nøyaktig ett element eller at a[v:h] er tom. I de to tilfellene er intervallet a[v:h] å anse som sortert og metoden skal ikke gjøre noe mer. Krav 2 er oppfylt siden de rekursive kallene hele tiden skjer på intervaller som blir kortere og kortere og dermed at et av basistilfellene før eller senere må inntreffe.
Kvikksortering slik den er laget i Programkode 1.5.7 a), kan i noen spesialtilfeller være svært ineffektiv for store tabeller. Hvis f.eks. midtelementet i a[v:h] er det største av alle i a[v:h], vil k bli lik h og dermed vil a[v:k−1] ha kun ett element mindre enn a[v:h]. Slik vil det gå hvis vi f.eks. starter med flg. tabell:
| 4 | 8 | 5 | 3 | 10 | 7 | 2 | 9 | 1 | 6 |
Hvis dette forsetter videre, dvs. at k enten blir lik v eller lik h ved hver tabelldeling, vil det bli utført så mange som n − 1 metodekall (n er tabellens lengde) før det blir et basistilfelle. I så fall blir sorteringen ineffektiv. Det finnes flere teknikker for å unngå dette. Kvikksortering er i gjennomsnitt av orden n·log2(n) , men av orden n2 i det verste tilfellet. Dette og andre aspekter ved kvikksortering vil vi ta opp til grundig behandling i et senere kapittel.
| 1. | a) Legg en utskriftssetning med teksten
"Kallet med [" + v + ":" + h + "] starter!" først og en med
"Kallet med [" + v + ":" + h + "] er ferdig!" sist i
Programkode 1.5.7 a). Kjør så kvikksortering
på en permutasjon av tallene fra 1 til 10.
Hva blir utskriften? b) Utskriften fra a) vil vise at både tomme intervaller (h < v) og intervaller med lengde 1 legges på stakken. Men de er allerede sortert. Legg inn kode i Programkode 1.5.7 a) slik at kun intervaller med lengde større enn 1 behandles. |
| 2. | I Programkode 1.5.7 a) gjøres det første rekursive kallet på intervallet a[v:k-1] og det andre på a[k+1:h]. Hva vil skje hvis vi bytter om de to kallene? |
| 3. | Lag en permutasjon av tallene fra 1 til 10 slik at hvis Programkode 1.5.7 a) brukes på de verdiene, vil hver tabelldeling gjøre at k blir lik h, dvs. at a[v:k-1] hver gang kun blir én mindre enn a[v:h]. Hvilken rekursjonsdybde vil det gi? |
| 4. | Hvis en alltid gjør det første rekursive kallet på det korteste av de to delintervallene, så vil rekursjonsdybden maksimalt være av orden log2(n) uansett hvordan tabellen a er på forhånd. Sjekk at det stemmer. |
![]() 1.5.8 Flettesortering
1.5.8 Flettesortering
I Avsnitt 1.3.11
laget vi denne rekursive implementasjonen av flettesortering:
private static void flettesortering(int[] a, int[] b, int fra, int til) { if (til - fra <= 1) return; // a[fra:til> har maks ett element int m = (fra + til)/2; // midt mellom fra og til flettesortering(a,b,fra,m); // sorterer a[fra:m> flettesortering(a,b,m,til); // sorterer a[m:til> // fletter a[fra:m> og a[m:til> flett(a,b,fra,m,til); // Programkode 1.3.11 f) } public static void flettesortering(int[] a) { int[] b = new int[a.length/2]; // en hjelpetabell for flettingen flettesortering(a,b,0,a.length); // kaller metoden over } Programkode 1.5.8 a)
Her starter vi med å finne midtposisjonen m. Så gjør vi først et rekursivt kall på det halvåpne intervallet a[fra:m> og så på det halvåpne intervallet a[m:til>. Krav 1 er oppfylt siden hvert av de to intervallene er halvparten så store som delintervallet a[fra:til>. Når vi hele tiden halverer vil vi til slutt ende opp med et delintervall som inneholder kun én verdi. Dette basistilfellet behandles i koden uten noen flere rekursive kall. Dermed er også krav 2 oppfylt.
Effektiviteten til flettesortering er uavhengig av hvordan verdiene i tabellen a er fordelt. Tabellen deles alltid på midten og metoden er dermed alltid av orden n·log2(n). Det er mulig å lage en noe mer effektiv implementasjon enn den i Programkode 1.5.8 a). Det vil vi se mer på i et senere kapittel.
| 1. | Legg inn en utskriftssetning i som første setning i Programkode 1.5.8 a). La den f.eks. ha flg. tekst: "Nå legges a[" + fra + ":" + til + "> på programstakken". Kjør så flettesortering på en tabell med en eller annen permutasjon av tallene fra 1 til 10. |
![]() 1.5.9 Hanois tårn
1.5.9 Hanois tårn
I brikkespillet Hanois tårn har brikkene form av en skive med hull i midten og
alle har forskjellige diameter. Det er tre pinner og spillet starter med
at alle brikkene ligger på første pinne. De må ligge ordnet etter størrelse
– brikken med størst diameter nederst og den med minst diameter
øverst. Dermed vil brikkene på første pinne se ut som et kjegleformet tårn.
Spillet går ut på å flytte brikkene fra pinne A til pinne C slik at det også blir et kjegleformet tårn på C. Under flyttingen er det ikke lov å legge en brikke oppå en som er mindre.
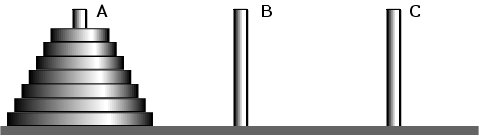 |
| De tre pinnene og brikker i spillet Hanois tårn |
De tre pinnene betegnes med A, B og C. Anta at vi har n brikker eller skiver. Først flytter vi de n - 1 øverste brikkene på A fra A til B ved å bruke C som hjelpepinne. Så flyttes den nederste/siste brikken på A fra A til C. Deretter flyttes alle brikkene på B fra B til C ved å bruke A som hjelpepinne. Dette kan simuleres ved hjelp av flg. kode:
public static void HanoisTårn(char> A, char B, char C, int n) { if (n == 0) return; // ingen brikker - tomt tårn HanoisTårn(A, C, B, n - 1); System.out.println("Brikke " + n + " fra " + A + " til " + C); HanoisTårn(B, A, C, n - 1); } Programkode 1.5.9 a)
Flg. eksempel viser hvordan vi kan bruke den rekursive metoden til finne trekkene for tre brikker og der pinnene heter A, B og C. Brikke 1 ligger øverst, brikke 2 nest øverst, osv:
HanoisTårn('A','B','C',3); // Brikke 1 fra A til C // Brikke 2 fra A til B // Brikke 1 fra C til B // Brikke 3 fra A til C // Brikke 1 fra B til A // Brikke 2 fra B til C // Brikke 1 fra A til C Programkode 1.5.9 b)
| 1. | Gjennomfør spillet på papir med 3 brikker uten å se på de trekkene som ble generert i Programkode 1.5.9 b). Prøv deretter med 4 og 5 brikker. Hvis du ikke får det til får du en løsning ved å utføre metodekallet i Programkode 1.5.9 b) med parameterverdi 4 og 5. Hva er det minste antallet trekk som trengs hvis det er n brikker? |
| 2. | Det ligger mange versjoner av spillet på web. Bruk "Tower of Hanoi" som søkeord! |
![]() 1.5.10 En vei gjennom en labyrint
1.5.10 En vei gjennom en labyrint
Labyrinten er satt opp som en todimensjonal tabell. Ytterveggene har kun fått en smal strek. Alle grå ruter
er lukket (representerer innervegger). Det er én inngang og én utgang. Det første målet er å finne en vei
gjennom labyrinten. Det er ikke tillatt å gå på skrå!
 |
| Figur 1.5.10 a) : En labyrint med 20 rader og 20 kolonner |
I hver rute har vi derfor fire muligheter: høyre, ned, venstre eller opp. En eller flere av
dem kan imidlertidig være ulovlige på grunn av vegger. Datateknisk lar vi labyrinten være gitt som en
heltallstabell a der hver åpen rute er 0 og hver
lukket rute (grå bakgrunn) 1. Ruten (i,j) er gjeldende rute og (iut,jut)
er utgangen. Vi lager en foreløpig metode, dvs. versjon 0:
public static void finnVei0(byte[][] a, int i, int j, int iut, int jut) { if (i == iut && j == jut) return; // utgangen int m = a.length; // antall rader int n = a[0].length; // antall kolonner if (j + 1 < n && a[i][j+1] == 0) finnVei0(a,i,j+1,iut,jut); // til høyre if (i + 1 < m && a[i+1][j] == 0) finnVei0(a,i+1,j,iut,jut); // nedover if (j > 0 && a[i][j-1] == 0) finnVei0(a,i,j-1,iut,jut); // til venstre if (i > 0 && a[i-1][j] == 0) finnVei0(a,i-1,j,iut,jut); // oppover } Programkode 1.5.10 a)
I metoden finnVei0 brukes «prøving og feiling» (eng: brute force). Fra hver rute (i,j)
prøves fortløpende alle de fire potensielle mulighetene. Først mot høyre, så nedover, osv. Vi kan sjekke
hva som skjer hvis vi starter i inngangen, dvs i rute (0,0) i
Figur 1.5.10 a).
Først går vi mot høyre så langt vi kan, dvs. til rute (0,2). Dermed vil det gå nedover til rute (2,2).
Så mot høyre til rute (2,7). Men der stopper det. Vi har kommet inn i en blindgate.
Den tredje muligheten dvs. å gå til venstre (tilbake), vil nå bli valgt. Dermed kommer vi tilbake til rute
(2,6). Derfra er det to muligheter - til venstre eller til høyre. Men det å gå til
høyre er første setning og dermed vil vi gå dit, dvs. til rute (2,7)
enda en gang. Deretter vil algoritmen hoppe frem og tilbake mellom (2,6) og
(2,7). En evig løkke!!
Den enkleste måten å løse problemet med «evig løkke» på er å markere hver rute som vi har vært på, som «besøkt». Vi kan f.eks. sette tallet 2 der. Dermed vil 0 fortelle at ruten er åpen, 1 at den er lukket og 2 at vi har vært der før. Dette vil også løse et annet problem. Det vil være labyrinter der Programkode 1.5.10 a) vil gå rundt i en «sirkel». Men med endringen vil den stoppe når den kommer til en rute som allerede er «besøkt». Hvis vi også lar metoden skrive ut en melding når utgangen er nådd, vil flg. kode virke (versjon 1):
public static void finnVei1(byte[][] a, int i, int j, int iut, int jut) { a[i][j] = 2; // ruten er besøkt if (i == iut && j == jut) // utgangen { System.out.println("En vei er funnet!"); } int m = a.length, n = a[0].length; // m rader, n kolonner if (j + 1 < n && a[i][j+1] == 0) finnVei1(a,i,j+1,iut,jut); // til høyre if (i + 1 < m && a[i+1][j] == 0) finnVei1(a,i+1,j,iut,jut); // nedover if (j > 0 && a[i][j-1] == 0) finnVei1(a,i,j-1,iut,jut); // til venstre if (i > 0 && a[i-1][j] == 0) finnVei1(a,i-1,j,iut,jut); // oppover } Programkode 1.5.10 b)
Hva vil skje nå hvis denne metoden brukes på labyrinten i
Figur 1.5.10 a)? Vi vil fortsatt komme til rute
(2,7). Men derfra er det ikke mulig å komme videre. Den rekursive metoden «trekker seg tilbake»
til det kallet der det står igjen muligheter. Det betyr tilbake til rute (2,4). Derfra vil det gå
oppover til rute (0,4), så til høyre til rute (0,9), osv. Igjen vil den havne i en
blindgate, dvs. i rute (0,19). Deretter vil rekursjonen «trekke seg tilbake» til rute
(3,15) og gå videre til venstre derfra. Osv.
Det trengs en labyrint til testing av Programkode 1.5.10 b).
Vi kan sette opp a direkte i koden, men det blir lite fleksibelt. Det enkleste er
å ha tabellverdiene på en fil. Nedenfor står de tre første linjene på filen
labyrint.txt. Det er tabellen til
Figur 1.5.10 a):
00010000001110001000
01010111100000101011
osv.
De to tallene på første linje angir dimensjonen til tabellen (først antall rader og så antall kolonner). Deretter
kommer innholdet. Som nevnt over angir 0 en «åpen» rute og 1 en som er «lukket».
Følgende metode leser en slik fil der filnavnet er gitt på url-form (obs: du må ha med
import java.net.URL;):
public static byte[][] hentLabyrint(String url) throws IOException { BufferedReader inn = new BufferedReader(new InputStreamReader((new URL(url)).openStream())); String[] dim = inn.readLine().split(" "); // filens første linje int m = Integer.parseInt(dim[0]); // m er antall rader int n = Integer.parseInt(dim[1]); // n er antall kolonner byte[][] a = new byte[m][n]; // oppretter tabellen for (int i = 0; i < m; i++) { String linje = inn.readLine(); // leser en linje for (int j = 0; j < n; j++) { if (linje.charAt(j) == '1') a[i][j] = 1; } } inn.close(); return a; } Programkode 1.5.10 c)
Filen kan hentes fra: "https://www.cs.hioa.no/~ulfu/appolonius/kap1/5/labyrint.txt".
Hvis du imidlertid har flyttet filen over til deg selv, må du oppgi filnavnet på url-form. Som
"file:///c:/algdat/labyrint.txt" hvis den f.eks. er lagt under c:/algdat.
Flg. kodebit tester det vi har laget så langt:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/5/labyrint.txt"; byte[][] a = hentLabyrint(url); finnVei1(a,0,0,19,19); Programkode 1.5.10 d)
Programkode 1.5.10 d) vil gi utskriften: En vei er funnet! Men hvilken vei? Det kan vi kanskje få informasjon
om hvis hele tabellen skrives ut til konsollet:
public static void skrivLabyrint(byte[][] a) { for (int i = 0; i < a.length; i++) { for (int j = 0; j < a[i].length; j++) { System.out.print(a[i][j]); } System.out.println(); } } Programkode 1.5.10 e)
Hvis et kall på skrivLabyrint legges inn som siste setning i
Programkode 1.5.10 d), vil utskriften vise at samtlige
«åpne» ruter ha blitt besøkt. Dvs. at samtlige 0-er i tabellen har blitt erstattet av 2-ere. Dermed er
det umulig å se hvilken vei som er funnet. Dette må vi reparere! For det første bør vi få en utskrift som viser
de rutene som utgjør veien som er funnet og ingen andre. Det betyr at eventuelle blindgater ikke skal være med.
For det andre skal metoden «stoppe» når vi har kommet frem til utgangen. Det betyr at kun de rutene
som det er nødvendige å besøke for å komme frem til utgangen, skal besøkes.
Vi unngår blindgatene i utskriften hvis «besøkt» fjernes når metoden «trekker seg tilbake».
Med andre ord kan vi la a[i][j] = 0 være siste setning i
Programkode 1.5.10 b). Men dette er ikke nok. Det å
«stoppe» metoden kan gjøres på flere måter. Det er mulig å bruke en global (static) variabel for
det formålet, men det er en kunstig teknikk. Det beste er å bruke en parameter eller å la metoden returnere
sann (true) hvis utgangen er funnet. Her bruker vi den siste varianten. Se også
i Oppgave 6. Vi bruker navnet finnVei på siste versjon:
public static boolean finnVei(byte[][] a, int i, int j, int iut, int jut) { a[i][j] = 2; // ruten er besøkt if (i == iut && j == jut) return true; // utgangen er funnet int m = a.length; // antall rader int n = a[0].length; // antall kolonner boolean funnet = false; // hjelpevariabel if (!funnet && j + 1 < n && a[i][j+1] == 0) funnet = finnVei(a,i,j+1,iut,jut); // til høyre if (!funnet && i + 1 < m && a[i+1][j] == 0) funnet = finnVei(a,i+1,j,iut,jut); // nedover if (!funnet && j > 0 && a[i][j-1] == 0) funnet = finnVei(a,i,j-1,iut,jut); // til venstre if (!funnet && i > 0 && a[i-1][j] == 0) funnet = finnVei(a,i-1,j,iut,jut); // oppover if (!funnet) a[i][j] = 0; // blindvei return funnet; } Programkode 1.5.10 f)
Programkode 1.5.10 f) vil gjøre det vi ønsker. Hvis et av de fire mulige rekursive kallene returnerer
true, vil funnet få verdien true. De rekursive kallene som kommer etterpå
vil derfor ikke bli utført. Hvis ingen av de fire kallene har returnert med true,
er (i,j) inne i en blindgate og ruten settes tilbake til 0.
For å få en bedre presentasjon av resultatet kan vi lage en html-fil ved hjelp av tabellen. Metoden
tilHTML
gjør det. Kopier den inn i programsystemet ditt. Dermed vil flg. kodebit kunne kjøres. Resultatet ser
du hvis du åpner filen labyrint.html i en webleser:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/5/labyrint.txt"; byte[][] a = hentLabyrint(url); // labyrinten boolean funnet = finnVei(a, 0, 0, 19, 19); // fra inngang til utgang System.out.println(funnet ? "En vei er funnet!" : "Ingen vei!"); tilHTML(a,"labyrint.html"); // labyrinten i html-format Programkode 1.5.10 g)
En ser fort at labyrinten i Figur 1.5.10 a)
har mange veier fra inngangen (0,0) til utgangen(19,19). Det er faktisk hele 202 forskjellige.
Metoden finnVei i Programkode 1.5.10 f) finner
den veien som ligger lengst til høyre. Det kommer av at den fra hver rute først går videre til høyre hvis det er mulig.
Vi finner andre veier hvis vi bytter om på rekkefølgen av de reksursive kallene i
Programkode 1.5.10 f). En kan også eksperimentere
med å ha inngangen og utgangen andre steder, fjerne vegger eller legge inn flere. Spesielt bør en sjekke
hva som skjer hvis en ekstra vegg fører til at det ikke finnes noen vei.
Se Oppgavene 2 − 5.
Veiens lengde Vi definerer at lengden på veien er antall «skritt» fra startruten og til (og med) utgangen. Dette kan vi selvfølgelig finne ved å telle opp manuelt. F.eks. har den veien vi fant her en lengde på 84 (én mindre enn antall kryss). Men det er også enkelt å gjøre om Programkode 1.5.10 f) slik at vi også får veiens lengde. Se Oppgave 7.
Neste oppgave er å finne den korteste veien. Til den oppgaven finnes det flere smarte teknikker som vi skal studere nærmere i Delkapittel 11.2. Det å finne korteste vei i en labyrint er et spesialtilfelle av det å finne korteste vei i en graf. Men her i dette avsnittet handler det først og fremst om rekursjon, om å forstå hvordan rekursjon virker og om å lage rekursive metoder. Derfor skal vi her finne korteste vei med samme type rekursiv teknikk som ovenfor selv om det i dette tilfellet er en ineffektiv teknikk.
Det er enkelt (men som sagt ineffektivt) å finne lengden på den korteste veien ved å bruke samme idé som i Programkode 1.5.10 b). For hver vei vi finner, sjekker vi om den er kortere enn den til da korteste veien:
public static void finnKortestVei(byte[][] a, int i, int j, int iut, int jut, int lengde, int[] kortest) // to ekstra parametere { a[i][j] = 2; // ruten er besøkt if (i == iut && j == jut) // utgangen { if (lengde < kortest[0]) kortest[0] = lengde; // oppdaterer } int m = a.length, n = a[0].length; // m rader og n kolonner if (j + 1 < n && a[i][j+1] == 0) finnKortestVei(a,i,j+1,iut,jut,lengde+1,kortest); // til høyre if (i + 1 < m && a[i+1][j] == 0) finnKortestVei(a,i+1,j,iut,jut,lengde+1,kortest); // nedover if (j > 0 && a[i][j-1] == 0) finnKortestVei(a,i,j-1,iut,jut,lengde+1,kortest); // til venstre if (i > 0 && a[i-1][j] == 0) finnKortestVei(a,i-1,j,iut,jut,lengde+1,kortest); // oppover a[i][j] = 0; // nuller ruten } Programkode 1.5.10 h)
Programkode 1.5.10 h) er ineffektiv fordi vi går til utgangen hver gang selv om en ny vei bare skiller seg litt fra den forrige veien. Det betyr at vi går gjennom de samme rutene mange ganger. Metoden kan brukes slik:
public static void main(String[] args) throws IOException { String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/5/labyrint.txt"; byte[][] a = hentLabyrint(url); int[] minimum = {Integer.MAX_VALUE}; finnKortestVei(a, 0, 0, 19, 19, 0, minimum); if (minimum[0] == Integer.MAX_VALUE ) System.out.println("Det er ingen vei!"); else System.out.println("Korteste vei har lengde " + minimum[0]); } Programkode 1.5.10 i)
Det er mulig å utvide Programkode 1.5.10 i) til også å finne den korteste veien og ikke bare dens lengde. Men som nevnt er dette en ineffektiv teknikk. (Avsnitt 11.1.5 har en bedre metode.) En mulig teknikk som bruker en litt «brutal» fremgangsmåte, er å lage en kopi av hele labyrinten hver gang metoden finner en vei som er kortere enn tidligere. Se Oppgave 8.
| 1. | Programbiten i Programkode 1.5.10 d) bruker
finnVei1 fra Programkode 1.5.10 b). Legg
også inn i programbiten et kall på utskriftsmetoden fra Programkode 1.5.10 e).
Kjør så programbiten. Har alle rutene blitt besøkt?
|
| 2. | Kjør programbiten i Programkode 1.5.10 g). Pass da på
at det versjonen av finnVei fra Programkode 1.5.10 f)
du bruker.
|
| 3. | Bytt om de rekursive kallene i Programkode 1.5.10 f) slik at det først blir venstre, så nedover, så høyre og til slutt oppover. Hvilken vei blir det da? Bruk programbit Programkode 1.5.10 g). |
| 4. | Legg inn en ekstra vegg i labyrinten i Figur 1.5.10 a)
slik at det ikke finnes noen vei fra inngangen til utgangen. Sett f.eks. 1 i rute (14,11). Det kan du gjøre ved
å legge inn setningen a[14][11] = 1; rett etter at labyrinten er lest inn.
Hva blir da resultatet
av å kjøre programbit Programkode 1.5.10 g).
|
| 5. | Eksperimenter med å ha inngangen og utgangen andre steder, ta vekk vegger eller legg inn nye. Programbit Programkode 1.5.10 g) viser resultatet. Hva skjer hvis inngang og utgang er samme rute? |
| 6. | I Programkode 1.5.10 f) brukes returverdien til
å stoppe rekursjonen. Vi kan isteden gjøre det med en parameter. Men da kan vi ikke bruke en vanlig
parameter siden Java bruker verdioverføring (eng: call by value). Vi kan isteden bruke en boolsk tabell med kun
ett element. Referansen (eller adressen) til tabellen verdioverføres, men innholdet i tabellelementet kan endres.
Lag en versjon av finnVei som bruker denne teknikken.
|
| 7. | Legg inn int lengde som ekstra parameter i
Programkode 1.5.10 f). Legg inn
en utskriftssetning som skriver ut verdien til lengde når utgangen er funnet.
I de fire rekursive kallene brukes lengde + 1 som parameterverdi.
|
| 8. | Lag først en metode public static int[][] kopi(int[][] a) som lager og
returnerer en kopi av parametertabellen a. Utvid så
Programkode 1.5.10 h) med en parameter
int[][][] b. Når det er funnet en kortere vei legges en kopi av labyrinten inn
i b[0]. Kanskje du kan finne en annen og mindre ressurskrevende måte å registrere
den nye og kortere veien på?
|
![]() 1.5.11 Hvordan gjøre om fra rekursjon til iterasjon
1.5.11 Hvordan gjøre om fra rekursjon til iterasjon
Teorien sier at det alltid går an å gjøre om en metode fra å være rekursiv til å bli iterativ.
I noen tilfeller er det lett å få det til, mens det andre ganger kan være ganske krevende.
Det å prøve å få til en slik omgjøring kan gi god innsikt i hvordan rekursjon fungerer.
En rekursiv metode kan ha et eller flere rekursive kall. Hvis siste setning i en metode er et rekursivt kall, kalles det halerekursjon. Et slikt kall kan enkelt erstattes med en løkke. Det som skjer er at metoden starter på nytt − med en endring på parameterverdien eller verdiene. Ta kvikksortering i Programkode 1.5.7 a) som eksempel. Der er siste setning et rekursivt kall. Det som skjer er at venstre endepunkt endres fra v til k + 1. Men det kan vi gjøre i en løkke og dermed vil vi få en kvikksortering med kun ett rekursivt kall:
public static void kvikksortering2(int[] a, int v, int h) { while (v < h) { int k = Tabell.sParter(a,v,h,(v + h)/2); // Programkode 1.3.9 f) if (v < k - 1) kvikksortering2(a,v,k-1); // minst to i a[v:k-1] v = k + 1; } } Programkode 1.5.11 a)
Denne versjonen av kvikksortering gir kun en marginal forbedring med tanke på effektivitet i forhold til Programkode 1.5.7 a), men fordelen er at vi nå har kun ett rekursivt kall. Dette kallet skjer på det venstre delintervallet, dvs. på a[v:k-1]. Videre ser vi at kallet skjer kun hvis v < k − 1, dvs. hvis intervallet a[v:k-1] har minst to verdier. Hvis intervallet har én eller ingen verdier, er det ikke nødvendig å gå videre siden intervallet da allerede er sortert.
Diskusjonen i Avsnitt 1.5.2 viste at hvert rekursivt kall førte til et nytt aktivitetslag på programstakken. Først når det oppstod et basistilfelle ble det tilhørende laget fjernet. Antall lag til enhver tid kalles rekursjonens dybde og det maksimale antallet lag under kjøringen av en rekursiv metode kalles den maksimale rekursjonsdybden. Et problem med kvikksortering er at det finnes tabeller som gjør den maksimale rekursjonsdybden svært stor. Faktisk så stor som n − 1 for en tabell med n verdier.
| 1 | 4 | 6 | 8 | 10 | 12 | 14 | 15 | 2 | 9 | 5 | 11 | 3 | 13 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 1.5.11 a) : En tabell med 15 verdier | ||||||||||||||
Partisjoneringen i vår versjon av kvikksortering bruker verdien på midten av intervallet a[v:h] som skilleverdi. Tabellen i Figur 1.5.11 a) har tallet 15 på midten (dvs. i posisjon 7) og det er også tabellens største verdi. I et kall på kvikksortering i Programkode 1.5.11 a) med v = 0 og h = 14 som verdier, vil derfor sParter flytte 15 bakerst (15 og 7 bytter plass) og gi k verdien 14. Det rekursive kallet vil så skje på intervallet a[v:k - 1] = a[0:13]. Men midt på a[0:13] (posisjon 6) ligger 14. Dermed vil sParter flytte 14 bakerst i a[0:13] og returnere med 13. Så blir et nytt rekursivt kall utført på a[0:12]. Osv. Tallene i Figur 1.5.11 a) er slik at hvert nytt rekursivt kall vil skje på et intevall som er én mindre enn det det var. Se Oppgave 3. Det vil bli utført 14 kall på kvikksortering før det oppstår et basistilfelle, dvs. v < k − 1 er usann.
Programstakken krever plass og hvis rekursjonsdybden blir for stor (for mange aktivitetslag), kan det «renne over» (eng: stack overflow). Da avbrytes programkjøringen. Det finnes heldigvis en enkel måte å hindre dette på. I Programkode 1.5.7 a) kunne vi ha valgt å utføre det rekursive kallet på det andre delintervallet, dvs. på a[k + 1 : h]. I en slik versjon av kvikksortering ville tabellen i Figur 1.5.11 a) bli sortert med kun ett kall. Se Oppgave 4. Men det er selvfølgelig mulig å lage en tabell med 15 verdier hvor også denne versjonen utfører 14 kall før et basistilfelle inntreffer.
Løsningen på problemet vårt er å sjonglere mellom a[v : k − 1] og a[k + 1 : h]. Vi utfører det rekursive kallet på det korteste av de to og f.eks på det venstre hvis de er like lange. Med en slik strategi vil det bli kun ett kall for tabellen i Figur 1.5.11 a). Maksimal rekursjonsdybde får vi nå hvis sParter alltid deler intervallet a[v : h] på midten. Slik blir det feks. for en tabell som inneholder tallene fra 1 til 15 i sortert rekkefølge. En halvering i hvert rekursivt kall vil gjøre at det aldri blir flere enn log 2 n kall før det kommer et basistilfelle. Men normalt vil maksimal rekursjonsdybde bli mindre enn log 2 n . Dette koder vi slik:
public static void kvikksortering3(int[] a, int v, int h) // ny versjon { while (v < h) { int m = (v + h) / 2; // m er midten på intervallet int k = Tabell.sParter(a, v, h, m); // a[m] er skilleverdi if (k <= m) // a[v:k-1] er minst { if (v < k - 1) kvikksortering3(a, v, k - 1); v = k + 1; } else // a[k+1:h] er minst { if (k + 1 < h) kvikksortering3(a, k + 1, h); h = k - 1; } } } Programkode 1.5.11 b)
Har Programkode 1.5.11 b) to rekursive kall? Ikke når det er if - else. Hvis denne versjonen brukes på tabellen i Figur 1.5.11 a) , vil det ikke bli noe rekursivt kall. Alt arbeidet vil foregå ved hjelp av while-løkken. Den vil gå n − 1 ganger og hver gang vil sParter gå gjennom hele a[v : h]. Det betyr at metoden er av kvadratisk orden for denne tabellen. Det er mulig å lage slike tabeller for enhver dimensjon n. Det betyr at kvikksortering er av kvadratisk orden i de mest ugunstige tilfellene, men av orden n log 2 n i gjennomsnitt.
Det finnes teknikker som gjør de ugunstige tilfellene mindre sannsynlige. La m = (v + h) / 2. Våre versjoner av kvikksortering bruker alltid a[m] som skilleverdi under partisjoneringen. Det har som vi så i Figur 1.5.11 a) , uheldige konsevenser. En mulig forbedring er å velge den miderste av a[v], a[m] og a[h], i sortert rekkefølge, som skilleverdi. I Figur 1.5.11 a) vil det være den midterste av 1, 7 og 15, dvs. 7. Med 7 som skilleverdi vil tabellen i Figur 1.5.11 a) nesten halveres i første partisjonering. Mer om dette i et senere kapittel der vi skal studere både kvikksortering og andre sorteringsteknikker nærmere. Se også Oppgave 5.
Poenget med versjonen i Programkode 1.5.11 b) er at der kan vi på forhånd vite hvor stor programstakken maksimalt kan bli. Med tanke på denne størrelsen, får vi som nevnt over, det mest ugunstige tilfellet når hver partisjonering deler intervallet i to like store deler. Hvis intervallengden n er et oddetall, f.eks. n = 2k + 1, vil neste kall skje på et intervall med lengde k, osv. Det betyr at programstakken, hvis vi starter med en tabell med lengde n > 1, aldri får flere enn ⌈log2(n+1)⌉ − 1 aktivitetslag. Selv om n er stor, blir dette et lite antall.
Programkode 1.5.11 b) skal nå omformes til
en iterativ metode ved at programstakken erstattes med en
eksplisitt stakk. I en stakk legges verdier på
og tas fra «toppen». Det rekursive kallet i
Programkode 1.5.11 b) skjer på det korteste
av intervallene a[v : k − 1] og
a[k + 1 : h]. Kallet må gjøre seg ferdig
før programkontrollen kan gå til neste setning og dermed behandle det lengste
av de to intervallene. I vår iterative versjon lagrer vi
isteden «informasjon» om det lengste intervallet på stakken.
Løkkekontrollen while (v < h) avgjør så om
det korteste intervallet skal behandles videre eller, hvis det har færre enn to verdier,
si at det er ferdigbehandlet. Hvis det korteste intervallet er ferdigbehandlet,
jobber vi videre med det intervallet som ligger øverst på stakken. Osv.
Begrepet stakk er svært viktig i databehandling og vil bli diskutert nøye i et senere kapittel. Her skal vi isteden få til det samme ved hjelp av en int-tabell. Hvis vi tenker oss at tabellen står loddrett med posisjon 0 nederst, vil en innlegging på første ledige plass kunne ses på som å legge verdien på «toppen». Tilsvarende vil det å hente den verdien som sist ble lagt inn, kunne ses på som å ta fra «toppen». I en int-tabell kan vi kun legge inn heltall, men det holder for oss siden venstre og høyre indeks gir nok«informasjon» om et intervall. Vi kan også dimensjonere «stakken» på forhånd siden vi vet hvor stor den maksimalt vil bli:
public static void kvikksortering4(int[] a) // iterativ versjon { int dim = ((int)Math.ceil(Math.log(a.length + 1)/Math.log(2)) - 2); int[] s = new int[Math.max(2,dim*2)]; // int-tabell som stakk int i = 0; s[i++] = 0; s[i++] = a.length - 1; // endepunktene til a while (i > 0) // fortsetter så lenge stakken ikke er tom { int h = s[--i], v = s[--i]; // tar fra stakken while (v < h) { int m = (v + h) / 2; // m er midten int k = Tabell.sParter(a, v, h, m); // partisjonerer if (k <= m) // a[v:k-1] er kortest { if (k + 1 < h) { s[i++] = k + 1; s[i++] = h; } // det lengste h = k - 1; // det korteste } else // a[k+1:h] er kortest { if (v < k - 1) { s[i++] = v; s[i++] = k - 1; } // det lengste v = k + 1; // det korteste } } } } Programkode 1.5.11 c)
Programstakkens størrelse vil aldri overstige ⌈log2(n+1)⌉ − 1 i Programkode 1.5.11 b) . Den iterative versjonen i Programkode 1.5.11 c) bruker en eksplisitt stakk s. Istedenfor et rekursivt kall legges intervallendepunkter på stakken, dvs. to verdier om gangen. Dermed må stakken dimensjoneres til å være dobbelt så stor som maksimal programstakkstørrelse (minus 1 siden det ikke trengs plass til å kalle metoden første gang). Videre må s alltid ha plass til minst to verdier for å kunne takle tilfellet a.length < 4.
Alle versjonene vi har laget av kvikksortering er like effektive. Kanskje er den iterative versjonen hårfint raskere enn de andre. Se Oppgave 6.
Vi tok utgangspunkt i Programkode 1.5.11 b) når vi laget den itertive versjonen, men det hadde også vært mulig å ta utgangspunkt Programkode 1.5.7 a) . Da må den imidlertid omkodes litt slik at det første rekursive kallet alltid skje på det korteste av de to intervallene. Dermed kan en eksplisitt stakk dimensjoneres på samme måte som i Programkode 1.5.11 c) . Se Oppgave 7.
| 1. | Første setning i kvikksorteringsversjonen fra Programkode 1.5.7 a) inneholder en sjekk på om intervallet a[v : h] inneholder minst to verdier. Antallet rekursive kall kan reduseres hvis sjekken isteden gjøres før de rekursive kallene. Gjør disse endringene i koden. |
| 2. | Gjør om versjonen av kvikksortering som du ble bedt om å lage i Oppgave 1, slik at den returnerer det maksimale antallet aktivitetslag på programstakken under en kjøring. Hvis metoden brukes på en tabell med tallene fra 1 til 15 i sortert rekkefølge, skal metoden returnere 3. Hvis den brukes på tabellen i Figur 1.5.11 a) skal den returnere 14. |
| 3. | Versjonene av kvikksortering i Programkode 1.5.11 a) og b) sorterer et intervall a[v : h]. Lag i begge tilfellene også versjoner som sorterer hele tabeller ved å kalle opp den som sorterer a[v : h]. Lag testkjøringer som viser at metodene sorterer korrekt. |
| 4. | Sjekk at programstakken får en dybde på 14 når tabellen i Figur 1.5.11 a) brukes i Programkode 1.5.11 a) . Gjennomfør kjøringen for «hånd». |
| 5. | Lag en versjon av kvikksortering på samme måte som i Programkode 1.5.11 a) , men der kallet hele tiden gjøres på det andre intervallet. Sjekk at det da ikke vil skje et eneste rekursivt kall for tabellen Figur 1.5.11 a) . |
| 6. | La m = (v + h) / 2. Lag en versjon der den miderste av a[v], a[m] og a[h], i sortert rekkefølge, brukes som skilleverdi. |
| 6. | Sjekk effektiviteten til de forskjellige versjonene av kvikksortering ved å måle tidsforbruket når de kjøres på store og tilfeldige tabeller. Sammenlign med den versjonen av kvikksortering som ligger i class Arrays og som sorterer int-tabeller. |
| 7. | Ta utgangspunkt i Programkode 1.5.7 a) og lag en som fortsatt har to rekursive kall, men der det første kallet alltid skjer på det korteste av de to intervallene. Bruk så det til å lage en ny iterativ versjon. |
| 8. | Lag en iterativ versjon av flettesortering i Programkode 1.5.8 a) . Der blir alltid tabellintervallet delt på midten. Dermed er det lett å dimensjonere en eksplisitt stakk på forhånd. |
![]() 1.5.12 Rekursjon, rekursjonsligninger og induksjonsbevis
1.5.12 Rekursjon, rekursjonsligninger og induksjonsbevis
Her vil det etter hvert komme mer stoff!
| 1. | xxxx |

|