![]() 11.1.1 Generelt om grafer
11.1.1 Generelt om grafer
Dette avsnittet inneholder kun en kort innføring i de viktigste grafbegrepene. Det forventes at de som leser dette har
fått nok kunnskap om grafteori fra annet hold. Emnet Algoritmer og datastrukturer
bygger på Diskret matematikk og der inngår det normalt mye grafteori.
En graf har noder (eng: node/nodes eller vertex/vertices)
og kanter (eng: edge/edges) mellom dem.
En kant er formelt et par av noder. Kanten kalles rettet hvis paret er ordnet
og urettet hvis paret er uordnet.
En graf tegnes vanligvis ved å la nodene være små sirkler og kantene streker mellom noder. En rettet kant
tegnes normalt som en pil. En kant kan ha en vekt (eller lengde)
i form av et tall.
Vi skiller nodene fra hverandre ved å gi hver av dem et unikt «navn», dvs.
en identifikator.
 |
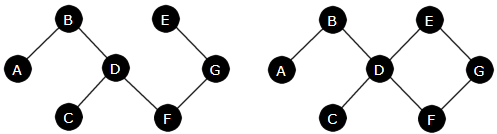
| Figur 11.1.1 a): En graf med bokstaver som navn |
En kant er et nodepar. Nå er det ingen fast praksis når det gjelder formen på et par. Spørsmålet er hvordan man skal skille mellom ordnet og uordnet. Hvis f.eks. A og B er to noder, brukes ofte (A,B). Er dette et ordnet eller et uordnet par? Normalt vil det fremgå av sammenhengen, dvs. av hva slags type graf det handler om. Men noen velger å bruke (A,B) for ordnet par (dvs. kanten går fra A til B) og <A,B> for uordnet par (en urettet kant).
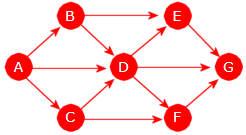
Urettet og uvektet graf
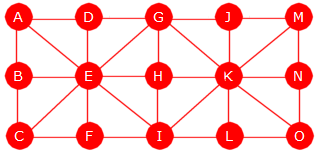
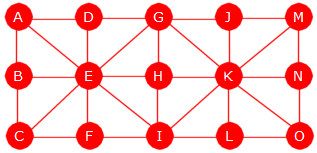
Figur 11.1.1 b) under til venstre viser en urettet og uvektet graf
med 7 noder og 12 kanter. Der brukes en bokstav som identifikator:
 |
 |
|
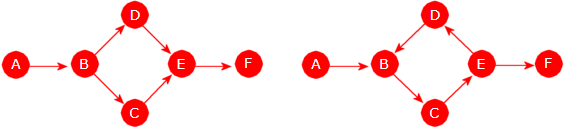
| Figur 11.1.1 b): 7 noder og 12 kanter | Figur 11.1.1 c): En rettet graf |
Rettet og uvektet graf
En graf kalles rettet (eng: directed graph eller digraph) hvis alle kantene har en retning, dvs. at
de er representert som ordnede par.
Figur 11.1.1 c) over til høyre viser en rettet (og uvektet) graf. Den er laget ved at hver
av kantene i grafen i Figur 11.1.1 b) har fått retning. En vanlig måte
å markere retning på er å bruke en pil.
Urettet og vektet graf
En graf kalles vektet (eng: weighted) hvis det til hver kant er tilordnet
en vekt (et tall). Verdien kalles generelt kantens vekt, men
i mange situasjoner er det mer naturlig å si at det er kantens lengde.
Grafen i Figur 11.1.1 d) under til venstre er urettet og vektet:
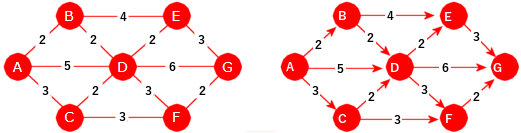 |
| Figur 11.1.1 d): En urettet og vektet graf Figur 11.1.1 e): En rettet og vektet |
Rettet og vektet graf
Grafen i Figur 11.1.1 e) over til høyre er rettet og vektet:
Vi kan oppsummere dette ved å si at det er fire hovedtyper av grafer, men det er også grafer som er en kombinasjon av disse hovedtypene:
1) Urettet og uvektet, 2) Rettet og uvektet, 3) Urettet og vektet og 4) Rettet og vektet.
En kant er et nodepar. Hvis de to nodene i paret er like,
kalles det en sløyfe (eng: loop). En graf uten sløyfer kalles sløyfefri.
Det kan også være to eller flere like par, dvs. flere kanter mellom
to noder. Det gir flg. graftyper:
- Enkel urettet graf − maksimalt én kant mellom to noder og sløyfefri.
- Enkel rettet graf − maksimalt én kant i samme retning mellom to noder og sløyfefri.
- Multigraf − det kan være flere kanter mellom to noder, men sløyfefri.
- Pseudograf − det kan være flere kanter mellom to noder og noder kan ha sløyfer.
Urettet graf Vi har blant andre flg. begreper:
NaboTo noder X og Y kalles naboer hvis det går en kant mellom dem. I Figur 11.1.1 b) er A og B naboer, men ikke nodene A og E. Naboene til A er B, C og D. På engelsk er to noderadjacent(tilstøtende) hvis de er naboer.NodegradGraden til en node er lik kantantallet. En sløyfe utgjør to kanter. F.eks. er graden til A i Figur 11.1.1 b) lik 3 og den til D lik 6.Vei og veilengdeDet går en vei mellom to noder X og Y hvis det er mulig å gå fra X til Y ved å følge kanter. Hvis grafen er uvektet, er veilengden lik antallet kanter og hvis den er vektet, er veilengden summen av kantvektene.Enkel veiEn vei kalles enkel hvis alle kantene på veien er forskjellige.SykelEn enkel vei som starter i en node X, inneholder minst én kant og som ender der den startet (dvs. i X ), kalles en sykel eller en krets (eng: circuit). En graf uten sykler kallesasyklisk.Korteste veiHvis det går flere enn én vei mellom to noder X og Y, er den veien kortest som inneholder færrest kanter eller minst kantvektsum hvis grafen er vektet.SammenhengGrafen kalles sammenhengende hvis det går en vei mellom hvert par av forskjellige noder X og Y. Hvis den ikke er sammenhengende, så består den av to eller flere sammenhengende komponenter.SubgrafEn subgraf (eller en delgraf) S av en graf G er en graf som består av en eller flere noder fra G og med kanter som også er kanter i G.TrærGrafen kalles et tre hvis den er sammenhengende og uten sykler (asyklisk).
Rettet graf Vi har blant andre flg. begreper:
Direkte etterfølgerEn node Y kalles en direkte etterfølger til en node X hvis det er en kant med retning fra X til Y. I Figur 11.1.1 c) er B en direkte etterfølger til A.Vei og veilengdeDet går en vei fra en node X til en node Y hvis det er mulig å gå fra X til Y ved å følge kanter i kantenes retning. I en uvektet graf er veilengden lik antall kanter på veien og i en vektet graf er den summen av kantenes lengde/vekt.EnkelveiEn vei kalles enkel hvis alle kantene på veien er forskjellige.SykelEn enkel vei som starter i en node X, inneholder minst én kant og som ender der den startet (dvs. i X ), kalles en sykel eller en krets (eng: circuit). En rettet graf uten sykler kalles asyklisk.Korteste veiHvis det går flere enn én vei fra en node X til en node Y, er den veien kortest som har minst lengde. I Figur 11.1.1 d) er det mange veier fra A til G og den korteste av dem har lengde 8 (veien A, C, F, G).EtterfølgerEn node Y kalles en etterfølger til en node X hvis det går en vei fra X til Y. I Figur 11.1.1 c) er G en etterfølger til A (G er der en etterfølger til alle de andre).Direkte forgjenger og forgjengerEn node X kalles en direkte forgjenger til en node Y hvis det går en kant fra X til Y. Dvs. at Y er en direkte etterfølger til X. En node X kalles en forgjenger til en node Y hvis Y er en etterfølger til X.KildeogslukEn node med kun utkanter er en kilde. En med kun innkanter er et sluk.SterksammenhengGrafen kalles sterkt sammenhengende hvis det finnes en vei fra enhver node til enhver annen node.SvaksammenhengGrafen kalles svakt sammenhengende hvis den urettede grafen vi får ved å fjerne retningen på alle kantene, blir sammenhengende.
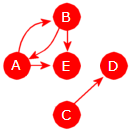 |
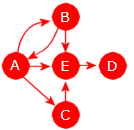 |
 |
||
| Ingen av delene | Svakt smh. | Sterkt smh. |
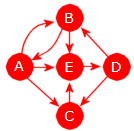
Grafen til venstre i figuren over er hverken svakt eller sterkt sammenhengende. Hvis retningene på kantene tas vekk, blir den ikke sammenhengende som urettet graf. Den på midten er derimot svakt sammenhengende, men ikke sterkt sammenhengende. Det går f.eks. ingen vei fra D til C. Den til høyre er sterkt sammenhengende. Der kan vi starte i hvilken som helst node og finne en vei til en hvilken som helst annen node.
| 1. | Tegn en urettet graf som har nodene A, B, C, D, E og F og der det er én og bare én kant mellom hvert par av forskjellige noder. Hvor mange kanter vil grafen få? |
| 2. | Graden grad(X) til en node X i en urettet graf er dens
kantantall. En sløyfe telles som to kanter. La n være antallet kanter i grafen.
Håndhilsingssetningen (eng: the handshaking theorem) sier at 2n = ∑ grad(X)
der summes tas over alle noden i grafen. Sjekk at denne setningen stemmer for grafen i
Figur 11.1.1 b) og for den i
Oppgave 1.
|
| 3. | Sriv opp alle mulige veier fra A til G i grafen i Figur 11.1.1 e) (det er 10 stykker) og lengden på dem. Hvem er kortest og hvem er lengst? Har den kilde eller sluk? |
![]() 11.1.2 Listerepresentasjon av uvektede grafer
11.1.2 Listerepresentasjon av uvektede grafer
Vi har fire hovedtyper av grafer og det er mulig
å lage en felles datastruktur for alle fire. Men her gjør vi det foreløpig litt enklere og lager en struktur
felles for uvektede grafer. I figuren
under til venstre er A og B naboer i en urettet graf. Når vi beveger oss i en slik graf skal vi
kunne gå begge veier, dvs. både fra A til B og fra B og A. Det kan vi få til
ved å la en urettet kant være representert med to rettede kanter. Se figuren under til høyre:
| Figur 11.1.2 a): Naboer har har en «dobeltkant» |
En urettet graf representeres normalt ved hjelp av
naboskapslister (eng: adjacency list) eller ved en naboskapsmatrise (se Avsnitt 11.1.3).
Naboskapslisten til en node er en liste med
referanser til den eller de nodene som den er nabo til. Nodene selv kan ligge
i en datastruktur der det er enkelt å finne dem - f.eks. en tabell. Vi
tenker oss at de 7 nodene i Figur 11.1.1 b)
ligger i en tabell. Siden A og B er naboer må B ligge i listen til A og A i listen til B.
D er nabo til alle de andre. Dermed må A, B, C, E, F og G ligge i listen til
D og omvendt. Det gir:
 |
| Figur 11.1.2 b): Naboskapslister for grafen i Figur 11.1.1 a) |
Det er enklere å representere den rettede grafen i Figur 11.1.1 c) siden en liste nå kun skal inneholde de nodene som det går en (rettet) kant til, dvs. de direkte etterfølgerne. F.eks. går det kanter fra noden A til nodene B, C og D. Dermed skal listen til A inneholde nettopp de nodene. Det går ingen (rettet) kant fra G og dermed skal listen til G være tom:
 |
| Figur 11.1.2 c): Grafen i Figur 11.1.1 b) |
I Figur 11.1.2 b) og c) ligger
nodene i en (loddrett) tabell og hver av dem har en liste. Denne strukturen kunne vi ha brukt siden søking i en (sortert) tabell er
effektivt. Men hvis grafen skal være dynamisk (innlegging og fjerning), er det enklere å velge ferdige strukturer som har
de nødvendige operasjonene fra før. F.eks. en Map
for nodene og en List til kantlistene:
import java.util.*; // Map og List import java.io.*; // graf fra fil import java.net.URL; // graf fra internett public final class Graf implements Iterable<String> // final: skal ikke arves { private static final class Node // en indre nodeklasse { private final String navn; // navn/identifikator private final List<Node> kanter; // nodens kanter private byte innkanter = 0; // antall innkanter private boolean besøkt = false; // hjelpevariabel brukes senere private Node forrige = null; // hjelpevariabel brukes senere private Node(String navn) // nodekonstruktør { this.navn = navn; // nodens navn kanter = new LinkedList<>(); // oppretter kantlisten } public String toString() { return navn; } // nodens navn } // Node private final Map<String, Node> noder; // en map til å lagre nodene public Graf() { noder = new HashMap<>(); } // standardkonstruktør public boolean leggInnNode(String navn) // ny node { if (navn == null || navn.length() == 0) throw new IllegalArgumentException("Noden må ha et navn!"); if (noder.get(navn) != null) return false; // finnes navnet fra før? return noder.put(navn, new Node(navn)) == null; } public boolean nodeFinnes(String navn) // finnes denne noden? { return noder.get(navn) != null; } public Iterator<String> iterator() // klassen er iterable { return noder.keySet().iterator(); } public String[] nodenavn() // nodenavnene som en tabell { return noder.keySet().toArray(new String[0]); } } // Graf Programkode 11.1.2 a)
Vi bruker en
HashMap
siden den normalt er mest effektiv. Hadde vi trengt sortering kunne vi ha brukt en
TreeMap.
Metoden leggInnNode(String navn)
sjekker først om navnet finnes fra før. Hvis ikke,
opprettes en node med gitt navn og noden legges inn i vår HashMap (med navnet som nøkkelverdi).
Hvis du har flyttet klassen Graf over i ditt system, kan dette testes.
I flg. programbit lages starten på grafen i
Figur 11.1.1 b),
men foreløpig uten kanter/naboer:
String[] nodenavn = "ABCDEFG".split(""); // A, B, C, D, E, F og G Graf graf = new Graf(); for (String navn : nodenavn) graf.leggInnNode(navn); for (String navn : graf) System.out.print(navn + " "); // A B C D E F G Programkode 11.1.2 b)
I en rettet graf går en kant fra en node og til en annen node.
En urettet graf må ha kanter begge veier.
Metoden leggInnKant(String franode, String tilnode) som vi nå skal lage,
må derfor kalles to ganger hvis nodene er naboer i en urettet graf.
Både franode og tilnode må eksistere på forhånd. Hvis ikke,
kastes et unntak. Vi bestemmer her (som et valg) kun å tillate enkle grafer. Dvs. at en node ikke kan ha en kant
til seg selv og hvis X og Y er to forskjellige noder, kan det ikke være to kanter fra X til Y.
public void leggInnKant(String franode, String tilnode) { if (franode.equals(tilnode)) throw // sjekker om de er like new IllegalArgumentException(franode + " er lik " + tilnode + "!"); Node fra = noder.get(franode); // henter franode if (fra == null) throw new NoSuchElementException(franode + " er ukjent!"); Node til = noder.get(tilnode); // henter tilnode if (til == null) throw new NoSuchElementException(tilnode + " er ukjent!"); if(fra.kanter.contains(til)) throw new IllegalArgumentException("Kanten finnes fra før!"); til.innkanter++; // en ny innkant fra.kanter.add(til); // legger til i kantlisten } public void leggInnKanter(String franode, String... tilnoder) { for (String tilnode : tilnoder) leggInnKant(franode, tilnode); } Programkode 11.1.2 c)
Flg. kode i tillegg til Programkode 11.1.2 b) bygger opp grafen i Figur 11.1.1 b):
graf.leggInnKanter("A", "B","C","D"); // fra A til B,C,D graf.leggInnKanter("B", "A","D","E"); // fra B til A,D,E graf.leggInnKanter("C", "A","D","F"); // fra C til A,D,F graf.leggInnKanter("D", "A","B","C","E","F","G"); // fra D til A,B,C,E,F,G graf.leggInnKanter("E", "B","D","G"); // fra E til B,D,G graf.leggInnKanter("F", "C","D","G"); // fra F til C,D,G graf.leggInnKanter("G", "D","E","F"); // fra G til D,E,F Programkode 11.1.2 d)
Det er den urettede grafen i Figur 11.1.1 b) vi får da det legges inn to kanter for alle nabopar. F.eks. blir kanten fra A til B lagt inn i det første kallet og den fra B til A i det andre.
Flg. metode som hører til klassen Graf,
finner alle kantene fra noden node:
public String kanterFra(String node) { Node fra = noder.get(node); // henter noden if (fra == null) return null; // finnes noden? return fra.kanter.toString(); // listens toString-metode } Programkode 11.1.2 e)
Vi kan sjekke om alt fungerer ved å legge flg. kodebit til slutt i Programkode 11.1.2 d). Fjernes utskriftssetningen nederst i Programkode 11.1.2 b, bør vi få flg. utskrift:
for (String node : graf) // bruker iteratoren i grafen { System.out.println(node + " -> " + graf.kanterFra(node)); } // A -> [B, C, D] // B -> [A, D, E] // osv. Programkode 11.1.2 f)
I Programkode 11.1.2 b) og
Programkode 11.1.2 d) er navnene på nodene og nodene det går kanter til,
lagt direkte inn i koden. Dette fungerer for små testgrafer, men er lite fleksibelt. En bedre løsning
er å ha grafinformasjonen på en fil som graf1.txt (klikk for å se filen).
Hver linje starter med et nodenavn og så kommer navnet på de nodene det går kanter til.
Flg. konstruktør for klassen Graf lager en graf ved hjelp av dataene på en fil:
public Graf(String url) throws IOException { this(); // standardkonstruktøren BufferedReader inn = new BufferedReader // leser fra fil (new InputStreamReader((new URL(url)).openStream())); String linje; while ((linje = inn.readLine()) != null) { String[] navn = linje.split(" "); // deler opp linjen leggInnNode(navn[0]); // noden kommer først for (int i = 1; i < navn.length; i++) // så nodene det går kant til { leggInnNode(navn[i]); // navnet på naboen leggInnKant(navn[0], navn[i]); // legges inn som nabo } } inn.close(); } Programkode 11.1.2 g)
Når leggInnNode() kalles i for-løkken, kan det finnes
en node med det navnet fra før. I så fall returneres false og ingen innlegging.
Hvis filen er tom, opprettes en tom graf.
I flg. eksempel
lages en graf ved hjelp av dataene på filen graf1.txt,
dvs. den urettede grafen i Figur 11.1.1 b).
Hvis du ikke allerede har laget din egen versjon av klassen Graf, finner du en med alle de instansmetodene vi har laget til nå,
her.
Du kan også teste dette med filer på eget område, men
da må du, for å få url-syntaks, ha file:/// som første del av filnavnet. Du må også passe på ha kun ett mellomrom mellom hvert nodenavn.
Bruk gjerne noe annet enn en stor bokstav som nodenavn:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf1.txt"; Graf graf = new Graf(url); Programkode 11.1.2 h)
Urettet graf
Klassen Graf er
i utgangspunktet tilrettelagt for rettede (og uvektede) grafer, men vil også kunne brukes for urettede grafer.
I så fall må en passe på at det enten er ingen kant eller kant begge veier mellom to noder. To nabonoder
må ha kant begge veier. Men det er fort gjort å glemme en kant, dvs. at det er lagt inn kant kun én vei
mellom to noder. Da kan det hende at en algoritme som forventer at grafen er urettet, vil feile.
Det vi trenger er en metode som avgjør om en graf er urettet. For hver kant (X,Y) som grafen har, må det sjekkes at også (Y,X) er kant. Spesielt må en node alltid ha like mange innkanter som utkanter. Tester vi på det først, vil det svært effektivt avsløre de fleste grafer som ikke er urettet. Men dessverre ikke alltid. Ta f.eks. en rettet graf i form av en sirkel. Der vil hver node ha én innkant og én utkant. Vi må derfor gå grundigere til verks:
public boolean erUrettet() // sjekker om grafen er urettet { for (Node p : noder.values()) { if (p.innkanter != p.kanter.size()) return false; } for (Node p : noder.values()) { for (Node q : p.kanter) { if (!q.kanter.contains(p)) return false; } } return true; } Programkode 11.1.2 i)
Uheldigvis er denne metoden relativt kostbar å bruke hvis grafen er urettet. Problemet ligger bl.a. i setningen der det letes etter p i kantlisten til q. La grafen ha n noder og m kanter. Da vil en node ha i gjennomsnitt k = m/n kanter. Hvis grafen er urettet, vil metoden i så fall ha orden n + m k. Men for en «tynn» graf (k liten) blir ikke dette altfor ille.
 |
| Figur 11.1.2 d): En graf |
Figuren over viser en graf som mangler en kant fra C til A for å kunne være urettet.
Flg. kodbit (data for grafen ligger på graf1b.txt) tester metoden.
Metoden rapporterer imidlertid ikke hvor det er feil.
Se Oppgave 17.
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf1b.txt"; Graf graf = new Graf(url); System.out.println(graf.erUrettet()); // Utskrift: false graf.leggInnKant("C", "A"); // en ny kant System.out.println(graf.erUrettet()); // Utskrift: true Programkode 11.1.2 j)
| 1. | Legg inn Programkode 11.1.2 f) i Programkode 11.1.2 h). Hva blr utskriften? | ||
| 2. | På filen graf2.txt ligger data som svarer til den rettede grafen i
Figur 11.1.1 c). Bruk den i
Programkode 11.1.2 h). Sjekk at utskriften blir som den skal.
| ||
| 3. |
graf3.txt med det som trengs for å bygge opp
grafen på figuren over. Den må inneholde
det som konstruktøren i Programkode 11.1.2 g) forventer.
Bruk så den i Programkode 11.1.2 h).
| ||
| 4. | Gjør som i Oppgave 3, men med flg. graf (la filen hete f.eks. graf4.txt):
| ||
| 5. | Lag kode som lager en urettet graf med noder med navn fra A til Z.
Det skal gå en kant mellom A og B, mellom B og C,
mellom C og D osv. Til slutt skal det gå en kant mellom Z og A.
Dvs. en «sirkel av noder». Avslutt med utskrift som i Programkode 11.1.2 f).
| ||
| 6. | Lag kode som lager en urettet graf med noder med navn fra 1 til 10 (oppgitt som tegnstrenger)
og der det går en kant mellom hvert par av forskjellige noder.
Avslutt med utskrift som i Programkode 11.1.2 f).
| ||
| 7. | Lag metoden public int antallNoder() i klassen Graf. Den skal returnere
antallet noder i grafen.
|
| 8. | Lag metoden public boolean equals(Object o) i klassen Node. Den skal returnere
true hvis noden har like navn og false ellers.
|
| 9. | Lag metoden public boolean erIsolert(String nodenavn) i klassen Graf. Den skal returnere
true hvis det det hverken går kanter til noden eller kanter fra noden og false ellers.
|
| 10. | Lag metoden public boolean erKant(String franode, String tilnode) i klassen Graf.
Den skal returnere true hvis franode − tilnode
utgjør en kant og false ellers.
|
| 11. | Lag metoden public int grad(String nodenavn) i klassen Graf. Den
skal returnere graden til noden med navn nodenavn. Graden til en node er antallet
kanter fra noden. Hvis det ikke finnes noen node med det gitte navnet, skal metoden
kaste en NoSuchElementException.
|
| 12. | Lag metoden public void skrivGraf(String filnavn) throws IOException i klassen Graf. Den skal skrive ut informasjon om
grafen til filen med navn filnavn. Filen skal se ut slik som konstruktøren i
Programkode 11.1.2 g) forventer at den skal være.
|
| 13. | Metoden public String kanterFra(String node) i
Programkode 11.1.2 e) returnerer en tegnstreng med nodenavn. Lag
metoden public String[] kantTabellFra(String node) i klassen Graf. Den skal returnere nodenavnene som
en String-tabell. Hvis noden ikke finnes, skal metoden returnere null og hvis den finnes, men ikke har noen kanter, skal
en tom tabell returneres.
|
| 14. | Lag metoden public int antallInnkanter(String node). Den skal returnere
antallet kanter som går til parameternoden.
|
| 15. | Lag metoden public String kanterTil(String node). Den skal returnere en tegnstreng med navnene på de nodene
som har en kant til parameternoden. Lag så metoden public String[] kantTabellTil(String node) som gjør det samme,
men nå med nodenavnene i en String-tabell.
|
| 16. | I Programkode 11.1.2 b) blir iteratoren i klassen Graf
brukt til å skrive ut navnet på alle nodene. Lag metoden
public String[] nodenavn() i klassen Graf. Den skal returnere en String-tabell med nodenavnene.
|
| 17. | Metoden erUrettet() returnerer false hvis
den oppdager en node der antall innkanter er forskjellig fra antall utkanter eller hvis den finner to noder med en kant den ene
veien, men ikke den andre veien. Utvid metoden slik at den rapporterer hva den fant, f.eks. via en tegnstreng (String som returtype).
|
![]() 11.1.3 Matriserepresentasjon av uvektede grafer
11.1.3 Matriserepresentasjon av uvektede grafer
En graf kan representeres ved hjelp av en todimensjonal tabell (eller matrise). Hvis grafen har n noder, vil tabellen
få dimensjon n × n. Hver rad hører til en bestemt node og i raden
er de nodene markert som det går en kant til fra denne noden. Hver kolonne hører også til en bestemt node.
I kolonnen er det markert fra hvilke noder det går en kant til noden. En slik representasjon
kalles en naboskapsmatrise (eng: adjacency matrix).
Matrisene for Figur 11.1.1 b), Figur 11.1.1 c) og Figur 11.1.1 e) er vist i figuren under.
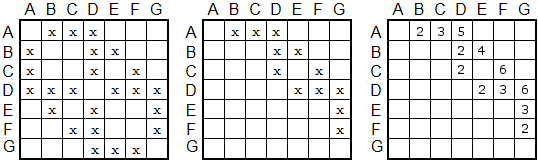 |
| Figur 11.1.3 a): En urettet graf, en rettet graf og en rettet og vektet graf |
Matrisen lengst til venstre representerer grafen i Figur 11.1.1 b).
I den første raden (dvs. raden til A) står det kryss i kolonnene til B, C og D.
Det betyr at det går en kant fra A til de tre nodene. I den første kolonnen (dvs. den til A)
står det kryss i radene til B, C og D. Det betyr at det går en kant fra disse tre
til A. Dette blir riktig siden det er en urettet graf og dermed kant begge veier. Matrisen til en urettet graf blir
derfor symmetrisk.
Den midterste matrisen over representerer grafen i Figur 11.1.1 c). Den er rettet
og dermed blir det færre kryss. I raden til f.eks. D er det tre kryss og de forteller at det går en kant til
E, F og G. Kolonnen til D har også tre kryss og
de forteller at det går en kant til D fra A, B og C.
Matrisen lengst til høyre representerer den vektede grafen i Figur 11.1.1 e). Der står det tall og ikke kryss. Det betyr at tallet både kan ses på som et kryss, dvs. at det er en kant og som lengden (eller vekten) på kanten.
En matrise har heltall som indekser. I Figur 11.1.3 a)
er det imidlertid satt på bokstaver, dvs. nodenavnene. Det er gjort for illustrasjonens skyld.
Det vi egentlig trenger er en navnetabell i tillegg, f.eks. slik:
| A | B | C | D | E | F | G |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Figur 11.1.3 b): Navnetabell | ||||||
Vi slår opp i tabellen vha. navnet og finner indeks. Den brukes så i matrisen. Tabellen over viser at noden D
har indeks 3. Hvis matrisen heter graf, er det dermed
raden graf[3] som inneholder nodene som det går en kant til. Hvis f.eks. graf[3][6]
er avkrysset, så går det en kant fra D til noden som har indeks 6 i navnetabellen, dvs. til G.
Det blir imidlertid ikke fullt så enkelt når dette skal implementeres. Da må vi kunne legge inn én og én node og da ikke nødvendigvis med nodenavnene i sortert rekkefølge. Hvis vi dessuten ønsker å legge en ny node inn i en eksisterende graf, vil den kunne ha et navn som alfabetisk kommer innimellom de andre nodenavnene.
Vi kunne derfor la navnetabellen inneholde nodenavnene i den rekkefølgen de ble lagt inn. Men da får vi et annet problem. Det er
at vi ofte vil ha behov for å lete i navnetabellen og det kan ikke gjøres effektivt hvis den er usortert. Løsningen på dette
er å bruke to navnetabeller og en indekstabell som knytter dem sammen. Ta grafen i
Figur 11.1.1 b) som eksempel. Vi ønsker nå å bygge
den opp ved å legge inn nodene i flg. rekkefølge: A, B, E, G, F, C og D:
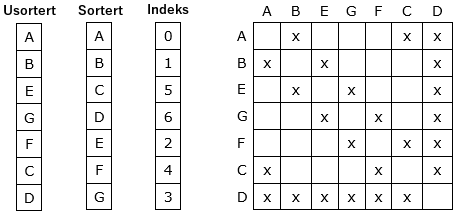 |
| Figur 11.1.3 c): Tabeller og naboskapsmatrise |
Lengst til venstre i figuren over står den (usorterte) tabellen der nodenavnene legges inn fortløpende. Den
samme rekkefølgen er det på radene og kolonnene i grafmatrisen. Fordelen er at hver ny node får tildelt rad
på bunnen og kolonne lengst til høyre i matrisen. Med andre ord ingen endringer i eksisterende matrise.
Neste tabell inneholder nodenavnene sortert. Der må hvert nytt nodenavn plasseres inn på riktig sted.
Indekstabellen knytter de to tabellene sammen. Ta D som eksempel. Den har indeks 3 (0 er første indeks)
i den sorterte tabellen. På indeks 3 i indekstabellen står tallet 6 og det er indeksen til D i den usorterte
tabellen. Ekstrakostnadene er kun arbeidet med å holde tabellene sortert og indeks oppdatert.
Matriserepresentrasjonen er imidlerid kostbar når det gjelder plassbehov. Vi ser i
Figur 11.1.3 c) at matrisen har mange tomme
felter. Hvis en graf har relativt sett få kanter sammenlignet med antall noder, vil matrisen bli slik. Enda «tommere»
vil det kunne bli for en rettet graf siden det der normalt kun er kanter én vei mellom to noder. I de fleste tilfellene
er nok listerepresentasjon best.
Men det er mye interessant kodeteknisk ved matriseteknikken.
Ut fra diskusjonen over bør klassen MGraf (M for matrise) for uvektede grafer ha flg. variabeler
der matrisen graf er av typen boolean. Dvs.
true for «avkrysset» og false ellers:
public final class MGraf { private boolean[][] graf; // grafmatrisen private int antall; // antall noder private String[] navn; // nodenavn - usortert private String[] snavn; // nodenavn - sortert private int[] indeks; // indekser private int[] forrige; // for senere bruk // Konstruktører og metoder skal inn her } // MGraf Programkode 11.1.3 a)
Et naturlig valg er å la MGraf ha to konstruktører. En der vi bestemmer startdimensjonen på tabellene og en
standardkonstruktør (parameterløs) med en fast dimensjon (f.eks. 10):
public MGraf(int dimensjon) // konstruktør { graf = new boolean[dimensjon][dimensjon]; // grafmatrisen antall = 0; // foreløpig ingen noder navn = new String[dimensjon]; // nodenavn - usortert snavn = new String[dimensjon]; // nodenavn - sortert indeks = new int[dimensjon]; // indekstabell } public MGraf() // standardkonstruktør { this(10); } Programkode 11.1.3 b)
En god del metoder kan nå kodes på direkten. F.eks. en som gir oss antallet noder, en som gir tabelldimensjonen, en som gir oss grafens nodenavn sortert og en som som forteller om et nodenavn finnes:
public int antallNoder() // antall noder i grafem { return antall; } public int dimensjon() // dimensjonen til tabellene { return graf.length; } public String[] nodenavn() // navn på alle nodene { return Arrays.copyOf(snavn, antall); } private int finn(String nodenavn) // privat hjelpemetode { return Arrays.binarySearch(snavn, 0, antall, nodenavn); } public boolean nodeFinnes(String nodenavn) // finnes denne noden? { return finn(nodenavn) >= 0; } Programkode 11.1.3 c)
Vi må kunne legge inn en ny node. Dermed trengs metoden leggInnNode() i MGraf.
Da dukker det imidlertid opp et problem. Hva skal vi gjøre hvis datastrukturen er fylt opp, dvs. at antall er lik
dimensjonen til tabellene. Vi kan «nekte» en innlegging, dvs. la metoden returnere false
eller eventuelt kaste et unntak. Alternativt kan vi «utvide» datastrukturen og dermed få
større plass. En utvidelse skjer egentlig ved at det opprettes en ny og større datastruktur og at den gamle kopieres over i den nye.
Dermed kan den gamle strukturen gå til resirkulering. Det siste er imidlertid litt kostbart, men mye mer dynamisk.
Vi velger derfor å «utvide» når det er fullt. I flg. metode bruker vi ferdige kopieringsmetoder. Det er
copyOf() fra klassen Arrays
og arraycopy() fra System:
private void utvid() { int nydimensjon = graf.length == 0 ? 1 : 2*graf.length; // dobler navn = Arrays.copyOf(navn, nydimensjon); // usortert navnetabell snavn = Arrays.copyOf(snavn, nydimensjon); // sortert navnetabell indeks = Arrays.copyOf(indeks, nydimensjon); // indekstabell boolean[][] gammelgraf = graf; graf = new boolean[nydimensjon][nydimensjon]; // grafmatrisen for (int i = 0; i < antall; i++) { System.arraycopy(gammelgraf[i], 0, graf[i], 0, antall); } } Programkode 11.1.3 d)
Nå er vi klare til å lage
metoden leggInnNode(). Den skal først sjekke om noden finnes. Hvis ja, returneres false. Hvis
ikke, legges navnet inn sortert i navnetabellen. Den får samme posisjon der og i indekstabellen. Indekstabellen skal inneholde
indeks til graftabellens tilhørende rad og kolonne. Det betyr at vi ikke behøver å gjøre endringer i graftabellen. Vi
bruker neste ledige rad og kolonne:
public boolean leggInnNode(String nodenavn) // ny node { if (navn == null || nodenavn.length() == 0) throw new IllegalArgumentException("Noden må ha et navn!"); int rad = finn(nodenavn); // raden i den sorterte navnetabellen if (rad >= 0) return false; // finnes fra før! if (antall >= graf.length) utvid(); // sjekker om det er fullt rad = -(rad + 1); // for å få innsettingspunktet for (int i = antall; i > rad; i--) { snavn[i] = snavn[i - 1]; // forskyver i snavn[] indeks[i] = indeks[i - 1]; // forskyver i infeks[] } snavn[rad] = nodenavn; // på rett sortert plass i snavn[] navn[antall] = nodenavn; // på neste ledige plass indeks[rad] = antall; // antall blir indeks i navn[] antall++; // en ny node return true; // vellykket innlegging } Programkode 11.1.3 e)
Det er mulig allerede nå å teste de metodene som er laget. Hvis du ikke allerede har kodet klassen MGraf hos deg selv, kan du finne en versjon med alt vi har laget til nå, her. Nodene legges inn i rekkefølgen A, B, E, G, F, C, D:
MGraf graf = new MGraf(0); // starter med tomme tabeller String[] navn = "ABEGFCD".split(""); // usortert rekkefølge for (String n : navn) graf.leggInnNode(n); // legger inn System.out.println(Arrays.toString(graf.nodenavn())); // [A, B, C, D, E, F, G] Programkode 11.1.3 f)
Grafen ble opprettet med 0 som startdimensjon. Dermed må det ha skjedd flere utvidelser underveis. Fra 0 til 1 og så til 2, 4 og 8. Den sorterte innleggingen ser også ut til å fungere. Dermed ser koden ok ut så langt.
Det er nå rett frem å lage denne klassens versjon av LeggInnKant().
Vi må finne rad- og kolonneindeks til de to nodene og så «krysse av» (sette true) i tilhørende plass i matrisen:
public void leggInnKant(String franode, String tilnode) { if (franode.equals(tilnode)) throw // sjekker om de er like new IllegalArgumentException(franode + " er lik " + tilnode + "!"); int i = finn(franode); // indeks i den sorterte navnetabellen if (i < 0) throw new NoSuchElementException(franode + " er ukjent!"); int j = finn(tilnode); // indeks i den sorterte navnetabellen if (j < 0) throw new NoSuchElementException(tilnode + " er ukjent!"); int rad = indeks[i]; // raden i matrisen int kolonne = indeks[j]; // kolonnen i matrisen if (graf[rad][kolonne]) throw // true for avkrysset new IllegalArgumentException("Kanten finnes fra før!"); graf[rad][kolonne] = true; // krysser av } public void leggInnKanter(String franode, String... tilnoder) { for (String tilnode : tilnoder) leggInnKant(franode, tilnode); } Programkode 11.1.3 g)
Til testing trenger vi en metode som gir oss en nodes kanter.
Informasjonen vi trenger ligger i form av true i den raden som hører til franoden:
public String kanterFra(String nodenavn) { int i = finn(nodenavn); // indeksen i den sorterte navnetabellen if (i < 0) return null; int rad = indeks[i]; // indeksen i den usorterte navnetabellen StringJoiner sj = new StringJoiner(", ", "[", "]"); for (int kolonne = 0; kolonne < antall; kolonne++) if (graf[rad][kolonne]) sj.add(navn[kolonne]); return sj.toString(); } Programkode 11.1.3 h)
Metodene over kan nå testes på samme måte som det ble gjort for de tilsvarende metodene i klassen
Graf. Bruk Programkode 11.1.3 f) der
MGraf inngår og i tillegg det fra Programkode 11.1.2 d).
I tillegg må du ha kode som ved hjelp av metoden kanterFra()
lager utskrift. Men siden klassen MGraf ikke er itererbar (har ikke en iterator), vil ikke
Programkode11.1.2 f) virke for MGraf.
Bruk isteden metoden nodeNavn().
Hvis du ikke allerede har laget din egen versjon av MGraf,
finner du en med alle de instansmetodene vi har laget til nå, her.
En ulempe med matriserepresentasjonen er at det brukes mye unødvendig plass for «tynne» grafer,
dvs. grafer med relativt sett få kanter. I slike tilfeller vil også mange av metodene bli ineffektive.
Ta metoden kanterFra() som eksempel. Der vil letingen
alltid gå bortover hele raden (orden n) også hvis tilhørende node har ingen eller få utkanter.
Det er tungvint å bygge opp en graf direkte i koden. Det er enklere å hente informasjonen fra en fil. Da kan vi gjøre på samme
måte som for klassen Graf, dvs. ha en konstruktør som har et filnavn på url-form som parameter. Vi kan bruke
den i Graf (Programkode 11.1.2 g)
hvis vi skifter navn fra Graf til MGraf. Med den kan flg. kode kjøres:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf1.txt"; MGraf graf = new MGraf(url); for (String n : graf.nodenavn()) System.out.println(n + " -> " + graf.kanterFra(n)); Programkode 11.1.3 i)
| 1. | Flytt klassen MGraf over til ditt system. På
filen MGraf ligger klassen med de metodene vi har laget så langt.
|
| 2. | Lag testprogram. Bruk f.eks. Programkode 11.1.3 f)
og så det fra Programkode 11.1.2 d).
I tillegg må du ha kode som ved hjelp av metoden kanterFra()
lager utskrift. Men siden klassen MGraf ikke er itererbar (har ikke en iterator), vil ikke
Programkode11.1.2 f) virke for MGraf.
Bruk isteden metoden nodeNavn().
|
| 3. | Sjekk at Programkode 11.1.3 i) virker.
Prøv også med graf2.txt.
|
| 4. | Flg. kode vil ikke virke hvis graf er en instans av klassen MGraf:
for (String n : graf) { System.out.println(n + " -> " + graf.kanterFra(n)); }Skal dette virke må MGraf implementere Iterable<String>.
Se klassen Graf. Gjør det som trengs for at
MGraf skal bli «itererbar». Bruk så dette i
Programkode11.1.3 i).
|
| 5. | Lag metoden public void skrivGraf(String filnavn) throws IOException i klassen MGraf.
Se Oppgave 12 i Avsnitt 11.1.2.
|
| 6. |
I Oppgavene 9, 10, 11, 13, 14 i Avsnitt 11.1.2 ble det bedt
om en serie metoder for klassen Graf. Lag de samme metodene for glassen MGraf.
|
| 7. |
Metoden erUrettet() tester om en graf er urettet eller ikke.
Den er laget for klassen Graf. Hvis bruker en matriserepresentasjon
(klassen MGraf), svarer dette til å sjekke om matrisen er symmetrisk. Til det er en algoritme av
orden n² det beste mulige. Lag metoden erUrettet() for klassen MGraf.
|
![]() 11.1.4 Traverseringer
11.1.4 Traverseringer
Traversering handler om å kunne gå fra node til node ved å følge kanter. En oppgave kan være å finne mulige veier
mellom to noder og dermed også korteste vei eller å avgjøre om grafen har sykler. Det er mange forskjellige oppgaver
der traversering blir benyttet.
Vi ser først på traverseringer som starter i en oppgitt node og som derfra går innom de nodene som det er mulig å komme til ved
å følge kanter. Da er det to vanlige teknikker som brukes: 1) dybde-først og 2) bredde-først.
Vi starter med dybde-først og tar utgangspunkt i den rettede grafen i
Figur 11.1.1 c). Dens naboskapsliste står
Figur 11.1.2 c). Vi starter med å «besøke» A
(dvs. A er startnoden).
Dybde-først-traversering
For hver node vi kommer til, skal
den markeres som «besøkt». Det gjør vi ved å endre fargen på navnet fra hvit til svart:
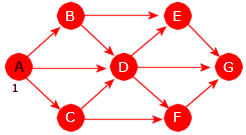 |
| Figur 11.1.4 a) - Starten på dybde-først |
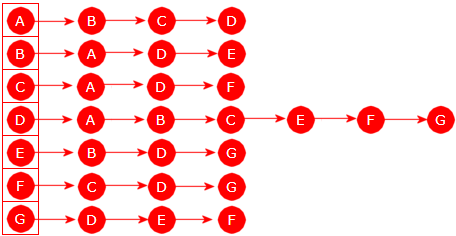
Det går en kant fra A til (i alfabetisk rekkefølge) B, C og D. Det er vanlig å snakke om dem som den første, andre og tredje, men det er ingen regel om hva som skal være rekkefølgen. Det blir bestemt av den datstrukturen vi bruker som grafrepresentasjon. Men her velger vi alfabetisk rekkefølge. Det betyr at den første av de nodene som det går en kant til (fra A) er B, osv. I dybde-først går vi så dit:
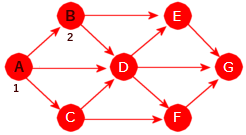 |
| Figur 11.1.4 b) - A og B er besøkt |
Det går kanter fra B til D og E. Da går vi videre til den første av dem, dvs. til D:
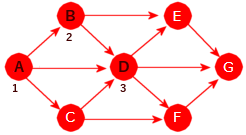 |
| Figur 11.1.4 c) - A, B og D er besøkt |
Fra D går det kanter til E, F og G. Vi går til den første (dvs. E) og derfra er det kun én mulighet, dvs. til G. Fra G kommer vi ikke videre:
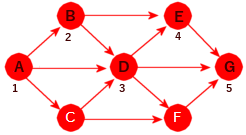 |
| Figur 11.1.4 d) - A, B, D, E og G er besøkt |
Siden vi ikke kommer videre fra G, må vi «trekker oss tilbake» langs veien vi har gått til der det står igjen flere muligheter. Det er tilbake til D. Der har vi igjen å gå først til F og så G. Vi går til F. Fra F går det kun kant til G, men der har vi vært. Den siste muligheten fra D er G, men der har vi jo vært. Dermed:
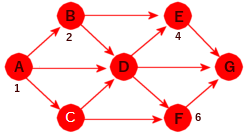 |
| Figur 11.1.4 e) - A, B, D, E, G og F er besøkt |
Nå har vi prøvd alle muligheter fra D. Da «trekker vi oss igjen tilbake». Først til B. Der står det igjen å gå til E, men der har vi vært. Vi «trekker oss tilbake» til A. Der står mulighetene C og D igjen. Vi går først til C, men ikke videre siden de to som kommer etter C allerede er besøkt. Den siste muligheten fra A er å gå til D, men der har vi vært. Dermed er vi ferdig! I figuren under er nodene nummerert i besøksrekkefølgen, dvs. A, B, D, E, G, F og C.
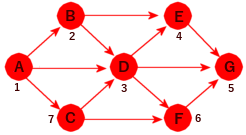 |
| Figur 11.1.4 f) - A, B, D, E, G, F, C |
En implementasjon av dybde-først-teknikken (som er beskrevet ovenfor) er selvfølgelig avhengig
av hva slag grafstruktur vi bruker. Her skal vi først implementere den i klassen Graf som
bruker naboskapslister.
Hvis du ikke allerede har den i ditt system, er dette siste versjon:
Graf. Den inneholder det
som er laget i Avsnitt 11.1.2 og i
avsnittets oppgaver. Hvordan teknikken skal kodes
i klassen MGraf (der det brukes en naboskapsmatrise) tas opp i
siste del av dette avsnittet.
Når en algoritme skal kodes vil en ofte ha valget mellom å bruke rekursjon eller lage en iterativ løsning.
Men teknikken dybde-først er nærmest rekursiv i sin natur. Vi bruker derfor rekursjon. Da
lager vi en privat rekursiv metode og en offentlig metode som setter den rekursive metoden i gang. Metoden
er avhengig av at variabelen besøkt i utgangspunktet er false i alle noder.
Hvis vi ønsker å kjøre metoden flere ganger på samme graf, må grafen «nullstilles» for hver gang.
Vi lager først en metode som gjør det:
public void nullstill() { for (Node p : noder.values()) { p.besøkt = false; p.forrige = null; } } Programkode 11.1.4 a)
Når en node «besøkes» kan vi utføre en «oppgave» med en gang eller vi kan vente til vi er ferdige
med dens etterfølgere. Dvs. en preoppgave eller en postoppgave
(se Oppgave 2).
Hva oppgaven går ut på bestemmes senere vha. funksjonsgrensesnittet
Consumer:
private void dybdeFørstPre(Node p, Consumer<String> oppgave) { p.besøkt = true; oppgave.accept(p.navn); // preoppgave - accept() er eneste metode i Consumer for (Node q : p.kanter) // tar alle kantene fra p { if (!q.besøkt) dybdeFørstPre(q, oppgave); // rekursivt kall } } Programkode 11.1.4 b)
Variabelen besøkt oppdateres og vi ser at det kun er de direkte etterfølgerne (de som det går en kant til)
som ikke er besøkt, som vi går videre til. Hvis noden p ikke har direkte etterfølgere (kantlisten er tom), er metoden ferdig.
For at dybde-først-traverseringen skal virke må vi ha en metode som setter rekursjonen i gang. Den har en startnode og en oppgave
av typen Consumer som parametre:
public void dybdeFørstPretraversering(String startnode, Consumer<String> oppgave) { Node p = noder.get(startnode); if (p == null) throw new IllegalArgumentException(startnode + " er ukjent!"); dybdeFørstPre(p, oppgave); // kaller den rekursive metoden } Programkode 11.1.4 c)
Vi kan teste dette ved å bruke filen graf2.txt (klikk for å se filen) som input. Da får vi
den rettede grafen i eksemplet over. Vi bruker konsollutskrift som oppgave, dvs. vi legger inn et lambda-utrykk for det. Hvis
alle metodene er lagt inn i klassen Graf
(du må ha import java.util.function.Consumer; øverst), vil flg. kode virke:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); graf.dybdeFørstPretraversering("A", x -> System.out.print(x + " ")); // Utskrift: A B D E G F C Programkode 11.1.4 d)
I koden over brukes lambda-uttrykket x -> System.out.print(x + " ") som oppgave. Hvis en vil ha en mer
«innpakket» utskrift, kunne en bruke en StringJoiner til å bygge opp en tegnstreng som så skrives ut. Dette
kan f.eks. gjøres slik:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); StringJoiner sj = new StringJoiner(", ", "[", "]"); graf.dybdeFørstPretraversering("A", sj::add); System.out.println(sj.toString()); // Utskrift: [A, B, D, E, G, F, C] Programkode 11.1.4 e)
Oppgave 1 handler om å teste dette på andre grafer.
Oppgave 2 tar opp posttraversering.
Bredde-først-traversering I dybde-først gikk vi så «dypt» vi kunne i grafen før vi
«trakk oss tilbake» for å kunne prøve resten av kantene ut fra en node.
I bredde-først går vi i «bredden» før dybden. Vi bruker samme graf som sist og starter med å besøke noden A:
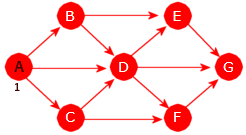 |
| Figur 11.1.4 g) - Starten på bredde-først |
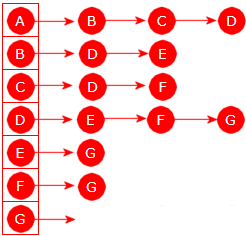
Fra A går det kanter til B, C og D. De tre nodene utgjør første «bredde». En annen måte å si det på er at første «bredde» er de nodene som det går en kant til fra A. Vi besøker dem fortløpende (alfabetisk rekkefølge) − først B, så C og til slutt D:
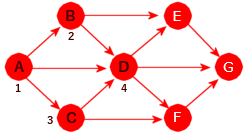 |
| Figur 11.1.4 h) - De fire første |
Andre «bredde» består av de nodene som det går en vei til med to kanter fra A. I alfabetisk rekkefølge er det D, E, F og G. Men D har vi allerede vært innom. Derfor er det E, F og G vi besøker. Flere er det ikke. Det gir:
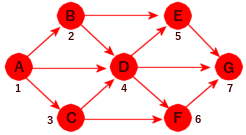 |
| Figur 11.1.4 i) - Alle er besøkt |
Hadde grafen vært et tre med A som rot, ville bredde-først-traversering vært det samme som
nivåtraversering.
En kø-teknikk vil derfor virke. En besøkt node legges i køen:
public void breddeFørstTraversering(String startnode, Consumer<String> oppgave) { Node p = noder.get(startnode); // henter startnoden if (p == null) throw new IllegalArgumentException(startnode + " er ukjent!"); Queue<Node> kø = new ArrayDeque<>(); // oppretter en nodekø p.besøkt = true; // noden p er den første vi besøker kø.offer(p); // legger noden p i køen while (!kø.isEmpty()) // så lenge køen ikke er tom { p = kø.poll(); // tar ut en node fra køen oppgave.accept(p.navn); // utfører oppgaven for (Node q : p.kanter) // nodene det går en kant til { if (!q.besøkt) // denne er ikke besøkt { q.besøkt = true; // nå er den besøkt kø.offer(q); // legger noden i køen } } } } Programkode 11.1.4 f)
Bytter vi dybde-først med bredde-først i
Programkode 11.1.4 e), får vi flg. testprogram
(husk å nullstille
hvis du kjører begge traverseringene på samme graf):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); StringJoiner sj = new StringJoiner(", ", "[", "]"); graf.breddeFørstTraversering("A", sj::add); System.out.println(sj.toString()); // Utskrift: [A, B, C, D, E, F, G] Programkode 11.1.4 g)
I Oppgave 3 blir du bedt om å teste dette på andre grafer.
Traversering i MGaf Metoden dybdeFørstPre() for klassen
MGraf blir nærmest en kopi av
Programkode 11.1.4 b) og
c) og så ta hensyn til den interne strukturen MGraf har.
For å markere at en node er besøkt bruker vi en boolsk hjelpetabell:
private void // rekursiv hjelpemetode dybdeFørstPre(int i, boolean[] besøkt, Consumer<String> oppgave) { besøkt[i] = true; // noden er besøkt oppgave.accept(navn[i]); // oppgaven utføres for (int j = 0; j < antall; j++) // kantene til noden { if (graf[i][j] && !besøkt[j]) dybdeFørstPre(j, besøkt, oppgave); // rekursivt kall } } Programkode 11.1.4 h)
Vi trenger også her en offentlig metode som setter rekursjonen i gang. Der opprettes en boolsk hjelpetabell med
navn besøkt:
public void dybdeFørstPretraversering(String startnode, Consumer<String> oppgave) { int i = finn(startnode); // indeks i den sorterte navnetabellen if (i < 0) throw new IllegalArgumentException(startnode + " er ukjent!"); i = indeks[i]; // indeks i matrisen boolean besøkt[] = new boolean[antall]; // hjelpetabell dybdeFørstPre(i, besøkt, oppgave); // kaller den rekursive metoden } Programkode 11.1.4 i)
For å teste at dette virker kan en bytte ut Graf med MGraf i Programkode 11.1.4 e).
Resten skal være som det er. Også metoden breddeFørstTraversering() for klassen
Graf kan brukes som utgangspunkt for å lage en versjon i klassen MGraf.
Se Oppgave 5 - 7.
| 1. | a) I utledningen av dybde-først-traversering ble den rettede grafen i
Figur 11.1.1 c) brukt som eksempel.
Finn ut i hvilken rekkefølge nodene vil bli besøkt i dybde-først-traversering (med A som startnode) i den urettede grafen i
Figur 11.1.1 b). Gjør det slik at de nodene det
går en kant til behandles i afabetisk rekkefølge. Du får en test på svaret ditt hvis du kjører
Programkode 11.1.4 d) med filen
graf1.txt. Hvis du ikke allerede har klassen Graf
i ditt system, finner du klassen med alle metodene her.
|
b) Gjør som i a), men med grafen i
Figur 11.1.2 d).
Test så med filen
graf3.txt.
| |
c) Som i a), men med grafen i
Figur 11.1.2 e).
Test så med filen
graf4.txt.
| |
| 2. | a) Lag dybdeFørstPost() i Graf. Den skal være som
Programkode 11.1.4 b), men
accept-setningen skal stå etter for-løkken. Husk å skifte navn også
i det rekursive kallet. Lag så dybdeFørstPosttraversering() maken til den i
Programkode 11.1.4 c), men nå med et
kall på dybdeFørstPost().
|
b) Gjør som i Oppgave 1 a), b) og c) med post-traversering.
Bruk Programkode 11.1.4 e)
som testprogram.
| |
| c) Lag en Consumer slik at du får utskriften motsatt vei. | |
| 3. | Gjør som i Oppgave 1 a), b) og c) med bredde-først-traversering.
Bruk Programkode 11.1.4 g)
som testprogram.
|
| 4. | I Programkode 11.1.4 d)
og e) blir nodenavnene skrevet til konsollet ved hjelp
av lambda-utrykk (en Consumer). Lag det slik at navnene først legges i en liste (ArrayList eller
LinkedList) og så at listens innhold skrives ut.
|
| 5. | Lag kode som tester dybde-først-traversering
(Programkode 11.1.4 h
og i ) i MGraf.
Hvis du ikke allerede har klassen og dens metoder
i ditt system, finner du den siste versjonen av den (med alle metodene fra teksten og fra oppgavene) her.
|
| 6. | Lag posttraversering for MGraf. Se Oppgave 2 når det gjelder det samme for Graf.
|
| 7. | Lag bredde-først-traversering i MGraf. Ta utgangspunkt i
den i
Graf og gjør de endringene som trengs for MGraf.
Du vil trenge en boolsk tabell besøkt til å markere at en node er besøkt. Se
dybdeFørstTraversering() for MGraf.
I denne klassen trengs foreløpig ingen nullstill-metode siden besøkt
er en lokal tabell.
Test dette ved å bruke MGraf
i Programkode 11.1.4 g). Du bør få samme resultat.
|
![]() 11.1.5 Korteste vei i en uvektet graf
11.1.5 Korteste vei i en uvektet graf
En vei i en graf består av en start- og en sluttnode
og av nodene på veien. Den er med andre ord en oppramsing x0 ,
x1 , x2 , . . . , xn
der x0 er startnoden og xn sluttnoden og der det går en kant fra
xi til xi+1 for
i fra 0 til n - 1.
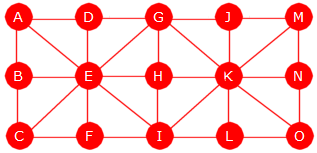 |
| Figur 11.1.5 a): En graf - 15 noder og 30 kanter |
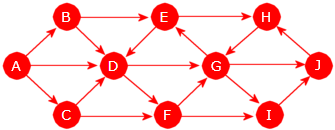
Så sant det finnes en vei fra en node X til en node Y, må det også finnes en korteste vei eller eventuelt flere korteste veier. Ta som eksempel at vi skal finne korteste vei fra A til en av de andre nodene i grafen i Figur 11.1.5 a) over. Algoritmen er ganske enkel. Vi gjør rett og slett en bredde-først-traversering. Når vi besøker en node for første gang, noterer vi hvilken node vi kom fra. Ved å gå motsatt vei (til startnoden) får vi korteste vei. Dette gir korteste vei siden bredde-først-traverseringen beveger seg vekk fra startnoden men én kant om gangen.
Vi lager først en metode for dette i klassen Graf
(se Oppgave 5 for MGraf).
Der har nodene en forrige-referanse og den vi skal bruke til å finne korteste vei (men i motsatt rekkefølge).
Metoden finner korteste vei fra startnoden til samtlige andre noder som det går en vei til. Dette er så og si samme kode
som i Programkode 11.1.4 f):
public void kortestVeiFra(String node) { Node p = noder.get(node); // henter startnoden if (p == null) throw new IllegalArgumentException(node + " er ukjent!"); Queue<Node> kø = new ArrayDeque<>(); // oppretter en kø p.besøkt = true; // p er den første vi besøker kø.offer(p); // legger p i køen while (!kø.isEmpty()) // så lenge køen ikke er tom { p = kø.poll(); // tar ut en node fra køen for (Node q : p.kanter) // kantene fra p { if (!q.besøkt) // denne er ikke besøkt { q.besøkt = true; // nå er den besøkt q.forrige = p; // vi kom dit fra p kø.offer(q); // legger noden i køen } } } } Programkode 11.1.5 a)
Vi finner den korteste veien fra en node tilbake til startnoden vha. referansen forrige. Hvis vi f.eks.
legger nodene på en stakk og så tar dem ut, får vi dem i rett rekkefølge:
public String veiTil(String node) // returnerer veien i rett rekkefølge { Node p = noder.get(node); if (p == null) throw new IllegalArgumentException(node + " er ukjent!"); if (p.forrige == null) return "[]"; // ingen vei til p Deque<String> stakk = new ArrayDeque<>(); // bruker en deque som stakk while (p != null) { stakk.push(p.navn); // legger nodenavnet på stakken p = p.forrige; // går til forrige node på veien } return stakk.toString(); } Programkode 11.1.5 b)
Flg. programbit finner korteste vei fra A til alle de andre nodene i grafen i Figur 11.1.5 a). Legg merke til at det er flere korteste veier. Her finner vi én av dem:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf3.txt"; Graf graf = new Graf(url); graf.kortestVeiFra("A"); // fra A til O System.out.println(graf.veiTil("O")); // Utskrift: [A, D, G, K, O] Programkode 11.1.5 c)
Det er mange korteste veier fra A til O i grafen i Figur 11.1.5 a).
[A, D, G, K, O] er en av dem. En versjon av kortestVeiFra() for klassen MGraf kan ta utgangspunkt i
dens breddeFørstTraversering(). Se Oppgave 5 i
Avsnitt 11.1.4 og Oppgave 5 nedenfor.
| 1. | Test at Programkode 11.1.5 c). Hvis du ikke allerede har
klassen Graf med metodene for kortest vei i ditt system, så finner du en full versjon
her.
|
| 2. | Programkode 11.1.5 c) gir veien til én node. Gjør om koden
slik at korteste vei fra A til samtlige noder blir skrevet ut - en linje for hver node. Gjør om veiTil() slik
den f.eks. for veien fra A til O gir: [A, D, G, K, O], 4. Dvs. veilengden i tillegg.
|
| 3. | På filen graf6.txt ligger data for en graf. Lag en tegning
som viser hvordan grafen ser ut. Bruk så det du laget i Oppgave 1 og 2
på den grafen. Sjekk at svarene stemmer med det du ser av tegningen.
|
| 4. | Programkode 11.1.5 a) gir korteste vei
fra en startnode til alle noder som det går en vei til. Hvis målet kun er å finne korteste vei mellom en franode og en
tilnode, gjøres litt unødvendig arbeid. Metoden kunne stoppe når den har kommet til rett node.
Lag public String kortestVei(String franode, String tilnode) slik at den gjør det.
|
| 5. | Lag metodene i Programkode a)
og b) i klassen MGraf. Hvis du ikke har den i ditt
system, finner du siste versjon her. Lag også metoden i Oppgave 4 for MGraf.
|
![]() 11.1.6 Korteste vei i en labyrint
11.1.6 Korteste vei i en labyrint
I Avsnitt 1.5.10 brukte vi rekursive teknikker for
å finne veier (og korteste vei) i en labyrint. Labyrinten i Figur 11.1.6 a) under ble brukt som eksempel:
 |
| Figur 11.1.6 a) : En labyrint med 20 rader og 20 kolonner |
En labyrint kan ses på som en uvektet graf der
hver «åpen» rute er en node. Fra hver rute går det kanter til maksimalt fire andre ruter (til høyre,
nedover, til venstre eller oppover). Vi kan bruke samme idé som i
Avsnitt 11.1.5.
Klassen Labyrint
inneholder det som ble laget der, bl.a. en rekursiv metode som kun fant lengden på kortest vei. Nå er det i tillegg satt opp fire konstanter - en for hver retning ut fra en rute.
I Graf har hver node en forrige-peker
Isteden kan vi, når vi kommer til en rute, markere i den hvilken retning som bragte oss dit.
Det mest effektive er en bredde-først traversering (vha. en kø). Da må nodene som vi skal til, legges i køen. I en heltallskø (int/Integer) kan vi, for å spare på plassen, la rutens i-koordinat utgjøre de 16 første og dens j-koordinat de 16 siste bitene i en int. Når vi tar fra køen må vi separere de to delene.
I utgangspunktet inneholder rutene enten tallet 0 (åpen rute) eller tallet 1 (en vegg). Hvis vi kommer
til en åpen rute f.eks. ved å gå til høyre, legger vi inn et tall (konstanten HØYRE) i
ruten. For de andre retningene blir det tilsvarende. Dermed kan vi finne veien tilbake. Hvis f.eks.
en rute inneholder HØYRE, går vi til venstre siden det er der veien kommer fra. Da passer
vi samtidig på å sette et «kryss» i ruten for å markere at ruten hører til den korteste veien.
Konstantene står øverst på Labyrint. Flg. metode
hører til den klassen:
public static int kortestVei(byte[][] a, int iinn, int jinn, int iut, int jut) { int m = a.length, n = a[0].length; // m rader, n kolonner Queue<Integer> q = new ArrayDeque<>(); // en heltallskø q.offer((iinn << 16) | jinn); // de 16 første og 16 siste bitene while (!q.isEmpty()) // så lenge som køen ikke er tom { int koordinater = q.poll(); int i = koordinater >> 16, j = koordinater & ((1 << 16) - 1); if (i == iut && j == jut) break; // dette er utgangen if (j + 1 < n && a[i][j+1] == 0) // til høyre { a[i][j+1] = HØYRE; // markerer retningen q.offer(i << 16 | (j + 1)); // legger inn koordinatene } if (i + 1 < m && a[i+1][j] == 0) // nedover { a[i+1][j] = NED; // markerer retningen q.offer((i + 1) << 16 | j); // legger inn koordinatene } if (j > 0 && a[i][j-1] == 0) // til venstre { a[i][j-1] = VENSTRE; // markerer retningen q.offer(i << 16 | (j - 1)); // legger inn koordinatene } if (i > 0 && a[i-1][j] == 0) // oppover { a[i-1][j] = OPP; // markerer retningen q.offer((i - 1) << 16 | j); // legger inn koordinatene } } if (a[iut][jut] == ÅPEN) return 0; // ingen vei til utgangen int i = iut, j = jut, veilengde = 0; // starter i utgangen while (i != iinn || j != jinn) // går tilbake til inngangen { veilengde++; int retning = a[i][j]; // retningen hit a[i][j] = KRYSS; // del av veien if (retning == HØYRE) j--; // venstre er motsatt vei else if (retning == NED) i--; // opp er motsatt vei else if (retning == VENSTRE) j++; // høyre er motsatt vei else i++; // ned er motsatt vei } a[i][j] = KRYSS; // del av veien return veilengde; // lengden på veien } Programkode 11.1.6 a)
Vi kan teste Programkode 11.1.6 a) på labyrinten i
Figur 11.1.6 a). Hvis du har klassen
Labyrint i ditt system og har lagt inn Programkode 11.1.6 a)
i den klassen, vil flg. kode virke. Resultatet finner du på utskriftsfilen labyrint.html under «gjeldende område»
på ditt system. Men du kan selv bestemme hvor den skal havne ved å oppgi full vei. Legg også merke til at veilengden blir
som i en graf, dvs. én mindre enn antall ruter/noder på veien:
public static void main(String[] args) throws IOException { String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/5/labyrint.txt"; byte[][] a = Labyrint.hentLabyrint(url); int veilengde = Labyrint.kortestVei(a, 0, 0, 19, 19); if (veilengde < 1) System.out.println("Ingen vei!"); else { System.out.println("Lengden på kortest vei: " + veilengde); Labyrint.tilHTML(a,"labyrint.html"); } } Programkode 11.1.6 b)
| 1. | Flytt klassen Labyrint over i ditt system,
legg Programkode 11.1.6 a) inn i klassen
og sjekk at Programkode 11.1.6 b) virker.
Utskriften som er en html-fil, kan du selv velge navn på og dirigere dit du vil ha den. Du kan få nye veier ved
å ta vekk vegger eller legge inn nye vegger. Hva blir resultatet hvis du f.eks. tar vekk veggen i rute (15,8)? Dvs.
sett inn setningen a[15][8] = 0; i koden rett etter der labyrinten er lest inn. Hva blir
resultatet hvis du setter inn en vegg (f.eks. i rute (14,11)) slik at det ikke finnes noen vei?
|
| 2. | Programkode 11.1.6 a) er for lite robust. Det foretas
f.eks. ingen sjekk på at inngangen (koordinatene iinn og jinn) er på ytterkanten
av labyrinten og representerer en åpen rute. Det sammen gjelder utgangen (iut og jut).
Legg inn kode som sjekker at inngangen og utgangen er «lovlige». Hvis ikke skal metoden kaste et passelig unntak.
|
| 3. | Lag egne labyrinter. Du kan opprette byte-tabellen direkte i
Programkode 11.1.6 b) (og gi den innhold)
eller du kan lage filer av samme type som
labyrint.txt. Labyrinten behøver ikke være
kvadratisk. Hvis du lager en slik fil, må du oppgi den på url-form i
Programkode 11.1.6 b), dvs. som
"file:///c:/algdat/labyrint.txt" hvis den for eksempel ligger under c:/algdat.
|
| 4. | Lag metoden public static void skrivLabyrint(String filnavn, byte[][] a) throws IOException
i klassen Labyrint. Den
skal skrive labyrinten ut på fil. Filens innhold skal være slik metoden hentLabyrint() forventer.
|
| 5. | Det er mulig å gjøre om labyrinten i
Figur 11.1.6 a) til samme datastruktur som i
Programkode 11.1.2 a). Da kan teknikken fra
Avsnitt 11.1.5 brukes til å finne korteste vei. Lag kode som
gjør om labyrinten til en urettet graf. En åpen rute blir da en node og som nodenavn kan en f.eks. velge kordinatene. Dvs. ruten
(i,j) får navnet "i,j".
|
![]() 11.1.7 Spenntrær
11.1.7 Spenntrær
La G være en urettet graf. En subgraf (eller en delgraf) S av G er en graf som består av en eller flere
noder fra G og med kanter som også er kanter i G. Figuren under viser en urettet graf med 7 noder og
12 kanter:
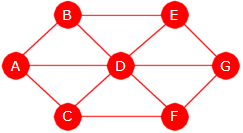 |
| Figur 11.1.7 a): En urettet graf |
I de to grafene under utgjør de svarte nodene og svarte kantene subgrafer til grafen over:
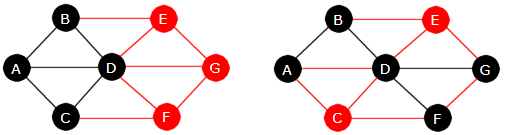 |
| Figur 11.1.7 b): To subgrafer |
Et tre er en urettet og sammenhengende graf uten sykler.
En graf er sammenhengende hvis det går en vei mellom ethvert par av forskjellige noder.
Husk at en sykel er en vei som går fra en node tilbake til den samme noden og som inneholder minst
én kant og der alle kantene er forskjellige.
Dermed vil det i et tre finnes én og bare én vei mellom to noder.
Vi ser at subgrafen (de svarte nodene og kantene) i
grafen til venstre i figuren over, ikke er et tre. Der er det mange sykler.
Men subgrafen til høyre er et tre.
En subgraf T til en urettet og sammengende graf G kalles et spenntre
(eng: a spanning tree) hvis den er et tre og inneholder alle nodene i G.
En graf har normalt mange spenntrær. Figuren under viser et spenntre (de svarte nodene og kantene) til
grafen i Figur 11.1.7 a):
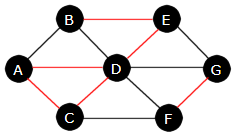 |
| Figur 11.1.7 c): Et spenntre |
Det er forholdsvis enkelt å finne et spenntre til en urettet og sammenhengende graf. En kan bruke en
dybde-først eller en bredde-først-algoritme. Med dybde-først blir det på samme måte som
for dybde-først-traverseringen i
Programkode 11.1.4 b)
og 11.1.4 c). Flg. metoder (en offentlig
og en privat og rekursiv) returnerer en graf som utgjør et spenntre for en gitt urettet og
sammenhengende graf:
public Graf spenntre(String navn) // hører til klassen Graf { Node p = noder.get(navn); if (p == null) throw new IllegalArgumentException(navn + " er ukjent!"); Graf tre = new Graf(); // oppretter en tom graf tre.leggInnNode(navn); // legger inn startnoden spenntre(p, tre); // kaller den rekursive metoden return tre; // returnerer spenntreet } private void spenntre(Node p, Graf tre) // hører til klassen Graf { p.besøkt = true; // denne er ferdig for (Node q : p.kanter) // alle kantene fra p { if (!q.besøkt) // hopper over de som er ferdig { tre.leggInnNode(q.navn); // legger inn en node tre.leggInnKant(p.navn, q.navn); // kant den ene veien tre.leggInnKant(q.navn, p.navn); // kant den andre veien spenntre(q, tre); } } } Programkode 11.1.7 a)
Vi kan teste dette på grafen i Figur 11.1.7 a)
og med A som startnode. Grafen har mange forskjellige spenntrer og vi får nå ett av dem:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf1.txt"; Graf graf = new Graf(url); // oppretter grafen Graf spenntre = graf.spenntre("A"); // starter i A for (String node : spenntre) // bruker iteratoren i grafen { System.out.print(node + " -> " + spenntre.kanterFra(node) + " "); } // A -> [B] B -> [A, D] C -> [D, F] D -> [B, C] E -> [G] F -> [C, G] G -> [F, E] Programkode 11.1.7 b)
Dette svarer til grafen/spenntreet under til venstre. Hadde vi isteden brukt f.eks. D som startnode, ville vi ha fått spenntreet under til høyre:
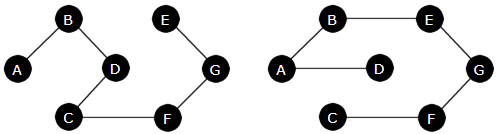 |
| Figur 11.1.7 d): To spenntrær for grafen i Figur 11.1.7 a) |
Det er også mulig å finne spenntrær ved hjelp av bredde-først. Da blir koden av samme slag som den for
bredde-først-traversering i Programkode 11.1.4 f).
Se Oppgave 3.
Disse teknikkene (dybde-først og bredde-først) kan også brukes i klassen
MGraf, dvs. den klassen
der grafen er implementert ved hjelp av en naboskapsmatrise.
Se Oppgave 4.
| 1. | Sjekk at Programkode 11.1.7 b)
virker som oppgitt. Prøv med flere startnoder enn A og D.
|
| 2. | Metoden i Programkode 11.1.7 a) finner
et spenntre under forutsetning av at grafen er sammenhengende. Hva skjer hvis det ikke er tilfellet. Legg
f.eks. en ny node med navn H inn i grafen i
Programkode 11.1.7 b). Kjør
så programmet.
|
| 3. | Lag metoden Graf spenntre(String navn) i
klassen Graf. Den skal returnere et spenntre til en urettet og sammenhengende graf slik som
metoden i Programkode 11.1.7 a).
Hvis klassen skal inneholde begge versjonene, bør kanskje den førte hete spenntre1 og den som skal lages her
spenntre2. Bruk
Programkode 11.1.4 f) som
utgangspunkt.
|
| 4. | Lag metoden MGraf spenntre(String navn) i
klassen MGraf. Se Avsnitt 11.1.3.
Bruk en dybde-først-teknikk og ta utgangspunkt i
Programkode 11.1.4 h)
og 11.1.4 i).
|
| 5. | Gjør som i Oppgave 4, men bruk en bredde-først-teknikk. Ta utgangspunkt i det som
er løsningen på Oppgave 7 i Avsnitt 11.1.4.
|
![]() 11.1.8 Asykliske grafer
11.1.8 Asykliske grafer
En sykel (eng: circuit) er en enkel vei
som starter i en node X, inneholder minst én kant og som ender der den startet (dvs. i X).
En graf uten sykler kalles asyklisk (eng: asyclic). En rettet asyklisk graf kalles på engelsk
en DAG (Directed Asyclic Graph).
I de algoritmene vi har studert til nå, har det ikke hatt betydning om grafen er asyklisk eller ikke. Det gjelder f.eks. traverseringer, korteste vei og spenntrær. Men det er situasjoner der grafen må være asyklisk (f.eks. i forbindelse med topologsik sortering). I dette avsnittet skal vi se på algoritmer som avgjør om en graf (rettet eller urettet) har en sykel.
Urettede grafer
En urettet, sammenhengende og asyklisk graf kalles et tre. Det betyr at hvis grafen er
sammenhengende og har en sykel, så er det ikke et tre. Det gjør det forholdsvis enkelt å lage en algoritme som avslører
om en sammenhengende graf har en sykel.
Vi kan starte i en hvilken som helst node og bruke en dybde-først-teknikk. Så fort vi
kommer til en node som allerede er besøkt, har vi funnet en sykel.
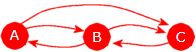
Det er imidlertid et teknisk problem vi må overvinne. En urettet kant blir representert ved hjelp av to rettede kanter. I figuren under til venstre er det en urettet graf som har en sykel. Men den er datateknisk representert som i figuren til høyre:
 |
| Figur 11.1.8 a): To versjoner av en rettet graf |
La oss starte dybde-først-traverseringen i A. Da markeres den som besøkt. A har B og C som naboer. Da går vi først til B og markerer den som besøkt. Men B har A og D som naboer. Men hvis vi nå sjekker A, så oppdager vi at den er besøkt. Men det betyr ikke at vi har funnet en sykel. Når vi generelt i traverseringen går fra en node X til en node Y, må vi, når vi går videre fra Y, ikke bry oss om noden som vi kom fra, dvs. X.
Hvordan løser vi det datateknisk? Jo, vi kan bruke variabelen
forrige. I startnoden setter vi den til null. Når vi kommer til en node som ikke
er besøkt, setter vi forrige i den til å være lik noden vi kom fra. Det betyr at hvis vi generelt har
kommet fra X til Y og skal videre, så sjekker vi de direkte etterfølgerne til Y om de er besøkt eller ikke. Anta at Z er
en slik node som er besøkt.
Hvis den er lik den forrige til Y, så må den være lik X. Dermed ingen sykel. Men hvis Z derimot ikke er lik den
forrige til Y, så har vi funnet en sykel.
Vi sier at en tom graf og en graf med én eller to noder er asyklisk. Husk av vi kun ser på enkle grafer, dvs. maksimalt én (urettet) kant mellom to noder og ingen sløyfer. Flg. metode avgjør om en sammenhengende graf er asyklisk.
public boolean asykliskUrettet() { if (noder.size() <= 2) return true; // tom graf eller maks to noder Node p = noder.values().iterator().next(); // en tilfeldig node boolean resultat = asykliskUrettet(p); // kaller den rekursive metoden nullstill(); // besøkt og forrige settes tilbake til null return resultat; }
private boolean asykliskUrettet(Node p) // rekursiv dybde-først-traversering { p.besøkt = true; for (Node q : p.kanter) // alle naboene til p { if (!q.besøkt) { q.forrige = p; if (!asykliskUrettet(q)) return false; // rekursivt kall } else if (p.forrige != q) return false; // en sykel } return true; } Programkode 11.1.8 a)
Vi kan teste dette på de to grafene under. Den til venstre er et tre (et spenntre til grafen i
Figur 11.1.7 a) og den til høyre har fått en ekstra kant
(mellom D og E) slik at den ikke lenger er asyklisk. Data for grafen (treet) til venstre ligger på
graf9.txt:
 |
| Figur 11.1.8 b): Til venstre et tre Til høyre en graf med sykel |
Grafen til høyre får vi til ved å legge inn en kant mellom D og E. Det gjøres ved hjelp av to rettede kanter - en den ene veien og en motsatt vei:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf9.txt"; Graf graf = new Graf(url); System.out.println(graf.asykliskUrettet()); // Utskrift: true graf.leggInnKant("D", "E"); // kant den ene veien graf.leggInnKant("E", "D"); // kant motsatt vei System.out.println(graf.asykliskUrettet()); // Utskrift: false Programkode 11.1.8 b)
Metoden asykliskUrettet() bruker den første noden som iteratoren gir, som startnode. Hvis grafen er usammenhengende,
vil kun den komponenten som som inneholder startnoden, bli undersøkt. Utvid koden
(Oppgave 2)
slik at alle komponentene blir undersøkt hvis den er usammenhengende. Metoden
returnerer false hvis den finner en sykel, men ingenting om hvor sykelen ble funnet.
Men det er ikke vanskelig å endre. Når vi kommer til en node som har vært besøkt tidligere, kan vi, både fra den noden vi står på og fra den
besøkte noden, gå «bakover» ved hjelp av forrige. Dermed kan vi finne hvilke noder som inngår i sykelen.
Dette er tema i Oppgave 3.
En versjon av metoden asykliskUrettet() for klassen MGraf er tema i
Oppgave 4.
Rettede grafer Vi må tenkel litt annerledes når det gjelder
å avgjøre om en en enkel
og rettet graf har en sykel. F.eks. får vi en sykel hvis det går kant begge veier mellom to noder.
Når en dybde-først-traversering treffer en node første gang, settes den som besøkt. Hvis den treffes på nytt,
dvs. via en annen vei, så får vi to muligheter. Se figuren under:
 |
| Figur 11.1.8 c): Graf uten sykel Graf med sykel |
La oss starte dybde-først-traverseringen i A. I grafen til venstre vil vi da gå videre til B, C, E og F. Deretter trekker vi oss tilbake til den nærmeste noden der det står igjen kanter, dvs. tilbake til B. Derfra går vi videre til D. Men der stopper vi siden dens eneste direkte etterfølger (dvs. E) allerede er besøkt. Så trekker vi oss tilbake til A. Her er det ingen sykel selv om vi i traverseringen kom til en node som allerede var besøkt.
Hvis vi gjentar dette i grafen til høyre, blir det først A, B, C, E og D. Men der stopper vi siden den eneste direkte etterfølgeren til D (dvs. B) allerede er besøkt. Så trekker vi oss tilbake til E. Deretter blir det F. Så trekker vi oss tilbake til A siden alle kanter er vurdert. Men det er en sykel. Hvordan skal vi klare å skille på disse to tilfellene?
I det første tilfellet kom vi til F. Så trakk vi oss tilbake til E, så til C og så til B før vi fortsatte til D. Det betyr at når vi kom til E på nytt, kom vi til en node som vi tidligere har trukket oss tilbake fra. Men slik var det ikke i det andre tilfellet. Når vi der kom til B for andre gang, hadde vi ennå ikke trukket oss tilbake fra B. Der ligger forskjellen. Vi løser dette ved å markere en node som besøkt første gang vi kommer dit og som ferdigbehandlet når vi trekker oss tilbake. Dermed kan vi teste på dette i algoritmen.
Vi starter med en algoritme for Graf (en for
MGraf
tas i Oppgave 5). Variabelen besøkt
i Node skal som før oppdateres første gang vi kommer dit. Men hvordan skal vi markere at vi har trukket oss
tilbake og at den dermed er ferdigbehandlet? Vi kan selvfølgelig legge inn en ny variabel i Node.
Men vi skal heller bruke variabelen forrige på en lur måte. Vi oppretter en
tom hjelpenode med f.eks. ferdig som referansenavn:
Node ferdig = new Node(""); // en tom hjelpenode
Når vi kommer til en node for første gang, setter vi besøkt til true og
forrige til den noden vi kom fra. Nå vi trekker oss tilbake, setter vi forrige
til ferdig. Hvis vi kommer til en sykel, dvs. til en node som er besøkt og der forrige ikke er ferdig, så kan
vi finne sykelen ved å gå baklengs ved hjelp av forrige.
Hvis en dybde-først-traversering starter i en bestemt node, vil det kun være den delen av grafen som det går veier til fra startnoden, som vil bli undersøkt. En metode for dette må derfor gjenta dette fortløpende på noder som ikke er besøkt, inntil hele grafen er undersøkt.
Flg. rekursive metode har to noder som argumenter. Den første p er den noden som rekursjonen foregår på og den andre
er hjelpenoden ferdig som det skal refereres til for å markere at en node er ferdigbehandlet. Metoden skal, hvis
den finner en sykel, returnere en node som inngår i sykelen og null ellers. Hvis grafen har en sykel, kan returnoden
brukes til å traversere sykelen og dermed gi informasjon om hvilke noder som inngår:
private Node asykliskRettet(Node p, Node ferdig) // dybde-først-traversering { p.besøkt = true; // første gang vi kommer til p for (Node q : p.kanter) // alle kantene ut fra p { if (!q.besøkt) { q.forrige = p; // p er forrige på veien til q Node r = asykliskRettet(q, ferdig); // den rekursive metoden if (r != null) return r; // stopper hvis vi finner en sykel } else if (q.forrige != ferdig) { q.forrige = p; return q; // en sykel er funnet og q inngår } } // for-løkken p.forrige = ferdig; // vi trekker oss tilbake fra p return null; // ingen sykel så langt } Programkode 11.1.8 c)
Metoden over vil traversere den delen av grafen som det fører veier til fra startnoden. Hvis den finner en sykel, vil en node
som inngår i sykelen bli returnert. Hvis ikke, returnerer den null. Flg. hjelpemetode
traverserer en sykel og returnerer en tegnstreng med navnet på nodene som inngår. For klart å markere at det er en sykel,
er den noden sykeltraverseringen starter med, tatt med både først og sist i oppramsingen:
private String sykel(Node r) { Deque<String> stakk = new ArrayDeque<>(); stakk.push(r.navn); // første node i sykelen Node s = r.forrige; // en hjelpenode while (s != r) // går rundt sykelen { stakk.push(s.navn); s = s.forrige; } stakk.push(r.navn); // legger inn denne på nytt return stakk.toString(); // fra stakk til String } Programkode 11.1.8 d)
Det som nå gjenstår er å lage en offentlig metode som kobler sammen de to metodene over. For å sikre at hele grafen blir undersøkt, er det nødvendig fortløpende å kalle den rekursive metoden på alle ikke besøkte noder. Normalt vil et kall på første node føre til at en serie andre noder blir besøkt. De hopper vi over i fortsettelsen:
public String asykliskRettet() { Node ferdig = new Node(""); // hjelpenode Node r = null; // hjelpenode for (Node p : noder.values()) // ser på alle nodene { if (!p.besøkt) // hopper over de som er besøkt { r = asykliskRettet(p, ferdig); // den rekursive metoden if (r != null) break; // stopper hvis det er en sykel } } String resultat = r != null ? sykel(r) : null; nullstill(); return resultat; } Programkode 11.1.8 e)
For å teste dette bruker vi flg. graf:
 |
| Figur 11.1.8 d): En graf med flere sykler |
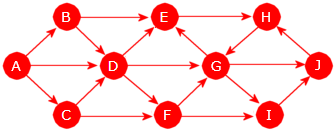
Grafen over har flere sykler. Da spørs det hvilken av dem metoden asykliskRettet() finner først. Data for grafen
ligger på graf10.txt:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf10.txt"; Graf graf = new Graf(url); System.out.println(graf.asykliskRettet()); // Utskrift: [D, F, G, E, D] Programkode 11.1.8 f)
Utskriften fra kodebiten over viser at kanten fra E til D inngår i den sykelen som ble funnet. Hva vil skje hvis vi snur retningen på den kanten, dvs. at grafen blir slik som i denne figuren:
 |
| Figur 11.1.8 e): En graf med flere sykler |
Grafen har fortsatt sykler. Hvem av dem vil asykliskRettet() nå finne?
Vi kan «snu» en kant ved å fjerne den og så legge inn den motsatte kanten. Flg.
metode fjerner en kant:
public void fjernKant(String franode, String tilnode) { Node fra = noder.get(franode); if (fra == null) throw new NoSuchElementException(franode + " er ukjent!"); Node til = noder.get(tilnode); if (til == null) throw new NoSuchElementException(tilnode + " er ukjent!"); if (!fra.kanter.remove(til)) throw new NoSuchElementException( "Kant " + franode + " -> " + tilnode + " finnes ikke!"); til.innkanter--; // tilnoden får en innkant mindre enn før } Programkode 11.1.8 g)
I flg. kodebit snus retningen på kanten fra E til D og deretter kanten fra H til G. I det siste tilfellet blir grafen sykelfri, dvs. asyklisk:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf10.txt"; Graf graf = new Graf(url); System.out.println(graf.asykliskRettet()); // Utskrift: [D, F, G, E, D] graf.fjernKant("E", "D"); graf.leggInnKant("D", "E"); // kanten "snus" System.out.println(graf.asykliskRettet()); // Utskrift: [G, E, H, G] graf.fjernKant("H", "G"); graf.leggInnKant("G", "H"); // kanten "snus" System.out.println(graf.asykliskRettet()); // Utskrift: null Programkode 11.1.8 h)
En alternativ teknikk
Husk at en kilde (eng: source)
er en node uten innkanter. En asyklisk rettet graf må ha minst én kilde. Hvorfor? Anta det motsatte, dvs. at
den er uten kilder. Det betyr at hver node har minst én direkte forgjenger.
La X være en node. La så Y være en direkte forgjenger til X. La videre Z være en direkte forgjenger til Y.
Osv. I denne prosessen må vi før eller senere komme til en node som vi allereder har tatt med,
siden grafen har endelig mange noder. Dermed har vi funnet en sykel. En selvmotsigelse!
Med andre ord må grafen ha minst én kilde.
Algoritme
Denne observasjonen kan vi bruke til å lage flg. algoritme: Sjekk grafens noder. Hvis den ikke har noen kilder, har den
en sykel. Hvis ikke, la X være en kilde. Fjern så X og dens kanter fra grafen. Hvis grafen som vi nå har, ikke har
noen kilder, må den ha en sykel (som også må være en sykel i den opprinnelige grafen). Osv. Hvis dette ikke stopper før
vi har gått gjennom alle nodene, så er grafen asyklisk. Ellers må den ha en sykel.
Vi kan illustrere dette på grafen i Figur 11.1.8 d).
Her med antall innkanter markert:
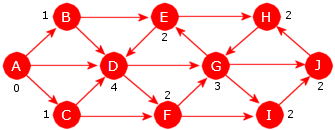 |
| Figur 11.1.8 f): En graf der antall innkanter er markert |
Grafen har kun A som kilde (node uten innkanter). Fjerner vi den (og dens kanter) får vi:
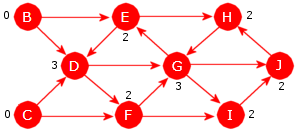 |
| Figur 11.1.8 g): En graf der antall innkanter er markert |
Nå er det to kilder, dvs. B og C. Fjerner vi begge (og kantene) blir dette resultatet:
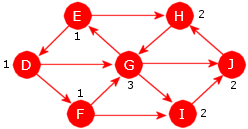 |
| Figur 11.1.8 h): En graf uten kilder |
Nå har vi fått en graf uten kilder og ifølge observasjonen over, har den da en sykel.
Den sykelen inngår da også i den opprinnelige grafen som dermed ikke er
asyklisk. I hver node er antall innkanter registrert (dvs. variabelen innkanter).
Det bruker vi i flg. kode:
public boolean asykliskRettet() // true hvis asyklisk { Deque<Node> stakk = new ArrayDeque<>(); // til å lagre noder byte[] innkanter = new byte[antallNoder()]; // hjelpetabell int antall = 0, i = 0; // hjelpevariabeler for (Node p : noder.values()) // alle nodene i grafen { innkanter[i++] = p.innkanter; // tar vare på innkanttallene if (p.innkanter == 0) stakk.push(p); // henter alle kildene } while (!stakk.isEmpty()) { Node p = stakk.pop(); // en kilde antall++; // øker antallet for (Node q : p.kanter) // kant fra p til q { if (--q.innkanter == 0) stakk.push(q); // "fjerner" kanten } } int j = 0; // hjelpevariabel for å gi innkanter opprinnelig verdi for (Node p : noder.values()) p.innkanter = innkanter[j++]; return antall == antallNoder(); // har alle nodene blitt vurdert? } Programkode 11.1.8 i)
Algoritmebeskrivelsen sier at noder fortløpende skal fjernes.
Men her «fjernes» en node ved at de nodene som det går kanter til fra noden, får redusert antall innkanter. Det betyr at variabelen
innkanter i noen eller i alle noder til slutt har blitt 0. Dermed vil grafen bli «ødelagt».
For å unngå dette, starter metoden med å ta vare på verdiene til innkanter og lagre dem i en tabell. Til
slutt blir de lagt tilbake.
Hvis en bruker denne versjonen av asykliskRettet() i
Programkode 11.1.8 h), vil utskriften bli
false, false og true. Hva må vi gjøre her for å få skrevet
ut nodene som inngår i en sykel hvis grafen ikke er asyklisk? Det lar seg løse,
men ikke på en effektiv måte. Men som en kodeoppgave kan det være av interesse.
Se Oppgave 8.
| 1. | Sjekk at Programkode 11.1.8 b) virker. Ta vekk kanten mellom
D og E. Legg inn isteden kanter mellom andre par av noder slik at det blir en sykel. Legg også inn flere noder og urettede kanter (kant begge veier)
slik at det skifter mellom å være et tre og ikke et tre. Sjekk at metoden
asykliskUrettet() hele tiden
gir rett svar. Det er en forutsetning at grafen er urettet, dvs. at hvis det går en kant én vei mellom to noder, må
det også gå en kant den motsatte veien. Dette kan sjekkes ved hjelp av metoden
erUrettet().
|
| 2. | I asykliskUrettet() starter traverseringen med den
første noden som iteratoren gir. Hvis grafen er usammenhengende, vil kun den komponenten som startnoden hører til,
bli undersøkt. Utvid metoden slik at alle komponentene blir undersøkt hvis grafen er usammenhengende.
|
| 3. | Gjør flg. endringer i metoden asykliskUrettet(): La den ha
String som returtype. Hvis metoden finner en sykel, skal den
returnere en tegnstreng med navnet til nodene som inngår i sykelen. Hvis grafen er asyklisk, returneres null. For
å få til dette må den rekursive metoden rapportere hvor den fant en node som inngår i en sykel. Da kan sykelen
traverseres ved hjelp av variabelen forrige.
|
| 4. | Metoden asykliskUrettet() som sjekker om en urettet graf er asyklisk, er laget
for klassen Graf. Lag metoden for klassen
MGraf. Sjekk at
Programkode 11.1.8 b) også virker for den. Lag
en utvidet versjon som returnerer nodene sykelnoden slik som i Oppgave 2.
|
| 5. | Programkode 11.1.8 h) tester
asykliskRettet(). Test den ytterliger ved å
fjerne, legge inn nye eller «snu» kanter.
|
| 6. | Lag en versjon av asykliskRettet() for
MGraf. Bruk f.eks.
Programkode 11.1.8 h) til å sjekke
at den virker som den skal.
|
| 7. | Sjekk at den versjonen av asykliskRettet() som står i
Programkode 11.1.8 i) også
virker i Programkode 11.1.8 h).
Siden det er to versjoner burde de ha ulike navn.
|
| 8. | Gjør om asykliskRettet() i
Programkode 11.1.8 i)
sli at den returnerer det samme som den i
Programkode 11.1.8 e).
Start i en node og gå «bakover» til det kommer en node som allerede er besøkt. Ta
kun med de nodene der variabelen innkanter er større enn 0.
|
| 9. | Lag en versjon av asykliskRettet() i
Programkode 11.1.8 i)
for klassen MGraf.
|
![]() 11.1.9 Topologisk sortering
11.1.9 Topologisk sortering
Et prosjekt betstår vanligvis av mange separate arbeidsoppgaver og dette kan representeres ved hjelp
av en rettet graf, dvs. et arbeidsskjema:
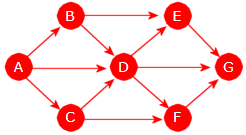 |
| Figur 11.1.9 a): Arbeidsskjema |
Figuren over viser et arbeidsskjema for de arbeidsoppgavene som kan tenkes å inngå i et prosjekt. Det er syv arbeidsoppgaver med navn fra A til G. I et prosjekt er det vanligvis slik at enkelte oppgaver må være fullført før andre oppgaver kan påbegynnes. I skjemaet er det markert med en pilformet kant. F.eks. går det en kant fra A til D og det betyr at A må være fullført før D kan starte.
I noen prosjekter kan det utføres kun én oppgave om gangen. Det er jo tilfellet hvis det er kun én person som skal gjennomføre prosjektet. Dermed er det nødvendig å kunne sette opp arbeidsoppgavene i en rekkefølge. Hvis oppgave X må utføres før oppgave Y, så må X komme foran Y i rekkefølgen. Hvis det derimot ikke er noen avhengighet mellom X og Y, så er den innbyrdes rekkefølgen av de to valgfri.
Ta flg. rekkefølge som et eksempel: A, B, D, C, E, F, G. Men det blir feil. Arbeidsskjemaet viser
at C må utføres før D, men i eksemplet kommer C etter D. Bytter vi om, dvs. til
A, B, C, D, E, F, G, vil det stemme. En slik rekkefølge kalles en topologisk sortering.
Definisjon Gitt en rettet og asyklisk graf. En topologisk sortering av grafen
er en rekkefølge av grafens noder der en nodes
etterfølger
alltid kommer etter noden i rekkefølgen.
I arbeidsskjemaet i Figur 11.1.9 a) ser
vi at arbeidsoppgave A må utføres først. En slik node, dvs. en som ikke har noen kanter inn til seg, men kun kanter
til andre noder, kalles en kilde.
Vi ser også at alle de andre oppgavene må være utført før
G kan begynne. En slik node, dvs. en som det kun går kanter inn til, men ingen kanter ut, kalles et
sluk.
I vårt arbeidsskjema er det én kilde og ett sluk. Det betyr at de må komme hhv. først og sist i en topologisk
sortering. Men for de andre er det flere muligheter. I vårt tilfelle er det fire mulige topologiske
sorteringer. Se Oppgave 1.
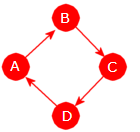 |
| Figur 11.1.9 b) |
Det som er målet nå er å lage en sorteringsalgoritme. Definisjonen over sier at grafen må være rettet og asyklisk. Det at den er asyklisk er et nødvendig krav. Ta grafen til venstre som eksempel. Der er alle nodene sine egne etterfølgere. Hvis vi f.eks. starter i A og følger kanter, kommer vi til A. Med andre ord er A sin egen etterfølger. Det betyr at A må være fullført før A kan påbegynnes. Det er jo en umulighet. Men hvis grafen er rettet og asyklisk (kalles en DAG på engelsk), så kan den sorteres toplogisk. Normalt vil det være mange mulige topologiske sorteringer.
Posttraversering I Avsnitt 11.1.4
så vi på to måter å traversere en graf. Den første brukte en dybde-først-teknikk. Den er forklart ved
hjelp av illustrasjoner. Men teknikken har en valgfrihet. Vi kan «behandle» en node første gang vi
kommer dit, dvs. før vi går videre til dens etterfølgere. Eller siste gang vi kommer dit, dvs. etter at
alle dens etterfølgere er ferdigbehandlet. Dette
svarer til preorden og postorden for binære trær. Se
Avsnitt 5.1.7.
Se på
grafen (eller arbeidsskjemaet) i Figur 11.1.9 a).
Hvis vi der starter i A og så bruker dybde-først (med alfabetisk rekkefølge på direkte etterfølgere),
så kommer vi til nodene første gang i denne rekkefølgen: A, B, D, E, G, F, C. Men siste gang til dem
i denne rekkefølgen: G, E, F, D, B, C, A. Det kalles pre- og posttraversering.
Hvis vi snur rekkefølgen på den siste, får vi A, C, B, D, F, E, G som jo er en topologisk sortering.
Det er ingen tilfeldighet. I posttraversering «behandles» (f.eks. at navnet skrives ut)
alle etterfølgerne til en node før noden. Med andre omvendt topologisk rekkefølge.
Oppgave 2 i Avsnitt 11.1.4
går ut på å kode en posttraversering. Løsningsforslaget har to metoder. En privat rekursiv metode
som gjør traverseringen og en offentlig en som setter i gang den rekursive metoden. Begge hører til
i klassen Graf (MGraf behandles lenger ned):
private void dybdeFørstPost(Node p, Consumer<String> oppgave) // rekursiv metode { p.besøkt = true; for (Node q : p.kanter) // tar alle kantene fra p { if (!q.besøkt) dybdeFørstPost(q, oppgave); // rekursivt kall } oppgave.accept(p.navn); // postoppgave - accept() er eneste metode i Consumer } public void dybdeFørstPosttraversering(String startnode, Consumer<String> oppgave) { Node p = noder.get(startnode); if (p == null) throw new IllegalArgumentException(startnode + " er ukjent!"); dybdeFørstPost(p, oppgave); // kaller den rekursive metoden } Programkode 11.1.9 a)
Data for grafen i Figur 11.1.9 a)
ligger på graf2.txt. I flg. kodebit bruker
vi innlegging (push) i en stakk (en ArrayDeque) som oppgave. Da vil vi få nodene i motsatt rekkefølge:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); Deque<String> stakk = new ArrayDeque<>(); graf.dybdeFørstPosttraversering("A", stakk::push); System.out.println(stakk); // Utskrift: [A, C, B, D, F, E, G] Programkode 11.1.9 b)
Koden over har to svakheter. For det første vil den gi et resultat selv om grafen ikke er asyklisk. Det kommer
av at en node settes som besøkt første gang vi kommer dit. Hvis vi så, i løpet av en sykel, kommer dit på nytt,
vil det stoppe der siden vi kun går videre til noder som ikke er besøkt. Data for grafen i
Figur 11.1.9 b) ligger
på graf8.txt. Hvis den brukes i
Programkode 11.1.9 b), vil vi
få [A, B, C, D] som utskrift. Kjør koden og sjekk at det blir slik!
Den andre svakheten er at kun den delen av en graf som nås fra startnoden, dvs. startnoden og dens etterfølgere, vil bli sortert. Ta flg. figur som eksempel:
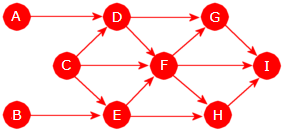 |
| Figur 11.1.9 c): Arbeidsskjema |
Hvis vi nå bruker A som startnode, vil vi kun komme til A, D, F, H, G , I. Data for grafen ligger
på graf7.txt. Bruk det i
Programkode 11.1.9 b) og se hva som skjer.
Hvis vi gjentar dette med B som startnode, vil vi komme til B og E, men ikke mer. De øvrige etterfølgerne til
B er allerede besøkt. Men B og E er ikke etterfølgere til A og dermed kan de settes foran A i en topologisk
sortering. Tilsvarende med C. Den kan settes foran B. Dette kan vi løse ved å utvide
Programkode 11.1.9 b):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf7.txt"; Graf graf = new Graf(url); Deque<String> stakk = new ArrayDeque<>(); graf.dybdeFørstPosttraversering("A", stakk::push); graf.dybdeFørstPosttraversering("B", stakk::push); graf.dybdeFørstPosttraversering("C", stakk::push); System.out.println(stakk); // Utskrift: [C, B, E, A, D, F, H, G, I] Programkode 11.1.9 c)
I koden over inngår fortløpende A, B og C som argumenter. De kunne vært tatt i en annen rekkefølge og det
kunne vært brukt flere (så sant de ikke allerede har blitt besøkt).
Dette vil ha gitt forskjellige rekkefølger til slutt,
men det er ok. Det eneste sikre er at A, B, C, D og E må komme foran F siden de er forgjengere til F. Videre
må F komme foran G, H og I siden de er etterfølgere.
Se Oppgave 2 og
3.
Men uansett er en slik måte å gjøre det på kun mulig i de tilfellene der vi har full oversikt over grafen, f.eks.
en tegning.
Vi må ha en mer generell teknikk. Og det er å prøve fortløpende alle noder som ennå ikke er besøkt. Dvs. slik der en (topologisk) sortert tabell returneres:
public String[] topologiskSortering() { Deque<String> stakk = new ArrayDeque<>(); for (Node p : noder.values()) // alle nodene i grafen { if (!p.besøkt) dybdeFørstPost(p, stakk::push); } return stakk.toArray(new String[0]); } Programkode 11.1.9 d)
Dette vil virke for alle rettede og asykliske grafer. Vi kan for eksempel sjekke at det virker for grafen i
Figur 11.1.9 c):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf7.txt"; Graf graf = new Graf(url); String[] sortert = graf.topologiskSortering(); System.out.println(Arrays.toString(sortert)); // Utskrift: [C, B, E, A, D, F, H, G, I] Programkode 11.1.9 e)
Hvor effektiv er metoden topologiskSortering()? Den tar for seg hver eneste node
og for hver node dens kanter. Den er da av orden m + n der m er antall kanter
og n antall noder.
Direkte sortering Teknikken over
(dvs. posttraversering) sorterer på en indirekte måte.
Flg. algoritme er mer direkte. Vi bruker flg. graf til å illustrere trinnene:
 |
| Figur 11.1.9 d): En rettet asyklisk graf |
Første trinn er å finne en node uten innkanter (en kilde). En rettet og asyklisk graf vil alltid ha minst én slik node. I grafen over er det noden A. Dermed blir A den første i sorteringen (det markeres med et 1.tall). Så fjernes alle utkantene til A. Det gir grafen under til venstre. Neste trinn er å finne en node uten innkanter i «restgrafen» (A regnes ikke med). Både B og C kan velges. Vi velger C (nå nr 2) og fjerner alle utkantene til C. Det gir grafen under til høyre:
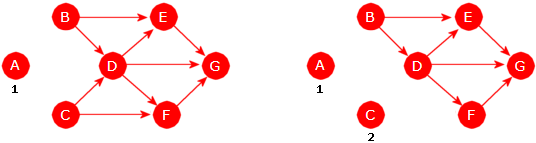 |
| Figur 11.1.9 e): Trinn 1 til venstre og trinn 2 til høyre |
Slik fortsetter vi. Velg en node uten innkanter i «restgrafen» (de nummererte nodene regnes ikke med). Fjern alle dens utkanter. Noden blir den neste i sorteringsrekkefølgen:
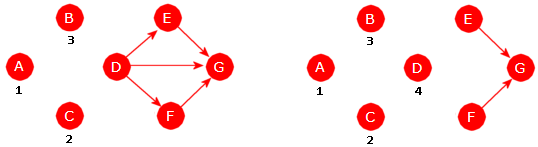 |
| Figur 11.1.9 f): Trinn 3 til venstre og trinn 4 til høyre |
I trinn 5 kan vi velge mellom E og F (se grafen i figuren over til høyre) siden ingen av dem har innkanter. Vi kan f.eks. velge F. Da må det bli E neste gang:
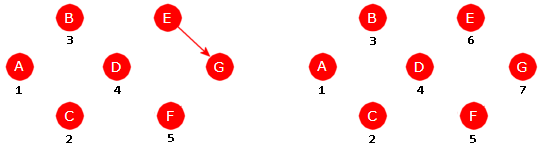 |
| Figur 11.1.9 g): Trinn 5 til venstre og trinn 6 til høyre |
Dermed blir rekkefølgen A, C, B, D, F, E, G. Vi kunne fått en annen rekkefølge ved å velge
B istedenfor C i 2. trinn og E istedenfor F i 5. trinn. En og samme graf kan tegnes på flere måter. Vi kan tegne
grafen i Figur 11.1.9 d) med nodene
i rekkefølgen A, C, B, D, F, E, G og dermed se at for hver node kommer alle dens etterfølgere senere:
 |
| Figur 11.1.9 h): Nodene i sortert rekkefølge |
Hvis vi isteden bruker grafen i
Figur 11.1.9 c), vil vi
se at der er det i utgangspunktet tre noder uten innkanter, dvs. A, B og C. Hvis vi f.eks. velger C, er neste
trinn å «fjerne» kantene som går fra C (utkantene). Etter det er A og B de eneste nodene uten innkanter. Velger
vi så B og fjerner utkantene, vil nå A og E være de uten innkanter. Osv. Se
Oppgave 5.
Hvordan skal dette kodes? Vi kan jo ikke, som i illustrasjonene over, ødelegge grafen. Det som kan hjelpe
oss er variabelen innkanter i den indre klassen
Node. Dens verdi skal være lik det antallet
innkanter som noden har. Den har 0 som utgangsverdi, men
blir oppdatert i metoden leggInnKant().
For å spare plass er den av typen byte og har dermed 127 som maksverdi.
Men det er mer enn nok for våre eksempler og øvingsoppgaver.
Oppgave 14 i
Avsnitt 11.1.2 handler om
metoden antallInnkanter() (se løsningsforslaget). Med den i klassen Graf
kan vi få sjekket om variabelen innkanter har fått korrekte verdier for
grafen i Figur 11.1.9 d):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); for (String node : graf) { System.out.print("(" + node + "," + graf.antallInnkanter(node) + ") "); } // Utskrift: (A,0) (B,1) (C,1) (D,3) (E,2) (F,2) (G,3) Programkode 11.1.9 f)
Vår direkte sorteringsmetode skal starte med å finne den eller de nodene som er uten innkanter. De tar vi vare på ved f.eks. å legge dem på en stakk. Så setter vi igang en løkke som går så lenge stakken ikke er tom. Hver gang tas det ut en node og den blir da den som kommer etter de vi allerede har, i rekkefølgen. Så går vi til dens direkte etterfølgere. Hver av dem får variabelen innkanter redusert med en. Hvis den blir 0, legges noden på stakken.
Flg. metode gjør som beskrevet over og vil virke som den skal. Men den har noen svakheter og de tar vi opp lenger ned:
public String[] topologiskSortering() // returnerer en topologisk sortert tabell { Deque<Node> stakk = new ArrayDeque<>(); // til å lagre noder String[] sortert = new String[antallNoder()]; // sortering for (Node p : noder.values()) // alle nodene i grafen { if (p.innkanter == 0) stakk.push(p); // de som er uten innkanter } int i = 0; while (!stakk.isEmpty()) { Node p = stakk.pop(); // en node uten innkanter sortert[i++] = p.navn; // legger navnet i tabellen for (Node q : p.kanter) // kant fra p til q { if (--q.innkanter == 0) stakk.push(q); } } return sortert; } Programkode 11.1.9 g)
Metoden over kan testes f.eks. ved å bruke Programkode 11.1.9 e).
Vi har nå to forskjellige metoder som sorterer topologisk. Hvis begge skal være tilgjengelige, må de ha ulike navn. F.eks.
topologiskSortering1() og topologiskSortering2().
Metoden i Programkode 11.1.9 g) har som nevnt over, noen svakheter. For det første har variablen
innkanter blitt «ødelagt», dvs. at den har blitt 0 i alle nodene. Dermed vil ikke metoder som er avhengig
av den virke lenger.
Metoden nullstill() kan ikke brukes siden den ikke tar med
variabelen innkanter. Vi kan isteden endre Programkode 11.1.9 g) noe. I starten der
det letes etter noder uten innkanter, kan vi fange opp alle verdiene og lagre dem i en tabell. Til slutt kan disse verdiene
legges tilbake i nodene. Se Oppgave 6.
Den andre svakheten er at vi får et resultat også for en graf som har en sykel.
Det fører til at det på
et bestemt trinn ikke lenger vil være noder uten innkanter. Dermed stopper while-løkken. Sjekk hva som skjer hvis det legges
inn en kant f.eks. fra I til D i grafen som inngår i
Programkode 11.1.9 e). Det betyr
at tabellen sortert ikke fylles opp. Spørsmålet er hva vi i så fall skal gjøre.
Skal det kastes et unntak eller skal metoden returnere et «signal» (f.eks. null) om at noe er feil.
Det at det kastes et unntak er egentlig et signal til brukere av metoden at det på forhånd bør sjekkes om grafen er asyklisk.
Hvis det isteden returneres en «feilverdi», kan testen foretas etterpå.
Se Oppgave 7.
Toplogisk sortering i MGraf
Algoritmen i
Programkode 11.1.9 d) for MGraf kan
oversettes til MGraf ved hjelp av metoden dybdeFørstPost()
fra Oppgave 6 i Avsnitt 11.1.4:
public String[] topologiskSortering() // hører til klassen MGraf { Deque<String> stakk = new ArrayDeque<>(); boolean besøkt[] = new boolean[antall]; // hjelpetabell for (int i = 0; i < antall; i++) { if (!besøkt[i]) dybdeFørstPost(i, besøkt, stakk::push); } return stakk.toArray(new String[0]); // returnerer stakkens innhold } Programkode 11.1.9 h)
Hvis du har dybdeFørstPost() og MGraf-versjonen
av topologiskSortering() hos deg i klassen MGraf, kan du ved å bytte ut Graf med MGraf i
Programkode 11.1.9 e), få testet dette. Se også
Oppgave 8.
En MGraf-versjon av Programkode 11.1.9 g) er litt vanskeligere
å få til slik at den blir effektiv. I
MGraf er det ingen eksplisitt informasjon om antall innkanter til
en node. Vi kan imidlertid finne det ved å telle opp antallet «kryss» (verdien true) i
den matrisekolonnen som hører til noden. En annen mulighet er å innføre en ny tabell i MGraf
for antall innkanter. Den må da oppdateres i metoden
leggInnKant().
Se Oppgave 10.
Effektivitet Programkode 11.1.9 g)
starter med en gjennomgang av alle nodene. Deretter blir én og én tatt ut fra stakken. For hver node blir den direkte etterfølgere
behandlet. Det betyr at metoden er av orden m + n der m er antall kanter og n antall noder
i grafen. Hvem er så best av denne og den i Programkode 11.1.9 d)?
De har samme orden og er nok forholdsvis like, men denne er antageligvis litt raskere.
Korrekthet
Setning En rettet graf kan sorteres topologisk hvis og bare hvis
den er asyklisk.
Anta at den kan sorteres topologisk og anta så at den har en sykel. La X være den av nodene i sykelen som kommer først i den topologiske rekkefølgen. Men siden X inngår i en sykel må den ha en direkte forgjenger Y i sykelen. Med andre ord går det da en kant fra Y til X. Men da må jo Y komme foran X i rekkefølgen. Umulig siden X var den første. Det betyr at grafen må være asyklisk.
Anta at grafen er asyklisk. Da gjelder for det første at den må ha minst én node uten innkanter. Anta at det ikke er tilfelle, dvs. alle noder har minst én innkant. Ta en vilkårlig node X. Den har en innkant. La Y være noden som en slik kant kommer fra. Den har også en innkant. La Z være noden den kommer fra. Osv. Dette kan ikke fortsette i det uendelige siden garfen har endelig mange noder. Det betyr at før eller senere må vi treffe på en node vi allerede har vært innom. Altså en sykel. Men det er umulig siden grafen er asyklisk. Altså må grafen ha minst én node uten innkanter.
Velg en node uten innkanter og la den være først. Det er i overenstemmelse med definisjonen siden dens eventuelle etterfølgere kommer senere. Ta vekk noden og dens eventuelle utkanter fra grafen. Det vi står igjen med kaller vi restgrafen. Velg så en node uten innkanter fra restgrafen. En slik node finnes siden restgrafen også er asyklisk. La den være den andre noden i rekkefølgen. Osv. Dette vil stoppe siden det er endelig mange noder. Det vi da får er en rekkefølge som oppfyller definisjonen. Med andre ord kan grafen sorteres topologisk.
| 1. | Sett opp de fire mulige topologiske sorteringene av grafen i
Figur 11.1.9 a).
|
| 2. | Bytt om rekkefølgen på A, B og C i Programkode 11.1.9 c)
og se hva som da blir resultatet. Prøv også med andre noder. Kravet er da at for hver node må noden ikke alllerede ha vært besøkt.
|
| 3. | Hvor mange forskjellige topologiske sorteringer er det av grafen i
Figur 11.1.9 c)?
|
| 4. | På xxx.html ligger en større graf. Sjekk at den er asyklisk. Bruk den i
Programkode 11.1.9 e). Data for grafen ligger
på xxx.txt.
|
| 5. | Gjennomfør (på papir) trinnene i direkte sortering for grafen i
Figur 11.1.9 c).
|
| 6. | Ta utgangspunkt i Programkode 11.1.9 g).
Opprett i staretn en byte-tabell f.eks. med navn antallInnkanter med plass til alle nodene. Fyll den
opp i den løkken der det letes etter noder uten innkanter. Bruk den (før den siste setningen) til å
oppdatere alle nodene med korrekte verdier på variabelen innkanter. Test at dette virker!
|
| 7. | Ta utgangspunkt i løsningsforslaget for Oppgave 6 og legg inn kode slik at det returneres null hvis grafen inneholder
en sykel, dvs. hvis tabellen sortert ikke fylles opp.
|
| 8. | Legg MGraf-versjonene av dybdeFørstPost()
og topologiskSortering() inn i din versjon av klassen MGraf.
Har du ingen slik versjon finner du en her. Sjekk så at
Programkode 11.1.9 e) virker når dy bytter ut Graf med MGraf.
|
| 9. | Gjør som i Oppgave 4 for MGraf-versjonen av topologiskSortering().
|
| 10. | a) Lag en MGraf-versjon av Programkode 11.1.9 g)
ved at metoden benytter en lokal hjelpetabell av type byte med navn antallInnkanter. Den gis verdi
for hver node ved å telle opp antallet «kryss» (verdien true) i den matrisekolonnen som hører til noden.
|
b) Utvid klassen MGraf med en byte-tabell innkanter
|
![]() 11.1.10 Sammenhengende grafer
11.1.10 Sammenhengende grafer
En urettet graf er sammenhengende hvis det går en vei mellom hvert par
av forskjellige noder. I en rettet graf er det vanlig å skille mellom
to typer av sammenheng. Grafen kalles sterkt sammenhengende hvis det går en vei fra enhver node til enhver annen node
og svakt sammenhengende hvis den urettede grafen vi får ved
å fjerne retningen på alle kantene, blir sammenhengende.
Urettet graf
Det er enkelt å avgjøre om en urettet graf er sammenhengende eller eventuelt få tak i dens komponenter hvis den
ikke er sammenhengende. Vi gjør en traversering (dybde-først eller bredde-først) fra en hvilken som helst startnode S.
Hvis alle nodene har blitt besøkt, er den sammenhengende, dvs. den har kun én komponent. Hvis ikke, gjentar vi dette fra
en node som ennå ikke har blitt besøkt. De ikke-besøkte nodene vi da kommer til, utgjør en ny komponent. Osv. til
alle nodene er besøkt.
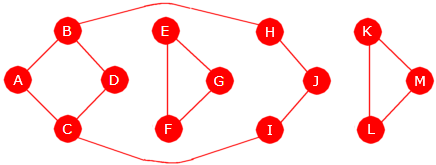 |
| Figur 11.1.10 a): En urettet og usammenhengende graf |
Grafen i figuren over har tre komponenter. Data ligger på
graf12.txt. Vi ønsker nå en metode
som gir oss navnet på nodene i hver komponent. F.eks. på formen:
{A, B, C, D, H, I, J} {E, F, G} {K, L, M}
Flg. offentlige metode skal gjøre en eller flere rekursive dybde-først-traverseringer avhengig av hvor mange
komponenter grafen har. Til traverseringene kan vi bruke en metode vi har laget
tidligere, dvs. dybdeFørstPre() der innlegging
i en StringJoiner er oppgaven:
public List<String> komponenter() { List<String> komponenter = new ArrayList<>(); for (Node p : noder.values()) { if (!p.besøkt) { StringJoiner sj = new StringJoiner(", ", "{", "}"); dybdeFørstPre(p, sj::add); // nodene som nås fra p komponenter.add(sj.toString()); // legger inn komponenten } } return komponenter; // returnerer listen } Programkode 11.1.10 a)
Flg. kodebit viser hvordan dette virker for grafen i Figur 11.1.10 a):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf12.txt"; Graf graf = new Graf(url); for (String s : graf.komponenter()) System.out.print(s + " "); // Utskrift: {A, B, D, C, I, J, H} {E, F, G} {K, L, M} Programkode 11.1.10 b)
Rettet graf En rettet graf er som tidligere nevnt, sterkt
sammenhengende hvis det går en vei fra enhver node til enhver annen node. Det betyr spesielt at hvis den har minst to noder,
vil det gå en vei fra en node tilbake til noden (en sykel).
For å kunne avgjøre
dette er det lurt å studere
den omvendte grafen, dvs. den grafen vi får ved å snu retningene på alle kantene.
Konstruksjon: Vi starter med en gitt graf og en ny tom omvendt graf.
Så lager vi noder i omvendt med samme navn som
dem i graf. Deretter setter vi igang to iteratorer som går i parallell i de to grafene
(nodene kommer sortert mhp. navn i begge).
Vi henter informasjon om kantene i graf og bruker det til å legge inn tilsvarende kanter
motsatt vei i omvendt.
public static Graf omvendt(Graf graf) // hører til klassen Graf { Graf omvendt = new Graf(); // ny og tom graf for (Node p : graf.noder.values()) // nodene i graf { omvendt.noder.put(p.navn, new Node(p.navn)); // nodene i omvendt } Iterator<Node> i = graf.noder.values().iterator(); // iterator i graf Iterator<Node> j = omvendt.noder.values().iterator(); // iterator i omvendt while (i.hasNext()) { Node p = i.next(), op = j.next(); // p i graf, op i omvendt for (Node q : p.kanter) // kant fra p til q i graf { omvendt.noder.get(q.navn).kanter.add(op); // kant fra q til p i omvendt } } return omvendt; // den omvendte grafen } Programkode 11.1.10 c)
Vi kan teste metoden på flg. graf:
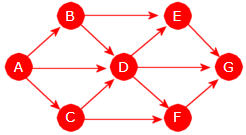 |
| Figur 11.1.10 b): En rettet graf |
Data for grafen ligger på graf2.txt. I flg. kodebit lages først grafen og så den
omvendte grafen. Nodene og kantene i den omvendte skrives ut:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/1/graf2.txt"; Graf graf = new Graf(url); Graf omvendt = Graf.omvendt(graf); for (String node : omvendt) // bruker iteratoren i grafen { System.out.println(node + " -> " + omvendt.kanterFra(node)); } // A -> [] B -> [A] C -> [A] D -> [A, B, C] E -> [B, D] F -> [C, D] G -> [D, E, F] Programkode 11.1.10 d)
Hvor kostbar er metoden? Hva med MGraf for denne og for metoden komponeneter()?
Hvordan kan vi bruke metoden for å løse problemet vårt? Generelt: Velg en vilkårlig node S i grafen. Gjennomfør så en dybde-først-traversering med S som startnode. Gjør det samme i den omvendte grafen, dvs. en traversering med S som startnode. Hvis alle nodene i grafen og alle nodene i den omvendte grafen har blitt besøkt, så er grafen sterkt sammenhengende. Hvorfor? Jo, la X og Y være to noder i grafen. Siden alle nodene i den omvendte har blitt besøkt, må spesielt X ha blitt besøkt. Dermed finnes det en vei fra X til S i grafen (fordi det finnes en fra S til X i den omvendte). Det finnes også en vei fra S til Y i grafen siden alle nodene har blitt besøkt. Dermed X -> S -> Y.
 Øverst
Øverst