![]() 11.2.1 Listerepresentasjon for vektede grafer
11.2.1 Listerepresentasjon for vektede grafer
En graf representeres normalt ved hjelp av naboskapslister
eller ved en naboskapsmatrise.
Naboskapslister er vanligst når grafen har relativt få kanter i forhold til antall noder.
Klassen Graf (uvektet graf) bruker naboskapslister.
Samme idé kan brukes for klassen VGraf (vektet graf -
eng: weighted graph).
I Avsnitt 11.2.4 skal vi se mer på matriserepresentasjoner.
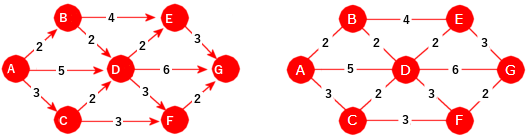 |
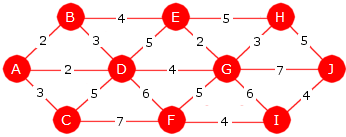
| Figur 11.2.1 a): To vektede grafer - en rettet til venstre og en urettet til høyre |
Kantene i en rettet graf har retning - fra én node til en annen. I en uretter graf kan en kant representeres vha. to rettede kanter.
| Figur 11.2.1 b): En urettet kant som to rettede kanter |
Det holder derfor å lage en datastruktur for rettede grafer. Den vil også fungere for urettede ved at en kant da registreres som to rettede kanter.
Rettede kanter: Ta noden A til venstre i
Figur 11.2.1 a) som eksempel.
Det går kanter fra den til B, C og D med vekter (eller lengder) på hhv. 2, 3 og 5.
Kanten består av en «pil» og et tall der pilen representerer en nodereferanse.
Her er vektene/lengdene heltall. Men det vil jo også være tilfeller der det er desimaltall.
Typen double vil dekke
alle behov siden et heltall kan konverteres til et desimaltall. Men her skal vi for enkelthets
skyld nøye oss med int
som datatype for vekt/lengde. Det gir flg. datatype (med konstruktør) for en (rettet) kant:
private static final class Kant // en indre klasse { private final Node til; // noden som kanten går til private int vekt; // kantens vekt private Kant(Node til, int vekt) // konstruktør { this.til = til; // tilordnes verdi this.vekt = vekt; // tilordnes verdi } } // Kant Programkode 11.2.1 a)
Det vil ofte være ønskelig å få skrevet ut informasjon om en kant fra en node. F.eks. kunne det være
(B,2) for en kant som går fra A til B med vekt/lengde 2.
Se Oppgave 1.
En node må ha et «navn» og en liste med kantreferanser. Konstruktøren gir navn en verdi
og oppretter en tom liste (som en lenket liste). Nå kan det hende at en node
ikke har noen kanter. Dermed er det strengt tatt ikke nødvendig å opprette en liste på forhånd.
En node uten kanter i en urettet graf kalles en isolert node.
De er det normalt få eller ingen av i en vanlig graf. I en rettet graf kalles en slik
node for et sluk, dvs. at det kan gå kanter inn til noden, men ingen
ut. Vi velger her å opprette kantlisten siden det forenkler kodingen av flere av de
metodene vi skal lage senere. Noden får også noen hjelpvariabler for senere bruk:
private static final class Node // en indre klasse { private static final int uendelig = 0x7fffffff; // maks int-verdi private final String navn; // navn/identifikator private List<Kant> kanter; // nodens kanter private int avstand = uendelig; // til senere bruk private boolean ferdig = false; // til senere bruk private Node forrige = null; // til senere bruk private Node(String navn) // konstruktør { this.navn = navn; // nodens navn kanter = new LinkedList<>(); // en tom liste } } // Node Programkode 11.2.1 b)
Dette skal inn i klassen VGraf (V for vektet). Vi bruker, som i
Graf,
en Map<String,Node>
for enkelt å kunne få tak i en node vha. navnet. Dermed blir koden til metoden leggInnNode()
identisk med den i Graf. Men dens
leggInnKant()
må vi omkode. En vekt må inn som tilleggsparameter
og den må med når kanten opprettes. Vi tillater kun
enkle grafer:
public void leggInnKant(String franode, String tilnode, int vekt) { if (franode.equals(tilnode)) throw // sjekker om de er like new IllegalArgumentException(franode + " er lik " + tilnode + "!"); Node fra = noder.get(franode); // henter franode if (fra == null) throw new NoSuchElementException(franode + " er ukjent!"); Node til = noder.get(tilnode); // henter tilnode if (til == null) throw new NoSuchElementException(tilnode + " er ukjent!"); for (Kant kant : fra.kanter) // sjekker om kanten finnes fra før { if (kant.til == til) throw new IllegalArgumentException("Kanten finnes fra før!"); } fra.kanter.add(new Kant(til, vekt)); // legger til i kantlisten } Programkode 11.2.1 c)
Det som er satt opp så langt og det som uten videre kan kopieres direkte fra
klassen Graf,
finner du i VGraf. Flytter du dette over i ditt system og bruker
en utviklingsmiljø (IDE) (f.eks. Netbeans, Eclipse eller IntelliJ), vil det nok komme flere
forslag (hints), f.eks. at enkelte klassevariabler kan være konstante (final). Men de fleste vil forsvinne når vi får kodet mer.
Det er «tungvint» å opprette en vektet graf direkte i koden. Det er mer hensiktsmessig å hente informasjon fra en fil og
så bygge grafen ved hjelp av den. Den informasjonen som trengs for å lage grafene i
Figur 11.2.1 a) setter vi opp på flg.form (se også
vgraf1.txt og
vgraf2.txt):
A B 2 C 3 D 5 A B 2 C 3 D 5
B D 2 E 4 B A 2 D 2 E 4
C D 2 F 3 C A 3 D 2 F 3
D E 2 F 3 G 6 D A 5 B 2 C 2 E 2 F 3 G 6
E G 3 E B 4 D 2 G 3
F G 2 F C 3 D 3 G 2
G G D 6 E 3 F 2
Figur 11.2.1 c): Grafene i Figur 11.2.1 a) - rettet til venstre, urettet til høyre
Hver linje starter med et nodenavn og så en oppramsing av de nodene (med tilhørende vekt) som det går en kant til. Vi kan la
VGraf få en konstruktør som har filnavnet (på url-form) som argument.
Den kan lages nesten maken til den tilsvarende for klassen Graf for uvektede grafer, dvs.
Programkode 11.1.2 g). Med
den ferdigkodet (gjør Oppgave 1) vil flg. kode virke:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf1.txt"; VGraf vgraf = new VGraf(url); for (String node : vgraf) { System.out.println(node + " -> " + vgraf.kanterFra(node) + " "); } Utskrift: A -> (B,2), (C,3), (D,5) B -> (D,2), (E,4) C -> (D,2), (F,3) D -> (E,2), (F,3), (G,6) E -> (G,3) F -> (G,2) G -> Programkode 11.2.1 d)
Sjekk at det også blir riktig med
vgraf2.txt. Hvis du isteden vil ha filen med grafdata lokalt, må du
oppgi filveien (path) på url-form. Dvs. hvis filen f.eks. ligger i en mappe under c, må
file:///c:/ utgjøre første del av url-en. Husk også at hvis du er i et windows-miljø, så kan du ikke bruke
\ . I Java tolkes \ som starten på et spesialtegn. Da må du eventuelt bruke \\ siden det tolkes som \ .
Grafstrukturen bør være dynamisk, dvs. det bør være mulig å legge inn nye og fjerne gamle noder og kanter. Et annet behov er å kunne
endre vekten på en eksisterende kant. Det kunne skje ved at kanten først fjernes og så opprettes på nytt med ny vekt. Men en bedre løsning
kunne være å omkode metoden leggInnKant()
slik at hvis kanten finnes fra før, får den ny vekt og hvis den ikke finnes, blir den opprettet. Da burde metoden returnere den gamle vekten.
Se Oppgavene.
| 1. | Flytt klassen VGraf over til deg.
Lag så konstruktøren public VGraf(String url) throws IOException
i klassen VGraf. Ta utgangspunkt i den versjonen som
klassen Graf har.
La så Kant ha en toString-metode.
La den returnere tegnstrengen "(B,2)" hvis kanten går til noden B med vekt 2. Lag også
en toString-metode for Node.
Den skal returnere navnet på noden.
|
| 2. | Lag metoden public void skrivGraf(String filnavn) throws IOException i klassen VGraf.
Den skal skrive ut informasjon om grafen til filen med navn filnavn. Filen skal se ut slik som konstruktøren
fra Oppgave 1 forventer at den skal være. Se Oppgave 12 i Avsnitt 11.1.2.
|
| 3. | Lag en endret versjon av leggInnKant() slik at
hvis kanten finnes fra før, skal vekten oppdateres vha. parameterverdien vekt. La metoden returnere
en heltallsverdi (en int) som er lik parameterverdien vekt hvis det er en ny kant og
den gamle vekten hvis det er oppdatering.
|
| 4. | Lag metoden public boolean erKant(String franode, String tilnode).
Den skal returnere true hvis det går en kant fra franode til tilnode og false ellers.
|
| 5. | Lag metoden public boolean fjernKant(String franode, String tilnode). Den
skal fjerne oppgitt kant og returnerer true. Hvis kanten ikke finnes, returneres false.
|
| 6. | Lag metoden public String[] .
Den skal returnere en Stringtabell med de nodene som det går en kant til fra node. Det er ikke det samme som
metoden kantFra(). Den returnerer en tegnstreng.
|
| 7. | Lag metoden public String[] .
Den skal returnere en Stringtabell med de nodene som det går en kant fra til node.
|
| 8. | En node kan fjernes kun hvis den ikke har noen kanter, dvs. ingen kanter ut fra noden og ingen inn til noden.
Lag metoden public boolean fjernNode(String node). Den skal
fjerne noden med oppgitt navn og returnere true. Hvis noden ikke finnes, skal den returnere false.
|
![]() 11.2.2 Dijkstras algoritme for korteste vei
11.2.2 Dijkstras algoritme for korteste vei
Det kalles generelt vektede grafer når hver kant har en «vekt».
Men i mange situasjoner er det mer naturlig å si at kantene har lengde. Dermed gir det mening å snakke
om veilengder og korteste vei. Med vekt på kantene burde en isteden bruke uttrykket
«letteste vei» eller vei med minst sammenlagt vekt. Men det er heller uvanlig.
Det finnes mange algoritmer for å finne korteste vei i en graf. Man skiller normalt mellom korteste vei fra én bestemt node (eng: single-source shortest paths) og korteste vei mellom alle par av noder (eng: all-pairs shortest paths). Det skilles også mellom grafer der kanter kan ha negativ vekt og de som ikke tillater det.
Den mest kjente av dem og kanskje også den mest brukte, kalles Dijkstras algoritme. Den stammer fra 1959 og ble laget av Edsger W. Dijkstra. Den hører til kategorien «single-source shortest paths». Den virker på grafer der det kan være flere kanter mellom to noder og der det kan være sykler, men den virker generelt ikke hvis det finnes kanter med negativ vekt. Den virker både for rettede og urettede grafer. En urettet kant mellom to noder kan jo ses på som at det går kant begge veier mellom de to nodene.
Som eksempel bruker vi flg. lille og enkle graf. Den har maksimalt én kant mellom to noder og ingen sykler. Vi ser på en litt større graf i neste eksempel.
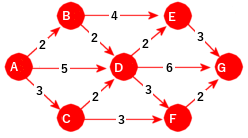 |
| Figur 11.2.2 a): En eksempelgraf |
Siden Dijkstras algoritme er en «single-source shortest paths», må vi velge en «source», dvs. en startnode. I prinsippet kan vi velge en hvilken som helst node, men her velger vi A siden det finnes veier fra A til alle de andre nodene. Korteste vei fra A til seg selv er 0 og det er i figuren under markert med tallet 0 (med svart) i A-noden. Vi kaller det avstanden til A:
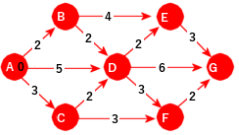 |
| Figur 11.2.2 b): A er startnode |
Neste skritt er å gå til de direkte etterfølgerne til startnoden A, dvs. til de nodene som det går en kant til. Her blir det de tre nodene B, C og D. I de nodene setter vi inn (som foreløpig avstandsverdi) lengden (med svart farge) på de tilhørende kantene. Med andre ord tallene 2 i B, 3 i C og 5 i D. Samtidig endrer vi fargen (fra svart til hvit) på avstandsverdien i A. Det vil gi oss flg. figur:
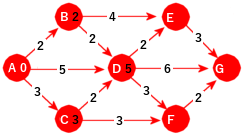 |
| Figur 11.2.2 c): As direkte etterfølgere |
Vi skal under algoritmens gang skille mellom tre typer noder. 1) De aktive, dvs. de nodene som har fått tilordnet en svart
avstandsverdi. I figuren over er det B, C og D. 2) De som er ferdigbehandlet, dvs. de som har fått tilordnet en hvit
avstandsverdi. Den representerer lengden på korteste vei fra startnoden. I figuren over er A ferdigbehandlet.
3) De som er ubehandlet, dvs. de som vi ennå ikke har vært innom (har ikke fått tilordnet avstandsverdi). I figuren over er
det E, F og G. Når algoritmen starter (dvs. startnode er valgt og fått 0 som svart avstandsverdi) er
startnoden den (eneste) aktive noden og alle de andre er ubehandlet.
Dijkstras algoritme kan nå beskrives slik:
- Velg en av nodene i grafen som startnode. Sett den som aktiv, dvs. la den få 0 som (svart) avstandsverdi.
- Velg den noden X blant de
aktivesom har minst avstandsverdi. Finnes det ikke aktive noder, er algoritmen ferdig. Er det flere aktive noder med minst verdi, spiller det ingen rolle hvem av dem vi velger. Sett den valgte noden X somferdigbehandlet, dvs. skift farge på avstansverdien fra svart til hvit. - Se på de direkte etterfølgerne til X (de nodene Y som det går en kant til fra X). La
sumvære avstandsverdien til X + lengden på kanten fra X til Y. a) Hvis Y erubehandlet, skal den fåsumsom (svart) avstandsverdi. b) Hvis Y eraktivogsumer mindre enn dens avstandsverdi, skal den fåsumsom ny (svart) avstandsverdi. Gå til punkt 2.
Hvis vi går tilbake til Figur 11.2.2 c), ser vi at det er B som den av de aktive nodene som har minst avstandsverdi (dvs. 2). Vi velger den og lar avstandsverdien bli hvit. Den har D og E som direkte etterfølgere. Avstansverdien til B er 2 og den pluss lengden på kanten fra B til D er 4. Dermed oppdaterer vi avstansverdien til D fra 5 til 4. E er ubehandlet. Den får derfor 2 + 4 = 6 som (svart) avstandsverdi:
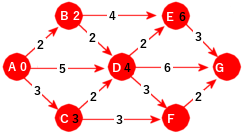 |
| Figur 11.2.2 d): D har blitt oppdatert |
I figuren over er det C, D og E som er aktive. Blant dem har C minst avstandsverdi og den settes som ferdigbehandlet. Fra C til D blir 3 + 2 = 5. Dermed ingen oppdatering av D. F får 3 + 3 = 6 som avstandsverdi:
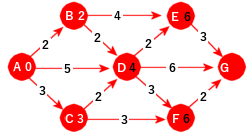 |
| Figur 11.2.2 e): C er ferdigbehandlet |
Så er det D sin tur. Fra D til E blir det 4 + 2 = 6. Men det er den verdien som E allerede har og derfor ingen oppdatering. Fra D til F blir det 4 + 3 = 7. Ingen oppdatering her heller. Fra D til G blir det 4 + 6 = 10. Dermed blir G aktiv med 10 som avstandsverdi:
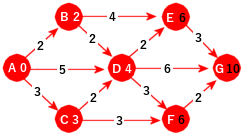 |
| Figur 11.2.2 f): D er ferdigbehandlet |
Nå har vi for første gang to aktive noder med samme verdi, dvs. E og F. Da spiller det ingen rolle hvem vi tar. Her velger vi alfabetisk, dvs. E. Fra E til G blir det 6 + 3 = 9 og siden 9 er mindre 10, oppdateres G:
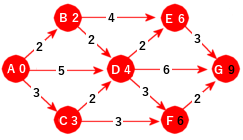 |
| Figur 11.2.2 g): G oppdateres |
Nå er det F sin tur og avstanden til G er 6 + 2 = 8. Dermed oppdateres G på nytt. Da står vi igjen kun med G. Men siden det ikke går noen kanter videre derfra, er vi ferdig. Hurra!
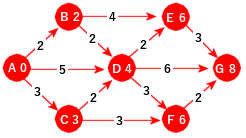 |
| Figur 11.2.2 h): Algoritmen er ferdig |
I figuren over inneholder hver node den korteste avstanden til startnoden A. Men hva med korteste vei? Når
en node får tildelt en avstandsverdi eller den blir oppdatert, noterer vi fra hvilken node vi kom (hjelpevariabelen
forrige i Node). I figuren under er dette
markert med grønne piler. Ved å gå fra G til A vha. grønne piler får vi A-C-F-G som kortest vei fra A til G.
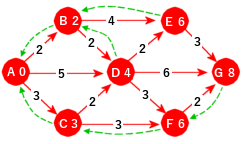 |
| Figur 11.2.2 i): Grønne veier tilbake |
Et større eksempel med 18 noder og 37 kanter:
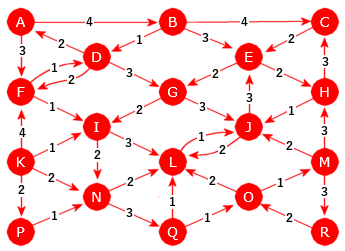 |
| Figur 11.2.2 j): En rettet graf med 18 noder og 37 kanter |
Den eneste forutsetningen for at Dijkstras algoritme skal virke er at ingen kanter har negativ vekt. Men grafen
kan være urettet eller rettet med sykler og kanter begge veier. Du kan teste din forståelse
av algoritmen ved f.eks. finne korteste vei fra A til G i den urettede grafen til høyre i
Figur 11.2.1 a) og korteste vei fra A til R i grafen rett over.
Se også Oppgave 1. Et bevis
for at Dijkstras algoritme gir et korrekt resultat finner du i
Avsnitt 11.2.8.
| 1. | La A være startnode i den urettede grafen (en urettet kant ses på som kant begge veier)
til høyre i Figur 11.2.1 a). Finn korteste
vei til G. Gjenta dette med den rettede grafen i
Figur 11.2.2 j). Finn korteste
vei til R. Gjenta, men med R som start og A som slutt.
|
| 2. | VGraf63 har 63 noder
nummerert fra 0 til 62. Finn korteste vei fra node 0 til node 62 vha. Dijkstras algoritme.
Deretter (når du har lest Avsnitt 11.2.3)
kan du sjekke svaret ved gjøre de nøvendige endringene i
Programkode 11.2.3 c).
Dataene ligger på vgraf63.txt.
|
| 3. | Avstandsverdien i hver node skal til slutt innholde lengden på den korteste veien fra startnoden.
Dijkstras algoritme starter med at avstandsverdien i startnoden settes til 0. Men i
Figur 11.2.2 a) er det egentlig ingen vei fra A til A.
I Figur 11.2.2 j) er det flere veier fra A til A, f.eks.
A, B, D, A med lengde 7. Er det mulig å endre algoritmen slik at den finner korteste vei fra startnoden til seg selv hvis
en slik finnes? Se også Oppgave 7 i Avsnitt 11.2.3.
|
| 4. | Det finnes mye stoff om Dijkstras algoritme på internett. Bruk Dijkstra's algorithm som søkeord. Det
finnes også mange animasjoner. Prøv f.eks.
denne.
|
![]() 11.2.3 Implementasjon av Dijkstras algoritme
11.2.3 Implementasjon av Dijkstras algoritme
Vi bruker beskrivelsen fra forrige avsnitt.
En node som er tatt ut er ferdig.
Hvis avstand
fortsatt er «uendelig» er den ubehandlet. Den aktiviseres ved å gi
den avstand. I flg. metode bruker vi en usortert liste som
datastruktur for de aktive nodene. Vårt foreløpige mål er å få en metode som virker, men som ikke nødvendigvis er effektiv.
Det tar vi opp lenger ned.
public void kortestVeiFra(String nodenavn) // en enkel versjon { Node start = noder.get(nodenavn); // henter startnoden if (start == null) throw new NoSuchElementException(nodenavn + " er ukjent!"); List<Node> aktiv = new ArrayList<>(); // usortert liste for aktive noder start.avstand = 0; // start har avstand lik 0 aktiv.add(start); // startnoden aktiviseres while (!aktiv.isEmpty()) { int m = 0; // leter i aktivlisten etter den med minst avstand for (int i = 1; i < aktiv.size(); i++) // resten av de aktive { if (aktiv.get(i).avstand < aktiv.get(m).avstand) m = i; } Node denne = aktiv.remove(m); // minst avstand - se Oppgave 2 denne.ferdig = true; // denne er tatt ut for (Kant k : denne.kanter) // kantene til denne { Node etterfølger = k.til; // direkte etterfølger til denne if (etterfølger.ferdig) continue; // tar ikke med de ferdige if (denne.avstand + k.vekt < etterfølger.avstand) // sammenligner { if (etterfølger.avstand == Node.uendelig) aktiv.add(etterfølger); etterfølger.avstand = denne.avstand + k.vekt; // oppdaterer etterfølger.forrige = denne; // vei til etterfølger går via denne } } // for } // while } // metode Programkode 11.2.3 a)
Det å lete i en usortert liste er ineffektiv. Det hadde vært mer effektivt å lagre de aktive nodene i f.eks. en heapbasert prioritetskø. Se lenger ned. Obs: Første gang vi i for-løkken for kanter kommer til en node, vil sammenligningen være sann siden noden da er «uendelig».
Vi trenger metodene avstand() som gir en nodes
avstandsverdi og veiTil() som gir selve veien.
Hvis metoden kortestVeiFra() skal brukes flere ganger på samme graf, må grafen «nullstilles»
for hver gang, dvs. at variablene i
Node må få tilbake sine utgangsverdier.
public int avstand(String nodenavn) { Node node = noder.get(nodenavn); if (node == null) throw new NoSuchElementException(node + " er ukjent!"); return node.avstand; } public String veiTil(String nodenavn) { Node node = noder.get(nodenavn); if (node == null) throw new NoSuchElementException(node + " er ukjent!"); Deque<String> kø = new LinkedList<>(); while (node != null) { kø.addFirst(node.navn); node = node.forrige; } return kø.toString(); } public void nullstill() { for (Node node : noder.values()) { node.avstand = Node.uendelig; node.ferdig = false; node.forrige = null; } } Programkode 11.2.3 b)
Hvis du har bygget opp klassen VGraf hos deg, med alle de aktuelle metodene, vil flg. kodebit kunne kjøres
(du finner også en ferdig klasse her):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf1.txt"; VGraf vgraf = new VGraf(url); String fra ="A", til = "G"; String tekst = "Vei fra " + fra + " til " + til + ": "; vgraf.kortestVeiFra(fra); System.out.println(tekst + vgraf.veiTil(til) + ", " + vgraf.avstand(til)); // Utskrift: Vei fra A til G: [A, C, F, G], 8 Programkode 11.2.3 c)
Dette stemmer med Figur 11.2.2 i).
Prøv også den rettede grafen til høyre i
Figur 11.2.1 a)
(vgraf2.txt) og grafen i
Figur 11.2.2 j)
(vgraf3.txt) med R som til.
Se Oppgavene.
En forbedret versjon: Metoden
kortestVeiFra() vil virke ok og være effektiv nok for små grafer.
Men svakheten er at vi leter i en usortert liste etter den «minste» noden for deretter ta den ut. Det er av orden n. Det
hjelper ikke med sortert liste. Der er isteden innlegging av orden n.
Vi bør velge en heapbasert prioritetskø. Der vil både innlegging og uttak i verste fall være av
logaritmisk orden. Men da dukker det imidlertid opp et annet problem.
Når vi går fra en node til dens direkte etterfølger og den er aktiv, vil det
kunne være via en kortere vei enn tidligere. I så fall må dens avstandsverdi oppdateres. Men det vil
kunne korrumpere den heapbaserte prioritetskøen siden nodens plassering i den
er basert på dens avstandsverdi.
En løsning på dette (som ofte velges) er å innføre en lokal klasse (record) med to variabler, dvs. en node og dens avstand. Prioritetskøen skal da inneholde instanser av denne. Når avstandsverdien til en node må oppdateres, legges isteden en ny instans (med den nye avstandsverdien) i køen. En konsekvens er at samme node kan være i flere instanser. Men det er den med minst avstandsverdi som blir tatt ut først. Dermed er noden ferdigbehandlet. Når neste instans med samme node tas ut, kan den overses:
public void kortestVeiFra(String nodenavn) // Dijkstras algoritme { Node start = noder.get(nodenavn); // henter startnoden if (start == null) throw new NoSuchElementException(nodenavn + " er ukjent!"); record Avstand(Node node, int avstand) {} PriorityQueue<Avstand> aktiv = // oppretter køen new PriorityQueue<>((a,b) -> a.avstand - b.avstand); start.avstand = 0; // avstand settes til 0 aktiv.offer(new Avstand(start, 0)); // startnoden er nå aktiv while (!aktiv.isEmpty() ) // så lenge køen ikke er tom { Avstand denne = aktiv.poll(); // den med minst avstandsverdi if (denne.node.ferdig) continue; // denne er vi ferdig med for (Kant k : denne.node.kanter) // ser på alle kantene til denne { Node etterfølger = k.til; // k er en kant fra denne if (!etterfølger.ferdig) // kun de som ikke er ferdige { if (denne.avstand + k.vekt < etterfølger.avstand) { etterfølger.avstand = denne.avstand + k.vekt; // oppdaterer aktiv.offer(new Avstand(etterfølger, etterfølger.avstand)); etterfølger.forrige = denne.node; // forrige på ny vei } } } // for denne.node.ferdig = true; // denne er ferdig } // while } Programkode 11.2.3 d)
En graf kan ha flere korteste veier mellom to noder. Denne versjonen vil derfor kunne finne en
annen vei enn den i Programkode 11.2.3 a).
Se Oppgave 4.
Obs: En implementasjon av Dijkstras algoritme for matriserepresentasjonen
(klassen VMGraf) står i Avsnitt 11.2.4.
| 1. | Programkode 11.2.3 c) viser korteste vei
fra startnoden A til G. Vis at metoden også gir rett resultat for de andre nodene (dvs. B, C, D, E og F). Se
Figur 11.2.2 i).
|
| 2. | Node denne = aktiv.remove(m);
i Programkode 11.2.3 a) kan forbedres. Hvordan?
|
| 3. | Bruk vgraf3.txt
(dvs. Figur 11.2.2 j) i
Programkode 11.2.3 c). Prøv med forskjellige startnoder.
Bruk så vgraf63.txt
(VGraf63) med 0 som startnode og 62 som sluttnode.
|
| 4. | Programkode 11.2.3 d) inneholder en
bedre (effektivere) versjon av kortestVeiFra() enn den i
Programkode 11.2.3 a).
Legg inn den forbedrede versjonen i klassen VGraf (kall
f.eks. den første versjonen for kortestVeiFra0) og
sjekk at vi med den forbedrede versjonen får samme lengde på korteste vei som sist i
Programkode 11.2.3 c)
og i Oppgave 1 og 2. Se spesielt på de korteste veiene fra 0 til 62 som vi får for
VGraf63 for de to versjonene. Det blir forskjellige veier?
Hvorfor? Sjekk i grafen at begge veiene er korrekte og at de begge har samme lengde. Se også
Oppgave 5.
|
| 5. | I versjonen av kortestVeiFra()
fra Programkode 11.2.3 a)
brukte vi en usortert liste for de aktive nodene, men i den fra
Programkode 11.2.3 d)
var det binærheap. Effektiviteten her vil jo i begge tilfellene være avhengig av hvor mange
noder som til enhver ligger der. Hvis det i gjennomsnitt er få, vil også første versjon være rimelig
effektiv. Generelt vil det ligge litt flere i binærheapen siden samme node kan ligge i flere
instanser av Avstand. Legg inn ekstra kode i de to versjonene som skriver hvor mange
noder/avstander som ligger der i hver runde. Sjekk så hva det blir for
VGraf63.
|
| 6. | Metoden kortestVeiFra() finner alltid
korteste vei. Men det hender ofte at det er flere korteste veier mellom to noder.
I VGraf63 har korteste vei mellom 0 og 62 lengde 18, men det er hele
fem forskjellige veier mellom de to nodene som har den lengden. Sjekk på figuren at det stemmer! Lag kode som finner alle de korteste veiene
i en graf hvis det er flere av dem.
|
| 7. | VGraf63 har 63 noder og 103 kanter. Du kan eksperimenter med å legge inn flere
kanter, eventuelt fjerne kanter eller endre kantlengder for å se hvordan det påvirker korteste vei. Da må du legge filen
vgraf63.txt
lokalt hos deg og legge inn endringene/tilleggene der.
|
| 8. | I Oppgave 3 i Avsnitt 11.2.2 tas opp et problem med en vei fra
startnoden til seg selv. Der foreslås det en mulig løsning. Den skal vi implementere her:a) La klassen VGraf ha en privat variabel start av type Node initiert til null.b) La den bli null også i metoden nullstill().c) Helt i begynnelsen av metoden kortestVeiFra() skal det være instansvariabelen start som får verdi
og ikke en lokal variabel.d) I kortestVeiFra() skal ikke startnoden gjøres aktiv og dens avstandsverdi skal ikke endres. Isteden
skal startnodens direkte etterfølgere gjøres aktive med avstandsverdi lik avstanden til startnoden (dvs. kantens vekt). Men
variabelen forrige i disse direkte etterfølgere skal ikke endres, dvs. fortsatt være null. Dette må
gjøres for å unngå en evig løkke vha. forrige. Det vil kunne skje hvis det finnes en vei fra A til A (dvs. en sykel).e) Resten av koden i kortestVeiFra() skal være som før.f) Metoden veiTil() må få et tillegg. Som en nest siste setning (før return)
legges startnodens navn først i køen (addFirst). Grunnen til dette er at forrige
i startnodens direkte etterfølgere er null.
|
![]() 11.2.4 Matriserepresentasjon for vektet graf
11.2.4 Matriserepresentasjon for vektet graf
Representasjonen blir ganske lik den for MGraf.
Forskjellen er at i matrisen for en uvektet graf er det nok å angi om det er en kant eller ikke. Med andre
ord kunne vi der bruke en boolsk matrise. En matrise for en vektet graf må i tillegg vekten angis.
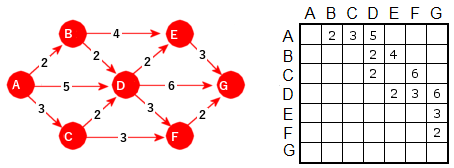 |
| Figur 11.2.4 a): Vektet graf representert som figur og matrise |
Figuren over viser hvorfor en matriserepresentasjon ressursmessig ofte er ugunstig. Matrisen
har 7 × 7 = 49 plasser, mens kun 12 av dem er i bruk. Det er først når det er mange kanter i forhold
til antall noder at matrise er den beste teknikken. Men matriserepresentasjonen er uansett
interessant kodemessig. Et spørsmål er hvor stor vekt en kant kan tenkes å ha. I
klassen VGraf ble typen int
brukt til vekt, men det er nok nærmest i alle tilfeller unødvendig. Da kan en jo ha vekter opp til
2147483647. I alle eksemplene våre er det brukt små vekter og dermed vil datatypen byte (-128 til 127)
være mer enn godt nok for oss. Dermed vil plassbehovet kun være en firedel av det som typen int trenger.
Hvis en skulle ha behov for større vekter enn det eller eventuelt desimale vekter, er det enkelt å kode om.
I MGraf inngår en boolsk matrise og der blir
alle plassene automatisk satt til false. I en uvektet graf er det kun to muligheter - kant eller ikke kant.
Men i en vektet graf er det annerledes. I prinsippet kan en kantvekt være både positiv, 0 og negativ. Det høres rart ut
med en negativ vekt, men det er eksempler der det er naturlig. Når en tallmatrise opprettes får alle plassene 0 som verdi.
Men det vil ikke fungere her siden en kantvekt kan være 0. Vi velger derfor å initialisere alle plassene til
det minste negative tallet, dvs. -128 for byte. Dette betyr at det kun er vekter fra -127 til 127
som kan tillates.
public final class VMGraf // final: skal ikke arves { private final byte IKKE_KANT = -128; // minst byte-verdi private byte[][] graf; // en todimensjonal tabell private int antall; // antall noder private String[] navn; // nodenavn - usortert private String[] snavn; // nodenavn - sortert private int[] indeks; // indekser private int[] avstand; // for senere bruk private int[] forrige; // for senere bruk } // VMGraf Programkode 11.2.4 a)
En konstruktør må opprette tabellene (borsett fra forrige og avstand som foreløpig ikke skal benyttes)
med en gitt dimensjon og sette alle plassene i matrisen til IKKE_KANT:
public VMGraf(int dimensjon) // konstruktør { graf = new byte[dimensjon][dimensjon]; // grafmatrisen antall = 0; // foreløpig ingen noder navn = new String[dimensjon]; // nodenavn - usortert snavn = new String[dimensjon]; // nodenavn - sortert indeks = new int[dimensjon]; // indekstabell for (int i = 0; i < dimensjon; i++) { Arrays.fill(graf[i], IKKE_KANT); // setter IKKE-KANT på alle plasser } } public VMGraf() // standardkonstruktør { this(10); // bruker 10 som startdimensjon } Programkode 11.2.4 b)
En serie metoder kan hentes fra MGraf som de er:
public int antallNoder() // antall noder i grafem { return antall; } public int dimensjon() // dimensjonen til tabellene { return graf.length; } public String[] nodenavn() // navn på alle nodene { return Arrays.copyOf(snavn, antall); } private int finn(String nodenavn) // privat hjelpemetode { return Arrays.binarySearch(snavn, 0, antall, nodenavn); } public boolean nodeFinnes(String nodenavn) // finnes denne noden? { return finn(nodenavn) >= 0; } Programkode 11.2.4 c)
Også her bør det være en dynamisk datastruktur, dvs. at strukturen «utvides» etter behov. Vi kan bruke den private metoden
utvid() i MGraf som utgangspunkt.
Men her skal både den gamle matrisen kopieres over i den nye og det som er selve «utvidelsen» må fylles
med verdien IKKE_KANT. Vi kan se på den gamle matrisen som et kvadrat som ligger oppe i det venstre hjørnet til
den nye matrisen.
private void utvid() { int nydimensjon = graf.length == 0 ? 1 : 2*graf.length; // dobler navn = Arrays.copyOf(navn, nydimensjon); // usortert navnetabell snavn = Arrays.copyOf(snavn, nydimensjon); // sortert navnetabell indeks = Arrays.copyOf(indeks, nydimensjon); // indekstabell byte[][] gammelgraf = graf; graf = new byte[nydimensjon][nydimensjon]; // grafmatrisen for (int i = 0; i < antall; i++) { System.arraycopy(gammelgraf[i], 0, graf[i], 0, antall); Arrays.fill(graf[i], antall, nydimensjon, IKKE_KANT); // resten av raden } for (int i = antall; i < nydimensjon; i++) { Arrays.fill(graf[i], IKKE_KANT); // hele raden } } Programkode 11.2.4 d)
Metoden leggInnNode() kan hentes
fra MGraf som den er. Men metoden leggInnKant()
må endres noe siden en kant nå har vekt. Bl.a. bør vi sjekke om vekten ligger innenfor [-127,127]. Hvis ikke, kastes et unntak:
public void leggInnKant(String franode, String tilnode, int vekt) { if (franode.equals(tilnode)) throw // sjekker om de er like new IllegalArgumentException(franode + " er lik " + tilnode + "!"); int i = finn(franode); // indeks i den sorterte navnetabellen if (i < 0) throw new NoSuchElementException(franode + " er ukjent!"); i = indeks[i]; // indeks i den usorterte navnetabellen int j = finn(tilnode); // indeks i den sorterte navnetabellen if (j < 0) throw new NoSuchElementException(tilnode + " er ukjent!"); j = indeks[j]; // indeks i den usorterte navnetabellen if (graf[i][j] != IKKE_KANT) throw new IllegalArgumentException("Kanten finnes fra før!"); if (vekt < -127 || vekt > 127) throw new IllegalArgumentException(vekt + " er ulovlig som vekt!"); graf[i][j] = (byte)vekt; // fra int til byte } Programkode 11.2.4 e)
Det er også greit å ha en metode som gir oss (som en tegnstreng) kantene fra en node. Ta node D i grafen i
Figur 11.2.4 a) som eksempel. Den har kanter til E, F og G med vekter 2, 3 og 6.
Da kunne metoden f.eks. returnere: [(E,2), (F,3), (G,6)]. Hvis det ikke går noen kanter, kan den returnere kun en tom hakeparentes, dvs. [].
public String kanterFra(String node) { int i = finn(node); // indeks i den sorterte navnetabellen if (i < 0) return null; i = indeks[i]; // indeks i den usorterte navnetabellen StringJoiner sj = new StringJoiner(", ", "[", "]"); for (int j = 0; j < antall; j++) { if (graf[i][j] != IKKE_KANT) { sj.add('(' + navn[j] + ',' + graf[i][j] + ')'); } } return sj.toString(); } Programkode 11.2.4 f)
Det som trengs før dette kan testes, er det å kunne lese grafinformasjon fra en fil. Da gjør vi som tidligere, dvs. lager en konstruktør
med et filnavn på url-form som parameter. Her kan vi bruke konstruktøren for
VGraf som den er bortsett fra å bytte
navn fra VGraf til VMGraf. Hvis du har bygget opp VMGraf hos deg selv
(hvis ikke finner du en fullstendig versjon her), vil flg. kodebit virke :
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf1.txt"; VMGraf vgraf = new VMGraf(url); for (String node : vgraf.nodenavn()) { System.out.println(node + " -> " + vgraf.kanterFra(node) + " "); } A -> [(B,2), (C,3), (D,5)] B -> [(D,2), (E,4)] C -> [(D,2), (F,3)] D -> [(E,2), (F,3), (G,6)] E -> [(G,3)] F -> [(G,2)] G -> [] Programkode 11.2.4 g)
Figur 11.2.2 j) inneholder en litt større graf. Du kan se hvorden dette virker
på den ved å bruke vgraf3.txt i koden over. Se også
Oppgave 1.
Dijkstras algoritme for VMGraf Her tar vi ta utgangspunkt i Dijkstras algoritme for
VGraf og så metoden for
bredde-først-traversering i MGraf (se Oppgave 5
i Avsnitt 11.1.4).
I metoden kortestVeiFra() må tabellene avstand og forrige
i VMGraf opprettes der verdiene i avstand
settes til «uendelig» og de i forrige til -1. Videre må vi ha en lokal boolsk
hjelpetabell ferdig. Den skal brukes til å markere at en node er ferdigbehandlet.
Det vil ikke være nødvendig med en nullstill-metode hvis metoden skal kjøres flere ganger på samme graf siden alle de nevnte tabellene opprettes på nytt hver gang:
public void kortestVeiFra(String nodenavn) // Dijkstras algoritme { int i = finn(nodenavn); // indeks i den sorterte navnetabellen if (i < 0) throw new NoSuchElementException(nodenavn + " er ukjent!"); i = indeks[i]; // indeks i den usorterte navnetabellen class Avstand // lokal hjelpeklasse { int node, avstand; Avstand(int node, int avstand) { this.node = node; this.avstand = avstand; } } Queue<Avstand> aktiv = new PriorityQueue<>((a,b) -> a.avstand - b.avstand); avstand = new int[antall]; // oppretter tabellen Arrays.fill(avstand, 0x7fffffff); // setter verdiene til "uendelig" forrige = new int[antall]; // oppretter tabellen Arrays.fill(forrige, -1); // setter verdiene til -1 boolean[] ferdig = new boolean[antall]; // lokal hjelpetabell avstand[i] = 0; // avstand i startnoden settes til 0 aktiv.offer(new Avstand(i, 0)); // startnoden er nå aktiv while (!aktiv.isEmpty()) // så lenge det er aktive noder { Avstand minst = aktiv.poll(); // den "minste" noden int denne = minst.node; // hjelpevariabel int avst = minst.avstand; // hjelpevariabel if (ferdig[denne]) continue; // denne er vi allerede ferdig med for (int neste = 0; neste < antall; neste++) // går gjennom matriseraden { if (graf[denne][neste] != IKKE_KANT) // en kant fra denne til neste { if (ferdig[neste]) continue; // denne er vi allerede ferdig med int vekt = graf[denne][neste]; // hjelpevariabel if (avst + vekt < avstand[neste]) // sammenligner { avstand[neste] = avst + vekt; aktiv.offer(new Avstand(neste, avstand[neste])); forrige[neste] = denne; // veien går fra denne til neste } } } // for ferdig[denne] = true; // nå er denne er ferdig } // while } Programkode 11.2.4 h)
Etter at denne metoden er brukt på en graf, vil tabellene avstand og forrige inneholde resultatet.
Dermed vil det være nyttig med en metode som til en gitt node returnerer den minste avstanden dit fra den startnoden som ble brukt:
public int avstand(String nodenavn) { int i = finn(nodenavn); // indeks i den sorterte navnetabellen if (i < 0) throw new NoSuchElementException(nodenavn + " er ukjent!"); i = indeks[i]; // indeks i den usorterte navnetabellen return avstand[i]; } Programkode 11.2.4 i)
Det er også viktig å kunne få ut de nodene som utgjør den korteste veien og ikke kun veiens lengde. Da må vi starte i en node og
gå bakover til startnoden vha. tabellen forrige. Med
Figur 11.2.4 a) som graf, vil metoden
kortestVeiFra() gi A, C, F, G som korteste vei fra A til G med lengde 8. Kanskje vi da kan la flg. metode returnere
[A, C, F, G]:
public String veiTil(String node) { int i = finn(node); // indeks i den sorterte navnetabellen if (i < 0) throw new IllegalArgumentException(node + " er ukjent!"); i = indeks[i]; // indeks i den usorterte navnetabellen if (forrige[i] == -1) return "[], 0"; // ingen vei til denne noden Deque<String> stakk = new ArrayDeque<>(); // bruker en deque som stakk while (i != -1) { stakk.push(navn[i]); // legger nodenavnet på stakken i = forrige[i]; // går til forrige node på veien } return stakk.toString(); } Programkode 11.2.4 j)
Flg. programbit finner og skriver ut korteste vei fra A til G i grafen i Figur 11.2.4 a).
Men metoden kortestVeiFra() finner ikke kun korteste vei til G, men korteste vei fra startnoden til alle de nodene som det går en
vei til. Se Oppgave 2.
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf1.txt"; VMGraf vgraf = new VMGraf(url); String fra ="A", til = "G"; String tekst = "Vei fra " + fra + " til " + til + ": "; vgraf.kortestVeiFra(fra); String s = tekst + vgraf.veiTil(til) + ", " + vgraf.avstand(til); System.out.println(s); // Utskrift: Vei fra A til G: [A, C, F, G], 8 Programkode 11.2.4 k)
| 1. | Sjekk at Programkode 11.2.4 g) virker. Har du
ikke klassen VMGraf i ditt system, finner du en full versjon her.
Prøv dette også på grafen i Figur 11.2.2 j), dvs.
bruk vgraf2.txt. Prøv også med grafen
VGraf63, dvs. bruk vgraf63.txt.
|
| 2. | Sjekk at Programkode 11.2.4 k) virker. Har du
ikke klassen VMGraf i ditt system, finner du en full versjon her. Utvid programmet slik
at korteste vei til samtlige noder blir skrevet ut. Prøv med andre startnoder enn A.
Prøv dette også på grafen i Figur 11.2.2 j), dvs.
bruk vgraf3.txt. Prøv også med grafen
VGraf63, dvs. bruk vgraf63.txt
med 0 som franode og 62 som tilnode.
|
| 3. | VMGraf er ikke itererbar, dvs. den implementerer ikke
grensesnittet Iterable<String> slik som VGraf.
Gjør det som trengs for å få VMGraf itererbar. Se f.eks. klassen MGraf.
|
| 4. | Lag metoden public void skrivGraf(String filnavn) throws IOException i klassen VMGraf. Den skal skrive ut informasjon om
grafen til filen med navn filnavn. Filen skal se ut slik som konstruktøren som leser fra fil (se
VMGraf), forventer at den skal være. Se også Oppgave 2
i Avsnitt 11.2.1.
|
![]() 11.2.5 Spenntrær og Prims algoritme
11.2.5 Spenntrær og Prims algoritme
I Avsnitt 11.1.7
ble et tre og spesielt et spenntre for en
urettet graf definert.
Hvis treet er vektet (kantene har vekt/lengde), definerer vi treets vekt til
å være summen av kantvektene. I en vektet og urettet graf er det av interesse å finne
et minimalt spenntre, dvs. et spenntre med minimal vekt.
Ta flg. vektede graf som eksempel:
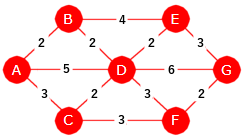 |
| Figur 11.2.5 a): Vektet graf med 7 noder |
Den vektede grafen over har mange spenntrær, f.eks. disse to:
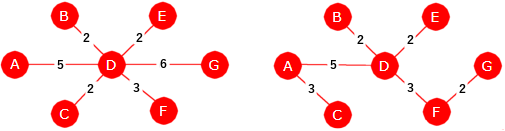 |
| Figur 11.2.5 b): Spenntrær - det venstre har vekt 20 og det høyre vekt 17 |
Ved å legge sammen kantvektene får vi at vekten til det venstre treet er 20 og til det til høyre 17. Men vi ser fort at dette ikke er minimale spenntrær. Målet nå er å finne et slikt et og det finnes normalt mange av dem. Det gjelder da å ta med færrest mulig av de «tunge» kantene og flest mulig av de «lette». Det finnes flere algoritmer. De to mest kjente er Prims algoritme (oppkalt etter Robert Prim) og Kruskals algoritme (oppkalt etter Joseph Kruskal). Vi starter med Prims algoritme og ser på Kruskals algoritme i neste avsnitt.
Viktige begreper: Kantene har formelt vekt, men her bruker vi lengde.
Dermed kan vi si at to nabonoder
X og Y har en avstand, dvs. kantens lengde. La T være et tre i en graf G (dvs. en subgraf som er sammenhengende
og uten sykler). En node X utenfor T sies å være en
nabo til T hvis X har minst
én nabonode i T. X sies å være nærmeste nabo til T hvis
X er den av naboene til T som har minst avstand til en node i T. Kanten mellom en slik X
og dens nærmeste nabo i T, kaller vi nærmeste kant.
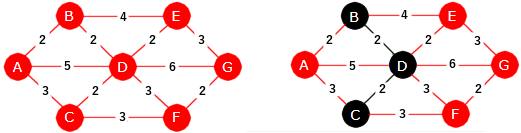 |
| Figur 11.2.5 c): Til venstre en graf G og til høyre et tre T i G |
Figur 11.2.5 c) over inneholder til venstre en graf G og til høyre et tre T i G. Treet T består av de tre svarte nodene og de to svarte kantene (mellom B og D og mellom C og D). Vi ser at alle de andre nodene nå er naboer til T siden hver av dem har minst en nabonode i T. F.eks. har A hele tre nabonoder i T. Men hvem av dem er nærmeste nabo til T? Det er både A og E. Den korteste kanten fra A til en node i T er den som går fra A til B med lengde 2. Tilsvarende er det for E. Korteste kant er den som går fra E til D (lengde 2). Kortest kant fra F (to kanter) har lengde 3 og korteste fra G lengde 6.
Prims algoritme har en ganske enkel idé. Start: En av grafens noder velges.
Den utgjør starttreet. Generelt: La T være treet vi har fått etter et antall trinn. Neste trinn er å innlemme
den nærmeste naboen til T (og dens nærmeste kant).
Hvis det er flere som ligger nærmest, er det likegyldig hvem som velges.
Hvis T ikke har noen nabonoder, er algoritmen ferdig.
Vi skal nå gjennomføre Prims algoritme på
grafen i Figur 11.2.5 a).
La f.eks. C være startnode. Den blir svart og utgjør starttreet T. Se til venstre
i figuren under. T har A, D og F som naboer og det er D som er nærmest (avstand 2). T
utvides med D og kanten fra C til D. Vi bruker svart farge på nodene og kantene i treet.
Se treet til høyre i figuren under:
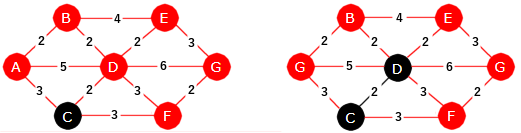 |
| Figur 11.2.5 d): Først velges en node (her C) og så noden som er nærmest C |
Nå er alle de røde nodene naboer til T (se til høyre i figuren over). Det er B og E som ligger nærmest T (begge med avstand 2). Da kan vi f.eks. velge B (og dermed kanten fra B til D):
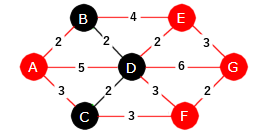 |
| Figur 11.2.5 e): Treet: to kanter, tre noder |
Nå er A og E nærmest treet T, begge med avstand 2 til T. Da kan vi f.eks. velge A (og kant A - B). I neste trinn må vi velge E (og kant E - D) siden den da vil være nærmest:
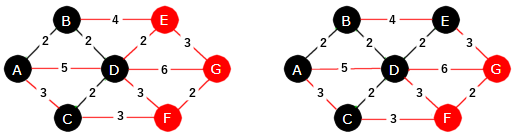 |
| Figur 11.2.5 f): Treet til venstre har 4 noder og det til høyre 5 |
Nå har T to naboer igjen, dvs. F og G. Begge har avstand 3 til T. Da spiller det ingen rolle hvem vi velger. Her velger vi F. Det er to kanter fra F til T med lengde 3. Begge kan velges og vi velger C - F. I neste runde må G velges og kanten F - G siden den er kortest:
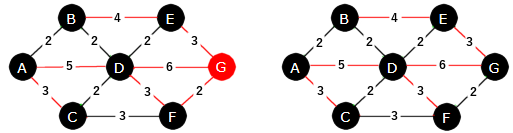 |
| Figur 11.2.5 g): Treet til venstre har 6 noder og det til høyre er et minimalt spenntre |
Vektsummen blir 13. Med kun de svarte kantene blir det flg. minimale spenntre:
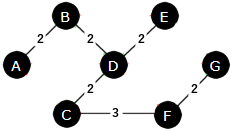 |
| Figur 11.2.5 h): Et minimalt spenntre |
Vi kan finne nærmeste nabo til et tre T ved å søke blant alle kantene fra treet til en nabo.
Dette blir brukbart effektivt hvis vi holder de aktuelle kantene i en heapbasert prioritetskø.
Noden innlemmes i treet ved at variabelen ferdig i noden
settes til true.
Flg. metode returnerer vekten til et minimalt spenntre, men ikke selve treet:
public int spenntrePrim0(String nodenavn) // 0. versjon, returnerer vekten { Node node = noder.get(nodenavn); // henter en node if (node == null) throw new NoSuchElementException(nodenavn + " er ukjent!"); PriorityQueue<Kant> kø = new PriorityQueue<>((a,b) -> a.vekt - b.vekt); kø.offer(new Kant(node,0)); // en 0-kant fra noden til seg selv int vekt = 0; // hjelpevariabel for summering for (int antallnoder = 0; antallnoder < noder.size(); ) { Kant kant = kø.poll(); // tar ut kanten med minst vekt Node nynode = kant.til; // noden som kanten går til if (!nynode.ferdig) // sjekker om noden hører til treet { nynode.ferdig = true; // innlemmes i treet vekt += kant.vekt; // øker vekten antallnoder++; // en node til i treet // de kantene til nynode som går til nabonoder utenfor treet for (Kant k : nynode.kanter) if (!k.til.ferdig) kø.offer(k); } } return vekt; // returnerer vekten til et minimalt spenntre } Programkode 11.2.5 a)
Vi kan teste dette på grafen i Figur 11.2.5 a)
(bruker vgraf2.txt) ved å la alle nodene etter tur
være første node i et tre. Du må ha med metoden nullstill() i din versjon av VGraf:
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf2.txt"; VGraf vgraf = new VGraf(url); for (char c = 'A'; c <= 'G'; c++) { String node = Character.toString(c); System.out.print(node + "-" + vgraf.spenntrePrim0(node) + " "); vgraf.nullstill(); } // Utskrift: A-13 B-13 C-13 D-13 E-13 F-13 G-13 Programkode 11.2.5 b)
Utskriften viser at lengden på et minimalt spenntre blir 13 uansett startnode. Obs: Metoden forutsetter
at grafen er sammenhengende. Hva skjer hvis den ikke er det?
Se Oppgave 2.
Det er litt mer krevende med en «manuell»
anvendelse av Prims algoritme på grafen under. Men prøv! Bruk f.eks. A som start. Du vil kunne få vekten på et minimalt
spenntre ved å bruke spenntrePrim0().
Data for grafen ligger på vgraf4.txt.
Se også Oppgave 3.
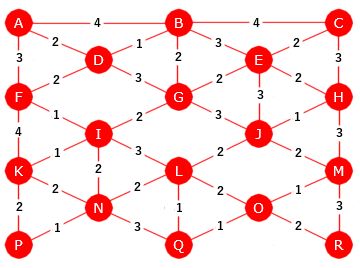 |
| Figur 11.2.5 i): En urettet graf med 18 noder og 36 kanter |
I den innerste for-løkken i
metoden spenntrePrim0()
blir alle kantene fra nynode til naboer utenfor treet, lagt inn i køen.
Når kanten med minst lengde tas ut, vil noden som kanten går til, være treets nærmeste nabo.
Hvis vi har n noder og m kanter, vil innlegging
og uttak fra køen i verste fall være av orden log(m). Se
også Prims algoritme - effektivitet.
Optimalisering Om mulig hadde det vært bedre med en kø med noder (og ikke kanter) slik at hver gang
vi tok ut en node, så ville det være den som var nærmeste nabo til det eksisterende treet. Da ville
innlegging og uttak isteden bli av orden log(n). Det er bedre siden n
normalt er en god del mindre enn m. Hvis vi benytter at klassen
Node i tillegg til ferdig, også har variablene
avstand og forrige, kan vi få til dette. Vi kan gjøre på samme måte som
den versjonen av Dijkstras metode vi har i
Programkode 11.2.3 d). Dvs. hver gang vi
tar ut en node (som så innlemmes i treet), så sjekker vi nodens naboer utenfor treet. Er det en vi ikke har sjekket før (har
«uendelig» som avstandsverdi), gir vi den kantlengden som verdi. Ellers, hvis kantlengden er mindre enn dens verdi,
oppdateres den. Dette kan gjøres i samme setning siden alle kantlengder er mindre enn «uendelig».
Hver gang en node får verdi (ny eller oppdatering), setter vi variablen forrige til franoden.
Dette gir bedre effektivitet:
public int spenntrePrim(String nodenavn) // ny og mer effektiv versjon { Node start = noder.get(nodenavn); // henter startnoden if (start == null) throw new NoSuchElementException(nodenavn + " er ukjent!"); record Avstand(Node node, int avstand) {} Queue<Avstand> kø = new PriorityQueue<>((a,b) -> a.avstand - b.avstand); start.avstand = 0; // avstand settes til 0 kø.offer(new Avstand(start, 0)); // legger startnoden i køen int vekt = 0; // hjelpevariabel for summering while (!kø.isEmpty()) { Avstand denne = kø.poll(); // den med minst avstandsverdi if (denne.node.ferdig) continue; // denne er allerede i treet for (Kant k : denne.node.kanter) // alle naboene til denne { Node nabo = k.til; // en av naboene if (!nabo.ferdig) // tar med kun de som ikke allerede er i treet { if (k.vekt < nabo.avstand) { nabo.avstand = k.vekt; // får ny verdi nabo.forrige = denne.node; // registrerer kanten kø.offer(new Avstand(nabo,nabo.avstand)); } } } // for denne.node.ferdig = true; // innlemmes i treet vekt += denne.node.avstand; // legger til kantvekten } // while return vekt; // treets vekt } Programkode 11.2.5 c)
Denne versjonen av spenntrePrim() returnerer som den
første, kun vekten på
et minimalt spenntre. Hva vil skje hvis den anvendes på en urettet og vektet graf som ikke er
sammenhengende. I den første førte det til en
NoSuchElementException. Se Oppgave 5.
En stor fordel med
denne versjonen er at det nå er lett å plukke ut informasjon fra grafen om hvilke kanter som inngår i treet.
Variabelen forrige forteller at det er kanten mellom node og
node.forrige
som hører til treet. Flg. metode returnerer en liste med kantinformasjon på
formen (A,B,2) hvis f.eks. kanten mellom A og B med lengde 2 inngår i treet:
public List<String> spenntrePrim()
{
if (noder.size() == 0) throw new IllegalStateException("Grafen er tom!");
String start = noder.keySet().iterator().next(); // en eller annen node
int vekt = spenntrePrim(start); // Programkode 11.2.5 c)
List<String> spenntre = new ArrayList<>(); // for kantene i spenntreet
for (Node n : noder.values()) // ser på alle nodene
{
StringJoiner sj = new StringJoiner(",", "(", ")");
if (n.forrige != null) // kanten mellom n og n.forrige
{
sj.add(n.navn).add(n.forrige.navn).add(Integer.toString(n.avstand));
spenntre.add(sj.toString()); // kanten legges i listen
}
}
spenntre.add("Vekt: " + vekt); // avslutter med å legge inn vekten
nullstill(); // setter variabelen forrige tilbake til false
return spenntre; // en liste med alle kantene i spenntreet
}
Programkode 11.2.5 d)
Prims algoritme virker uavhengig av hvilken startnode som velges. Det blir alltid et minimalt spenntre, men hvilke
kanter som inngår vil kunne variere. I metoden over brukes det første navnet som iteratoren i nøkkelmengden (keySet)
gir oss. Så brukes Programkode 11.2.5 c)
til å finne vekten av det minimale spenntreet. Deretter hentes de kantene som inngår og
det skjer ved hjelp av variablen forrige i nodene. Kantene legges i en liste.
Flg. kode tester dette på grafen i
Figur 11.2.5 a).
Resultatet blir ikke helt som Figur 11.2.5 h)
siden algoritmen starter med en annen node. I Figur 11.2.5 a)
inngar kanten mellom C og F i spenntreet, men den blir byttet ut med kanten mellom E og G i det som koden nedenfor vil gi.
Men det blir likevel et minimalt spenntre siden de to kantene har samme vekt.
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf2.txt"; VGraf vgraf = new VGraf(url); System.out.println(vgraf.spenntrePrim()); // Utskrift: [(B,A,2), (C,D,2), (D,B,2), (E,D,2), (F,G,2), (G,E,3), Vekt: 13] Programkode 11.2.5 e)
Metoden i Programkode 11.2.5 d)
gir en liste med kanter som tegnstrenger. Det er også mulig lage det slik at en graf returneres, dvs.
det minimale spenntreet som en egen graf uavhengig av den grafen spenntreet er laget for.
Se Oppgave 7.
Kan vi være sikre på at Prims algoritme alltid gir et minimalt spenntre? Dette tas opp under Prims algoritme - korrekthet.
En graf kan også representeres som en matrise - se
Avsnitt 11.2.4. Der er det også laget kode for Dijkstras algoritme
for å finne korteste vei i en rettet og vektet graf. Den samme teknikken kan brukes til å lage kode
for Prims algoritme i klassen VMGraf siden en urettet graf lages ved å ha en rettet kant hver vei.
Se Oppgave 8.
| 1. | Prims algoritme der C er startnode er vist fra
Figur 11.2.5 d) til
Figur 11.2.5 h).
Hvilket minimalt spenntre får vi med Prims algoritme hvis vi starter med A? Hva med G?
|
| 2. | Legg inn en ny node (f.eks. med navn H) i grafen i
Programkode 11.2.5 b),
men ingen flere kanter. Da vil H bli en isolert node og grafen blir usammenhengende. Hva
skjer hvis programmet kjøres? Legg inn kode i
spenntrePrim0() som
gir en feilmelding som sier at treet er usammenhengende hvis treet er det.
|
| 3. | a) Bruk Prims algoritme til å finne et minimalt spenntre for grafen i
Figur 11.2.5 i).
Start fra A. Det er mange minimale spenntrær. I algoritmens gang vil det ofte være
flere kanter med minst vekt som kan velges. Bruk f.eks. som strategi at i så fall
velges den av dem som sist ble «valgbar». Det vil ofte føre til at
en ny node som skal inn i treet, er nabo til den som sist ble innlemmet. Kanter
blir «valgbare» i sortert rekkefølge mhp. tilnoden.
|
b) Metoden spenntrePrim0()
gir vekten på et minimalt spenntre, men ikke de kantene som inngår. Gjør den om
slik at den returnerer en liste med det minimale spenntreets kanter.
Hvis f.eks. en kant mellom A og B med lengde 2 inngår, så skal listen inneholde tegnstrengen
(A,B,2). Siden grafen er urettet har ikke kantene retning. Derfor er det likegyldig om
det blir (A,B,2) eller (B,A,2). Kan du få det til at kantene kommer i den rekkefølgen
som den foreslåtte strategien i Oppgave 3a) vil gi?
| |
| 4. | Skal Prims algoritme fungere, må grafen være urettet. I utgangspunktet har en kant
retning. En urettet kant er derfor gitt som to rettede kanter med samme vekt, men
i hver sin retning. Lag metoden boolean erUrettet(). Den skal sjekke om en graf er urettet.
|
| 5. | Hvis versjonen av spenntrePrim() fra
Programkode 11.2.5 a)
blir brukt på en usammenhengende graf, kastes det en NullPointerException.
Se Oppgave 2. Hva skjer hvis vi bruker versjonen fra
Programkode 11.2.5 c)?
|
| 6. | Metoden i Programkode 11.2.5 d)
returnerer en liste over de kantene som inngår i det minimale spenntreet. Hvis grafen har kun én node,
så vil spenntreet kun bestå av den ene noden og dermed ingen kant. Slik som metoden nå er laget, returneres
ingen kanter i dette tilfellet. Gjør om koden slik at hvis navnet på den enslige noden er X, så returneres
(X,X,0). Dvs. en kant fra noden til seg selv med lengde 0.
|
| 7. | Metoden fra
Programkode 11.2.5 a)
returnerer vekten av et minimalt spenntre og endrer kun variablen ferdig i nodene.
Metoden fra
Programkode 11.2.5 c)
returnerer også vekten av et minimalt spenntre, men gjør endringer i alle variablene i nodene -
både ferdig, forrige og avstand.
Det muligjør metoden VGraf spenntrePrimGraf(). Den skal returnere det minimale spenntreet
som en separat graf. Lag den.
|
| 8. | Klassen VMGraf (se Avsnitt 11.2.4)
bruker matriserepresentasjon for vektede grafer. Lag metoden
int spenntrePrim(String node) for
denne klassen. Lag den med samme idé som i
Programkode 11.2.5 c). Hent
også ideer fra Dijkstras algoritme for VMGraf.
Lag også versjoner av Programkode 11.2.5 d)
og for metoden det bes om til slutt i Oppgave 7, for klassen VMGraf.
|
![]() 11.2.6 Union-Finn strukturer
11.2.6 Union-Finn strukturer
Avsnitt 11.2.5 handler om Prims algoritme
for å finne minimale spenntrær. Vi skal også se på Kruskals algoritme for det samme. Men for å kunne
implementere den er det gunstig å ha tilgang til en såkalt
Union-Finn
datastruktur. Vi velger derfor å lage en slik struktur før vi i neste
avsnitt (Avsnitt 11.2.7) ser på Kruskals algoritme.
En Union-Finn datastruktur inneholder disjunkte ikke-tomme mengder. Disjunkt betyr at to og to av dem ikke har noe felles. Mengdene {A, B}, {C}, {D, E, F, G} og {H, I, J} er disjunkte.
En Union-Finn datastruktur skal ha tre hovedoperasjoner.
1) Til et gitt element X må det være mulig å «få tak i» (Finn) den
mengden som X er element i. 2) Det må være mulig å opprette en ny mengde {X} med kun ett element.
Det forutsetter at elementet X ikke er element i noen av de mengdene som allerede finnes.
3) Det må være mulig å slå sammen (Union) to gitte mengder.
Den vanlige måten å lage en Union-Finn datastruktur på er å la hver mengde være representert ved
et tre - tilsammen en «skog». En isolert node er et tre med én node:
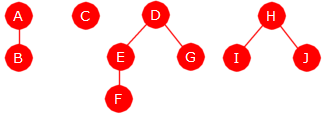 |
| Figur 11.2.6 a): {A, B}, {C}, {D, E, F, G} og {H, I, J} |
I figuren over har ingen av nodene mer enn to barn. Men generelt vil det ikke være noen grense for hvor mange barn en node kan ha. De tre sentrale operasjonene nevnt over kan lett implementeres i en slik datastruktur. 1) Vi lar hvert tre være representrert ved treets rotnode. Det å finne den mengden som inneholder et gitt element, går da først ut på å få tak i noden som inneholder elementet og så gå derfra opp til roten. Til det trenger vi en nodestruktur med forelderreferanser. 2) En ny mengde med kun ett element får vi til ved å opprette en ny isolert node med det elementet. 3) To mengder slås sammen ved at de tilhørende trærne «slås sammen». Det gjør vi ved å la roten i det av dem som har færrest noder, bli et barn til den andre roten. Flg. figur viser hvordan det blir etter at {D, E, F, G} og {H, I, J} er slått sammen:
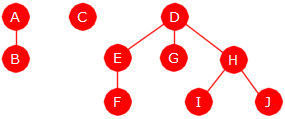 |
| Figur 11.2.6 b): {D, E, F, G} union {H, I, J} |
Sammenslåingen av {D, E, F, G} og {H, I, J} har gitt et tre der rotnoden har 3 barn. Poenget med å la rotnoden
i treet med færrest noder bli barn til den andre roten, er at det gir et «flatere» tre. Sjekk hva
som hadde skjedd hvis vi gjorde motsatt (se Oppgave 1)!
Det er
generelt et mål å få trærne så «flate» som mulig. Dermed vil ingen node ligge langt fra roten i
tilhørende tre. I hvert fall må avstanden minst være av logaritmisk orden mhp. antall noder.
Trærne kan gjøres «flatere» på enda en måte. Hver gang vi ønsker å finne mengden/treet som et bestemt element
hører til, må vi først finne elementets node og så gå derfra opp til roten. Da kan vi avslutte med å la noden bli et barn til rotnoden.
Ta som eksempel at vi skal finne mengden/treet til J i
Figur 11.2.6 b).
Da avslutter vi den prosessen med la forelderreferansen i J-noden
gå direkte til rotnoden, dvs. til D-noden. Hvis J-noden var rot i et (ikke-tomt) tre, ville treet «fulgt med på lasset»:
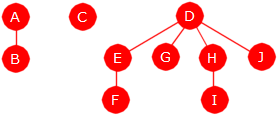 |
| Figur 11.2.6 c): J-noden har rykket opp |
Vi starter med flg. skjelett for klassen UnionFinn:
import java.util.*; public class UnionFinn<T> { private static final class Node { private Node forelder = null; private int antall = 1; } Map<T, Node> noder = new HashMap<>(); // Private hjelpemetoder skal inn her // Øvrige metoder skal inn her } Programkode 11.2.6 a)
Vi velger å lage klassen generisk, dvs. en generisk type T for elementene.
Det gjør klassen litt mer ressurskrevende, men gir enkel og gjennomsiktig kode. I noen
implementasjoner av en slik klasse brukes heltall (int) som elementer. Da kan de også inngå som tabellindekser
og dermed gi smarte løsninger. Mer her bruker vi de samme ideene som vi har brukt før i forbindelse med koding av
trestrukturer. Nodeklassen inneholder en referanse til forelderen og en antall-variabel. Hensikten med den siste er at
rotnoden i et tre skal ha informasjon om antallet noder i treet. En Map
der T er nøkkelverdi og Node tilhørende verdi, brukes til å finne noden til et gitt element.
1) Finn Vi gir private hjelpemetoder navn etter intern datastruktur (node/tre/rot),
mens offentlige metoder relateres til mengder og elementer. For å finne roten i treet som inneholder et gitt element,
må vi kunne gå fra elementets node p og oppover til roten:
private static Node finnRot(Node p) // første versjon { while (p.forelder != null) p = p.forelder; // vi går oppover return p; } Programkode 11.2.6 b)
Men som nevnt over, vil det være lurt samtidig å «løfte opp» noden (og det treet den er rotnode for hvis den ikke er en bladnode) til å bli rotnodens barn. Det koster svært lite ekstra, kun en hjelpevariabel og en avsluttende tilordning:
private static Node finnRot(Node p) // en bedre versjon { Node rotP = p; // hjelpevariabel while (rotP.forelder != null) rotP = rotP.forelder; // vi går oppover if (p != rotP) p.forelder = rotP; // har vi gått oppover? return rotP; } Programkode 11.2.6 c)
Internt i UnionFinn handler det om noder og trær. Men det er implementasjonsdetaljer. En bruker
av klassen vil tenke i form av elementer og mengder. En metode som returnerer mengden til et element, bør
derfor ha et navn som sier det. Men hva skal metoden returnere? I implementasjonen brukes rotnoden som representant for
mengden/treet. Men det gir ikke mening å returnere den. For det første er den lokale nodeklassen privat
og er dermed ikke tilgjengelig utenfor klassen UnionFinn. For det andre ville en nodereferanse gi direkte
tilgang til det indre av UnionFinn. Det kan vi ikke tillate. Her nøyer vi oss derfor med å la
metoden returnere et heltall, 0 hvis elementet er ukjent og ellers lik antallet elementer i den
mengden som inneholder det gitte elementet.
public int finnMengde(T e)
{
Node p = noder.get(e);
return p == null ? 0 : finnRot(p).antall;
}
Programkode 11.2.6 d)
2) Flg. offentlige metode oppretter en ny mengde med kun ett element. Hvis det er et nytt element, returneres true. Hvis ikke,
dvs. hvis det allerede finnes en mengde som inneholder elementet, returneres false. Vi tillater ikke null som element:
public boolean nyMengde(T e)
{
if (e == null) throw new NullPointerException("Ikke null som element!");
if (noder.get(e) != null) return false; // elementet finnes fra før
else
{
noder.put(e, new Node()); // legger inn det nye elementet
return true;
}
}
Programkode 11.2.6 e)
3) Union Vi skal slå sammen (danne unionen av) de to mengdene som inneholder henholdsvis
element e1 og element e2.
Men hva hvis e1 eller e2 er ukjent? En mulighet er å kaste et unntak. Men vi
kan isteden opprette en mengde med ett element (en node) hvis elementet er ukjent.
Det forenkler bruken av metoden union().
Videre skal metoden returnere 0 hvis e1 og e2 hører til samme mengde og ellers
returnere antall elementer i unionen. Vi lager først en privat hjelpemetode som finner noden til et kjent element
og hvis det er ukjent, lager en ny node for det elementet. Den blir delvis lik metoden
nyMengde():
private Node node(T e) { if (e == null) throw new NullPointerException("Ikke null som element!"); Node p = noder.get(e); if (p == null) // dette er et nytt element { p = new Node(); // ny node noder.put(e, p); // legger inn elementet og noden } return p; } Programkode 11.2.6 f)
To trær forenes (to mengder slås sammen) ved at roten i det
som har færrest noder blir barn til den andre roten.
Hvis de har like mange noder, blir det hipp som happ. Obs: Hvis et element (e1 eller e2)
er ukjent, blir det først opprettet en node for elementet:
public int union(T e1, T e2) // { Node rot1 = finnRot(node(e1)); Node rot2 = finnRot(node(e2)); if (rot1 == rot2) return 0; // e1 og e2 er i samme mengde if (rot1.antall < rot2.antall) // treet til e1 har færrest noder { rot1.forelder = rot2; rot2.antall += rot1.antall; return rot2.antall; } else // treet til e2 har færrest noder eller de har like mange { rot2.forelder = rot1; rot1.antall += rot2.antall; return rot1.antall; } } Programkode 11.2.6 g)
Legg merke til at metoden union() også kan brukes til å lage en mengde med ett element, dvs. slik
som også metoden nyMengde() kan gjøre. Det er kanskje en litt
kunstig måte å gjøre det på, men det går an:
UnionFinn<Character> mengder = new UnionFinn<>(); mengder.nyMengde('A'); // en mengde med kun A som element mengder.union('B','B'); // en mengde med kun B som element
Obs! Kallet: mengder.union('B','B') gir 0 som resultat
fordi B ligger i samme mengde som B. En kunne kanskje tro at det skulle bli 1 siden det er antallet elementer i den mengden som kun inneholder B.
Det hadde vært fordelaktig og da ikke minst for å kunne teste disse metodene, at vi kunne få skrevet ut de elementene som en mengde har. Ta f.eks. mengden {A, B, C, D, E}. Uansett hvilket av de fem elementene vi tar utgangspukt i, bør vi få at mengden som elementet hører til, er {A, B, C, D, E}. Det kan vi få til, men datastrukturen er ikke tilrettelagt for en slik oppgave. Vi lager likevel en metode for dette selv om den blir ineffektiv når det er mange elementer. Vi må først finne rotnoden til mengden/treet som inneholder det gitte elementet. Deretter må vi for hvert eneste element finne «dets rot» og så sjekke om den er lik. Heldigvis blir koden kort og enkel:
public String mengde(T e) { Node p = noder.get(e); if (p == null) throw new NoSuchElementException("Ukjent element " + e + "!"); StringJoiner s = new StringJoiner(", ", "{", "}"); Node rot = finnRot(p); for (T ee : noder.keySet()) { if (finnRot(noder.get(ee)) == rot) s.add(ee.toString()); } return s.toString(); } Programkode 11.2.6 h)
Flg. kodebit viser hvordan dette fungerer. Hvis du vil teste dette hos deg selv, må du ha klassen
UnionFinn i ditt prosjekt:
UnionFinn<Character> mengder = new UnionFinn<>(); mengder.union('A', 'B'); // {A, B} mengder.union('B', 'C'); // {A, B} U {C} = {A, B, C} mengder.union('D', 'E'); // {D, E} mengder.union('A', 'D'); // {A, B, C} U {D, E} = {A, B, C, D, E} System.out.println(mengder.mengde('A')); // Utskrift: {A, B, C, D, E} Programkode 11.2.6 i)
Algoritmeanalyse Effektiviteten til denne implementasjonen av en
UninonFinn datastrktur står og faller med hvordan trærne blir.
Det er som tidligere nevnt viktig å få trærne så «flate» som mulig slik at ingen
noder ligger langt fra roten i tilhørende tre. Hvordan vil det bli her? Det viktige er at
når to trær settes sammen, blir roten i det treet som har færrest noder barn til roten i det
andre treet. Hvis de har like mange noder, blir roten i det andre treet barn til roten i det første.
Dermed er det kun i dette tilfellet at det blir høydeendringer.
Trær som representerer mengder oppstår ved at to og to trær settes sammen hvor det ene (eller
begge) kan ha kun én node. Gitt at vi skal lage et tre med
n noder. Et ytterpunkt er at vi starter med én node og så legger til
en og en node fortløpende. Først får treet to noder, men så vil hver ny node på
grunn av innleggingsregelen, bli barn til den første noden. Dermed blir treet helt
«flatt». En rot og resten av nodene er barn til roten.
Motsatt blir det størst høyde når trær med like mange noder slås sammen. Et tre med
maksimal høyde (og n noder) kan lages slik: Først slås to og to noder sammen.
Det gir n/2 trær med 2 noder og høyde 1. Så slår vi sammen
to og to av disse og det gir n/4 trær med 4 noder og høyde 2. Osv. til vi får
ett tre. Det skjer etter log2(n) «runder» og treet
får også høyde log2(n). Ta n = 8 som eksempel
med bokstavene fra A til H som elementer. Den beskrevne prosessen vil gi et tre med
høyde log28 = 3, dvs. treet under til venstre:
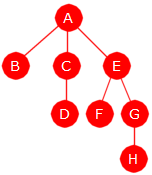 |
| Figur 11.2.6 d) |
Med andre ord vil et tre med
n noder av den typen som kan oppstå her, få en høyde mellom 0
og log2(n). Vi kan dermed konkludere med at
metodene finnMengde() og union() i verste fall er av logaritmisk orden.
Metoden mengde() som gir alle elementene i en gitt mengde, er imidlertid
ineffektiv, dvs. av orden nlog2(n) i verste fall og
orden n som best.
I beskrivelsen over har vi ikke sett på som skjer i hjelpemetoden finnRot().
Den starter på en node og går opp til roten og avslutter med at noden «flyttes opp» som
barn til rotnoden. Det gjør den gjennomsnittlige nodedyben mindre.
Tilsammen gir dette en UnionFinn struktur som er god nok for de fleste formål.
| 1. | Slå sammen trærne for {D,E,F,G} og {H,I,J} i
Figur 11.2.6 a) slik at rotnoden i treet
med flest noder blir barn til rotnoden i det andre treet.
|
| 2. | Gitt koden:
UnionFinn<Character> mengder = new UnionFinn<>(); mengder.nyMengde('A'); for (char c = 'B'; c <= 'E'; c++) mengder.union('A', c); System.out.println(mengder.mengde('A'));Hvordan vil det underliggende treet se ut? |
| 3. | Hver mengde er representert ved et tre. Målet er at trærne har liten høyde. Lag
metoden: public int maksHøyde() i klassen UnionFinn. Den skal returnere høyden til det treet som har størst høyde. Husk at høyden i et tre
er avstanden fra rotnoden til den noden som ligger lengst ned. Gjør så et kall på denne metoden
til slutt i koden i Oppgave 2.
|
| 4. | Lag kode som konstruerer et tre med bokstavene A til H som elementer slik som beskrevet under
Algoritmeanalyse.
Bruk så metoden maksHøyde() fra Oppgave 3 til å vise at høyden blir 3.
|
![]() 11.2.7 Kruskals algoritme
11.2.7 Kruskals algoritme
Denne algoritmen har som Prims algoritme, en enkel idé. Den tar for seg kantene etter tur
og da i stigende rekkefølge med
hensyn på vekten/lengden. I Prims algoritme er det et tre som hele tiden utvides. Men her
dannes det under algoritmens gang disjunkte subtrær som til slutt blir et spenntre.
Et subtre er en subgraf som er sammenhengende og uten sykler.
Her skal vi bruke en annen graf enn tidligere til å demonstrere gangen i algoritmen. Grafen i
Figur 11.2.5 a) har mange
kanter med samme vekt. Det ville ha gitt stor frihetsgrad i Kruskals algoritme. Vi skal isteden
bruke en graf der alle kantene har forskjellige vekt. I figuren under står grafen til venstre
og en graf med kun nodene (ingen kanter) til høyre:
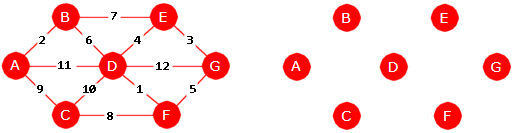 |
| Figur 11.2.7 a): En graf der kantene har forskjellig vekt |
Kanten mellom D og F har minst vekt. Så kommer kanten mellom A og B og så den mellom E og G. Tar vi med disse tre kantene blir det ingen sykler. Det gir flg. figur:
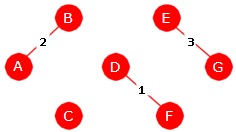 |
| Figur 11.2.7 b): Fire subtrær |
I figuren over har vi fire subtrær, tre med to noder og et med én node. Neste kant i rekkefølgen er den mellom D og E (vekt 4). Den tar vi med siden den ikke fører noen sykler. Se grafen under til venstre. Deretter kommer kanten mellom F og G (vekt 5). Men den kan vi ikke ta med siden vi da vil få en sykel. Vi hopper over den og tar den neste, dvs. kanten mellom B og D (vekt 6). Den er ok siden det ikke blir noen sykel av den. Se grafen til høyre på figuren under:
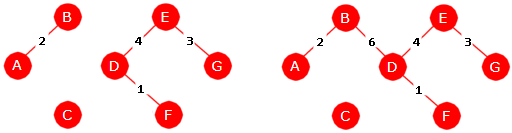 |
| Figur 11.2.7 c): Til venstre: tre subtrær Til høyre: to subtrær |
Nest kant i rekkefølgen er den mellom B og E (vekt 7), men den tar vi ikke med siden den fører til en sykel. Så er det kanten mellom C og F (vekt 8) og med den går det bra:
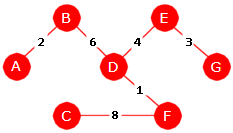 |
| Figur 11.2.7 d): Et minimalt spenntre |
Nå er vi ferdig sidene alle nodene er tatt med. Resultatet er et spenntre med sammenlagt vekt på
24. Påstanden er at dette er et minimalt spenntre. Det å bevise at Kruskals algoritme alltid
gir et minimalt spenntre tas opp i neste avsnitt
om algoritmeanalyse. Men hvis du har kode for
Prims algoritme (f.eks. Programkode 11.2.5 c )
i ditt system, kan du sjekke hva den finner frem til. Data for grafen ligger på
vgraf5.txt.
Kruskals algoritme er enklere og raskere å bruke på en tegning enn Prims algoritme. Ta f.eks. grafen i
Figur 11.2.5 i) som har 18 noder og
36 kanter. Hvis du har den på papir er det bare å markere fortløpende de kantene som skal være med og fjerne
(krysse ut) de som ikke kan være med fordi de fører til en sykel. Ta først alle kantene med vekt 1, så de
med vekt 2, osv. til alle nodene har kommet med. Se Oppgave 2.
Kruskals algoritme er imidlertid vanskeligere å kode enn Prims algoritme og spesielt det å få kode som er effektiv.
Første del er enkel. Den går ut på å legge alle kantene i en prioritetskø. Derfra får vi dem i
stigende rekkefølge. Men det vanskelige punktet er å avgjøre om en ny kant sammen med det vi har fra før,
fører til en sykel eller ikke. Men det kan heldigvis løses ved hjelp av en union-finn-struktur,
f.eks. klassen UnionFinn fra Avsnitt 11.2.6.
I Kruskals algoritme kan vi se på nodene som mengdeelementer.
Vi bruker grafen i Figur 11.2.7 a)
som eksempel. Kanten mellom D og F har lavest vekt og det gir mengden {D, F}. Nest lavest vekt har
kanten mellom A og B og dermed {D, F}. Så kommer {E, G}. Deretter kanten mellom D og E.
Men D ∈ {D, F} og E ∈ {E, G}. Da slås de to sammen til
{D, E, F, G}. Neste kant i rekkefølgen etter stigende vekt er den fra F til G.
Men de to ligger i samme mengde. Det betyr at det å ta med den kanten vil gi en sykel, så den hopper vi over.
Slik fortsetter vi. En kant der endepunktene allerede ligger i en mengde tas ikke med. Når en mengde
inneholder alle nodene, er vi ferdig.
Det er naturlig å la en metode som implementerer Kruskals algoritme, ligge i klassen VGraf.
Det er viktig å huske at begrepet spenntre kun har mening i urettede grafer. Klassen VGraf
er til både for rettede og urettede grafer. En kant i VGraf er et objekt av typen
Kant og den har retning. I en urettet graf har ikke
kantene retning. Ta som eksempel en kant mellom A og B. Det løses datateknisk ved at det opprettes
to kanter (to instanser av klassen Kant) med
retning hver sin vei. Dvs. en kant fra A til B og en fra B til A.
En implementasjon må starte med at kantene legges inn i en prioritetskø med hensyn på vekt.
Da kan vi ikke bruke klassen Kant siden
den ikke inneholder informasjon om den noden som kanten går fra. Den inneholder kun
kantvekten og noden kanten går til. Legg også merke til at i klassen VGraf
er et nodenavn alltid av typen String. Vi lager derfor en lokal record
for dette formålet. Men tanke på utskrifter velger vi å omkode dens toString-metode:
record NyKant(String fra, String til, int vekt) { public String toString() { return "(" + fra + "," + til + "," + vekt + ")"; } } Programkode 11.2.7 a)
Hvis en kant fra A til B har lengde 5, blir resultatet: (A,B,5)
Først må det opprettes en prioritetskø med en kompartor som ordner etter kantvekt:
PriorityQueue<NyKant> kø = new PriorityQueue<>((a,b) -> a.vekt - b.vekt);
I en urettet graf vil det, som nevnt over, gå kanter begge veier mellom noder. Men det holder å ta med den ene av dem.
Hvis det fra en node A går kanter til B, C og D, så tar vi med dem. Deretter setter vi A som ferdigbehandlet
(variabelen ferdig i klassen Node). Når vi
så kommer til B, tar vi ikke med kanten fra B til A siden A er ferdig:
for (Node p : noder.values()) // alle nodene { for (Kant kant : p.kanter) { if (!kant.til.ferdig) kø.offer(new NyKant(p.navn, kant.til.navn, kant.vekt)); } p.ferdig = true; } nullstill(); // setter ferdig tilbake til false Programkode 11.2.7 b)
For å kunne teste dette legger vi de kantene som er med i det minimale spenntreet som Kruskals algoritme finner, i en liste. Da er det bare å kode resten av algoritmen:
List<String> liste = new ArrayList<>(); // en liste for kanter UnionFinn<String> mengder = new UnionFinn<>(); // elementene er av typen String int vektsum = 0; // vekten til det minimale spenntreet while (!kø.isEmpty()) // tar fra køen { NyKant kant = kø.poll(); // tar ut en kant int antall = mengder.union(kant.fra, kant.til); // 0 hvis de er i samme mengde if (antall > 0) { vektsum += kant.vekt; // øker vekten liste.add(kant.toString()); // denne kanten hører til spenntreet } if (antall == noder.size()) break; // alle noder er tatt med } liste.add("Vekt: " + vektsum); // tar med vekten på treet Programkode 11.2.7 c)
Alt over hører hjemme i en metode som vi velger å kalle spenntreKruskal(). Den skal ha
List<String> som returtype for å kunne returnere listen med kanter som ble bygget opp.
Hvis du ikke selv vil sette sammen dette til en metode, kan du finne en ferdig versjon under
spenntreKruskal. Metoden hører hjemme
VGraf.
Hvis du har VGraf og
klassen UnionFinn
i ditt prosjekt, vil flg. programbit kunne
kjøres på data for grafen i Figur 11.2.7 a):
String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf5.txt"; VGraf vgraf = new VGraf(url); System.out.println(vgraf.spenntreKruskal()); // Utskrift: [(D,F,1), (A,B,2), (E,G,3), (D,E,4), (B,D,6), (C,F,8), Vekt: 24] Programkode 11.2.7 d)
| 1. | Bruk Kruskals algoritme direkte på tegningen av grafen i
Figur 11.2.5 a).
Den grafen har mange kanter med samme vekt. Rekkefølgen en tar dem i er likegyldig. Men det
vil kunne gi forskjellige minimale spenntrær. Kjør så
Programkode 11.2.7 d)
med data for den grafen, dvs. vgraf2.txt. Blir det samme resultat?
| ||
| 2. | Gjør som i Oppgave 1, men med grafen i
Figur 11.2.5 i).
Data på vgraf4.txt
| ||
| 3. | Hvis du har lagt inn
spenntrePrim(String nodenevn) og
spenntrePrim() i klassen
VGraf, så kan du bruke dem til å se hva Prims algoritme gir.
| ||
| 4. | Gitt flg. graf. Finn et minimalt spenntre ved hjelp av Kruskals algoritme. Lag så en fil med data
som genererer grafen (kanter begge veier) og bruk Programkode 11.2.7 d).
Obs: Lokale filer må oppgis på url-form og da med file som protokoll. F.eks. har undertegnede dette på
en lokale fil med url: file:///c:/EclipseAlgDat/AlgDat/graf.txt
| ||
| 5. | Tegn dine egne urettede grafer og bruk Kruskals algoritme på dem. Lag så datafiler med den informasjonen som trengs
for å bygge opp opp de urettede grafene. Husk at det må gå kanter begge veier. Hver linje starter med et
nodenavn (f.eks. en bokstav) og så nodenavn og vekt for de nodene det går en kant til. F.eks. ser datafilen til
Figur 11.2.7 a) slik ut:
A B 2 C 9 D 11 B A 2 D 6 E 7 C A 9 D 10 F 8 D A 11 B 6 C 10 E 4 F 1 G 12 E B 7 D 4 G 3 F C 8 D 1 G 5 G D 12 E 3 F 5Når du bruker egne filer må du likevel oppgi dem på url-form, men da med file som protokoll.
| ||
| 6. | Hvis du er usikker på om en graf er urettet, kan du lage en metode som sjekker grafen. En slik
metode er laget for uvektede grafer - se Programkode 11.1.2 i)
og det ble bedt om en for vektede grafer i Oppgave 4 i Avsnitt 11.2.5.
|
![]() 11.2.8 Algoritmeanalyse
11.2.8 Algoritmeanalyse
La n være «størrelsen» på den oppgaven som en
algoritme skal løse der ƒ( n ) gir antallet
arbeidsoperasjoner som funksjon av n. Det kan være vanskelig å finne en slik
funksjon og spesielt hvis algoritmen påvirkes av de verdiene som behandles.
Da skiller vi normalt mellom gjennomsnittlig effektivitet og effektiviteten i det verste tilfellet.
Som oftest er det enklere å finne en funksjon for det verste tilfellet enn for det gjennomsnittlige.
I analysen brukes
begrepene O (ƒ( n )),
Ω (ƒ( n )) og
Θ (ƒ( n )). Hvis en algoritme er
O (ƒ( n )), betyr det at ƒ( n )
er en asymptotisk øvre grense for antallet operasjoner og med Ω (ƒ( n )) en
asymptotisk nedre grense. Hvis de to er like, er algoritmen Θ (ƒ( n )).
Se Avsnitt 1.8.5.
Her i kompendiet har den mer upresise formen «av orden ƒ( n )» som oftest blitt brukt. I praksis har den som oftest blitt brukt når det korrekte hadde vært å bruke Θ (ƒ( n )). Dvs. tilfellene der det har vært mulig å beregne forholdsvis nøyaktig hvor mange operasjoner som utføres. Noen steder er også utrykket «maksimalt av orden ƒ( n )» brukt. Det er egentlig det samme som O (ƒ( n )). Vi fortsetter denne uformelle praksisen siden det gir en god nok indikasjon på hvordan algoritmer oppfører seg.
Dijkstras algoritme - Effektivitet
Anta at vi har en sammenhengende graf med n noder og m kanter.
Det betyr spesielt at m ≥ n - 1. En funksjon for arbeidsmengde
vil nå være en funksjon av både m og n.
Algoritmen må ha en startnode. Anta at alle noder kan nås fra den. En
forutsetning for at algoritmen skal virke er at ingen kanter har negativ vekt.
Metoden i Programkode 11.2.3 a)
er forholdsvis enkel å analysere. De aktive nodene holdes i
en usortert tabell (en ArrayList). En fordel med det er at hvis en aktiv node får endret sin
avstandsverdi, behøver ikke noden skifte plass i tabellen. Når den er usortert må vi uansett
lete gjennom hele tabellen for å finne den «minste». I koden blir den minste tatt ut
av tabellen ved en remove. Det betyr at «hullet» i tabellen må
tettes igjen. Det kan forbedres. Se Oppgave 2 i
Avsnitt 11.2.3.
I while-løkken tas ut én og én node. Hvis det i gjennomsnitt er k aktive noder,
er arbeidet med å ta ut en node av orden k. For hver node blir dens
direkte etterfølgere (kantene) behandlet (med en eller flere operasjoner). Problemet er at det ikke er
mulig å vite generelt hvor stor k er. Men den kan i verste fall være stor.
Ta f.eks. en graf der det går en kant fra startnoden til
samtlige andre noder. Etter at startnoden er tatt ut vil alle de andre nodene bli aktive, dvs.
n - 1 stykker. Deretter synker det med én om gangen. I gjennomsnitt blir
det n/2. Det betyr at
Programkode 11.2.3 a)
i verste fall er av orden m + n². Men i praksis vil dette fungere greit for små grafer.
Den versjonen av Dijkstras algoritme vi har i
Programkode 11.2.3 d)
er litt verre å analysere. Der bruker vi en binærheapbasert prioritetskø for de aktive nodene.
Hvis en ser analyser av dette andre steder, tenker man seg der at køen også tillater
endringer på noder som ligger i køen og at en slik endring er av logaritmisk orden mhp. n.
En slik prioritetskø er mulig å lage. I så fall kommer man til at
algoritmen er av orden n + m log( n ) i det verste tilfellet.
Men siden m ≥ n - 1, vil m log( n ) være
det dominerende leddet. Dermed orden m log( n ).
Men i vår prioritetskø
(PriorityQueue)
kan ikke verdier som allerede ligger i køen, endres. I
Programkode 11.2.3 d)
er det løst ved at køen isteden inneholder avstandsobjekter. Hvis avstanden i en node må reduseres,
legges et nytt avstandsobjekt i køen med samme node. Dermed vil den kunne ha
mange avstandsobjekter med samme node. While-løkken går så lenge køen ikke er tom og
dermed ofte mer enn n ganger. Nå er m < n² og
dermed log( m ) < log( n² ) = 2log( n ).
Det betyr at denne implementasjonen likevel er av orden m log( n )
i det verste tilfellet. I praksis vil denne versjonen være god nok for de aller fleste formål.
Det er mulig å implementere Dijkstras algoritme enda litt mer effektivt. Det kan en få til ved å bruke en Fibonacciheap og da vil det kunne bli av orden m + n log( n ) i det verste tilfellet.
Dijkstras algoritme - Korrekthet
Nodene er delt i tre: 1) de ubehandlede,
2) de aktive og 3) de ferdigbehandlede. Algoritmen har en løkke der den aktive noden X
som har minst avstandsverdi, tas ut. Så behandles de direkte etterfølgerne Y som
ikke er ferdigbehandlet. Lengden på veien dit er
X.avstand pluss lengden på kanten fra X til Y.
Hvis Y er ubehandlet, får den tilordnet denne veilengden og hvis
den er aktiv (vi har vært der før) og veilengden er mindre enn Y.avstand, blir
denne veilengden ny avstandsverdi.
Setning 1: Gitt en rettet og vektet graf der ingen vekt er negativ.
Når en node (i Dijkstras algoritme) tas ut, er dens avstandsverdi lik lengden på korteste vei dit.
Dette bevises ved hjelp av et induksjon:
Basistrinnet: Den første som tas ut er startnoden og den har 0 som avstandsverdi. Det stemmer med setningen.
Induksjonstrinnet: Anta at startnoden er tatt ut (og dermed ferdigbehandlet).
La så X stå for tur til å bli tatt ut. Induksjonsantagelsen er at setningen stemmer
for alle noder som er tatt ut tidligere. La vei være en korteste vei fra
startnoden til X og anta at lengden til vei er mindre enn X.avstand.
Følg vei fra start og la Z være den første noden vi kommer til som ikke er
tatt ut tidligere. Da vil den direkte forgjengeren U til Z på vei være
tatt ut.
 |
Figur 11.2.8 a): vei - en korteste vei fra start til X |
Z har avstandsverdi siden den i hvert fall fikk det
når U ble tatt ut. Men den kan ha blitt oppdatert senere.
Induksjonsantagelsen sier nå at U.avstand er lik lengden på korteste vei
til U og den må være like lengden av den delen av vei som går fra fra start til U.
Hvis det hadde vært en enda kortere vei til U, så ville det også ha gitt oss en enda kortere vei
til X. Videre kan ikke Z.avstand være større enn summen U.avstand
+ kantlengde(U,Z) og denne må igjen være mindre enn eller lik lengde(vei), dvs. lengden til vei.
Dermed får vi flg. ulikheter:
Z.avstand ≤ U.avstand + kantlengde(U,Z) ≤ lengde(vei)
< X.avstand
Med andre ord er det ikke X som står for tur til å bli tatt ut siden Z ikke er tatt ut og har mindre avstandverdi
enn X. En selvmotsigelse. Det betyr at antagelsen om at lengde(vei) < X.avstand
er gal. Dermed: lengde(vei) = X.avstand. Induksjonsprinsippet forteller derfor at
setningen er sann.
Legg merke til at hvis vi har en korteste vei til en node X, så vil denne også gi korteste vei til alle noder som ligger på veien. Ta VGraf63 som eksempel. En korteste vei (det er flere av dem) fra 0 til 62 er gitt ved nodene 0, 3, 8, 15, 24, 33, 42, 50, 57, 61, 62. Ta noden 50 som eksempel. Da vil 0, 3, 8, 15, 24, 33, 42, 50 være en korteste vei dit.
Prims algoritme - Effektivitet Den versjonen
vi har i Programkode 11.2.5 c)
har samme oppførsel som den for Dijkstras algoritme. Dermed
er den av orden m log( n ) i det verste tilfellet.
Prims algoritme - Korrekthet Algoritmen
starter med et tre som består av én node. Deretter utvides treet
med én og én node (og kanten mellom dem). Algoritmen er slik at vi hele tiden får et tre siden
den nye kanten alltid har én node i det forrige treet og én node utenfor. Dermed blir det ingen sykler. Det
betyr at vi får et tre til slutt og dermed et spenntre. Men det som mangler er et bevis på at
spenntreet er minimalt.
Setning 2: Gitt en urettet, vektet og sammenhengende graf. Etter hver
innlemmelse av en node, vil treet en da får være et subtre av
et minimalt spenntre.
Dette bevises ved hjelp av et induksjon:
Basistrinnet: I første runde inneholder treet kun startnoden og den er inneholdt i ethvert spenntre og dermed i et minimalt spenntre. Det stemmer med setningen.
Induksjonstrinnet: La X være noden som på et bestemt trinn (etter det første) i algoritmen skal innlemmes. La T være treet vi har. Induksjonsantagelsen er at setningen stemmer før hver nye innlemmelse. Det betyr at T da er et subtre av et minimalt spenntre S. Bruk figuren under til venstre som eksempel. Den viser resultet etter fem trinn. T består av de 5 svarte nodene og de kantene mellom dem som er svarte. T er et subtre av det minimale spenntreet S som består av alle nodene og alle de svarte kantene:
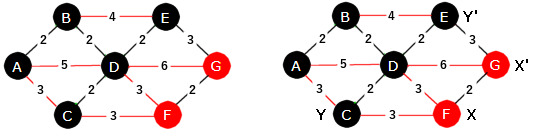 |
Figur 11.2.8 b): vei - en korteste vei fra start til X |
Siden det er X som står for tur til å bli innlemmet, må X være en nærmeste nabo til T. I figuren over til venstre kan både F og G være denne X-en siden begge har avstand 3 til T. Vi kan la F være X. Se figuren til høyre. La så Y være en nærmeste nabonode til X i T. I figuren kan det være både C og D. Vi lar C være Y. Det er markert i figuren til høyre. La så T' være treet vi får når X (og kanten fra Y til X) innlemmes i T. I figuren svarer det til vi får T' ved å utvide T med noden F og kanten fra C til F.
Anta at kanten fra Y til X allerede ligger i S. S omfatter T og dermed også T'. Dermed er setningen sann i dette tilfellet.
Anta isteden at kanten fra Y til X ikke ligger i S. Slik er det i figuren over. Men S er et tre og dermed sammenhengende. Det betyr at S inneholder en vei fra Y til X. I figuren er det veien C, D, E, G, F. Følg denne veien fra Y mot X og la Y' være den siste noden på veien som ligger i T (dvs. E i figuren). La X' være første node på veien etter Y' (dvs. G i figuren). Da ligger X' utenfor T. Det kan godt hende at Y = Y' eller X = X' (men ikke begge deler). La S' være spenntreet vi får ved å fjerne kanten mellom Y' og X' i S (kanten mellom E og G i figuren) og isteden sette inn den mellom Y og X (kanten mellom C og F i figuren). S' omfatter T', inneholder alle nodene, er sammenhengende og uten sykler, dvs. S' er et spenntre. Vi har:
vekt(S') = vekt(S) - kantvekt(Y',X') + kantvekt(Y,X)
Men vekten på kanten mellom Y' og X' kan ikke være mindre enn den mellom Y og X. I så fall ville X' vært en nærmere nabo til T enn det X er. Dette betyr at vekt(S') ≤ vekt(S) og dermed vekt(S') = vekt(S) siden S er et minimalt spenntre. Det betyr at S' er et minimalt spenntre som inneholder T'. Induksjonsprinsippet gir derfor at setningen er sann.
Kruskals algoritme - Korrekthet
Beviset er ganske likt det for
Prims algoritme. Algoritmen starter med at
vi har en subgraf som betsår av alle nodene, men ingen kanter. Så ser vi på én og én kant
i stigende rekkefølge mhp. vekt fra den opprinnelige grafen.
Hvis kanten vil føre til en sykel i subgrafen, blir den forkastet. Hvis ikke, legges den
inn i subgrafen. Osv. til alle nodene har blitt knyttet sammen.
Setning 3: Gitt en urettet, vektet og sammenhengende graf. Etter hver
(i Kruskals algoritme) innlemmelse av en kant subgrafen, vil subgrafen en da får være
en subgraf av et minimalt spenntre.
Dette bevises ved hjelp av et induksjon:
Basistrinnet: I første runde inneholder subgrafen alle nodene og ingen kanter. Men nodene er inneholdt i ethvert spenntre og dermed i et minimalt spenntre. Det stemmer med setningen.
Induksjonstrinnet: La k være kanten som på et bestemt trinn (etter det første) i algoritmen skal innlemmes. La S være subgrafen vi har. Induksjonsantagelsen er at setningen stemmer før hver nye innlemmelse. Det betyr at S da er en subgraf av et minimalt spenntre T.