 |
| D. Huffman |
Anta som et eksempel at vi har en sekvens med 100 bokstaver og at den kun
inneholder bokstavene fra A til H.
Vi antar også at disse 100 bokstavene består av 12 A-er, 7 B-er, 3 C-er, 14 D-er,
28 E-er, 9 F-er, 5 G-er og 22 H-er. Antallet forekomster av en bokstav kalles
bokstavens frekvens. Denne sekvensen på 100 bokstaver kan ikke være tatt ut fra
vanlig tekst. Da ville det ha vært mange flere forskjellige bokstaver (og andre tegn).
Men også i vanlig tekst er det slik at enkelte bokstaver forekommer ofte og andre sjelden eller
nesten aldri. I norsk tekst er det bokstaven (liten) e som er mest brukt.
I denne eksempelsekvensen på 100 bokstaver er
det E som er hyppigst og C som det er færrest av. En tabelloversikt over frekvensen
til hver bokstav kalles en frekvensfordeling:
| Tegn | A | B | C | D | E | F | G | H |
| Frekvens | 12 | 7 | 3 | 14 | 28 | 9 | 5 | 22 |
| Binærkode | 01000001 | 01000010 | 01000011 | 01000100 | 01000101 | 01000110 | 01000111 | 01001000 |
| Tabell 5.4.1 : En frekvenstabell for 8 tegn | ||||||||
|---|---|---|---|---|---|---|---|---|
En vanlig bokstav representeres normalt med en binærkode på 8 biter (en byte). Bokstaven A har binærkoden 01000101. Denne bitsekvensen kan også tolkes som tallet 65. Bokstaven B er representert ved 01000010 eller tallet 66, osv. Se Tabell 5.4.1. For å lagre informasjonen i den gitte sekvensen på 100 bokstaver brukes det en byte for hver bokstav, dvs. 100 byter og siden hver byte består av 8 biter, blir det tilsammen 800 biter. Spørsmålet er nå om det er mulig å lagre denne informasjonen med bruk av færre biter enn dette?
Når vi har så få som 8 forskjellige bokstaver kan vi gi hver bokstav en entydig bitkode ved hjelp av bare tre binære siffer. De kan kombineres på 8 mulige måter. Det er 000, 001, 010, 011, 100, 101, 110 og 111. Da kunne vi bestemme at A skal ha bitkoden 000, B bitkoden 001, osv. Dermed vil vi kunne lagre den informasjonen som ligger i sekvensen på 100 bokstaver, ved hjelp av bare 300 biter. Er 300 biter det beste vi kan oppnå?
| 1. | Klikk på navnet David Huffman og les om hans innsats. |
![]() 5.4.2 Prefikskoder
5.4.2 Prefikskoder
En mulighet er å bruke variabel bitkodelengde, dvs. at de forskjellige
bokstavene ikke har det samme antallet biter i sin bitkode. Vi komprimerer ved at
hver bokstav i sekvensen blir erstattet med sin bitkode.
For å få redusert den sammenlagte størrelsen vil det trolig være lurt å la
bokstaver som forekommer ofte, få kortest bitkode. Vi kan imidlertid få et problem
når dette deretter skal tolkes eller dekomprimeres. Hvordan skal vi,
når det er variabel bitkodelengde,
kunne vite når bitkoden for en bokstav slutter og bitkoden for neste bokstav starter?
I eksemplet vårt er det E som er hyppigst.
Vi kunne gi den bitkoden 0. Den nest hyppigste er H og den kunne vi gi bitkoden 1.
De fire deretter i hyppighet er D, A, F og B, og de kunne få kodene 00, 01, 10
og 11. Hvis vi nå komprimerer sekvensen ABAB ved å erstatte hver bokstav med
dens bitkode, får vi 01110111. Men hvordan skal dette kunne dekomprimeres?
Første biten er 0. Er det en E eller er det første biten i A?
Vi kan løse dette problemet ved å bruke det som kalles prefikskoder
(engelsk: prefix codes).
Det betyr at bitkoden for en bokstav ikke kan
være første delen av bitkoden for en annen bokstav. Med andre ord blir det ikke
tillatt å la E får bitkoden 0 og A bitkoden 01 fordi bitkoden for E da er første
del av bitkoden for A.
Vi kan finne prefikskoder for en samling bokstaver ved hjelp av et
fullt binærtre
med nøyaktig like mange bladnoder som det
er forskjellige bokstaver. Husk definisjonen: Et binærtre er fullt hvis hver node
enten har to eller ingen barn. Tegnene knyttes til bladnodene. Vi finner bitkoden
til en bokstav ved å gå veien fra rotnoden ned til bladnoden, dvs. en 0-bit når
vi går til venstre og en 1-bit når vi går til høyre. Vi kaller et slikt tre
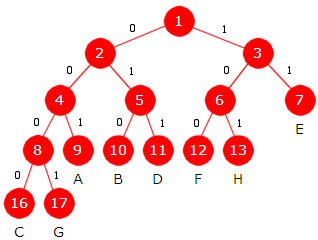
et prefikskodetre. Nedenfor er det satt opp et mulig prefikskodetre
for de 8 bokstavene i vårt eksempel:
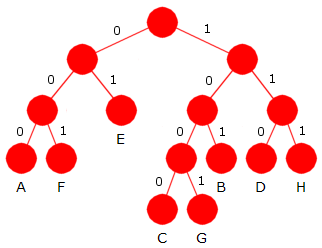 |
| Figur 5.4.2 a) Et fullt tre - 8 bladnoder med en bokstav til hver. |
Ved hjelp av treet i Figur 5.4.2 a) finner vi fort bitkoder for de 8 bokstavene. F.eks. går vi fra rotnoden og ned til noden med A ved venstre, venstre og venstre. Dermed blir bitkoden til A lik 000. Bitkodelengden er antall biter i bitkoden. Vi setter opp dette i en tabell:
| Tegn | A | B | C | D | E | F | G | H |
| Bitkode | 000 | 101 | 1000 | 110 | 01 | 001 | 1001 | 111 |
| Bitkodelengde | 3 | 3 | 4 | 3 | 2 | 3 | 4 | 3 |
| Tabell 5.4.2 b) : Kodetabell basert på binærtreet fra Figur 5.4.2 a) | ||||||||
|---|---|---|---|---|---|---|---|---|
Bitkodene i Tabell 5.4.2 b) blir prefikskoder. La X og Y være to bokstaver. Hvis bitkoden for Y utgjorde første del av bitkoden for X, måtte vi passere Y-noden på veien fra rotnoden ned til X-noden. Men det er umulig siden begge hører til bladnoder. En sekvens av 0- og 1-biter kan derfor «dekomprimeres» på en entydig måte ved hjelp av et prefikskodetre. Gitt sekvensen:
10011010001101100111010101
Dekomprimeringen starter i treets rotnode. Derfra til venstre ved 0-bit
og til høyre ved 1-bit.
Før eller senere kommer vi til en bladnode. Tegnet i bladnoden noteres. Så vi går opp til
rotnoden og forsetter. Prefikskodetreet i
Figur 5.4.2 a) gir oss
resultatet: GBADDEDBE
La T betegne et prefikskodetre og B (T ) bitsummen − dvs. antallet biter vi ender opp med når komprimeringen skjer ved hjelp av bitkodene som treet gir. B (T ) er summen av produktet av frekvensen og bitkodelengden for hver bokstav. I vårt eksempel med 8 bokstaver og frekvenser som gitt i Tabell 5.4.1, og der T er treet fra Figur 5.4.2 a), blir B (T ) slik:
B(T) = 12·3 + 7·3 + 3·4 + 14·3 + 28·2 + 9·3 +5·4 + 22·3 = 280
Resultatet blir at vår sekvens på 100 bokstaver kan komprimeres ned til 280 biter, dvs. B (T ) = 280. Nå er det ikke oppgitt hvordan denne bokstavsekvensen ser ut. Men det har heller ingen betydning. Ved prefikskoding er det frekvensen til bokstavene som teller.
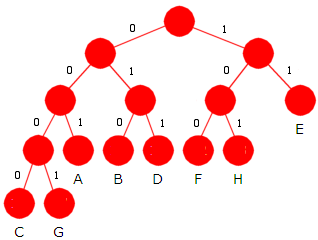
På slutten av Avsnitt 5.4.1 så vi på muligheten av å la hver bokstav få en bitkode med lengde 3, og det ble satt opp forslag til bitkode for hver bokstav. Da ville sekvensen bli komprimert ned til 300 biter. Dette er også prefikskoding. Flg. prefikskodetre gir nettopp de bitkodene:
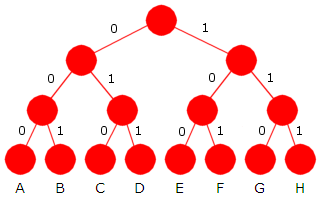 |
| Figur 5.4.2 c) Prefikskodetre - alle får bitkodelengde 3 |
B (T )-verdien til treet i Figur 5.4.2 c) er 300.
Det er dårligere enn Figur 5.4.2 a)
der B (T ) = 280. Som
sagt er det lurt at hyppige bokstaver får en kortere bitkode enn de sjeldne.
Det er årsaken til at treet i Figur 5.4.2 a) gir den beste prefikskoden
av de to. Bokstaven E har størst frekvens og i Figur 5.4.2 a) har
den kortere bitkode enn den har i Figur 5.4.2 c).
Spørsmål: Finnes det et optimalt prefikskodetre T, dvs.
et prefikskodetre som gir minst mulig verdi for B (T )?
I neste avsnitt skal vi se på en algoritme som gir et optimalt prefikskodetre.
| 1. | Et prefikskodetre T for vårt eksempel gir flg. bitkoder: A = 100, B = 11110, C = 111110, D = 101, E = 0, F = 1110, G = 111111 og H = 110. Tegn treet! Det hyppigste tegnet E har fått kortest mulig kode. Hva blir bitsummen B (T )? Gir det god komprimering? |
| 2. | Dekomprimer 11100010010110101110 ved hjelp av prefikskodetreet i Figur 5.4.2 a). Gjør det samme med 100100000100101 og 101011001100101. |
| 3. | Bokstavene i Morse-alfabetet består av prikker og streker. Hvis prikk og strek erstattes med 0 og 1, blir dette et system med variabel bitkodelengde. Finn Morse-koden til bokstavene fra A til H. Er det i dette systemet mulig å finne f.eks. hva 01110111 betyr? |
![]() 5.4.3 Huffmans metode
5.4.3 Huffmans metode
Hvis vi regner ut bitsummen B (T ) for alle prefikskodetrær,
må det naturligvis være minst ett av dem som gir minst mulig bitsum.
Et prefikskodetre T med minimal verdi på B (T )
kalles et optimalt prefikskodetre.
Huffmans metode er navnet på den algoritmen som konstruerer et optimalt
prefikskodetre. Resultatet kalles et Huffmantre.
Det er frekvensfordelingen som er utgangspunktet for algoritmen. Vi bruker det samme eksemplet som sist. Se Tabell 5.4.3 a) under:
| Tegn | A | B | C | D | E | F | G | H |
| Frekvens | 12 | 7 | 3 | 14 | 28 | 9 | 5 | 22 |
| Tabell 5.4.3 a) : Bokstaver og frekvenser | ||||||||
|---|---|---|---|---|---|---|---|---|
Huffmantreet består av noder. Hver node skal inneholde en bokstav (generelt et tegn), en frekvens (antall forekomster av tegnet) og to referanser - til venstre og høyre barn. Med Java-kode kan vi sette det opp slik:
class Node { private char tegn; // et tegn private int frekvens; // tegnets frekvens private Node venstre; // referanse til venstre barn private Node høyre; // referanse til høyre barn } Programkode 5.4.3 a)
Vi starter med å lage én node for hver bokstav og nodene legger vi fortløpende inn i
en kø som holdes ordnet. Køen ordnes etter frekvens, dvs. at noden med minst frekvens
kommer først og dermed den med størst frekvens sist. Når dette senere skal
implementeres er det naturlig å bruke en prioritetskø der frekvensen brukes som prioritet.
På tegningen nedenfor har vi satt frekvensen inne i noden og bokstaven rett under:
 |
| Figur 5.4.3 a) : «Bokstavene» er lagt i en ordnet kø |
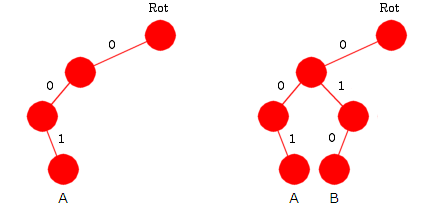
Vi tar så ut noden med minst frekvens og så den med nest minst frekvens, dvs. først den med frekvens 3 og så den med frekvens 5. Vi lager en ny node der frekvensen blir summen (dvs. 3 + 5 = 8) av frekvensene i de to nodene. Den nye noden trenger ikke ha noen bokstav (tegn). Den første vi tok ut blir venstre barn og den andre høyre barn. Deretter legger vi den nye noden inn på rett plass i den ordnede køen. (Egentlig legger vi inn det treet som har noden som rotnode). Resultatet blir slik:
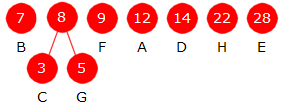 |
| Figur 5.4.3 b) : C og G er barn til en ny node |
Vi gjentar dette. De to nodene (eller de to trærne) med minst frekvens er den med frekvens 7 og den med frekvens 8. Disse tar vi ut. Vi lager en ny node med frekvens 7 + 8 = 15. Den første vi tok ut blir venstre barn og den andre høyre barn. Den nye noden (eller treet) legges inn i køen. På denne måten fortsetter vi til vi står igjen med én node som blir treets rotnode.
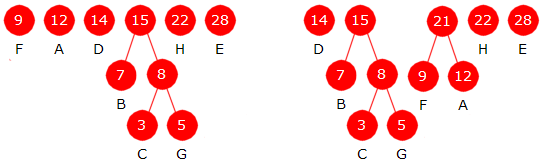 |
| Figur 5.4.3 c) : Til venstre blir 7 + 8 = 15 ny node. Til høyre blir 9 + 12 = 21 ny node. |
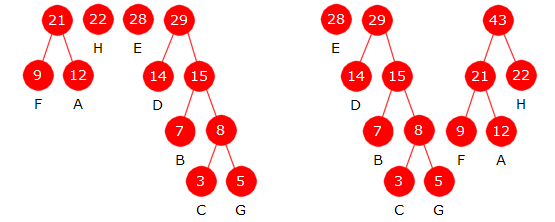 |
| Figur 5.4.3 d) : Til venstre blir 14 + 15 = 29 og til høyre blir 21 + 22 = 43 nye noder. |
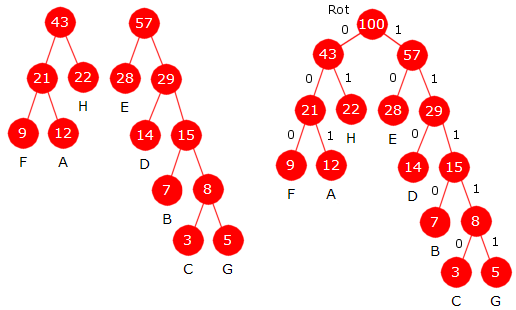 |
| Figur 5.4.3 e) : Til venstre blir 28 + 29 = 57 ny node. Til slutt blir 43 + 57 = 100 roten i treet. |
I Figur 5.4.3 c), d) og e) er «rundene» i Huffmans algoritme satt opp og nederst til høyre i Figur 5.4.3 e) står Huffmantreet. Bitkoden til A får vi ved å starte i rotnoden og så venstre, venstre og høyre, dvs. 001. B får bitkoden 1110, osv. Vi setter alle bitkodene inn i en tabell:
| Tegn | A | B | C | D | E | F | G | H |
| Bitkode | 001 | 1110 | 11110 | 110 | 10 | 000 | 11111 | 01 |
| Bitkodelengde | 3 | 4 | 5 | 3 | 2 | 3 | 5 | 2 |
| Tabell 5.4.3 b) : Bitkodetabell basert på treet til høyre i Figur 5.4.3 e) | ||||||||
|---|---|---|---|---|---|---|---|---|
Hvor godt vil disse bitkodene komprimere bokstavsekvensen vår? Vi regner ut B (T ):
B(T) = 12·3 + 7·4 + 3·5 + 14·3 + 28·2 + 9·3 +5·5 + 22·2 = 273
Dette gav bedre komprimering enn sist - fra 280 til 273 biter. Det kan bevises matematisk (se Avsnitt 5.4.13) at Huffmans algoritme gir et optimalt prefikskodetre. Dvs. at det ikke finnes noen andre prefikskodetrær som gir en bedre komprimering, dvs. mindre verdi på bitsummen B (T). Men det finnes mange andre som gir samme komprimering. Se Oppgave 6.
Oppsummert går Huffmans algoritme slik:
- Gitt at vi kjenner frekvensen (antall forekomster) til hvert av de forskjellige tegnene i en «melding». Disse tegnene omtales også som meldingens «alfabet».
- Lag en node for hvert av tegnene med tegnets frekvens som nodens frekvens og tegnet som nodens tegn. Se Figur 5.4.3 a) .
- Velg noden med minst og så den med nest minst frekvens. Hvis det er flere med minst frekvens, er rekkefølgen likegyldig. Lag en ny node der den første blir venstre og den andre høyre barn. Den nye nodens frekvens settes til summen av frekvensene til de to som ble valgt ut. Tegnet i den nye noden har ikke interesse og kan være hva som helst.
- Den nye noden legges sammen med de andre. Det betyr at antallet i samlingen av noder har blitt én mindre enn før (to tas ut, en legges inn). Se Figur 5.4.3 b) .
- Gjenta punkt 3. og 4. Se Figur 5.4.3 c) og Figur 5.4.3 d) .
- Når det er to noder igjen, vil den nye noden vi lager bli rotnode i Huffmantreet. Frekvensen i noden blir lik antallet tegn i «meldingen». Se Figur 5.4.3 e) .
- Vi finner bitkoden for et tegn ved å starte i rotnoden og gå ned til tegnets node. En 0-bit til venstre og en 1-bit til høyre.
Huffmans algoritme er ikke entydig. Hvis to eller flere noder har samme frekvens, kan ikke den minste velges på en entydig måte. Det betyr at vi kan få forskjellige Huffmantrær og hvert av dem gir et sett med bitkoder. Men alle disse er likeverdige i den forstand at de er optimale, dvs. at bitsummen B (T) blir den samme. Se Oppgave 5 - 6.
I et Huffmantre kommer nodefrekvensene i
avtagende rekkefølge i
speilvendt nivåorden, dvs. i
nivåvis orden fra roten og nedover og for hvert nivå fra høyre mot venstre.
Se på Huffmantreet til høyre i
Figur 5.4.3 e) . Der kommer de
slik i speilvendt nivåorden: 100, 57, 43, 29, 28, 22, 21, 15, 14, 12, 9, 8, 7, 5, 3.
Denne egenskapen karakteriserer et Huffmantre: Et prefikskodetre
er et Huffmantre hvis og bare hvis 1) nodefrekvensen til hver foreldernode er summen av barnas frekvenser
og 2) frekvensene kommer i avtagende rekkefølge i speilvendt nivåorden. Dette brukes
bl.a. i den «adaptive» Huffman-teknikken. Hvis en ikke kjenner frekvensfordelingen
i «meldingen» på forhånd, kan Huffmantreet bygges og endres og
komprimeringen kan gjennomføres fortløpende mens «meldingen» leses. Det betyr at
hvis frekvensen til et tegn øker, behøver ikke Huffmans algoritme utføres på nytt for å
finne Huffmantreet. Det holder å endre inne i treet.
Se Oppgave 13 og
Avsnitt 5.4.12.
| 1. | Bruk Huffmans algoritme, finn og tegn Huffmantreet der bokstavene A, B, C og D har frekvensene 1, 2, 4 og 13. Hva blir bitkodene? Komprimer teksten ABBAD. Dekomprimer 1000011000001. Hva blir bitsummen B (T)? |
| 2. | Som i Oppgave 1 med frekvenser 14, 7, 3, 16, 20 og 8 for bokstavene fra A til F. Komprimer teksten ABBAD. Dekomprimer 1000011000001. Hva blir bitsummen B (T)? |
| 3. | Som i Oppgave 1 med frekvenser 30, 20, 3, 18, 42, 25 og 10 for bokstavene fra A til G. Komprimer teksten ABBAD. Dekomprimer 10000110000011. Hva blir bitsummen B (T)? |
| 4. | Som i Oppgave 1 med frekvenser 17, 6, 3, 21, 25, 10, 5 og 13 for bokstavene fra A til H. Komprimer teksten ABBAD. Dekomprimer 10000110000010. Hva blir bitsummen B (T)? |
| 5. | Lag et Huffmantre for fordelingen 1, 1, 2 og 4 for A, B, C og D. Da vil det hver gang de to nodene med minst frekvens skal velges, være to like å velge mellom. Dermed vil treet avhenge av hvilken av dem som tas ut først. Hvor mange forskjellige trær vil det bli? |
| 6. | Lag et Huffmantre for fordelingen 1, 1, 1, 2 og 3 for A, B, C, D og E. Her vil de ulike valgene av minst blant flere like frekvenser føre til Huffmantrær med ulik form. Dvs. at samme bokstav kan få ulike bitkodelengder. Vis at det kan skje. |
| 7. | Huffmans algoritme gir alltid et optimalt prefikskodetre. Det finnes imidlertid mange optimale prefikskodetrær for samme frekvensfordeling. Ta utgangspunkt i Huffmantreet til høyre i Figur 5.4.3 e) . Sett opp det speilvendte treet, dvs. det treet vi får ved å la de to barna i hver indre node node bytte plass. Hvilke bitkoder gir dette treet? Er det optimalt, dvs. har det samme bitsum som det opprinnelige treet? |
| 8. | Hvis Huffmans algoritme omdefineres slik at den noden som tas ut først (har minst frekvens) blir høyre barn og den som så tas ut (nest minst frekvens) blir venster barn, kan vi si at vi også nå får et Huffmantre. Hvordan vil treet bli hvis vi bruker den samme frekvensfordelingen som i starten på Avsnitt 5.4.3. Sammenlign det treet med det som diskuteres i Oppgave 7. |
| 9. | Ta utgangspunkt i treet til høyre i Figur 5.4.3 e) . Bytt om noder slik at det blir et tre der nivåene er fylt opp fra venstre, men fortsatt med nøyaktig like mange noder på hvert nivå som før. Lag det også slik at bladnoder på samme nivå kommer i stigende rekkefølge med hensyn på nodenes tegn. Det gir også et optimalt prefikskodetre og kalles et kanonisk tre. |
| 10. | Finn en frekvensfordeling for de fem bokstavene A, B, C, D og E slik at to bokstaver i det tilhørende Huffmantreet får bitkodelengde 4. Prøv å få det til slik at summen av frekvensene blir minst mulig. Gjør det samme med de seks bokstavene fra A til F og da slik at to bokstaver får bitkodelengde 5. Anta at vi har n bokstaver. Finnes det en frekvensfordeling for de n bokstavene slik at to bokstaver får bitkodelengde lik n − 1? |
| 11. | Hvor mange forskjellige tegn må en «melding» inneholde og hvor stor må «meldingen» minst være for at et Huffmantre for frekvensfordelingen til «meldingen» får et tegn med bitkodelengde på 32? |
| 12. | Gitt bitkodene A = 11, B = 01, C = 1000, D = 101, E = 00 og F = 1001. Tegn det tilhørende prefikskodetreet. en frekvensfordeling som vil gi nettopp det treet. |
| 13. | Et prefikskodetre er et Huffmantre hvis 1) nodefrekvensen til hver foreldernode er summen av barnas frekvenser og 2) frekvensene kommer i avtagende rekkefølge i speilvendt nivåorden Hvis frekvensen for et eller flere tegn endrer seg, er det ikke nødvendig å gjennomføre Huffmans algoritme på nytt. Det holder å gå inn i treet og gjøre endringene der slik 1) og 2) blir oppfylt. Ta utgangspunkt i treet i Oppgave 1 og øk frekvensen til A med 2 (fra 1 til 3). Gjør så de nødvendige endringene i treet. |
En melding komprimeres ved at hvert tegn i meldingen erstattes med tegnets bitkode. Et problem med dette er at Huffmantreet (eller bitkodene) da må være kjent når den komprimerte meldingen skal dekomprimeres. En mulighet er å la første del av den komprimerte meldingen inneholde slik informasjon. Spørsmålet blir da: Hvor mye
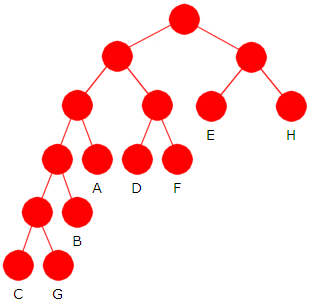 |
| Figur 5.4.4 a): Venstreorientert kanonisk tre |
Det er bedre å bruke bitkodene fra et annet optimalt prefikskodetre enn Huffmantreet. Vi tar utgangspunkt i Huffmantreet og lager et tre med de samme bladnodene på hvert nivå, men slik at nivåene er fylt opp fra venstre. I tillegg lar vi tegnene på hvert nivå være sortert alfabetisk. Ta treet til høyre i Figur 5.4.3 e) som utgangspunkt. Da vil denne teknikken gi oss treet i Figur 5.4.4 a) til venstre.
Treet i Figur 5.4.4 a) kalles det kanoniske treet. Det er
et optimalt prefikskodetre siden hvert tegn
(eller bladnode) har samme avstand til roten som i det opprinnelige Huffmantreet.
Huffmanskogen Alle prefikskodetrær som har de samme tegnene
og for hvert tegn samme avstand til roten som i et Huffmantre T, utgjør Huffmanskogen til T.
Kanonisk tre Det treet K i Huffmanskogen til et Huffmantre T som
har alle nivåene fylt opp med noder fra venstre og med tegn på samme nivå sortert alfabetisk,
kalles det (venstreorienterte) kanoniske treet. Hvis X og Y er to tegn
i K, vil X alltid ligge til venstre for Y hvis X har større avstand
fra roten enn Y eller hvis de har samme avstand og X kommer foran Y
alfabetisk.
Generelt vil Huffmanskogen bestå av mange forskjellige prefikskodetrær. Vi kan lage dem ved å bytte om på noder på samme nivå. Alle slike trær er optimale og bitkodene til hvilket som helst av dem kunne brukes til komprimeringen. Men det (venstreorienterte) kanoniske treet har den fordelen at det kan gjenskapes kun ved hjelp av lengdene til bitkodene. Bitkodene og bitkodelengdene som treet i Figur 5.4.4 a) gir, er:
| Tegn | A | B | C | D | E | F | G | H |
| Bitkode | 001 | 0001 | 00000 | 010 | 10 | 011 | 00001 | 11 |
| Bitkodelengde | 3 | 4 | 5 | 3 | 2 | 3 | 5 | 2 |
| Tabell 5.4.4 a) : Bitkodetabell basert på treet i Figur 5.4.4 a) | ||||||||
|---|---|---|---|---|---|---|---|---|
Obs. Det er også mulig å bruke det (høyreorienterte) kanoniske treet, dvs. det treet i Huffmanskogen som har alle nivåene fylt opp med noder fra høyre og der tegnene (eller blanodene) på samme nivå er sortert alfabetisk. Se Oppgave 6.
Påstanden er at det kanoniske treet kan gjenskapes kun ved hjelp av lengdene på bitkodene. Hvordan gjør vi det? Ta som eksempel at vi har flg. tegn og bitkodelengder:
| Tegn | A | B | C | D | E | F | G | H |
| Bitkodelengde | 3 | 3 | 4 | 3 | 2 | 3 | 4 | 3 |
| Tabell 5.4.4 b) : Tegn og bitkodelengder | ||||||||
|---|---|---|---|---|---|---|---|---|
Flg. regel gir antallet noder på hvert nivå. Verdiene i Tabell 5.4.4 b) brukes som eksempel:
- La n være størst bitkodelengde. Nivå n blir da nederste nivå. I vårt eksempel: n = 4.
- Nederste nivå skal ha noder, i alfabetisk rekkefølge, for de tegnene som har lengde n. Antallet slike er alltid et partall. I vårt eksempel er det C og G.
- La k < n. På nivå k får vi først foreldrene til de på nivå k + 1. Antallet blir halvparten av antallet noder på nivå k + 1. I tillegg kommer en node for hvert tegn som har lengde lik k. Antallet vil alltid bli et partall. Vårt eksempel: Antall noder på nivå 3 (k = 3) blir 2/1 + 5 = 6 (2 noder på nivå 4 og 5 tegn med bitkodelengde lik 3).
Vårt eksempel: 1), 2) og 3) gir henholdsvis 2, 6, 4, 2 og 1 noder på nivåene 4, 3, 2, 1 og 0. Hvert nivå vil bestå av foreldernoder og/eller bladnoder, skal være fylt opp fra venstre og være sortert med hensyn på tegnene (bladnodene). Det gir oss flg. kanoniske tre:
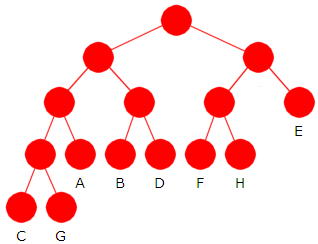 |
| Figur 5.4.4. b) : Kanonisk tre fra Tabell 5.4.4 b) |
La tabellen lengder inneholde tegnenes bitkodelengder og la n
være største lengde. Tabellen antall dimensjoneres til n + 1.
Først går vi gjennom lengder og teller opp hvor mange det er av hver lengde.
Resultatet havner i tabellen antall. Da vil spesielt antall[n]
inneholde antallet bladnoder på nederste nivå. Deretter bruker vi fortløpende regel 2
(i en for-løkke) til å finne det totale antallet noder på de øvrige nivåene:
int[] lengder = {3,3,4,3,2,3,4,3}; // bitkodelengdene int n = 4; // største lengde int[] antall = new int[n + 1]; // en tabell for nivåantallet for (int lengde : lengder) antall[lengde]++; // antall = {0,0,2,5,2} for (int k = n - 1; k >= 0; k--) antall[k] += antall[k + 1]/2; Tabell.skrivln(antall); // utskrift: 1 2 4 6 2 Programkode 5.4.4 a)
Programkode 5.4.4 a) gir oss antallet noder som det kanoniske treet skal ha på hvert nivå. Da kan treet konstrueres og vi kan finne bitkodene til tegnene. Men det er mulig å bruke en teknikk tilsvarende den i Programkode 5.4.4 a) til finne bitkodene direkte uten å måtte gå veien om treet. Det tar vi opp i Avsnitt 5.4.7.
Komprimering: Vi utvider nå Huffmans algoritme for å komprimere en «melding» til å bestå av følgende skritt:
- Finn tegnene og frekvensfordelingen i «meldingen» som skal komprimeres.
- Finn Huffmantreet og så det tilhørende (venstreorienterte) kanoniske treet.
- Sett opp bitkodene som det kanoniske treet gir.
- Den komprimerte meldingen skal bestå av a) informasjon om tegnene og lengdene på bitkodene og b) av at hvert tegn i «meldingen» er erstattet med sin bitkode.
Dekomprimering: Den komprimerte meldingen behandles i motsatt rekkefølge:
- Hent tegnene og bitkodelengdene.
- Sett opp det (venstreorienterte) kanoniske treet.
- Bitene bestemmer veien fra rotnoden og ned til et tegn (en bladnode).
| 1. | Anta at Huffmans algoritme på grunnlag av en bestemt frekvensfordeling for A, B, C og D gav bitkodelengder på henholdsvis 3, 3, 2 og 1. Tegn det tilhørende (venstreorienterte) kanoniske treet. |
| 2. | Som i Oppgave 1, men med A, B, C, D og E og lengder på henholdsvis 3, 3, 2, 2 og 2. |
| 3. | Som i Oppgave 1, men med A − F og lengder på henholdsvis 2, 4, 4, 2, 2 og 3. |
| 4. | Som i Oppgave 1, men med A − G og lengder på henholdsvis 2, 3, 4, 3, 2, 3 og 4. |
| 5. | Som i Oppgave 1, men med A − H og lengder på henholdsvis 3, 4, 5, 2, 2, 3, 5 og 3. |
| 6. | Finn det høyreorienterte kanoniske treet til Huffmantreet til høyre i Figur 5.4.3 e) . Dvs. finn treet som har de samme bladnodene som Huffmantreet på hvert nivå og slik at nivåene er fylt opp fra høyre. I tillegg skal tegnene (bladnodene) på hvert nivå være sortert alfabetisk. |
| 7. | Finn det høyreorienterte kanoniske treet til treet i Figur 5.4.4 b) . |
| 8. | Lag et program der du kjører koden i
Programkode 5.4.4 a) .
Bytt så ut int n = 4; med en setning der verdien til n finnes
ved at tabellen lengder gjennomsøkes. Bruk f.eks. maks-metoden som du bør
ha i samleklassen Tabell.
|
| 9. | Bytt ut vediene i tabellen lengder med 3, 4, 5, 3, 2, 3, 5, 2 i Oppgave 8.
Det svarer til treet i
Figur 5.4.4 a) .
|
| 10. | Bruk programmet fra Oppgave 8 til å finne antallet noder på hvert nivå for de kanoniske trærne i Oppgave 1 - 5. |
![]() 5.4.5 Implementasjon
5.4.5 Implementasjon
Programkode 5.4.3 a)
inneholder et nodeklasseforslag. Det er kun bladnoder som har tegn.
Derfor oppretter vi isteden en privat indre basisklasse Node med frekvens og referanser
og en privat subklasse BladNode med tegn. Se også Oppgave 3.
Legg
den under en ny mappe (package) med navn bitio - en samlemappe for bitbehandling.
package bitio; import java.io.*; // filbehandling import java.net.URL; // internett import hjelpeklasser.*; // diverse metoder public class Huffman // klasse for komprimering { private static class Node // en basisklasse { private int frekvens; // nodens frekvens private Node venstre; // referanse til venstre barn private Node høyre; // referanse til høyre barn private Node() {} // standardkonstruktør private Node(int frekvens, Node v, Node h) // konstruktør { this.frekvens = frekvens; venstre = v; høyre = h; } } // class Node private static class BladNode extends Node // en subklasse { private final char tegn; // bladnodens tegn private BladNode(char tegn, int frekvens) // konstruktør { super(frekvens, null, null); // basisklassens konstruktør this.tegn = tegn; } } // class BladNode } // class Huffman Programkode 5.4.5 a)
Vi skal her, for enkelhets skyld, kun komprimere «meldinger» som inneholder de vanlige
tegnene, dvs. de fra 0 til 255. En heltallstabell dimensjonert
til 256 kan derfor inneholde enhver frekvensfordeling. F.eks. får vi frekvensfordelingen
i Avsnitt 5.4.3 slik:
int[] frekvens = new int[256]; frekvens['A'] = 12; frekvens['E'] = 28; frekvens['B'] = 7; frekvens['F'] = 9; frekvens['C'] = 3; frekvens['G'] = 5; frekvens['D'] = 14; frekvens['H'] = 22;
Flg. metode bygger et tre (ved hjelp av frekvenser)
slik som beskrevet i Avsnitt 5.4.3.
Det lages en bladnode for hvert tegn i frekvenstabellen (med frekvens > 0)
og de legges i en ordnet kø (en prioritetskø). De to med minst frekvens (styrt av en komparator
gitt ved hjelp av et lamda-uttrykk) tas ut,
en ny node med dem som barn og frekvens lik summen av frekvensene, legges i køen, osv.
Treets rotnode returneres.
Huffmans algoritme krever at vi har minst to tegn, dvs. minst to av frekvensene
må være større enn 0. Metoden hører hjemme i
class Huffman:
private static Node byggHuffmanTre(int[] frekvens) { PrioritetsKø<Node> kø = // bruker et lamda-uttrykk new HeapPrioritetsKø<>((p,q) -> p.frekvens - q.frekvens); for (int i = 0; i < frekvens.length; i++) if (frekvens[i] > 0) // dette tegnet skal være med kø.leggInn(new BladNode((char)i, frekvens[i])); if (kø.antall() < 2) // må ha minst to noder throw new IllegalArgumentException("Det er for få tegn!"); while (kø.antall() > 1) { Node v = kø.taUt(); // blir venstre barn Node h = kø.taUt(); // blir høyre barn int sum = v.frekvens + h.frekvens; // summen av frekvensene kø.leggInn(new Node(sum, v, h)); // legger noden inn i køen } return kø.taUt(); // roten i treet } Programkode 5.4.5 b)
| 1. | Legg klassen Huffman Programkode 5.4.5 a)
under en ny mappe (package) med navn bitio. Legg deretter metoden byggHuffmanTre()
i Programkode 5.4.5 b)
inn i klassen.
|
| 2. | Det er fullt mulig å bruke en
PriorityQueue
fra java.util istedenfor en HeapPrioritetsKø i metoden byggHuffmanTre(). Hva må da endres?
|
| 3. | De indre nodene har ikke tegn, mens bladnodene ikke har barn. Nå arver likevel bladnodene to referanser. Vi kunne redusere plassbruken ved å ha en basisklasse (node) med frekvens og to subklasser (bladnode og indre node) med hhv tegn og to referanser. Gjør dette og gjør så de endringene som trengs der disse klassene brukes. |
| 4. |
Frekvenser kan være store. Kan det skape problemer i compare i komparatoren?
|
![]() 5.4.6 Bitkoder
5.4.6 Bitkoder
Med frekvenser som i
Avsnitt 5.4.3, vil metoden i
Programkode 5.4.5 b)
bygge opp treet til høyre i
Figur 5.4.3 e).
Bitkodene til tegnene finner vi ved traversere treet. I flg. metode
inngår en kodestreng og en kodetabell
som parametere. Kodestrengen kode utvides med '0'
til venstre og med '1' til høyre. I en bladnode
legges kode i kodetabellen:
private static void finnBitkoder(Node p, String kode, String[] koder) { if (p instanceof BladNode) koder[((BladNode)p).tegn] = kode; else { finnBitkoder(p.venstre, kode + '0', koder); // 0 til venstre finnBitkoder(p.høyre, kode + '1', koder); // 1 til høyre } } Programkode 5.4.6 a)
Flg. offentlig metode (legges i
class Huffman)
gir bitkoder som strenger, f.eks. "0101":
public static String[] stringBitkoder(int[] frekvens) { Node rot = byggHuffmanTre(frekvens); // bygger treet String[] bitkoder = new String[frekvens.length]; // en kodetabell finnBitkoder(rot,"",bitkoder); // lager bitkodene return bitkoder; // returnerer tabellen } Programkode 5.4.6 b)
Eksempel 1:
Hvis metodene er lagt inn i class Huffman, vil flg.
program kunne kjøres:
public static void main(String[] args) { int[] frekvens = new int[256]; frekvens['A'] = 12; frekvens['E'] = 28; frekvens['B'] = 7; frekvens['F'] = 9; frekvens['C'] = 3; frekvens['G'] = 5; frekvens['D'] = 14; frekvens['H'] = 22; String[] bitkode = Huffman.stringBitkoder(frekvens); for (int i = 0; i < frekvens.length; i++) if (frekvens[i] > 0) System.out.print((char)i + " = " + bitkode[i] + " "); // A = 001 B = 1110 C = 11110 D = 110 E = 10 F = 000 G = 11111 H = 01 } Programkode 5.4.6 c)
Vi kan velge andre tegn, flere tegn og andre frekvenser i Programkode 5.4.6 c). Men hvis vi har en tekst der frekvensfordelingen ikke er kjent, må vi først finne den.
Teksten som skal komprimeres kan f.eks. ligge i en tegnstreng.
Flg. metode finner frekvensfordelingen. Metoden hører hjemme i
class Huffman:
public static int[] stringFrekvens(String tekst) { int[] frekvens = new int[256]; for (int i = 0; i < tekst.length(); i++) frekvens[tekst.charAt(i)]++; return frekvens; } Programkode 5.4.6 d)
Eksempel 2: Gitt «Tarzan-skriket» "aaaaiiiooaaaaaaiiiiiooooaaaaaaaaiiiiiiiooooooh". Hvor mange biter trengs for å lagre dette ved hjelp av Huffman-teknikken? «Skriket» inneholder kun bokstavene a, i, o og h. Det gir flg. frekvensfordeling, bitkoder og bitkodelengder:
String tekst = "aaaaiiiooaaaaaaiiiiiooooaaaaaaaaiiiiiiiooooooh"; int[] frekvens = Huffman.stringFrekvens(tekst); // frekvensene String[] bitkoder = Huffman.stringBitkoder(frekvens); // bitkodene int antallBiter = 0; for (int i = 0; i < frekvens.length; i++) if (frekvens[i] > 0) { antallBiter += frekvens[i] * bitkoder[i].length(); System.out.print((char)i + " = " + bitkoder[i] + " "); } System.out.println("\nKan lagres med " + antallBiter + " biter!"); // Utskrift: // a = 0 h = 100 i = 11 o = 101 // Kan lagres med 87 biter! Programkode 5.4.6 e)
Hvis det er en «stream» (f.eks. en tekstfil) som skal komprimeres,
vil det normalt være
mange forskjellige tegn. Det er store og små bokstaver, siffer,
mellomrom, komma, punktum, osv. Der vil det også kunne være
«usynlige» tegn, dvs. kontrolltegn. F.eks. tabulatortegn,
tegn for linjeskift og sideskift. De første 32 tegnene (0 - 31) i
ascii-tabellen
er av den typen. Hvert slikt tegn har fått et navn på to eller tre bokstaver.
F.eks. står HT for (horisontal) tabulator, LF og CR for linjeskift
(eng: line feed, carriage return) og FF for sideskift (eng: form feed).
Dette er satt opp i flg. tabell. Legg den
i class Huffman:
public static String[] ascii = {"NUL","SOH","STX","ETX","EOT","ENQ","ACK","BEL","BS","HT","LF", "VT","FF","CR","SO","SI","DLE","DC1","DC2","DC3","DC4","NAK", "SYN","ETB","CAN","EM","SUB","ESC","FS","GS","RS","US"}; Programkode 5.4.6 f)
Følgende metode (som hører hjemme i
class Huffman)
finner frekvensfordelingen i det som en «stream»
inneholder:
public static int[] streamFrekvens(InputStream inn) throws IOException { int[] frekvens = new int[256]; int tegn = 0; while ((tegn = inn.read()) != -1) frekvens[tegn]++; inn.close(); return frekvens; } Programkode 5.4.6 g)
Eksempel 3: En fil kan oppgis ved en url (uniform resource locator).
For en lokal fil (på egen maskin) har den en spesiell form. Anta at filen
c:\algdat\hjelpeklasser\Tabell.java finnes. Da har den
file:///c:/algdat/hjelpeklasser/Tabell.java
som url. Legg merke til at den starter med file:///
og bruker vanlige skråstreker (/) alle steder.
I flg. eksempel inngår et av delkapitlene fra det nettbaserte kompendiet og da brukes vanlig url:
public static void main(String[] args) throws IOException { String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/3/kap13.html"; InputStream inn = new BufferedInputStream((new URL(url)).openStream()); int[] frekvens = Huffman.streamFrekvens(inn); String[] bitkoder = Huffman.stringBitkoder(frekvens); for (int i = 0; i < bitkoder.length; i++) if (bitkoder[i] != null) { String ut = (i < 32) ? Huffman.ascii[i] : "" + (char)i; System.out.printf("%-3s = %s %d\n",ut,bitkoder[i],frekvens[i]); } // Utskrift: De 10 første linjene: // ETX = 0110111100011101110 1 // LF = 110011 7299 // CR = 110110 7299 // = 100 45663 // ! = 000101001010 72 // " = 111100 8248 // # = 1010110101 423 // % = 1010111000110110 8 // & = 11011100 1909 // ' = 01101111000101 18 } // slutt på main Programkode 5.4.6 h)
Utskriften over viser viser at filen inneholder hvert av tegnene LF og CR 7299 ganger.
Når vi skriver et tekstdokument i et Windows-system og trykker Enter
for å skifte linje, avsettes de to tegnene CR og LF. Med andre ord er det 7299 linjer
på filen som inneholder
Delkapittel 1.3 fra
kompendiet. Men det er tegnet mellomrom (eng: space) som brukes overlegent
flest ganger, dvs. 45663 ganger. Dette tegnet bruker som alle de andre tegnene, åtte biter.
Men med denne komprimeringsteknikken vil det bli erstattet med 100, dvs. kun tre biter.
Eksempel 4: I Programkode 5.4.6 d)
ble det laget en metode som fant frekvensfordelingen i en tegnstreng og
i Programkode 5.4.6 g) en som
fant den for en InputStream. Egentlig kunne vi ha nøyd oss med den siste siden
den også kan (implisitt) brukes for en tegnstreng:
public static void main(String[] args) throws IOException { String s = "ABBCCCDDDDDEEEEEEEEFFFFFFFFFFFFFGGGGGGGGGGGGGGGGGGGGG"; InputStream inn = new ByteArrayInputStream(s.getBytes()); String[] bitkoder = Huffman.stringBitkoder(Huffman.streamFrekvens(inn)); for (int i = 0; i < bitkoder.length; i++) if (bitkoder[i] != null) System.out.print((char)i + " = " + bitkoder[i] + " "); // A = 111110 B = 111111 C = 11110 D = 1110 E = 110 F = 10 G = 0 } Programkode 5.4.6 i)
| 1. | På filen Huffman ligger klassen
Huffman med alle de metodene m.m. som er laget til nå. Legg den over til deg
under en mappe (package) med navn bitio. Da må du ha med import bitio.*;
øverst på de stedene der klassen skal brukes.
|
| 2. | Kjør programmet i Eksempel 1. Gjenta det med andre frekvenser. |
| 3. | Lag et program som kjører koden i Eksempel 2. Gjenta det med andre tegnstrenger. F.eks. en tekstreng på lengde 100 med 12 A-er, 7 B-er, osv. slik som i Tabell 5.4.1. |
| 4. | Kjør programmet i Eksempel 3. Legg inn kode slik at antallet forskjellige tegn på filen skrives ut (med en passende tekst) til slutt. Hvilke 10 tegn er det som brukes mest? Gjenta dette med pdf-versjonen av Delkapittel 1.3 (dvs. bytt ut kap13.html med kap13.pdf i url-en). Hvor mange forskjellige tegn inneholder den? Hvorfor? Gjenta dette med andre filer. Hvis du velger en lokal fil (på din egen maskin), må du passe på at url-en oppgis på rett form. Se den innledende teksten til Eksempel 3. |
| 5. | Komprimeringsgraden i prosent er 100 ganger forholdet mellom reduksjonen (differensen mellom original filstørrelse og det den komprimeres til) og original filstørrelse. Det betyr f.eks. at hvis komprimeringsgraden er 0%, så er de to like. Målet er å få høy komprimeringsgrad. Den kan imidlertid ikke bli 100%. I så fall måtte den komprimeres til 0 biter og det er selvfølgelig umulig. Gjør om koden Eksempel 3 slik at den finner original filstørrelse. Det er bare å summere alle frekvensene i frekvenstabellen. Finn så hvor mange biter dette komprimeres til, dvs. finn summen av frekvensen ganget med bitkodelengden for hvert tegn. Se Eksempel 2. Obs: Dette må deles med 8 for å finne antallet byter. Lag det så slik at komprimeringsgraden skrives ut. |
| 6. | Prøv koden fra Oppgave 5 på flere tekstfiler. Det heter at med Huffman-teknikken blir komprimeringsgraden for tekstfiler på 30-40%. Stemmer det for deg? Prøv med filer som kun inneholder Java-kode. Blir slike filer komprimert bedre (høyere komprimeringsgrad) enn tekstfiler. Prøv også word- og pdf-filer. Hva blir komprimeringsgraden? |
| 7. | I Avsnitt 5.4.3 gav Huffmans algoritme bitodene i Tabell 5.4.3 b). Bokstavene C og G fikk de lengste bitkodene, dvs. 5 biter. Hva er den lengste bitkoden Huffmans algoritme kan gi hvis «meldingen» kun inneholder de åtte bokstavene fra A til H ? Finn en frekvensfordeling som gjør at to bokstaver får denne lengste bitkoden. Se Oppgave 10 i Avsnitt 5.4.3. Test svaret ditt ved å bruke koden i Eksempel 1. |
![]() 5.4.7 Det kanoniske treet og «ekte» bitkoder
5.4.7 Det kanoniske treet og «ekte» bitkoder
I Avsnitt 5.4.4 ble det satt opp fire punkter
for å utføre en komprimering. Etter Huffmantreet er oppgaven å finne det kanoniske treet.
Da trengs kun bitkodelengdene. De kan finnes f.eks. ved metoden finnBitkoder
i Programkode 5.4.6 a).
Bitkodene blir da tegnstrenger og deres lengder blir bitkodelengder. Men det er bedre å ha
en direkte metode der lengdene blir verdier i en heltallstabell. Det kan gjøres
ved en rekursiv traversering. For hvert nivå nedover (forelder til barn) blir
avstanden til roten én mer enn før. I en bladnode vil «lengden»
til tegnet bli det samme som avstanden til roten. Metoden kalles med lengde lik 0:
private static void finnLengder(Node p, int lengde, int[] lengder) { if (p.venstre == null) // p er en bladnode { lengder[((BladNode)p).tegn] = lengde; // tegnets lengde } else { finnLengder(p.venstre, lengde + 1, lengder); // lengde øker med 1 finnLengder(p.høyre, lengde + 1, lengder); // lengde øker med 1 } } Programkode 5.4.7 a)
Det kanoniske treet kan lages ved hjelp av bitkodelengdene − se Avsnitt 5.4.4. Men det er egentlig bitkodene vi er på jakt etter og de kan vi faktisk finne uten å konstruere treet først. Vi bruker samme eksempel som i siste del av Avsnitt 5.4.4:
| Tegn | A | B | C | D | E | F | G | H |
| Bitkodelengde | 3 | 3 | 4 | 3 | 2 | 3 | 4 | 3 |
| Tabell 5.4.7 a) : Tegn og bitkodelengder | ||||||||
|---|---|---|---|---|---|---|---|---|
Bitkodelengdene i Tabell 5.4.7 a) gir flg. (venstreorienterte) kanoniske tre:
 |
| Figur 5.4.7. a) : Kanonisk tre fra Tabell 5.4.7 a) |
I hver node i treet Figur 5.4.7 a) står nodens posisjon − se Avsnitt 5.1.3. Husk sammen-hengen mellom nodeposisjon og bitkode: Bitkoden er lik de binære sifrene til posisjonen bortsett fra den første 1-eren. I Figur 5.4.7 a) har f.eks. A posisjon 9. Binært er det 1001. Tar vi vekk den første 1-eren får vi 001 og det er bitkoden til A.
Bitkodelengdene fra Tabell 5.4.7 a) overfører vi til flg. heltallstabell:
int[] lengder = {3,3,4,3,2,3,4,3};
Vi skal nå punktvis gå gjennom teknikken for å lage bitkoder ved hjelp av tabellen lengder.
1. Vi må først finne den største bitkodelengden. La det være n. I eksemplet vårt er n = 4.
Her antas at maks-metoden fra
Delkapittel 1.1
ligger i samleklassen Tabell:
int n = lengder[Tabell.maks(lengder)]; // metoden maks fra klassen Tabell
2. Treet i Figur 5.4.7 a)
forteller oss hvor mange bladnoder (eller tegn) det er på hvert nivå. Dette antallet kan vi
finne ved å gå gjennom tabellen lengder og telle opp siden nivå i treet svarer
til bitkodelengde:
int[] blader = new int[n + 1]; // antall bladnoder på hvert nivå for (int lengde : lengder) // for alle lengde i lengder if (lengde > 0) blader[lengde]++; // teller opp Tabell.skrivln(blader); // Utskrift: 0 0 1 5 2
3. Posisjonen til første tegn (alfabetisk rekkefølge) blant de med bitkodelengde
n, er 1 << n (dvs. 2 opphøyd i n).
I Figur 5.4.7 a) er det C
og som vi ser er posisjonen 1 << 4 = 16. Hvis pos[k] er posisjonen
til den første bladnoden på nivå k, vil pos[k] + blader[k]
være én mer enn posisjonen til den siste bladnoden på nivå k siden blader[k]
er antall bladnoder. Spesielt er posisjonen til første bladnode på nivå k − 1
lik (pos[k] + blader[k]) / 2.
I Figur 5.4.7 a)
er 16 posisjonen til den første på nivå 4. Da stemmer det fint at posisjonen
til første bladnode på nivå 3 er lik (16 + 2)/2 = 9 og at første på nivå 2
er lik (9 + 5)/2 = 7.
int[] pos = new int[n + 1]; // en posisjonstabell pos[n] = 1 << n; // betyr 2 opphøyd i n for (int k = n; k > 0; k--) pos[k - 1] = (pos[k] + blader[k])/2; // første bladnode på nivå k - 1 Tabell.skrivln(pos); // Utskrift: 2 4 7 9 16
4. Vi kjenner nå posisjonen til første bladnode (eller tegn) på hvert nivå. På et og samme nivå ligger de andre i alfabetisk rekkefølge og deres posisjoner får vi ved å starte med posisjonen til den første og forløpende øke den med 1:
int[] posisjoner = new int[lengder.length]; // en posisjonstabell for (int i = 0; i < posisjoner.length; i++) if (lengder[i] > 0) posisjoner[i] = pos[lengder[i]]++; for (int p : posisjoner) if (p > 0) System.out.print(p + " "); // Utskrift: 9 10 16 11 7 12 17 13
5. Forskjellen mellom bitkoden og posisjonen til en bladnode (et tegn) er at
posisjonen har en ekstra 1-bit foran. Denne trenger vi egentlig ikke siden
tabellen lengder forteller hvor mange biter som er aktuelle.
Dette tar vi hensyn til i flg metode. Der setter vi alle ideene sammen til en helhet.
Metoden forventer at ingen bitkodelengde er større enn 31. Hvorfor akkurat
31 diskuteres senere:
public static int[] finnBitkoder(int[] lengder) { int[] blader = new int[32]; // antall tegn av hver lengde for (int lengde : lengder) if (lengde < 32) blader[lengde]++; // teller opp else throw new IllegalStateException("Bitkodelengde > 31!"); int[] pos = new int[32]; // posisjonen til første bladnode for (int k = 31; k > 0; k--) pos[k - 1] = (pos[k] + blader[k])/2; int[] bitkoder = new int[lengder.length]; for (int i = 0; i < bitkoder.length; i++) if (lengder[i] > 0) bitkoder[i] = pos[lengder[i]]++; return bitkoder; } Programkode 5.4.7 b)
Hvis metoden finnBitkoder er lagt inn i klassen Huffman,
vil flg. kodebit kunne kjøres:
int[] lengder = {3,3,4,3,2,3,4,3}; int[] bitkoder = Huffman.finnBitkoder(lengder); Tabell.skrivln(bitkoder); // Utskrift: 1 2 0 3 3 4 1 5 Programkode 5.4.7 c)
Kodebiten over gir 1 2 0 3 3 4 1 5 som utskrift for bitkodene. Kan det stemme? Husk at en bitkode nå er et bestemt antall biter bakerst i et heltall. Hvis vi setter på en ekstre 1-bit foran de aktuelle bitene, blir resulatet det samme som posisjonen i treet. Hvis et heltall k slutter med f.eks. 0001, setter vi en 1-bit foran ved k | 1 << 4. Tar vi med flg. ekstra utskriftssetning i Programkode 5.4.7 c), vil vi imidlertid få det resultatet som forventes:
for (int i = 0; i < lengder.length; i++) System.out.print((bitkoder[i] | 1 << lengder[i]) + " "); // Utskrift: 9 10 16 11 7 12 17 13
| 1. | Legg metoden finnBitkoder i Programkode 5.4.7 b)
inn i klassen Huffman.
|
| 2. | Bitlengdene 3, 4, 5, 3, 2, 3, 5, 2 førte til treet i Figur 5.4.4 a). Kjør Programkode 5.4.7 c) (ta med den ekstra utskriftssetningen satt opp lenger ned) med disse bitlengdene og sjekk at resultatene stemmer med treet. |
| 3. | Gitt (se Oppgave 5 i Avsnitt 5.4.4 ) 3, 4, 5, 2, 2, 3, 5, 3. Gjør som i Oppgave 1. |
| 4. | La 3, 3, 5, 3, 2, 4, 4, 3, 4, 5 være bitkodelngder for bokstavene fra A til J. Tegn det tilhørende (venstreorienterte) kanoniske treet og gjør så som i Oppgave 1. |
| 5. | Lag en metode tilsvarende den i Programkode 4.5.7 b), men der vi får bitkodene som hører til det høyreorienterte kanoniske treet. Sjekk resultatet ved f.eks. å tegne treet for bitkodelengdene 3, 3, 4, 3, 2, 3, 4, 3 og så bruke den metoden i Programkode 5.4.7 c). |
![]() 5.4.8 Komprimering
5.4.8 Komprimering
En «melding» komprimeres ved at hvert tegn erstattes med tilhørende bitkode.
Dette skaper et problem siden bitkodene kan ha forskjellige lengder. F.eks. kan de to første
tegnene ha bitkodelengder på 5 og 7. Men minste enhet for lagring (eller utskrift)
er en byte (8 biter). Derfor må bitkodene «skjøtes sammen». Så fort vi har fått
8 biter lagres de (eller skrives ut) som én enhet (en byte). Klassen
BitOutputStream
har utskriftsmetoder som gjør dette for oss. Kopier klassen over til deg. Legg den under mappen (package)
bitio.
Vedlegg A1
inneholder en beskrivelse av metodene i
BitOutputStream
og eksempler på hvordan de brukes. F.eks. skriver en av dem ut et oppgitt antall biter
fra et heltall:
public void writeBits(int value, int numberOfBits)
Flg. enkle metode skal komprimere innholdet i
InputStream
inn og skrive resultatet til
OutputStream
ut.
Da må følgende punkter utføres: 1) inn leses en gang for å finne
frekvensfordelingen, 2) Huffmantreet bygges ved hjelp av frekvensfordelingen,
3) en traversering av treet gir bitkodelengdene,
4) det kanoniske treet og bitkodene konstrueres ved hjelp av bitkodelengdene og
5) inn leses en gang til og bitkoden til hvert tegn skrives
til ut. Legg metoden inn i klassen Huffman:
public static int komprimer(InputStream inn, OutputStream ut) throws IOException { if (inn.markSupported() == false) throw new IllegalStateException("InputStream kan ikke resettes!"); int[] frekvens = streamFrekvens(inn); // punkt 1 inn.reset(); // lesingen kan starte på nytt Node rot = byggHuffmanTre(frekvens); // punkt 2 int[] lengder = new int[frekvens.length]; finnLengder(rot, 0, lengder); // punkt 3 int[] bitkoder = finnBitkoder(lengder); // punkt 4 BitOutputStream bitUt = new BitOutputStream(ut); int antallBiter = 0, tegn = 0; while ((tegn = inn.read()) != -1) // punkt 5 { bitUt.writeBits(bitkoder[tegn],lengder[tegn]); antallBiter += lengder[tegn]; // teller opp } inn.close(); bitUt.close(); // lukker return antallBiter; } Programkode 5.4.8 a)
Komprimeringsmetoden i Programkode 5.4.8 a) vil virke kun for instanser av
InputStream
som tillater at «strømmen» resettes, dvs. tillater
at lesingen kan starte på nytt fra begynnelsen. Dette gjelder f.eks. for klassen
ByteArrayInputStream
der lesingen skjer fra en underliggende byte-tabell. Metoden markSupported() returnerer sann
for denne klassen.
Eksempel 1 I flg. eksempel skal vi «komprimere» meldingen "Dette er en test!". Den har 8 forskjellige og tilsammen 17 tegn (bokstaver, mellomrom og utropstegn). Bokstaven e forekommer 5 ganger og vil komme til å få en kort bitkode (10), mens f.eks. bokstaven D forekommer kun én gang og vil dermed få en «lang» bitkode (00000). Se Oppgave 2.
String melding = "Dette er en test!"; InputStream inn = new ByteArrayInputStream(melding.getBytes()); ByteArrayOutputStream ut = new ByteArrayOutputStream(); System.out.println(Huffman.komprimer(inn, ut)); // Utskrift: 46 Programkode 5.4.8 b)
Utskriften fra Programkode 5.4.8 b) forteller at de 17 tegnene i meldingen har
blitt komprimert ned til 46 biter. Det betyr i gjennomsnitt 2,7 biter per tegn. Men
hvordan ser den komprimerte meldingen ut? Resultatet ligger i en byte-tabell inne i enheten
ut. Vi kan hente ut byte-tabellen og oversette innholdet
til en string der en 0-bit blir til tegnet '0' og en 1-bit til tegnet '1'. Legg flg. kode
inn på slutten av Programkode 5.4.8 b):
String komprimering = BitOutputStream.toBitString(ut.toByteArray()); System.out.println(komprimering); // Utskrift: 00000101 11110011 00011011 00010011 11000001 11000100 Programkode 5.4.8 c)
Utskriften i Programkode 5.4.8 c) viser bitene i hver byte i byte-tabellen som
inneholder den komprimerte meldingen. Tilsammen 6·8 = 48 biter.
Men utskriften i Programkode 5.4.8 b) sa at det var 46 biter og det er korrekt.
Men 46 biter er for få til å fylle 6 byter. Klassen
BitOutputStream
er laget slik at når en utskrift gjøres ferdig (flush eller close ),
blir det lagt til så mange ekstra 0-biter på slutten at den siste byten blir fylt opp. Det betyr at de
to siste 0-bitene i den siste byten i utskriften i Programkode 5.4.8 c), ikke
hører til den komprimerte meldingen. Dette betyr at ved en eventuell dekomprimering er det viktig
å vite hvor de egentlige bitene stopper og dermed hvor ekstrabitene starter.
Eksempel 2 Anta at filen "test.txt" er tilgjengelig. Vi kan forsøke å «komprimere» den:
InputStream inn = new FileInputStream("test.txt"); ByteArrayOutputStream ut = new ByteArrayOutputStream(); System.out.println(Huffman.komprimer(inn, ut)); Programkode 5.4.8 d)
Kjører vi koden over vil det imidlertid bli kastet et unntak av
typen IllegalStateException med feilmeldingen
"InputStream kan ikke resettes!" . Hvis en fil skal leses
på nytt, må vi først avbryte kontakten med filen (close) og så opprette
en ny kontakt ved hjelp av en konstruktør. Vi må derfor lage en annen metode for komprimering
av vanlige filer.
Vi gjør som i Eksempel 3 i Avsnitt 5.4.6 og lar en fil være representert ved sin url. Dermed kan vi åpne filen for lesning ved hjelp av flg. kode:
InputStream inn = new BufferedInputStream((new URL(url)).openStream());
Under dekomprimering må vi kjenne til bitkodene som ble brukt under komprimeringen. De kan gjenskapes eksakt hvis vi kjenner tegnene og deres bitkodelengder. Hvert av de 256 tegnene fra 0 til 255 kan i prinsippet forekomme. I Eksempel 3 i Avsnitt 5.4.6 ble filen som inneholder Delkapittel 1.3 analysert. Den inneholdt 97 forskjellige tegn. Det er vanlig å legge informasjon om hvilke tegn som forekommer, på begynnelsen av filen som vi komprimerer til. Det leses først under en dekomprimering. Et mål er å bruke så liten plass som mulig til dette.
Vi kan f.eks. først skrive ut hvor mange forskjellige tegn det er og så skrive ut de tegnene det handler om. Med f.eks. 97 forskjellige tegn vil det da bli 7 biter (tallet 97) + 97·8 = 783 biter. Et alternativ er å bruke 256 biter (én bit for hvert mulig tegn) med en 1-bit hvis tegnet er med og en 0-bit hvis det ikke er med. Den siste teknikken er best hvis det er mange tegn, mens den første er best hvis det er få tegn. Grensen går ved 32 forskjellige tegn. Med 32 tegn vil det bli 32·8 = 256 biter. Det er også andre måter å gjøre det på. Se Oppgave 4.
Også tegnenes bitkodelengder må skrives ut.
I Eksempel 3 var 18 største lengde.
For å skrive ut tall fra 1 til 18 holder det med 5 biter. Med 15 som største bitkodelengde hadde det
holdt med 4 biter, osv. Flg. hjelpemetode
som legges i klassen Huffman, finner antallet signifikante binære
siffer i et heltall:
public static int antBinSiffer(int k) // antall binære siffer { return k == 0 ? 0 : 32 - Integer.numberOfLeadingZeros(k); } Programkode 5.4.8 e)
Det totale antallet biter etter at alle bitkodene er skrevet ut, behøver ikke bli et helt antall byter. Hvis ikke legges det på, før utskriftsfilen lukkes, et ekstra antall 0-biter (fra 1 til 7 stykker). Hvis de tas med under en dekomprimering, kan vi risikere å få en større fil enn vi opprinnelig hadde. En enkel måte å løse det på kunne være å skrive ut det totale antallet tegn først på filen. Dermed kunne vi stoppe når det antallet tegn var dekomprimert.
En mer interessant måte å løse det på er å bruke en «vaktpost». Til det velger vi det tegnet (eller et av de tegnene) som har størst bitkodelengde. Bitkoden for vaktposten skrives ut helt til slutt. Dermed kan dekomprimeringen stoppe når vi har funnet vaktposttegnet rett antall ganger. Vi finner hva som skal være vaktpost ved å finne størst lengde i tabellen lengder (ved hjelp av metoden maks fra klassen Tabell ).
Frekvensen til vaktposten kan være fra 1 og oppover. Den må skrives et sted på starten av den komprimerte filen og helst med så få biter som mulig. Antallet biter kan i prinsippet variere fra 1 til 31. Alle tall fra 1 til 31 kan skrives med kun fem biter siden 31 = 11111. Dermed bruker vi 5 biter til å oppgi hvor mange biter frekvensen har og så skrives frekvensen ut med nøyaktig det antallet biter. Vaktpostfrekvensen vil normalt være et lite tall, kanskje bare 1. I Eksempel 3 i Avsnitt 5.4.6 der filen som inneholder Delkapittel 1.3 inngår, er 18 størst bitkodelengde. Det første av dem er '@' som har frekvens 2. Dermed blir det 5 + 2 + 18 = 25 ekstra biter for dette vaktpostopplegget. Vi kunne brukt et annet tegn som vaktpost, men det er fordelaktig å velge et som har størst bitkodelengde. Se Oppgave 5.
Det normale er å la den komprimerte filen starte med et såkalt filhode (eng: file header). Filhodet består av et antall biter komponert slik at det bl.a. kan brukes til å identifisere filen som en fil komprimert ved hjelp av Huffmans metode. Dermed kan en metode for dekomprimering gi en feilmelding (kaste et unntak) hvis filen er av feil type. Filhodet kan også brukes i forbindelse med spesialtifeller. I flg. komprimeringsmetode bruker vi ikke filhode. Utforming og bruk av et filhode tas opp i Oppgave 2 og i andre oppgaver.
public static void komprimer(String fraUrl, String tilFil) throws IOException { InputStream inn = new BufferedInputStream ((new URL(fraUrl)).openStream()); // åpner inn-filen int[] frekvens = streamFrekvens(inn); // frekvenstabellen Node rot = byggHuffmanTre(frekvens); // bygger Huffmantreet int[] lengder = new int[frekvens.length]; finnLengder(rot, 0, lengder); // bitkodelengdene int[] bitkoder = finnBitkoder(lengder); // bitkodene int vaktpost = Tabell.maks(lengder); // vaktposttegnet int k = antBinSiffer(lengder[vaktpost]); // antall siffer BitOutputStream ut = new BitOutputStream(tilFil); // ut-filen ut.writeBits(k, 3); // maks antall siffer for (int lengde : lengder) // tegn og lengder { if (lengde == 0) ut.write0Bit(); // ikke med hvis 0 else ut.writeBits(lengde | 1 << k, k + 1); // 1 + lengde } int s = antBinSiffer(frekvens[vaktpost]); // antall siffer ut.writeBits(s, 5); // skriver ut ut.writeBits(frekvens[vaktpost], s); // vaktpostens frekvens inn = new BufferedInputStream ((new URL(fraUrl)).openStream()); // åpner på nytt int tegn = 0; while ((tegn = inn.read()) != -1) // leser ett og ett tegn { ut.writeBits(bitkoder[tegn], lengder[tegn]); // skriver bitkoden } ut.writeBits(bitkoder[vaktpost], lengder[vaktpost]); // vaktposten inn.close(); // lukker inn-filen ut.close(); // lukker ut-filen } Programkode 5.4.8 f)
Hvor god er denne komprimeringsteknikken? I Eksempel 3 i Avsnitt 5.4.6 ble filen som inneholder Delkapittel 1.3, analysert. Filen er på 392.010 byter. Flg. figur viser hva som blir skrevet på utskriftsfilen hvis filen med Delkapittel 1.3 komprimeres:
| 3 | 741 | 7 | 1.978.152 | 18 |
| Siffer | Bitkodelengder | Vaktpost | Komprimeringen | Vaktpost |
| Figur 5.4.8 a) : Bitene på uskriftsfilen | ||||
Bitkodelengder kan variere fra 1 til 31. Hvis største bitkodelengde er mindre enn 16, kan vi skrive ut hver av dem 4 binære siffer. Men vi må bruke 5 binære siffer hvis noen av dem er 16 eller større. Første utskrift forteller hvor mange binære siffer som vi bruker for lengdene. Maks antall er 5 siden ingen bitkodelengde kan være større enn 31. For å skrive et tall som er 5 eller mindre trengs kun 3 binære siffer. I vårt eksempel er 19 største bitkodelengde (lengden til vaktposten) og dermed må vi bruke 5 binære siffer for å skrive ut lengdene. Det betyr at variabelen k blir 5 og dermed at 101 (= 5) blir de tre første bitene på utskrifsfilen.
Videre har vi 256 biter der en 1-bit forteller at tilhørende tegn er med og en 0-bit at det ikke er med. I Eksempel 3 er det med 97 tegn av de 256 mulige og for hvert av de 97 tegnene skrives tegnets bitkodelengde med 5 biter. Tilsammen blir det 256 + 95·5 = 741 biter. Deretter kommer data om vaktposten. Normalt vil vaktposten ha liten frekvens, ofte kun 1. Men i teorien kan den være stor. Hvis vi har en stor fil med bare to forskjellige tegn, vil et av dem bli vaktpost. Uansett hvor stor frekvensen til vaktposten er, holder det med 5 biter for å fortelle hvor mange biter frekvensen kan skrives med. I vårt eksempel er '@' vaktpost med frekvens 2. Dermed får variabelen s verdien 2. Tilsammen blir det 5 + 2 = 7 biter.
I selve komprimeringen blir hvert av de 392.010 tegnene (bytene) erstattet med sin bikode. Det utgjør 1.978.152 biter. Det hele avsluttes med de 18 bitene i vaktpostens bitkode. Sammenlagt 1.978.921 biter. Tallet 1.978.921 gir 1 i rest når vi deler med 8. Med andre ord mangler det syv biter for å fylle opp den siste byten. De bitene legges til etterpå og utskriftsfilen vil derfor komme til å inneholde 247.366 byter.
Komprimeringsgrad er definert som differensen mellom gammel og ny filstørrelese delt med gammel filstørrelse. I vårt eksempel blir det (392.010 − 247.366) / 392.010 = 0,37 = 37 %. En frekvensfordeling er skjev hvis noen tegn forekommer ofte, mens andre tegn er sjeldne og jevn hvis alle tegnene forekommer omtrent like ofte. Jo skjevere fordeling er, jo høyere komprimeringsgrad gir Huffmans metode. Tekstfiler er gode eksempler på skjeve fordelinger.
Hvis en fil inneholder alle eller de fleste av de 256 aktuelle tegnene og i tillegg har jevn frekvensfordeling, kan det hende at komprimeringsgraden blir lav og til og med negativ. Den blir negativ hvis den komprimerte filen blir større enn den opprinnelige. Ta pdf-versjonen av Delkapittel 1.3 som eksempel. Den er på 2.157.917 byter. Programkode 5.4.8 f) brukt på den vil gi en utskriftsfil på 2.154.536 byter, dvs. en komprimeringsgrad på 0,2 %.
Første del av den komprimerte filen skal inneholde nok informasjon til at tegnenes bitkoder kan rekonstrueres. Hvis vi har en stor fil slik som i Figur 5.4.8 a), har størrelsen på denne informasjonen lite å si for komprimeringsgraden. Men for små filer kan det bli annerledes. Da er det gunstig at informasjonen tar så liten plass som mulig. En mulighet er å bruke Huffmans metode også på bitkodelengdene. Flg. tabell viser fordelingen:
| 1 | 6 | 7 | 9 | 8 | 11 | 8 | 12 | 13 | 2 | 6 | 2 | 2 | 2 | 3 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Bitkodelengde 3 forekommer bare én gang, mens lengdene 10 og 11 forkommer 12 og 13 ganger. I Figur 5.4.8 a) ble alle bitkodelengdene skrevet ut med 5 binære siffer. Men kan vi isteden la de bitkodelengdene det er mange av få en kortere bitkode og dermed en lenger bitkode for de lengdene det er få av (f.eks. lengdene 3 og 18). Dette tas opp i Oppgave 7.
Det finnes komprimeringsteknikker som gir en vesentlig høyere komprimeringsgrad enn Huffmans metode. Det skal vi se mer på et annet sted. Huffmans metode er likevel i bruk, men da først og fremst som et ledd i andre algoritmer. F.eks. algoritmen Deflate som brukes bl.a. i filformatet PNG.
| 1. | Kopier klassene BitOutputStream
og BitInputStream
over til deg. Legg dem under mappen (package) bitio.
|
| 2. | Legg metoden i Programkode 5.4.8 a)
inn i klassen Huffman.
Finn så bitkodene som blir brukt under komprimering av meldingen "Dette er en test!"
og sjekk at det stemmer med utskriften i
Eksempel 1.
|
| 3. | Huffmans metode virker best hvis «meldingen» har en skjev frekvensfordeling, f.eks. tekstfiler eller filer med javakode. På slike filer vil de aller fleste tegnene ligge i intervallet 0 − 127. På norsk er det imidlertid noen unntak siden bokstavene Æ, æ, Ø, ø, Å og å ligger i intervallet 128 − 255. Gjør om metoden i Programkode 5.4.8 f) slik at det brukes 128 biter for å markere hvilke tegn i intervallet 0 − 127 som finnes. Tegnene fra 128 − 255 oppgis ved at antallet oppgis og så en byte (nok med 7 biter siden tegnet starter med en 1-bit) for hvert tegn. Hvor mange biter ville dette ha blitt for tegnene i Eksempel 3? |
| 4. | Hvis det er få forskjellige tegn, kan det lønne seg å oppgi hvilke tegn det er ved å ramse dem opp (antallet og så tegnene). Da kan det lønne seg å dele det i to grupper: 1) de i intervallet 0 − 127 og 2) de i intervallet 128 − 255. Da er det nok å bruke 7 biter per tegn siden alle tegn i gruppe 1) starter med 0 og alle i gruppe 2) med 1. Hvor går grensen (antall forskjellige tegn) for at dette lønner seg i forhold til slik det gjøres i Oppgave 3? Gjør disse endringene i Programkode 5.4.8 f). La dette tilfellet svare til at tallet 1 (0001) skrives ut som filhode. |
| 5. | Et hvilket som helst av tegnene kan brukes som «vaktpost». Hva blir fordelen og hva blir ulempen ved å velge et annet tegn som «vaktpost» enn et som har lengst bitkode? |
| 6. | Lag tillegg i Programkode 5.4.8 f) som behandler spesialtilfellene 1) filen er tom og 2) alle tegnene er like. Signaliser tilfellene 1) og 2) ved å bruke henholdsvis 2 (0010) og 3 (0011) som filhode. |
| 7. | Det antallet biter vi bruker for å skrive ut bitkodelengdene kan reduseres. Lengdene har en skjev frekvensfordeling og kan derfor representeres med variabel bitkodelengde. Se f.eks. tabellen med bitkodelengder hentet fra Eksempel 3. Hvis metoden i Programkode 5.4.8 f) brukes på den filen, vil lengdene bli skrevet ut med 5 biter for hver lengde, dvs. 95·5 = 475 biter. Hvor mange biter vil det bli hvis vi bruker Huffmans metode på bitkodelengdene? Gjør om Programkode 5.4.8 f) slik at denne ideen brukes. |
| 8. | Alle bitkodelengder er større enn 0. Dermed kan vi skrive dem ut redusert med 1. Dermed kan det være mulig å bruke færre siffer. F.eks. kun 4 siffer hvis største lengde var 16 siden 16 - 1 = 15 krever kun fire siffer. Eller vi kan redusere med lengden til minste lengde. Hvis den er 3 reduseres med 3. Hvis f.eks. lengdene går fra 3 til 18, vil det isteden bli fra 0 til 15 og vi trenger kun fire siffer. |
| 9. | Som vaktpost brukes et tegn med maksimal bitkodelengde. Et slikt tegn finner vi allerede da treet bygges siden den tas ut først fra prioritetskøen. Kan det benyttes videre? |
![]() 5.4.9 Enkel dekomprimering
5.4.9 Enkel dekomprimering
Å dekomprimere er å reversere det som ble utført under komprimeringen. Vi tar
utgangspunkt i komprimeringsmetoden slik den er satt opp i
Programkode 5.4.8 f).
Hvis metoden er endret og/eller har fått tillegg (se oppgavene i
Avsnitt 5.4.8), må
dekomprimeringsmetoden endres tilsvarende. I komprimeringsmetoden ble det
først skrevet ut tre biter. Vi må derfor starte med å lese dem. De tre
bitene gir oss et tall (variabelen k) som sier hvor
mange biter som bitkodelengdene er skrevet ut med.
Neste oppgave er å lese den informasjonen som forteller hvilke tegn det handler om,
deres bitkodelengder og vaktpostinformasjonen. En dekomprimeringsmetode må
derfor starte slik (obs: du må ha tilgang til
BitInputStream):
public static void dekomprimer(String fraUrl, String tilFil) throws IOException { BitInputStream inn = new BitInputStream((new URL(fraUrl)).openStream()); // åpner filen int k = inn.readBits(3); // antall biter i lengdene int[] lengder = new int[256]; // 256 mulige tegn for (int i = 0; i < lengder.length; i++) { if (inn.readBit() == 1) { lengder[i] = inn.readBits(k); } } int vaktpost = Tabell.maks(lengder); // tegn med størst lengde int s = inn.readBits(5); // antall siffer i vaktpostens frekvens int vaktpostfrekvens = inn.readBits(s) + 1; // her vil det komme mer kode inn.close(); // lukker inn-filen } Programkode 5.4.9 a)
Gitt at vi har laget et kanonisk tre ved hjelp av bitkodelengdene. Dekomprimeringen kan da utføres ved at én og én bit leses. Fra rotnoden går vi til venstre ved en 0-bit og til høyre ved en 1-bit, osv. Før eller senere kommer vi til et tegn (en bladnode). Hvis det er vaktposten og vi har funnet den for siste gang, er vi ferdige. Hvis ikke, skriver vi ut tegnet og starter på nytt i rotnoden. Dette er en enkel, men ikke effektiv dekomprimeringsteknikk. Vi skal finne en vesentlig mer effektiv måte i neste avsnitt, dvs. i Avsnitt 5.4.10.
Vi må først lage det kanoniske treet. Det kan gjøres på flere måter. Den enkleste måten er nok å gjøre det ved hjelp av bitkodene. Vi har allerede en metode som finner dem ved hjelp av bitkodelengdene. Se Programkode 5.4.7 b). Bitkoden for hvert aktuelt tegn utgjør en gren i treet. Husk at en gren i et binærtre består av rotnoden og nodene på veien ned til en bladnode. Vi bygger treet ved å bygge det gren for gren. En ny gren kan bestå av noder som allerede ligger i treet og av nye noder. Grenens nye noder må lages fortløpenede nedover mot den aktuelle bladnoden.
Ta som eksempel
at vi har de åtte tegnene fra A til H med flg. bitkoder:
A = 001, B = 010,
C = 0000, D = 011, E = 11,
F = 100, G = 0001 og H = 101. Vi legger inn «grenene»
fortløpende, først A = 001. Deretter B = 010, men da kun noder som er nye i forhold til A:
 |
| Grenen A = 001 er lagt inn Grenen B = 010 er lagt inn |
Med utgangspunkt i en lengdetabell kan dette kodes slik (metoden legges i class Huffman):
private static Node byggKanoniskTre(int[] lengder) { int[] bitkoder = finnBitkoder(lengder); // bitkodene Node rot = new Node(); // rotnoden for (int i = 0; i < lengder.length; i++) // går gjennom tabellen { if (lengder[i] > 0) // denne skal være med { int n = bitkoder[i]; // bitkoden til tegnet i int k = (1 << lengder[i]) >> 1; // posisjonen til første bit Node p = rot; // starter i roten while (k > 1) // alle unntatt siste bit { if ((k & n) == 0) // biten på plass k { if (p.venstre == null) p.venstre = new Node(); p = p.venstre; } else { if (p.høyre == null) p.høyre = new Node(); p = p.høyre; } k >>= 1; // flytter k en posisjon mot høyre } // lager bladnoden til slutt if ((n & 1) == 0) p.venstre = new BladNode((char)i,0); else p.høyre = new BladNode((char)i,0); } } return rot; // roten til det kanoniske treet } Programkode 5.4.9 b)
Hvis vi bruker Programkode 5.4.9 b) på en lengdetabell der A = 3, B = 3, C = 4, D = 3, E = 2, F = 3, G = 4 og H = 3, får vi flg. kanoniske tre:
 |
| Figur 5.4.9 a) : Et kanonisk tre |
Programkode 5.4.9 a) inneholder starten på dekomprimeringen. Som fortsettelse må vi først konstruere det kanoniske treet, så åpne utskriftsfilen, opprette en frekvensvariabel og sette i gang selve dekomprimeringen. Ved hjelp av én og én bit går vi fra rotnoden ned til et tegn (en bladnode). Tegnet telles med hvis det er vaktposttegnet og vi avslutter hvis det var siste forekomst. Hvis ikke, skrives tegnet ut og vi starter på nytt fra rotnoden. Flg. kodebit skal legges inn i Programkode 5.4.9 a) der det står // her vil det komme mer kode:
Node rot = byggKanoniskTre(lengder); // bygger treet BitOutputStream ut = new BitOutputStream(tilFil); int frekvens = 0; // opptellingsvariabel for (Node p = rot; ; p = rot) { while (p.venstre != null) // p er ikke en bladnode p = inn.readBit() == 0 ? p.venstre : p.høyre; if (((BladNode)p).tegn == vaktpost) { if (++frekvens == vaktpostfrekvens) break; // ferdig } ut.write(((BladNode)p).tegn); // skriver ut } ut.close(); Programkode 5.4.9 c)
Filen "komprimert.huf" inneholder en komprimert «melding» der filtypen "huf" signaliserer at Huffmans metode er brukt. Hvis programbiten i Programkode 5.4.9 c) er lagt inn i metoden i Programkode 5.4.9 a) og den igjen er lagt inn i class Huffman, vil flg. kodebit virke:
String inn = "https://www.cs.hioa.no/~ulfu/appolonius/kap5/4/komprimert.huf"; Huffman.dekomprimer(inn,"ut.txt"); Programkode 5.4.9 d)
Kjør programbiten over og sjekk utskriftsfilen "ut.txt". Den skal inneholde den originale «meldingen» og skal kunne leses uten problemer. I tillegg kan det sjekkes om den dekomprimerte filen er nøyaktig like stor som den opprinnelige filen. Men for å være helt sikker på at komprimeringen og dekomprimeringer fungerer korrekt, bør det sjekkes om filene er nøyaktig like, dvs. like byte for byte. Se Oppgave 3.
| 1. | Legg Programkode 5.4.9 b)
inn i class Huffman.
|
| 2. | Legg Programkode 5.4.9 a)
inn i class Huffman og legg så programbiten i
Programkode 5.4.9 c)
inn i metoden der det står // her vil det komme mer kode.
|
| 3. | Lag en metode som sjekker om to filer er identiske, dvs. om de er like byte for byte. Bruk metoden til å sammenligne utskriftsfilen "ut.txt" i Programkode 5.4.9 d) med originalfilen "https://www.cs.hioa.no/~ulfu/appolonius/kap5/4/test.txt". |
| 4. | Komprimer og dekomprimer kap13.html |
| 5. | Som i Oppgave 4 men med kap13.pdf. |
| 6. | Ta hensyn til de endringene i komprimer som er gjort i Oppgave ...... |
![]() 5.4.10 Effektiv dekomprimering
5.4.10 Effektiv dekomprimering
Dekomprimeringsteknikken som brukes i
Programkode 5.4.9 c)
er ikke effektiv. For det første leses én og én bit og det er kostbart.
For det andre må vi sammenligne for hver bit for å kunne gå nedover i treet.
Tilsammen blir dette mye arbeid. En bedre teknikk er å kunne «hoppe ned»
til rett tegn i én operasjon. Vi bruker treet i
Figur 5.4.9 a) som utgangspunkt.
Fyller vi opp med nodene som mangler på hver rad, får vi et perfekt binærtre.
Ekstranodene har fått grå farge på figuren under:
 |
| Figur 5.4.10 a) : Et utvidelse til et perfekt tre |
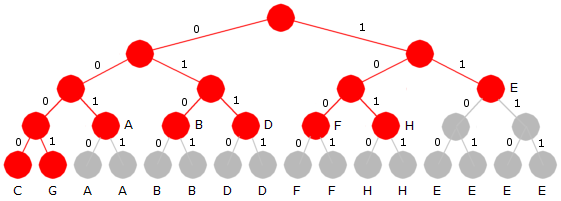
I treet over er det C og G som har lengst bitkode og lengden er fire. Anta nå at vi leser fire biter om gangen. Et eksempel er bitene 0101. De første tre bitene bringer oss ned til den røde noden med bokstaven B. Den siste biten bringer oss videre ned til siste rad og da til en grå node som også har bokstaven B. Hvis de fire bitene isteden hadde vært 0100, ville det samme ha skjedd bortsett fra at vi nå vil teffe en annen grå node med bokstaven B.
Anta nå at vi har fire biter der de to første er 11. Det vil bringe oss først ned til den røde noden med boktsven E. Men uansett hva de to neste bitene er (00, 01, 10 eller 11), vil de bringe oss ned til en grå node med bokstaven E. Siste rad i treet i Figur 5.4.10 a) har 16 noder. De kan nummereres fra 0 til 15. Bokstaven C ligger lengst til venstre. Den har bitoden 0000 og det svarer til tallet 0 skrevet med fire binære siffer. Bokstaven G har bitkoden 0001 og det gir tallet 1 skrevet med fire binære siffer. Den første grå noden med bokstaven A har bitkoden 0010 og det er tallet 2 med fire binære siffer. Osv.
Vi kan erstatte den siste raden i treet med flg. tabell:
| C | G | A | A | B | B | D | D | F | F | H | H | E | E | E | E |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Figur 5.4.10 b) : En tegntabell med samme innhold som nederste rad i treet | |||||||||||||||
Tabellindeksene går fra 0 til 15. Det betyr at når fire biter tolkes som et heltall fungerer det som en tabellindeks. Dermed kan vi lese rett ut fra tabellen hvilken bokstav det er. F.eks. er 1101 = 13 og det gir bokstaven E. Det er imidlertid et lite problem. Det er kun de to bitene 11 som er den egentlige bitkoden til E. Det betyr at de to siste bitene, dvs. 01, må «legges tilbake» og utgjøre de første to bitene ved neste lesing av fire biter. Tabellen under viser hvor mange biter som må «legges tilbake» for hver bokstav. F.eks. er det 2 for bokstaven E:
| 1 | 1 | 0 | 1 | 2 | 1 | 0 | 1 |
| A | B | C | D | E | F | G | H |
| Figur 5.4.10 c) : Antall biter for mange | |||||||
Hvis n er største bitkodelengde, vil nederste rad i utvidelsen av det kanoniske treet til et perfekt tre få 2n noder. Den tilhørende tabellen vil dermed få indekser fra 0 til 2n − 1. Tabellen som skal fortelle hvor mange biter som skal «legges tilbake», skal ha plass til alle de 256 mulige tegnene. I dekomprimeringen leses n og n biter. En samling på n biter, tolket som et heltall, utgjør en indeks i tabellen. Dermed får vi tak i rett tegn ved å «slå opp» i tabellen. Deretter bruker vi tegnet som indeks i den andre tabellen og får vite hvore mange biter som skal «legges tilbake» og dermed utgjøre de første bitene i neste innlesing på n biter.
For et tegn X med bitkodelengde k vil det være d = n − k biter som skal «legges tilbake». Første posisjon for X i tegntabellen finner vi ved å legge d stykker 0-biter bakerst i bitkoden til X. I tegntabellen vil det være 2d forekomster av X. Ta treet i Figur 5.4.10 a), tegntabellen i Figur 5.4.10 b) og bokstaven E som eksempel. Da vil n = 4, k = 2 og d = 2. Første posisjon for E er 11 pluss to 0-biter, dvs. 1100 = 12. Antall forekomster av E er 2d = 22 = 4, dvs. E går fra 12 til (men ikke med) 12 + 4 = 16.
Flg. metode som skal legges i class Huffmann, tar i mot en lengdetabell,
en tabell for antall biter som skal «legges tilbake» og
største bitkodelengde (obs: 1 << n er lik 2n ):
public static byte[] lagTegntabell(int[] lengder, int[] tilbake, int n) { int[] bitkoder = finnBitkoder(lengder); // finner bitkodene byte[] tegntabell = new byte[1 << n]; // en byte-tabell for (int i = 0; i < lengder.length; i++) // går gjennom tabellen if (lengder[i] > 0) // tegn nr. i er med { int d = n - lengder[i]; // d er lengdeforskjellen tilbake[i] = d; // antall tilbake int fra = bitkoder[i] << d; // starten på tegn nr. i int til = fra + (1 << d); // slutten på tegn nr. i for (int j = fra; j < til; j++) // fyller ut intervallet tegntabell[j] = (byte)i; // med tegn nr. i } return tegntabell; } Programkode 5.4.10 a)
Eksempel: I flg. kodebit brukes tegnene og birkodelengdene fra Figur 5.4.9 a):
int[] lengder = new int[256]; int[] tilbake = new int[256]; lengder['A'] = 3; lengder['B'] = 3; lengder['C'] = 4; lengder['D'] = 3; lengder['E'] = 2; lengder['F'] = 3; lengder['G'] = 4; lengder['H'] = 3; byte[] tegntabell = Huffman.lagTegntabell(lengder, tilbake, 4); for (byte b : tegntabell) System.out.print((char)(b & 255) + " "); // Utskrift: C G A A B B D D F F H H E E E E Programkode 5.4.10 b)
Teknikken krever, som nevnt flere steder, at biter som er lest må kunne
«legges tilbake» slik at de kan leses på nytt. Klassen
BitInputStream
har flere metoder som gjør nettopp det, f.eks. metoden
void unreadBits(int numberOfBits) som «legger tilbake»
en, noen eller alle de bitene som sist ble lest inn. Antallet oppgis ved hjelp av
parameteren numberOfBits.
Det kan oppstå et problem med tabellstørrelsen hvis det er store bitkodelengder.
Setningen byte[] tegntabell = new byte[1 << n]; oppretter en
tabell med 2 opphøyd i n som størrelse. I
Eksempel 3 i
Avsnitt 5.4.6 ble filen som
innholder Delkapittel 1.3
analysert. Der ble n = 19 største bitkodelengde. Det
vil gi en tabell på størrelse 524.288 byter = 512kb. Det er ikke spesielt stort.
Men hvis n blir en del større og nærmer seg 31, kan det bli problemer med
minnet. Hvis det ikke er plass, kommer Java-feilmeldingen
OutOfMemoryError: Java heap space. Dette problemet
tas opp lenger ned.
I Programkode 5.4.9 a) laget vi starten på en dekomprimering. Der det står // her vil det komme mer kode, setter vi inn flg. kode:
int n = lengder[vaktpost]; // lengden til vaktposten int[] tilbake = new int[lengder.length]; // for tilbakelegging byte[] tegntabell = lagTegntabell(lengder, tilbake, n); BitOutputStream ut = new BitOutputStream(tilFil); // for utskrift int frekvens = 0; // forekomster av vaktposttegnet for(;;) { int tegn = tegntabell[inn.readBits(n)] & 255; // finner et tegn if (tegn == vaktpost) { if (++frekvens == vaktpostfrekvens) break; } ut.write(tegn); // skriver ut tegnet inn.unreadBits(tilbake[tegn]); // legger biter tilbake } ut.close(); // lukker ut-filen Programkode 5.4.10 c)
Hvis metoden lagTegntabell i
Programkode 5.4.10 a)
legges inn i klassen Huffman og kodebiten i
Programkode 5.4.10 c)
legges inn der det står // her vil det komme mer kode
i Programkode 5.4.9 a),
vil flg. kodebit virke:
String inn = "https://www.cs.hioa.no/~ulfu/appolonius/kap5/4/komprimert.huf"; Huffman.dekomprimer(inn,"ut.txt"); Programkode 5.4.10 d)
Kjør programbiten i Programkode 5.4.10 d) og sjekk utskriftsfilen "ut.txt". Den skal inneholde den originale «meldingen» og skal kunne leses uten problemer.
Store bitkodelengder La n være største bitkodelengde. Hvis n = 19 vil tegntabellen få 1 << 19 = 524.288 byter = 512kb = 0,5mb som størrelse. Dette er ikke spesielt mye. Men for hver 1-er som n øker med, dobles størrelsen. Derfor er det viktig å ha en teknikk for å unngå «Out Of Memory» for store verdier av n.
En mulig løsning er å lese inn bitene i to etapper. La oss dele det kanoniske treet på «midten», dvs. la nivåene fra og med m = (n + 1)/2 og oppover være én del og nivåene nedenfor m en annen del. Ta filen som inneholder Delkapittel 1.3 som eksempel. Analysen av den filen viste at det kanoniske treet har flg. antall noder på nivåene fra 0 til 19:
| Antall bladnoder: | 0 | 0 | 0 | 1 | 6 | 7 | 9 | 8 | 11 | 8 | 12 | 13 | 2 | 6 | 2 | 2 | 2 | 3 | 1 | 2 |
| Antall indre noder: | 1 | 2 | 4 | 7 | 8 | 9 | 9 | 10 | 9 | 10 | 8 | 3 | 4 | 2 | 2 | 2 | 2 | 1 | 1 | 0 |
| Antall noder: | 1 | 2 | 4 | 8 | 14 | 16 | 18 | 18 | 20 | 18 | 20 | 16 | 6 | 8 | 4 | 4 | 4 | 4 | 2 | 2 |
| Nivå: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figur 5.4.10 d) : Antall bladnoder, antall indre noder og totalt antall noder på hvert nivå | ||||||||||||||||||||
Her er n = 19 og dermed m = (19 + 1)/2 = 10. Tabellen viser at det på nivå 10 er totalt 20 noder derav 12 bladnoder og 8 indre noder. Nå «glemmer» vi for en kort stund den delen av treet som ligger under nivå 10. Hvis vi da utvider det vi har igjen til et perfekt tre slik som i Figur 5.4.10 a), vil det bli 2 opphøyd i m noder på nivå m = 10. Disse nodene kan som før «erstattes» med en byte-tabell med størrelse 1 << m = 1 << 10 = 1024. De første 8 posisjonene hører til indre noder, mens resten skal fylles med tegn. De 12 posisjonene fra 8 til 19 skal ha hver sin bokstav siden de representerer tegn med m = 10 som bitkodelengde. På de neste posisjonene vil det komme flere av hvert tegn. F.eks. to forekomster av alle tegn med bitkodelengde 9, fire forekomster av alle med bitkodelengde 8, osv. Tabellen fylles opp med verdier omtrent slik som i Programkode 5.4.10 a).
Dekomprimeringen skjer nå ved at m = 10 biter leses. Hvis tallet som disse representerer, er større enn 7, vil vi få tegnet ved å slå opp i tabellen og så i tabellen for «tilbakelegging» for å finne hvor mange biter som skal «legges tilbake». Filen med Delkapittel 1.3 inneholder 330.520 tegn og av dem er det hele 327.702 stykker som har en bitkodelengde på 10 eller mindre. Det betyr at det å lese med 10 biter gir oss rett tegn i hele 99% av tilfellene.
 |
| Figur 5.4.10 e) : Den nederste delen av treet |
På nivå 18 er det kun én indre node og det tilhørende treet har høyde 1. På nivå 17 er det også kun én indre node og treet har høyde 2. På nivå 16 er det to indre noder. Treet til den første har høyde 3 og det til den andre høyde 1. Tabellen sier at det også er to indre noder på nivå 15. Tegningen viser at de tilhørende trærne har høyde 4 og 1.
Høyden til en node (eller treet med noden som rot)
er én mer en høyden til det største
(størst høyde) av nodens to subtrær. Flg. metode tar i mot en tabell blader
som forteller hvor mange bladnoder det er på hvert nivå og returnerer en tabell som
viser høyden til trærne til de indre nodene på et oppgitt nivå.
Returtabellens lengde er lik antallet indre noder:
public static int[] treHøyde(int[] blader, int nivå) { int n = blader.length; // n er antall nivåer i treet (0 til n-1) int[] noder = new int[n]; // antall noder på hvert nivå (0 til n-1) noder[n-1] = blader[n-1]; // kun bladnoder på nederste nivå for (int k = n - 1; k > nivå; k--) // n-1 er nederste nivå noder[k - 1] = noder[k]/2 + blader[k-1]; // antall noder på nivå k-1 int maks = noder[Tabell.maks(noder)]; // maks antall noder på et nivå int[] høyder = new int[maks]; for (int i = n - 2; i >= nivå; i--) { int k = noder[i] - blader[i]; // antall indre noder på nivå i for (int j = 0; j < k; j++) { høyder[j] = Math.max(høyder[2*j],høyder[2*j+1]) + 1; } for (int j = k; j < noder[i+1]; j++) høyder[j] = 0; } int[] h = new int[noder[nivå] - blader[nivå]]; System.arraycopy(høyder,0,h,0,h.length); return h; } Programkode 5.4.10 e)
Tabellen i Figur 5.4.10 d)
inneholder antallet bladnoder på hvert nivå. Flg. eksempel viser
hvordan metoden treHøyde kan brukes til å finne
høyden til trærne på gitte nivåer:
int[] blader = {0,0,0,1,6,7,9,8,11,8,12,13,2,6,2,2,2,3,1,2}; for (int nivå = 8; nivå < 13; nivå++) { System.out.print("nivå " + nivå + ": "); Tabell.skrivln(Huffman.treHøyde(blader,nivå)); } // Utskrift: // nivå 8: 11 3 2 2 2 1 1 1 1 // nivå 9: 10 2 2 2 1 1 1 1 1 1 // nivå 10: 9 2 1 1 1 1 1 1 // nivå 11: 8 2 1 // nivå 12: 7 1 1 1 Programkode 5.4.10 f)
Det er nå en hel serie med «detaljer» som må på plass før selve dekomprimeringen kan starte. Vi tar utgangspunkt i Programkode 5.4.9 a). Flg. «detaljer» skal inn der det står // her vil det komme mer kode:
int n = lengder[vaktpost]; // lengden til vaktposten int[] blader = new int[n + 1]; // n er nederste nivå for (int lengde : lengder) if (lengde > 0) blader[lengde]++; // finner antallet på hvert nivå int[] bitkoder = finnBitkoder(lengder); // finner bitkodene
Neste skritt er å dele det kanoniske treet på midten. Vi behandler den delen av treet som går ned til og med nivå m = (n + 1)/2 for seg. Vi lager først en byte-tabell med størrelse 1 << m og fyller den med tegn på samme måte som i Programkode 5.4.10 a). Et heltall gitt ved m biter blir da en indeks. Dermed kan vi finne tilhørende tegn ved å slå opp i tabellen og så bruke tegnet til å slå opp i tilbakeleggingstabellen. Forskjellen er at de første posisjonene i byte-tabellen nå representerer indre noder i det kanoniske treet. I de posisjonene legger vi derfor høyden til de tilhørende trærne:
int m = (n + 1)/2; // det midterste nivået i treet byte[] tegntabell = new byte[1 << m]; // en byte-tabell int[] høyder = treHøyde(blader, m); // de indre nodene på nivå m int grense = høyder.length; // skiller indre noder og blader for (int i = 0; i < grense; i++) { tegntabell[i] = (byte)høyder[i]; // høydene først i tegntabellen } int[] tilbake = new int[lengder.length]; // for tilbakelegging
Variabelen grense er skillet mellom de indre nodene og resten. Hvis heltallet representert med m biter er mindre enn grense, betyr det at vi må lenger ned i det kanoniske treet for å finne rett tegn. I vårt eksempel (Figur 5.4.10 d ) er n = 19, m = (19 + 1)/2 = 10 og grense = 8. Utskriften fra Programkode 5.4.10 f) sier at høydene til trærne til de 8 indre nodene er henholdsvis 9, 2, 1, 1, 1, 1, 1 og 1. Det første treet har høyde 9. Hvis vi fyller ut det med nodene som mangler vil nederste nivå der få 1 << 9 = 512 noder. Denne raden erstatter vi med en byte-tabell som fylles med tegn. Dermed kan et heltall gitt med 9 biter gi oss rett tegn ved et tabelloppslag. Osv. Vi trenger imidlertid 8 byte-tabeller. Da passer det å bruke en to-dimensjonal byte-tabell, dvs. en tabell med 8 rader. Størrelsene på de 8 radene blir da 1 << 9 = 512, 1 << 2 = 4, 1 << 1 = 2, osv:
byte[][] tegntabeller = new byte[grense][]; // en to-dimensjonal tabell for (int i = 0; i < grense; i++) { tegntabeller[i] = new byte[1 << høyder[i]]; // størrelse 1 << høyder[i] }
Legg merke til at i vårt eksempel vil hele systemet med byte-tabeller bestå av tabeller med størrelser 1024, 512, 4, 2, 2, 2, 2, 2 og 2. Tilsammen 1552 byter. Dette er dramatisk mindre bruk av minne enn å ha én byte-tabell på 1 << 19 = 524288 byter.
Den mest kompliserte oppgaven gjenstår. Det er å fylle alle byte-tabellene med
de riktige tegnene. Da skal tegn med lengde <= m legges i den «store»
tabellen tegntabell og tegn med lengde > m i en av de «små»
tabellene i tegntabeller:
for (int i = 0; i < lengder.length; i++) // går gjennom alle lengdene { int lengde = lengder[i]; // hjelpevariabel if (lengde > 0) // tegnet i skal være med { if (lengde <= m) // den store tabellen { // tegntabell skal fylles ut med tegnet asciiverdi i } else // de små tabellene { // en av tabellene i tegntabeller skal fylles ut med tegnet i } } }
Det å legge tegnet med ascii-verdi i inn i tegntabell gjøres
som i Programkode 5.4.10 a):
int d = m - lengde; // lengdeforskjellen tilbake[i] = d; // antall tilbake int fra = bitkoder[i] << d; // starten på tegn nr. i int til = fra + (1 << d); // slutten på tegn nr. i for (int j = fra; j < til; j++) tegntabell[j] = (byte)i; // fyller ut
Er bitkodelengden > m, skal tegnet ligge i en av tabellene
i tegntabeller. I vårt eksempel
er m = 10. La tegnet i ha en bitkodelengde på 15. De
10 første bitene i bitkoden bringer oss ned til en av de indre nodene på nivå 10.
Tallet gitt ved de 10 bitene vil være et av tallene fra 0 til 7 siden nivået har 8
indre noder. Trærne til de 8 nodene har høyder på henholdsvis 9, 2, 1, . . . 1.
Siden lengden er 15, skal tegnet legges i treet med høyde 9. Dermed skal
det leses 9 biter til (og 9 − 5 = 4 av dem må legges tilbake).
De 10 første bitene i bitkoden må utgjøre tallet 0 (alle bitene
er 0-biter). De 5 siste bitene sammen med 4 ekstra 0-biter bakerst, bestemmer
posisjonen til første forekomst av tegnet i. Antallet forekomster er 1 << 4 = 16.
Istedenfor tallene 10, 15 og 9 skal vår kode bruke variablene m, lengde og d1 :
int kode = bitkoder[i]; // bitkoden til tegnet med i som asciiverdi int d1 = lengde - m; // differensen mellom lengde og m int kode1 = kode >> d1; // de m første bitene i kode int kode2 = kode & ((1 << d1) - 1); // de d1 siste bitene i kode byte[] b = tegntabeller[kode1]; // finner rett tabell int d2 = tegntabell[kode1] - d1; // differensen mellom høyden og d1 tilbake[i] = d2; // antall tilbake int fra = kode2 << d2; // starten på tegn i int til = fra + (1 << d2); // slutten på tegn i for (int j = fra; j < til; j++) b[j] = (byte)i; // fyller ut
Nå gjenstår selve dekomprimeringen. Kjernen der er at m biter leses.
Det tilhørende heltallet gir en indeks til tabellen tegntabell.
Hvis indeksen ikke hører til en indre node, finner vi tegnet i tabellen.
Hvis den hører til en indre node, finne vi høyden til det tilhørende treet og det
sier hvor mange biter vi skal lese i neste innlesning. Videre finner vi
hvilken av tabellene til tegntabeller som vi da skal slå opp.
Har vi lest for mange biter legges de overflødige tilbake.
Hvis tegnet er lik vaktposttegnet, teller vi opp. Osv:
BitOutputStream ut = new BitOutputStream(tilFil); // for utskrift int frekvens = 0; // forekomster av vaktposttegnet for(;;) { int lest = inn.readBits(m); // leser m biter int tall = tegntabell[lest] & 255; // slår opp i tegntabellen if (lest < grense) // lest gir en indre node { byte[] b = tegntabeller[lest]; // finner rett tabell lest = inn.readBits(tall); // leser flere biter tall = b[lest] & 255; // slår opp i tabellen } // tall er nå ascii-verdien til et tegn if (tall == vaktpost) { if (++frekvens == vaktpostfrekvens) break; } ut.write(tall); // skriver ut tegnet inn.unreadBits(tilbake[tall]); // legger biter tilbake } ut.close(); // lukker ut-filen
I dette avsnittet behandler vi først hele det kanoniske treet under ett. Da
holder det med å lage én tegntabell og bruke kun én bit-innlesing for hvert tegn.
Men tabellen kan bli stor hvis største bitkodelengde n er stor. En annen teknikk
er å dele treet på midten. Da bruker vi flere tegntabeller, men sammenlagt bruker
de dramatisk mindre plass en den ene store tabellen. Ulempen er at vi får én ekstra
sammenligning lest < grense. Men den vil sjelden være sann. I vårt
eksempel er den sann for kun én prosent av innlesningene. Dette er en helt marginal kostnad.
Derfor bør vi alltid bruke todelingsteknikken. Det å sette alt sammen til en metode for
todelingsteknikken gis som Oppgave xx.
| 1. | xxx |
![]() 5.4.11 Huffmans metode med begrenset bitkodelengde
5.4.11 Huffmans metode med begrenset bitkodelengde
| 1. | xxx |
![]() 5.4.12 Den adaptive Huffmanteknikken
5.4.12 Den adaptive Huffmanteknikken
Den statiske Huffmanteknikken krever at frekvensfordelingen for tegnene i
den «meldingen» som
skal komprimeres, er kjent. Hvis ikke må «meldingen»
leses en gang først. Under komprimeringen må den så leses på nytt.
Det er selvfølgelig uheldig med to innlesinger hvis det å lese
tar lang tid. Det vil også være situasjoner der det ikke
er mulig å lese «meldingen» to ganger og da kan ikke denne teknikken brukes.
I den adaptive (eller dynamiske) Huffmanteknikken bygges Huffmantreet fortløpende mens «meldingen» leses. For hvert tegn som leses er det to muligheter:
- Hvis tegnet finnes fra før, brukes bitkoden som treet gir. Deretter økes tegnets frekvens og treet oppdateres slik at det blir et korrekt Huffmantre.
- Hvis tegnet er nytt, skrives det først ut et «signal» (en spesiell bitkode) og så tegnets ordinære bitkode (ascii-kode). I tillegg legges det nye tegnet inn i treet.
Hvis denne teknikken skal virke, må vi for det første ha en regel som forteller når et tre er et korrekt Huffmantre og for det andre en algoritme som på en forholdsvis effektiv måte vil oppdatere et korrekt Huffmantre til et tre som fortsatt er korrekt.
 |
| Figur 5.4.12 a) : Tomt tre |
 |
| Figur 5.4.12 b) : E er satt inn |
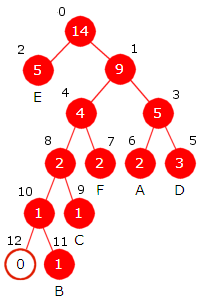 |
| Figur 5.4.12 c) : Totalt 14 tegn |
Anta som eksempel at teksten "EDEAEEFECDAFDB" utgjør første del av en melding. På forhånd har vi et «tomt» Huffmantre, dvs. et tre som kun består av «nullnoden». Den skal representere tegn som ennå ikke har blitt observert og har dermed frekvens lik 0. Se Figur 5.4.12 a) til venstre.
E er første tegn. Når det legges inn får vi Figur 5.4.12 b). Det kan ses på som et Huffmantre siden rotnodens frekvens er summen av barnas frekvenser og venstre barns frekvens er mindre enn eller lik høyre barns frekvens. Nodene er nummerert slik at nummerrekkefølgen gir avtagende frekvenser. Her blir det 0, 1 og 2 med frekvenser 1, 1 og 0.
Vi trenger et litt større tre for å kunne forklare gangen i oppdateringen. Anta at hvert av de 13 øvrige tegnene i meldingen er lagt inn og at treet har blitt oppdatert etter hver innlegging. Resultatet er Figur 5.4.12 c). Vi ser at frekvensen i hver indre node er lik summen av barnas frekvenser og at nummerrekkefølgen 0, 1, . . 12 (i dette tilfellet svarer det til speilvendt nivåorden) gir avtagende frekvenser, dvs. 14, 9, 5, 5, 4, 3, 2, 2, 2, 1, 1, 1, 0.
La p og q være to noder i treet. Vi sier at p kommer foran q hvis p har et lavere plassnummer enn q. Videre sier vi at p er den første (eller den minste) noden i en samling noder hvis p har det laveste plassnummeret. Ta f.eks. alle nodene som har frekvens 1 i Figur 5.4.12 c), dvs. nodene på plassene 9, 10 og 11. Da er det noden på plass 9 (bokstaven C) som er den første (eller den minste) av dem. Noden på plass 6 (bokstaven A) er den første av de som har frekvens 2.
Anta at B er neste tegn i meldingen. Vi må først avgjøre om B ligger i treet. I vårt eksempel - Figur 5.4.12 c) - ligger B i noden på plass 11. Den skal nå bytte plass med den første av de som har samme frekvens (dvs. 1) som B-noden, dvs. med noden på plass 9 (bokstaven C). Etter flyttingen økes frekvensen med 1. Figur 5.4.12 d) viser resultatet:
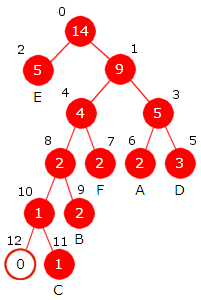 |
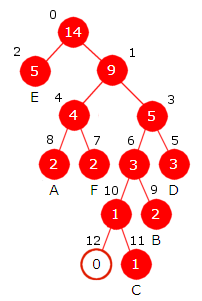 |
|
| Figur 5.4.12 d) : B og C har byttet plass |
Figur 5.4.12 e) : To noder har byttet plass |
Neste skritt er å gå til forelderen til den som nettopp ble flyttet, dvs. til noden på plass 8. Se Figur 5.4.12 d). Den skal bytte plass med den første av de nodene som har samme frekvens. Dvs. noden på plass 8 flyttes til plass 6 (og omvendt). Etter flyttingen økes frekvensen med 1. Se Figur 5.4.12 e) over. Legg merke til at en node flyttes ved at hele treet til noden flyttes.
På nytt går vi til forelderen til noden som ble flyttet (noden på plass 6), dvs. til noden på plass 3. Se Figur 5.4.12 e) over. Den skal som vanlig byttes med den første av de nodene som har samme frekvens, dvs. frekvens 5. Med andre ord skal den byttes med noden på plass 2 (bokstaven E). Frekvensen økes med 1. Så går vi til dens forelder, men siden det er rotnoden er vi ferdig. Til slutt økes rotnodens frekvens med 1. Se Figur 5.4.12 f) under:
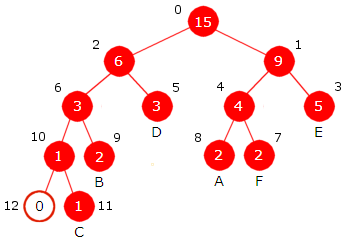 |
| Figur 5.4.12 f) : Nodene på plass 2 og 3 er byttet |
Legg merke til at det bare er noder med samme frekvens som bytter plass. Det betyr at etter hver ombytting vil frekvensen i hver indre node fortsatt være summen av frekvensene til nodens to barn. Etter en ombytting økes frekvensen med 1 i den første av nodene med samme frekvens. Det betyr dens frekvens fortsatt blir mindre enn eller lik frekvensen i den noden som kommer rett foran i rekkefølgen. Med andre ord vil frekvensene fortsatt komme i avtagende rekkefølge med hensyn på nodenes nummerrekkefølge.
Vi må ta hensyn til et spesialtilfelle: Anta at tegnet C skal inn i treet i Figur 5.4.12 f). Da starter vi i noden på plass 11. Men den første av de som har samme frekvens (frekvens 1), er noden på plass 10, dvs. foreldernoden. I et slikt tilfelle skal det ikke skje en ombytting. Vi øker isteden frekvensen og går rett til foreldernoden på plass 10. Den er først blant de med samme frekvens, men å bytte den med seg selv er helt unødvendig. Vi øker frekvensen og går så rett til foreldernoden, dvs noden på plass 6. Den må byttes med noden på plass 5 og så få sin frekvens økt. Det hele fortsetter i dens forelder, dvs. noden på plass 2. Den er «enslig», dvs. den er alene om å ha den frekvensen den har. Dermed kun frekvensøkning, men ingen ombytting. Dens forelder er rotnoden og etter at vi har økt dens frekvens, er vi ferdig. Figur 5.4.12 g) under viser resultatet:
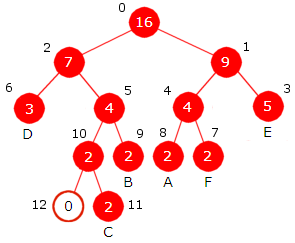 |
| Figur 5.4.12 g) : En ny forekomst av C |
Hvis det er et nytt tegn, blir det litt annerledes. I Figur 5.4.12 g) inngår bokstavene A , B , C , D , E og F. Anta at G skal inn. Det gjøres ved at nullnoden på plass 12 blir en indre node med frekvens 1, med bokstaven G som høyre barn og en ny nullnode som venstre barn. Så går vi rett til forelderen til den gamle nullnoden, dvs. til noden på plass 10. Se Figur 5.4.12 g). Derfra er oppdateringen som før. Noden bytter plass med den på plass 7 og frekvensen økes. Så går vi til dens forelder på plass 4, osv. Figur 5.4.12 h) viser resultatet:
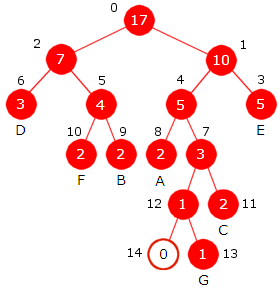 |
| Figur 5.4.12 h) : G er lagt inn som nytt tegn |
Legg merke til at når et helt nytt tegn legges inn, får treet to nye noder. Det betyr at hvis treet inneholder n forskjellige tegn vil det ha 2n + 1 noder. Treet i Figur 5.4.12 h) har 7 forskjellige tegn og 2·7 + 1 = 15 noder (nummerert fra 0 til 14).
OBS. Første gang det legges inn et tegn, dvs. når vi starter med et tomt Huffmantre, blir det som Figur 5.4.12 b) viser.
Et prefikskodetre med frekvenser har søskenegenskapen (eng: the sibling property) hvis:
- Frekvensen i hver indre node er lik summen av frekvensene til de to barna.
- Nodene kan nummereres i avtagende rekkefølge med hensyn på frekvens. I nummereringen skal alltid det venstre barnet i et søskenpar følge rett etter det høyre barnet og forelderen alltid ha et nummer som kommer foran disse.
Det kan bevises at et prefikskodetre som har søskenegenskapen, er et Huffmantre. Legg merke til at treet i Figur 5.4.12 h) har søskenegenskapen. Det samme har alle de andre trærne vi har tegnet. Algoritmen beskrevet over sørger for at denne egenskapen bevares ved hver oppdatering.
I alle trærne som er tegnet svarer nummereringen til speilvendt nivåorden. Den starter i roten (nr. 0) og går nedover nivå for nivå og for hvert nivå fra høyre mot venstre. Men kravet i søskenegenskapen er ikke fullt så strengt. Algoritmen sørger for at egenskapen bevares, men ikke nødvendigvis at nummereringen er i speilvendt nivåorden. Se Oppgave 3. Men det vil hele tiden være slik at frekvensene kommer i avtagende rekkefølge både i denne spesielle nummereringen og i speilvendt nivåorden selv om de to kan være forskjellige.
Beskrivelsen over svarer til det som kalles FGK-algoritmen (etter Newton Faller, Robert Gallager og Donald Knuth). En forskjell er at når FGK-algortimen beskrives, er det vanlig å nummerere nodene motsatt vei. I en slik nummerering kommer nullnoden først og rotnoden sist. Ulempen er at alle nodene må renummereres når det kommer inn nye noder. Alternativt kan en la rotnoden fra starten av få et stort nummer. Anta at «meldingen» kun kan inneholde ascii-tegn (tallverdier fra 0 til 255). Det betyr at treet kan ha maksimalt 256 bladnoder og dermed maksimalt 513 noder. Dermed kunne rotnoden få nummer 512 og de øvrige nummereres nedover. I treet i Figur 5.4.12 h) ville da nullnoden bli nummer 498.
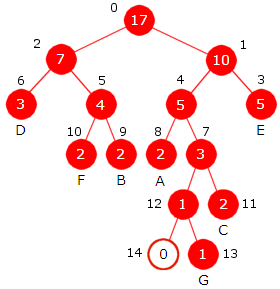 |
| Figur 5.4.12 i) : Huffmantre med 15 noder |
frekvens, tegn og nummer,
og som ellers variabler for venstre og høyre barn.
Hvis to noder skal bytte plass, gjøres det implisitt ved at nodene bytter foreldre.
Noden må derfor ha forelder som variabel. Et ledd i algoritmen er
at en node skal bytte plass med den første av de som har samme frekvens. Ta
f.eks. noden på plass 11 i treet til venstre. Den første av de med frekvens 2 er den på
plass 8. Hvordan skal vi på en effektiv måte kunne finne den ved å starte fra
plass 11? Det kan f.eks. løses ved hjelp av en nodetabell med referanse til hver node
i treet. Hvis tabellindeksen til en referanse og nummeret til noden den går til er like,
blir det effektivt.
private final static class Node // en indre nodeklasse { private int frekvens; // nodens frekvens private int c; // nodens tegn private int nummer; // nodens nummer private Node forelder; // referanse til forelder private Node venstre = null; // referanse til venstre barn private Node høyre = null; // referanse til høyre barn private Node(int frekvens, int c, int nummer, Node forelder) { this.frekvens = frekvens; this.c = c; this.nummer = nummer; this.forelder = forelder; } } // Node Programkode 5.4.12 a)
Tabellen noder under har 15 verdier. Den kobles til treet
i Figur 5.4.12 i) ved at
noder[0] går til roten, noder[1] til den på plass 1, osv.
til noder[14] som går til nullnoden.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Figur 5.4.12 k) : En tabell som skal koblet til treet i Figur 5.4.12 j) | ||||||||||||||
En node har et eksplisitt nummer (variablen nummer) og et implisitt
nummer (det samme tallet) gjennom sin plassering i tabellen noder. Vi finner
den første av de som har samme frekvens som p ved å slå opp i tabellen
med p.nummer som indeks. Derfra leter vi mot venstre.
To noder p og q bytter plass ved at de implisitt bytter plass i treet
(bytter foreldre) og eksplisitt ved at de bytter plass i tabellen. Nodene må også
bytte (interne) nummer:
private static void bytt(Node p, Node q, Node[] noder) { Node f = p.forelder, g = q.forelder; // finner foreldrene if (p == f.venstre) f.venstre = q; // f får q som barn else f.høyre = q; if (q == g.høyre) g.høyre = p; // g får p som barn else g.venstre = p; p.forelder = g; // p får g som forelder q.forelder = f; // q får f som forelder noder[q.nummer] = p; // p flyttes til plassen til q noder[p.nummer] = q; // q flyttes til plasen til p int nummer = p.nummer; // p og q bytter nummer p.nummer = q.nummer; q.nummer = nummer; } Programkode 5.4.12 b)
Tabellen tegn skal være slik at
hvis 'A' er i treet, skal tegn['A'] gå til noden til
'A'. Hvis 'B' ikke er der, skal tegn['B'] være
null. Siden alle ascii-tegn kan forekomme, får den 257 (256 + 1) som
dimensjon. Tegnet EOC = 256 står for «End of Compression»:
public class AdHuffman // adaptiv Huffman { private static final int EOC = 256; // End of Compression // Nodeklassen fra Programkode 5.4.12 a) skal inn her private Node rot, NULL; // referanser til rotnoden og nullnoden private Node[] noder; // nodetabell for nodene private Node[] tegn; // nodetabell for tegn int antall = 0; // antall noder i treet public AdHuffman() // kontruktør - lager et tomt tre { rot = NULL = new Node(0,-1,0,null); // rotnoden er lik nullnoden noder = new Node[2*8 + 1]; // plass til 17 noder (8 tegn) noder[antall++] = rot; // roten legges i posisjon 0 tegn = new Node[257]; // alle ascii-verdier + EOC } // Metoden bytt fra Programkode 5.4.12 b) skal inn her } Programkode 5.4.12 c)
Et nytt tegn c legges som høyre barn til nullnoden. Barnet legges
på første ledige plass i nodetabellen og i tegn[c].
Venstre barn blir ny nullnode og legges i nodetabellen på neste
ledige plass. Se beskrivelsen mellom Figur 5.4.12 g)
og Figur 5.4.12 h).
Det må være samsvar mellom nodenumrene og plasseringene i nodetabellen:
private Node nyttTegn(int c) // et nytt tegn { if (antall == noder.length) // er tabellen full? { noder = Arrays.copyOf(noder,2*antall - 1); // dobler } Node p = NULL; // p settes lik nullnoden p.høyre = new Node(1,c,antall,p); // ny node som høyre barn tegn[c] = p.høyre; // noden inn i tegn-tabellen noder[antall++] = p.høyre; // noden inn i nodetabellen p.venstre = new Node(0,-1,antall,p); // ny node som venstre barn noder[antall++] = p.venstre; // noden inn i nodetabellen NULL = p.venstre; // ny nullnode if (p == rot) return p; // returnerer roten p.frekvens = 1; // frekvens lik 1 return p.forelder; } Programkode 5.4.12 d)
Nå har vi de byggestenene som trengs for å lage en oppdateringsmetode, dvs. en metode som enten øker frekvensen til et eksistrende tegn eller som legger inn et nytt tegn, og som deretter oppdaterer treet slik som beskrevet i første del av dette avsnittet:
private void oppdater(int c) { Node p = tegn[c]; // slår opp i tegntabellen if (p == null) p = nyttTegn(c); // er det et nytt tegn? while (p != rot) // går fra p og opp mot roten { // sammenligner p med noden rett foran if (noder[p.nummer - 1].frekvens == p.frekvens) { int k = p.nummer - 1; // leter videre mot venstre while (noder[k-1].frekvens == p.frekvens) k--; Node q = noder[k]; // q er minst if (q != p.forelder) bytt(p,q,noder); // p og q bytter plass } p.frekvens++; // øker frekvensen p = p.forelder; // går til forelderen } } Programkode 5.4.12 e)
Ytterste while-løkke i Programkode 5.4.12 e) stopper når p
kommer til roten. Men frekvensen økes ikke. Det betyr at rotnodens frekvens blir stående på 0.
Dermed kan den brukes som en «vaktpost». Den innerste while-løkken inneholder
k-- og det er situasjoner der k da kan bli negativ. Se på situasjonen etter at
det første tegnet er lagt inn slik som i
Figur 5.4.12 b). Hvis det samme
tegnet (bokstaven E) skal legges inn en gang til, vil letingen etter den første
blant de som har frekvens 1 kunne bringe oss ut av tabellen. Men det kan ikke skje nå siden
rotnodens frekvens er 0. Derfor trengs ingen sammenligning
av typen k > 0 for å stoppe while-løkken. Hvis det var nødvendig å vite
hva rotnodens frekvens skulle ha vært hvis den hadde vært oppdatert på vanlig måte, er
det bare å legge sammen barnas frekvenser.
Hvis vi skal skrive ut nodene i et tre for å sjekke at ting stemmer, kan det være
lurt å ha en toString-metode i nodeklassen. Hvis meldingen inneholder
«usynlige» tegn, kan vi legge tabellen ascii fra
Programkode 5.4.6 f) inn i
class ADHuffman. Metoden kan da lages slik:
public String toString() { String s = "(" + nummer + "," + frekvens; if (c >= 0) // bladnoder har c = -1 { if (c < 32) s += "," + ascii[32]; else s += "," + (char)c; } return s + ")"; } Programkode 5.4.12 f)
Flg. metode bygger opp et tre ved hjelp av «melding» i form av en tegnstreng og skriver ut nodenes innhold i nummerrekkefølge:
public static void skrivTre(String melding) { AdHuffman h = new AdHuffman(); // lager et tomt tre char[] tegn = melding.toCharArray(); // gjør om til en tegntabell for (char c : tegn) h.oppdater(c); // bygger opp treet for (int i = 0; i < h.antall; i++) // skriver ut nodene System.out.print(h.noder[i] + " "); } Programkode 5.4.12 g)
All den koden som er laget til nå, ligger på
class AdHuffman. Hvis du flytter den
over til ditt system, vil flg. kodebit skrive ut nodene i treet fra
Figur 5.4.12 c).
I «utskriften» er bare de åtte første nodene tatt med.
Se også Oppgave 2.
public static void main(String[] args) { AdHuffman.skrivTre("EDEAEEFECDAFDB"); } // Utskrift: (0,0) (1,9) (2,5,E) (3,5) (4,4) (5,3,D) (6,2,A) (7,2,F) . . . Programkode 5.4.12 h)
Bitkoder For hvert tegn i meldingen må det avgjøres om det er et helt nytt tegn eller om tegnet har forekommet tidligere. Hvis tegnet er nytt skal først bitkoden til nullnoden skrives ut og deretter tegnet på vanlig form (ascii-verdi). Hvis tegnet har forkommet før, skrives bitkoden til tegnet slik det ligger i treet.
Problemet er at treet endrer seg etter hvert som vi leser tegn og oppdaterer treet.
Dermed vil både nullnoden og bladnodene kunne skifte plasser. Bitkoden
til et tegn er gitt ved veien fra roten ned til tegnet. Men den veien vil endre
seg når treet endrer seg. Det betyr at vi må finne denne veien på nytt for hvert
tegn vi leser. Et oppslag i tabellen tegn gir oss direkte aksess til den bladnoden
som inneholder tegnet. Derfor er det enklest og mest effektivt å gå motsatt vei, dvs.
fra noden og opp til roten. Da finner vi imidlertid bitene i en rekkefølge som er
motsatt av den vi må ha, men det fikser vi.
La biter og lengde være en int-variabler og p
en nodereferanse. Vi starter med at alle bitene i biter er 0 og at
lengde er 0. For hver node oppover skyves bitene i
biter en enhet mot høyre. Da kommer det inn en 0-bit fra venstre.
Hvis p er et venstre barn, så lar vi 0-biten stå. Men hvis p derimot
er et høyre barn, må vi ersatte den med en 1-bit. Til det bruker vi
tallet 0x80000000, dvs. tallet som har en 1-bit lengst til venstre og
resten 0-biter:
lengde++; // lengden øker med 1 biter >>>= 1; // skyver inn en 0-bit fra venstre if (p.forelder.høyre == p) biter |= 0x80000000; // er p et høyre barn? p = p.forelder; Programkode 5.4.12 i)
Når vi kommer til roten, vil tegnets bitkode ligge i venstre del av biter og
lengde sier hvor mange det er. Da kan vi bruke metoden
writeLeftBits fra klassen BitOutputStream.
Den skriver ut så mange biter fra venstre i biter som lengde
sier.
Hvis det er et helt nytt tegn, skal som nevnt bitkoden til nullnoden skrives ut og deretter tegnet. Da dukker det opp et problem. Helt til slutt kan vi stå igjen med færre enn 8 biter. Da legges det på ekstra 0-biter for å få en full byte. Vi trenger derfor en «vaktpost» som som sier fra når «våre» biter slutter. Det må være et tegn som helt sikkert ikke forekommer i meldingen, f.eks. tegnet med ascii-verdi 256 og som vi har kalt EOC (eng: end of compression). EOC har imidlertid 9 biter og dermed må også alle andre tegn skrives ut med 9 istedenfor de normale 8 bitene. Kostnaden er 1 ekstra bit for hvert av de ulike tegnene. Men det utgjør lite siden det maksimalt kan være 256 forskjellige tegn, normalt vesentlig færre:
private void skrivBitkode(int c, BitOutputStream ut) throws IOException { int biter = 0, lengde = 0; Node blad = tegn[c]; Node p = blad != null ? blad : NULL; // p tegnnode eller nullnoden while (p != rot) // går oppover mot roten { lengde++; biter >>>= 1; if (p.forelder.høyre == p) biter |= 0x80000000; p = p.forelder; } ut.writeLeftBits(biter,lengde); if (blad == null) ut.writeBits(c,9); // tegnet med 9 biter } Programkode 5.4.12 j)
Metoden komprimer henter tegn fra en fil og skriver resultatet
til en annen fil. For hvert tegn som leses sørger metoden
skrivBitkode for å få ut bitene og metoden oppdater
for å legge tegnet inn i Huffmantreet:
public static void komprimer(String fraUrl, String tilFil) throws IOException { InputStream inn = new BufferedInputStream((new URL(fraUrl)).openStream()); // inn BitOutputStream ut = new BitOutputStream(tilFil); // ut AdHuffman h = new AdHuffman(); // oppretter et tomt Huffmantre int c = 0; while ((c = inn.read()) != -1) // leser til filslutt { h.skrivBitkode(c,ut); // skriver ut bitkoden h.oppdater(c); // oppdaterer Huffmantreet } h.skrivBitkode(EOC,ut); // Vaktpost: End of Compression inn.close(); ut.close(); // lukker filene } Programkode 5.4.12 k)
Dekomprimeringen foregår på en tilsvarende måte som for den statiske Huffmanteknikken. Bitene leses en for en og ved hjelp av dem kommer vi ned til en bladnode i treet. Hvis det er nullnoden, vil de 9 neste bitene representere et helt nytt tegn. Hvis ikke, innholder bladnoden det aktuelle tegnet. Tegnet skrives ut, treet oppdateres og vi fortsetter inntil «vaktposten» EOC kommer:
public static void dekomprimer(String fraUrl, String tilFil) throws IOException { BitInputStream inn = new BitInputStream((new URL(fraUrl)).openStream()); // inn OutputStream ut = new BufferedOutputStream(new FileOutputStream(tilFil)); // ut AdHuffman h = new AdHuffman(); // et tomt Huffmantre for (Node p = h.rot; ; p = h.rot) // starter i roten { while (p.venstre != null) // er p er en bladnode? { if (inn.readBit() == 0) p = p.venstre; // til venstre ved 0-bit else p = p.høyre; // til høyre ved 1-bit } int c = p.c; // tegnet i noden if (c == -1) c = inn.readBits(9); // er p lik nullnoden? if (c == EOC) break; // End of Compression ut.write(c); // skriver ut tegnet h.oppdater(c); // oppdaterer Huffmantreet } inn.close(); ut.close(); // lukker filene } Programkode 5.4.12 l)
Hvis du legger skrivBitkode, komprimer og dekomprimer
inn i class AdHuffman, vil
flg. programbit kunne kjøres:
String fraUrl = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/3/kap13.html"; AdHuffman.komprimer(fraUrl,"ut.txt"); Programkode 5.4.12 m)
I siste del av Avsnitt 5.4.8 fant vi at metoden i Programkode 5.4.8 f) (den statiske Huffmanteknikken) komprimerte filen Delkapittel 1.3 ned til 207.538 byter. Hvis en kikker på filen "ut.txt", vil en se at den er på 207.631 byter. Dette er imidlertid noen få byter mer, men til gjengjeld leser den adaptive Huffmanteknikken filen kun én gang. Se Oppgave 5. Sjekk at dekomprimeringsmetooden virker som den skal - se Oppgave 6.
Effektivitet Anta at «meldingen» innholder tilsammen n tegn derav k forskjellige. I den adaptive Huffmanteknikken bygges treet fortløpende og for hvert tegn er treet et Huffmantre for de tegnene som er lest inntil da. Hvis alle de k tegnene forekommer like ofte, vil treet kunne være nær perfekt med en gjennomsnittlig bitkodelengde for de leste tegnene på omtrent log2 k. Men hvis det er skjev fordeling vil gjennomsnittlig bitkodelengde være mindre enn det. Det betyr at både komprimeringen og dekomprimeringen vil være av orden n log2 k. I vanlige tilfeller er k svært mye mindre enn n og da vil metodene i praksis være av orden n.
Det kommer her stoff om Vitters adaptive Huffmanteknikk.
| 1. | Start med et tomt tre og legg så inn bokstavene A, B, C og D slik som beskrevet i første del av dette avsnittet. Hvordan ser treet ut? Lag en tegning. Bygg det videre ut med E, A og A. Tegn treet. Avslutt med å legge inn B, D, B, E og F. Tegn treet. |
| 2. | Ta class AdHuffman
over til deg og lag et program som kjører
Programkode 5.4.12 h). Det
andre tallet i hver parentes er frekvensen. Sjekk at de (bortsett fra den første som er
rotnoden) kommer i avtagende rekkefølge. Gjør om
Programkode 5.4.12 g)
slik at det blir korrekt frekvens også i utskriften av rotnoden.
Husk at rotnodens frekvens skal være lik summen av barnas frekvenser. Gjør om
Programkode 5.4.12 h) slik
at du får treet/trærne fra Oppgave 1.
|
| 3. | Lag en metode public static void skrivTre2(String melding) som
skriver ut nodene slik som
Programkode 5.4.12 g) gjør, men
skriver dem i speilvendt nivåorden. Da må du bruke en kø.
Sjekk at det da blir samme utskriftsrekkefølge for "EDEAEEFECDAFDB" som
i Programkode 5.4.12 g).
Blir det samme rekkefølge hvis du bruker "ABCDEAA"?
|
| 4. | Vi har tidligere sett på den statiske Huffmanteknikken. Frekvensfordelingen i Tabell 5.4.1 førte da til Huffmantreet til høyre i Figur 5.4.3 e). Lag en tegnstreng med 100 tegn med bokstavene fra A til H slik at det blir denne frekvensfordelingen. Kjør så Programkode 5.4.12 g) med denne tegnstrengen. Sammenlign resultatet med Figur 5.4.3 e). |
| 5. | I den adaptive Huffmanteknikken legges det ikke ut noen informasjon i starten av komprimeringen slik som i den statiske Huffmanteknikken. Likevel blir resultatet en fil som er litt større. Hva tror du er årsaken? |
| 6. | Legg inn Programkode 5.4.12 j),
Programkode 5.4.12 k) og
Programkode 5.4.12 l) i
class AdHuffman og kjør programmet
i Programkode 5.4.12 m). Sjekk
størrelsen på filen "ut.txt". Lag en programbit der
"ut.txt" dekomprimeres. Da må du bruke dens url.
Sjekk at resultatet blir korrekt.
|
| 7. | Bruk både den statiske og adaptive Huffmanteknikken på noen filer som inneholder få forskjellige tegn. Hvem av dem komprimerer best i slike tilfeller? |
| 8. |
![]() 5.4.13 Algoritmeanalyse
5.4.13 Algoritmeanalyse
Et alfabet defineres som en vilkårlig samling av forskjellige "tegn". Hva
slags tegn det er snakk om spiller ingen rolle, men for oss vil det være nærliggende
å tenke på en samling ascii-tegn. Vi sier at alfabetet har prefikskoder hvis
det til hvert tegn i alfabetet er tilordnet en bitkode, dvs, en sekvens med biter (0 og 1),
slik at ingen tegn har en bitkode som utgjør første delen av bitkoden for et annet tegn.
En bitkodelengde er antallet biter i en bitkode.
Prefikskodene til et alfabet kan representeres som veier i et binærtre. Treet har da nøyaktig like mange bladnoder som det er tegn og hvert tegn er tilknyttet en bladnode. Veien fra rotnoden til bladnoden representerer prefikskoden - en 0 når vi går til venstre og en 1 til høyre. Se f.eks. figur 5.4.2 a). Et slikt tre kalles et prefikskodetre. I avsnitt 5.4.2 ble det krevd at et prefikskodetre måtte være fullt, men det er egentlig for strengt. Ethvert binærtre med like mange bladnoder som det er tegn i alfabetet, definerer et sett med prefikskoder. Men vi skal straks se at et prefikskodetre som ikke er fullt, er av liten interesse for oss.
Vi sier at alfabetet har en frekvensfordeling hvis det til hvert tegn er tilordnet en frekvens (et positivt heltall). Hvis T er et prefikskodetre til et alfabet med en gitt frekvensfordeling, så skal B(T) betegne bitsummen, dvs. summen av produktene av frekvens og bitkodelengde for hvert tegn. Se avsnitt 5.4.2.
Hvis vi tar for oss alle mulige prefikskodetrær T for et alfabet med en gitt frekvensfordeling, så vil minst et av dem gi minst mulig verdi på B(T). Et slikt tre kalles et optimalt prefikskodetre.
Lemma 5.4.13 a) Et optimalt prefikskodetre er fullt.
Bevis Hvis et optimalt prefikskodetre T ikke er fullt, må det være en indre node som har kun ett barn. Denne noden kan vi fjerne ved at den erstattes av sitt barn. Da vil alle tegn/bladnoder i det tilhørende subtreet få bitkoder som er kortere enn før og dermed vil B(T) bli mindre. Men det er umulig siden T er optimalt.
Lemma 5.4.13 b) La x og y være to bladnoder/tegn i et optimalt prefikskodetre med frekvenser f(x) og f(y). La l(x) og l(y) være bitkodelengdene. Hvis f(x) < f(y), så er l(x) <= l(y).
Bevis Anta omvendt at det finnes bladnoder/tegn x og y slik at f(x) < f(y) og l(x) > l(y). Da vil produktet (f(y) - f(x))(l(x) - l(y)) være større enn 0. La T' være det treet vi får ved å bytte om x og y, dvs. x får bitkoden og frekvensen til y og omvendt. Da vil B(T') = B(T) - f(x)l(x) - f(y)l(y) + f(x)l(y) + f(y)l(x) = B(T) + (f(y) - f(x))(l(x) - l(y)) > B(T). Men dette er i strid med forutsetningen at B(T) er optimalt. Dermed må l(x) <= l(y).
Det kommer mer stoff her.
