Oppgave 1

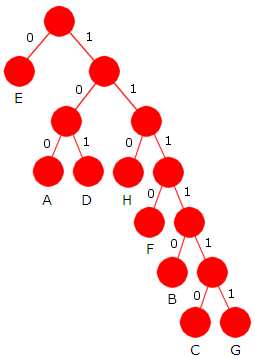Bitsummen B (T ) blir her 12·3 + 7·5 + 3·6 + 14·3 + 28·1 + 9·4 + 5·6 + 22·3 = 291. Dette er dårligere enn for treet i Figur 5.4.2 a) der bitsummen ble 280. Men det er bedre enn å la alle de åtte tegnene få en bitkode på lengde 3. Det gir en bitsum på 300.

Oppgave 2

1. HAGEBED   2. GAFFE   3. BEGGE

Oppgave 3

Du finner Morse-alfabetet f.eks. på Wikipedia.

I Morse-alfabetet har hver bokstav fått en kode som består av «prikker» og «streker». Hyppige bokstaver har fått kort kode. F.eks. er koden for E kun en «prikk». En melding kan overføres ved hjelp av lyd eller lys. Ved lyd brukes en kort lyd som «prikk» og en litt lenger lyd som «strek». Ved lys brukes et kort lyssignal og et litt lenger lyssignal. Men det må alltid være et opphold mellom to bokstaver når dette sendes. Ellers er det ikke mulig å vite hvor «prikkene» eller «strekene» for én bokstav slutter og den neste starter.

Hvis en «prikk» erstattes med en 0-bit og en «strek» med en 1-bit, kan det se ut som om vi kan bruke Morse-alfabetet til å komprimere en tekst. Men under «sending» av en tekst der Morse-alfabetet brukes, inngår implisitt et tredje «tegn». Det er oppholdet eller den korte pausen. Men i vår type komprimering har vi kun 0- og 1-biter til disposjon og dermed kan ikke Morse-alfabetet brukes siden det ikke består av prefikskoder.