Oppgave 1

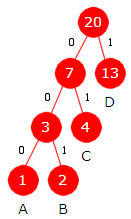Bitkoder: A = 000, B = 001, C = 01, D = 1   ABBAD = 0000010010001   1000011000001 = DACDAB   B (T) = 1·3 + 2·3 + 4·2 + 13·1 = 30

Oppgave 2

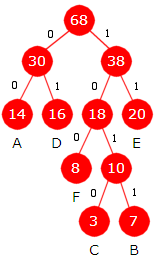Bitkoder: A = 00, B = 1011, C = 1010, D = 01, E = 11, F = 100   ABBAD = 0010110001   1000011000001 = FAEAAD   B (T) = 14·2 + 7·4 + 3·4 + 16·2 + 20·2 + 8·3 = 164

Oppgave 3

Bitkoder: A = 00, B = 110, C = 0100, D = 011, E = 10, F = 111, G = 0101 ABBAD = 0011011000011 10000110000011 = EADAAD B (T) = 30·2 + 20·3 + 3·4 + 18·3 + 42·2 + 25·3 + 10·4 = 385

Oppgave 4

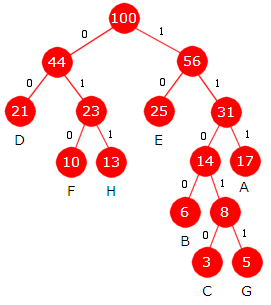Bitkoder: A = 111, B = 1100, C = 11010, D = 00, E = 10, F = 010, G = 11011, H = 011 ABBAD = 1111100110011100 10000110000010 = EDHDDF B (T) = 17·3 + 6·4 + 3·5 + 21·2 + 25·2 + 10·3 + 5·5 + 13·3 = 276

Oppgave 5

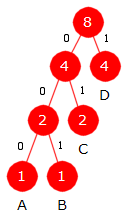I hver iterasjon i algoritmen skal de to nodene med minst frekvens velges. Den første (minst frekvens) blir venstre barn og den andre høyre barn. Hvis to eller flere noder har samme minste frekvens, er det egentlig likegyldig hvilken vi velger først av dem. Et sett med slike valg vil gi treet til venstre med bitkoder A = 000, B = 001, C = 01 og D = 1. Med denne frekvensfordelingen vil det hver gang være to noder med samme minste frekvens. Det betyr at det kan bli 2 · 2 · 2 = 8 forskjellige Huffmantrær. Alle blir optimale. Bitkodene for de fire bokstavene blir forskjellige, men vil alltid ha samme lengde for hvert tre. Hvis en melding komprimeres ved hjelp av bitkodene, må nøyaktig de samme bitkodene være kjent ved en senere dekomprimering. Det kun å kjenne frekvensene vil da ikke være tilstrekkelig.

Oppgave 6

Fordelingen 1, 1, 1, 2 og 3 for A, B, C, D og E vil kunne gi mange forskjellige Huffmantrær avhengig av hva som velges først når den minste blant flere like frekvenser skal velges. Figuren under viser to mulige trær:

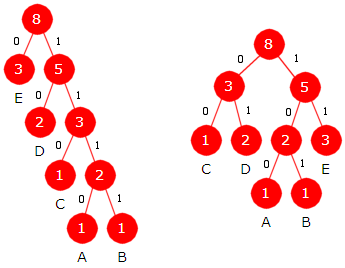Begge trærne er optimale prefikskodetrær. I treet til venstre blir A = 1110, B = 1111, C = 110, D = 10 og E = 0. Det gir bitsummen 4 + 4 + 3 + 2·2 + 3·1 = 18. I treet til høyre blir A = 100, B = 101, C = 00, D = 01 og E = 11. Bitsum: 3 + 3 + 2 + 2·2 + 3·2 = 18. Legg også merke til at i begge kommer frekvensene i avtagende rekkefølge i speilvendt nivåorden.

Oppgave 7

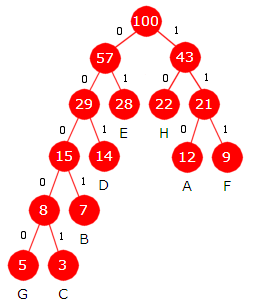Treet til venstre er det speilvendte til treet til høyre i Figur 5.4.3 e) . Bitkodene blir nå:   A = 110   B = 0001   C = 00001   D = 001   E = 01   F = 111   G = 00000   H = 10. Bitsummen B(T) blir selvfølgelig den samme som før siden alle bokstavene har like lange bitkoder som de har det det opprinnelige treet. Legg merke til at vi får de nye bitkodene ved å bytte om på 0-er og 1-ere i de gamle.

Oppgave 8

Her får vi nettopp det speilvendte treet fra Oppgave 7.

Oppgave 9

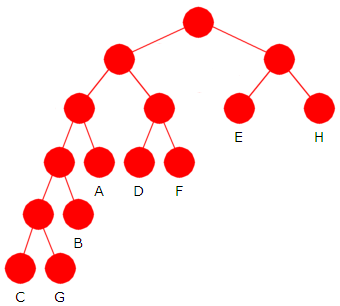Treet til venstre kalles et kanonisk tre siden alle nivåene er fylt opp fra venstre og på hvert nivå kommer bokstavene i sortert rekkefølge. Bitkodene blir nå:   A = 001   B = 0001   C = 00000   D = 010   E = 10   F = 011   G = 00001   H = 11. Bitsummen B(T) blir selvfølgelig den samme som før siden alle bokstavene har like lange bitkoder som de har det det opprinnelige treet. Dette treet kan gjenskapes hvis vi kun kjenner lengdene til bitkodene.

Oppgave 10

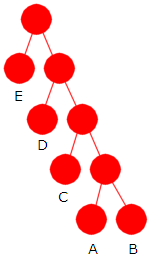1) Vi må finne frekvenser for A, B, C, D og E slik at Huffmantreet blir som treet til venstre. En mulighet er å bruke Fibonacci-tallene 1, 1, 2, 3, 5 og 8 som frekvenser. Da kan vi få treet til venstre med bitkoder A = 1110, B = 1111, C = 110, D = 10 og E = 0 og dermed lengde 4 på bitkodene til A og B. Summen av frekvensene blir 1 + 1 + 2 + 3 + 5 = 12.

Vi kan også få til treet til venstre med frekvenser 1, 1, 1, 2 og 3 og med sum lik 8, men da må vi bruke flg. algoritme for å bygge opp treet: Lag en node for hver av de fem bokstavene med dette som frekvenser og sett dem opp i alfabetisk rekkefølge. I hver iterasjon blir de to nodene lengst til venstre henholdsvis venstre og høyre barn i en ny node med frekvens lik summen av frekvensene. Hvis den får en frekvens lik en frekvens som ligger der fra før, legger vi den først blant de med samme frekvens. Prøv dette!

2) Det blir på samme måte for de seks bokstavene A, B, C, D, E og F som for de fem bokstavene i 1). Vi får et tilsvarende tre som det i figuren med frekvenser lik Fibonacci-tallene 1, 1, 2, 3, 5 og 8 (sum = 20). Vi kan få en mindre sum hvis vi isteden bruker 1, 1, 1, 2, 3 og 5 (sum = 13) hvis vi bruker samme algoritme som i 1). Da får vi bitkoder: A = 11110, B = 11111, C = 1110, D = 110, E = 10 og F = 0. Det gir A og B en bitkodelengde på 5.

3) Anta at vi har n bokstaver. Da kan vi bruke de n første Fibonacci-tallene 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, osv. som frekvenser. Hvis f.eks. n = 15 (bokstavene fra A til O) blir frekvensene 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 og 610 med frekvenssum lik 1596. Også her går det an å bruke 1, 1, 1, 2, 3, 8, 13, 21, 34, . . . , 377 (sum = 987) isteden. Huffmantreet vil gi A = 111111111111110 og B = 111111111111111.

Oppgave 11

La f_k , k = 0, 1, 2, . . . være Fibonacci-tallene, dvs. f₀ = 0, f₁ = 1, f₂ = 1, f₃ = 2, osv. Vi lar 33 tegn ha frekvenser lik 1, 1, 1, 2, 3, 5, 8, 13, . . , f₃₂ der f₃₂ = 2.178.309. En kjent formel sier at summen av dette er lik f₃₄ = 5.702.887. Denne frekvensfordelingen vil føre til at i Huffmantreet vil to tegn få en bitkodelengde på 32. Hvis meldingen ligger på en fil med 1 byte for hvert tegn, vil filstørrelsen bli omtrent 5,4MB. Se Se f.eks. Oppgave 12 i Avsnitt 1.5.1 når det gjelder å regne ut store Fibonacci-tall.

Oppgave 12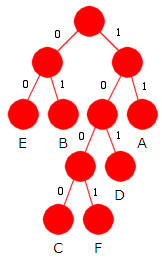

Oppgave 13