 |
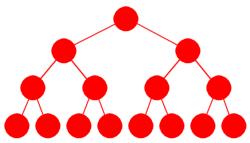
| Figur 9.1.1 a) : Et perfekt binærtre |
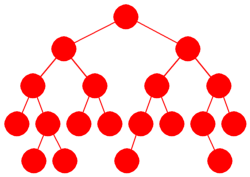 |
| Figur 9.1.1 b) : Et balansert binærtre |
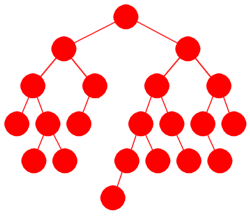 |
| Figur 9.1.1 c) : Et høydebalansert binærtre |
balanse, likevekt og skjevhet brukes
i forbindelse med binære trær og da spesielt binære søketrær. Men begrepene defineres og brukes litt forskjellig i faglitteraturen.
Figur 9.1.1 a) til venstre viser et
perfekt binærtre. Et slikt tre må
kunne kalles balansert. Hver node har like mye på hver side.
For treet i Figur 9.1.1 b) er det annerledes. Ta f.eks. rotnodens venstre
barn. Dens venstre subtre har høyde 2 og 5 noder, mens det høyre har høyde 1 og 3 noder.
Men det er ikke mulig å lage noe «bedre» tre med
tanke på balanse når vi som her har 19 noder. Her er alle nivåene, bortsett fra det nederste,
fylt opp med noder. Slike trær har høyde h =
⌊log2(n)⌋ (obs: ⌊⌋ er
avrunding nedover) der n er antall noder. Generelt for binærtrær gjelder
⌊log2(n)⌋ ≤ h ≤ n − 1.
Uformelt kunne vi derfor si at jo nærmere høyden til et tre er ⌊log2(n)⌋,
jo mer balansert er det.
Obs: Høyden til et tre har to forskjellige definisjoner
i faglitteraturen. En sier at det er lik antall nivåer i treet, mens en annen sier at det er største avstand mellom roten og en node
(eller lengden på treets lengste gren). Forskjellen på de to er 1. Her brukes den siste og den er i
henhold til NIST.
Et binærtre kalles høydebalansert hvis det for hver node er slik at
høydeforskjellen mellom nodens to subtrær ikke er mer enn 1.
Treet i Figur 9.1.1 b) og det i
Figur 9.1.1 c) oppfyller dette. Sjekk at det stemmer! Husk at et tre med kun
én node har høyde 0 og et tomt tre har høyde −1. For slike trær gjelder
h < 1,44 log2(n + 2) − 1,328, dvs.
god balanse. Et binært søketre av denne typen kalles et
AVL-tre.
Et AVL-tre har i tillegg algoritmer for å holde treet
høydebalansert etter en innlegging eller en fjerning.
Et alternativ er antallbalanse eller
vektbalanse
(antall tolkes som vekt).
Her må antallet noder i en vilkårlig nodes subtrær utgjøre en gitt minsteandel α av antallet i treet med
noden som rot.
Hvis p er en vilkårlig node, må
antall(p.venstre) ≥ α · antall(p) og
antall(p.høyre) ≥ α · antall(p).
Her er det viktig å sette rett verdi på andelsfaktoren α. Hvis vi f.eks. bruker
α = 1/5, vil treet i Figur 9.1.1 c) bli antallbalansert med 1/5 = 0,2
som andelsfaktor. Sjekk det!
Søking er den viktigste operasjonen i et binært søketre.
Det er viktig at den er effektiv, dvs. av logaritmisk orden. Tiden det tar å finne en node er
bestemt av hvor langt ned i treet den ligger. Hvis treet har en høyde av logaritmisk orden, så
blir søkingen effektiv. Et annet begrep er gjennomsnittlig nodedybde.
Dybden til en node er lik avstanden fra noden til roten og gjennomsnittet tas over alle nodene.
Gjennomsnittlig nodedybde er alltid mindre enn treets høyde. Det optimale er
et tre der alle nivåene, eventuelt bortsett fra det nederste, er fylt opp med noder. Det
motsatte er et tre der ingen noder har to barn. For disse ytterpunktene finnes det formler
for gjennomsnittlig nodedybde gnd(n) av antallet n. Dermed:
(9.1.1) ((n + 1) k − 2(2k − 1)) / n
≤ gnd(n) ≤ (n − 1)/2,
k = ⌊log2(n + 1)⌋
Uttrykket på venstre side i (9.1.1) er for store verdier av n tilnærmet lik log2(n + 1) − 2
og dermed log2(n + 1) − 2 ≤ gnd(n) ≤ (n − 1)/2.
I Avsnitt 5.2.4
fant vi at et gjennomsnittlig binært søketre med n forskjellige verdier (n stor) har en
gjennomsnittlig nodedybde på 1,386·log2(n + 1) − 2,846.
Dvs. at søking i et binært søketre i gjennomsnitt er effektivt. Men hvis søking alltid skal være effektivt, må
en bruke teknikker for å balansere treet hvis det etter en innleggging eller fjerning har kommet i en eller annen
form for ubalanse. En mulighet er å bruke høydebalanse og dermed et AVL-tre.
En annen mulighet er «fargebalanse». I et
rød/svart
binærtre er en node enten «rød» eller «svart». En ny node er alltid rød og hvis
forelderen også er rød, starter en balanseoperasjon. Et slikt tre har en høyde som maksimalt er det dobbelte av
det optimale (⌊log2(n)⌋), men normalt en del bedre.
Ubalanse Et binærtre der ingen noder har to barn, er det mest ubalanserte av alle.
Et slikt tre har høyde n − 1 og gjennomsnittelig nodedybde
(n − 1)/2.
Det er to ytterpunkter. Et binærtre kalles
ekstremt høyreskjevt hvis ingen noder har venstre barn og
ekstremt venstreskjevt hvis ingen noder har høyre barn.
| 1. | Treet Figur 9.1.1 b) er et eksempel på et binærtre med 19 noder og alle
nivåene bortsett fra det nederste, er fulle av noder. Hvor mange slike trær er det?
|
| 2. | Gitt et binærtre med n noder. Hvis alle nivåene, eventuelt bortsett fra det nederste, er fylt opp med noder,
har treet høyde ⌊log2(n)⌋. Er det motsatte sant?
|
| 3. | Hvor mange forskjellige binære trær finnes det med n noder der ingen node har to barn.
|
| 4. | Setning 9.1.1 har på venstre side en formel for den
gjennomsnittlige nodedybden for et binærtre der alle nivåene eventuelt bortsett fra det nederste, er fulle
av noder. a) Sjekk at formelen stemmer for trærne i Figur 9.1.1 a og b).b) Vis at formelen stemmer for alle n. Hint: Start med å lage en formel som gjelder
for perfekte trær. Formel G.1.9
kommer til nytte her.
|
![]() 9.1.2 Fra tabell til balansert tre
9.1.2 Fra tabell til balansert tre
Anta at vi har verdier i en tabell. En aktuell problemstilling er å lage et balansert
binærtre som inneholder tabellverdiene.
Vi kan bruke flg. idé: La tabellens midtverdi bli rotnodens verdi. Gå så til hver side av midtverdien. La midtverdien av tabellens venstre side bli verdien i rotnodens venstre barn og midtverdien på høyre side verdien i rotnodens høyre barn. Osv. Dette gjøres enklest ved at en rekursiv metode kalles først på den delen av tabellen som ligger til venstre for midten og deretter på den delen som ligger til høyre:
private static <T> Node<T> balansert(T[] a, int v, int h) { if (v > h) return null; // et tomt intervall int m = (v + h)/2; // midten return new Node<>(a[m], balansert(a, v, m - 1), balansert(a, m + 1, h)); } Programkode 9.1.2 a)
Treet blir balansert siden vi alltid går inn på midten av intervallet. Da alle verdiene til venstre for midten havner i venstre subtre og alle til høyre i høyre subtre, vil en inorden traversering gi verdiene i tabellrekkefølgen. OBS: Hvis tabellen er sortert og uten duplikater, blir treet et binært søketre. Men ikke nødvendigvis hvis tabellen har duplikater. Se Avsnitt 5.2.5.
Metoden balansert() kan legges i enhver klasse som har en tilsvarende nodestruktur,
f.eks. i klassen
BinTre. Da må
klassen ha en offentlig metode som kaller den private metoden:
public static <T> BinTre<T> balansert(T[] a) { BinTre<T> tre = new BinTre<>(); // et tomt tre tre.rot = balansert(a,0,a.length-1); // treet bygges opp tre.antall = a.length; // antall som i tabellen return tre; // treet returneres } Programkode 9.1.2 b)
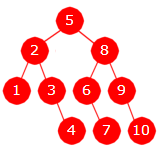 |
| Figur 9.1.2 a) |
Hvis dette ligger i klassen
BinTre, vil
flg. eksempel vise hvordan det kan brukes. Utskriften viser
at treets verdier i inorden svarer til hvordan de ligger i tabellen.
Figur 9.1.2 a) viser hvordan treet blir:
Integer[] a = {1,2,3,4,5,6,7,8,9,10};
BinTre<Integer> tre = BinTre.balansert(a);
tre.inorden(Oppgave.konsollutskrift()); // Se inorden
// Utskrift: 1 2 3 4 5 6 7 8 9 10 og Oppgave
Programkode 9.1.2 c)
| 1. | Hvordan blir treet Programkode 9.1.2 c) hvis tabellen inneholder tallene fra 1 til 19?
|
| 2. | Metoden public boolean erBalansert() i klassen BinTre skal returnere
true hvis alle nivåene eventuelt borsett fra det nederste, er fulle av noder og false ellers. Lag metoden og bruk den
i Programkode 9.1.2 c).
|
| 3. | Lag metoden public boolean erHøydeBalansert() i klassen BinTre.
Den skal returnere true hvis treet er høydebalansert
og false ellers.
|
![]() 9.1.3 Komplette trær
9.1.3 Komplette trær
Det kan være ønskelig å bygge opp et komplett
binærtre ved hjelp av verdiene i en
tabell og f.eks. lage treet slik at en traversering i inorden eller
eventuelt i nivåorden, gir verdiene i samme rekkefølge som de har i tabellen. Det siste er
det enkleste å få til siden den første verdien da må høre til rotnoden, de to neste til rotnodens
to barn, osv. Flg. private rekursive metode gjør nettopp det. En offentlig metode setter
rekursjonen i gang:
private static <T> Node<T> komplett(T[] a, int posisjon) { if (posisjon > a.length) return null; Node<T> venstre = komplett(a, 2*posisjon); // venstre subtre Node<T> høyre = komplett(a, 2*posisjon + 1); // høyre subtre return new Node<>(a[posisjon - 1], venstre, høyre); // rotnoden } public static <T> BinTre<T> komplettNivåorden(T[] a) { BinTre<T> tre = new BinTre<>(); tre.antall = a.length; tre.rot = komplett(a,1); return tre; } Programkode 9.1.3 a)
Vi trenger en metode som sjekker om et binærtre er komplett. Dermed kan vi få testet om Programkode 9.1.3 a) virker som den skal. Et binærtre med n noder er komplett hvis og bare hvis nodene har posisjonstall fra 1 til n. Vi lager derfor en rekursiv metode som traverserer treet og sjekker nodenes posisjonstall:
private static <T> boolean sjekkPosisjon(Node<T> p, int pos, int n) { if (p == null) return true; // et tomt tre er komplett return pos <= n // sjekker posisjonstallet && sjekkPosisjon(p.venstre, 2*pos, n) // sjekker venstre subtre && sjekkPosisjon(p.høyre, 2*pos + 1, n); // sjekker høyre subtre } public boolean erKomplett() { return sjekkPosisjon(rot,1,antall); // kaller den rekursive metoden } Programkode 9.1.3 b)
Hvis Programkode 9.1.3 a) og b) ligger i klassen
BinTre, vil
flg. eksempel virke:
Integer[] a = {1,2,3,4,5,6,7,8,9,10};
BinTre<Integer> tre = BinTre.komplettNivåorden(a);
tre.nivåorden(Oppgave.konsollutskrift());
System.out.println(" " + tre.erKomplett());
// Utskrift: 1 2 3 4 5 6 7 8 9 10 true
Programkode 9.1.3 c)
Det å lage et komplett binærtre der en traversering i inorden gir verdiene i samme rekkefølge som de har i tabellen, er vanskeligere å få til.
En mulig fremgangsmåte er å lage et komplett binærtre med plass til så mange verdier som det er i tabellen og så fylle det med verdier fra tabellen gjennom en inorden traversering. Det komplette treet kan f.eks. lages på samme måte som i Programkode 9.1.3 a):
private static <T> Node<T> komplett(int n, int posisjon) // n verdier { if (posisjon > n) return null; Node<T> venstre = komplett(n, 2*posisjon); // venstre subtre Node<T> høyre = komplett(n, 2*posisjon + 1); // høyre subtre return new Node<>(null,venstre,høyre); // null som nodeverdi } Programkode 9.1.3 d)
Neste skritt er legge inn verdiene mens treet traverseres. Det kan gjøres rekursivt eller iterativt (se Oppgave 2 og 3 for iterative løsninger). Under traverseringen må vi holde orden på hvilket nummer noden har i inorden og så legge inn tilsvarende verdi fra tabellen. Som «teller» bruker vi en int-tabell med kun én verdi:
private static <T> void leggInnInorden(Node<T> p, T[] a, int[] indeks) { if (p.venstre != null) leggInnInorden(p.venstre, a, indeks); p.verdi = a[indeks[0]]; // setter inn tabellverdi indeks[0]++; // øker indeks if (p.høyre != null) leggInnInorden(p.høyre, a, indeks); } public static <T> BinTre<T> komplettInorden(T[] a) { BinTre<T> tre = new BinTre<>(); int[] indeks = {0}; tre.rot = komplett(a.length,1); leggInnInorden(tre.rot, a, indeks); tre.antall = a.length; return tre; } Programkode 9.1.3 e)
Flg. programbit der tabellen inneholder bokstaver, viser hvordan dette vil virke:
String[] s = "ABCDEFGHIJKL".split(""); // = {"A","B","C", . . . } BinTre<String> tre = BinTre.komplettInorden(s); // bygger opp treet tre.inorden(Oppgave.konsollutskrift()); // skriver ut i inorden System.out.println(" " + tre.erKomplett()); // sjekker om det er komplett // Utskrift: A B C D E F G H I J K L true Programkode 9.1.3 f)
Det er mulig å lage et komplett binærtre med verdiene fra en tabell i inorden på en tilsvarende måte som i Programkode 9.1.2 a). Der var det tabellens midtverdi som ble rotnodeverdi. Men det vil ikke fungere for et komplett binærtre siden det der normalt er flere noder i rotnodens venstre subtre enn i høyre subtre. Figuren under til venstre viser et komplett binærtre med 17 noder:
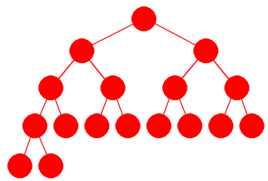 |
| Figur 9.1.3 a): 17 noder |
I dette treet er det 9 noder i rotnodens venstre subtre og 7 i høyre subtre. Hvis vi
har en tabell a, må derfor de 9 første verdiene i a (indekser fra 0 til 8)
legges i venstre subtre, den 10-ende verdien ( a[9] ) i rotnoden og resten i høyre subtre.
Hvis vi isteden vil lage et komplett binærtre med 18 noder, blir det 10 noder i venstre subtre
og dermed er det verdi nr. 11 ( a[10] ) som skal inn i rotnoden. Osv.
Men for komplette trær med fra 23 og oppover til 31 noder vil antallet noder i venstre subtre
være fast lik 15.
Dette kan oppsummeres slik: Gitt at verdiene i en tabell a med lengde n skal legges
inn i et komplett binærtre slik at verdienes rekkefølge i inorden er den samme som i tabellen.
Hvis m er antallet noder i rotnodens venstre subtre, er det verdien a[m] som
skal inn i rotnoden. Oppgaven blir derfor å finne m som funksjon av n.
Treet i Figur 9.1.3 a) har 17 noder. Tallet 17 skrives som 10001 på binærform.
Hvis vi «stripper» tallet, dvs. setter alle 1-ere til 0 bortsett fra den første,
får vi det binære tallet k = 10000 som svarer til 16. Videre gir 16 - 1 = 15 antallet
noder i det perfekte treet vi får ved å fjerne nederste rad. Dermed vil antallet noder
på nederste rad være lik n − k + 1. Vi ser at antallet noder
i venstre subtre er avhengig av om antallet på nederste rad er mindre enn eller lik
antallet på nest nederste rad eller ikke. Dvs. hvis n − k + 1 ≤
k/2 (eller n − k < k/2 eller
n − k/2 < k),
blir antallet m i venstre subtre lik
n − k/2. Hvis ikke, blir antallet m i venstre subtre
lik k − 1.
Det finnes en ferdig metode som «stripper» et positivt heltall. Den ligger
i klassen Integer
og heter highestOneBit(). Dermed kan vi lage flg. metode:
private static <T> Node<T> komplett(T[] a, int v, int h) { if (v > h) return null; // tomt intervall int n = h - v + 1; // antallet i intervallet int k = Integer.highestOneBit(n); // stripper n int m = n - (k >> 1); // k >> 1 svarer til k/2 m = (m < k ? m : k - 1) + v; // m relativt til v Node<T> venstre = komplett(a, v, m - 1); // venstre subtre Node<T> høyre = komplett(a, m + 1, h); // høyre subtre return new Node<>(a[m], venstre, høyre); } Programkode 9.1.3 g)
Det er mulig å optimalisere Programkode 9.1.3 g) noe. Vi vet at i et
komplett binærtre er minst ett av rotnodens to subtrær
et perfekt binærtre. I noen tilfeller er
begge perfekte. Hvis vi skal bygge opp et perfekt tre ved hjelp av verdiene i et
tabellintervall, vil det være intervallets midtverdi som skal inn i rotnoden.
Dermed kan vi isteden bruke metoden balansert() i
Programkode 9.1.2 a).
Dette innebærer en effektivisering siden det er litt mindre arbeid å finne midten i en
tabell enn å utføre den beregningen som inngår i starten av Programkode 9.1.3 g).
Se Oppgave 6.
Vi trenger en offentlig metode som kaller den rekursive metoden i Programkode 9.1.3 g):
public static <T> BinTre<T> komplettInorden(T[] a) // ny versjon { BinTre<T> tre = new BinTre<>(); tre.antall = a.length; tre.rot = komplett(a,0,a.length-1); return tre; } Programkode 9.1.3 h)
Flg. programbit tester dette:
Integer[] a = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20};
BinTre<Integer> tre = BinTre.komplettInorden(a);
System.out.println(tre.erKomplett());
tre.inorden(Oppgave.konsollutskrift());
System.out.println();
tre.nivåorden(Oppgave.konsollutskrift());
// Utskrift:
// true
// 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
// 13 8 17 4 11 15 19 2 6 10 12 14 16 18 20 1 3 5 7 9
Programkode 9.1.3 i)
| 1. | Ta utgangspunkt i Programkode 9.1.3 c).
Sett opp tallene fra 1 til 10 i en slik rekkefølge at når treet bygges med metoden
komplettNivåorden(),
vil en inorden traversering gi tallene i sortert rekkefølge. Sjekk svaret
ved å bruke traverseringsmetoden inorden(). Gjør deretter det samme med tallene fra 1 til 20.
|
| 2. |
Hvor mange bladnoder har et komplett binærtre med n noder?
|
| 3. |
Metoden komplettNivåorden() bruker en
rekursiv hjelpemetode. Lag den uten rekursjon, f.eks. ved å bruke en kø.
|
| 2. |
Lag metoden public static <T> BinTre<T> komplettInorden(T[] a) uten
rekursjon.
I koden skal det først opprettes et tomt binærtre, så skal treet bygges ved et kall på
metoden i Programkode 9.1.3 d).
Deretter skal det gjøres en iterativ traversering ved hjelp av en stakk
(bruk samme teknikk som i Programkode 5.1.8 g )
der verdiene fra tabellen fortløpende legges inn i nodene. Til slutt returneres treet. Lag en
programbit som tester det du har laget.
|
| 3. | Ta utgangspunkt i Figur 9.1.3 a). Legg på noder forløpende slik at treet hele tiden er komplett. Hvor mange noder er det i rotnodens venstre subtre når treet får 18, 19, 20, 21, 22, 23, 24, 25 og 26 noder? |
| 4. | Det påstås i teksten at i et komplett binærtre er minst ett av rotnodens to subtrær et perfekt binærtre. Tegn et komplett binærtre med 20 noder. Hvilket av rotnodens to subtrær er perfekt? Gjør det samme for 23 noder og 25 noder. |
| 5. | Gjør om Programkode 9.1.3 g) slik
at metoden balansert() fra Programkode 9.1.2 a)
kalles hvis tabellintervallet er slik at treet vil bli
perfekt.
|
![]() 9.1.4 Balansering ved hjelp av rotasjoner
9.1.4 Balansering ved hjelp av rotasjoner
Figur 9.1.4 a) under viser til venstre et utsnitt av et binærtre. Vi har to noder p og q
med verdier x og y der q er venstre barn til p. Bokstavene a, b og c står for subtrær. Et eller
flere av dem kan være tomme.
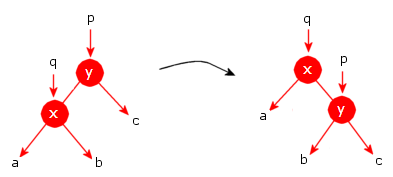 |
| Figur 9.1.4 a) : En høyrerotasjon med hensyn på p |
Til høyre i Figur 9.1.4 a) står resultatet av en høyrerotasjon med hensyn på p. Vi ser at noden q har «gått opp» og noden p har «gått ned» og dermed at p nå har blitt høyre barn til q. Videre har b, som opprinnelig var høyre subtre til q, nå blitt venstre subtre til p. Den krumme pilen i midten markerer at det er utført en rotasjon.
En viktig egenskap ved en høyrerotasjon er at nodene vil ha nøyaktig samme rekkefølge i inorden etter som før rotasjonen. Før rotasjonen, til venstre i figuren, er rekkefølgen i inorden lik a − x − b − y − c og det er nøyaktig slik det er til høyre etter rotasjonen.
Flg. metode, som har p som parameter, gjør en høyrerotasjon med hensyn på p og returnerer en referanse til det som opprinnelig var p sitt venstre barn:
private static <T> Node<T> høyreRotasjon(Node<T> p) { Node<T> q = p.venstre; p.venstre = q.høyre; q.høyre = p; return q; } Programkode 9.1.4 a)
En venstrerotasjon gjør det motsatte av en høyrerotasjon. Hvis vi gjør en venstrerotasjon med hensyn på p i treutsnittet til venstre i Figur 9.1.4 b) under, blir resultatet treutsnittet til høyre. Noden p går ned og noden q opp:
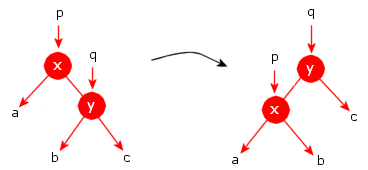 |
| Figur 9.1.4 b) : En venstrerotasjon med hensyn på p |
En venstrerotasjon får vi ved å bytte venstre med høyre i Programkode 9.1.4 a):
private static <T> Node<T> venstreRotasjon(Node<T> p) { Node<T> q = p.høyre; p.høyre = q.venstre; q.venstre = p; return q; } Programkode 9.1.4 b)
Hvis vi kombinerer to eller flere rotasjoner, vil vi kunne oppnå ulike effekter. Hvis vi starter med utsnittet under til venstre i Figur 9.1.4 c), så gjør en venstrerotasjon med hensyn på q og så en høyrerotasjon med hensyn på p, får vi det som står under til høyre i Figur 9.1.4 c):
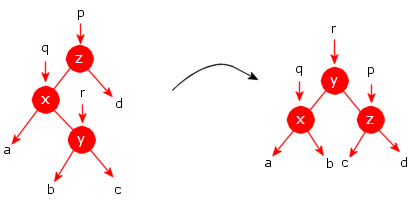 |
| Figur 9.1.4 c) : En venstre- og en høyrerotasjon |
Vi ser spesielt at rekkefølgen i inorden bevares. Den var lik a − x − b − y − c − z − d og det er den også etterpå. Denne kombinasjonen av rotasjoner kalles en dobbel høyrerotasjon. Selv om den kan uføres ved hjelp av de to rotasjonsmetodene vi allerede har, er det likevel vanlig å lage en egen metode for det. Se Oppgave 1.
Det er mulig å «brette ut» et hvilket som helst binærtre til et «ekstremt høyreskjevt» tre ved hjelp av en serie høyrerotasjoner. Et binærtre kalles ekstremt høyreskjevt hvis ingen noder har venstre barn. I Figur 9.1.4 d) under er det utført to høyrerotasjoner. Den første (på treet til venstre) der rotasjonen er med hensyn på rotnoden (verdien D). Det gir det midterste treet som resultat. På det treet er det på nytt utført en høyrerotasjon med hensyn på rotnoden (den har verdi B):
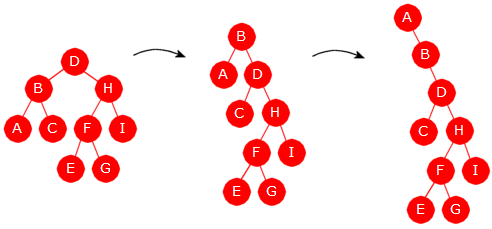 |
| Figur 9.1.4 d) : To høyrerotasjoner med hensyn på rotnoden |
Vi kan fortsette «utbrettingen» ved å gå fra rotnoden i det høyre treet (verdien A) og nedover mot høyre. For hver node nedover som har venstre barn, gjør vi roteringer inntil det ikke lenger er venstre barn. Osv. Da vil vi ende opp med et ekstremt høyreskjevt tre:
public void gjørEkstremtHøyreskjevt() { if (antall() <= 1) return; while (rot.venstre != null) rot = høyreRotasjon(rot); Node<T> f = rot; // forelder while (f.høyre != null) { Node<T> p = f.høyre; // roterer med hensyn på p while (p.venstre != null) p = høyreRotasjon(p); f.høyre = p; f = f.høyre; } } Programkode 9.1.4 c)
Vi kan teste om «utbrettingsteknikken» virker ved f.eks. å traversere treet i både inorden og nivåorden. Hvis treet er ekstremt høyreskjevt, vil vi få samme utskrift i de to tilfellene. Men vi kan også lage en egen metode som sjekker dette. Da er det bare å starte i rotnoden og for hver node nedover til høyre må det undersøke om noden har et venstre barn. Hvis en node har det, så er treet ikke ekstremt høyreskjevt. Dette kan kodes slik:
public boolean erEkstremtHøyreskjevt() { for (Node<T> p = rot; p != null; p = p.høyre) if (p.venstre != null) return false; return true; } Programkode 9.1.4 d)
Flg. programbit tester om «utbrettingsteknikken» i Programkode 9.1.4 c) virker som den skal. Vi starter med å bygge opp treet til venstre i Figur 9.1.4 d):
char[] verdi = "DBHACFIEG".toCharArray(); // nodeverdier int[] posisjon = {1,2,3,4,5,6,7,12,13}; // nodeposisjoner BinTre<Character> tre = new BinTre<>(); // tomt tre for (int i = 0; i < verdi.length; i++) // bygger treet tre.leggInn(posisjon[i], verdi[i]); tre.gjørEkstremtHøyreskjevt(); // rotasjoner tre.nivåorden(Oppgave.konsollutskrift()); // nivåorden System.out.print(" "); // mellomrom tre.inorden(Oppgave.konsollutskrift()); // inorden System.out.println(" " + tre.erEkstremtHøyreskjevt()); // Utskrift: A B C D E F G H I A B C D E F G H I true Programkode 9.1.4 e)
Overskriften på dette avsnittet er «balansering ved hjelp av rotasjoner». Så langt har vi imidlertid kun gjort det motsatte av balansering, dvs. laget et tre som er så ubalansert som det er mulig å få til. Neste skritt imidlertid å «brette sammen» det skjeve treet til et komplett binærtre. Figur 9.1.4 e) under viser hvordan vi kan «brette sammen» et ekstremt høyreskjevt tre slik at det blir et komplett tre:
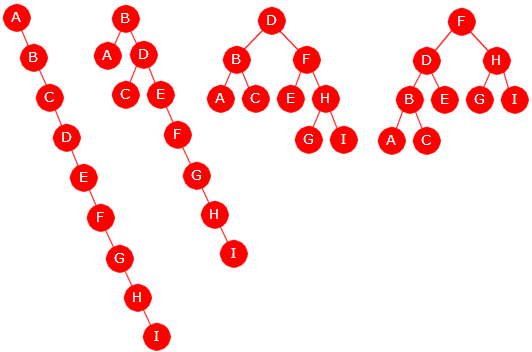 |
| Figur 9.1.4 e) : Fire stadier i sammenbrettingsprosessen for et ekstremt høyreskjevt tre |
«Sammenbrettingen» er litt mer komplisert enn «utbrettingen». Figur 9.1.4 e) viser noen av skrittene. Det komplette treet lengst til høyre har to noder på nederste rad. Dermed må det utføres to rotasjoner i første runde: Den første på roten og det gir en ny rotnode. Neste rotasjon utføres på dens høyre barn. La n være antallet noder. La videre m være det største tallet av typen 2k − 1 som er mindre enn eller lik n. Differansen n − m er antallet noder på nederste rad i det komplette treet. I eksempelet i Figur 9.1.4 e) er n = 9 og m = 23 − 1 = 7 og dermed n − m = 2. Det andre (fra venstre) treet i Figur 9.1.4 e) viser resultatet av de to første rotasjonene.
Videre i rotasjonene tar vi utgangspunkt i m = 7. I neste runde gjøres det m / 2 = 3 rotasjoner. Da får vi det tredje treet i Figur 9.1.4 e). Så settes m = 3 og det utføres m / 2 = 1 rotasjon. Dermed vi vi det siste treet i Figur 9.1.4 e).
Rotasjonene starter på rotnoden og utføres så forløpende nedover på høyre barn så mange ganger som trengs. Flg. hjelpemetode gjør dette:
private void rotasjoner(int m) { rot = venstreRotasjon(rot); Node<T> p = rot; for (int i = 1; i < m; i++) p = p.høyre = venstreRotasjon(p.høyre); } Programkode 9.1.4 f)
Dette settes sammen til en private metode som «bretter sammen» et ekstremt høyreskjevt binærtre og en offentlig metode som starter med et vilkårlig tre og ender opp med et komplett binærtre der nodene har nøyaktig samme rekkefølge i inorden som de hadde i det opprinnelige treet:
private void brettSammen()
{
int k = Integer.highestOneBit(antall);
int m = (antall == (k << 1) - 1) ? antall : k - 1;
rotasjoner(antall - m); // første runde
while (m > 1) // resten av rundene
{
m /= 2;
rotasjoner(m);
}
}
public void gjørKomplett()
{
gjørEkstremtHøyreskjevt();
brettSammen();
}
Programkode 9.1.4 g)
Teknikken bak metoden gjørKomplett() kalles
DSW-algoritmen etter Day,
Stout og Warren.
Flg. programbit demonstrerer bruken av metoden. Først lages det et fullstendig venstreskjevt tre med bokstavene fra A til Z i inorden og deretter blir treet «komplettisert»:
BinTre<Character> tre = new BinTre<>(); // tomt tre for (char c = 'Z'; c >= 'A'; c--) tre.leggInn(1 << ('Z' - c), c); tre.gjørKomplett(); tre.inorden(Oppgave.konsollutskrift()); System.out.println(" " + tre.erKomplett()); // Utskrift: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z true Programkode 9.1.4 h)
Effektivitet: Hvor effektiv er metoden
gjørKomplett()? Her er det naturlig å
se på antallet rotasjoner, dvs. antallet ganger det utføres en venstrerotasjon eller en
høyrerotasjon. I metoden
gjørEkstremtHøyreskjevt()
er det kun høyrerotasjoner. Hvis vi starter i roten og går mot høyre så langt det går, kalles
nodene på den veien for treets høyre ryggrad (eng: backbone). Hvis treet har n noder
og k av dem utgjør den høyre ryggraden, så vil det bli utført n − k
høyrerotasjoner. Det verste tilfellet er når treet er ekstremt venstreskjevt, dvs.
at ingen noder har høyre barn. Da blir det n − 1 høyrerotasjoner. Det beste tilfellet
er når treet er ekstremt høyreskjevt siden det gir ingen høyrerotasjoner. I gjennomsnitt vil
k være av størrelsesorden log2(n) og dermed vil antallet høyrerotasjoner
i gjennomsnitt være ikke så langt unna n.
I metoden brettSammen() utføres det
kun venstrerotasjoner. Det kan vises at det der alltid blir utført
n − ⌊log2(n+1)⌋ venstrerotasjoner når det er n noder.
I sum får vi derfor at antallet rotasjoner i metoden
gjørKomplett() alltid er mindre enn 2n
både i gjennomsnitt og i det verste tilfellet. Metoden er derfor av orden n.
Se også Oppgave 3.
Det er også mulig å «komplettisere» et binærtre ved å legge nodene, i inorden, i en tabell og så bygge et komplett tre ved hjelp av tabellen. Ulempen er at vi bruker ekstra plass til tabellen, men den vil bli noe raskere enn metoden over. Se Oppgave 4-6.
Referanser:- Colin Day, Balancing a Binary Tree, Computer Journal 19 (1976), 360-361.
- Quentin Stout and Bette Warren, Tree Rebalancing in Optimal Time and Space, Communications of the ACM 29 (1986), 902-908.
| 1. | Lag metoden private static <T> Node<T> dobbelHøyreRotasjon(Node<T> p).
Den skal gjøre som i
Figur 9.1.4 c). Inputparameter er p
og den skal returnere noden r.
|
| 2. | Lag metoden private static <T> Node<T> dobbelVenstreRotasjon(Node<T> p).
Den skal gjøre det motsatte av metoden i Oppgave 1.
|
| 3. | Lag et program som bygger opp et f.eks. balansert binærtre med 1 million noder og finn så ut hvor lang tid
metoden gjørKomplett() bruker på din maskin.
|
| 4. | Lag en metode f.eks. med navn tilTabell. Den skal traversere treet i inorden
og fortløpende legge nodene inn i enn nodetabell a, dvs. en tabell av typen
Node<T>[].
|
| 5. | Lag en metode komplett maken til den i
Programkode 9.1.3 g). Metoden
skal sette sammen treet ved hjelp av nodene i tabellen a av typen Node<T>[]. Da skal det ikke lages noen nye
noder. Metoden skal returnere roten til treet.
|
| 6. | Lag en ny versjon av metoden gjørKomplett()
der «komplettiseringen» utføres ved hjelp av metodene i Oppgave 4 og 5. Når det
skal opprettes en nodetabell må det brukes en «rå» type (eng: raw type), dvs. uten
typeparameter: Node[] a = new Node[antall]; Sammenlign så tidsbruken med den andre versjonen.
Se Oppgave 3.
|
