Oppgave 1

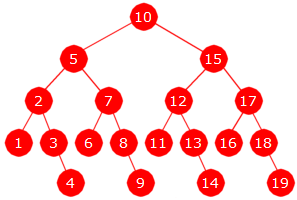Tallene fra 1 til 19

Oppgave 2

Hvis vi traverserer treet i nivåorden ved hjelp av en kø, vil køen, når vi er ferdig med ett nivå, innholde alle nodene på neste nivå. Dermed vet vi hvor mange det er og kan sammeligne det med hvor mange det må være for at nivået skal være fullt. Hvis det ikke er fullt, avbrytes traverseringen. Deretter sjekker vi om dette nivået er det nederste. Hvis minst en av nodene har barn, er det ikke nederste nivå. Hvis treet er perfekt, vil dette også fungere. Da stopper traverseringen ved at det er 0 noder på neste nivå og det er mindre enn det maksimale antallet på det nivået.

  public boolean erBalansert()
  {
    if (tom()) return true;  // vi sier at et tomt tre er balansert

    Kø<Node<T>> kø = new TabellKø<>();  // hjelpekø
    int k = 1;  // maks antall på et nivå

    kø.leggInn(rot);    // legger roten i køen

    while (true)
    {
      int antall = kø.antall();  // antallet på dette nivået
      if (antall != k) break;    // er det forskjellig fra maks?

      for (int i = 0; i < antall; i++)  // alle på nivået
      {
        Node<T> p = kø.taUt();

        if (p.venstre != null) kø.leggInn(p.venstre);
        if (p.høyre != null) kø.leggInn(p.høyre);
      }
      k <<= 1;  // k = 1, 2, 4, 8, 16, osv.
    }

    // sjekker om dette er det nederste nivået i treet
    while (!kø.tom())
    {
      Node<T> p = kø.taUt();
      if (p.venstre != null || p.høyre != null) return false;
    }

    return true;
  }

Oppgave 3

Her kan en lage en rekursiv hjelpemetode som normalt returnerer høyden til treet med p som rot. Men hvis treet ikke er høydebalansert kan det signaliseres med en negativ verdi. Vi kan ikke bruke -1 siden et tomt tre har høyde -1. Derfor bruker vi her -2.

  private static <T> int erHøydebalansert(Node<T> p)
  {
    if (p == null) return -1;                   // tomt tre
    int venstre = erHøydebalansert(p.venstre);  // høyden til venstre subtre
    if (venstre == -2) return -2;  // venstre subtre er ikke høydebalansert
    int høyre = erHøydebalansert(p.høyre);      // høyden til høyre subtre
    if (høyre == -2) return -2;    // høyre subtre er ikke høydebalansert
    if (Math.abs(venstre - høyre) <= 1)
      return Math.max(venstre, høyre) + 1;  // returnerer høyden
    else return -2;                         // treet er ikke høydebalansert
  }

  public boolean erHøydebalansert()
  {
    return erHøydebalansert(rot) != -2;
  }