![]() 6.1.1 Hva er hashing?
6.1.1 Hva er hashing?
Det engelske ordet hash kan være både substantiv og verb. Substantivet hash er definert slik
i «Webster's Dictionary»:
«a dish of diced or chopped meat and often vegetables, as of leftover corned beef,
veal, etc., and potatoes, sautéed in a frying pan or of meat, potatoes, and carrots
cooked together in gravy». Dette minner sterkt om den matretten vil kaller lapskaus.
Verbet hash har betydningen: «to chop into small pieces».
I databehandling er hashing en teknikk for å legge objekter i en tabell på en slik måte at både innlegging, søking og fjerning blir effektive operasjoner. Målet er at alle tre operasjonene skal være av konstant orden. Teknikken består normalt av tre trinn:
- Objektet deles opp («hakkes i biter») og delene brukes til å konstruere et (stort) heltall. Dette heltallet kalles objektets hashverdi.
- Hashverdien (heltallet) konverteres ved hjelp av en bestemt regel til en tabellposisjon, f.eks.
ved å bruke
restennår hashverdien heltallsdivideres med tabellengden. - Hvis tabellposisjonen allerede er i bruk (kollisjon - et annet objekt ligger der), skal det likevel være mulig (ved hjelp av en fast regel) å lagre objektet og da på en slik måte at det lett kan gjenfinnes. Dette kalles kollisjonsbehandling.
Hashing er en så viktig teknikk at de som konstruerte Java valgte å la basisklassen
Object få metoden hashCode(). Den er satt opp slik i klassen Object:
public native int hashCode();
Dette betyr at enhver klasse arver metoden hashCode(). Se på flg.
eksempel:
public static void main(String... args)
{
class MinKlasse { } // en klasse uten innhold
MinKlasse objekt = new MinKlasse(); // en instans av klassen
System.out.println(objekt.hashCode()); // utskrift: vil variere
}
Programkode 6.1.1 a)
Metoden hashCode() er satt opp som native i basisklassen Object.
Det betyr at koden ikke er synlig for oss. Metoden vil da normalt være kodet i et annet språk (f.eks. C eller C++) pga.
effektivitet. Det gjelder først og fremst metoder som er direkte avhengig av operativsystemet. Men dette er ikke så relevant
lenger siden moderne Java har en effektivitet som ikke ligger langt under den som C og C++ har.
I programmeringsspråket Java er det ikke bestemt hvordan hashCode() skal implementeres, men i dens API står det:
«This is typically implemented by converting the internal address of the object into
an integer, but this implementation technique is not required by the Java(TM) programming language».
En kjøring av Programkode 6.1.1 a) gav 366712642 som
utskrift. Det er nok rimelig å anta at tallet er basert på minneadressen. Det betyr spesielt at
hvis samme kode kjøres på nytt (et annet program, en annen maskin eller
en annen plattform), vil det kunne komme et annet tall. Men kravet (eng: contract) er at hvis hashCode()
kalles flere ganger for samme objekt under samme programkjøring, så skal det alltid bli samme tall. Det vil være oppfylt her.
I programmering skjelner vi mellom «identisk» likhet og «logisk» likhet.
La o1 og o2 være to Java-objekter. Vi sier objekter, men o1 og o2
er egentlig to referanser, dvs. minneadresser til der innholdet ligger. Vi sier
at de er identisk like (eller identiske) hvis de refererer til det samme objektet. Motsatt sier vi at de er
logisk like hvis de referer til to objekter med likt innhold. Det betyr selvfølgelig at hvis de er identiske, så er de også logisk like.
Objektene kan generelt sammenlignes slik:
o1 == o2 // indentisk likhet - sammenligner minneadresser
o1.equals(o2) // logisk likhet - sammenligner innholdet
Programkode 6.1.1 b)
Metoden equals() er også en metode i basisklassen Object. Der er den kodet slik:
public boolean equals(Object obj)
{
return (this == obj);
}
Programkode 6.1.1 c)
Hvis vi, i våre klasser, ikke overstyrer (eng: override) equals(), vil den virke på
samme måte som indentitetsoperatoren == . Det betyr at det er minneadressene som sammenlignes,
og ikke innholdet. Dermed må equals() alltid overstyres (omkodes)
i klasser der det er aktuelt å sammenligne objekter «logisk». Videre må vi passe på
at vi alltid bruker equals() og aldri operatoren == , hvis formålet er
å sammenligne mhp. innhold (logisk sammenligning).
Det er viktig å se metodene hashCode() og equals()
i sammenheng. Kravet (eng: contract) er at hvis equals() sier at to objekter er
(logisk) like, så må hashCode() gi samme verdi for de to. Det betyr at hvis equals()
overstyres i vår klasse, så må også hashCode() overstyres.
| 1. |
Hva blir innholdet til verdiene lik1, lik2, lik3, eq1,
eq2, eq3, h1, h2, h3 og h4 i koden under?
Lag et program der verdiene skrives ut.
String[] s = {"A"};
String a = "A", b = "A", c = new String("A"), d = s[0];
boolean lik1 = (a == b), lik2 = (a == c), lik3 = (a == d);
boolean eq1 = a.equals(b), eq2 = a.equals(c), eq3 = a.equals(d);
int h1 = a.hashCode(), h2 = b.hashCode(), h3 = c.hashCode(), h4 = d.hashCode();
|
| 2. | Hva blir verdiene til lik1, lik2 og lik3 i denne koden:
int[] a = {1,2,3}, b = a, c = {1,2,3}; boolean lik1 = (a == b), lik2 = (a == c), lik3 = a.equals(c); |
![]() 6.1.2 Perfekte hashfunksjoner
6.1.2 Perfekte hashfunksjoner
Gitt at vi har en fast samling verdier (f.eks. ord) som skal organiseres slik at søking blir mest mulig effektiv.
De 50 reserverte ordene i Java er et eksempel på en slik samling. I et Java-program
inngår både reserverte ord og ordinære variabelnavn. Under kompilering er det viktig at det raskt
kan avgjøres hva som er hva. En mulighet er å legge dem sortert i en tabell og så bruke binærsøk.
Det er en effektiv teknikk. Men er det mulig å gjøre det enda bedre?
Spørsmål: Kan tabellen organiseres slik at det er mulig å gå direkte til ordet, dvs. uten å søke seg frem.
En slik teknikk kalles å gjøre et direkte oppslag. Målet er å lage en hashfunksjon
som er definert for alle ord (eller tegnstrenger), men som har den egenskapen at når den kalles for et av de
reserverte ordene, så returneres indeksen
til der ordet ligger i tabellen:
Definisjon 6.1.2 La U være en universalmengde og A en delmengde av U med n verdier,
N de naturlige tallene og B tallene fra 0 til n - 1.
En perfekt hashfunksjon på A er en
funksjon f : U → N som er en-til-en når den restrikteres til A. En minimal perfekt hashfunksjon på A er en
funksjon f : U → B som er en-til-en når den restrikteres til A.
Her kunne f.eks. A være mengden av de 50 reserverte ordene i Java og universalmengden U lik
mengden av alle ord (eller tegnstrenger). Da ville vi kunne få mer effektiv søking enn binærsøk
hvis vi klarte å finne en minimal perfekt hashfunksjon på A. I teorien er det
alltid mulig å lage en slik funksjon, men hvis A har mange verdier er det en vanskelig
oppgave. En metode som kalles Cichellis algoritme (se
også oppgave 4) virker i mange tilfeller (ikke alltid).
Den benytter ordets lengde sammen med første og siste bokstav.
Her skal vi for eksemplets skyld gjøre det svært enkelt. Vi plukker ut noen av de reserverte ordene (10 stykker) og setter opp en minimal perfekt hashfunksjon for dem:
String[] reserverteord =
{"class","default","else","extends","if","implements",
"interface","protected","static","synchronized"};
Programkode 6.1.2 a)
Hashfunksjonen skal som nevnt over, benytte ordets lengde sammen med første og siste bokstav, dvs. slik:
hash(ord) = (lengde(ord) + g(førstebokstav(ord)) + g(sistebokstav(ord))) mod n
der funksjonen g() gjør om en bokstav til et heltall. Siden det er 10 ord i tabellen, blir det
n = 10. Det er funksjonen g som Cichellis algoritme finner. Her setter vi kun opp resultatet:
public static int g(char c)
{
return c == 'd' || c == 'p' ? 1 : 0;
}
public static int hash(String ord, int n)
{
return (ord.length() + g(ord.charAt(0)) + g(ord.charAt(ord.length() - 1))) % n;
}
Programkode 6.1.2 b)
Bruker vi flg. kode på tabellen i Programkode 6.1.2 a),
vil vi få ut indeksene til der ordene må legges i en tabell for at vi skal kunne gjøre direkte oppslag:
for (String ord : reserverteord) System.out.print(hash(ord, 10) + " ");
// Utskrift: 5 8 4 7 2 0 9 1 6 3
Programkode 6.1.2 c)
Utskriften sier at det første ordet (class) må legges på indeks 5, det andre ordet
(default) på indeks 8, osv. til det siste ordet (synchronized) som må
inn på indeks 3.
Dette kan vi teste slik:
String[] reserverteord =
{"implements","protected","if","synchronized",
"else","class","static","extends","default","interface"};
String[] testord = {"else","Else","if","iff"};
for (String ord : testord)
{
if (ord.equals(reserverteord[hash(ord, 10)])) ord += " er et reservert ord";
else ord += " er ikke et reservert ord";
System.out.println(ord);
}
// Utskrift:
// else er et reservert ord
// Else er ikke et reservert ord
// if er et reservert ord
// iff er ikke et reservert ord
Programkode 6.1.2 d)
Funksjonen g() fra Programkode 6.1.2 b)
er enkel. Hvis vi skulle ha funnet en g() for en tabell med alle de 50 reserverte i Java,
ville den ha blitt vesentlig mer komplisert.
Et problem når det gjelder en minimal perfekt hashfunksjon for en stor datamengde, er at den kan bli kostbar å bruke.
Gevinsten ved å kunne gjøre direkte oppslag i tabellen kan tapes ved at hashfunksjonen må gjøre så mye arbeid hver gang den kalles.
Hvis samlingen med verdier er liten, er det enklere (og effektivt nok) å bruke konstruksjonen
switch - case. Flg. metode avgjør om et ord hører til de
ti reserverte ordene:
public static boolean erReservert(String ord)
{
switch (ord)
{
case "class":
case "default":
case "else":
case "extends":
case "if":
case "implemnets":
case "interface":
case "protected":
case "static":
case "synchronized": return true;
default: return false;
}
}
Programkode 6.1.2 e)
| 1. | Det finnes en masse stoff om perfekte og minimale perfekte hashfunksjoner på internett. Bruk «minimal perfect hash function» som søkestreng. |
| 2. |
Sjekk at metoden erReservert() virker. Se
f.eks. Programkode 6.1.2 d).
|
| 3. |
Lag en metoden som den i Programkode 6.1.2 d), men
med en sortert String-tabell med de ti reserverte ordene som parameter.
Metoden skal bruke binærsøk.
|
| 4. |
I boken Adam Drozdek, Data Structures and Algorithms in Java, Brooks/Cole er det som eksempel laget to
forskjellige minimale perfekte hashfunksjoner for de ni musene fra gresk
mytologi, dvs. for Calliope, Clio, Erato, Euterpe, Melpomene, Polyhymnia, Terpsichore, Thalia og Urania.
Den første er laget ved hjelp av Cichellis algoritme.
I algoritmen telles først forekomstene av de bokstavene som står først eller sist. Siden det er både
små og store bokstaver, blir alle gjort om til store. Bokstaven E forekommer flest (6) ganger. Den står først eller sist
i Calliope, Erato, Euterpe, Melpomene og Terpsichore. Dernest kommer A (3 ganger), C(2), O(2), osv.
Så settes ordene opp i rekkefølge etter hyppigheten av bokstavene. Da kommer Euterpe først siden den har
E først og E sist. Dermed 6 + 6 = 12. Dernest kommer Calliope (2 + 6 = 8), så Erato (6 + 2 = 8), osv. Bokstaven
E får verdi 0 ( public static int g(char c) { c = Character.toUpperCase(c); if (c == 'P') return 2; else if (c == 'U') return 4; else return 0; }Hashfunksjonen er den i Programkode 6.1.2 b). Når den brukes
må n = 9 siden det er ni muser. Lag kode som sjekker at dette gir en minimal perfekt hashfunksjon.
En minimal perfekt hashfunksjon av denne typen er ikke entydig. Det er flere andre muligheter.
|
![]() 6.1.3 Generelle hashfunksjoner
6.1.3 Generelle hashfunksjoner
Oppskriften sier at
en hashfunksjon skal returnere et heltall som så skal brukes til å konstruere en indeks
for lagringstabellen. Hvis vi kjenner de verdiene som det er aktuelt å lagre, kunne begge disse
delene gjøres i ett (først et heltall og så en indeks). Et eksempel på dette kommer i forbindelse med
LZW-metoden for komprimering. Se Avsnitt 7.2.6.
Men hvis vi skal gjøre det generisk, må det gjøres i to operasjoner. Det betyr at instanser
(objekter av datatypen) som det er aktuelt å lagre, må kunne «omformes» til et heltall.
Deretter blir det hashsystemet (tabellstruktur og kollisjonsbehandling) som bruker dette
heltallet. Slik er den generiske måten i Java.
Integer I Java arver som nevnt i Avsnitt 6.1.1, enhver klasse metoden
hashCode() fra basisklassen Object. Den er overstyrt (eng: overridden)
i alle Javas vanlige referansetyper, f.eks. Integer og String. I Integer
returnerer den instansen verdi. Se flg. eksempel:
Integer i = 10;
System.out.println(i.hashCode()); // Utskrift: 10
Programkode 6.1.3 a)
Denne metoden, som til et tall tilordner det samme tallet, er en
perfekt hashfunksjon.
Det kan imidlertid være gunstig
å gjøre en primtallsbasert forskyvning. Klassen Heltall
er et eksempel på en «omslagsklasse» (for datatypen int). Den er laget på
samme måte som Integer. Hvis vi ikke koder hashCode() og
equals() i Heltall,
vil både NetBeans og Eclipse foreslå hvordan de skal kodes.
NetBeans kommer med flere forslag.
Et av dem er som følger (der verdi er instansvariabelen i klassen):
public int hashCode()
{
int hash = 7;
hash = 97 * hash + this.verdi;
return hash;
}
Programkode 6.1.3 b)
I Eclipse kommer det kun ett forslag og det ser slik ut:
public int hashCode()
{
final int prime = 31;
int result = 1;
result = prime * result + verdi;
return result;
}
Programkode 6.1.3 c)
Begge versjonene gir en perfekt hashfunksjon siden funksjonsverdien er forskjøvet en fast verdi i forhold til argumentet.
Double Hashfunksjonen til datatypen double er litt mer komplisert. Se på flg. eksempel:
Double d = 3.14;
System.out.println(d.hashCode()); // Utskrift: 300063655
Programkode 6.1.3 d)
Tallet 3,14 kan skrives på vitenskaplig form (eng: scientific notation), dvs.
som 0,314·101 der 0,314 er mantissen og 1-tallet (som 10 er opphøyd i)
er eksponenten. Vi kan også oppgi tall på denne formen i programkode. Mantissen kommer først
(foran e/E) og så eksponenten:
Double d = 0.314e1; // mantisse: 0.314 eksponent: 1
System.out.println(d); // Utskrift: 3.14
Programkode 6.1.3 e)
Et double-tall lagres også internt på vitenskaplig form, men da med 2 som grunntall (og ikke 10).
De 64 bitene som inngår er delt opp slik: første bit er fortegnsbit, de neste 11 bitene brukes til
eksponenten og resten (de 52 siste bitene) til mantissen. Klassen Double har en metode som
tolker de 64 bitene som et long-tall:
long biter = Double.doubleToRawLongBits(3.14);
System.out.println(biter); // Utskrift som long: 4614253070214989087
// 64 biter: 0 10000000000 1001000111101011100001010001111010111000010100011111
Programkode 6.1.3 f)
Metoden hashCode() deler bitene i to. De første og de siste 32 bitene «flettes
sammen» ved hjelp av operatoren ^ (eksklusiv eller) og «flettingen» blir hashverdien:
int hash = (int) ((biter >>> 32) ^ biter); // innholdet i metoden hashCode()
String
En tegnstreng kan
«hakkes opp» i sine enkelte deler, dvs. i sine tegn og hvert tegn kan brukes til å konstruere et stort
heltall. Dette kan gjøres på mange måter. I Java har man valgt å bruke
en konstruksjon der hvert tegn inngår som om det skulle være siffer i et tallsystem med
31 som «grunntall». Ta tegnstrengen "abcd" som eksempel:
a · 313 + b · 312 + c · 31 + d
I dette regnestykket inngår tall-verdiene til tegnene. Resultatet blir derfor:
97 · 313 + 98 · 312 + 99 · 31 + 100 = 2987074
Denne teknikken kalles polynomisk hashing og kan kodes slik for en generell tegnstreng s:
public static int hash(String s) { int n = s.length(), h = 0; for (int i = 0; i < n; i++) h = h*31 + s.charAt(i); return h; } Programkode 6.1.3 g)
En hashfunksjon bør i størst mulig grad unngå at to ulike objekter får samme hashverdi.
Det ser ut som at polynomisk hashing med 31 som «grunntall» fungerer godt for dette. Men også grunntall lik
33, 37, 39 og 41 skal gi god spredning.
En ulempe med polynomisk hashing er at utregningen koster en del arbeid
hvis tegnstrengen er lang. Det finnes imidlertid mange andre teknikker for å «hashe» en tegnstreng.
Se Oppgave 2 - 4.
Polynomisk hashing kan føre
til at det «flyter over» hvis tegnstrengen er lang, dvs. verdien til
variabelen h i
Programkode 6.1.3 g)
kan bli større enn datatypen int tillater. En konsekvens er
at metoden vil kunne returnere et negativt tall. Se på flg. eksempel:
String s = "abcdef"; System.out.println(hash(s) + " " + s.hashCode()); // Utskrift: -1424385949 -1424385949 Programkode 6.1.3 h)
Metoden Programkode 6.1.3 g)
er laget nøyaktig slik som hashCode() i klassen String og
dermed samme resultat. Men det spesielle er at returverdien er negativ for tegnstrengen
"abcdef". Dette må en ta hensyn til i et «hashsystem». Hvis h er
en hashverdi og n størrelsen på hashtabellen, så vil
h % n (dvs. resten) bli negativ hvis
h er negativ og kan dermed ikke være indeks i tabellen.
En mulighet er da
er å skifte fortegn. Men det kan være problematisk siden det finnes et int-tall
h som har egenskapen at −h = h. Det
er tallet −2147483648, dvs. den minste mulige int-tallet.
Andre muligheter er 1) å ta komplementet (0-biter blir 1-biter og omvendt), 2) å fjerne
fortegnsbiten eller 3) å se på hashverdien som fortegnsløs (eng: unsigned) og bruke
metoden remainderUnsigned(). Her ser vi på 2). De to andre (1 og 3)
tas opp i Oppgave 5 - 6.
Hvis hashverdien er negativ, kan vi fjerne fortegnsbiten (sette den til 0) og beholde resten av bitene som de er. Denne teknikken brukes i hashingklassene i Java. Det gjøres slik:
int h = -1424385949; // 10101011000110011001100001100011 int m = 0x7fffffff; // 01111111111111111111111111111111 h &= m; // 00101011000110011001100001100011 System.out.println(h); // 723097699 Programkode 6.1.3 i)
Objekter med sammensatt identifikator Ofte vil de objektene som skal lagres i en tabell, ha flere enn én
instansvariabel som bestemmer objektets tilstand. Ta klassen
Person
som eksempel. Der bestemmer både fornavn og etternavn hvilken person det er.
Vi kan ikke kun bruke etternavnet i en hashfunksjon. Det kan være mange med samme etternavn. En vanlig måte (som
det er tilrettelagt for i Java) er å bruke polynomisk hashing med 31 som «grunntall». Hvis
det gjelder Elin Olsen, kunne det gjøres slik:
hash (Olsen) · 31 + hash (Elin)
I Javas teknikk (Objects.hash() eller Arrays.hashCode())
blir tallet enda litt større, dvs. lik:
312 + hash (Olsen) · 31 + hash (Elin)
Dette kan kodes på en generisk måte:
public static int hash(Object... verdier) { if (verdier == null) return 0; int h = 1; for (Object o : verdier) { h = h*31 + (o == null ? 0 : o.hashCode()); } return h; } Programkode 6.1.3 j)
Dette virker slik:
int hash1 = Objects.hash("Olsen", "Elin"); // metode fra class Objects int hash2 = hash("Olsen", "Elin"); // Programkode 6.1.3.j int hash3 = 31*31 + "Olsen".hashCode()*31 + "Elin".hashCode(); // direkte System.out.println(hash1 + " " + hash2 + " " + hash3); // Utskrift: -1927833970 -1927833970 -1927833970 Programkode 6.1.3 k)
| 1. | Finn to forskjellige tegnstrenger, begge med to bokstaver, med like hashCode()-verdier. |
| 2. | Ofte vil tegnstrenger som skal legges i en tabell, være ulike i kun ett eller i kun noen få av tegnene. Vi
tenker oss nå at A000, A001, A002, . . . , A399 er de aktuelle tegnstrengene. Lag en int-tabell med plass
til n verdier der n = 197 (et primtall). La s være en av strengene fra
A000 til A399. Da vil s.hashCode() % n bli en indeks i tabellen. Finn ut hvor mange det blir
av de forskjellige indeksene? Vil alle de aktulle indeksene bli brukt. Finn ut hvor mange indekser det
var ingen av, hvor mange det var én av, to av, osv. Prøv deretter med
n lik primtallene 193, 199 og 211. |
| 3. |
Flg. hashfunksjon ble lansert en gang. Bruk den i Oppgave 2.
public static int hash(String s) { int h = 0; for (int i = 0; i < s.length(); i++) { h = (h << 5) ^ s.charAt(i) ^ h; } return h; } |
| 4. |
Flg. hashfunksjon går under navnet ElfHash. Prøv den i Oppgave 2.
public static int hash(String s) { int h = 0; for (int i = 0; i < s.length(); i++) { h = (h << 4) + s.charAt(i); int g = h & 0xf0000000; if (g != 0) h ^= (g >>> 24); h &= ~g; } return h; } |
| 5. | Hvis k er negativ, er fortegnsbiten lik 1.
Lag en kodebit der variabelen k inngår, slik at hvis k er negativ,
så skal k erstattes av sitt
komplement. Da blir k positiv. |
| 6. |
Hva blir resten: -1 % 3 ? Vi kan isteden se bort fra fortegnet og la den første biten være en vanlig bit. Hva blir
Integer.remainderUnsigned(-1, 3) ?
|
| 7. |
Hashfunksjonen i Programkode 6.1.3 j)
har Object som parametertype. Dermed kan vi gjøre slik:
int h = hash("ABC", 10, 3.14). Sjekk at det virker! Hva blir verdien?
|
![]() 6.1.4 Lukket adressering
6.1.4 Lukket adressering
Gitt at vi skal plassere navnene Olga, Basir, Ali, Per, Elin, Siri, Ole og Mette i en tabell der det skal
være plass til enda flere verdier. Siden vi har hørt at det skal være fordelaktig med en tabelldimensjon som er
et primtall, velger vi å la den ha plass til 13 verdier (navn). Dvs. slik:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.4 a) : En tabell med plass til 13 verdier (indekser fra 0 til 12) | ||||||||||||
Da «hasher» vi hvert navn, deler med tabellengden (13) og får en indeks for hver av dem:
String[] navn = {"Olga","Basir","Ali","Per","Elin","Siri","Ole","Mette"};
for (String n : navn) System.out.print(n + ": " + (n.hashCode() % 13) + " ");
// Utskrift: Olga: 5 Basir: 1 Ali: 8 Per: 6 Elin: 0 Siri: 12 Ole: 3 Mette: 7
Programkode 6.1.4 a)
Hvert navn legges så inn på den plassen som indeksen sier, dvs. Olga på plass/indeks 5, osv.
| Elin | Basir | Ole | Olga | Per | Mette | Ali | Siri | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.4 b) : 8 verdier er lagt inn - ingen kollisjoner | ||||||||||||
Tabellen inneholder 8 verdier, men har plass til 13. Det ble ingen kollisjoner (like indekser) for de 8 verdiene. Sannsynlighten for kollisjoner vil selvfølgelig vokse etter som tabellen blir fullere. Men selv om tabellen kun inneholder én verdi, kan det bli kollisjon. La nå Anne være neste navn. Da får vi:
"Anne".hashCode() % 13 = 2045636 % 13 = 8
Men indeks 8 er opptatt - med andre ord en kollisjon. Hva gjør vi da? Det må jo være mulig å legge inn Anne siden tabellen ikke er full. Det er vanlig å håndtere dette på én av to måter:
Lukket adresseringbetyr at ved kollisjon skal objektet legges inn på den indeksen vi fikk. Men da må vi ha en datastruktur som tillater flere objekter på samme indeks.Åpen adresseringbetyr at objektet skal legges, så sant tabellen ikke er full, på en annen ledig plass og det må være en fast regel for hvordan det skal foregå.
Her skal vi se nærmere på lukket adressering. Åpen adressering tas opp i
neste avsnitt. Som nevnt over, må hashsystemet tillate flere objekter på
samme indeks. En vanlig teknikk er å la tabellen være en tabell av nodereferanser (en lenket liste). Dvs. slik:
 |
| Figur 6.1.4 c) : En tabell med nodereferanser |
La tabellen hete hash. Innlegging, søking og fjerning kan da gjøres på denne måten:
Innlegging: 1) Lag en ny node som inneholder objektet. 2) Finn objektets tabellindeksindeks. 3) Sjekkhash[indeks]. 4) Hvis den ernull, la den referere til den nye noden. 5) Hvis den ikke ernull, la den nye noden bli første node i den tilhørende listen. 6) Øk antallvariabelen.Søking: 1) Finn tabellindeksen. 2) Søk i den (eventuelt tomme) (lenkede) listen som hører til indeksen. 3) Hvis objektet ikke ligger der, så finnes ikke objektet.Fjerning: 1) Finn tabellindeksen. 2) Søk i den (eventuelt tomme) (lenkede) listen som hører til indeksen. 3) Fjern den (hvis den er der) på vanlig måte (ved å endre på en referanse). 4) Reduser antallvariabelen.
Hvis Olga, Basir, Ali, Per, Elin, Siri, Ole og Mette (se indeksene) legges inn, får vi flg. tabell:
 |
| Figur 6.1.4 d) : En tabell med nodereferanser |
Anne skal legges inn: En ny node med Anne som verdi legges først i den lenkede listen som hører til indeks 8, dvs. foran Ali. Vi kan legge inn enda flere, f.eks. Åse, Leif, Mona og Lise:
String[] navn = {"Anne","Åse","Leif","Mona","Lise"};
for (String n : navn) System.out.print(n + " " + (n.hashCode() % 13) + ", ");
// Utskrift: Anne 8, Åse 11, Leif 3, Mona 8, Lise 9
Programkode 6.1.4 b)
Etter innleggingene blir tabellinnholdet slik:
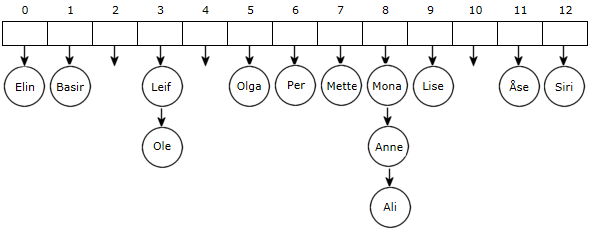 |
| Figur 6.1.4 e) : En tabell med lister - 3 tomme, 8 med 1 node, 1 med 2 noder og 1 med 3 noder |
Vi ser nå at hele problemstillingen med lukket adressering er redusert til å legge inn, søke og fjerne i lenkede lister. Målet er imidlertid at listene skal være så korte som mulig - helst ha kun én node. Det mest ekstreme er at alle verdiene ligger i en og samme liste. I så fall vil dette være en ineffektiv lagringsstruktur.
Figur 6.1.4 e) har 13 som tabelldimensjon
og det er lagt inn 13 verdier. Sannsynligheten for lange lister kan reduseres hvis tabelldimensjonen holdes større
enn antall verdier. Forholdet mellom de to (antall/dimensjon) kalles tettheten (eng: load factor). Jo mindre tetthet,
jo mindre sannsynlighet for kollisjoner. Ofte setter man en grense for tettheten, f.eks. 75%. Hvis den, etter en
innlegging, passerer grensen, er det vanlig å «utvide» tabellen. Da må alle verdiene
legges inn på nytt. Derfor er det også vanlig å lagre hashverdien i hver node slik at den ikke må regnes ut på nytt.
En hashtabell skal ha muligheter for å legge inn, søke etter og fjerne verdier. I tillegg bør den ha metoder for å finne antall,
gjøre utskrift og traversere, osv. Den bør derfor implementere grensesnittet
Beholder. Men det kommenterer vi vekk inntil videre:
public class LenketHashTabell<T> // implements Beholder<T> { private static class Node<T> // en indre nodeklasse { private final T verdi; // nodens verdi private final int hashverdi; // lagrer hashverdien private Node<T> neste; // peker til neste node private Node(T verdi, int hashverdi, Node<T> neste) // konstruktør { this.verdi = verdi; this.hashverdi = hashverdi; this.neste = neste; } } // class Node private Node<T>[] hash; // en nodetabell private final float tetthet; // eng: loadfactor private int grense; // eng: threshold (norsk: terskel) private int antall; // antall verdier public LenketHashTabell(int dimensjon) // konstruktør { // mangler kode } public LenketHashTabell() // standardkonstruktør { this(13); // velger 13 som startdimensjon inntil videre } public int antall() { return antall; } public boolean tom() { return antall == 0; } // flere metoder skal inn her } // class LenketHashTabell Programkode 6.1.4 c)
Det eneste nye i forhold til det som har vært diskutert, er instansvariabelen grense. Poenget
er at hvis antall verdier delt med tabelldimensjonen overstiger gitt tetthet, må
vi «utvide». Dette må
sjekkes i leggInn-metoden. Hvis vi setter grense (en heltallsvariabel) lik
tetthet ganget med tabelldimensjon, kan antall sammenlignes
med grense. Da sammenlignes to heltall og det er «billigere» enn å sammenligne
to desimaltall.
Den første konstruktøren skal opprette en nodetabell med oppgitt dimensjon. Men tabelltypen er generisk og i Java er det ikke mulig å opprette en tabell av en generisk type:
hash = new Node<T>[dimensjon]; // Feilmelding: "generic array creation"
En mulighet er å bruke «raw type» eller som vi har gjort tidligere, å gå vi en objekttabell:
1) hash = (Node<T>[]) new Node[dimensjon]; // bruker raw type 2) hash = (Node<T>[]) new Object[dimensjon]; // går via Object
1) «Raw type» betyr at nodetabellen opprettes med Object som type for T. Så konverteres
den til Node<T>[]. NetBeans «kommenterer» at
en eksplisitt konvertering er unødvendig. Med andre ord at det holder med:
hash = new Node[dimensjon].
Eclipse sier «Type safety: Unchecked cast from Node[] to Node<T>[]».
2) Dette går det ikke an å bruke som teknikk. Det kommer ingen syntaksfeil, men derimot en kjørefeil
(ClassCastException). Dette kan vi derfor glemme som idé.
Eventuelle «kommentarer» fra NetBeans, Eclipse eller
andre verktøy, kan «undertrykkes» ved hjelp av en annotasjon. Det er slik
det gjøres i Javabibliotekene (Java.util):
@SuppressWarnings({"rawtypes","unchecked"}) // en annotasjon
public LenketHashTabell(int dimensjon) // konstruktør
{
if (dimensjon < 0) throw new IllegalArgumentException("Negativ dimensjon!");
hash = new Node[dimensjon]; // bruker raw type
tetthet = 0.75f; // maksimalt 75% full
grense = (int)(tetthet * hash.length); // gjør om til int
antall = 0; // foreløpig ingen verdier
}
Programkode 6.1.4 d)
Metoden leggInn() må først finne hashverdien og om nødvendig gjøre den om til et ikke-negativt
tall. En innlegging fører til at antallet økes. Hvis det gjør at grensen passeres, skal tabellen «utvides». Men det venter
vi med. Deretter er det kun å finne rett plass i tabellen og så legge inn en node først i den tilhørende listen.
I denne versjonen er like verdier tillatt:
public boolean leggInn(T verdi) { Objects.requireNonNull(verdi, "verdi er null!"); if (antall >= grense) { // her skal metoden utvid() kalles, men det tas opp senere } int hashverdi = verdi.hashCode() & 0x7fffffff; // fjerner fortegn int indeks = hashverdi % hash.length; // finner indeksen // legger inn først i listen som hører til indeks hash[indeks] = new Node<>(verdi, hashverdi, hash[indeks]); // lagrer hashverdi antall++; // en ny verdi return true; // vellykket innlegging } Programkode 6.1.4 e)
Etter leggInn() bør vi lage toString(). Først da får vi muligheten å sjekke at
dette virker. Vi går gjennom tabellen fra start til slutt og henter fortløpende verdiene
i de tilhørende listene:
public String toString() { StringJoiner s = new StringJoiner(", ", "[", "]"); for (Node<T> p : hash) // går gjennom tabellen { for (; p != null; p = p.neste) // går gjennom listen { s.add(p.verdi.toString()); } } return s.toString(); } Programkode 6.1.4 f)
Flg. eksempel viser at dette virker slik som i Figur 6.1.4 e):
String[] navn = {"Olga","Basir","Ali","Per","Elin","Siri",
"Ole","Mette","Anne","Åse","Leif","Mona","Lise"};
LenketHashTabell<String> hashtabell = new LenketHashTabell<>();
for (String n : navn) hashtabell.leggInn(n);
System.out.println(hashtabell);
// [Elin, Basir, Leif, Ole, Olga, Per, Mette, Mona, Anne, Ali, Lise, Åse, Siri]
Programkode 6.1.4 g)
Kravet er at HashTabell skal
implementere Beholder. Det som mangler
er inneholder(), fjern(), nullstill() og
iterator(). De tre første tas opp i Oppgave 4 - 6.
For å lage metoden iterator() må vi først lage en intern iteratorklasse. Det tas opp lenger ned.
En viktig sak står igjen. Det er å «utvide» tabellen når grensen overskrides.
Et primtall som dimensjon gir best spredning. Standardkonstruktøren
bruker 13 som startdimensjon. Ved utvidelse er det vanlig enten å øke med 50% eller å doble. Men det vil normalt
ikke gi et primtall. Dessuten tillater den generelle konstruktøren
et hvilket som helst ikke-negativt heltall som dimensjon. Her skal vi derfor (og foreløpig) nøye oss med en enkel form
for utvidelse, dvs. dobling pluss 1. Det gir i hvert fall et oddetall og dermed også i noen tilfeller et primtall.
Teknikker for å lage primtallsdimensjoner tas opp lenger ned.
I metoden leggInn() skal tabellen
«utvides» hvis antall >= grense. Kommentaren erstattes
med et kall på flg. metode (den bruker 2*hash.length + 1 som ny dimensjon):
private void utvid() // hører til LenketHashTabell { @SuppressWarnings({"rawtypes","unchecked"}) // bruker raw type Node<T>[] nyhash = new Node[2*hash.length + 1]; // dobling + 1 for (int i = 0; i < hash.length; i++) // den gamle tabellen { Node<T> p = hash[i]; // listen til hash[i] while (p != null) // går nedover { Node<T> q = p.neste; // hjelpevariabel int nyindeks = p.hashverdi % nyhash.length; // indeks i ny tabell p.neste = nyhash[nyindeks]; // p skal legges først nyhash[nyindeks] = p; p = q; // flytter p til den neste } hash[i] = null; // nuller i den gamle } hash = nyhash; // bytter tabell grense = (int)(tetthet * hash.length); // ny grense } Programkode 6.1.4 h)
Hvis du har lagt inn utvid()
i LenketHashTabell og
oppdatert leggInn() med et kall
på utvid(), vil
Programkode 6.1.4 g)
virke som før, men med en annen rekkefølge i utskriften. Med 13 som startdimensjon vil
grense = (int)(13 * 0.75) = (int)9.75 = 9. Dermed «utvides» tabellen når
det 10-ende navnet skal legges inn og hele systemet blir omorganisert.
Sjekk også at det også virker hvis 0 brukes som startdimensjon.
Til slutt gjør vi det som trengs for å kunne «iterere», dvs. klassen
HashTabellIterator. Itereringen i vår hashtabell kan deles i to. Først går vi
«bortover» i tabellen og så «nedover» i den lenkede listen hvis
den inneholder flere noder. Dette blir med andre ord en kombinasjon av idéene fra
TabellListeIterator og
EnkeltLenketListeIterator.
Vi trenger en indeks som flytter seg i tabellen og en nodereferanse
p som går nedover i listen:
private class HashTabellIterator implements Iterator<T> { private int indeks = 0; private Node<T> p = null; private HashTabellIterator() { // skal flytte p til første verdi } public boolean hasNext() { // avgjør om det er flere verdier } public T next() { // returnerer p.verdi og flytter p til neste verdi } } // class HashTabellIterator Programkode 6.1.4 i)
Hashtabellen er alltid større enn antall verdier. Det betyr at mange av tabellelementene
er null. I konstruktøren må derfor variabelen indeks flyttes til det første som ikke er
null og p vil da referere til første node i tilhørende liste:
private HashTabellIterator() { while (indeks < hash.length && hash[indeks] == null) indeks++; p = indeks < hash.length ? hash[indeks] : null; } Programkode 6.1.4 j)
Hvis det er tomt (alle tabellelementene er null) eller den siste verdien er
«besøkt», vil indeks bli lik hash.length
og p lik null.
Det betyr at både indeks < hash.length og
p != null kan brukes som en test på om det er flere igjen.
Her velger vi den siste:
public boolean hasNext() { return p != null; } Programkode 6.1.4 k)
I metoden next() må vi først ta vare på «denne» (current) verdien,
dvs. p.verdi. Hvis p ikke er den siste i listen, flytter
vi den til neste node. Hvis ikke, må indeks flyttes til første tabellelement som ikke er null. Hvis
det ikke er noe slike elementer igjen, blir indeks satt til hash.length
og p til null. Til
slutt returneres «denne» verdien:
public T next() { if (!hasNext()) throw new NoSuchElementException("Ingen flere verdier"); T verdi = p.verdi; // tar vare på verdien if (p.neste != null) { p = p.neste; // hvis p ikke er den siste } else // må gå til neste indeks der hash[indeks] er ulik null { while (++indeks < hash.length && hash[indeks] == null); p = indeks < hash.length ? hash[indeks] : null; } return verdi; // returnerer verdien } Programkode 6.1.4 l)
Metoden iterator() skal returnere en instans av klassen HashTabellIterator:
public Iterator<T> iterator() { return new HashTabellIterator(); }
Iteratorens remove-metode tas opp i Oppgave 7.
I Programkode 6.1.4 g)
skrives innholdet ut ved hjelp av metoden toString(). Hvis den ikke var tilgjengelig,
kunne vi ha fått til det samme ved hjelp av defaultmetoden forEach() i
grensesnittet Iterable.
Vi kan også få skrevet ut innholdet ved hjelp av en generell forAlle-løkke. Slik løkker virker for tabeller
og for klasser som implementerer Iterable. Flg. kode krever imidlertid at kommentartegnet
foran Beholder<T> i LenketHashTabell<T>
fjernes og at metodene inneholder(), fjern(),
nullstill() og iterator() har kode
(se Oppgave 2):
String[] navn = {"Olga","Basir","Ali","Per","Elin","Siri",
"Ole","Mette","Anne","Åse","Leif","Mona","Lise"};
Beholder<String> hashtabell = new LenketHashTabell<>(); // er en Beholder
for (String n : navn) hashtabell.leggInn(n); // legger inn
StringJoiner sj = new StringJoiner(", ", "[", "]");
hashtabell.forEach(n -> sj.add(n)); // bruker forEach fra Iterable
System.out.println(sj.toString());
for (String n : hashtabell) System.out.print(n + " "); // en forAlle-løkke
Programkode 6.1.4 m)
Primtallsdimensjoner Denne delen er ikke laget ennå.
Oppsummering
Denne teknikken, dvs. lukket adressering med separat lenking (eng: closed adressing with separate chaining) er
den som er mest brukt i praksis. Den inngår i de fleste klassebibliotekene, f.eks. i hashingklassene i Java
(HashSet,
LinkedHashSet,
Hashtable,
HashMap,
IdentityHashMap og
LinkedHashMap).
Hvis referansetypen som skal legges inn, har en god hashmetode (sprer verdiene godt) og tabellen har en primtallslengde,
blir innlegging, søking og fjerning svært
effektivt. Ulempen er at den bruker mye
plass. Teknikken med åpen adressering som vi skal se på i neste avsnitt, vil nok ofte være like
effektiv. Men der er spesielt fjerning av verdier et problematisk område. Men den bruker mindre plass siden det ikke
inngår lenkede lister.
| 1. | Flytt klassen LenketHashTabell over til deg
(f.eks. under hjelpeklasser). Erstatt så konstruktøren med den i
Programkode 6.1.4 d).
Sett inn
metodene leggInn() og
toString() og sjekk at
Programkode 6.1.4 g) virker. |
| 2. | Sett inn metodene inneholder, fjern, nullstill og
iterator i LenketHashTabell. De skal se ut
(parameter- og returtype) som i Beholder.
La metodene inntil videre kun ha setningen:
throw new UnsupportedOperationException();
Etter det kan du ta vekk kommentartegnet // øverst i
LenketHashTabell.
|
| 3. |
Legg metoden utvid()
i klassen LenketHashTabell
og gjør et kall på den i
leggInn().
Gjør om eksempelet i Programkode 6.1.4 g) slik
at tabellen starter med lengde 11. Gjør det også slik at innholdet skrives ut etter hver innlegging istedenfor til slutt.
Hvorfor skifter utskriftene? Lag tegninger som viser hvordan den interne datastrukturen endrer seg etterhvert.
Da må du lage en egen programbit som gir deg tabellindeksene for de aktuelle tabelldimensjonene (først 11 og så 23 siden
utvidelsen går fra 11 til 23).
Bruk så 0 som startlengde på tabellen og gjenta dette.
|
| 4. |
Lag metoden public boolean inneholder(T verdi) i
klassen LenketHashTabell. Den skal returnere
true hvis verdi ligger der og false ellers.
Gjør som i leggInn() når det gjelder fortegn i hashverdien.
|
| 5. |
Lag metoden public boolean fjern(T verdi) i
klassen LenketHashTabell.
Den skal, hvis den finnes, fjerne verdi. Hvis det er flere forekomster
av verdi, skal kun en av dem fjernes. Metoden skal returnere true hvis
fjerningen var vellykket og false ellers.
|
| 6. |
Lag metoden public void nullstill() i
klassen LenketHashTabell.
|
| 7. |
Legg inn klassen HashTabellIterator i
LenketHashTabell.
Bruk de oppdaterte versjonene av konstruktøren,
hasNext() og
next().
Iteratorens remove() skal fjerne verdien som sist ble returnert av
next(). I tillegg gjelder kravene i
Tabell 3.1.1.
Legg inn instansvariabelen fjernOK i
iteratoren. Den skal i utgangspunktet være
false og settes til true i next().
I remove() sjekkes det om den er true. I så fall
settes den til false. Lag metoden remove() og gjør den nødvendige
endringen i metoden next()! La så metoden iterator() returnere
en instans av itertaorklassen.
Se også avsnittene
3.2.4 (TabellListeIterator) og
3.3.4 (EnkeltLenketListeIterator).
|
| 8. |
Det kan være problematisk med flere iteratorer. Gjør slik som i avsnitt
3.2.5 og i slutten av
avsnitt 3.3.4.
|
| 9. |
Utskrifter fra LenketHashTabell (toString eller
iterator) vil endre seg etter utvidelser.
Lag klassen DobbeltlenketHashTabell. Bruk LenketHashTabell som grunnlag og
la nodeklassen få en ekstra referanse slik at nodene kan lenkes sammen i den rekkefølgen de blir laget.
Klassen må da ha et hode og en hale for denne lenken.
Se Avsnitt 3.3.2.
Dette får konsekvenser for leggInn(), toString(),
nullstill() og fjern().
Videre må både hele iteratorklassen endres. Nå skal den isteden gå langs lenken som starter
i hode og ender i hale.
|
![]() 6.1.5 Åpen adressering
6.1.5 Åpen adressering
Som nevnt i forrige avsnitt (Avsnitt 6.1.4)
er det to hovedtyper av teknikker når det gjelder kollisjonsbehandling i hashing.
Lukket adresseringbetyr at en verdi skal, også når det blir en kollisjon, legges inn på «hashindeksen». Men det krever en datastruktur som tillater flere på samme indeks.Åpen adresseringbetyr at ved kollisjon skal verdien, så sant tabellen ikke er full, legges på en annen ledig plass. Da må det være en fast regel for hvor den skal legges.
I Avsnitt 6.1.4 så vi på lukket adressering
med separat lenking. Her skal vi se på åpen adressering.
Vi starter med en tabell med plass til 13 verdier. I den legger vi inn
Olga, Basir, Ali, Per, Elin, Siri, Ole og Mette. Da havner Olga på indeks 5 siden
"Olga".hashCode() % 13 = 5. Osv.
| Elin | Basir | Ole | Olga | Per | Mette | Ali | Siri | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.5 a) : 8 verdier er lagt inn - ingen kollisjoner | ||||||||||||
Foreløpig har det ikke vært kollisjoner. Men sannsynligheten for det øker når tettheten øker.
Den er definert som antall delt med tabelldimensjon
og er her lik 8 / 13 = 0,62 = 62%. Hvis f.eks. Bodil skal legges inn, blir det en kollisjon
og den kommer på indeks 5 siden "Bodil".hashCode() % 13 = 64358650 % 13 = 5.
Vi må derfor finne en annen (og ledig) plass for henne. Det er tre vanlig teknikker for å finne
hvor hun da skal legges. I all tre letes det ved fortløpende å «hoppe» bortover i tabellen
der «hopplengden» kan være fast eller variabel. La tabellen ha lengde 13 slik som i
Figur 6.1.5 a), i en indeks som er opptatt og
hopplengde et positivt heltall. Da «hopper» vi slik:
i = (i + hopplengde) % 13;
Vi må unngå at vi «hopper» ut av tabellen. Hvis for eksempel i = 5
og hopplengde = 9, så vil i + hopplengde bli lik 14.
Men 14 % 13 = 1. Dermed er vi fortsatt innenfor tabellen, men fra den andre siden. Et krav til denne teknikken
er at hvis tabellen ikke er full, så skal vi ved ett eller flere hopp helt sikkert treffe en ledig
plass. Hvis vi i Figur 6.1.5 a) gjør et hopp til (fra indeks 1) med lengde 9,
vil vi komme til indeks 10 og den er ledig. Du kan selv sjekke at dette stemmer for andre indekser.
Start f.eks. med i = 3. Hvor mange hopp trengs da?
Teknikken med å «hoppe» bortover i tabellen for å finne en ledig plass for innlegging, brukes også
ved søking og fjerning. Gitt at vi skal finne
verdi. Hvis den ligger på sin hashindeks, så er alt ok. Hvis plassen derimot er
ledig, så finnes ikke verdi. Men hvis det ligger noe annet der,
må vi lete videre. Vi må da «hoppe» på nøyaktig samme måte som ved en innlegging.
Kommer vi til en plass som inneholder verdi, så er saken klar. Hvis vi derimot kommer
til en ledig plass, kan vi gi opp. Men hvis plassen inneholder noe annet, «hopper» vi videre.
Hvis vi skal fjerne en verdi og har funnet den, får vi et problem hvis plassen markeres som ledig.
Plassen/indeksen kan jo ha inngått i «hopp»-serien for en annen verdi. Endres plassen
fra opptatt til ledig, ødelegges denne serien. En løsning kan være å ha tre
typer tabellplasser: 1) tom (markert med null), 2) opptatt (inneholder en verdi) og 3) ledig
(markert på en spesiell måte). Ved søking og fjerning hopper vi forbi
både opptatt og ledig, mens en innlegging kan skje både på en tom og en ledig plass.
Mer om dette senere.
Som nevnt over er det tre typer «hopp»-teknikker som er i bruk:
1. Lineær prøving (eng: linear probing) betyr at hvis verdiens «hashindeks»
er opptatt, så leter vi videre med fast «hopplengde» på 1. Se tabellen i
Figur 6.1.5 a). Vi så tidligere at
hvis Bodil skulle legges inn, ville det bli en kollisjon siden hennes «hashindeks» var 5.
Vi «hopper» da videre, først til 6, så til 7,
så til 8 og til 9 og der stopper vi. Bodil må legges inn på indeks 9 siden det er den første ledige plassen vi finner:
| Elin | Basir | Ole | Olga | Per | Mette | Ali | Bodil | Siri | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.5 b) : Lineær prøving - Bodil legges inn på indeks 9 | ||||||||||||
Allerede i dette lille eksempelet ser vi et av problemene med lineær prøving. Det er en tendens til at
verdier hoper seg opp. Det blir med andre ord lange intervaller med plasser som er opptatt. Det lengste
intervallet i Figur 6.1.5 b) er
på 5. Hvis en ny verdi har hashindeks fra 5 til 9, vil den havne på indeks 10. Da øker intervallet med en
og får lengde 6. Dette fenomenet kalles primær opphopning
(eng: primary clustering) og fører til at vi i gjennomsnitt må gjøre mange «hopp» for å finne
plassen til en ny verdi.
Det er mulig å tallfeste problemet med primær opphopning. La λ være hashtabellens tetthet.
Da kan det vises at i gjennomsnitt må omtrent
(1 + 1/(1 − λ)²)/2 indekser undersøkes for å finne plassen til en ny verdi.
I Figur 6.1.5 b) er
λ = 9/13 = 0,69 = 69%. En innlegging i en tabell med en slik tetthet skulle da
i gjennomsnitt kreve at 5,7 indekser måtte undersøkes. Hvis tabellen er tom, dvs. λ = 0, vil
formelen gi tallet 1. Ved søking
vil samme formel gjelde hvis verdien vi søker etter ikke er der. Hvis verdien derimot er der,
vil gjennomsnittet bli omtrent (1 + 1/(1 − λ))/2. Med λ = 0,69 blir det 2,1.
Det er enkelt å implementere lineær prøving, men den brukes normalt ikke. Den er ikke håpløst ineffektiv hvis tettheten holdes på et lavt nivå, f.eks. at den aldri overstiger 50%. Men siden det finnes andre og bedre teknikker, brukes de isteden.
2. Kvadratisk prøving (eng: quadratic probing) betyr at hvis «hashindeksen»
er opptatt, leter vi videre på en «kvadratisk» måte. Hvis i er hashindeksen,
forsøker vi med i + 1, så med i + 4, så
i + 9, så i + 16, osv. Nå er det ikke 1, 4, 9, 16, · · · som
er hopplengder. En hopplengde er avstanden mellom to plasser i rekken. Vi «hopper» fra i
til i + 1 (lengde 1), fra i + 1 til i + 4
(lengde 3), fra i + 4 og i + 9 (lengde 5), osv. Med
andre ord er det 1, 3, 5, 7, 9, osv. som er hopplengder.
Vi legger inn Ali, Anna, Bodil, Heidi, Olga og Per i en tabell med lengde 13. De har hhv. 8, 4, 9, 2, 5 og 6 som hashindekser. Alle er forskjellige. Dermed ingen kollisjoner så langt:
| Heidi | Anna | Olga | Per | Ali | Bodil | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.5 c) : 6 verdier er lagt inn - ingen kollisjoner | ||||||||||||
Hvis Bodil (hashindeks: 64358650 % 13 = 5) skal legges inn, får vi en kollisjon. Kvadratisk søking sier at neste mulighet er 5 + 1 = 6, men den er også opptatt. Så kommer 6 + 3 = 9. Forsatt opptatt. Da blir det 9 + 5 = 14. Men det er utenfor. Det blir isteden 14 % 13 = 1 og den er ledig. Bodil skal dermed legges på indeks 1:
| Bodil | Heidi | Anna | Olga | Per | Ali | Bodil | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Figur 6.1.5 d) : Kvadratisk prøving - Bodil er lagt inn på indeks 1 | ||||||||||||
Kvadratisk prøving fører ikke til primær opphopning slik som i
lineær prøving. Med andre ord er det uvanlig med lange intervaller av
plasser som er opptatt. Dermed vil i gjennomsnitt færre indekser
bli sjekket. Vi får isteden
sekundær opphopning (eng: secundary clustering). Hvis f.eks. en ny
verdi med hashindeks 5 skal inn, må vi følge samme letevei som sist og så minst et «hopp» til.
Men sekundær opphopning er et mindre alvorlig problem.
La λ være hashtabellens tetthet. I gjennomsnitt
må omtrent: 1/(1 − λ) − λ − log (1 − λ) indekser
sjekkes i kvadratisk prøving. Det betyr at i en hashtabell med samme tetthet som den i
Figur 6.1.5 d)
(7/13 = 0,54 = 54%), vil en innlegging i gjennomsnitt kreve at 2,5 indekser sjekkes.
For et mislykket søk gjelder samme formel, mens for et vellykket et gjelder omtrent:
1 − log (1 − λ) − λ/2. Med λ = 0,54 blir
det 1,5.
Lineær prøving vil, så sant det ikke er fullt, alltid føre til en ledig plass.
Men er det slik med kvadratisk prøving? Hvis Bill skal legges inn i tabellen i
Figur 6.1.5 d), blir det en kollisjon da
"Bill".hashCode() % 13 = 2070567 % 13 = 5. Med kvadratisk prøving blir hopplengdene fortløpende lik
1, 3, 5, 7, 9, 11, 13, 15, 17, osv. Flg. kode gir oss de aktuelle indeksene:
for (int i = 5, k = 1; k < 13; k++) // starter på i = 5 og gjør 12 hopp { i = (i + (2*k - 1)) % 13; // hopplengde 2*k - 1, dvs. 1, 3, 5, . . . System.out.print(i + " "); // indekser: 6 9 1 8 4 2 2 4 8 1 9 6 } Programkode 6.1.5 a)
Her ser vi noe som ikke er gunstig. Etter det 6. «hoppet» ( k = 6)
får vi samme indekser som før, men i motsatt rekkefølge. Hvis vi hadde gjort et hopp til
( k = 13), ville i ha blitt 5. Hvis vi da fortsetter
«hoppingen», kommer samme sekvens med indekser på nytt.
I Figur 6.1.5 d) er alle disse indeksene
opptatt. Med andre ord er det umulig å få plassert Bill med kvadratisk prøving. Dette problemet
gjelder ikke kun tabeller med lengde lik «ulykkestallet» 13. Det er slik for alle primtall.
Men heldigvis har vi flg. regel (et bevis finner du i Avsnitt 6.1.8):
Setning 6.1.5 a) La hashtabellen ha et odde primtall p
( p > 2) som lengde.
La n = (p − 1) / 2 og
i en indeks i tabellen. Da vil i og de n
første indeksene (n + 1 indekser) i kvadratisk prøving,
bli forskjellige. Det betyr at
hvis tabellens tetthet λ < 50%, vil vi alltid kunne finne en
ledig plass for en ny verdi.
I tilfellet p = 13 betyr det at hvis tabellen inneholder 6 eller færre verdier (den er mindre
enn halvfull), så
vil det ved kvadratisk prøving alltid bli funnet en plass til en ny verdi. Men hvis tabellen inneholder
7 eller flere verdier, gis det ingen garanti. Hvis hashindeksen til en ny verdi hører til en av de ledige
plassene, så kan verdien legges inn. Men dette gjelder ikke generelt. Tabellen i
Figur 6.1.5 d) inneholder 7 verdier
(tabellen er mer enn halvfull) og der var det ikke mulig å legge inn Bill ved hjelp av kvadratisk prøving.
Men hvis vi, eventuelt ved å utvide, sørger for at tabellen alltid er mindre enn halvfull, så vil det
fungere.
Men dette kan heldigvis gjøres smartere. Det var en som fant ut
(se Avsnitt 6.1.8) at hvis en bruker primtall
på formen p = 4k + 3, så er det nye muligheter. Legg merke
til at 13 ikke er på formen 4k + 3, men derimot på formen 4k + 1.
Vi prøver isteden med 11 = 4·2 + 3:
for (int i = 5, k = 1; k < 11; k++) // starter på i = 5 og gjør 10 hopp { i = (i + (2*k - 1)) % 11; // hopplengde 2*k - 1, dvs. 1, 3, 5, . . . System.out.print(i + " "); // indekser: 6 9 3 10 8 8 10 3 9 6 } Programkode 6.1.5 b)
Dessverre skjer det samme med 11 som med 13. Med i = 5 som startindeks vil
kvadratisk prøving deretter gi indeksene 6, 9, 3, 10, 8, 8, 10, 3, 9, 6. Med andre ord kun de 6
forskjellige indeksene 5, 6, 9, 3, 10 og 8. Men vi har en mulighet til. Det er å «hoppe» motsatt vei.
Starter vi med i = 5, får vi da 4, så 1, osv. Dette kan enkelt illustreres hvis vi tenker
oss tabellen formet som en sirkel:
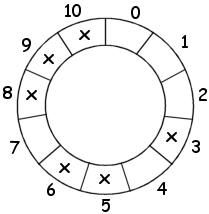 |
| Figur 6.1.5 e) |
I sirkelen til venstre er de 6 forskjellige indeksene vi fikk ved å starte med 5 og deretter gjøre (11 - 1)/2 = 5 hopp i «positiv» retning (med klokken) med hopplengder 1, 3, 5, 7 og 9, markert med et kryss. Hopper vi f.eks. videre fra 9 med hopplengde 5, kommer vi, ved å følge sirkelen med klokken, til indeks 3 (obs: 9 + 5 = 14 og 14 % 11 = 3).
Hvis vi isteden «hopper» motsatt vei («negativ» retning eller mot klokken) kommer vi, hvis vi starter i indeks 5, først til 4 siden 5 - 1 = 4. Fra 4 gjør vi et «hopp» med lengde 3, dvs. 4 - 3 = 1. Med andre ord kommer vi til indeks 1. Videre fra 1 skal vi ha en hopplengde på 5. Ved å følge sirkelen (mot klokken) kommer vi da til indeks 7. Så til 0 når vi «hopper» med en lengde på 7 videre fra 7. Til slutt bruker vi 9 som hopplengde videre fra 0 og da kommer vi til 2. Dermed har vi vært innom samtlige indekser. Dette gjelder ikke kun når vi starter i indeks 5. Uansett hvor vi starter vil 5 slike «hopp» med klokken (der hopplengden øker med 2 om gangen) og 5 tilsvarende «hopp» mot klokken, garantert «prøve» samtlige indekser.
Når dette skal kodes, må vi være påpasselige. Et «hopp» mot klokken får vi til ved å ta differensen mellom indeks og hopplengde. Men det kan gi et negativt tall og da kan vi ikke bruke Java's modulo-operator %. I flg. kode brukes 11 som primtall, 5 som startindeks og «hoppene» går vekselsvis med klokken og mot klokken:
int p = 11, indeks = 5; // p et primtall på formen 4k + 3 int i = indeks, j = indeks; // i med klokken, j mot klokken System.out.print(indeks + " "); // skriver ut startindeks for (int hopplengde = 1; hopplengde < p; hopplengde += 2) // 1, 3, 5, 7, 9 { if ((i += hopplengde) >= p) i -= p; // hopper med klokken if ((j -= hopplengde) < 0) j += p; // hopper mot klokken System.out.print(i + " " + j + " "); // Utskrift: 5 6 4 9 1 3 7 10 0 8 2 } Programkode 6.1.5 c)
Utskriften viser at indeksene fra 0 til 10 kommer én og bare én gang. Dette virker for alle primtall på
formen 4k + 3, men ikke for noen som er på formen 4k + 1. Se hva
som skjer hvis du f.eks. setter p = 13, p = 17,
p = 19 og p = 23 i Programkode 6.1.5 c). Prøv også med andre
startindekser enn 5.
3. Dobbelt hashing (eng: double hashing) betyr at hvis «hashindeksen»
er opptatt, så letes det videre med en «hopplengde» definert av en annen hashfunksjon.
I en hashfunksjon kan det bli utført relativt mye arbeid. F.eks. inneholder hashfunksjonen til
en String, hvis den er lang, et stort regnestykke. Derfor kan det være gunstig å bruke
den første hashverdien til å konstruere en fast hopplengde. Ta utgangspunkt i
Figur 6.1.5 a) der tabellen
har lengde 13. Vi kan bruke 11 som primtall nr. 2 og finne en hopplengde ved hjelp av det tallet.
Ta som eksempel at Bodil skal legges inn:
int p = 13, q = 11; // to primtall int h = "Bodil".hashCode() & 0x7fffffff; // hashverdi int i = h % p; // hashindeks int hopplengde = q - (h % q); // bruker q for (int k = 0; k < p; k++) // p ganger { System.out.print(i + " "); // skriver ut indeksen if ((i += hopplengde) >= p) i -= p; // hopper videre } // Utskrift: 5 12 6 0 7 1 8 2 9 3 10 4 11 Programkode 6.1.5 d)
Hadshindeksen i til Bodil er 5. Så brukes hashverdien h til å konstruere en hopplengde som
alltid er større enn 0 siden h % q alltid er mindre enn q. Maksimal
hopplengde blir q. Hvis indeks i er opptatt, vil vi ved å bruke denne faste hopplengden før eller
senere kommet til en ledig plass så sant tabellen ikke er full. Vi ser av utskriften at hopplengden
der ble 7 og at det må gjøres mange «hopp» før det kommer en ledig plass (indeks 2).
Denne idéen vil også virke for
søking og fjerning hvis vi der «hopper» på samme måte som ved en innlegging.
| 1. | Sjekk at alle indekser blir skrevet ut i
Programkode 6.1.5 c) når
p er et primtall på formen 4k + 3, f.eks. 19 og 23. Sjekk
at det skjer uansett hvilken startindeks som brukes (så lenge den går fra 0 til
p − 1. Sjekk så at hvis primtallet p er på
formen 4k + 1 (f.eks. 13, 17 og 29), så kommer det bare
(p + 1)/2 forskjellige indekser.
|
| 2. | Gitt en tabell med primtallet p som lengde. Hvis i er et ikke negativt
heltall, vil i % p gi en lovlig indeks i tabellen. Men det virker ikke
hvis i er negativ siden i % p da blir negativ.
I Programkode 6.1.5 c) brukes
en annen teknikk for i og j. Hvorfor virker det?
|
| 3. | Teknikken dobbelt hashing virker for alle primtall p som er
større enn 2. Se
f.eks. hva utskriften blir fra
Programkode 6.1.5 d) når
p = 17 og q = 13. Hva blir da hashindeksen for Bodil og hva
blir hopplengden? Hva blir indeksene til Olga, Basir, Ali, Per, Elin, Siri, Ole, Mette og Bodil
hvis de legges inn i den gitt rekkefølgen i en på forhånd tom String-tabell med lengde 17?
|
![]() 6.1.6 En implementasjon av åpen adressering
6.1.6 En implementasjon av åpen adressering
Vi har sett på tre ulike teknikker for kollisjonsbehandling ved
åpen adressering. Den første
(lineær prøving) er ugunstig
på grunn av primær opphopning. Den tredje
(dobbelt hashing) vil normalt gi best
spredning siden den hverken har primær eller sekundær opphopning. Den andre
(kvadratisk prøving) har sekundær opphopning,
men det er et mindre alvorlig problem. Alle tre er forholdsvis enkle å implementere.
Vi velger her kvadratisk prøving. Det
å lage en implementasjon som bruker dobbelt hashing, er
satt opp som øvingsoppgave.
Et problem som så vidt ble nevnt i forrige avsnitt, er at rekkefølgen av «hopp» blir brutt ved en fjerning. Teknikken sier at vi ved søking må følge den rekkefølgen av hopp som ble gjort ved innlegging. Det betyr at hvis vi da kommer til en ledig plass, så er det et signal om at verdien ikke finnes. Men hvis vi ved fjerning setter en plass som ledig, vil det kunne bryte hopprekkefølgen til en verdi som ble lagt inn senere. Ta som eksempel at vi skal legge inn Ove, Bodil, Ali, Mette, Kim og Ole i en tabell med plass til 11 verdier:
| Kim 1 | Ole 3 | Bodil 4 | Ove 5 | Ali 6 | Mette 9 | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Figur 6.1.6 a) : Seks verdier som ligger på sin egen indeks | ||||||||||
I figuren over har hvert navn fått navnets hashindeks som tilleggsindeks. Alle
har forskjellig hashindeks og ligger derfor på den plassen i tabellen som indeksen sier. Hvis vi
så skal legge inn Tone som har hashindeks 5, blir det en kollisjon. Ove ligger der. Kvadratisk prøving
sier (se Programkode 6.1.5 c)
at vi da skal sjekke indeksene 6, 4, 9, 1, 3, 7, 10, · · · og velge den første
av dem som er ledig. Det er indeks 7. Der skal Tone legges:
| Kim 1 | Ole 3 | Bodil 4 | Ove 5 | Ali 6 | Tone 5 | Mette 9 | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Figur 6.1.6 b) : Tone er lagt inn på indeks 7 | ||||||||||
Vi fjerner så Ali. Vi finner ham på hans hashindeks 6. Etterpå vil tabellen se slik ut:
| Kim 1 | Ole 3 | Bodil 4 | Ove 5 | Tone 5 | Mette 9 | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Figur 6.1.6 c) : Ali på indeks 6 er fjernet | ||||||||||
Men nå vil det ikke lenger være mulig å finne Tone. Siden hun har hashindeks 5, starter vi med å sjekke hva som ligger på den indeksen. Deretter følger vi hopprekkefølgen, dvs. vi går til indeks 6. Men den er ledig og det er et signal om at Tone ikke finnes. Det er mulig å finne Tone ved å gå gjennom hele tabellen, men det er ikke det som er poenget med hashing. Idéen er at vi normalt skal kunne finne en verdi ved å sjekke én eller noen få indekser.
En vanlig løsning på dette problemet er å markere på en spesiell måte at verdien på en plass er fjernet. Det betyr at den plassen da kan betraktes som ledig ved innlegging av en ny verdi, men som opptatt ved søking etter en verdi:
| Kim 1 | Ole 3 | Bodil 4 | Ove 5 | X | Tone 5 | Mette 9 | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Figur 6.1.6 d) : Verdien på indeks 6 er markert med X som betyr at verdien er fjernet | ||||||||||
Hvis tabellen skal være av typen T[] der T er en generisk type
(T kan f.eks. være String som i eksemplene), får vi et problem.
I en slik tabell kan vi kun skille mellom null og ikke null.
Da er det ikke mulig å markere en plass som fjernet, dvs. med en verdi som hverken er null eller ikke
null. Vi løser det imidlertid med å la det være en tabell av hashobjekter der hvert
objekt inneholder en verdi (av typen T) og verdiens hashverdi (et heltall):
private static final class HashObjekt<T> // en indre klasse { private final T verdi; // verdi av typen T private final int hashverdi; // hashverdien private HashObjekt(T verdi, int hashverdi) // konstruktør { this.verdi = verdi; this.hashverdi = hashverdi; } } // HashObjekt private final HashObjekt<T> x // et fast objekt = new HashObjekt<>(null, 0); // kun null-verdier private boolean ledig(int indeks) // ledig for innlegging { HashObjekt<T> o = hash[indeks]; // objektet på indeks return o == null || o == x; // sammenligner } Programkode 6.1.6 a)
Det er satt opp et fast objekt med det korte navnet x. Det bruker vi for å markere at en verdi
i tabellen er fjernet. Dermed kan en innlegging skje der verdien er null eller er lik
x (fjernet). Hjelpemetoden ledig() sjekker dette. Ved søking
(i metodene inneholder() og fjern())
må en plass med en x anses som opptatt, men uten verdi.
Med kvadratisk prøving må tabellen ha et
primtall på formen 4k + 3 som lengde. Vi må også kunne «utvide» tabellen når
tettheten blir for stor. Vi må derfor ha tilgang til en serie med primtall av den typen og der hvert av dem er
ca. det dobbelte av det foregående. Da bruker vi tallene som laget for lukket adressering
(se Programkode 6.1.4 h).
Klassen KvadratiskHashTabell skal ha flg. instansvariabler:
private HashObjekt<T>[] hash; // en tabell med hashobjekter private final float tetthet; // eng: loadfactor private int grense; // eng: threshold, norsk: terskel private int antall; // antall verdier private int iprim; // indeks i primtallstabellen Programkode 6.1.6 b)
Et klasseskjelett finner du under
KvadratiskHashTabell. Det er satt opp to
konstruktører. Standardkonstruktøren bruker 11 (et primtall på formen 4k + 3) som hashtabeldimensjon.
I den andre konstruktøren, som ikke er kodet, inngår tabelldimensjonen
som parameter. Det betyr at den reelle dimensjonen eventuelt må settes til noe annet enn parameterverdien.
For det første krever vi at dimensjonen ikke er negativ. For det andre bruker vi det
minste tallet fra primtallstabellen som er større enn parameterverdien, som reell dimensjon:
@SuppressWarnings({"rawtypes","unchecked"}) // en annotasjon
public KvadratiskHashTabell(int dim) // konstruktør
{
if (dim < 0) throw new IllegalArgumentException("Ulovlig dimensjon!");
for (; iprim < prim.length; iprim++) // leter i tabellen prim
{
if (dim <= prim[iprim]) break; // stopper her
}
dim = iprim < prim.length ? prim[iprim] : prim[iprim - 1];
hash = new HashObjekt[dim]; // bruker raw type
tetthet = 0.75f; // maksimalt 75% full
grense = (int)(tetthet * dim); // gjør om til int
antall = 0; // foreløpig ingen verdier
}
Programkode 6.1.6 c)
Hvis en bruker 0 eller 1 som dimensjon, vil 1 bli brukt. Men 1 er ikke primtall. Poenget er at det ikke skal være
nødvendig å bruke ekstra plass før det eventuelt skal legges inn noe. Dette ordnes derfor i
leggInn-metoden. Videre ser vi at hvis 11 inngår som parameter, vil tabellen få dimensjon 11. Men
hvis en bruker 12, vil dimensjonen isteden bli 19. Osv.
Ofte må en konvertere fra en datatype til en annen. Hvis det gjøres på feil måte, vil en få
ClassCastException under programkjøring. I utviklingsmiljøer
(f.eks. NetBeans og Eclipse) kan det komme meldinger
eller advarsler (eng: warning) om slike ting. Hvis en er helt sikker på at det en gjør er korrekt,
kan meldingen (eller advarselen) «undertrykkes» ved hjelp av annotasjonen SuppressWarnings.
I setningen:
hash = new HashObjekt[dim]
bes det om en konvertering fra «raw type» til HashObjekt<T>[].
«Raw type» betyr at det opprettes en tabell der datatypen er Object istedenfor T.
Dette er slik det må (og skal) gjøres. Derfor brukes annotasjonen her. Hvis du undersøker
Java-klassene i java.util, vil du se samme teknikk.
Metoden leggInn() skal legge verdien på den plassen som hashindeksen sier. Dette er klassens
viktigste metode. Hvis den inneholder feil, vil hverken søking eller
fjerning virke. I denne versjonen tillates det like verdier. Det er det imidlertid enkelt
å endre på. I så fall må leggInn() kodes slik at det letes etter verdien først.
Oppgaver i leggInn(T verdi):
- Kaste feilmelding hvis parameterverdien er
null - Utvide hashtabellen hvis den er minst 75% full
- Finn parameterverdiens hashverdi og hashindeks
- Lage et nytt hashobjekt
- Hvis hashindeks er ledig, legges hashobjektet der
- Hvis hashverdien ikke er ledig, må det letes kvadratisk etter en ledig plass. Da letes det vekselsvis med klokken og mot klokken.
- Hvis tabellen ikke er full, vil leteprosessen garantert stoppe på en ledig plass
De fire første kulepunktene handler om å lage et HashObjekt og de fire siste om å plassere objektet i
hashtabellen. Det vil være nyttig å ha en hjelpemetode som gjør det siste siden det må
gjøres om igjen når/hvis tabellen skal utvides:
// privat hjelpemetode som brukes i den offentlige leggInn-metoden private void leggInn(HashObjekt<T> o, int h) // h = hashindeks { HashObjekt<T>[] hash1 = hash; // hashtabellen int dim = hash1.length; // dimensjonen if (ledig(h)) hash1[h] = o; // legger inn else { for (int hopplengde = 1, v = h; ; hopplengde += 2) // øker med 2 { if ((h += hopplengde) >= dim) h -= dim; // med klokken if (ledig(h)) { hash1[h] = o; return; } // legger inn if ((v -= hopplengde) < 0) v += dim; // mot klokken if (ledig(v)) { hash1[v] = o; return; } // legger inn } } // else } // leggInn public boolean leggInn(T verdi) { Objects.requireNonNull(verdi, "verdi er null!"); // sjekker verdi if (antall >= grense) utvid(); // utvider int hverdi = verdi.hashCode() & 0x7fffffff; // fjerner fortegn int dim = hash.length; // tabellens dimensjon int h = hverdi % hash.length; // hashindeks HashObjekt<T> o = new HashObjekt<>(verdi, hverdi); // nytt hashobjekt leggInn(o, h); // legger inn antall++; // øker antallet return true; // vellykket innlegging } Programkode 6.1.6 d)
Nå er vi istand til å opprette en hashtabell og legge inn verdier. Men for å kunne sjekke at dette faktisk virker,
må vi kunne se hva som ligger der. Vi trenger en metode som skriver ut innholdet, dvs.
toString(). Vi lar den skrive ut i den rekkefølgen verdiene har i tabellen:
public String toString() { StringJoiner s = new StringJoiner(", ", "[", "]"); for (HashObjekt<T> o : hash) { if (o != null && o != x) s.add(o.verdi.toString()); } return s.toString(); } Programkode 6.1.6 e)
Flg. eksempel viser hvordan dette virker når åtte navn legges inn:
Beholder<String> hash = new KvadratiskHashTabell<>(); String[] navn = {"Ove","Bodil","Ali","Mette","Kim","Ole","Tone","Jon"}; for (String s : navn) hash.leggInn(s); // legger inn i hashtabellen System.out.println(hash); // skriver ut // Utskrift: [Kim, Ole, Bodil, Ove, Ali, Tone, Jon, Mette] Programkode 6.1.6 f)
Hvis vi forsøker å legge inn ett navn til, kommer det en UnsupportedOperationException. Med
11 som tabelldimensjon blir:
grense = (int)(tetthet * dim)
= (int)(0.75 * 11) = 8. Dermed blir utvid() kalt i
leggInn-metoden.
Men den er ikke kodet ennå. Da gjør vi det:
@SuppressWarnings({"rawtypes","unchecked"}) // en annotasjon
private void utvid() // utvidelsesmetode
{
if (iprim == prim.length - 1) return; // ingen utvidelse
HashObjekt<T>[] gammelhash = hash; // den gamle tabellen
hash = new HashObjekt[prim[++iprim]]; // en ny tabell
int dim = hash.length; // dimensjon
for (int i = 0; i < gammelhash.length; i++) // den gamle tabellen
{
HashObjekt<T> o = gammelhash[i]; // skal o legges inn?
if (o == x) gammelhash[i] = null; // nuller
else if (o != null) leggInn(o, o.hashverdi % dim); // legger inn
}
grense = (int)(tetthet * hash.length); // ny grense
}
Programkode 6.1.6 g)
Vi kan sjekke at metoden utvid() virker ved å gjenta eksemplet i
Programkode 6.1.6 f), men denne gangen
med flere verdier og med en liten startlengde på hashtabellen:
Beholder<String> hash = new KvadratiskHashTabell<>(0); // starter med 0 String[] navn = {"Ove","Bodil","Ali","Mette","Kim","Ole","Tone","Jon","Unn"}; for (String s : navn) hash.leggInn(s); // legger inn i hashtabellen System.out.println(hash); // skriver ut // Utskrift: [Ole, Bodil, Ali, Kim, Unn, Ove, Tone, Jon, Mette] Programkode 6.1.6 h)
Metoden fjern(T verdi) må (ved kvadratisk søking) finne verdien og så
erstatte objektet med x
(«signalet» at verdien er fjernet).
Metoden inneholder(T verdi) må finne verdien og i leteprosessen «hoppe over»
de som er «fjernet». Hvis det er fjernet mange uten at nye er lagt inn (mange
x-er i tabellen),
vil det redusere effektivteten. Se øvingsoppgavene.
Klassen skal ha en iterator. Teknikken blir omtrent den samme som den som er brukt i klassen
TabellListe.
Forskjellen er at her må vi hoppe over null-objekter og objekter som er fjernet
(markert med x) når vi leter videre
etter neste verdi. Rekkefølgen av verdier blir den samme som i metoden
toString():
public Iterator<T> iterator() { return new KvadratiskHashTabellIterator(); } private class KvadratiskHashTabellIterator implements Iterator<T> { private int i = 0; // tabellindeks starter i 0 private KvadratiskHashTabellIterator() // konstruktør { // flytter tabellindeks i til første objekt - hopper over null og x while (i < hash.length && (hash[i] == null || hash[i] == x)) i++; } public boolean hasNext() { return i < hash.length; // er i innenfor tabellen? } public T next() { if (!hasNext()) throw new NoSuchElementException("Ingen flere verdier"); T verdi = hash[i].verdi; // flytter tabellindeksen i videre - hopper over null og x while (++i < hash.length && (hash[i] == null || hash[i] == x)); return verdi; } } // Iterator Programkode 6.1.6 i)
Klassen KvadratiskHashTabell er en
Beholder og er dermed Iterable.
Det betyr at vi kan traversere innholdet ved hjelp av en for-alle-løkke (da er det egentlig iteratoren som brukes):
Beholder<String> hash = new KvadratiskHashTabell<>(); String[] navn = {"Ove","Bodil","Ali","Mette","Kim","Ole","Tone","Jon","Unn"}; for (String s : navn) hash.leggInn(s); // legger inn i hashtabellen hash.forEach(s -> System.out.print(s + " ")); // en type for-alle-løkke System.out.println(); // linjeskift for (String s : hash) System.out.print(s + " "); // en annen for-alle-løkke // [Ole, Bodil, Ali, Kim, Unn, Ove, Tone, Jon, Mette] // [Ole, Bodil, Ali, Kim, Unn, Ove, Tone, Jon, Mette] Programkode 6.1.6 h)
| 1. | Det som er kodet til nå finner du under
KvadratiskHashTabell. Tre metoder gjenstår: |
i) public boolean fjern(T verdi) Metoden skal
fjerne objektet som inneholder verdi (hvis det finnes) og erstatte det med
objektet x (det som signaliserer
at objekter er fjernet). Hvis et objekt ble fjernet, skal metoden returnere true
(og false ellers). Hvis det finnes flere objekter som inneholder
verdi, skal kun ett av dem fjernes. |
|
ii) public boolean inneholder(T verdi) Metoden skal
returnere true hvis det finnes et objekt som inneholder verdi
og returnere false ellers. |
|
iii) public void nullstill() Metoden skal tømme tabellen,
dvs. alle tabellelementene settes til null og variabelen antall settes til 0. |
|
| 2. | Lag metoden public void remove() i
KvadratiskHashTabellIterator.
Den skal fjerne verdien (objektet) som ble returnert ved sist kall på next().
Reglene for unntak
står i Tabell 3.1.1.
La boolean fjernOK
være en privat instansvariabel i iteratorklassen og la den ha false som
startverdi. Den settes til
true i next(). I remove() sjekkes den. Hvis den
er false kastes en IllegalStateException. Hvis ikke, settes den til false.
|
| 3. | Når en iterator settes i gang, har hashtabellen et bestemt innhold. Dermed er
det formelt sett forutsigbart hvilke verdier iteratoren vil levere. Men forutsigbarheten
ødelegges hvis det skjer endringer i tabellen etter at iteratoren har startet. En måte å hindre
dette på er å legge inn en privat instansvariabel
int endringer i
KvadratiskHashTabell og en privat instansvariabel
int iteratorendringer i
iteratorklassen. Den siste settes lik den første som utgangspunkt. I de metodene i
KvadratiskHashTabell der det er endringer (såkalte mutatorer) økes
endringer med 1. I både next() og
remove() i iteratoren sammenlignes de to variablene. Hvis de er ulike,
kastes en ConcurrentModificationException. Metoden remove()
fjerner den som sist ble returnert av next(). En slik fjerning er ok
siden iteratoren allerede har vært innom den verdien. I remove() skal
derfor begge de to endringsvariablene økes med 1.
|
| 4. | I klassen KvadratiskHashTabell er det tillatt med duplikater, dvs. at samme verdi
kan legges inn flere ganger. Det er metoden leggInn() som styrer dette. Lag en
ny versjon av leggInn() der dupikater stoppes. Dvs. hvis en verdi allerede ligger
i hashtabellen, skal den ikke legges inn på nytt og metoden skal da returnere false.
|
| 5. | Et problem med KvadratiskHashTabell er at en traversering (ved hjelp av iteratoren)
eller en utskrift (toString-metoden) gir et uforutsigbart resultat mhp.
rekkefølgen av verdiene. Ved
kollisjon vil en verdi havne på annet sted. Videre vil verdiene bli omplassert ved tabellutvidelser.
La HashObjekt ha en
neste-peker og klassen et hode
og en hale. Dette for å kunne lenke sammen objektene til en
enkeltlenket liste. Ved hver innlegging skal da tilhørende HashObjekt havne
bakerst i listen. Dermed kan iteratoren og toString kodes slik at verdiene kommer
i samme rekkefølge som de ble lagt inn. Det er best å lage en ny klasse med denne idéen,
f.eks. med navn LenketKvadratiskHashTabell. Metoden fjern()
vil også bli påvirket av dette.
|
| 6. | Lag klassen DobbeltHashTabell. Den skal virke som KvadratiskHashTabell, men
bruke dobbelt hashing
istedenfor kvadratisk søking.
Hvis primtallet p er tabellengde, kan en bruke primtallet rett foran
p i tabellen prim som primtallet q i den andre hashfunksjonen.
Da vil q = 3 hvis p = 7, q = 7 hvis
p = 11, q = 11 hvis p = 19, osv.
|
![]() 6.1.7 Hashing i Java
6.1.7 Hashing i Java
I Java er det mange klasser som benytter hashing:
HashSet(subtype avSetog dermed avCollection)LinkedHashSet(subtype avHashSet)Hashtable(subtype av bådeDictionaryogMap)HashMap(subtype av bådeAbstractMapogMap)IdentityHashMap(subtype av bådeAbstractMapogMap)LinkedHashMap(subtype tilHashMap)
HashSet
virker på samme måte som «våre» klasser,
dvs. som KvadratiskHashTabell
og HashTabell.
De metodene som brukes mest, er:
int size(); antall boolean isEmpty(); tom boolean add(T e); leggInn boolean contains(Object o); inneholder boolean remove(Object o); fjern void clear(); nullstill String toString(); toString Iterator<T> iterator(); iterator() Programkode 6.1.7 a)
HashSet
bruker lukket adressering
med separat kjeding, men bruker ikke primtall som
tabelldimensjon. Startdimensjonen er (hvis ikke noe annet er oppgitt) 16. Hvis det så, etter innlegginger,
blir for stor tetthet, dobles tabellen - først til 32, så til 64, osv. Med slike tall
kan en hashverdi konverteres til en indeks på en «billig» måte.
Hvis n er tabellens dimensjon (av typen over), så vil:
(n - 1) & hashverdi gi samme indeks
som: hashverdi % n:
int n = 1 << 4; // n = 16, << = bitshift int hashverdi = "Kari".hashCode(); // en hashverdi int indeks1 = hashverdi % n; // modulo-operatoren int indeks2 = (n - 1) & hashverdi; // og-operatoren System.out.println(indeks1 + " " + indeks2); // Utskrift: 13 13 Programkode 6.1.7 b)
Her er det et problem. Med n = 2k vil kun de k siste bitene i
hashverdi bestemme indeksen. De øvrige bitene har ingen betydning. Det betyr at alle
hashverdier som er like på de k siste bitene, vil gå til samme indeks. Men slik er
det ikke hvis en bruker primtall. Da vil alle bitene i en hashverdi være med på å bestemme indeksen
når vi bruker modulo (resten ved divisjon). De som har laget
HashSet
har derfor valgt å «bearbeide» hashverdien først slik at også de 16 første bitene (av de 32) får
betydning, dvs. slik:
int n = 1 << 4; // n = 16, << = bitshift int hashverdi = "Kari".hashCode(); // en hashverdi hashverdi ^= (hashverdi >>> 16); // ^ = xor, >>> = bitshift int indeks = (n - 1) & hashverdi; // de fire siste bitene System.out.println(indeks); // Utskrift: 14 Programkode 6.1.7 c)
HashSet tillater
null-verdier, men ikke duplikater. Hvis en forsøker (f.eks. ved add-metoden) å legge inn en verdi
som finnes fra før, vil den ikke bli lagt inn og metoden returnerer false. To verdier
a og b vil her bli sett på som like (som duplikater) hvis og bare hvis
de er like mhp. både equals() og hashCode().
HashSet<String> h = new HashSet<>(); // oppretter tabellen System.out.println(h.add(null)); // returnerer true System.out.println(h.add("Kari")); // returnerer true System.out.println(h.add("Kari")); // returnerer false - duplikat System.out.println(h); // Utskrift: [null, Kari] Programkode 6.1.7 d)
Et problem med hashtabeller er at en traversering (ved hjelp av iteratoren) eller en utskrift (toString-metoden), gir et uforutsigbart resultat mhp. rekkefølgen. Hvis en bruker åpen adressering, vil verdier ved kollisjoner havne på andre steder. Videre vil alle verdiene bli omplassert når tabellen utvides. Også ved lukket adressering blir verdiene omplassert ved tabellutvidelser. Se på flg. eksempel:
HashSet<String> h = new HashSet<>(4); // oppretter tabellen String[] navn = {"Elin","Ole","Berit"}; // tre navn for (String s : navn) h.add(s); // legger inn System.out.println(h); // [Elin, Ole, Berit] h.add("Jens"); // legger inn Jens System.out.println(h); // [Ole, Berit, Jens, Elin] Programkode 6.1.7 e)
Ved første utskrift kom Elin først, men så sist i neste utskrift. Det kommer av at tabellen har blitt utvidet fra lengde 4 til
lengde 8. Hvis det er viktig at at verdiene kommer ut i samme rekkefølge som de ble lagt inn, kan en bruke klassen
LinkedHashSet.
Der har nodene fått en ekstra sammenlenkning. En ny verdi havner alltid bakerst i den lenken:
Set<String> h = new LinkedHashSet<>(4); // oppretter tabellen String[] navn = {"Elin","Ole","Berit"}; // tre navn for (String s : navn) h.add(s); // legger inn System.out.println(h); // [Elin, Ole, Berit] h.add("Jens"); // legger inn Jens System.out.println(h); // [Elin, Ole, Berit, Jens] Programkode 6.1.7 f)
Klassen HashMap<K,V>
er en Map<K,V> og dermed
heter de vanlige metodene:
int size(); // antall boolean isEmpty(); // tom V put(K key, V value); // legger inn V get(Object key); // henter boolean containsKey(Object key); // søker etter nøkkel boolean containsValue(Object value); // søker etter verdi V remove(Object key); // fjerner void clear(); // nullstiller Programkode 6.1.7 g)
Klassene HashSet og
HashMap er
egentlig laget på samme måte eller rettere sagt er HashSet laget ved hjelp av HashMap.
Når verdi legges inn (add-metoden) i en HashSet, er det egenlig put i
HashMap som brukes. Da går verdi inn som key, mens
value blir satt til en fast verdi (en konstant) med navn PRESENT. Men dette ser ikke vi når vi bruker
HashSet. Det foregår bak «kulissene». Det betyr at HashSet bruker mer plass enn
egentlig nødvendig.
Det er er tillatt å ha null både som nøkkel (key) og verdi (value) i en HashMap. En
nøkkel må være entydig, dvs. hvis en legger inn ( put ) et par nøkkel/verdi der nøkkel allerde finnes, blir den gamle
verdien erstattet med den nye og den gamle returnert. Første gang en nøkkel blir brukt returneres null:
HashMap<String,String> map = new HashMap<>(); // en map System.out.println(map.put(null, null)); // Utskrift: null System.out.println(map.put("Kari", "Jensen")); // Utskrift: null System.out.println(map.put("Kari", "Olsen")); // Utskrift: Jensen System.out.println(map); // Utskrift: {null=null, Kari=Olsen} Programkode 6.1.7 h)
HashMap har ingen iterator. Men mengden av nøkkelverdier, og av tilhørende verdier, har en iterator.
Se Oppgave 2. Men vi kan traversere ved hjelp av
metoden forEach(). Den har en
BiConsumer
som argument. (Se også Programkode 1.9.2 d.)
I flg. eksempel oppretter vi en kobling, mellom personer (navn) og karakterer på en bestemt eksamen, ved hjelp av en map.
Deretter lages en tegnstreng ved hjelp av forEach() og
en StringJoiner:
String[] navn = {"Per","Kari","Ole","Åse","Jens","Elin","Ali"};
Character[] karakter = {'F','C','E','D','F','A','B'};
Map<String,Character> map = new HashMap<>(); // en map
int i = 0;
for (String s : navn) map.put(s, karakter[i++]); // bygger opp
StringJoiner sj = new StringJoiner(", "); // en StringJoiner
map.forEach((s,k) -> sj.add(s + " -> " + k)); // legger inn
System.out.println(sj); // skriver ut
// Jens -> F, Åse -> D, Ole -> E, Per -> F, Elin -> A, Kari -> C, Ali -> B
Programkode 6.1.7 i)
Klassen HashMap har flere andre metoder enn forEach() der funksjonsobjekt/er inngår
som argument (BiConsumer i forEach). Eksempelet over var fra en tenkt eksamen. Det kan se ut som at det gikk dårlig siden
det var mange svake resultater - f.eks. F (stryk), E og D. Det kan skyldes at oppgavene var for vanskelige. Her
sier vi at det var tilfellet og at karakterene derfor skal justeres. Alle skal få sin karakter satt opp én enhet, dvs.
de som har fått F skal isteden få E, osv. Men de som har fått A, må bli stående på samme karakter. Det er ikke noe som
er bedre enn A.
Oppgaven er derfor å gjøre om vår map slik at den inneholder de justerte resultatene.
Men vi skal ikke gjøre det ved å justere tabellen karakter. Vi skal justere «mappen».
Først gjør vi det på en konvensjonell måte - uten bruk av funksjonell programmering (dvs. med teknikk fra før Java 1.8).
Flg. kode er en fortsettelse av
Programkode 6.1.7 i):
for (String s : map.keySet()) // går gjennom alle nøkkelverdiene { Character k = map.get(s); // henter karakteren og justerer if (k != 'A') map.replace(s, (char)(k - 1)); // om nødvendig } Programkode 6.1.7 j)
En mer «moderne» mulighet er f.eks. å bruke metoden compute() fra HashMap.
Den har to argumenter. Først en nøkkelverdi og så en
BiFunction.
En BiFunction er som navnet sier, en funksjon med to argumenter. I vårt tilfelle skal den
(som første argument) ha en «nøkkel» i form av et navn og så en karakter (den som hører til nøkkelen). Funksjonverdien
(returen) er den nye karakteren til nøkkelen. I flg. kode brukes et lambda-uttrykk som BiFunction:
for (String s : map.keySet()) // går gjennom alle nøkkelverdiene { map.compute(s, (n,k) -> (k != 'A') ? (char)(k - 1) : k); } Programkode 6.1.7 k)
Hvilken av Programkode 6.1.7 j) og k) er best? Det er nok
j) som er enklest å forstå. Der står det direkte hva som skjer. Men k)
er nok noe mer effektiv. I j) må objektet som har s som nøkkelverdi,
finnes to ganger - både i get() og i replace(), mens i k)
skjer endringen mens en har tak i objektet. Sjekk hvordan compute() er kodet i HashMap!
| 1. | Sjekk at Programkode 6.1.7 j) og
k) gir samme resultat. |
| 2. | HashMap
har ingen iterator, men mengden av alle nøkkelverdier utgjør en Set og den
har en iterator. Den brukes implisitt (for-løkken) i
Programkode 6.1.7 j) og
k).
Mengden av alle verdier utgjør en Collection og den har en iterator.
Lag kode som bruker den til å skrive ut alle verdiene. |
| 3. | Klassen LinkedHashMap
er en subklasse til klassen HashMap,
men med det tillegget at itereringsmetodene henter nøkkelverdiene i den rekkefølgen de ble lagt inn. Bruk den
i Programkode 6.1.7 i)!
|
| 4. | HashMap
har flere metoder som bruker funksjonsobjekter (funksjonell programmering). F.eks.
computeIfAbsent(), computeIfPresent(), merge()
og removeAll(). Når kan disse brukes? Lag eksempler!
|
| 5. | Typen Map<K,V>
er generisk. Det betyr at vi nesten kan velge hva som helst som konkrete typer for K og V.
I eksemplene over ble karakterer koblet til personer. Men en person kan jo ha flere karakterer og de kan
legges i en liste. Gitt en tabell med navn (personer) og en todimensjonal tabell med karakterer (bokstaver).
Karakterene i første rad hører til første person i navnetabellen, osv. En map der
K er String og V er List<Character> er satt opp.
Lag kode som bygger opp «mappen»! Bruk den listetypen du finner enklest. Lag så kode
som finner (og skriver ut) de (kun navnet) som har fått minst én A.
String[] navn = {"Per","Kari","Ole","Åse","Jens","Elin"};
Character[][] kar = {{'E','C'},{'A','B','A'},{},{'B'},{'D','E','F'},{'A'}};
Map<String,List<Character>> map = new HashMap<>();
|
![]() 6.1.8 Algoritmeanalyse - kvadratisk søking
6.1.8 Algoritmeanalyse - kvadratisk søking
Gitt en hashtabell med lengde p der p er et primtall større enn 2.
La h være hashindeksen til et objekt. Hvis indeks h er opptatt,
må vi finne et annet sted å legge objektet. Kvadratisk søking går ut på at vi da først prøver med
indeks h + 1, så med h + 4, så h + 9, osv.
Vi må imidlertid passe på at vi ikke går ut av tabellen. Derfor brukes generelt
(h + i²) mod p
for i = 1, 2, 3, osv. Men får vi på denne måten alle indeksene i tabellen?
Svaret er dessverre nei. Men heldigvis er den første halvparten av dem forskjellige.
La k være lik
(p − 1)/2. La i og j være
slik at 1 ≤ i < j ≤ k. Anta at
(h + j²) mod p =
(h + i²) mod p. Det betyr at p går opp
i (h + j²) − (h + i²).
Dette kan vi utvikle videre til:
(6.1.8.1) (h + j²) − (h + i²)
= j² − i²
= (j − i)(j + i)
Men, siden 1 ≤ i < j ≤ k, vil
1 ≤ j − i < p og
1 ≤ j + i < p. Men p er et primtall
og kan ikke gå opp i
(j − i)(j + i). I så fall måtte
p gå opp i j − i eller i
j + i. Men det er umulig. Dette betyr at
(h + j²) mod p ≠
(h + i²) mod p. Med andre ord vil de
k første indeksene av typen (h + i²) mod p
være forskjellige. Hvis tabellen er mindre enn halvfull, så vil dette helt sikkert føre til
en ledig plass. Men hvis den er mer enn halvfull, er ingen garanti.
Hva slags indeksverdier får vi hvis vi forsetter med i-er etter k, dvs. indekser
(h + i²) mod p for i > k?
Vi bruker h = 0 og p = 13 som eksempel. Da blir
k = (13 − 1)/2 = 6. Dette gir at i² mod 13
for i = 1, 2, . . , 6 blir
lik 1, 4, 9, 3, 12, 10. De er som forventet forskjellige. Men hvis vi fortsetter med
i = 7, 8, . . , 12, får vi 10, 12, 3, 9, 4, 1. Med andre ord det samme som sist, men
i motsatt rekkefølge. Dette er ikke tilfeldig. Generelt blir det som dette:
La k = (p − 1)/2. Da blir
k + 1 = (p + 1)/2. La m være
et ikke negativt heltall (dvs. m ≥ 0). La i =
k − m og j =
k + 1 + m. Da vil
(h + j²) mod p =
(h + i²) mod p
fordi (h + j²) − (h + i²)
= j² − i² =
(j − i)(j + i)
= (2m + 1)(2k + 1) = (2m + 1)p.
Dette betyr at det som ble vist i eksemplet med p = 13, gjelder generelt.
Lar vi i gå fra 1 til p − 1, vil
(h + i²) mod p først gi k
forskjellige indekser og så kommer de samme indeksene på nytt, men i motsatt rekkefølge.
Men vi har enda en mulighet. Vi kan gå motsatt vei, dvs. se om noen av indeksene
h − 1, h − 4, h − 9, osv.
(eller generelt
(h − i²) mod p)
er ledige. Får vi da andre indekser enn før? For å kunne avgjøre det må vi bruke ideer fra tallteori.
La mengdene A, B og P være gitt ved:
A = {(h + i²) mod p | i = 1, 2, . . . , k}, k = (p − 1)/2, 0 ≤ h ≤ p − 1
B = {(h − i²) mod p | i = 1, 2, . . . , k}, k = (p − 1)/2, 0 ≤ h ≤ p − 1
P = {0, 1, . . . , h − 1, h + 1, . . . , p − 1}
Som vist over er det k forskjellige tall i A.
Legg merke til at hashindeks h ikke er i A. Hvis den var,
måtte h ≡ h + i² (mod p),
dvs. i² ≡ 0 (mod p).
Men det er er umulig siden i < p.
Mengden B inneholder også k = (p − 1)/2
forskjellige tall fra P (samme bevis som for A).
Setning 1.6.8 a)
La p > 2 og r ∈ P.
Da er
r ∈ A hvis og bare hvis
(r − h)k ≡ 1 (mod p).
Bevis La r ∈ A, dvs.
r ≡ h + i² (mod p),
1 ≤ i ≤ k. Det gir
r − h ≡ i² (mod p)
og dermed at
(r − h)k ≡ i2k (mod p).
Siden p ikke går opp i i, sier Fermats teorem
at i p − 1 ≡ 1 (mod p).
Men i p − 1 = i2k
og dermed får vi (r − h)k ≡ 1 (mod p).
Omvendt sier Lagranges teorem at ligningen
xk ≡ 1 (mod p) kan ha maksimalt
k løsninger modulo p. Det betyr at det ikke finnes andre tall r
∈ P
enn de fra A som oppfyller
(r − h)k ≡ 1 (mod p).
Setning 1.6.8 b)
La p > 2 og r ∈ P.
Da er
r ∉ A hvis og bare hvis
(r − h)k ≡ −1 (mod p).
Bevis La r ∈ P. Da er
r − h ≠ 0 siden h ∉ P.
Største verdi for r er p − 1 og minste verdi for h er 0.
Dermed r − h ≤ p − 1. Tilsvarende
får vi at −(p − 1) ≤ r − h.
Dette betyr at p ikke kan gå opp i r − h
og dermed at (Fermats teorem) p går opp i
(r − h) p − 1 − 1
= (r − h) 2k − 1
= ((r − h) k − 1)((r − h) k + 1).
Altså må p gå opp i (r − h) k − 1 eller
i (r − h) k + 1, men ikke i begge.
I så fall: (r − h) k
≡ 1 (mod p) og
(r − h) k
≡ −1 (mod p) og dermed
1 ≡ −1 (mod p). Umulig siden p > 2.
Konklusjon: r ∉ A hvis og bare hvis
(r − h)k ≡ −1 (mod p).
Setning 1.6.8 c) (Radke)
La p være et primtall.
- Hvis
p≡ 1 (mod 4), så er mengdeneAogBlike. - Hvis
p≡ 3 (mod 4), så er mengdeneAogBdisjunkte, dvs.A∩B= ∅ ogA∪B=P.
Bevis La s ∈ B, dvs.
s ≡ h − i² (mod p)
eller s − h ≡ −i² (mod p).
Det gir oss
(s − h)k ≡
(−1)k i 2k (mod p)
≡ (−1)k i p − 1 (mod p)
≡ (−1)k (mod p).
Siste likhet får vi av at siden p ikke går opp i i p − 1,
vil (Fermats teorem) p gå opp i
i p − 1 − 1, dvs.
i p − 1 ≡ 1 (mod p).
I tilfelle 1. blir k = (p − 1)/2 et partall og dermed
(s − h) k ≡ 1 (mod p), dvs.
s ∈ A. Det betyr at
B ⊂ A og dermed A = B
siden de har like mange elementer.
I tilfelle 2. blir k et oddetall og dermed
sk ≡ −1 (mod p), dvs.
s ∉ A. Dermed A ∩ B = ∅
og A ∪ B = P.
Viktige definisjoner og setninger for kongruensregning
Definisjoner:
- (Divisjonsalgoritmen) La
avære et heltall ogdet positivt heltall. Da finnes det entydige heltallqogrslik at 0 ≤r<doga=qd+r. Her kallesqfor kvotienten ogrfor resten ved divisjonen. Vi sier atdgår opp ia(eller ataer delelig medd) hvisr= 0. - Uttrykket
amodder definert som restenri divisjonsalgoritmen. Hvisdikke går opp ia(hvisr≠ 0), så er (−a) modd=d− (amodd). a≡b(modd) hvis og bare hvisdgår opp ia−b.
Regneregler:
- Hvis
m> 0,a≡b(modm) ogc≡d(modm), så era + c≡b + d(modm). - Hvis
m> 0,a≡b(modm) ogc≡d(modm), så erac≡bd(modm). - Hvis
m> 0,k> 0 oga≡b(modm), så erak≡bk(modm). - Hvis
m> 0,mikke går opp icogac≡bc(modm), så era≡b(modm).
Setning 1.6.8 d) - Fermats teorem La p være et primtall og a
et heltall slik at p ikke går opp i a. Da er
a p − 1 ≡ 1 (mod p).
Bevis La P = {1, 2, . . . , p − 1} og
A = {ai mod p | i ∈ P }.
Tallene i A er forskjellige. Hvis ikke, må det finnes i og j
med i < j slik at aj mod p =
ai mod p. Da må p gå opp i
aj − ai = a(j - i).
Men p går hverken opp i a eller i j - i.
Derfor er det for hver i ∈ P en i' ∈ P
slik at i ≡ ai' (mod p). Produktet av
i'-ene er c = 1 · 2 · . . . · p - 1.
Dermed c ≡
a p − 1 c
(mod p) og a p − 1 ≡
1 (mod p).
Setning 1.6.8 e) - Lagranges teorem
La p være et primtall og
f(x) et n-te grads
polynom der koeffisientene er hele tall som
ikke alle er delelig med p. Da har kongruensligningen
f(x) ≡ 0 (mod p) maksimalt
n forskjellige røtter modulo p.
Bevis Legg merke til at teoremet sier at kongruensligningen
kan ha maksimalt n forskjellige røtter modulo p. Det betyr
at den kan ha færre enn n og også ingen.
Et induksjonsbevis. i) La n = 1. Da må
ligningen være på formen
a x + b ≡ 0 (mod p).
Hvis p ikke går opp i a, er det én løsning modulo p.
Siden gcd (a,p) = 1, finnes det hele tall
s og t slik at sa
+ tp = 1. Dermed vil
x ≡ sb (mod p)
være en løsning. Det er den eneste modulo p. For hvis x og y er to løsninger,
dvs. a x + b ≡ 0 (mod p)
og a y + b ≡ 0 (mod p),
så må vi ha a(x − y) ≡ 0 (mod p).
Da må p gå opp i x − y siden
p ikke går opp i a. Det betyr at
x ≡ y (mod p).
Hvis derimot p går opp i a,
er det ingen løsning. For hvis det hadde vært en løsning, måtte p gå opp i b,
men det er i strid med forutsetningen. Dette betyr at Lagranges teorem stemmer for n = 1.
ii) La n være større enn 1. Hvis f(x) ikke
har noen røtter modulo p, er det ingenting å bevise. Vi kan derfor anta at
f(x) har minst én rot
x ≡ a (mod p). En polynomdivisjon gir oss et
polynom q(x) og et heltall r slik at
f(x) = (x − a) q(x) + r
Men siden a er en rot modulo p, dvs. f(a) ≡ 0 (mod p),
må r ≡ 0 (mod p). Følgelig er
f(x) = (x − a) q(x) ≡ 0 (mod p).
Hvis x ≡ b (mod p) er en annen rot i
f(x), så er
0 ≡ f(b) = (b − a) q(b) (mod p)
Men siden a er forskjellig fra b modulo p, vil q(b) ≡ 0 (mod p).
Polynomet har grad n − 1 og har minst én koeffisient som p ikke går opp i.
Hvis ikke, måtte alle koeffisientene til f være delelig med p.
Induksjonshypotesen gir derfor at q(x) har maksimalt n − 1
røtter modulo p. Dermed har f(x) maksimalt n
røtter modulo p.
Korollar 1.6.8 f) Hvis n går opp i p − 1,
vil x n ≡ 1 (mod p) ha nøyaktig n
røtter.
Bevis Da n går opp i p − 1, finnes
m slik at p − 1 = mn og
da kan x p − 1 − 1 faktoriseres slik:
x p − 1 − 1 =
(x n − 1)(x n(m-1)
+ x n(m-2) + . . . +
x n + 1)
Siden p ikke går opp i noen av tallene fra 1 til p − 1,
sier Fermats teorem at hvert av dem er en rot
i polynomet x p − 1 − 1. Med andre
ord har polynomet p − 1 røtter modulo p. De to polynomene
på høyre side i faktoriseringen av x p − 1 − 1
har, i henhold til Lagranges teorem, maksimalt henholdsvis n og n(m − 1)
røtter. Men skal vi få det samme på begge sider må siden
p − 1 = n + n(m − 1),
de to polynomene på høyre side ha nøyaktig n og n(m − 1)
røtter. Med andre ord har x n ≡ 1 (mod p) nøyaktig n
røtter.
Korollar 1.6.8 g) Hvis p ≡ 1 (mod 4), så har
x 2 ≡ −1 (mod p) en løsning.
Bevis La p =
4 m + 1. Dermed blir p − 1 = 4 m og
x p − 1 − 1 =
(x 2m − 1)(x 2m + 1).
Fermats teorem sier at x p − 1 − 1 har nøyaktig
p − 1 = 4 m røtter modulo p. Hvert av de to polynomene
(x 2m − 1) og
(x 2m + 1) har iflg. Lagranges teorem maksimalt
2m røtter og da de ikke kan ha noen felles, må derfor begge ha nøyaktig 2m røtter.
La derfor x ≡ a (mod p) være en løsning av
x 2m + 1, dvs.
(a m ) 2 ≡ −1 (mod p).
Dvs. x ≡ a m (mod p)
blir en rot i x 2 ≡ −1 (mod p).
Eksempel La p = 5.
Korollar 1.6.8 g) sier at
x 2 ≡ −1 (mod 5) har en løsning. Det sier
ikke noe om hvordan vi kan finne den. Vi får prøve oss frem. Legg merke til at 4 ≡ −1 (mod 5).
Vi har 02 ≡ 0 (mod 5),
12 ≡ 1 (mod 5), 22 ≡ 4 ≡ −1 (mod 5),
32 ≡ 9 ≡ 4 ≡ −1 (mod 5) og til slutt
42 ≡ 16 ≡ 1 (mod 5). Med andre ord har x 2 ≡ −1 (mod 5)
både 2 og 3 som røtter.
La så p = 7. Da er p ≡ 3 (mod 4).
Korollar 1.6.8 g) kan ikke brukes
for x 2 ≡ −1 (mod 7). Vi prøver oss frem.
Husk at 6 ≡ −1 (mod 7). Vi har 02 ≡ 0 (mod 7), 12 ≡ 1 (mod 7),
22 ≡ 4 (mod 7), 32 ≡ 9 ≡ 2 (mod 7),
42 ≡ 16 ≡ 2 (mod 7), 52 ≡ 25 ≡ 4 (mod 7) og
62 ≡ 36 ≡ 1 (mod 7). Altså ingen røtter.
Korollar 1.6.8 f) sier at
x 2 ≡ 1 (mod 7) har nøyaktig 2 og
x 3 ≡ 1 (mod 7) har nøyaktig 3 forskjellige røtter siden både 2 og 3 går
opp i 7 − 1 = 6. Vi kan sjekke at det stemmer. For tilfellet 2 kan vi bruke det som vi nettopp regnet ut. Vi ser
at x = 1 og x = 6 er de eneste løsningene.
For tilfellet 3 er det litt mer arbeid:
03 ≡ 0 (mod 7), 13 ≡ 1 (mod 7),
23 ≡ 8 ≡ 1 (mod 7), 33 ≡ 27 ≡ 6 (mod 7),
43 ≡ 64 ≡ 1 (mod 7), 53 ≡ 125 ≡ 6 (mod 7) og
63 ≡ 216 ≡ 6 (mod 7). Med andre ord er
x = 1, 2 og 4 røtter.
Referanser:
Charles E. Radke, The Use of Quadratic Residue Research, Comm. of the ACM, Volume 13, Number 2, 1970.
| 1. | La p = 11, dvs. p ≡ 3 (mod 4). Sjekk om
x 2 ≡ −1 (mod 11) likevel har en løsning.
Både 2 og 5 går opp i 11 − 1 = 10. Vis ved utregning at
Korollar 1.6.8 f)
stemmer for disse verdiene.
|
| 2. | La p = 13, dvs. p ≡ 1 (mod 4). Sjekk ved å prøve deg
frem at Korollar 1.6.8 g)
stemmer. Både 2, 3, 4 og 6 går opp i 13 − 1 = 12. Vis ved utregning at
Korollar 1.6.8 f)
stemmer for disse verdiene. Kan du på grunnlag av det du nå har funnet avgjøre om
x 3 ≡ −1 (mod 13) har løsninger?
|
