1.9.1  Funksjonsgrensesnitt og lambda-uttrykk
Et funksjonsgrensesnitt (eng: functional interface) har nøyaktig én abstrakt metode. Metoden kan ha ingen, ett eller flere argumenter og ingen (void) eller én returverdi. Hvis den abstrakte metoden matematisk sett ikke er en funksjon, dvs. hvis den enten ikke har argumenter eller er void, kalles det likevel et funksjonsgrensesnitt.

I Avsnitt 1.5.5 ble funksjonsgrensesnittet Oppgave innført:

  @FunctionalInterface              // en annotasjon
  public interface Oppgave<T>       // legges under hjelpeklasser
  {
    void utførOppgave(T t);         // en eller annen oppgave
  }
              Programkode 1.9.1 a)

Definisjonen av grensesnittet Oppgave starter med en annotasjon (eng: annotation). Den gjør at en kompilator kan sjekke om Oppgave er korrekt satt opp, dvs. at den har nøyaktig én abstrakt metode. Se Oppgave 1.

En vanlig arbeidsoppgave er å skrive ut innholdet av en datastruktur. Flg. metode skriver innholdet av den generiske tabellen a til konsollet:

  public static <T> void skrivTilKonsoll(T[] a)
  {
    for (T t : a) System.out.print(t + " ");  // går gjennom tabellen
  }
                   Programkode 1.9.1 b)

Dette kan generaliseres ved hjelp av grensesnittet Oppgave. I flg. generiske metode inngår en oppgave som argument (eller parameter):

  public static <T> void tabellOppgave(T[] a, Oppgave<? super T> oppgave)
  {
    for (T t : a) oppgave.utførOppgave(t);   // går gjennom tabellen
  }
                   Programkode 1.9.1 c)

Men hvordan skal vi få meddelt metoden tabellOppgave() at oppgaven er å skrive til konsollet? Vi kan bruke et lambda-uttrykk (eng: a lambda expression). I Java er dette en ny teknikk for å kunne sende en metode inn som argument til en annen metode.

La A og B være to mengder. I matematikk brukes notasjonen f : A → B. Det betyr at f er en funksjon fra definisjonsmengden A til verdiområdet B. Hvis x ∈ A og f(x) ∈ B er tilhørende funksjonsverdi, kan vi skrive: x → f(x). Dette leses som at x går til f(x). Uttrykket x → f(x) er et lambda-uttrykk.

Et lambda-uttrykk for oppgaven å skrive noe (en x) til konsollet, kan da settes opp slik:

  x -> System.out.print(x + " ");

                   Programkode 1.9.1 d)

Et lambda-uttrykk må imidlertid knyttes til et funksjonsgrensesnitt. F.eks. på flg. måte:

  Oppgave<String> oppgave = x -> System.out.print(x + " ");

Nå er lambda-uttrykket knyttet til det konkrete grensesnittet Oppgave<String>. Datatypen til x blir avledet (eng: inferred) av typen til oppgaven, dvs. x blir av typen String. Her ser vi imidlertid ingenting til metoden utførOppgave(). Men det er heller ikke nødvendig siden x er dens argument og System.out.print(x + " "); dens «kropp». Med andre ord har vi ikke metoden utførOppgave() som sådan, men vi har dens innhold. Vi skal senere se eksempler på metoder med en «kropp» som består av mer enn ett metodekall.

Vi kobler dette sammen med metoden tabellOppgave() til flg. programbit:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};   // en String-tabell
  Oppgave<String> oppgave = x -> System.out.print(x + " ");  // et lambda-uttrykk
  tabellOppgave(s, oppgave);                                 // bruker metoden
  // Utskrift: Sohil Per Thanh Ann Kari Jon

                   Programkode 1.9.1 e)

Vi kan imidlertid gjøre det kortere. Lambda-uttrykket kan gå rett inn som argument:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, x -> System.out.print(x + " "));

                   Programkode 1.9.1 f)

Koden over har ingen eksplisitt forbindelse mellom lambda-uttrykket og grensesnittet. Den er implisitt siden Oppgave er argumenttype i metoden tabellOppgave(). Typen til argumentet x blir her avledet av typen til tabellen s.

I et lambda-uttrykk kan det refereres til en variabel utenfor uttrykket. I flg. utvidelse av Programkode 1.1.9 f) skrives kun de navnene fra tabellen s som er kortere enn lengde:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};   // en String-tabell
  int lengde = 4;                                            // en int-variabel

  Oppgave<String> oppgave = x ->                             // et lambda-uttrykk
  {
    if (x.length() < lengde) System.out.print(x + " ");      // sjekker lengden
  };                                                         // obs: semikolon

  tabellOppgave(s, oppgave);    // Utskrift: Per Ann Jon

                   Programkode 1.9.1 g)

Det kan refereres til en variabel (eller variabler) fra et lambda-uttrykk hvis den er konstant (eng: final) eller i praksis er konstant (eng: effectively final). I Programkode 1.1.9 g) burde det derfor ha stått: final int lengde = 4; Men det går bra slik det er fordi lengde ikke endres noe sted. Da er den i praksis konstant. Se Oppgave 2.

I neste eksempel skal vi prøve å finne antallet navn i String-tabellen med lengde kortere enn lengde. Vi gjør flg. forsøk:

  int lengde = 4, antall = 0;                                // int-variabler

  Oppgave<String> oppgave = x ->                             // et lambda-uttrykk
  {
    if (x.length() < lengde) antall++;                       // teller opp
  };
                   Programkode 1.9.1 h)

Koden over har imidlertid en syntaksfeil (markert med rødt). F.eks. gir NetBeans meldingen: «local variables referenced from a lambda expression must be final or effectively final». Det er med andre ord ikke tillatt å oppdatere variabelen antall.

I Java skilles det mellom grunnleggende typer (int, char, osv.) og referansetyper. En tabell er en referansetype. Tabellnavnet er «adressen» til der tabellelementene ligger. Holder vi navnet fast, men endrer på tabellens innhold, vil likevel tabellen ses på som i praksis å være konstant. Dette kan vi utnytte som en «utvei» (eng: a hatch) i Programkode 1.1.9 h). Istedenfor int-variabelen antall bruker vi en int-tabell med ett element:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};   // en String-tabell
  int lengde = 4;                                            // en int-variabel
  int[] antall = {0};                                        // en int-tabell

  Oppgave<String> oppgave = x ->                             // et lambda-uttrykk
  {
    if (x.length() < lengde) antall[0]++;                    // teller opp
  };

  tabellOppgave(s, oppgave);                                 // kaller metoden
  System.out.println(antall[0]);    // Utskrift: 3

                   Programkode 1.9.1 i)

Metoden utførOppgave() i Oppgave har et argument, men returnerer ikke noe. Det betyr at det til høyre for pilen (→) i et lambda-uttrykk kan være et metodekall (som i Programkode 1.1.9 d ) eller en samling av (ingen, en eller flere) programsetninger. I det siste tilfellet må setningene stå i en blokk { . . . } og må avsluttes med semikolon (se f.eks. Programkode 1.1.9 i ). Flg. lambda-utrykk vil være lovlig, men har ingen effekt siden blokken er tom:

  Oppgave<String> oppgave = x ->  { };    // en tom blokk

                   Programkode 1.9.1 j)

Legg merke til at «blokken» i lambda-uttrykket må avsluttes med et semikolon når lambda-uttrykket står som separat kode slik som i Programkode 1.9.1 j). Men det skal ikke være semikolon når et slikt lambda-uttrykk går direkte inn som argument i en metode, dvs. slik:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, x ->  { });

«Blokken» til et lambda-uttrykk kan inneholde flere programlinjer. Den funger som en vanlig kodeblokk og kan dermed også ha lokale variabler, løkker m.m. Se Oppgave 4.

Et grensesnitt (også et funksjonsgrensesnitt) kan, i tillegg til abstrakte metoder, ha statiske metoder og metoder som er standard (eng: default). F.eks. er det å skrive til konsollet en såpass vanlig oppgave at vi kunne lage et fast lambda-uttrykk for det. En statisk metode i grensesnittet Oppgave kan gjøre det for oss:

  @FunctionalInterface              // en annotasjon
  public interface Oppgave<T>       // legges under hjelpeklasser
  {
    void utførOppgave(T t);         // en abstrakt metode

    public static <T> Oppgave<T> konsollutskrift()  // en statisk metode
    {
      return x -> System.out.print(x + " ");  // returnerer et lambda-uttrykk
    }
  }                Programkode 1.9.1 k)

Nå kan Programkode 1.1.9 f) isteden skrives på en måte som er lettere å huske:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, Oppgave.konsollutskrift());

Metoden konsollutskrift() i Oppgave legger et mellomrom etter x. Her hadde det vært bedre og mer fleksibelt å la utskriften av x være hovedoppgaven og isteden la «mellomrom» være en eventuell tilleggsoppgave. Vi tar vekk «mellomrommet» i konsollutskrift(). En tilleggsoppgave kan vi få til ved hjelp av en standard/default metode:

  @FunctionalInterface              // en annotasjon
  public interface Oppgave<T>       // legges under hjelpeklasser
  {
    void utførOppgave(T t);         // en abstrakt metode

    public static <T> Oppgave<T> konsollutskrift()  // en statisk metode
    {
      return x -> System.out.print(x);  // returnerer et lambda-uttrykk
    }

    default Oppgave<T> deretter(Oppgave<? super T> etter)  // default metode
    {
      if (etter == null) throw new NullPointerException("null-argument!");

      return x ->                    // returnerer et lambda-uttrykk
      {
        this.utførOppgave(x);        // hovedoppgaven
        etter.utførOppgave(x);       // tilleggsoppgaven
      };
    }
  }                Programkode 1.9.1 l)

Hvis vi ønsker mellomrom, kan vi gjøre det slik:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, Oppgave.konsollutskrift().deretter(x -> System.out.print(' ')));

                   Programkode 1.9.1 m)

Hvis vi isteden vil ha ny linje for hvert navn, kan vi gjøre det slik:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, Oppgave.konsollutskrift().deretter(x -> System.out.println()));

                   Programkode 1.9.1 n)

I lamda-uttrykket x → f(x) kan f(x) være ett metodekall eller mer generelt en programblokk (med en eller flere programsetninger). Hvis f(x) er ett metodekall, kan lambda-uttrykket x → f(x) oppgis på en kortere måte. Ta x -> System.out.println(x); som eksempel. Metoden println() er en instansmetode i out som er en instans av klassen PrintStream. Dermed kan vi isteden bruke: System.out::println. Se flg. eksempel:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, Oppgave.konsollutskrift().deretter(System.out::println));

                   Programkode 1.9.1 o)

I Java (java.util.function) finnes det en serie ferdige funksjonsgrensesnitt. De kan deles inn i flg. fem hovedtyper:

1. Konsumenter (eng: Consumer)
2. Produsenter (eng: Supplier)
3. Funksjoner (eng: Function)
4. Predikater (eng: Predicate)
5. Operatorer (unær og binær) (eng: Operator)

I avsnittene nedenfor vil hvert av disse grensesnittene bli diskutert.

1.	Legg inn en abstrakt metode til i grensesnittet Oppgave. Hva sier kompilatoren?
2.	Gi variablen lengde i Programkode 1.1.9 g) en ny verdi helt til slutt, dvs. etter kallet på metoden tabellOppgave(). Hva skjer?
3.	I Programkode 1.1.9 f) blir innholdet av en String-tabell skrevet ut til konsollet ved hjelp av metoden tabellOppgave() og et lamda-uttrykk. Gjør det om slik at det isteden bygges opp en tegnstreng der navnene rammes inne med [ og ] og skilles med komma og mellomrom. Dvs. samme tegnstreng som metoden Arrays.toString() gir. Bruk f.eks. en StringJoiner som hjelpemiddel.
4.	Lag et lambda-uttrykk som skriver ut argumentet x f.eks. 3 ganger og med mellomrom mellom første og andre gang og mellom andre og trdeje gang (men ikke til slutt). Det avsluttes med linjeskift. Bruk den i Programkode 1.1.9 f).
5.	I den nye versjonen av konsollutskrift() (se Oppgave) er det ikke lagt inn et melomrom. Det kan en få til med metoden deretter() slik som i Programkode 1.9.1 m). Lag metoden public static <T> Oppgave<T> konsollutskrift(String format) i grensesnittet Oppgave. Den skal bruke printf() istedenfor print(). Bruk så den til å få samme utskrift som Programkode 1.9.1 m).
6.	Hvor mange av de fem typene av funksjonsgrensesnitt er det i java.util.function

  1.9.2  Konsumenter
Det generiske funksjonsgrensesnittet Consumer<T> fra java.util.function er definert slik:

  @FunctionalInterface            // en annotasjon
  public interface Consumer<T>    // en konsument
  {
    void accept(T t);             // accept - ett argument, ingen returverdi

    default Consumer<T> andThen(Consumer<? super T> after)  // default metode
    {
      // kode som returnerer et lambda-uttrykk
    }
  }                Programkode 1.9.2 a)

Legg merke til at metoden accept() i Consumer er av samme type som utførOppgave() i grensesnittet Oppgave, dvs. ett generisk argument og ingen returverdi (void). Det betyr at vi kan bytte ut en Oppgave med en Consumer i Programkode 1.1.9 c):

  public static <T> void tabellOppgave(T[] a, Consumer<? super T> oppgave)
  {
    for (T t : a) oppgave.accept(t);
  }
                   Programkode 1.9.2 b)

Her kan vi få et problem. Hvis begge versjonene av tabellOppgave() er tilgjengelig (både den i Programkode 1.9.2 b) og den i Programkode 1.1.9 c), vil flg. kode gi en feilmelding:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, x -> System.out.print(x));

Lambda-uttrykket x -> System.out.print(x) passer til både Oppgave og Consumer. Dermed: «reference to tabellOppgave is ambiguous». Kompilatoren klarer ikke å adskille dem. Hvis vi spesifiserer det grensesnittet som lambda-uttrykket skal høre til, så forsvinner tvetydigheten:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  Consumer<String> oppgave =  x -> System.out.print(x);
  tabellOppgave(s, oppgave);

                   Programkode 1.9.2 c)

Consumer har også metoden andThen(). Den er kodet og virker på nøyaktig samme måte som metoden deretter() i Oppgave.

En BiConsumer<T,U> har to generiske typeparametere. Den har, som alle «konsumenter», en abstrakt og void metode med navn accept(). Den kan brukes når en Map traverseres ved hjelp av metoden forEach(BiConsumer<? super K,? super V> action). I en Map kobles en nøkkelverdi K (eng: key) til en annen verdi V. Ta som eksempel at Per, Kari og Ole har tatt en eksamen og fått henholdsvis B, A og C som karakterer:

  Map<String,Character> map = new TreeMap<>();    // String er nøkkelverditype
  map.put("Per", 'B'); map.put("Kari", 'A'); map.put("Ole", 'C');

  map.forEach((x,y) -> System.out.print(x + ": " + y + "  "));
  // Utskrift: Kari: A  Ole: C  Per: B

                   Programkode 1.9.2 d)

Lambda-uttrykket (x,y) -> System.out.print(x + ": " + y + " ") starter med (x,y) fordi metoden accept() i BiConsumer har to argumenter. Datatypene til x og y avledes av typen til map, dvs. x blir av typen String og y av typen Character. Legg merke til at utskriften er sortert mhp. x-verdiene. Det kommer av at map er en TreeMap. Her kunne det også vært brukt en HashMap. Se Oppgave 1.

Grensesnittet BiConsumer<T,U> har T og U som typeparametere. I java.util.function har også de tre grensesnittene ObjIntConsumer<T>, ObjLongConsumer<T> og ObjDoubleConsumer<T> to parametere. Her er T typeparameter. Den andre parameteren er konkret. Det er en int i ObjIntConsumer<T>, en long i ObjLongConsumer<T> og en double i ObjDoubleConsumer<T>.

I flg. metode inngår en ObjIntConsumer<T>:

  public static <T> void tabellOppgave(T[] a, ObjIntConsumer<? super T> oppgave)
  {
    for (int i = 0; i < a.length; i++) oppgave.accept(a[i], i);
  }
                   Programkode 1.9.2 e)

Metoden over kan f.eks. brukes slik:

  String[] s = {"Sohil","Per","Thanh","Ann","Kari","Jon"};
  tabellOppgave(s, (x,y) -> System.out.print("s[" + y + "] = " + x + " "));
  // Utskrift: s[0] = Sohil s[1] = Per s[2] = Thanh s[3] = Ann . . . .

                   Programkode 1.9.2 f)

I java.util.function er det også tre «konsumenter» som ikke er generiske. Det er de tre konkrete grensesnittene IntConsumer, LongConsumer og DoubleConsumer. Fordelen er at hvis vi ønsker å bruke en av typene int, long eller double, får vi ved hjelp av dem en mer direkte og effektiv kode. Da er det ikke nødvendig å gå via «omslagstypen» (f.eks. int til Integer).

Flg. metode traverserer en int-tabell og utfører en «oppgave» på hvert element:

  public static void tabellOppgave(int[] a, IntConsumer oppgave)
  {
    for (int k : a) oppgave.accept(k);   // går gjennom tabellen
  }
                   Programkode 1.9.2 g)

Denne metoden kan f.eks. brukes slik:

  int[] a = {1,2,3,4,5,6,7,8,9,10};
  tabellOppgave(a, k -> System.out.print(k + " "));
  // Utskrift: 1 2 3 4 5 6 7 8 9 10

                   Programkode 1.9.2 h)

1.	I Programkode 1.9.2 d) brukes en TreeMap. Sjekk at det også virker med en HashMap.
2.	I listeklassene ArrayList og LinkedList har metoden forEach() en Consumer som parameter. Opprett f.eks. en ArrayList, legg inn en del tegnstrenger (f.eks. navn) og skriv ut ved hjelp av forEach().

  1.9.3  Produsenter
I java.util.function er det satt opp fem funksjonsgrensesnitt av denne typen - et generisk og fire konkrete. Det generiske heter Supplier<T> og er definert slik:

@FunctionalInterface            // en annotasjon
public interface Supplier<T>    // produsent
{
  T get();                      // get - ingen argumenter, returverdi
}
                   Programkode 1.9.3 a)

Det er ikke satt opp noen krav til hva metoden get() skal returnere bortsett fra at det må være en instans av datatypen T. F.eks. er det ingen krav om at den må gi forskjellige verdier hver gang den kalles. En Supplier kan ses på som en kilde til verdier. Flg. metode bruker den til å fylle inn verdier i en generisk tabell:

  public static <T> void settInn(T[] a, Supplier<T> kilde)
  {
    for (int i = 0; i < a.length; i++) a[i] = kilde.get();
  }
                   Programkode 1.9.3 b)

Et lambda-uttrykk med ett argument settes opp slik: x -> f(x) eller slik: (x) -> f(x). Men hva hvis det ikke er noen argumenter slik som for get() i Supplier? Ja, da setter vi det opp slik: () -> f(). I flg. eksempel blir en Character-tabell fylt med A-er (se også Oppgave 1):

  Character[] c = new Character[10];
  settInn(c, () -> 'A');
  System.out.println(Arrays.toString(c));
  // Utskrift: [A, A, A, A, A, A, A, A, A, A]

                   Programkode 1.9.3 c)

En litt mer avansert teknikk er å lage en metode som gir en tilfeldig bokstav fra A til Z:

  public static char tilfeldigBokstav()
  {
    Random r = new Random();
    return (char)(r.nextInt(26) + 65);
  }
                   Programkode 1.9.3 d)

Med denne funksjonen som «kilde», kan Character-tabellen få tilfeldige bokstaver:

  Character[] c = new Character[10];
  settInn(c, () -> tilfeldigBokstav());
  System.out.println(Arrays.toString(c));
  // Utskrift (f.eks. dette): [D, K, D, A, C, I, Z, K, G, M]

                   Programkode 1.9.3 e)

Metoden tilfeldigBokstav() må ligge i en klasse. Hvis den f.eks. er lagt i samleklassen Tabell, vil lambda-uttrykket kunne settes opp slik: Tabell::tilfeldigBokstav. Prøv det!

I metoden tilfeldigBokstav() blir det opprettet en randomgenerator på nytt hver gang metoden kalles. Dette kan forenkles. Som tidligere nevnt kan det refereres til en variabel (eller variabler) fra et lambda-uttrykk hvis den er konstant (eng: final) eller i praksis er konstant (eng: effectively final). Dermed kan vi gjøre det slik:

  final Random r = new Random();
  Character[] c = new Character[10];
  settInn(c, () -> (char)(r.nextInt(26) + 65));
  System.out.println(Arrays.toString(c));

                   Programkode 1.9.3 f)

Hvis vi skulle ønske å lage et tilsvarende opplegg for å legge inn verdier i en heltallstabell, kan vi isteden bruke funksjonsgrenesnittet IntSupplier:

  public static void settInn(int[] a, IntSupplier kilde)
  {
    for (int i = 0; i < a.length; i++) a[i] = kilde.getAsInt();
  }
                   Programkode 1.9.3 g)

I flg. eksempel blir en heltallstabell fylt med heltall i intervallet fra 1 til 100:

  final Random r = new Random();
  int[] a = new int[10];

  settInn(a, () -> r.nextInt(100) + 1);
  System.out.println(Arrays.toString(a));

  // Eksempel på en utskrift:
  // [56, 24, 70, 87, 7, 65, 97, 25, 92, 27]

                   Programkode 1.9.3 h)

Grensesnittene LongSupplier, DoubleSupplier og BooleanSupplier virker på samme måte som IntSupplier. Se Oppgave 5.

1.	I eksemplet i Programkode 1.9.3 c) brukes en Supplier til å fylle en tabell med A-er. Klassen Arrays i java.util har allerede metoden fill(). Den fyller en tabell med en og samme verdi. Bruk den til å oppnå samme effekt som i Programkode 1.9.3 c).
2.	Gjør om metoden tilfeldigBokstav() slik at også Æ, Ø og Å kan forekomme og bruk den i Programkode 1.9.3 e).
3.	Gjør om Programkode 1.9.3 f) slik at det også der vil komme Æ, Ø og Å.
4.	Lag metoden public static String tilfeldigDag(). Den skal returnere en tilfeldig dag der mandag er "man", tirsdag er "tirs", osv. til søndag med "søn". Bruk så den og metoden settInn() til å fylle en String-tabell med tilfeldige dager.
5.	Sjekk hva metodene heter i LongSupplier, DoubleSupplier og BooleanSupplier.

  1.9.4  Funksjoner
I funksjonsgrensesnitt av typen konsument/produsent er den abstrakte metoden matematisk sett ikke en funksjon. I matematikk er en funksjon f en avbildning fra en definisjonsmengde A til et verdiområde B og vi skriver f : A → B. En matematisk funksjon må ha argument og funksjonsverdi. I en konsument er det ingen returverdi og i en produsent ikke noe argument.

Men i funksjonsgrensesnitt av typene funksjon, operator og predikat er den abstrakte metoden matematisk sett en funksjon. Operatorer og predikater kan på mange måter ses på som «subtyper» av funksjoner. Det mest generelle «en-dimensjonale» (ett argument) grensesnittet er Function<T,R> (T argumenttype og R returtype) er definert slik:

@FunctionalInterface               // en annotasjon
public interface Function<T,R>     // function
{
  R apply(T t);                    // apply - ett argument og returverdi

  // + default-metodene andThen() og compose()
  // + den statiske metoden identity()
}
                   Programkode 1.9.4 a)

Eksempel 1: Funksjon som til en tegnstreng (String) tilordner dens lengde (Integer):

  Function<String,Integer> f = s -> Integer.valueOf(s.length());
  System.out.println(f.apply("Kari"));  // 4

I Eksempel 1 blir heltallet s.length() (av typen int) eksplisitt konvertert til en Integer. Det blir kortere kode hvis vi lar det skje implisitt, dvs. slik (se også Oppgave 1):

  Function<String,Integer> f = s -> s.length();

Eksempel 2: Funksjon som til en tegnstreng (String) tilordner dens første tegn (Character):

  Function<String,Character> g = s -> s.charAt(0);
  System.out.println(g.apply("Kari"));  // K

I Eksempel 1 brukes det generiske funksjonsgrensesnittet Function<T,R>. Der må både T og R være referansetyper, dvs. at int ikke kan brukes. Uttrykket Function<String,int> gir syntaksfeil. Det blir tilsvarende i Eksempel 2, dvs. der char ikke kan brukes.

Fra matematikken vet vi at funksjoner kan settes sammen. Hvis f : A → B og g : B → C, så kan f og g settes sammen til g o f. I funksjonsgrensesnittet Function<T,R> svarer både f.andThen(g) og g.compose(f) til sammensetningen g o f (som leses g ring f):

  Function<String,Character> f = s -> s.charAt(0);  // første tegn i s
  Function<Character,Integer> g = c -> (int)c;      // tegnets ascii-verdi

  System.out.println(f.andThen(g).apply("Ole"));    // 79
  System.out.println(g.compose(f).apply("Anne"));   // 65

  // g.andThen(f) og f.compose(g) gir ikke menig her!

                   Programkode 1.9.4 b)

Den statiske metoden identity() i Function<T,R> svarer til lamda-uttrykket: x -> x.

Funksjonsgrensesnittet BiFunction<T,U,R> er «to-dimensjonalt», dvs. den abtrakte metoden er en funksjon med to argumenter - det første av type T og det andre av type U og med R som returtype. Det ser slik ut:

@FunctionalInterface                  // en annotasjon
public interface BiFunction<T,U,R>    // bifunction
{
  R apply(T t, U u);                  // apply - to argumenter og returverdi

  // + default-metoden andThen()
}
                   Programkode 1.9.4 c)

Eksempel 3: Funksjon som konkatenerer (skjøter) to strenger (med en blank mellom):

  BiFunction<String,String,String> sum = (x,y) -> x.concat(" ").concat(y);
  System.out.println(sum.apply("Per", "Olsen"));  // Per Olsen

Sammenskjøting (med en blank mellom) kan gjøres på flere måter. Se Oppgave 3 - 4.

I java.function er det tilsammen 17 funksjonsgrensesnitt av typen «Function», dvs. der den abstrakte metoden matematisk sett er en funksjon (den har argument og funksjonsverdi). De skiller seg fra Function<T,R> og BiFunction<T,U,R> ved at de er mer spesialiserte.

Type funksjonsgrensesnitt	Den abstrakte metoden
Function<T,R>	R apply(T t)
BiFunction<T,U,R>	R apply(T t, U u)
ToIntFunction<T>	int applyAsInt(T t)
ToLongFunction<T>	long applyAsLong(T t)
ToDoubleFunction<T>	double applyAsDouble(T t)
ToIntBiFunction<T,U>	int applyAsInt(T t, U u)
ToLongBiFunction<T,U>	long applyAsLong(T t, U u)
ToDoubleBiFunction<T,U>	double applyAsDouble(T t, U u)
IntFunction<R>	R apply(int verdi)
LongFunction<R>	R apply(long verdi)
DoubleFunction<R>	R apply(double verdi)
IntToLongFunction	long applyAsLong(int verdi)
IntToDoubleFunction	double applyAsDouble(int verdi)
LongToIntFunction	int applyAsInt(long verdi)
LongToDoubleFunction	double applyAsDouble(long verdi)
DoubleToIntFunction	int applyAsInt(double verdi)
DoubleToLongFunction	long applyAsLong(double verdi)
Tabell 1.9.4 - Oversikt over funksjonsgrensesnitt

Eksempel 4: I Eksempel 1 er funksjonen fra String til Integer. Det hadde blitt mer effektivt med en funksjon fra String til int. Det kan vi få til ved hjelp av funksjonsgrensesnittet ToIntFunction<T>. Da kan det settes opp slik:

  ToIntFunction<String> f = s -> s.length();
  System.out.println(f.applyAsInt("Kari"));  // 4

Grensesnittet IntFunction<R> er det omvendte av ToIntFunction<T>. Det representerer funksjoner fra int til den generiske typen R. Det kan f.eks. benyttes til å sette inn verdier i en generisk tabell. Klassen Arrays har flg. metode:

  public static <T> void setAll(T[] array, IntFunction<? extends T> generator)
  {
    Objects.requireNonNull(generator);
    for (int i = 0; i < array.length; i++) array[i] = generator.apply(i);
  }
                   Programkode 1.9.4 d)

Eksempel 5: Hvert element i en Integer-tabell med navn lengder skal inneholde lengden på det tilsvarende elementet i en String-tabell navn. Med andre ord skal for hver i lengder[i] være lik navn[i].length():

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};
  Integer[] lengder = new Integer[navn.length];   // en tom tabell
  Arrays.setAll(lengder, i -> navn[i].length());  // setter inn
  System.out.println(Arrays.toString(lengder));   // [3, 4, 4, 6, 9, 6]

Eksempel 6: Hvert element i en Character-tabell med navn forbokstav skal inneholde første bokstav i det tilsvarende elementet i en String-tabell navn:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};
  Character[] forbokstav = new Character[navn.length];  // en tom tabell
  Arrays.setAll(forbokstav, i -> navn[i].charAt(0));    // setter inn
  System.out.println(Arrays.toString(forbokstav));      // [P, K, A, P, M, J]

Eksempel 7: I Programkode 1.9.3 f) brukte vi en produsent (supplier) til å fylle en Character-tabell med tilfeldige bokstaver. Det kan vi også få til ved setAll-metoden:

  Random r = new Random();
  Character[] c = new Character[10];
  Arrays.setAll(c, i -> (char)(r.nextInt(26) + 65));
  System.out.println(Arrays.toString(c));
  // Eksempel på utskrift: [G, Q, H, K, M, G, I, F, N, P]

Eksempel 8: I Eksempel 7 ble tabellen c fylt med tilfeldige bokstaver. Flg. kode fyller den fortløpende med bokstavene A, B, C osv:

  Character[] c = new Character[10];
  Arrays.setAll(c, i -> (char)(i + 65));

Eksempel 9: Flg. kode fyller en Integer-tabell med tallene 1, 2, 3, osv:

  Integer[] a = new Integer[10];
  Arrays.setAll(a, i -> i + 1);

Eksempel 10: I Eksempel 9 får en Integer-tabell tallene 1, 2, 3, osv. Men samme kode kan brukes på en int-tabell. Se nedenfor. Men det er egentlig en annen versjon av setAll() som brukes. Det ser vi på i Avsnitt 1.9.5 om operatorer. Se også Oppgave 9.

  int[] a = new int[10];
  Arrays.setAll(a, i -> i + 1);

1.	I Eksempel 1 brukes instansmetoden length() i klassen String. Den kan også refereres til ved hjelp av :: - operatoren. Gjør det.
2.	I Eksempel 2 inngår implisitt konvertering fra char til Character. Gjør det eksplisitt.
3.	I Eksempel 3 brukes instansmetoden concat() for å skjøte sammen en tegnstreng, en blank og en tegnstreng. a) Hva skjer hvis det står String::concat istedenfor (x,y) -> x.concat(" ").concat(y). b) Gjør det direkte med + - operatoren. c) Gjør det ved hjelp av den statiske metoden join().
4.	En Person har fornavn og etternavn. Lag en BiFunction som returnerer en Person (bruk konstruktøren) ved hjelp av fornavn og etternavn som argumenter. Lag så en Function som returnerer en tegnstreng med personens navn (bruk toString-metoden). Sett metodene sammen (andThen) til en metode som returnerer en tegnstreng med fornavn og etternavn (og en blank mellom).
5.	Eksempel 5 starter med String-tabellen navn. Bruk setAll() til å gjøre den om slik at alle navnene får kun store bokstaver.
6.	Eksempel 5 starter med String-tabellen navn. Bruk setAll() til å lage Boolean-tabellen b der b[i] er true hvis navn[i] inneholder bokstaven A (stor eller liten) og false ellers.
7.	I Java er det definert hvilke tegn og bokstaver som kan være første tegn i et variabelnavn. Det gjelder f.eks. vanlige bokstaver og _ (understrekingstegn/underscore), men også andre. Sett opp en Character-tabell med tegn du vet kan stå først og tegn du er usikker på. Bruk så setAll() til å lage en Boolean-tabell som har true hvis tegnet kan stå først og false ellers.
8.	Bruk setAll() til å lage en double-tabell med de 10 verdiene 1.0, 1.1, 1.2, . . . , 1.9. Da er det setAll()-metoden som har en IntToDoubleFunction som argument, som brukes.
9.	I Eksempel 10 brukes setAll() til å legge verdier i en int-tabell. I den versjonen av setAll() er det ingen «Function» som er argument, men en IntUnaryOperator. Alle lambda-uttrykk av typen i -> f(i) der f har int som returtype, er da tillatt. Start med en tom int-tabell a med plass til 10 verdier. Bruk så setAll() til å fylle int-tabellen slik at den blir (bruk et lambda-uttrykk) lik:
	a)   {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}   (de naturlige tallene)
	b)   {10, 9, 8, 7, 6, 5, 4, 3, 2, 1}   (motsatt vei)
	c)   {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}   (de første oddetallene)
	d)   {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}   (de første kvadrattallene)
	e)   {0, 1, 1, 2, 3, 5, 8, 13, 21, 34}   (de første Fibonacci-tallene)
	f)   {0, 1, 0, 1, 0, 1, 0, 1, 0, 1}   (0 og 1 annenhver gang)
	g)   {1, -2, 3, -4, 5, -6, 7, -8, 9, -10}   (pluss og minus annenhver gang)
10.	Gitt: String[] tall = {"10","12","9","13","5","20","17","3","11","10"}; Bruk setAll() til å lage int-tabellen: {10, 12, 9, 13, 5, 20, 17, 3, 11, 10}n.

  1.9.5  Operatorer
Vi skiller mellom binære og unære operatorer.

• Ta regnestykket 2 + 3 = 5. Der er + en binær operator og den omtales ofte som addisjonsoperatoren. Den er binær fordi den virker på de to tallene på hver side.
• La b være en boolsk variabel, dvs. at den kan være sann eller usann. Da vil !b bli det motsatte av b. Tegnet ! er en unær operator og den omtales ofte som negasjons-operatoren. Den er unær fordi den virker kun på det som kommer rett etterpå.
• De to elementene som en binær operator virker på, kalles operander - venstre og høyre operand. Elementet som en unær operator virker på, kalles operanden.

Operatorer er spesialtilfeller av funksjoner. La A være en mengde og f : A × A → A. Da vil f kunne ses på som en binær operator. Den virker på to elementer og returnerer et element av samme type. Tilsvarende vil g : A → A, kunne ses på som en unær operator. Legg merke til at i Tabell 1.9.4 er det ingen funksjonsgrensesnitt der argumenttypen og returtypen er like. Slike funsjonsgrensenitt har isteden blitt definert som operatorer.

Den mest generelle av operatorene heter BinaryOperator og er en subtype til BiFunction:

  @FunctionalInterface
  public interface BinaryOperator<T> extends BiFunction<T,T,T>
  {
    T apply(T t1, T t2);         // binær operator - arves fra BiFunction
    + default-metoden andThen() og de to statiske metodene minBy og maxBy 
  }
                   Programkode 1.9.5 a)

I Eksempel 3 i forrige avsnitt er det en enkel bruk av BiFunction. Men der kunne vi like gjerne ha brukt en BinaryOperator:

  BinaryOperator<String> sum = (x,y) -> x.concat(" ").concat(y);
  System.out.println(sum.apply("Per", "Olsen"));  // Per Olsen

Funksjonsgrensesnittet BinaryOperator har to statiske metoder minBy() og maxBy() der begge har en Comparator som argument og returnerer en BinaryOperator. Metoden i de to operatorene gir henholdsvis den minste og den største verdien:

  BinaryOperator<String> minst = BinaryOperator.minBy(String::compareTo);
  System.out.println(minst.apply("Per", "Kari"));  // Utskrift: Kari

I java.function er det tilsammen åtte operatorer:

Type funksjonsgrensesnitt	Den abstrakte metoden
UnaryOperator<T>	T apply(T operand)
BinaryOperator<T>	T apply(T v, T h)
IntUnaryOperator	int applyAsInt(int operand)
IntBinaryOperator	int applyAsInt(int v, int h)
LongUnaryOperator	long applyAsLong(long operand)
LongBinaryOperator	long applyAsLong(long v, long h)
DoubleUnaryOperator	double applyAsDouble(double operand)
DoubleBinaryOperator	double applyAsDouble(double v, double h)
Tabell 1.9.5 - Oversikt over funksjonsgrensesnitt

Funksjonsgrensesnittet IntUnaryOperator så vi på i Eksempel 10 og i Oppgave 9 i forrige avsnitt. Den inngår i flg. setAll-metode fra klassen Arrays:

  public static void setAll(int[] array, IntUnaryOperator generator)
  {
    Objects.requireNonNull(generator);
    for (int i = 0; i < array.length; i++) array[i] = generator.applyAsInt(i);
  }
                   Programkode 1.9.5 b)

IntUnaryOperator representerer funksjoner med int som argument- og returtype. Det betyr at det mulig å sette dem sammen. Det gjøres ved hjelp av metodene andThen og compose. Da vil f.andThen(g) være det samme som g.compose(f):

  int[] a = new int[10];                    // plass til 10 verdier
  IntUnaryOperator f = i -> i + 1;          // øker i med 1
  IntUnaryOperator g = i -> i * i;          // kvadrerer i
  Arrays.setAll(a, f.andThen(g));           // setter sammen g og f
  System.out.println(Arrays.toString(a));   // skriver ut

  // Utskrift: [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

                   Programkode 1.9.5 c)

I matematikk er det mange formeler og algoritmer der kun et funksjonsnavn inngår. Ta som eksempel at vi skal finne integralet til en funksjon f over intervallet [a,b]. Hvis vi deler det i åtte like store delintervaller, vil hvert delintervall få lengde h lik (b - a)/8. Videre setter vi x0 = a, x1 = a + h, x2 = a + 2h, osv. til x8 = a + 8h = b. Figuren under har x0 til x8 på x-aksen. På kurven som representerer f, er de tilhørende funksjonsverdiene satt opp.

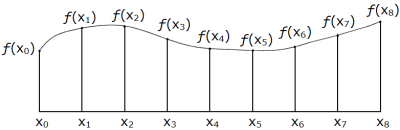Figur 1.9.5 a): Intervallet fra a = x0 til b = x8 er delt i åtte deler

Simpsons metode gir en god tilnærming til integralet og jo flere delintevaller vi lager jo bedre blir tilnærmingen. Formelen ser slik ut med åtte delintervaller:

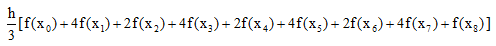Figur 1.9.5 b): Simpsons metode for åtte delintervaller

Det vi nå trenger en generell funksjon f : R → R der R er de reelle tallene. Til det formålet kan vi bruke en DoubleUnaryOperator siden den abstrakte metoden har double som type både for argumentet og returverdien.

Flg. algoritme bruker den generelle versjonen av Simpsons metode. Intervallet [a,b] blir delt i 2n delintervaller. Ønsker vi åtte delintervaller, må vi sette n lik 4:

  public static double Simpson(DoubleUnaryOperator f, double a, double b, int n)
  {
    double d = (b - a) / n;                   // h = d/2

    double x1 = a + d / 2, sum1 = 0.0;        // x1 = a + d/2 = a + h 

    for (int i = 0; i < n; i++)               // går n ganger
    {
      sum1 += f.applyAsDouble(x1); x1 += d;   // summerer og øker
    }

    double x2 = a + d, sum2 = 0.0;            // x2 = a + d = a + 2h

    for (int i = 1; i < n; i++)               // går n ganger
    {
      sum2 += f.applyAsDouble(x2); x2 += d;   // summerer og øker
    }

    return (f.applyAsDouble(a) + f.applyAsDouble(b)
            + 4*sum1 + 2*sum2)*d/6;           // d/6 = h/3
  }
                   Programkode 1.9.5 d)

Vi kan teste dette på et tilfellet der vi vet svaret. Integralet av sin(x) fra 0 til π kan regnes ut ved vanlig integrasjon (svar = 2). I flg. løkke går n fra 1 til 5, dvs. fra 2 til 10 delintervaller. Utskriften som har 4 desimalers nøyaktighet, viser at resultatet blir mer og mer lik 2:

  for (int n = 1; n <= 5; n++)
  {
    double integral = Simpson(Math::sin, 0, Math.PI, n);
    System.out.printf("%8.4f", integral);
  }

  // Utskrift: 2.0944  2.0046  2.0009  2.0003  2.0001

                   Programkode 1.9.5 e)

Grafen til funksjonen f (se under) over intervallet [0,1] utgjør en kvartsirkel. Integralet blir da lik π/4 = 0.7853981 . . . . Vi kan se hva Simpsons formel gir oss med åtte delintervaller:

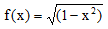  System.out.println(Simpson(x -> Math.sqrt(1 - x*x), 0, 1, 4));
  // Utskrift: 0.7802972924438544

1.	Sjekk at g.compose(f) gir samme resultat som f.andThen(g) i Programkode 1.9.5 c).
2.	Løs, hvis du ikke allerede har gjort det, Oppgave 9 i Avsnitt 1.9.4.
3.	Det er ikke mulig å finne en eksakt verdi for integralet av funksjonen sin(x)/x. Bruk Simpsons metode til å finne tilnærmingsløsninger for intervallet fra π/4 til π/2.
4.	Hvor god er Simpsons metode? Søk på internett eller i se en bok. Sjekk hva feilleddet sier.

  1.9.6  Predikater
Predikater og predikatfunksjoner er kjent fra diskret matematikk. Det kalles også en logisk eller en boolsk funksjon. Det betyr at en dens funksjonverdi er enten sann eller usann. I Java betyr det at den har datatypen boolean som returtype. Flg. funksjon er av denne typen:

  public static boolean f(int n)
  {
    return n > 0;
  }

Uansett hvilken verdi argumentet n har, vil f(n) enten være sann eller usann.

I alle de fem funksjonsgrensesnittene av typen predicate i java.function er den abstrakte metoden test() av denne typen:

Type funksjonsgrensesnitt	Den abstrakte metoden
Predicate<T>	boolean test(T t)
BiPredicate<T,U>	boolean test(T t, U u)
IntPredicate	boolean test(int verdi)
LongPredicate	boolean test(long verdi)
DoublePredicate	boolean test(double verdi)
Tabell 1.9.6 - Oversikt over funksjonsgrensesnitt

Funksjonsgrensesnittet Predicate<T> er definert slik:

  @FunctionalInterface                 // en annotasjon
  public interface Predicate<T>        // predikat
  {
    boolean test(T t);                 // test - ett argument

    // + default-metodene and, or og negate
    // + den statiske metoden isEqual
  }
                   Programkode 1.9.6 a)

Metoden tabellOppgave() i Programkode 1.9.2 b) går gjennom en tabell og en konsument (Consumer) bestemmer hva som skal gjøres med hvert tabellelement. Gitt en String-tabell med navn. Hvis vi ønsker bruke denne metoden til å skrive ut de navnene som inneholder bokstaven A (stor eller liten), kan vi få til det ved å lage f.eks. denne konsumenten:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  Consumer<String> oppgave = x ->              // en konsument
  {
    if (x.toUpperCase().indexOf('A') != -1)    // stor eller liten A?
      System.out.print(x + " ");               // skriver ut
  };

  tabellOppgave(navn, oppgave);                // bruker metoden

  // Utskrift: Kari Arne Margrethe Jasmin

                   Programkode 1.9.6 b)

Legg merke til at oppgave starter med: if (x.toUpperCase().indexOf('A') != -1). Hvis vi skulle være interessert i en annen bokstav enn A, måtte vi lage en ny konsument. Men fortsatt vil siste del av jobben være å skrive ut. Dette kan vi generalisere ved å lage en tabellOppgave-metode med et predikat og en konsument som argumenter. Dvs. slik:

  public static <T> void
  tabellOppgave(T[] a, Predicate<? super T> predikat, Consumer<? super T> konsument)
  {
    for (T t : a) if (predikat.test(t)) konsument.accept(t);
  }
                   Programkode 1.9.6 c)

Dermed kan vi erstatte Programkode 1.9.6 b) med flg. kode:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  Predicate<String> bokstav = x -> x.toUpperCase().indexOf('A') != -1;
  Consumer<String> utskrift = x ->  System.out.print(x + " ");

  tabellOppgave(navn, bokstav, utskrift);
  // Utskrift: Kari Arne Margrethe Jasmin

                   Programkode 1.9.6 d)

Slike idéer som dette er allerede en del av Java. Ved hjelp av en pipeline og en stream (se Avsnitt 1.9.7). I flg. eksempel er bokstav og utskrift som i Programkode 1.9.6 d):

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};
  Arrays.stream(navn).filter(bokstav).forEach(utskrift);
  // Utskrift: Kari Arne Margrethe Jasmin

                   Programkode 1.9.6 e)

En stream er en strøm av verdier. I koden over «omgjøres» tabellen navn til en slik strøm og predikatfunksjonen bokstav plukker ut (det kalles filtrering) de aktuelle verdiene.

I neste eksempel bruker vi samme teknikk som i Programkode 1.9.6 e) til å få skrevet ut partallene i en heltallstabell. Her kan vi bruke et Predicate<Integer>, men her er det mer effektivt med et IntPredicate (se Tabell 1.9.6):

  IntPredicate partall = x -> (x & 1) == 0;            // sann hvis x er partall
  IntConsumer utskrift = x ->  System.out.print(x + " ");

  int[] a = {7, 3, 6, 10, 5, 4, 12, 17, 8, 16};  // en samling heltall
  Arrays.stream(a).filter(partall).forEach(utskrift);
  // Utskrift: 6 10 4 12 8 16

                   Programkode 1.9.6 f)

Funksjonsgrensesnittet IntPredicate har negate, and og or som default-metoder. Hvis vi ønsker å få ut oddetallene, kan vi gjøre det slik:

  Arrays.stream(a).filter(partall.negate()).forEach(utskrift);

I flg. eksempel filtrerer vi slik at vi kun får tallene mellom 5 og 10. Vi lager et predikat p som gir oss de som er større enn 5 og et predikat q som gir de som er mindre enn 10:

  IntPredicate p = x -> x > 5, q = x -> x < 10;
  Arrays.stream(a).filter(p.and(q)).forEach(utskrift);

                   Programkode 1.9.6 g)

DeMorgans to lover sier at hvis p og q er to logiske utsagn, så vil

1. ¬(p ∧ q) = ¬p ∨ ¬q
2. ¬(p ∨ q) = ¬p ∧ ¬q

Vi kan bruke det til å finne tallene som er mindre enn eller lik 5 eller større enn eller lik 10:

  Arrays.stream(a).filter(p.and(q).negate()).forEach(utskrift);

eller

  Arrays.stream(a).filter(p.negate().or(q.negate())).forEach(utskrift);

Legg merke til at p.negate().or(q.negate()) ikke er lik p.negate().or(q).negate(). Her må en være nøye med hvor parentesene står. Se Oppgave 2.

1.	Lag metoden public static String navnlengde(String[] navn, int lengde). Den skal returnere en tegnstreng med de navnene som har en bestemt lengde. F.eks. med tabellen navn i Programkode 1.9.6 e) og lengde = 4, skal metoden returnere strengen [Kari, Arne].
2.	Hva blir resultatet hvis vi bruker p.negate().or(q).negate()?

  1.9.7  «Pipelines» og «streams»
Det engelske ordet pipeline oversettes normalt med rørledning, f.eks. noe som transporterer olje eller gass. Men ordboken «Webster's Dictionary» oppgir også « a channel of information » som betydning. I Java omtales pipeline som « a sequence of aggregate operations ».

En stream (en strøm) er en «bevegelse» av elementer. Det er ikke en datastruktur som lagrer dem. Isteden henter strømmen elementene fra en kilde (eng: source) og fører dem gjennom en serie av operasjoner. En slik operasjon kalles avsluttende (eng: terminal) hvis den avslutter strømmen. Hvis ikke, kalles den mellomliggende (eng: intermediate). Det er serien av operasjoner som definerer «rørledningen».

Programkode 1.9.6 e) inneholder et eksempel på en strøm og operasjoner på strømmen. Vi utvider eksemplet her. For å gjøre det klarere, deler vi opp koden:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};
  Predicate<String> bokstav = x -> x.toUpperCase().indexOf('A') != -1;
  Consumer<String> utskrift = x ->  System.out.print(x + " ");

  Stream<String> s = Arrays.stream(navn);    // en strøm med tabellen som kilde
  s = s.filter(bokstav);                     // en mellomliggende operasjon
  s = s.sorted();                            // en mellomliggende operasjon
  s.forEach(utskrift);                       // Arne Jasmin Kari Margrethe

                   Programkode 1.9.7 a)

I Programkode 1.9.7 a) opprettes det en strøm s ved hjelp av metoden stream() fra klassen Arrays. String-tabellen navn er kilden. Enhver tabell (og også andre datastrukturer) kan være kilde. Setningen: s = s.filter(bokstav); «filtrerer» strømmen. I vårt tilfelle er det de strengene som ikke inneholder bokstaven A, som filtreres vekk. Resultatet er en ny strøm av samme type. Men siden s er en referanse, kan den settes til å referere den nye strømmen.

Det er ikke mulig å utføre flere enn én operasjon på samme strøm. I Programkode 1.9.7 a) ser det ut som at det utføres hele tre operasjoner. Men i setningen s = s.filter(bokstav); returnerer metoden filter() en ny strøm og referansen s blir satt til å peke på den nye strømmen. Det blir på samme måte i setningen: s = s.sorted(); Flg. eksempel viser hva som skjer hvis vi forsøker å utføre to operasjoner på en og samme strøm:

  Stream<String> s = Arrays.stream(navn);    // en strøm med tabellen som kilde
  s.filter(bokstav);                         // første operasjon på s
  s.sorted();                                // andre operasjon på samme strøm
                   Programkode 1.9.7 b)

Programkode 1.9.7 b) gir ingen syntaksfeil, men en kjøring av et program med koden vil gi en IllegalStateException med meldingen: stream has already been operated upon or closed.

De fire siste setningene i Programkode 1.9.7 a) kan skrives som én setning. I tillegg kan koden for predikatet bokstav og konsumenten utskrift settes opp direkte i metodekallene. Dermed kan alt utføres i én lang setning:

  Arrays.stream(navn)                                 // strømmen opprettes
    .filter(x -> x.toUpperCase().indexOf('A') != -1)  // mellomliggende operasjon
    .sorted()                                         // mellomliggende operasjon
    .forEach(x ->  System.out.print(x + " "));        // avsluttende operasjon

                   Programkode 1.9.7 c)

En mellomliggende operasjon (eller instansmetode) er en som som returnerer en Stream. Det gjelder operasjoner som filter(), sorted(), distinct(), limit(), peek() og skip(). Se grensesnittet Stream. Ta f.eks. operasjonen distinct(). Hvis tabellen navn som brukes i Programkode 1.9.7 c), inneholder duplikater, vil operasjonen fjerne dem. Se Oppgave 2.

En avsluttende operasjon (eller instansmetode) er en som terminerer strømmen. I praksis er det operasjoner som ikke returnerer en Stream. Operasjonen forEach() er et eksempel. Den har void som returtype. Grensesnittet Stream har mange slike operasjoner. I flg. eksempel skal vi finne det første (i alfabetisk rekkefølge) av de navnene som inneholder bokstaven A. Operasjonen min() returnerer en Optional og er dermed avsluttende. Den inneholder, hvis det finnes, det første navnet. Her passer vi også på å opprette strømmen på en annen måte:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  Optional<String> min = Stream.of(navn)              // strømmen opprettes
    .filter(x -> x.toUpperCase().indexOf('A') != -1)  // mellomliggende operasjon
    .min(Comparator.naturalOrder());                  // avsluttende operasjon

  System.out.println(min.get());                      // Utskrift: Arne

                   Programkode 1.9.7 d)

Det vil ofte være tilfeller der de eksisterende operasjonene i Stream ikke løser det vi ønsker. Da kan vi opprette en iterator og hente ut elementene fra strømmen ved hjelp av den. I flg. eksempel lager vi som før, en strøm med String-tabellen navn som kilde. Men nå bruker vi en iterator til å finne navnene som inneholder bokstaven A:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  for (Iterator<String> i = Stream.of(navn).iterator(); i.hasNext(); )
  {
    String x = i.next();
    if (x.toUpperCase().indexOf('A') != -1) System.out.print(x + " ");
  }

  // Utskrift: Kari Arne Margrethe Jasmin

                   Programkode 1.9.7 e)

Hvis verdiene allerede ligger i en tabell, kan vi opprette en strøm ved hjelp av den statiske metoden stream() i klassen Arrays eller den statiske metoden of() i grensesnittet Stream:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  Stream<String> s1 = Arrays.stream(navn);    // statisk metode fra Arrays
  Stream<String> s2 = Stream.of(navn);        // statisk metode fra Stream

                   Programkode 1.9.7 f)

Grensesnittet Collection har default-metoden stream(). Det betyr at alle klasser som implementerer Collection har denne metoden. Det gjelder f.eks. klassene ArrayDeque, ArrayList, LinkedList, PriorityQueue, HashSet og TreeSet. Det er klasser som vi kommer til å jobbe med i dette faget. I flg. eksempel flytter vi først verdiene fra en tabell over i en liste (en subtype av List) og deretter lager vi en strøm ved hjelp av metoden stream():

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};

  List<String> liste = Arrays.asList(navn);

  System.out.println(liste.stream().max(Comparator.naturalOrder()).get());
  // Utskrift: Petter
                   Programkode 1.9.7 g)

Hvis vi skal bygge opp en tegnstreng, er det vanlig å bruke en StringBuilder. Det finnes en tilsvarende måte å lage en strøm:

  Stream.Builder<String> sb = Stream.builder();

Legg merke til syntaksen Stream.Builder. Det er fordi grensesnittet Builder er definert inne i grensesnittet Stream. Videre er builder() en statisk metode i Stream som returnerer en instans av en klasse som implementerer Builder. En «strømbygger» kan brukes slik:

  Stream.Builder<String> sb = Stream.builder();       // Stream.Builder

  sb.add("Per").add("Kari").add("Arne").add("Åse")    // legger inn
    .build()                                          // oppretter strømmen
    .filter(x -> x.toUpperCase().indexOf('A') != -1)  // filtrerer
    .sorted()                                         // sorterer
    .forEach(x ->  System.out.print(x + " "));        // Utskrift: Arne Kari

                   Programkode 1.9.7 h)

Det er også mulig å opprette en strøm med en fil som kilde. Filen navn.txt inneholder de samme navnene som String-tabellen navn med ett navn per linje. Hvis du er oppkoblet, kan filen leses ved å bruke "https://www.cs.hioa.no/~ulfu/appolonius/kap1/9/navn.txt" som url. Klassen BufferedReader har metoden lines(). Den returnerer en Stream<String> der hver linje på filen utgjør et strømelement. Flg. eksempel viser hvordan dette virker:

import java.io.*;
import java.net.URL;

public class Program
{
  public static void main(String... args) throws IOException
  {
    String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/9/navn.txt";

    BufferedReader innfil = new BufferedReader
      (new InputStreamReader((new URL(url)).openStream()));    // åpner filen

    innfil                                                     // filen
      .lines()                                                 // en strøm
      .sorted()                                                // sorterer
      .forEach(x -> System.out.print(x + " "));                // skriver ut

    innfil.close();                                            // lukker filen

    // Utskrift: Arne Jasmin Kari Margrethe Per Petter
  }
}
                   Programkode 1.9.7 i)

Hvis en skal teste algoritmer, trenger en ofte tilgang på tilfeldige verdier, f.eks. tilfeldige heltall. Klassen Random har flere metoder som lager tallstrømmer med tilfeldige tall. I flg. eksempel lages en IntStream med 10 tilfeldige heltall fra intervallet [1,100]:

  (new Random()).ints(10, 1, 101).forEach(k -> System.out.print(k + " "));

  // Eksempel på utskrift: 54 97 59 78 46 10 35 74 20 91

                   Programkode 1.9.7 j)

Hvis vi isteden vil ha de tilfeldige tallene i en tabell, kan vi gjøre det slik:

  int[] a = (new Random()).ints(10, 1, 101).toArray();

                   Programkode 1.9.7 k)

I dette avsnittet har vi konsentrert oss om det generiske grensesnittet Stream. De konkrete grensesnittene IntStream, LongStream og DoubleStream fungerer på omtrent samme måte. Hvis vi jobber med heltall eller desimaltall, er disse mer effektive. F.eks. er det normalt mer effektivt å bruke IntStream enn Stream<Integer>. I flg. eksempel er utgangspunktet en int-tabell. Da kan vi finne den største verdien ved hjelp av metoden max() i IntStream. Vi kan få til det samme ved hjelp av metoden max() i Stream<Integer>. Men da trengs en serie konverteringer mellom int og Integer som koster ekstra:

  int[] a = {7,3,12,4,8,11,13,10,9,6};                // int-tabell

  IntStream intStream = IntStream.of(a);              // IntStream
  int maks1 = intStream.max().getAsInt();             // Største verdi lik 13

  Integer[] b = new Integer[a.length];                // Integer-tabell
  for (int i = 0; i < a.length; i++) b[i] = a[i];     // kopierer

  Stream<Integer> integerStream = Stream.of(b);       // Stream<Integer>
  Comparator<Integer> c = Comparator.naturalOrder();  // Comparator
  int maks2 = integerStream.max(c).get();             // Største verdi lik 13

  System.out.println(maks1 + " " + maks2);            // Utskrift: 13 13

                   Programkode 1.9.7 l)

1.	Hva skjer hvis det søkes etter navn med bokstaven B i Programkode 1.9.7 c)?
2.	Legg inn navnet Kari til slutt i tabellen navn som brukes i Programkode 1.9.7 c). Hvis dette kjøres, vil Kari bli skrevet ut to ganger. Legg så inn operasjonen distinct() som nest siste operasjon. Hva skjer da?
3.	Hva skjer hvis det søkes etter navn med bokstaven B i Programkode 1.9.7 d)?

  1.9.8  «Collector» og «Collectors»
Vi må kunne analysere elementene i en strøm, bearbeide dem og eventuelt samle dem i en datastruktur. Målet er å kunne gjøre det på et overordnet nivå, dvs. at strømmen behandles som en helhet og ikke elementene enkeltvis. Slike operasjoner kalles «bulk operations».

Det generiske grensesnittet Stream har mange operasjoner der elementene aksesseres enkeltvis, men egentlig ingen «bulk operations». Ta som eksempel at elementene i en strøm av tegnstrenger skal samles i en liste. Dette kunne vi gjøre slik:

  String[] navn = {"Per","Kari","Arne","Petter","Margrethe","Jasmin"};
  Stream<String> navnstrøm = Stream.of(navn);     // en strøm av navn

  List<String> liste = new ArrayList<>();         // oppretter en liste
  navnstrøm.forEach(x -> liste.add(x));           // legger inn i listen

  System.out.println(liste);                      // skriver ut
  // Utskrift: [Per, Kari, Arne, Petter, Margrethe, Jasmin]

                   Programkode 1.9.8 a)

I koden over bruker vi operasjonen forEach() til å legge ett og ett element over i listen. Heldigvis har Stream to collect-operasjoner. Den ene har en Collector som parametertype og den kan hjelpe oss her. Den har flg. syntaks:

  <R,A> R collect(Collector<? super T, A, R> collector)    // operasjon i Stream

Her inngår hele tre generiske typeparametere. T er typen til elementene i strømmen og R er typen til returverdien. Parameter A kan i en del tilfeller være hva som helst. Java har ingen egen eksplisitt klasse som implementerer Collector, men samleklassen Collectors har en serie med (statiske) metoder som returnerer en Collector. F.eks. denne:

  public static <T> Collector<T, ? ,List<T>> toList()     // metode i Collectors

Når den brukes i operasjonen collect(), står T for elementtypen og List<T> for returtypen R. Det inngår også et spørsmålstegn ?. Det betyr at typeparameter A ikke har betydning. Vi kan nå få til det samme som i Programkode 1.9.8 a) ved hjelp av flg. kode:

  List<String> liste = navnstrøm.collect(Collectors.toList());

                   Programkode 1.9.8 b)

Det fremgår ikke av koden over hva slags liste vi får. Det er nok enten ArrayList eller LinkedList. Men dette kan vi finne ut ved å be om navnet på klassen til den instansen som variabelen liste refererer til. Da vil vi finne at det er en ArrayList (se også Oppgave 1):

  System.out.println(liste.getClass().getName());  // Utskrift: java.util.ArrayList

I forrige avsnitt brukte vi metoden filter() i Stream til å «filtrere» en strøm. Navn som ikke inneholdt bokstaven A ble filtrert vekk. Nå skal vi isteden samle dem i to lister der den ene skal inneholde navnene der A inngår og den andre de øvrige navnene. Klassen Collectors har metoden partitioningBy() som gjør dette for oss:

  public static <T> Collector<T, ?, Map<Boolean,List<T>>>
    partitioningBy(Predicate<? super T> predicate)

Nå vil String svare til T og vi kan bruke samme predikat som i Programkode 1.9.7 a):

  Predicate<String> bokstav = x -> x.toUpperCase().indexOf('A') != -1;

  Map<Boolean,List<String>> map =      // navnstrøm er som i Programkode 1.9.8 a)
    navnstrøm.collect(Collectors.partitioningBy(bokstav));

  System.out.println(map.get(true) + " " + map.get(false));
  // Utskrift: [Kari, Arne, Margrethe, Jasmin] [Per, Petter]  

                   Programkode 1.9.8 c)

Metoden partitioningBy() deler strømmen i to og samler delene i to lister. Collectors har også metoden groupingBy():

public static <T,K> Collector<T,?,Map<K,List<T>>>
  groupingBy(Function<? super T,? extends K> classifier)

Den kan f.eks. brukes til å gruppere navn etter lengde. I tabellen navn er det ett navn med tre bokstaver (Per), to med fire bokstaver, ingen med fem, osv. Metoden vil returnere en Map der strenglengde (K = Integer) blir nøkkelverdi (key) og en liste (List<String>) som verdi:

  Map<Integer,List<String>> map =      // navnstrøm er som i Programkode 1.9.8 a)
    navnstrøm.collect(Collectors.groupingBy(String::length));

  for (Integer i : map.keySet()) System.out.print(map.get(i) + " ");
  // Utskrift: [Per] [Kari, Arne] [Petter, Jasmin] [Margrethe]

                   Programkode 1.9.8 d)

Legg merke til kortformen String::length. Det står får funksjonen som til en tegnstreng gir strengens lengde. Dette kunne også vært satt opp slik: x -> x.length().

Collectors har mange andre metoder enn toList(), partitioningBy() og groupingBy(). Noen av dem blir tatt opp i oppgavene.

1.	I Programkode 1.9.8 b) fikk vi ArrayList. Bruker vi isteden metoden toCollection() i Collectors, kan vi selv velge listetype, f.eks. LinkedList. Gjør det!
2.	Collectors har metoden toSet(). Den samler elementene i en mengde (Set). Bruk den! Ta f.eks. utgangspunkt i Programkode 1.9.8 b). Vi får en HashSet. Vis at det stemmer! Bruk så toCollection() til å gi en TreeSet. Vi kan bruke toCollection() til å samle elementene i en hvilken som helst datastruktur av typen Collection. Prøv f.eks. med en PriorityQueue.
3.	Bruk en joining()-metode i Collectors til å samle alle elementene i en tegnstreng. Ta f.eks. utgangspunkt i strømmen navnstrøm og lag en tegnstreng som inneholder alle navnene adskilt med komma og mellomrom og innrammet med [ og ]. Lag også den metoden det blir bedt om i Oppgave 1 i Avsnitt 1.9.6 ved hjelp av kun én setning.
4.	Ta utgangspunkt i klassen Student og Student-tabellen Avsnitt 1.4.5. Lag en Map som i Programkode 1.9.8 d) der klasse (String) er nøkkelverdi.