LZW-algoritmen er den som ligger under GIF-formatet (Graphics Interchange Format) for grafikk på web-sider og er oppkalt etter A.Lempel, J.Ziv og T.Welch. Den komprimerer uten tap (eng: lossless compression). En dekomprimering gir dermed nøyktig det som opprinnelig ble komprimert. Lempel og Ziv beskrev i 1978 en algoritme som i dag går under navnet LZ78. En modifisering av algoritmen, gjort av T.Welch i 1983, gjorde at den fikk stor utbredelse. Algoritmen ble imidlertid patentert. Men det var først flere år senere og etter at GIF-formatet var lansert, at Unisys, selskapet som eide patentet, begynte å håndheve det. Det førte til mange kontroverser og resulterte bl.a. i utarbeidelsen av det patentfrie PNG-formatet (Portable Network Graphics). Der brukes en kombinasjon av LZ77 (også laget av Lempel og Ziv) og Huffmans algoritme. I dag er alle patenter utløpt og LZW-algoritmen kan brukes fritt.
På dagens web-sider vil en finne grafikk både i GIF- og PNG-format. Alle grafikkverktøy tilbyr begge formatene. Disse to egner seg først og fremst når det er få farger og store flater med samme farge, f.eks. for tegninger. Men hvem av dem skal en velge? Det heter seg at PNG generelt komprimerer litt bedre enn GIF, men det er også eksempler der GIF er best. Hvis en kjenner detaljene i algoritmene som ligger bak de to formatene, vil det i mange tilfeller være mulig å forutsi hvilken som gir best komprimering. Men løsningen er nok å bruke begge formatene og så sjekke hvilket av dem som gir best resultat.
 |
 |
 |
 |
|||
| PNG: 2102 byter | GIF: 2685 byter | PNG: 1261 byter | GIF: 1213 byter |
I figuren over er det fire forekomster av Java-logoen. De to første er identiske - den første har PNG-format og den andre GIF-format. Her ser vi at PNG er bedre enn GIF. De to siste er også identiske, men hvis en ser nøyere etter vil en oppdage at de to har færre farger enn de to første. Det gir bedre komprimering og i dette tilfellet er GIF litt bedre enn PNG.
Filene over er laget med samme grafikkverktøy. Et annet verktøy vil kunne gi andre filstørrelser. Det finnes
mange optimaliseringsteknikker. Det er også forskjeller mellom GIF og PNG på andre områder enn
komprimeringsgrad. PNG tillater flere farger enn GIF. GIF tillater animasjon, men ikke PNG. Se
oppgavene.
| 1. | Les mer om de to grafikkformatene. Start f.eks. med Wikipedia-artiklene om PNG og GIF. |
| 2. | I Windows har «Snipping Tool» formatene PNG, GIF og JPEG. Gjør en «snip» og ta vare på resultatet i alle de tre formatene. Sammenlign filstørrelsene. |
| 3. | Lag en GIF-animasjon. De fleste grafikkverktøyene tilbyr denne muligheten. |
Gitt at vi har en «melding» (en sekvens med tegn). Komprimeringsidéen er at hyppige «ord» i meldingen skal erstattes med tall. Hvis tallet har få siffer vil det kunne representeres med færre biter enn «ordet». Husk at idéen i Huffmans algoritme var å bruke prefikskoder og at hyppige
tegn skulle representeres med en kort bitkode (færre enn 8 biter).
Idéen i LZW er å bygge opp en «ordbok» mens meldingen leses. Hvert nytt «ord» i meldingen legges inn i ordboken og får samtidig tilordnet en tallkode. Hvis et ord blir funnet i ordboken, blir det isteden representert ved tallkoden. Hvis tallkodene i gjennomsnitt blir kortere (har færre biter) enn ordene, får vi en komprimering. Grunnen til at «ord» står i anførselstegn er at det her ikke menes vanlige ord, men kun «ord» i form av tegnkombinasjoner på minst to tegn. F.eks. er det i dette lille avsnittet på 8 linjer 17 vanlige ord som slutter med en n. Det betyr at tegnkombinasjonen «n » (n + mellomrom) forekommer 17 ganger. Målet er da å få den representert med et heltall som har færre enn 16 biter (2 byter).
Algoritmen for komprimering med LZW kan beskrives slik:
- Vi har en «melding» i form av en tegnsekvens. I algoritmen
inngår tegnetc, tegnstrengensog heltallenekodeognestekode.
- La
cvære første tegn i meldingen. - La
sha tegnetcsom innhold. - La
kodevære tallverdien tilc. - La
nestekodevære lik 256.
- La
- Er det flere tegn i sekvensen?
- Hvis nei, skriv ut
kodeog avslutt! - Hvis ja, sett
clik neste tegn i sekvensen.
- Hvis nei, skriv ut
- Ligger tegnstrengen
s+ci ordboken?- Hvis nei,
- legg
s+ci ordboken mednestekodesom ordkode - la
sfåcsom innhold - skriv ut
kode - sett så
kodelik tallverdien tilc - øk
nestekodemed 1
- legg
- Hvis ja,
- la
kodevære ordkoden tils+c - sett
sliks+c
- la
- Hvis nei,
- Gå tilbake til 2.
Algoritme 7.2.2 - komprimering
Eksempel 1: La "ABBABABAC" være en «melding».
I pkt. 1 settes startverdier for variablene c, s,
kode og nestekode. Vi sier at det er starten eller «runde» 0.
Der blir c = 'A', s = "A", kode = 65 og
nestekode = 256. Vi går så til pkt. 2 i algoritmen. Det kan vi si er «runde» 1.
Der blir c = 'B'. I pkt. 3 legges s + c = "AB"
(sammen med nestekode = 256) i ordboken, s settes lik "B",
kode = 65 skrives ut og settes så lik 66 (tallverdien til c = 'B') og
nestekode økes med 1 til 257.
Flg. tabell viser innholdet i de forskjellige variablene, hva som legges i ordboken og hva som skrives ut i
de forskjellige rundene i algoritmen:
runde | c | ordbok | s | utskrift | kode | nestekode |
| 0 | A | A | 65 | 256 | ||
| 1 | B | AB - 256 | B | 65 | 66 | 257 |
| 2 | B | BB - 257 | B | 66 | 66 | 258 |
| 3 | A | BA - 258 | A | 66 | 65 | 259 |
| 4 | B | AB | 256 | |||
| 5 | A | ABA - 259 | A | 256 | 65 | 260 |
| 6 | B | AB | 256 | |||
| 7 | A | ABA | 259 | |||
| 8 | C | ABAC - 260 | C | 259 | 67 | 261 |
| 9 | 67 |
Ord i ordboken har minst to tegn. Et enkelt tegn kunne også ha bli sett på som et ord. Men de trengs ikke i ordboken. De har allerede tallkode, dvs. tegnets bitsekvens tolket som et tall.
Eksempel 2:
Hvis meldingen har lange sekvenser med samme tegn, bedres komprimeringen.
Ta "AAAAAAAAAAA" som eksempel. Flg. tabell viser hva som da vil skje:
runde | c | ordbok | s | utskrift | kode | nestekode |
| 0 | A | A | 65 | 256 | ||
| 1 | A | AA - 256 | A | 65 | 65 | 257 |
| 2 | A | AA | 256 | |||
| 3 | A | AAA - 257 | A | 256 | 65 | 258 |
| 4 | A | AA | 256 | |||
| 5 | A | AAA | 257 | |||
| 6 | A | AAAA - 258 | A | 257 | 65 | 259 |
| 7 | A | AA | 256 | |||
| 8 | A | AAA | 257 | |||
| 9 | A | AAAA | 258 | |||
| 10 | A | AAAAA - 259 | A | 258 | 65 | 260 |
| 11 | 65 |
| 1. | Tall (uten fortegn, eng: unsigned) mindre enn 256 trenger 8 biter og tall fra 256 til 511 trenger 9 biter. Hvor mye plass trengs
da for utskriftene i Eksempel 1 og
Eksempel 2?
|
| 2. | I Eksempel 2 har meldingen 11 A-er. Hvordan blir det
med 16 A-er?
|
| 3. | Hva blir resultatet for flg. meldinger:
a) "ABAABBAAABBBC", b) "ABABABABABAB", c) "MISSISSIPPI", d) "AABACADAEAFAG". |
| 4. | Hvis grafikk med striper (f.eks. et flagg) roteres 180 grader, vil stripene skifte retning. Da vil horisontale striper gi bedre komprimering (med GIF) enn vertikale. Sjekk det! |
Beskrivelsen av
LZW-algoritmen (og eksemplene 1 og
2) gir en del utfordringer når
dette skal kodes profesjonelt. Målet er da å lage en metode som komprimerer innholdet
av en fil og som legger resultatet på en annen fil:
- Komprimeringen resulterer i en serie heltall. De må «lagres» med minst mulig bruk av plass, men samtidig på en slik form at de kan dekomprimeres.
- De fleste ordene i ordboken vil ikke bli brukt senere. Hvis meldingen er stor, vil også ordboken kunne bli stor. Ordboken må derfor utformes på en slik måte at vi ikke sløser med plassen.
- Det er søking og innlegging i ordboken kontinuerlig. De to operasjonene må derfor være effektive for at algoritmen skal bli effektiv.
- Tallkoden
nestekodeøker med én om gangen. For en stor melding vil tallkodene kunne bli så store at de krever større plass enn de ordene de skal erstatte.
Vi lager først en metode som demonstrerer logikken i algoritmen. Der bryr vi oss ikke om de «problemene» som er
skissert ovenfor. Optimaliseringene tar vi senere. Vi lar «meldingen» være en tegnstreng, dvs. en instans av
klassen String. Vi skal kunne slå opp i
ordboken med et ord (en tegnstreng) som oppslagsord og få tilbake ordets tallkode.
Til det bruker vi en Map, f.eks. en HashMap med
String og Integer som typeparametere:
Map<String, Integer> ordbok = new HashMap<>();
Vi trenger to metoder. Først en som komprimerer og deretter en som dekomprimerer. Men dekomprimeringen venter vi
med. Den tas opp i neste avsnitt. Metodene legger vi i klassen LZW. Den hører hjemme i samme
mappe som klassen Huffman, dvs.
under bitio.
I algoritmebeskrivelsen står det at tallkodene
«skrives ut». Her skal vi gjøre det litt mer anvendbart og isteden legge tallene i en liste. Dekomprimeringen gjøres
fra en tilsvarende liste og resultatet blir en tegnstreng:
package bitio; import java.util.*; import java.io.*; import java.net.URL; public class LZW { public static List<Integer> komprimer(String melding) // komprimeringsmetode { throw new UnsupportedOperationException(); } public static String dekomprimer(List<Integer> koder) // dekomprimeringsmetode { throw new UnsupportedOperationException(); } } // LZW Programkode 7.2.3 a)
Flg. metode er en direkte oversettelse av algoritmebeskrivelsen.
Den skal erstatte det som er satt opp i klassen LZW:
public static List<Integer> komprimer(String melding) { char c = melding.charAt(0); // første tegn i meldingen String s = String.valueOf(c); // tegnstrengen med c som innhold int kode = c; // tallkoden til c int nestekode = 256; // første ledige tallkode Map<String,Integer> ordbok = new HashMap<>(); // en ordbok List<Integer> resultat = new ArrayList<>(); // resultatliste for (int i = 1; i < melding.length(); i++) // resten av meldingen { c = melding.charAt(i); // neste tegn i meldingen Integer ordkode = ordbok.get(s + c); // søker etter s + c if (ordkode == null) // s + c er ikke i ordboken { ordbok.put(s + c, nestekode++); // legger s + c i ordboken s = String.valueOf(c); // setter s = c resultat.add(kode); kode = c; // kode blir tallkoden til c } else // s + c er i ordboken { kode = ordkode; // kode = ordkoden til s + c s = s + c; // setter s = s + c } } resultat.add(kode); // alle tegn er behandlet return resultat; } Programkode 7.2.3 b)
I flg. eksempel «komprimereres» meldingene fra
Eksempel 1 og
Eksempel 2. Kjør koden
og sjekk at utskriften blir som oppgitt i tabellene:
System.out.println(LZW.komprimer("ABBABABAC")); // [65, 66, 66, 256, 259, 67] System.out.println(LZW.komprimer("AAAAAAAAAAA")); // [65, 256, 257, 258, 65] Programkode 7.2.3 c)
| 1. | Sjekk at resultatet blir likt
Programkode 7.2.3 b)
med TreeMap istedenfor HashMap.
|
| 2. | Bruk meldingene fra Oppgave 3 i Avsnitt 7.2.2 i
Programkode 7.2.3 c).
|
| 3. | Vi kan sjekke ordbokens innhold
Programkode 7.2.3 b) for eksempel ved å bruke
Map<String,Integer> som returtype og avslutte med
return ordbok;.
|
| 4. | Legg inn utskriftssetninger i
Programkode 7.2.3 b)
slik at innholdet i alle variablene blir skrevet ut i hver runde. Dvs. slik tabellen
i Eksempel 1 viser.
|
Komprimeringen i LZW-algoritmen genererer en sekvens med heltall der første tall er mindre enn 256. Denne sekvensen er utgangspunktet for dekomprimeringen. Tallene brukes da til å bygge opp en ordbok med samme innhold som den som ble laget under komprimeringen, men nå blir tallkoden «nøkkel» og ordet den tilhørende verdien. I dekomprimeringen skal vi også ha en variabel
nestekode som starter på 256. Det betyr at hver gang
vi i tallsekvensen får et tall som er mindre enn nestekode, så må det tallet være
mindre enn 256 (hører til et ord med ett tegn) eller ligge i ordboken som ordkode til et ord.
Algoritmen for dekomprimering med LZW kan beskrives slik:
- Vi har en sekvens med tallkoder der den første er mindre enn 256. I algoritmen
inngår heltallenekodeognestekode, tegnetcog tegnstrengenesogt.
- La
kodevære første tallkode i sekvensen. - La
tforeløpig være udefinert. - La
svære tegnstrengen som harkodesitt tegn som innhold. Hvis f.eks.kodeer lik 65, så blirslik "A". - La
cforeløpig være udefinert. - Skriv ut
s. - La
nestekodevære lik 256.
- La
- Er det flere tallkoder igjen i sekvensen?
- Hvis nei, avslutt.
- Hvis ja,
- sett
kodelik neste tallkode fra sekvensen - sett
tliks.
- sett
- Er
kodemindre ennnestekode?- Hvis ja, (da hører
kodetil et tegn eller til et ord i ordboken)- sett
slik ordet som hører tilkode - sett
clik første tegn is
- sett
- Hvis nei, (da er
kode- sett
clik første tegn it - sett
slikt+c
- sett
- Hvis ja, (da hører
- Deretter:
- skriv ut
s - legg
nestekodei ordboken medt+csom tilhørende ord - øk
nestekodemed 1 - gå tilbake til 2.
- skriv ut
Algoritme 7.2.4 - dekomprimering
Eksempel 3: I eksempel 1 ble
«meldingen» "ABBABABAC" komprimert og det gav 65, 66, 66, 256, 259, 67 som resultat. Dette betyr
at det i dekomprimeringen blir færre «runder» enn komprimeringen siden det er færre tallkoder (6 stykker)
enn tegn i meldingen (9 tegn). Men ordboken inneholder det samme. Forskjellen er at i komprimeringen er det ord med
tihørende ordkode, mens det i dekomprimeringen er ordkoder med tilhørende ord:
runde | kode | t | s | c | utskrift | ordbok | nestekode |
| 0 | 65 | A | A | 256 | |||
| 1 | 66 | A | B | B | B | 256-AB | 257 |
| 2 | 66 | B | B | B | B | 257-BB | 258 |
| 3 | 256 | B | AB | A | AB | 258-BA | 259 |
| 4 | 259 | AB | ABA | A | ABA | 259-ABA | 260 |
| 5 | 67 | ABA | C | C | C | 260-ABAC | 261 |
I 4. runde er koden lik 259, men det hører ikke til et ord som allerede ligger i ordboken. Der inngår
kun kodene 256, 257 og 258 med AB, BA og BB som tilhørende ord. Vi ser at 259 sammen med ordet ABA blir
lagt inn i ordboken etterpå. Dette problemet oppstår når det i meldingen inngår en delsekvens med en
bestemt symmetri og innhold. Det er i slike tilfeller variabelen t kommer til nytte.
Hvis vi ikke, ville det vært nok med variabelen s.
Dette tar vi opp lenger ned.
Kode for dekomprimeringen får vi ved nærmest å gjøre en avskrift av
Algoritme 7.2.4:
public static String dekomprimer(List<Integer> koder) { int kode = koder.get(0); // første tallkode er < 256 String t; // foreløpig udefinert String s = String.valueOf((char)kode); // ord med ett tegn char c; // foreløpig udefinert StringBuilder resultat = new StringBuilder(s); // til å lagre resultatet int nestekode = 256; // nestekode lik 256 Map<Integer,String> ordbok = new HashMap<>(); // en ordbok for (int i = 1; i < koder.size(); i++) // resten av tallene { kode = koder.get(i); // neste tall t = s; // t settes lik s if (kode < nestekode) // kode er i ordboken { s = kode < 256 ? String.valueOf((char)kode) // ny verdi på s : ordbok.get(kode); c = s.charAt(0); // c lik første tegn i s } else // kode er ikke i ordboken { c = t.charAt(0); // c lik første tegn i t s = t + c; // s lik t + c } resultat.append(s); // lagrer s ordbok.put(nestekode, t + c); // legger inn i ordboken nestekode++; // øker nestekode med 1 } return resultat.toString(); } Programkode 7.2.4 a)
I flg. eksempel komprimeres først meldingen "ABBABABAC" der tallkodene havner i en liste. Så dekomprimeres dette ved å hente tallkodene fra listen og resultatet skrives ut:
System.out.println(LZW.dekomprimer(LZW.komprimer("ABBABABAC"))); // Utskrift: ABBABABAC Programkode 7.2.4 b)
Komprimeringen av "ABBABABAC" (se Eksempel 1) gav
utskriften 65, 66, 66, 256, 259, 67. Dekomprimeringen av den vises i
Eksempel 3. Der ser vi
at koden 259 blir lest inn i 4. runde og så blir den lagt inn ordboken sammen med "ABA". Men hvordan
kan vi vite at 259 hører til "ABA" når ordboken ikke på forhånd inneholder 259 som oppslagskode?
Svaret finner vi i Eksempel 1. Generelt
gjelder (se algoritmen) at hvis
s + c
ikke ligger i ordboken, så legges den inn og koden til s blir skrevet ut.
I Eksempel 3 ser vi at 259 leses inn
rett etter 256. Men 256 representerer "AB" siden 256 allerede ligger i ordboken. Det betyr at
i komprimeringen ble s + c der s = "AB" og
c foreløpig er ukjent, lagt inn i ordboken før 256 ble skrevet ut. I algoritmen
settes så s = c og c settes lik neste tegn i meldingen.
Anta at s ikke er lik "A". Hvis s + c
ikke lå i ordboken, så måtte koden til s (s har bare ett tegn)
ha blitt skrevet ut. Men det var 259 som ble
skrevet. Anta at s + c lå ordboken. Da blir
s satt lik s + c og
c lik neste tegn. Hvis det som nå er s + c ikke lå der,
så ville koden til s ha blitt skrevet ut.
Men da må den ha blitt lagt inn der tidligere. Osv. I komprimeringen må det med andre ord ha
vært "ABA" som ble lagt inn i ordboken i samme runde som 256 ble skrevet ut.
Komprimeringen vil nå forsette med å sette c = A (siste tegn i "ABA"), så
s = c og c lik neste tegn. Da må
c være lik B. Hvis ikke, kan vi ved hjelp av argumenter som de over, si at da måtte en
kode som allerede lå i ordboken, ha blitt skrevet ut. Neste tegn i meldingen må være A. Hvis ikke, måtte
en kjent kode ha blitt skrevet ut. Dermed (i komprimeringen) må vi ha fått
s = "ABA". Uansett hva neste tegn c er, så kan ikke
s + c ligge i ordboken. Dermed skrives koden til "ABA" ut og må være
259 siden det er den vi fikk etter 256.
Det at det i dekomprimeringen kommer en tallkode før et ord med den koden er lagt inn i ordboken,
oppstår når ordboken på forhånd inneholder Tegn+Ord og det senere i
meldingen kommer kombinasjonen
Tegn+Ord+Tegn+Ord+Tegn.
I eksemplet over var Tegn = A og Ord = "B". Her kan Ord være et tomt ord.
Ta meldingen "ABAAA" som et eksempel. Komprimeringen (se algoritmen)
vil gi 65, 66, 65, 258 som utskrift. Dette dekomprimeres slik:
runde | kode | t | s | c | utskrift | ordbok | nestekode |
| 0 | 65 | A | A | 256 | |||
| 1 | 66 | A | B | B | B | 256-AB | 257 |
| 2 | 65 | B | A | A | A | 257-BA | 258 |
| 3 | 258 | A | AA | A | AA | 258-AA | 259 |
I 3. runde kommer koden 258, men den ligger ikke i ordboken. Der ligger kun 256 og 257.
| 1. | Sjekk hva som skjer når "ABAAA" komprimeres. |
| 2. | I meldingen "ABAAA" er Tegn = A og Ord = "" (dvs. tomt) og i
"ABBABABAC" er Tegn = A og Ord = "B". Lag et
eksempel der Tegn = A og Ord har to tegn.
|
| 3. | Bruk en ArrayList som ordbok i Programkode 7.2.4 a)
istedenfor en HashMap.
|
Metodene
komprimering
og dekomprimering er laget for å demonstrere
hvordan LZW virker. Men nå skal vi lage versjoner av dem som kan brukes i praksis - f.eks. til å komprimere
innholdet av en fil og legge resultatet på en annen fil. I begynnelsen av
Avsnitt 7.2.3 ble det satt opp en del problemstillinger som
en må ta utgangspunkt i når dette skal kodes:
1) Variabelen nesteKode øker med 1 for hver ordboksinnlegging. Hvis «meldingen» er
stor, vil ordboken kunne bli stor og dermed føre til store tallkoder.
Komprimeringen kan «stoppe opp» hvis de blir for store. En tallkode som skal erstatte et ord, vil
da kunne bruke mer plass enn ordet selv. Flg. tabell viser plassbehovet for heltall:
 |
Vi skal senere teste dette på et av kompendiets største delkapitler, dvs. Delkapittel 1.3. Filen er på 411kB (høsten 2021). En komprimering vil gi 65278 ord i ordboken. Vi kan her klare oss med 16 biter som grense (til og med tallet 65535). Deretter legger vi ikke flere ord i ordboken. Men komprimeringen fortsetter. Mange av ordboksordene vil bli funnet på nytt. En mulighet er å øke grensen til f.eks. 17 eller 18 biter.
2) De heltallene som komprimeringen gir, må lagres med minst mulig bruk av plass. Første heltall er alltid i intervallet 0 - 255 siden en hvilket som helst kombinasjon av 8 biter (en byte) kan være første tegn i meldingen. Deretter vil det normalt, før eller senere, komme et heltall som er minst 256. Men da holder det ikke lenger med 8 biter. Bitkoden for 256 er 100000000, dvs. 9 biter. Neste grense er 512 = 1000000000 som har 10 biter. Osv.
Vi bør derfor skrive ut tallkodene med 8 biter så lenge som de er mindre enn 256, deretter med 9 biter så lenge som de er mindre enn 512, osv. Ved innlesing må vi da først lese 8 biter om gangen. Men når skal vi da gå over fra å lese 8 til å lese 9 biter? Vi trenger et «flagg», dvs. en tallkode som signaliserer at her skal vi skifte innlesingsformat. Vi kan ikke velge et tall fra 0 til 255 som flagg siden et slikt tall representerer et mulig tegn i meldingen. Første mulighet for et flagg er derfor 256. Men vi kan ikke finne 256 ved å lese 8 biter om gangen. Det løser vi med å skrive ut med 9 biter fra starten av og gjøre det så lenge som tallkodene er mindre enn 512, så går vi over til 10 biter, osv. «Flagget» 256 skrives ut når skiftet skjer.
Til disse formålene innfører vi flg. tallkonstanter i klassen
LZW:
private static final int LZW_GRENSE = 16; // maks antall biter private static final int MAKS = (1 << LZW_GRENSE) - 1; // maks tallkode private static final int NYTT_BITFORMAT = 256; // et flagg private static final int FØRSTE_KODE = 257; // første ledige kode Programkode 7.2.5 a)
Vi bruker klassen BitOutputStream til filutskift med variabelt antall biter. Dermed
kan vil lage flg. generelle komprimeringsmetode. Den henter «meldingen» fra
en InputStream og sender
resultatet til en BitOutputStream. Legg merke
til at første ledige kode er nå 257 (og ikke 256 som i oppskriften):
public static int komprimer(InputStream inn, BitOutputStream ut) throws IOException { int bitformat = 9, bitGrense = 512; // starter med 9 biter int c = inn.read(); // leser inn første byte if (c == -1) return 0; // inn er tom int antallInnlesteTegn = 1; // første tegn Map<String,Integer> ordbok = new HashMap<>(); // ordboken String s = String.valueOf((char)c); // må bruke char her int kode = c; // setter kode = c int nesteKode = FØRSTE_KODE; // første ledige tallkode while ((c = inn.read()) != -1) // slutt hvis c er -1 { antallInnlesteTegn++; // et nytt tegn Integer ordkode = ordbok.get(s + (char)c); // søker etter s + c if (ordkode == null) // fant ikke s + c { while (kode >= bitGrense) // sjekker størrelsen { ut.writeBits(NYTT_BITFORMAT,bitformat); // setter inn flagget bitformat++; // øker bitformat med 1 bitGrense <<= 1; // dobler bitGrense } ut.writeBits(kode, bitformat); // skriver ut koden if (nesteKode < MAKS) // sjekker størelsen { ordbok.put(s + (char)c, nesteKode); // nytt ord i ordboken nesteKode++; // øker nesteKode med 1 } s = String.valueOf((char)c); // setter s = c kode = c; // setter kode = c } else // fant s + c i ordboken { kode = ordkode; // tallkoden til s + c s += (char)c; // legger c bakerst i s } } while (kode >= bitGrense) // sjekker før utskrift { ut.writeBits(NYTT_BITFORMAT,bitformat); // setter inn flagget bitformat++; // øker bitformat med 1 bitGrense <<= 1; // dobler bitGrense } ut.writeBits(kode,bitformat); // skriver ut siste kode return antallInnlesteTegn; // returnerer antallet } Programkode 7.2.5 b)
Vi lager en tilsvarende dekomprimeringsmetode.
Utgangspunktet er Programkode 7.2.4 a).
Men nå skal kodene hentes fra en
BitInputStream og utskriften skal gå til en
OutputStream:
public static void dekomprimer(BitInputStream inn, OutputStream ut) throws IOException { int bitformat = 9; // starter med 9 biter int kode = inn.readBits(bitformat); // leser først tallkode if (kode == -1) return; // inn er tom Map<Integer,String> ordbok = new HashMap<>(); // oppretter ordboken int nesteKode = FØRSTE_KODE; // første ledige tall String s = String.valueOf((char)kode); // første kode String t; // hjelpevariabel char c; // hjelpevariabel ut.write(kode); // skriver ut while ((kode = inn.readBits(bitformat)) != -1) // resten av kodene { while (kode == NYTT_BITFORMAT) // skifter bitformat { bitformat++; // øker bitformat med 1 kode = inn.readBits(bitformat); // leser neste kode } t = s; // setter t = s if (kode < nesteKode) // kode er i ordboken { s = kode < 256 ? String.valueOf((char)kode) : ordbok.get(kode); c = s.charAt(0); // c = første tegn i s } else // ukjent kode { c = t.charAt(0); // c = første tegn i t s = t + c; // setter s = t + c } ut.write(s.getBytes()); // skriver ut s ordbok.put(nesteKode++, t + c); // nytt ord i ordboken } } Programkode 7.2.5 c)
Programkode 7.2.3 b) har en tegnstreng som parameter.
Programkode 7.2.5 b) er mer generell, men kan
brukes på en tegnstreng. Ta "ABBABABAC" som eksempel
(Eksempel 1). Vi konverterer den til
en byte-tabell og den legges i en ByteArrayInputStream som jo er en InputStream.
Under komprimeringen blir bitene implisitt lagt i en ByteArrayOutputStream.
Har du Programkode 7.2.5 b)
og c) i klassen
LZW og i tillegg de to klassene
BitInputStream og
BitOutputStream i ditt prosjekt, vil flg. kode virke:
public static void main(String... args) throws IOException { byte[] b = "ABBABABAC".getBytes(); // byte-tabell InputStream fra = new ByteArrayInputStream(b); // InputStream ByteArrayOutputStream ut = new ByteArrayOutputStream(); // OutputStream BitOutputStream til = new BitOutputStream(ut); // BitOutputStream LZW.komprimer(fra, til); // komprimerer fra.close(); til.close(); // lukker byte[] c = ut.toByteArray(); // byte-tabell System.out.println(Arrays.toString(c)); // komprimert melding // Utskift: [32, -112, -120, 80, 24, 33, 12] } Programkode 7.2.5 d)
Kan dette stemme? I Programkode 7.2.3 c)
er utskriften [65, 66, 66, 256, 259, 67], men det kan vi ikke forvente nå. Som nevnt over brukes
256 som et «flagg» for å signalisere en bitlengdeøkning. Nå er 257 første nye tallkode.
Derfor må det bli [65, 66, 66, 257, 260, 67].
Nå brukes imidlertid variabel bitkodelengde - 9 biter fra start, så 10 biter når det trengs, osv.
Med 9 biter: 65 = 001000001, 66 = 001000010, 257 = 100000001, osv.
Tilsammmen for de 6 tallene får vi flg. sekvens der 9 og 9 biter har fått rød/blå farge:
001000001001000010001000010100000001100000100001000011 65 66 66 257 260 67
Når dette skal lagres i en byte-tabell må sekvensen deles opp i 8 og 8 biter:
001000001001000010001000010100000001100000100001000011 32 -112 -120 80 24 33
De første 8 bitene er 00100000 og det er bitkoden for 32. De neste 8 bitene er 10010000 og det er et negativt byte-tall
siden 1 er første binære siffer. Komplementet (dvs. 01101111) pluss 1 blir 01110000
og det er bitkoden for 112 (dvs. 64 + 32 + 16). Dermed er 10010000 som vi startet med, lik −112. Tilsvarende blir det for
resten. Til slutt i bitsekvensen står det 000011. Her legges det på to ekstra 0-biter for å få 8. Dermed
00001100 = 12.
Vi kan utvide Programkode 7.2.5 d) og
gjøre en dekomprimering. Den komprimerte meldingen ligger i ut, dvs. i en ByteArrayOutputStream.
Internt har den en bytetabell c og den kan vi legge i en ByteArrayInputStream.
Utskriften kan gå direkte til konsollet, dvs. til System.out.
Det går bra siden System.out er en OutputStream. Legg flg. nederst
i Programkode 7.2.5 d):
InputStream tallkoder = new ByteArrayInputStream(c); // InputStream BitInputStream les = new BitInputStream(tallkoder); // BitInputStream LZW.dekomprimer(les, System.out); System.out.close(); // ABBABABAC Programkode 7.2.5 e)
Normalt vil det en skal komprimere eller dekomprimere ligge på en fil. Resultatet vil en normalt sende til en lokal fil.
For å gjøre det enkelt lager vi metoder der filnavnene inngår som parametre. Generelt vil vi kreve at
navnet oppgis på URL-form (normalt https som protokoll fra nettet og file som protokoll lokalt)
for filer som skal leses.
Flg. to metoder benytter de generelle metodene
Programkode 7.2.5 b)
og c). Det vi gjør er å konvertere filnavn til en Stream
av passende type:
public static int komprimer(String fraUrl, String tilFil) throws IOException { InputStream fra = new BufferedInputStream((new URL(fraUrl)).openStream()); BitOutputStream til = new BitOutputStream(new FileOutputStream(tilFil)); int antallInnlesteTegn = LZW.komprimer(fra, til); fra.close(); til.close(); return antallInnlesteTegn; } public static void dekomprimer(String fraUrl, String tilFil) throws IOException { BitInputStream fra = new BitInputStream((new URL(fraUrl)).openStream()); OutputStream til = new BufferedOutputStream(new FileOutputStream(tilFil)); dekomprimer(fra, til); fra.close(); til.close(); } Programkode 7.2.5 f)
Vi kan teste dette på en tekstfil. Delkapittel 1.3 er et
av dette kompendiets største kapitler. Det ligger på
https://www.cs.hioa.no/~ulfu/appolonius/kap1/3/kap13.html.
Obs: Hvis en isteden ønsker å bruke en fil på en lokal enhet (harddisk, cd eller minnepinne), må det starte
med file:///. Undertegnede har en lokal kopi av Delkapittel 1.3 på en minnepinne med flg. URL:
file:///d:/www/appolonius/kap1/3/kap13.html. Komprimeringsmetoden returnerer
antallet innleste tegn. Dermed får vi vite hvor stor innlesningsfilen er og vi kan regne ut komprimeringsgraden.
Se flg. eksempel:
public static void main(String... args) throws IOException { String fraUrl = "https://www.cs.hioa.no/~ulfu/appolonius/kap1/3/kap13.html"; long n = LZW.komprimer(fraUrl, "ut.lzw"); // lengden på innfilen long m = (new File("ut.lzw")).length(); // lengden på utfilen System.out.println("Opprinnelig fil: " + n + " byter"); System.out.println("Komprimert fil: " + m + " byter"); double grad = 100 * (1 - (double) m / n); System.out.printf("Komprimeringsgrad: %5.1f%1s\n", grad, "%"); } Programkode 7.2.5 g)
Hvor filen "ut.lzw" havner hos deg er avhengig av hvordan du
har satt opp prosjektet ditt. Hvis du vil dekomprimere må den oppgis på URL-form, dvs. med file som protokoll.
Skriv den ut til en html-fil. Problemet er at html-filen ikke vil bli spesielt lesbar i en web-leser siden stillark, tegninger og bilder
ikke er tilgjengelig. Men den er lesbar som en tektfil og hvis du sjekker filstørrelsen, vil du se at den er lik størrelsen
på den opprinnelige filen.
| 1. | Skjøt sammen Programkode 7.2.5 d)
og e) og bruk andre meldinger enn "ABBABABAC".
|
| 2. | Filen https://www.cs.hioa.no/~ulfu/appolonius/kap7/2/mystisk.txt inneholder resultatet av en komprimering. Sjekk innholdet. Dekomprimer og skriv resultatet til konsollet. |
I både komprimeringen og dekomprimeringen (f.eks. i
Programkode 7.2.5 b)
bygges det fortløpende opp en ordbok. Den er implementert
ved hjelp av en HashMap. Ordboken kan bli ganske stor. I forrige avsnitt ble kompendiets
Delkapittel 1.3 komprimert. Hvor stort dette delkapitlet er vil variere ettersom det ofte blir oppdatert og
eventuelt utvidet. Men høsten 2021 var det på 411.507 byter. Ordboken vokste under komprimeringen til 65.278 ord
med gjennomsnittsstørrelse på 7,3 tegn. De lengste var på 39 tegn. Dette er ett av dem:
</td><td> </td><td> </t
Som vi ser er ikke dette et vanlig ord. Det er en del av html-koden for en tabell. Men disse 39 tegnene/bytene
vil under komprimeringen, hvis den gjenfinnes, bli erstattet av tallkoden 62200 som lagres med kun 16 biter (2 byter).
Koden som forekommer tre ganger i det lange «ordet», er html-koden for
No Break Space.
Ordboken inneholder ord på to tegn og ord som er en utvidelse med ett tegn av et ord som allerede er der.
Det betyr f.eks at hvis ordboken inneholder abcdef, så vil den også inneholde abcde,
abcd, abc og ab. Det betyr at ikke bare det lange «ordet»
på 39 tegn ligger i ordboken, men også de 37 «ordene» med lengde fra 38 til 2 vi får ved å fjerne
ett og ett tegn. Dette kan ses på som unødvendig stor plassbruk. En bedre måte ville være at for hvert nytt
ord ble kun tegnet og en refranse til ordet som det var en utvidelse av, lagret. Dette kan organiseres i en
trestruktur.
Ta meldingen "ABBABABAC" som eksempel
(Eksempel 1). Der fikk ordboken
fortløpende ordene AB, BB, BA, ABA og ABAC.
Det gir flg. trestruktur (to trær):
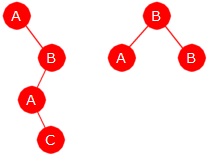 |
| Figur 7.2.6 a) : Ordboktrestruktur |
Hvis vi utvider meldingen til "ABBABABACAABCBA", vil ordboken få ordene CA, AA,
ABC og CB i tillegg. Da blir trestrukturen slik (tre trær):
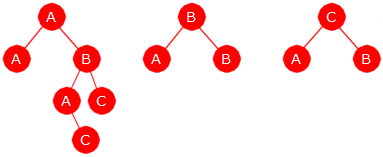 |
| Figur 7.2.6 b) : En utvidelse |
En node lagres ved at dens tegn og dens forelderreferanse (et heltall) lagres. I tillegg må det til noden kobles en tallkode. Et barn av noden får da det tallet som forelderreferanse:
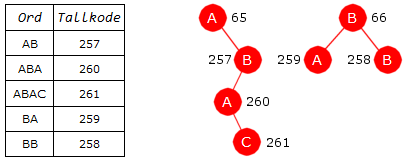 |
| Figur 7.2.6 c) : Til venstre: Ordbok Til høyre: Trestruktur |
Vi ser på "ABBABABAC" igjen, men nå med 257 som første ledige kode.
Nodene legges f.eks. i en hashmap med paret (tegn,forelder) som nøkkelverdi.
Først leses A som har tallkode 65 (ascii-verdi). Så B. Noden (B,65) representerer ordet AB siden forelder 65 nettopp er A.
Den legges inn med 257 som tilhørende tallkode.
Så B igjen. Forrige tegn var også B med tallkode 66. Da må vi sjekke om noden (B,66) er lagret. Nei! (B,66)-258 lagres.
Så kommer A. Noden (A,66) er ikke lagret. (A,66)-259 lagres. Så kommer B. Men noden (B,65) finnes fra før med tilhørende
kode 257. Da leser vi et nytt tegn, dvs. A og sjekker om noden (A,257) er lagret. Nei! (A,257)-260 lagres. Deretter
vil vi finne at noden (B,65) er lagret med tilhørende kode 257, så at noden (A,257) med tilhørende kode 260 er der. Men paret
noden (C,260) finnes ikke. Dermed lagres (C,260)-261. Det gir treet i
Figur 7.2.6 c
I Figur 7.2.6 c) har en node kun en bokstav og et
tall ved siden av. Hadde det vært plass på tegningen skulle det også ha vært et tall inne i noden ved siden av bokstaven.
I node C med tilhørende tall 261 skulle 260 stått inne i noden siden 260 er forelderen.
I en trenode har det også vært vanlig å ha referanser til nodens barn. Men det blir umulig her siden en node i prinsippet kan ha hele 256 barn - et barn for hver av de 256 aktuelle tegnene. Det som er entydig for en node er kombinasjonen av dens tegn og forelderreferanse. Ved hjelp av de to kan vi lete oss frem til riktig node hvis nodene legges i en søkbar datastruktur.
Men vil vi vinne noe på å bruke en trestruktur istedenfor å lagre ordene som tegnstrenger? Når
Delkapittel 1.3 ble komprimert fikk vi som nevnt over, et ord på hele 39 tegn. Hvert tegn i en tegnstreng
er en char og har dermed to byter. I tillegg til dette ordet ligger det i ordboken 37 andre ord
med lengder på henholdsvis 38, 37, 36, osv.
Det blir på samme måte som at hvis ordboken inneholder abcdef, så vil den også inneholde abcde,
abcd, abc og ab. Tilsammen blir dette 2(39 + 38 + . . . + 3 + 2) byter =
2·779 byter = 1558 byter. Men i et tre vil disse 38 ordene utgjøre deler av en og samme gren. Hver
node i grenen inneholder et tegn (en byte) og en forelderreferanse (en int), dvs. 5 byter. Sammenlagt
38·5 byter = 190 byter. Dermed bruker en trestruktur vesentlig mindre plass - 190 mot 1558 byter.
Det er ikke vanskelig å implementere dette. Vi tar utgangspunkt i
Programkode 7.2.5 b). I stedet for
den HashMap-typen som brukes der, bruker vi nå en HashMap der datatypen Node er nøkkelverdi:
Map<Node,Integer> ordbok = new HashMap<>();
og til en node bruker vi den nye konstruksjonen record (fra og med Java 16). Dvs. så enkelt og elegant som dette:
record Node(byte tegn, int forelder) {}
Det gir flg. forbedrede versjon av metoden komprimering:
public static int komprimer(InputStream inn, BitOutputStream ut) // Ny versjon throws IOException { int bitformat = 9, bitGrense = 512; // starter med 9 biter int c = inn.read(); // leser inn første tegn if (c == -1) return 0; // inn er tom int antallInnlesteTegn = 1; // første tegn record Node(byte tegn, int forelder) {} // nodedefinisjon Map<Node,Integer> ordbok = new HashMap<>(); // ordboken som trestruktur int kode = c; int nesteKode = FØRSTE_KODE; // første ledige tall while ((c = inn.read()) != -1) // slutt hvis c er -1 { antallInnlesteTegn++; // et nytt tegn Node node = new Node((byte)c,kode); // lager en node Integer ordkode = ordbok.get(node); // søker etter noden if (ordkode == null) // fant ikke noden { if (kode >= bitGrense) // sjekker størelsen { ut.writeBits(NYTT_BITFORMAT,bitformat); // setter inn flagget bitformat++; // øker bitformat med 1 bitGrense *= 2; // dobler bitGrense } ut.writeBits(kode,bitformat); // skriver ut koden if (nesteKode < MAKS) // sjekker størelsen { ordbok.put(node,nesteKode); // legges i trestrukturen nesteKode++; // øker nesteKode med 1 } kode = c; // setter kode = c } else // vi fant noden { kode = ordkode; // tallkoden til noden } } if (kode >= bitGrense) // siste utskrift { ut.writeBits(NYTT_BITFORMAT,bitformat); // setter inn flagget bitformat++; // øker bitformat med 1 } ut.writeBits(kode,bitformat); // siste kode return antallInnlesteTegn; // returnerer } Programkode 7.2.6 a)
Den nye komprimer bør testes, f.eks. ved hjelp av
Programkode 7.2.5 d). For å sikre at rett versjon brukes kan
den i Programkode 7.2.5 b) kalles
komprimer0. Se også Oppgave 2.
Dekomprimeringen blir litt annerledes. Nå er det tallkoder som leses inn og da må vi finne hvilken node tallkoden hører til. Det får vi til ved å legge nodene i en tabell der tallkoden blir tabellindeks. Når noden er funnet, finner vi ordet ved å gå oppover i treet til og med roten. Da kommer ordets tegn i motsatt rekkefølge. Men ved fortløpende å legge dem inn på en stakk kan vi få dem i rett rekkefølge. Vi starter med å legge inn som noder de 256 første tegnene og da med -1 som forelder:
public static void dekomprimer(BitInputStream inn, OutputStream ut) // Ny versjon throws IOException { int bitformat = 9; // starter med 9 biter int kode = inn.readBits(bitformat); // første tallkode if (kode == -1) return; // inn er tom record Node(byte tegn, int forelder) {} // en nodedefinisjon List<Node> ordbok = new ArrayList<>(); // en tabell // De 256 første nodene med -1 som forelder, 256 "nulles" vekk for (int i = 0; i < FØRSTE_KODE; i++) ordbok.add(new Node((byte)i,-1)); Deque<Integer> stakk = new ArrayDeque<>(); // en stakk int forelder = 0, forrige = kode; int c = kode; ut.write(c); // det første tegnet while ((kode = inn.readBits(bitformat)) != -1) { while (kode == NYTT_BITFORMAT) // er det et flagg? { bitformat++; // øker bitlengden kode = inn.readBits(bitformat); // leser med ny bitlengde } if (kode < ordbok.size()) forelder = kode; else { forelder = forrige; stakk.push(c); // legger på stakken } while (forelder != -1) { Node node = ordbok.get(forelder); // henter fra ordboken stakk.push((int)node.tegn); // legger på stakken forelder = node.forelder; // fortsetter oppover } c = stakk.peek(); // tar vare på toppen while (!stakk.isEmpty()) ut.write(stakk.pop()); ordbok.add(new Node((byte)c,forrige)); forrige = kode; } } Programkode 7.2.6 b)
| 1. | Trestrukturen i Figur 7.2.6 b)
kommer fra meldingen "ABBABABACAABCBA". Sett på for hver node den tilhørende tallkoden.
|
| 2. | La versjonen i Programkode 7.2.5 b) hete
komprimer0. Test så den nye versjonen ved hjelp av
Programkode 7.2.5 d). Legg merke til
at hvis den nye versjonen heter komprimer, vil den bli brukt i
Programkode 7.2.5 f).
|
| 3. | Sjekk at den ny versjonen i Programkode 7.2.6 b)
virker som den skal.
|

