Oppgave 2

Hvis en graf ikke er sammenhengende, kan den deles opp i en samling sammenhengende komponenter. Det som skjer i metoden er at den finner et spenntre for den komponenten der startnoden inngår. Bruk H som startnode i Programkode 11.1.7 b) hvis du har lagt inn en node med navn H. Da utgjør H en egen komponent og du får at spenntreet kun består av H.

Oppgave 3

  public Graf spenntre(String navn)        // bredde-først
  {
    Node p = noder.get(navn);              // henter startnoden
    if (p == null) throw new IllegalArgumentException(navn + " er ukjent!");

    Graf tre = new Graf();                  // oppretter en tom graf
    tre.leggInnNode(navn);                  // legger inn startnoden

    Queue<Node> kø = new ArrayDeque<>();    // oppretter en nodekø
    p.besøkt = true;                        // p er den første vi besøker
    kø.offer(p);                            // legger noden p i køen

    while (!kø.isEmpty())                   // så lenge køen ikke er tom
    {
      p = kø.poll();                        // tar ut en node fra køen

      for (Node q : p.kanter)               // nodene det går en kant til
      {
        if (!q.besøkt)                      // denne er ikke besøkt
        {
          tre.leggInnNode(q.navn);          // legger inn noden
          tre.leggInnKant(p.navn, q.navn);  // kant den ene veien
          tre.leggInnKant(q.navn, p.navn);  // kant den andre veien          

          q.besøkt = true;                  // nå er den besøkt
          kø.offer(q);                      // legger noden i køen
        }
      }
    }
    return tre;                             // returnerer spenntreet
  }

Hvis du bruker versjonen over (kall f.eks. dybde-først-versjonen for spenntre1 og den over for spenntre2 hvis begge skal inngå i klassen Graf) i Programkode 11.1.7 b), vil det gi spenntreet under til venstre med A som startnode og det under til høyre med D:

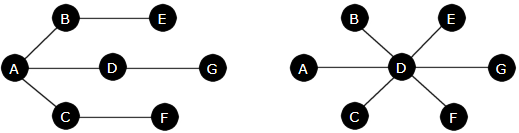To spenntrær for grafen i Figur 11.1.7 a)

Oppgave 4

  private void                              // rekursiv hjelpemetode
  spenntre(int i, boolean[] besøkt, MGraf tre)
  {
    besøkt[i] = true;                       // noden er besøkt

    for (int j = 0; j < antall; j++)        // kantene til noden
    {
      if (graf[i][j] && !besøkt[j])
      {
        tre.leggInnNode(navn[j]);           // legger inn noden
        tre.leggInnKant(navn[i], navn[j]);  // legger inn kant den ene veien
        tre.leggInnKant(navn[j], navn[i]);  // legger inn kant den andre veien
        spenntre(j, besøkt, tre);           // rekursivt kall
      }
    }
  }

  public MGraf spenntre(String startnode)   // hører til klassen MGraf   
  {
    int i = finn(startnode);  // indeks i den sorterte navnetabellen
    if (i < 0) throw new IllegalArgumentException(startnode + " er ukjent!");

    i = indeks[i];                          // indeks i den usorterte tabellen 

    MGraf tre = new MGraf();
    tre.leggInnNode(navn[i]);

    boolean besøkt[] = new boolean[antall]; // hjelpetabell
    spenntre(i, besøkt, tre);               // kaller den rekursive metoden

    return tre;                             // returnerer et spenntre
  }

Oppgave 5

  public MGraf spenntre(String startnode)
  {
    int i = finn(startnode);  // indeks i den sorterte navnetabellen
    if (i < 0) throw new IllegalArgumentException(startnode + " er ukjent!");

    i = indeks[i];  // indeks i den usorterte navnetabellen

    boolean[] besøkt = new boolean[antall];   // hjelpetabell

    MGraf tre = new MGraf();                  // oppretter en tregraf
    tre.leggInnNode(navn[i]);                 // legger inn startnoden
    besøkt[i] = true;                         // node i besøkes først

    Queue<Integer> kø = new ArrayDeque<>();   // oppretter en kø
    kø.offer(i);                              // legger i i køen

    while (!kø.isEmpty())                     // så lenge køen ikke er tom
    {
      i = kø.poll();                          // tar ut en node fra køen

      for (int j = 0; j < antall; j++)        // nodene det går en kant til
      {
        if (graf[i][j] && !besøkt[j])         // denne er ikke besøkt
        {
          tre.leggInnNode(navn[j]);           // legger inn noden
          tre.leggInnKant(navn[i], navn[j]);  // legger inn kant den ene veien
          tre.leggInnKant(navn[j], navn[i]);  // legger inn kant den andre veien          

          besøkt[j] = true;                   // nå er den besøkt
          kø.offer(j);                        // legger noden i køen
        }
      }
    }

    return tre;
  }