Oppgave 1

Uansett hvilken startnode man velger, vil det minimale spenntreet man får alltid inneholde kantene A - B, B - D, C - D og D - F. Men i tilfellene det er valg siden det er to noder som begge ligger nærmest treet man til da har fått, vil treet være avhengig av hva man velger. Mulighetene er da C - F og F - G, D - F og F - G eller E - G og F - G.

Oppgave 2

Det vil bli kastet en NullPointerException. For-løkken i metoden spenntrePrim0() går til at alle nodene er innlemmet i treet. Men siden det ikke er noen kant til H, vil etterhvert alle kanter som er lagt inn, bli tatt ut av køen. Når køen er tom, returnerer metoden poll() null. Dermed kommer det en NullPointerException i neste setning. Det vi derfor kan gjøre er å legge inn flg. setning rett etter poll()-setningen:

  if (kant == null) throw new NullPointerException("Treet er usammenhengende!");

En annen mulighet hadde vært å bruke remove() istedenfor poll(). De gjør det samme. Men remove() kaster en NoSuchElementException hvis køen er tom. Men det er kanskje ingen god feilmelding å få. Den sier ikke hva som er årsaken, dvs. at grafen er usammenhengende.

Oppgave 3 a)

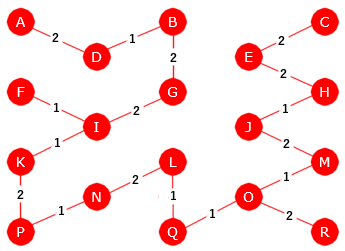Et minimalt spenntre for grafen i Figur 11.2.5 i)

Oppgave 3 b)

Klassen Kant inneholder kun noden som kanten går til. Men vi trenger også noden som kanten går fra. Men den mister vi når kanten legges inn i køen. En løsning er å bruke en lokal hjelpeklasse UtvidetKant som inneholder begge nodene og vekten. I tillegg skal den ha en «teller» som øker med 1 for hver innlegging. Dermed kan vi lage komparatoren for prioriteskøen slik at med lik vekt er det den med seneste tellerverdi som tas ut.

  public List<String> spenntrePrim0(String nodenavn)
  {
    Node node = noder.get(nodenavn); // henter startnoden
    if (node == null) throw new NoSuchElementException(nodenavn + " er ukjent!");

    record UtvidetKant(Node fra, Node til, int vekt, int nr)
    {
      public String toString()
      {
        return "(" + fra.navn + "," + til.navn + "," + vekt + ")";
      }
    }

    List<String> liste = new LinkedList<>();

    PriorityQueue<UtvidetKant> kø =
      new PriorityQueue<>((a,b) ->
        a.vekt - b.vekt != 0 ? a.vekt - b.vekt : b.nr - a.nr);

    int nr = 0;
    kø.offer(new UtvidetKant(node, node, 0, nr));  // 0-kant fra noden til seg selv

    int vekt = 0;  // hjelpevariabel for summering

    for (int antallnoder = 0; antallnoder < noder.size(); )
    {
      UtvidetKant kant = kø.poll();   // tar ut kanten med minst vekt
      if (kant == null) throw new NullPointerException("Treet er usammenhengende!");

      Node nynode = kant.til;        // noden som kanten går til

      if (!nynode.ferdig)            // en ferdig node ligger allerede i treet
      {
        liste.add(kant.toString());  // legger kanten i listen

        vekt += kant.vekt;           // øker vekten
        nynode.ferdig = true;        // innlemmes i treet
        antallnoder++;               // en node til i treet

        for (Kant k : nynode.kanter)
          if (!k.til.ferdig)
            kø.offer(new UtvidetKant(nynode, k.til, k.vekt, nr++));
      }
    }
    liste.add("Vekt: " + vekt);

    liste.remove(0);  // fjerner den første 0-kanten
    return liste;     // returnerer en liste med spenntreets kanter
  }

Flg. program tester metoden:

  String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf2.txt";
  VGraf vgraf = new VGraf(url);
  System.out.println(vgraf.penntrePrim0("C"));
  // Utskrift: [(C,D,2), (D,E,2), (D,B,2), (B,A,2), (E,G,3), (G,F,2), Vekt: 13]

Oppgave 4

  public boolean erUrettet()
  {
    for (Node node : noder.values())
    {
      for (Kant kant : node.kanter)
      {
        Node til = kant.til;

        boolean funnet = false;

        for (Kant k : til.kanter)
        {
          if (k.til == node && k.vekt == kant.vekt)
          {
            funnet = true;
            break;
          }
        }
        if (!funnet) return false;
      }
    }
    return true;
  }

Oppgave 5

Hvis Programkode 11.2.5 c) brukes på en ikke sammenhengende graf, vil vi få returnert vekten til et minimalt spenntre for den delen av grafen som nås fra startnoden. Det kommer ingen feilmeldinger.

Oppgave 6

Legg f.eks.

  if (noder.size() == 1)
  {
    StringJoiner sj = new StringJoiner(",", "(", ")");
    String node = nodenavn()[0];
    sj.add(node).add(node).add("0");
    spenntre.add(sj.toString());
    return spenntre;
  }

mellom setningene

  List<String> spenntre = new ArrayList<>();  // for kantene i spenntreet

og

  for (Node n : noder.values())  // ser på alle nodene

Oppgave 7

  public VGraf spenntrePrimGraf(String nodenavn)
  {
    spenntrePrim(nodenavn);  // finner et minimalt spenntre

    VGraf spenntre = new VGraf();  // ny og tom graf

    for (Node node : noder.values())
    {
      spenntre.leggInnNode(node.navn);  // legger alle nodenavnene inn i ny graf
    }

    if (noder.size() < 2) return spenntre;

    for (Node node : noder.values())
    {
      if (node.forrige != null)
      {
        // legger inn kantene i spenntreet i den nye grafen
        spenntre.leggInnKant(node.navn, node.forrige.navn, node.avstand);
        spenntre.leggInnKant(node.forrige.navn, node.navn, node.avstand);
      }
    }

    nullstill();  // nullstiller variablene forrige og avstand

    return spenntre;  // returnerer grafen
  }

Her er et eksempel på hvordan metoden kan brukes:

  String url = "https://www.cs.hioa.no/~ulfu/appolonius/kap11/2/vgraf2.txt";
  VGraf vgraf = new VGraf(url);

  VGraf tre = vgraf.spenntrePrimGraf("C");

  for (String node : tre)
  {
    System.out.println(node + " -> " + tre.kanterFra(node) + " ");
  }

  // Utskrift
  // A -> (B,2) 
  // B -> (A,2), (D,2) 
  // C -> (D,2) 
  // D -> (B,2), (C,2), (E,2) 
  // E -> (D,2), (G,3) 
  // F -> (G,2) 
  // G -> (F,2), (E,3) 

Oppgave 8

  public int spenntrePrim(String nodenavn)  // Prims algoritme
  {
    int i = finn(nodenavn);  // indeks i den sorterte navnetabellen
    if (i < 0) throw new NoSuchElementException(nodenavn + " er ukjent!");
    i = indeks[i];           // indeks i den usorterte navnetabellen   

    class Avstand  // lokal hjelpeklasse
    {
      int node, avstand;

      Avstand(int node, int avstand)
      {
        this.node = node; this.avstand = avstand;
      }
    }

    Queue<Avstand> kø = new PriorityQueue<>((a,b) -> a.avstand - b.avstand);

    avstand = new int[antall];           // oppretter tabellen
    Arrays.fill(avstand, 0x7fffffff);    // setter verdiene til "uendelig"

    forrige = new int[antall];           // oppretter tabellen
    Arrays.fill(forrige, -1);            // setter verdiene til -1

    boolean[] ferdig = new boolean[antall];  // lokal hjelpetabell

    avstand[i] = 0;                      // avstand i startnoden settes til 0
    kø.offer(new Avstand(i, 0));         // startnoden legges i køen

    int vektsum = 0;                     // hjelpevariabel for treets vekt

    while (!kø.isEmpty())                // så lenge køen ikke er tom
    {
      Avstand minst = kø.poll();         // den "minste" noden
      int denne = minst.node;            // hjelpevariabel

      if (ferdig[denne]) continue;       // denne er vi allerede ferdig med

      for (int neste = 0; neste < antall; neste++)  // går gjennom matriseraden
      {
        if (graf[denne][neste] != IKKE_KANT) // en kant fra denne til neste
        {
          if (ferdig[neste]) continue;   // denne er vi allerede ferdig med

          int vekt = graf[denne][neste]; // hjelpevariabel

          if (vekt < avstand[neste])     // sammenligner
          {
            avstand[neste] =  vekt;
            kø.offer(new Avstand(neste, avstand[neste]));
            forrige[neste] = denne;      // veien går fra denne til neste
          }
        }
      } // for

      ferdig[denne] = true;           // nå er denne er ferdig
      vektsum += avstand[denne];      // legger til kantvekten

    } // while

    return vektsum;                   // spenntreets vekt
  }

  public VMGraf spenntrePrimGraf()
  {
    VMGraf spenntre = new VMGraf();

    for (int i = 0; i < antall; i++)
    {
      spenntre.leggInnNode(snavn[i]);
    }

    if (antall < 2) return spenntre;

    for (int i = 0; i < antall; i++)
    {
      if (forrige[i] != -1)
      {
      spenntre.leggInnKant(navn[i], navn[forrige[i]], avstand[i]);
      spenntre.leggInnKant(navn[forrige[i]], navn[i], avstand[i]);
      }
    }

    return spenntre;
  }

  public List<String> spenntrePrim()
  {
    List<String> tre = new LinkedList<>();

    if (antall == 1)
    {
      StringJoiner sj = new StringJoiner(",", "(", ")");
      sj.add(navn[0]).add(navn[0]).add("0");
      tre.add(sj.toString());
      return tre;
    }

    for (int i = 0; i < antall; i++)
    {
      if (forrige[i] != -1)
      {
        StringJoiner sj = new StringJoiner(",", "(", ")");
        sj.add(navn[i]).add(navn[forrige[i]]).add(Integer.toString(avstand[i]));
        tre.add(sj.toString());
      }
    }

    return tre;
  }