![]() 1.8.1 En algoritmes arbeidsmengde
1.8.1 En algoritmes arbeidsmengde
I Delkapittel 1.1 ble det definert
og diskutert flere begreper knyttet til algoritmeanalyse. Her kommer en kort oppsummering:
| • | Arbeidsoperasjoner En algoritme er en beskrivelse av de arbeidsoperasjonene som skal til for å løse en bestemt oppgave. |
| • | Oppgave, algoritme og implementasjon Våre «oppgaver» vil være slike som kan løses ved hjelp et program (eller en metode) skrevet i f.eks. Java. Vi skiller mellom selve oppgaven, en algoritme for å løse oppgaven og en implementasjon (kode) av algoritmen. Det er ofte flere måter å løse en oppgave, dvs. flere mulige algoritmer for samme oppgave og en bestemt algoritme kan ofte kodes på flere måter. |
| • | Dominerende operasjon Blant arbeidsoperasjonene er det vanligvis en som er viktigere, er mer sentral eller er mer kostbar og utføres oftere enn de andre. Det kalles den dominerende operasjonen. F.eks. er det å sammenligne to verdier en dominerende operasjon i vanlig sortering. I numeriske algoritmer (algoritmer med tallberegninger) kan f.eks. en multiplikasjon (eller kanskje en divisjon) være en dominerende operasjon. |
| • | Arbeidsmengde I mange algoritmer er det mulig å «telle opp» antallet ganger den dominerende operasjonen utføres. Dette antallet utgjør algoritmens arbeidsmengde. |
| • | Orden Arbeidsmengden kan ofte uttrykkes som en funksjon av oppgavens størrelse n. Denne funksjonen definerer algoritmens orden. |
Eksempel I Delkapittel 1.1 diskuterte vi «oppgaven» å finne posisjonen til den største verdien i en heltallstabell. Flg. metode løser oppgaven:
public static int maks(int[] a) { int m = 0; // indeks til største verdi int maksverdi = a[0]; // største verdi for (int i = 1; i < a.length; i++) if (a[i] > maksverdi) { maksverdi = a[i]; // største verdi oppdateres m = i; // indeks til største verdi oppdaters } return m; // returnerer indeks/posisjonen til største verdi } // maks Programkode 1.8.1
Den dominerende operasjonen i Programkode 1.8.1 er sammenligningen
a[i] > maksverdi. Anta at tabellen a har n verdier, dvs.
at n = a.length.
For-løkken går da n − 1 ganger og siden sammenligningen utføres
hver gang, blir det n − 1 operasjoner. Med andre ord er arbeidsmengden gitt
ved ƒ( n ) = n − 1. Algoritmen er dermed av orden n (lineær orden).
![]() 1.8.2 Den asymptotiske rangeringen av funksjoner
1.8.2 Den asymptotiske rangeringen av funksjoner
Som nevnt i Avsnitt 1.8.1 kan
arbeidsmengden til en algoritme ofte uttrykkes ved hjelp av en funksjon
ƒ(n) der n er «størrelsen» på oppgaven.
Det er forskjellige typer funksjoner som
kan inngå i en slik sammenheng. Tabellen under viser de typene som
oftest inngår:
| Funksjonstype | n = 1 | n = 10 | n = 100 | n = 1000 | Beskrivelse | |
| ƒ1( n ) = 1 | 1 | 1 | 1 | 1 | konstant | |
| ƒ2( n ) = log2 n | 0 | 3,3 | 6,6 | 9,97 | logaritmisk | |
| ƒ3( n ) = √n | 1 | 3,2 | 10 | 31,6 | kvadratrot | |
| ƒ4( n ) = n | 1 | 10 | 100 | 1000 | lineær | |
| ƒ5( n ) = n log2 n | 0 | 33,2 | 664,4 | 9.965,8 | lineæritmisk | |
| ƒ6( n ) = n² | 1 | 100 | 10.000 | 1.000.000 | kvadratisk | |
| ƒ7( n ) = n³ | 1 | 1.000 | 1.000.000 | 10 siffer | kubisk | |
| ƒ8( n ) = 2 n | 2 | 1.024 | 31 siffer | 302 siffer | eksponensiell | |
| ƒ9( n ) = n! | 1 | 3.628.800 | 158 siffer | 2568 siffer | faktoriell | |
| Tabell 1.8.2 - Asymptotisk rangering av funksjonstyper | ||||||
|---|---|---|---|---|---|---|
Funksjonene i Tabell 1.8.2 er satt opp i rekkefølge (rangert) etter asymptotisk «oppførsel». Det er funksjonsverdiene for store argumentverdier n som er avgjørende. For n = 1 er mange av funksjonsverdiene like. Men allerede for n = 10 ser vi at rekkefølgen på funksjonene er nesten helt i samsvar med rekkefølgen på funksjonsverdiene. Det er kun log2 n og √n med funksjonsverdier 3,3 og 3,2 som er i utakt. Men for n = 100 stemmer det helt. Ellers ser vi at det er til dels enormt store forskjeller mellom funksjonsverdiene for store verdier av n.
Men hensyn på asymptotisk «oppførsel» sier vi at jo høyere opp i Tabell 1.8.2 en funksjon står, jo «mindre» er funksjonen. Det betyr for eksempel at funksjonen ƒ2( n ) = log2 n er asymptotisk sett «mindre enn» funksjonen ƒ3( n ) = √n. Se Avsnitt 1.8.5.
I Tabell 1.8.2 inngår logaritmefunksjonen med grunntall 2, dvs. ƒ( n ) = log2 n. Det kan være aktuelt med andre grunntall, f.eks. 10 eller e. I det første tilfellet (grunntall 10) vil logaritmen bli skrevet log10 n og i det andre (grunntall e) kun log n. Med andre ord hvis det ikke står noen indeks som indikerer grunntall, tas det som gitt at grunntallet er e = 2,718 · · · . Logaritmen med grunntall e kalles også den naturlige logaritmen og mange betegner den med ln n. Her vil vi konsekvent skrive log n siden den heter det i Java. Funksjonen n log2 n (eller bare n log n) kalles lineæritmisk (eng: linearithmic). Ordet er en «sammentrekning» av ordene lineær og logaritmisk. På norsk kalles den også loglineær.
En funksjon ƒ( n ) for arbeidsmengden til en algoritme er vanligvis en lineærkombinasjon av flere ledd, dvs. på formen a1 ƒ1( n ) + a2 ƒ2( n ) + · · · + ak ƒk( n ) der a1 til ak er konstanter og ƒ1( n ) til ƒk( n ) er funksjoner for eksempel fra Tabell 1.8.2.
For eksempel kan en slik funksjon være gitt som følgende lineærkombinasjon:
(1.8.2.1) ƒ( n ) = 2 n² + 3 n + log2 n − 1
I (1.8.2.1) inngår funksjonene n² , n , log2 n og 1 fra Tabell 1.8.2. Av disse er det n² som står lengst ned i tabellen. Det er derfor den som avgjør den asymptotiske oppførselen til ƒ( n ). Verdiene til de andre leddene blir bare «småtterier» i forhold til verdiene til n² for store verdier av n. Derfor kalles n² det dominerende leddet i ƒ( n ).
I funksjonen i (1.8.2.1) står det et 2-tall foran n² , dvs. 2 n² . Men 2-tallet er en konstant og det ser vi bort fra. Det er n² som er det dominerende leddet.
Eksempel 1 Hvis arbeidsmengden til en algoritme er gitt ved ƒ( n ) = 2 n² + 3 n + log2 n − 1, så er algoritmen av orden n² eller av kvadratisk orden.
Eksempel 2 La arbeidmengden til en algoritme være gitt ved ƒ( n ) = 0,2 √n + 10 log2 n + 8. Da er algoritmen av orden √n eller av kvadratrotorden.
| 1. | Hva er det dominerende leddet i funksjonen ƒ( n ) = 0,1 n² + 10 n log2 n | |||||
| 2. | Ta grafene til ƒ1 ( n ) = 0,1 n² og ƒ2 ( n ) = 10 n log2 n for n ≥ 2. De vil krysse hverandre for en n0 til høyre for 2. Dvs. grafen til ƒ1 ligger under den til ƒ2 mellom 2 og n0 og grafen til ƒ1 ligger over den til ƒ2 for alle verdier av n større enn n0. Denne verdien n0 er selvfølgelig et desimaltall. Finn det minste heltallet som er større n0, dvs. finn k = ⌈n0⌉. | |||||
| 3. |
I Tabell 1.8.2 står de
funksjonene som oftest inngår i algoritemanalyse. Men det er flere. Utvid
tabellen og sett flg. funksjoner på rett plass med hensyn på asymptotisk oppførsel:
|
![]() 1.8.3 Eksempler på arbeidsmengde og algoritmeorden
1.8.3 Eksempler på arbeidsmengde og algoritmeorden
Tabell 1.8.2 gir en oversikt over de
funksjonstypene som oftest inngår som ledd i en funksjon som definerer
arbeidsmengden i en algoritme. Her er noen eksempler på dette:
Eksempel 1 Flg. metode returnerer den siste verdien i en heltallstabell:
public static int sisteVerdi(int[] a) { int n = a.length; if (n > 0) return a[n - 1]; else throw new NoSuchElementException("Tabellen er tom!"); }
I metoden i Eksempel 1 hentes (og returneres) siste verdi i tabellen a.
Her er det rimelig å si at tabelloperasjonen a[n - 1]
er dominerende og den utføres kun én gang uansett hvor mange verdier tabellen måtte ha.
Tabellens lengde er n og funksjonen f som angir antallet ganger
den dominerende operasjonen utføres som funksjon av n, er gitt ved
ƒ( n ) = 1. Dvs. en konstant funksjon. Algoritmen er
derfor av konstant orden.
Eksempel 2 Heltallene 1, 2, 4, 8, 16, · · · osv. kalles potenser av 2 siden hvert av dem er på formen formen 2k. Flg. metode skriver ut alle potenser av 2 som er mindre enn eller lik n :
public static void skriv2potens(int n) { for (int k = 1; k <= n; k *= 2) System.out.print(k + " "); }
Metoden kan brukes til f.eks. å skrive ut alle 2-potenser som er mindre enn 1000:
skriv2potens(1000); // Utskrift: 1 2 4 8 16 32 64 128 256 512
I metoden i Eksempel 2 inngår multiplikasjonen k *= 2 og en
utskriftssetning. De utføres nøyaktig like mange ganger. Utskriftssetningen er
vesentlig mer kostbar enn multiplikasjonen og det er derfor rimelig å kalle
den dominerende. Men hvor mange ganger utføres den? Antallet har åpenbart noe med
logaritmen å gjøre siden vi får skrevet ut 10 potenser
når n = 1000. Vi ser også at hvis n = 1023, vil vi fortsatt få 10
potenser, men hvis n = 1024 vil det bli skrevet ut 11. Hvis n = 1,
får vi kun ut tallet 1. Dette forteller oss at antallfunksjonen (arbeidsmengden) må være
ƒ( n ) = ⌊log 2 n⌋ + 1
eller ƒ( n ) = ⌈log 2 ( n + 1)⌉
om en vil. Siden dette er en logaritmisk funksjon vil algoritmen være av logaritmisk orden.
Eksempel 3 Flg. metode finner summen av verdiene i en heltallstabell:
public static int tabellSum(int[] a) { if (a.length == 0) throw new IllegalStateException("Ingen verdier!"); int sum = a[0]; for (int i = 1; i < a.length; i++) sum += a[i]; return sum; }
La tabellen a i Eksempel 3 ha lengde n. Setningen
sum += a[i] utføres nøyaktig n − 1 ganger.
Her blir det hipp som happ om det er tabelloperasjonen eller addisjonen som
kalles dominerende. Addisjonen utføres nøyaktig
n − 1 ganger, mens tabelloperasjonen utføres n ganger
siden den også inngår i setningen int sum = a[0]. Hvis vi kaller
addisjonen dominerende, blir funksjonen for arbeidsmengden lik ƒ( n ) = n − 1 ,
dvs. en lineær funksjon (et 1. grads polynom i n). Algoritmen er dermed av
lineær orden.
Eksempel 4 En av de sorteringsmetodene vi har sett på tidligere kalles utvalgssortering. Metoden kan kodes på flere måter, f.eks. slik:
public static void utvalgssortering(int[] a) { for (int k = a.length; k > 1; k--) { int m = 0, maksverdi = a[0]; for (int i = 0; i < k; i++) if (a[i] > maksverdi) { maksverdi = a[i]; m = i; } Tabell.bytt(a,m,k-1); } }
I Eksempel 4 er det sammenligningen if (a[i] > maksverdi) som
er dominerende. La tabellen a ha n verdier. I første runde
finner vi den største verdien i intervallet a[0:n> og til det trengs
n − 1 sammenligninger. Så flyttes den største verdien bakerst ved
en ombytting. I neste runde finner vi den største verdien i
a[0:n − 1> , dvs. den nest største verdien i a. Til det
trengs n − 2 sammenligninger. Så flyttes den nest bakerst.
Osv. Legger vi sammen blir det n − 1 + n − 2
+ · · · + 3 + 2 + 1
sammenligninger. Dette er en aritmetisk rekke med sum lik
½ n ( n − 1) =
½ n2 − ½ n. Legg merke til
at vi alltid får dette antallet uansett hva slags verdier a måtte
ha og hvordan de er fordelt i tabellen. Arbeidsmengden er med andre ord kun avhenig av tabellens
størrelse n. I antallfunksjon ƒ( n ) =
½ n2 − ½ n er
n2 det dominerende leddet.
Utvalgssorteringen er derfor av kvadratisk orden.
Gitt flg. metoder:
public static int sum1(int n) { int sum = 0; int v = 1, h = n ; while (v < h) sum += v++ + h--; if (n % 2 != 0) sum += n/2; return sum; } public static int sum2(int n) { int sum = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < i; j++) sum++; } return sum; } public static int sum3(int n) { int sum = 0; for (int i = 0; i < n; i++) { for (int j = n; j > i; j--) sum++; } return sum; } public static int sum4(int n) { int sum = 0; for (int i = 1; i <= n; i *= 2) { for (int j = 0; j < n; j++) sum++; } return sum; } public static int antallA(String s) { int antall = 0; int n = s.length(); for (int i = 0; i < n; i++) { char c = s.charAt(i); if (c == 'A' || c == 'a') antall++; } return antall; } public static int[][] produkt(int[][] a, int[][] b) { int n = a.length; int[][] c = new int[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { int sum = 0; for (int k = 0; k < n; k++) { sum += a[i][k]*b[k][j]; } c[i][j] = sum; } } return c; } |
|
| 1. | Metoden sum1 summerer tallene fra 1 til n. La addisjon være dominerende operasjon. Finn en funksjon ƒ( n ) som gir antallet ganger den utføres. Ta kun med de addisjonene som summerer, dvs. += og +, men ikke den som øker tellevariabelen v (++). |
| 2. |
Finn, for hver av de tre metodene sum2, sum3 og
sum4, funksjoner ƒ( n ) som gir antallet
ganger addisjonen sum++ utføres.
Se Eksempel 2 i tilfellet sum4.
|
| 3. | I metoden antallA er n lik lengden til strengen s. Metoden finner antall forekomster av bokstaven A (stor eller liten) i tegnstrengen s. Hvilken operasjon kan en si er dominerende? Finn en funksjon ƒ( n ) som gir antallet ganger den utføres. |
| 4. | Metoden produkt multipliserer to n × n - matriser. Finn en funksjon ƒ( n ) som gir antallet multiplikasjoner som utføres. Lag kode som bruker produkt-metoden. |
| 5. | Lag en metode som returnerer antallet desimale siffer i et ikke-negativt heltall n. Det kan løses ved fortløpende divisjon med 10. Hva blir dominerende operasjon? Finn en formel (en funksjon av n) som gir antallet ganger den dominerende operasjonen utføres. |
![]() 1.8.4 Gjennomsnittlig arbeidsmengde og orden
1.8.4 Gjennomsnittlig arbeidsmengde og orden
I eksemplene Avsnitt 1.8.3 fant vi, som
funksjon av størrelsen n, hvor mange ganger den dominerende operasjonen
ble utført. Dvs. en formel for arbeidsmengden. Vi fant disse funksjonene:
- ƒ(n) = 1
- f ( n ) = ⌈log 2 ( n + 1)⌉
- ƒ(n) = n − 1
- ƒ(n) = ½ n ( n − 1) = ½ n2 − ½ n
I de fire eksemplene var formlene kun avhengig av n og ikke avhengig av hva slags verdier som ble behandlet og hvordan de var fordelt. Men dette er egentlig ikke det normale. I mange algoritmer, f.eks. algoritmer som arbeider i tabeller, vil arbeidsmengden i tillegg til å være avhengig tabellstørrelsen n, også være avhengig hva slags verdier tabellen har.
Eksempel 1 Flg. metode sjekker om en gitt verdi ligger i en (usortert) heltallstabell. Hvis den ligger i tabellen returneres verdiens posisjon (indeks) og hvis ikke returneres −1:
public static int søkUsortert(int[] a, int verdi) { for (int i = 0; i < a.length; i++) { if (verdi == a[i]) return i; // verdi funnet } return -1; // verdi ikke funnet }
I Eksempel 1 er det naturlig å se på sammenligningen verdi == a[i]
som dominerende operasjon. Minst arbeid blir det hvis verdi ligger først
i tabellen a. Da returnerer metoden etter å ha utført nøyaktig én
sammenligning. Mest arbeid blir det hvis verdi enten ligger som siste element i
a eller hvis den ikke ligger der i det hele tatt. Da returnerer metoden etter å ha utført
nøyaktig n sammenligninger der n er tabellens lengde.
For å finne gjennomsnittlig arbeidsmengde er det nødvendig å gjøre noen forutsetninger. Vi antar for det første at alle verdiene i a er forskjellige, så at alle verdiene blir søkt etter med samme sannsynlighet og til slutt at a inneholder verdien det søkes etter. Ligger verdi først blir det 1 sammenligning, 2 sammenligninger hvis den ligger nest først, osv. Til slutt hvis den ligger bakerst blir det n sammenligninger. Tilsammen 1 + 2 + · · · + n = ½ n ( n + 1) sammenligninger. Gjennomsnittet får vi ved å dele på n. Med andre ord ½ (n + 1) sammenligninger i gjennomsnitt med hensyn på de gitte forutsetningene.
I Eksempel 1 over så vi at algoritmens arbeidsmengde (antall dominerende operasjoner) var avhengig av både hvor den søkte verdien lå i tabellen og av tabellens størrelse. Vi innfører flg. tre begreper for en algoritmes arbeidsmengde:
- Arbeidsmengde i det beste tilfellet
- Gjenomsnittlig arbeidsmengde
- Arbeidsmengde i det mest ugunstige (verste) tilfellet
Det beste tilfellet i Eksempel 1 (verdien lå først) gav en arbeidsmengde på ƒ( n ) = 1. Gjennomsnittet (under de gitte forutsetningene) ble ƒ( n ) = ½ (n + 1). Arbeidsmengden i det «verste» tillfellet (verdien lå bakerst eller var ikke der i det hele tatt) ble ƒ( n ) = n. Dvs. konstant orden i det beste tilfellet og lineær orden i gjennomsnitt og i det verste tilfellet.
Det er arbeidsmengden i det mest ugunstige tilfellet og den gjennomsnittlige arbeidsmengden som har mest interesse. I mange algoritmer kan det være gradsforskjeller mellom disse. Dette gjelder f.eks. den viktige sorteringsalgoritmen kvikksortering som vi skal analysere nærmere et annet sted. Den er gjennomsnittlig svært effektiv (lineæritmisk orden), men ineffektiv (kvadratisk orden) i de mest ugunstige tilfellene.
Eksempel 2 Flg. metode undersøker om en heltallstabell er sortert stigende eller ikke:
public static boolean erSortert(int[] a) { for (int i = 1; i < a.length; i++) if (a[i-1] > a[i]) return false; // ikke sortert stigende return true; // a er sortert stigende }
Her er operasjonen a[i-1] > a[i] dominerende.
La a ha lengde n. Det mest «ugunstige» tilfellet får vi
hvis alle verdiene (eller alle bortsett fra den siste) er sortert. Da vil
sammenligningen bli utført n − 1 ganger. Men hva blir gjennomsnittet?
For å kunne avgjøre det må vi som vanlig gjøre en del forutsetninger.
Vi antar at a inneholder permutasjoner av tallene fra 1 til n og
at hver permutasjon har samme sannsynlighet.
Hvis a inneholder tallene 1 og 2, vil det bli én sammenligning uansett. Gjennomsnittet
blir 1. Hvis a inneholder en av de 6 permutasjonene av tallene fra 1 til 3, ser vi fort
at for tre av dem blir det utført to og for de tre øvrige kun én sammenligning. Det
gir 9/6 = 3/2 = 1 + 1/2 som gjennomsnitt. Ser vi på de 24 permutasjonene av tallene
fra 1 til 4, finner vi at gjennomsnittet blir 40/24 = 10/6 = 1 + 1/2 + 1/6. Det lar seg vise
(se Avsnitt 1.8.6) at hvis a inneholder
tallene fra 1 til n, vil det gjennomsnittlige antallet ganger
operasjonen a[i-1] > a[i] utføres være gitt ved:
ƒ( n ) = 1 + 1 / 2! + 1 / 3! + · · · + 1 / (n − 1)! ≈ e − 1
Summen over er de n − 1 første leddene i en kjent rekkeutvikling av tallet e − 1. Rekken konvergerer svært raskt. Vi har e − 1 = 1,718281828 · · · , men for oss er en avrunding til 1,7 godt nok. Dermed er den gjennomsnittlige arbeidsmengden for metoden erSortert konstant og tilnærmet lik 1,7. Med andre ord er dette et eksempel på en algoritme der det er gradsforskjell mellom arbeidsmengden i det mest ugunstige tilfellet ( ƒ( n ) = n − 1, lineær orden) og den gjennomsnittlige arbeidsmengden ( ƒ( n ) ≈ 1,7, konstant orden).
Eksempel 3 I Delkapittel 1.1 fant vi posisjonen til den største verdien i en tabell:
public static int maks(int[] a) { int m = 0; // indeks til største verdi int maksverdi = a[0]; // største verdi for (int i = 1; i < a.length; i++) if (a[i] > maksverdi) { maksverdi = a[i]; // største verdi oppdateres m = i; // indeks til største verdi oppdateres } return m; // returnerer indeks/posisjonen til største verdi }
Sammenligningen a[i] > maksverdi er dominerende operasjon
i Eksempel 3 og
den utføres alltid n − 1 ganger. Dvs. metoden er av lineær orden.
Her kan det også være av interesse å finne antallet ganger en ikke-dominerende
operasjon utføres. Hvis
a[i] > maksverdi i Eksempel 3 er sann,
vil også variablene maksverdi og m bli oppdatert.
Hvor mange ganger skjer det? Færrest antall ganger, dvs. 0 ganger, blir
det hvis den største verdien ligger først. Det «verste» tilfellet, dvs.
flest antall ganger, blir det hvis verdiene i a er forskjellige og er sortert
stigende. Da blir det n − 1 oppdateringer.
I Avsnitt 1.1.6
fant vi at a[i] > maksverdi var sann (forutsatt at alle
verdiene i a var forskjellige)
gjennomsnittlig 1/2 + 1/3 + · · · + 1/n =
Hn − 1 ganger. Men Hn ≈
log (n) + 0,577 og dermed Hn − 1 ≈
log (n) − 0,423. Med andre ord vil oppdateringen av
maksverdi og m i gjennomsnitt bli utført log (n) − 0,423 ganger.
Tilsammen får vi at arbeidmengden for oppdateringene av maksverdi og m i Eksempel 3 er konstant (lik 0) i det beste tilfellet, lik log (n) − 0,423 i gjennomsnitt og lik n − 1 i det verste tilfellet. Dette er igjen et eksempel på at det kan være gradsforskjeller mellom antall ganger en operasjon utføres i en algoritme når det gjelder beste tilfelle, i gjennomsnitt og i verste tilfelle. Med f.eks. n = 100.000, blir log (n) − 0,423 ≈ 11,1, mens n − 1 = 99999.
Eksempel 4 I Avsnitt 1.3.12 så vi på en sorteringsmetode med navnet innsettingssortering. Den er også et eksempel på at det er forskjell i arbeidsmengden i de tre tilfellene: best, gjennomsnitt og verst. Koden ser slik ut:
public static void innsettingssortering(int[] a) { for (int i = 1; i < a.length; i++) { int temp = a[i]; // flytter a[i] til en hjelpevariabel // verdier flyttes inntil rett sortert plass i a[0:i> er funnet int j = i-1; for (; j >= 0 && temp < a[j]; j--) a[j+1] = a[j]; a[j+1] = temp; // verdien settes inn på rett sortert plass } }
Vi fant flg. formeler for arbeidsmengde:
- Best: ƒ( n ) = n − 1 når tabellen er sortert stigende, lineær orden
- Gjennomsnitt: ƒ( n ) = ¼ n(n + 3) - Hn , kvadratisk orden
- Verst: ƒ( n ) = ½ n(n − 1) når tabellen er sortert avtagende, kvadratisk orden
Innsettingssorteringen er av kvadratisk orden både i gjennomsnitt og i det verste tilfellet. Formelene sier imidlertid at det utføres dobbelt så mange sammenligninger i det verste tilfellet som det gjør i gjennomsnitt.
| 1. |
public static void boblesortering(int[] a)Hvilken orden har boblesortering i det beste, i gjennomsnitt og i det verste tilfellet? |
![]() 1.8.5 Notasjon med O , Ω og Θ
1.8.5 Notasjon med O , Ω og Θ
Avsnitt 1.8.2 har en tabell med funksjonstyper
rangert etter asymptotisk «oppførsel». Der ble det sagt at jo høyere opp i tabellen
er funksjon står, jo «mindre» er den asymptotisk sett. I dette avsnittet skal vi
definere dette på en mer formell måte.
Hva betyr det at ƒ er O(g)? I |ƒ(n)| ≤ a|g(n)| inngår det tallverditegn. Men i praksis vil funksjoner i algoritmeanalyse være positive for aktuelle verdier av argumentet n. I så fall kan vi droppe tallverdier. Under har vi tegnet grafen til funksjonen ƒ(n) og den funksjonen vi får ved å gange g(n) med en positiv konstant a. Det er laget slik at grafene skjærer hverandre for n = n0 . Dermed ligger grafen til ƒ(n) under grafen til a g(n) for verdier av n til høyre for n0 . Kravet i definisjonen er med andre ord oppfylt og vi kan si at ƒ er O(g). En annen måte å uttrykke dette på er å si at g er en asymptotisk øvre grense for ƒ.
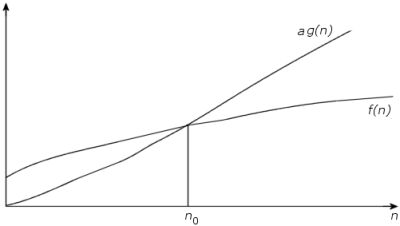 |
| Figur 1.8.5 a): Grafene til ƒ(n) og a g(n) skjærer hverandre i n0 |
De to konstantene a og n0 er ikke entydige. Finnes det først et slikt par, finnes det uendelig mange. Tallet n0 må ikke nødvendigvis stå for et skjæringspunkt. Poenget er at fra n0 og utover skal grafen til ƒ(n) ligge under grafen til a g(n). Dermed kunne n0 gjerne velges lenger til høyre enn der den står i Figur 1.8.5 a). I mange tilfeller kan a velges lik 1. Men generelt gjelder at jo større verdi på a, jo mindre verdi kan vi velge for n0. Hadde vi valgt en enda større a i Figur 1.8.5 a), ville grafen til a g(n) blitt brattere og dermed krysset grafen til ƒ(n) lenger til venstre.
Eksempel 1 La g(n) = n2 og ƒ(n) = 3n2 + 5n + 10. Vi skal vise at ƒ er O(g). Både ƒ og g er positive funksjoner. Derfor kan vi se bort fra tallverditegnet. Vi har 42 = 16. Dermed gjelder spesielt at n2 ≥ 10 for n ≥ 4. Videre har vi at hvis n ≥ 1, så er n2 ≥ n og dermed 5n2 ≥ 5n. Men hvis n ≥ 4, så er allerede n ≥ 1. Dermed får vi, hvis n ≥ 4, at
Derfor blir ƒ(n) ≤ a g(n) for n ≥ n0 hvis vi velger a = 9 og n0 = 4. Som nevnt over er ikke a og n0 entydige. La a = 18. Vi har ƒ(1) = 18 og 18 g(1) = 18. Grafene til ƒ og 18 g er parabler. De to skjærer hverandre for n = 1 og til høyre for 1 må dermed grafen til ƒ ligge under grafen til 18 g. Med andre ord blir ƒ(n) ≤ a g(n) for for alle n ≥ n0 hvis vi velger a = 18 og n0 = 1.
Eksempel 2 For funksjonstypene i tabellen i Avsnitt 1.8.2 vil det være slik at ƒ er O(g) hvis ƒ står høyere opp tabellen enn g. La for eksempel ƒ(n) = log2 n og g(n) = √n. Definér funksjonen h ved h(n) = g(n) − ƒ(n). Vi ser fort at h'(n) = 1/(2√n) − 1/(n ln 2) og at h(n) = 0 for n = 4/(ln 2)2 ≈ 8,33. Det betyr spesielt at h(n) er voksende for n ≥ 8,33. Videre har vi at h(16) = 0 og av det følger at h(n) ≥ 0 for n ≥ 16. Med andre ord vil |ƒ(n)| ≤ a |g(n)| for for alle n ≥ n0 hvis vi velger a = 1 og n0 = 16.
Det finnes en serie formeler for O-notasjon. Her er noen av dem:
- Anta at ƒ er O(g) og g er O(h). Da vil ƒ være O(h).
- Anta at ƒ er O(g) og at a er en konstant. Da vil aƒ være O(g).
- Anta at både ƒ1 og ƒ2 er O(g). Da vil ƒ1 + ƒ2 være O(g).
- Anta at ƒ1 er O(g1) og at ƒ2 er O(g2). Da vil ƒ1ƒ2 være O(g1g2).
Det finnes også en Ω-notasjon som er den omvendte av O-notasjonen. Den er definert slik:
Hvis begge er positive, betyr ƒ er Ω(g) at grafen til ƒ ligger over grafen til a g for n ≥ n0 .
O-notasjon og Ω-notasjon er som nevnt det omvendte av hverandre. Hvis ƒ er O(g), så vil g være Ω(ƒ) og hvis ƒ er Ω(g), så vil g være O(ƒ).
Til slutt har vi Θ-notasjon. Den er definert slik:
Hvis både ƒ og g er positive, betyr ƒ er Θ(g) at grafen til ƒ ligger mellom grafene til a1 g og a2 g for n ≥ n0 . Det følger forøvrig av definisjonene at ƒ er Θ(g) hvis og bare hvis ƒ er O(g) og g er O(ƒ). Dette betyr ikke at ƒ og g er like. Men de oppfører seg på samme måte for store verdier av n og kalles derfor asymptotisk «like».
Eksempel 3 Funksjonene n2, 2 n2, 5 n2 og 100 n2 er alle asymptotisk «like».
Eksempel 4 g(n) = n2 og ƒ(n) = 3n2 + 5n + 10 er asymptotisk «like».
Vi har tidligere sagt når det gjelder funksjonstypene i tabellen i Avsnitt 1.8.2, at jo høyere opp i tabellen er funksjon står, jo «mindre» er den asymptotisk sett. Vi kan nå definere begrepet asymptotisk «mindre enn» slik:
I Avsnitt 1.8.1 ble arbeidsmengden til en algoritme definert som antallet ganger algoritmens dominerende operasjon utføres. Hvis den oppgaven som algoritmen løser, har størrelse n, kan dette antallet ofte uttrykkes som en funksjon av n. Denne funksjonen ble det sagt definerer algoritmens orden. Dette kan nå gis en mer presis definisjon.
Eksempel 5 I Eksempel 1.8.4.4 fant vi at for en heltallstabell med lengde n, ville algoritmen innsettingssortering i gjennomsnitt utføre ƒ(n) = ¼ n2 + ¾ n − Hn sammenligninger. Nå vet vi at ƒ er Θ(n2). Med andre ord er algoritmen i gjennomsnitt av orden n2 eller kvadratisk orden.
| 1. | Bevis at hvis ƒ er O(g) og g er O(h), så vil ƒ være O(h). |
| 2. | Bevis at hvis ƒ er O(g) og a er en konstant, så vil aƒ være O(g). |
| 3. | Bevis at hvis både ƒ1 og ƒ2 er O(g), så vil ƒ1 + ƒ2 være O(g). |
| 4. | Bevis at hvis ƒ1 er O(g1) og ƒ2 er O(g2), så vil ƒ1ƒ2 være O(g1g2). |
![]() 1.8.6 Analyse av metoden erSortert
1.8.6 Analyse av metoden erSortert
I Eksempel 2
i Avsnitt 1.8.4 ble metoden erSortert diskutert. Den
gjennomsnittlige arbeidsmengden ble påstått å være gitt ved ƒ( n ) ≈ 1,7.
Her kommer et bevis for dette.
Gitt at tabellen a inneholder en permutasjon av tallene fra 1 til n.
La så k være et heltall slik at 1 ≤ k < n. Da vil operasjonen
if (a[i-1] > a[i]) bli utført k ganger hvis de k første
elementene i a er sortert, dvs. a[0] < a[1] <
a[2] < . . . <
a[k − 1] , men ikke de k + 1 første,
dvs. a[k − 1] > a[k]. La
B(n , k) være binomialkoeffisienten.
Da kan vi velge k sorterte tall først
i en permutasjon på B(n,k) måter og de siste n − k
tallene i permutasjonen kan velges på (n − k)! måter.
Dermed finnes det B(n , k)·(n − k)!
= n! / k! permutasjoner der de k første elementene
er sortert.
Antall permutasjoner der de k første er sortert, men ikke de k + 1 første, er dermed gitt ved:
(1.8.6.1) (n! / k!) − (n! / (k + 1)!) = n! (1/k! − 1/(k + 1)!) = n! k / (k + 1)!
Sammenlagt for alle permutasjonen blir dermed if (a[i-1] > a[i]) utført:
(1.8.6.2) n!·[1(1 − 1/2!) + 2(1/2! − 1/3!) + · · · + (n − 1)(1/(n − 1)! − 1/n!)] + n − 1
ganger. Det siste leddet i summen (dvs. n − 1) får vi fordi operasjonen blir utført n − 1 ganger for den ene permutasjonen som har alle tallene sortert. Hvis vi regner litt på summen i (1.8.6.2) og deretter deler med n! for å få gjennomsnittet, blir det flg. resultat:
(1.8.6.3) 1 + 1/2! + 1/3! + · · · + 1/(n − 1)!
Summen i (1.8.6.3) er de n − 1 første leddene i en kjent rekkeutvikling av tallet e − 1. Denne rekken konvergerer svært raskt. Vi har e − 1 = 1,718281828 . . . og allerede for n = 6 blir summen lik 1,717. For vårt formål er en avrunding til 1,7 godt nok. Dermed kan vi si at gjennomsnittlig arbeidsmengde er gitt ved ƒ(n) = 1,7.

|