![]() 1.6.1 Endimensjonale tabeller
1.6.1 Endimensjonale tabeller
Vi kan opprette en tabell (eng: array) i et Java-program på minst fire forskjellige måter.
Vi kan 1) opprette tabellen ved å ramse opp hvilke verdier den skal inneholde, 2) ved
å bruke new, 3) ved en kombinasjon av 1) og 2) eller 4) ved å klone en eksisterende tabell.
1) Flg. kode oppretter tabeller ved at vi i hvert tilfelle ramser opp tabellens verdier:
int[] a = {1,2,3,4,5,6,7,8,9,10}; double[] d = {3.14,2.718,0.577,1.4142,0.3010}; boolean[] b = {true,false,true,false}; String[] s = {"Sohil","Per","Thanh","Fatima","Kari","Jasmin"}; Programkode 1.6.1 a)
Det vi ramser opp må være av rett type eller at verdiene har implisitte konverteringsrutiner til rett type. F.eks. kan vi ha med heltall i oppramsingen for en desimaltallstabell siden et heltall implisitt konverteres til et desimaltall. Men normalt bør en oppgi det som desimaltall. Det omvendte er ikke tillatt med mindre en gjør en eksplisitt typekonvertering:
double[] d = {1,2,3}; // lovlig, 1 gjøres om til 1.0, osv. int[] a = {1.0,2.0,3.0}; // ulovlig, kan ikke gjøre om fra double til int Programkode 1.6.1 b)
I int-tabellen a er det ramset opp desimaltall og det er ulovlig. Hvis vi i steden eksplisitt hadde konvertert desimaltallene til heltall, dvs. (int)1.0, osv. ville koden vært syntaksmessig lovlig. Men slik kode skal en normalt ikke bruke.
Verdier av grunnleggende typer (int, double, osv) og av typen String kan lett ramses opp. Hvis
tabellen skal inneholde referansetyper, er det litt mer komplisert. Da må vi enten på
forhånd ha instanser av typen eller instansene må opprettes direkte i oppramsingen ved
hjelp av new.
Hvis tabelltypen er en av omslagsklassene, f.eks. Integer, så holder det
å ramse opp verdier av den tilhørende grunnleggende typen. Det er typens autoboksing
som tar seg av konverteringen til rett type:
Point[] p = {new Point(0,0),new Point(1,0),new Point(0,1)};
Integer[] i = {1,2,3,4,5,6,7,8,9,10}; // autoboksing, int til Integer
Double[] d = {1.0,2.0,3.0,4.0,5.0}; // autoboksing, double til Double
Programkode 1.6.1 c)
Typer kan blandes i oppramsingen så sant alle er subtyper av samme klasse:
Object[] o = {1,"Kari",new Point(0,0)}; // lovlig kode Programkode 1.6.1 d)
Konklusjon: Det å opprette tabeller ved å ramse opp verdier, er aktuelt kun når det er få verdier. Når vi lager testprogrammer for ulike metoder gjør vi det ofte ved hjelp av små tabeller med utvalgte verdier. Da er denne teknikken gunstig. Men det er også mange tilfeller der vi faktisk trenger små tabeller i våre programmer. For eksempel kan det hende vi trenger en tabell med ukedagenes navn eller en tabell med månedsnavnene. Da er det gunstig å bruke denne teknikken:
String[] dag = {"Man","Tirs","Ons","Tors","Fre","Lør","Søn"};
String[] måned = {"Jan","Feb","Mar","Apr","Mai","Jun",
"Jul","Aug","Sep","Okt","Nov","Des"};
Programkode 1.6.1 e)
2) En tabell av en bestemt datatype og med en bestemt lengde n oppretter vi normalt ved hjelp av operatoren new:
datatype[] a = new datatype[n]; // n er en konstant eller en variabel
Her kan datatype være f.eks. int, double, String, Integer, Object eller noe annet. Hvis vi skulle komme i skade for å bruke en negativ verdi på n, kastes et unntak med det lange navnet NegativeArraySizeException. Ellers, hvis n ≥ 0, er dette ok kode. Da blir det reservert plass til n verdier av typen datatype. Tabellen blir også «nullet», dvs. det legges inn nullverdier på alle plassene. Hva som er en nullverdi er avhengig av datatypen. F.eks. er det 0 for datatypen int, 0.0 for datatypen double, false for boolean og null for objekttyper. Det er lovlig med n = 0, men da får vi en tom tabell, dvs. uten plass til verdier:
int[] a = new int[100]; // plass til 100 heltall String[] s = new String[50]; // plass til 50 tegnstrenger Integer[] i = new Integer[0]; // en tom tabell Programkode 1.6.1 f)
Tabellen a får lengde 100, dvs. det blir reservert plass til 100 heltall og tallet 0 legges inn på hver plass. Tabellen s får lengde 50 og her legges det inn null på hver plass. I tabellen i er det ikke plass til noen verdier og dermed heller ingen null-verdier.
Konklusjon: Hvis vi i våre programmer trenger store tabeller, så opprettes de ved hjelp av new. Hvis vi ønsker bestemte verdier i tabellene, må vi lage kode for det:
Eksempel: Vi trenger en tabell som inneholder heltallene fra 1 til 100:
int[] a = new int[100]; // 100 heltall for (int i = 0; i < a.length; i++) a[i] = i + 1; // legger inn tallene Programkode 1.6.1 g)
3) Vi kan kombinere teknikkene fra 1) og 2). Flg. programkode oppretter en int-tabell med tallene fra 1 til 10 som tabellverdier:
int[] a = new int[] {1,2,3,4,5,6,7,8,9,10}; Programkode 1.6.1 h)
Dette kan være nyttig i en metode som returnerer en tabell. Gitt at vi har metodene min og maks. Anta at metoden minmaks skal returnere posisjonene til både den minste og den største verdien i tabellen a. Da kan den kodes på flg. enkle (men ikke effektive) måte:
public static int[] minmaks(int[] a) { return new int[] { min(a), maks(a) }; } Programkode 1.6.1 i)
4) Hvis vi allerede har en tabell a, kan vi lage en ny tabell ved å klone den:
datatype[] b = a.clone();
Hvis tabelltypen til a er en av de grunnleggende typene (int, double, osv),
så må klonetypen datatype være av samme type som a. Hvis tabelltypen til a er
en objekttype, så må klonetypen datatype være enten samme type som a eller
være en supertype til denne typen.
I flg. eksempel klones en int-tabell og en String-tabell:
int[] a = {1,2,3,4,5}; String[] s = {"Sohil","Thanh","Fatima"}; int[] b = a.clone(); // a og b er av samme type String[] t = s.clone(); // s og t er av samme type Object[] u = s.clone(); // u er en supertype til s Programkode 1.6.1 j)
I programkoden over blir heltallstabellen b en kopi av a.
Tabellene a og b er to forskjellige tabeller, med de har samme
innhold. Også s og t er to forskjellige tabeller med samme
innhold. En variabel av en objecttype, f.eks. String, er en referanse til
en instans av typen. Med andre ord er tabellverdiene i s og t
referanser til String-instanser. Både s[0] og t[0]
refererer til den String-instanser som inneholder navnet Sohil.
Etter kloningen er det fortsatt bare én slik String-instans, men det blir
referert til den fra to forskjellige tabeller. Typen til tabellen u
(dvs. Object) er en supertype til String. Derfor vil også den
kloningen fungere. Også her inneholder u de samme referansene som s.
En tabell har en tilhørende int-konstant length, og dens verdi er lik
tabellens lengde eller antaller reserverte plasser om en vil. Det at length
er konstant gjør at koden
a.length = 5; // syntaksfeil!!
gir syntaksfeil. Kompilatoren vil komme med en feilmelding omtrent som dette: variable length is declared final; cannot be assigned.
Det er mulig å opprette tomme tabeller, dvs. tabeller der det ikke er plass til noen
verdier. Det kan vi få til på en av flg. måter (datatype er en eller annen
datatype):
datatype[] a = new datatype[0]; // a er en tom tabell datatype[] b = {}; // b er en tom tabell datatype[] c = new datatype[]{}; // c er en tom tabell Programkode 1.6.1 k)
I begge tilfellene får vi en fysisk tabell der det ikke er plass til noen verdier, dvs. a.length er 0. Vi skal skille mellom en tom tabell og en null-tabell (dvs. en ikke eksisterende tabell). Flg. kode gir en null-tabell:
datatype[] a = null; // vi kaller a en null-tabell
Konklusjon: Hvis vi trenger en tabell som skal være en kopi av en eksisterende tabell, er det mest effektivt å bruke metoden clone. Metoden clone er native og er derfor trolig kodet så effektivt som mulig på den bestemte plattformen som JVM-en er laget for.
| 1. | Klassen Arrays har metoder for utskrift av tabeller. La a være en tabell av en eller annen type. Kallet Arrays.toString(a) returnerer en tegnstreng som inneholder verdiene til a adskilt med komma og med hakeparenteser på begge sider. Dette kan så skrives ut ved hjelp av System.out.println. Prøv dette! |
![]() 1.6.2 Metodene arraycopy, copyOf, copyOfRange, fill og equals
1.6.2 Metodene arraycopy, copyOf, copyOfRange, fill og equals
Metoden arraycopy fra klassen System i java.lang kopierer hele
eller deler av en tabell over i en annen tabell. Hvis tabellen er av en
objekttype, vil det, som for kloning, være referanser som kopieres.
Metoden har flg. signatur:
arraycopy(datatype1[] fra, int m, datatype2[] til, int n, int antall)
Det kopieres antall verdier fra og med posisjon m i tabellen fra over i tabellen til der kopieringen starter i posisjon n. Hvis datatype1 er en grunnleggende type må datatype2 være det samme som datatype1. Hvis datatype1 er en objektttype må datatype2 enten være det samme som datatype1 eller være en supertype til datatype1.
En «dynamisk» tabell «utvider seg». Det som egentlig skjer er at det lages en ny og større tabell av samme type og den gamle tabellen kopieres over i første del av den nye. Deretter får den nye tabellen navnet til den gamle. Til dette kan vi bruke arraycopy:
int[] a = {1, 2, 3}; a[3] = 4; // må fjernes, gir ArrayIndexOutOfBoundsException int[] b = new int[2*a.length]; // b dobbelt så stor som a System.arraycopy(a,0,b,0,a.length); // kopierer a over i b a = b; // a er "utvidet" a[3] = 4; // nå er dette ok Programkode 1.6.2 a)
Det som arraycopy gjør i Programkode 1.6.2 a), kunne vi selvfølgelig ha gjort ved hjelp av en vanlig for-løkke. Metoden arraycopy er native. Det betyr at den er kodet i den virtuelle javamaskinen (JVM) og forhåpentligvis laget så optimal som mulig for den gitte plattformen.
Det å «utvide» tabeller er såpass vanlig at Java har fått egne metoder for det. Da brukes arraycopy implisitt. Programkode 1.6.2 a) kunne vært erstattet med flg. kode:
int[] a = {1,2,3}; a[3] = 4; // må fjernes, gir ArrayIndexOutOfBoundsException a = Arrays.copyOf(a, 2*a.length); a[3] = 4; // nå er dette ok Programkode 1.6.2 b)
Metoden copyOf fra klassen Arrays har flg. signatur:
T[] copyOf(T[] a, int nylengde)
Datatypen T kan være en grunnleggende type (byte, short, int, long, float, double, char, boolean) eller en objekttype. Hvis nylengde er større enn a.length, returnerer metoden en ny tabell med inneholdet til a som første del. Resten består av «nuller». Hvis nylengde er lik a.length, får vi en kopi av a og hvis nylengde er mindre enn a.length, får vi en tabell som inneholder så mange verdier fra a som nylengde sier. Vi kan ha nylengde lik 0. Da returneres en tom tabell. Men hvis nylengde er negativ, får vi en NegativeArraySizeException.
Metoden copyOfRange er litt mer generell enn copyOf. Den har flg. signatur:
T[] copyOfRange(T[] a, int fra, int til)
Den returnerer en tabell med lengde til − fra. Her må fra ≥ 0, til ≥ fra og fra ≤ a.length. Men til kan godt være større enn a.length. Se flg. eksempel:
String[] s = {"Per","Kari","Ola"};
s = Arrays.copyOfRange(s, 2, 4); // lengde 4 - 2 = 2;
s[1] = "Åse";
System.out.println(Arrays.toString(s)); // [Ola, Åse]
Programkode 1.6.2 c)
Metoden fill fra klassen Arrays kan brukes til å fylle hele eller deler av en tabell med en bestemt verdi og equals tester om to tabeller er like, dvs. er like lange, er av samme type og har det samme innholdet. Se på flg. eksempel:
int[] a = new int[5]; // a = {0,0,0,0,0} Arrays.fill(a, 1); // a = {1,1,1,1,1} int[] b = {1,1,1,1,1}; int[] c = {1,2,3,4,5}; boolean x = Arrays.equals(a, b); // x = true boolean y = Arrays.equals(a, c); // y = false Programkode 1.6.2 d)
![]() 1.6.3 Flerdimensjonale tabeller
1.6.3 Flerdimensjonale tabeller
To- og flerdimensjonale tabeller opprettes på en tilsvarende måte som
de endimensjonale. Det betyr at vi kan opprette en flerdimensjonal tabell
ved 1) å ramse opp verdier, 2) ved hjelp av new, 3) ved å kombinere 1) og 2) eller ved
4) å klone en eksisterende tabell.
1) Vi ønsker en tabell med 3 rader og 5 kolonner som inneholder tallene fra 1 til 15:
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| Figur 1.6.3 a) : 3 rader, 5 kolonner | ||||
|---|---|---|---|---|
Vi kan opprette tabellen ved å ramse opp verdiene 1, . . , 15 på denne måten:
int[][] a = {{1,2,3,4,5}, {6,7,8,9,10}, {11,12,13,14,15}}; Programkode 1.6.3 a)
I oppramsingen har vi tre grupper med 5 verdier, en gruppe for hver rad i den todimensjonale tabellen. Det blir på samme måte for tabeller av andre datatyper. Når det gjelder hva slags verdier som er «lovlige» å ramse opp, er reglene de samme som for endimensjonale tabeller.
Hver rad i Figur 1.6.3 a) er selv en endimensjonal tabell. Vi kan derfor også gjøre det slik:
int[] rad1 = {1,2,3,4,5}; int[] rad2 = {6,7,8,9,10}; int[] rad3 = {11,12,13,14,15}; int[][] a = {rad1, rad2, rad3}; Programkode 1.6.3 b)
2) Hvis vi skal opprette en todimensjonal tabell ved hjelp av new må vi oppgi dimensjonen, dvs. antall rader og antall kolonner. Hvis målet er tabellen i Figur 1.6.3 a), blir det slik:
int[][] a = new int[3][5]; // 3 rader, 5 kolonner Programkode 1.6.3 c)
Tabellen «nulles», dvs. fylles med 0-verdier (tallet 0 siden det er int).
Hvis den i steden skal inneholde tallene fra 1 til15 slik som i
Figur 1.6.3 a), må de
legges inn, f.eks. slik:
for (int i = 0; i < 3; i++) // 3 rader { for (int j = 0; j < 5; j++) // 5 kolonner { a[i][j] = 5*i + j + 1; } } Programkode 1.6.3 d)
3) Det er også mulig å kombinere oppramsing av verdier og bruk av new. Hvis vil vil lage tabellen i Figur 1.6.3 a), blir det slik:
int[][] a = new int[][] {{1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15}}; Programkode 1.6.3 e)
4) Kloning av en todimensjonal tabell blir annerledes enn for en som er endimensjonal. La a være heltallstabellen med 3 rader og 5 kolonner som ble laget over. Et første forsøk på å klone a kunne være flg. kode:
int[][] b = a.clone(); // a klones Programkode 1.6.3 f)
Men dette virker ikke som forventet. Den todimensjonale tabellen b blir ingen «ekte» klone av a. Vi må se litt nærmere på hva som skjer når en todimensjonal tabell opprettes. La oss gjenta den koden som oppretter tabellen a ved hjelp av new:
int[][] a = new int[3][5]; Programkode 1.6.3 g)
Flg. tegning gir et godt inntrykk av det som skjer:
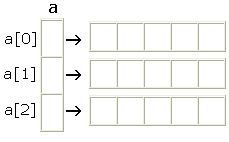 |
| Figur 1.6.3 b) : Tabellens oppbygging |
Systemet består av fire endimensjonale tabeller. Den ene er tegnet vertikalt og
de tre andre horisontalt. Navnet på den vertikale er a med datatype
int[], dvs. hvert element i tabellen a inneholder en referanse til
en int-tabell.
Dette er illustrert på tegningen ved at det går piler fra hvert element i a,
det vil si fra a[0], a[1] og a[2], til deres tilhørende
int-tabeller. Dette betyr at den todimensjonale tabellen a kan opprettes
på en alternativ måte:
int[][] a = new int[3][]; // lager den vertikale tabellen a[0] = new int[5]; // lager a[0]-tabellen a[1] = new int[5]; // lager a[1]-tabellen a[2] = new int[5]; // lager a[2]-tabellen Programkode 1.6.3 h)
Setningen int[][] b = a.clone(); kloner
kun referansetabellen a, dvs. den vertikale tabellen i
Figur 1.6.3 b).
Hvis kloning skal lage en kopi av hele den todimensjonale tabellen, må vi
klone både referansetabellen og de tre andre tabellene. F.eks. slik:
int[][] b = a.clone(); // kloner a b[0] = a[0].clone(); // kloner a[0] b[1] = a[1].clone(); // kloner a[1] b[2] = a[2].clone(); // kloner a[2] Programkode 1.6.3 i)
Figur 1.6.3 b) viser hvilken verdi a.length har. Det er lengden på den vertikale tabellen og det er det samme som antallet rader. Antallet kolonner får vi f.eks. ved hjelp av a[0].length.
Metodene arraycopy fra class System og fill og equals fra class Arrays kan ikke brukes på direkten for todimensjonale tabeller. Hvis a og b er to slike tabeller vil arraycopy kun kopiere referansetabellen a over i referansetabellen b. Tilsvarende blir det med fill og equals. Det er referansetabellene som vil inngå.
Gir det mening å ha en «tom» todimensjonal tabell? I flg. kodebit er alle setninger lovlige:
int[][] a = {}; int[][] b = {{}}; int[][] c = new int[0][0]; int[][] d = new int[2][0]; int[][] e = new int[0][2]; int[][] f = {null,{}}; Programkode 1.6.3 j)
Tabellene a og c i Programkode 1.6.3 j) har begge ingen rader og ingen kolonner. Tabellen b har 1 rad og ingen kolonner, d har 2 rader og ingen kolonner og e ingen rader og 2 kolonner. Vi kaller dette «tomme» tabeller. I noen tilfeller kan det være aktuelt å ha slike tabeller, men ingen av dem kan inneholde verdier. Tabellen f er litt spesiell. Den har 2 rader. Den første raden er null og den andre raden er tom. Hvis én eller flere rader er null er det ikke vanlig å kalle det en tom tabell. Se Oppgave 1 og 2.
| 1. | Vi trenger en tabell med 5 rader og 3 kolonner der tallene 1, 2 og 3 står i første rad, tallene 4, 5 og i andre rad, osv. Lag det på alle de måtene som står beskrevet fra Programkode 1.6.3 a) til Programkode 1.6.3 e). |
| 2. | Lag en programbit som inneholder
Programkode 1.6.3 j). Lag i tillegg kode som fortløpende skriver ut
a.length, b.length, osv. Blir utskriften det du forventer?
|
| 3. | Gjør som i Oppgave 2, men skriv nå ut
a[0].length, b[0].length, osv. Blir utskriften (og feilmeldingene)
som du forventer?
|
| 4. | Lag kode som lager en tabell b som kun består av de to første radene i tabellen a i
Programkode 1.6.3 a).
Kan du få brukt metoden copyOf
fra Avsnitt 1.6.2 her?
|
| 5. | Lag kode som «utvider» tabellen a i
Programkode 1.6.3 a) slik
at den får en rad til. Den skal inneholde tallene fra 16 til 20.
Kan du få brukt metoden copyOf
fra Avsnitt 1.6.2 her?
|
| 6. | Lag kode som oppretter en tabell a med 3 rader og 5 kolonner der tallene 1, 2 og 3 står i første
kolonne, tallene 4, 5 og 6 i andre kolonne, osv. Den skal så «utvides»
til å få 7 kolonner der tallene 16, 17 og 18 skal stå i den nest siste kolonnen og tallene
19, 20 og 21 i den siste kolonnene. Kan du få brukt metoden copyOf
fra Avsnitt 1.6.2 her?
|
| 7. | La n være en heltallsvariabel. Lag kode som oppretter en tabell a med n rader og n kolonner slik at det står 1-ere på hoveddiagonalen (elementene fra øverste venstre hjørne ned til nederste høyre hjørne) og 0-er alle andre steder. |
| 8. | La m og n være en heltallsvariabler. Lag kode som oppretter en tabell a med m rader og n kolonner. Første rad skal inneholde tallene fra 1 til n, andre rad tallene fra n + 1 til 2n, osv. |
| 9. | Lan m og n være en heltallsvariabler. Lag kode som oppretter en tabell a med m rader og n kolonner. Første kolonne skal inneholde tallene fra 1 til m, andre kolonne tallene fra m + 1 til 2m, osv. |
| 10. | Lang n være en heltallsvariabel. Lag kode som oppretter en tabell a med n rader og n kolonner slik at tallene fra 1 til n2 er satt inn i «sirkelform». Dvs. at tallene fra 1 til n står i første rad. Videre tallene fra n til 2n − 1 i nedover i siste kolonne. Deretter tallene fra 2n − 1 til 3n − 2 fra høyre mot venstre i nederste rad, osv. Se figuren under for tilfellet n = 5. |
| 1 | 2 | 3 | 4 | 5 |
| 16 | 17 | 18 | 19 | 6 |
| 15 | 24 | 25 | 20 | 7 |
| 14 | 23 | 22 | 21 | 8 |
| 13 | 12 | 11 | 10 | 9 |
![]() 1.6.4 Operasjoner på todimensjonale tabeller
1.6.4 Operasjoner på todimensjonale tabeller
Aktuelle operasjoner kan være å speile, rotere og transponere.
Men først ser vi på hvordan vi kan lage metoder som gir
«pene» utskrifter.
Utskrift En utskrift av en vanlig (endimensjonal) tabell kan vi få til
ved å bruke toString-metoden fra klassen
Arrays.
Metoden kan også brukes for en todimensjonal tabell siden den egentlig er en tabell av tabeller
(se Figur 1.6.3 b). Men resultatet blir ikke det
vi ønsker. Vi får noe som dette:
int[][] a = {{1,2,3,4,5}, {6,7,8,9,10}, {11,12,13,14,15}}; // tabellen System.out.println(Arrays.toString(a)); // toString // [[I@4322394, [I@77bdcbb2, [I@4d885088] // utskrift Programkode 1.6.4 a)
Det vi får ut er minneadressene til a[0], a[1] og a[2]. Vi må isteden kalle
toString-metoden på både a[0], a[1] og a[2]:
int[][] a = {{1,2,3,4,5}, {6,7,8,9,10}, {11,12,13,14,15}}; // tabellen for (int i = 0; i < a.length; i++) // radene i tabellen System.out.println(Arrays.toString(a[i])); // skriver ut raden // [1, 2, 3, 4, 5] // utskrift // [6, 7, 8, 9, 10] // [11, 12, 13, 14, 15] Programkode 1.6.4 b)
En utskrift blir normalt mest lesbar og «penest» hvis den kommer på rektangulær form. Det betyr at elementene i en og samme kolonne i tabellen kommer rett under hverandre. For å få til det må vi la utskriftskolonnene ha en fast bredde (eng: width). Den må være større enn bredden til det «bredeste» elementet tabellen. For hele tall er bredden det samme som antall siffer og eventuelt et ekstra tegn (fortegnet) for et negativt tall.
Hvis vi tar utgangspunkt i den todimensjonale tabellen i eksemplene over og bruker 4 som fast kolonnebredde, er det vanlig å velge en av følgende to måter for rektangulær utskrift:
1. eksempel: 2. eksempel:
1 2 3 4 5 1 2 3 4 5
6 7 8 9 10 6 7 8 9 10
11 12 13 14 15 11 12 13 14 15
Figur 1.6.4 a) : To rektangulære utskrifter
I 1. eksempel brukes høyrejustering (utskrift til høyre) og i 2. eksempel venstrejustering (utskrift til venstre) i det reserverte feltet. For tall er høyrejustering vanligst, mens det f.eks. for tegnstrenger er mest vanlig med venstrejustering.
Utskriften i Figur 1.6.4 a) kalles formatert. Hvis utskriften skal direkte til skjermen, er det enklest å bruke metoden printf (bokstaven f i navnet står for formatert). Når et heltall skal skrives ut trengs to parameterverdier. Først et utskriftsdirektiv i form av en tegnstreng og så tallet som skal skrives ut. I direktivet må vi oppgi feltbredde, hvilken type som skal skrives ut og eventuelt hva slags justering vi skal ha. Høyrejustering er standard. Flg. metode har tabellen og feltbredden som parametre:
public static void skriv(int[][] a, int feltbredde) { for (int i = 0; i < a.length; i++) // i følger radene { for (int j = 0; j < a[i].length; j++) // j følger kolonnene { System.out.printf("%" + feltbredde + "d", a[i][j]); } System.out.printf("\n"); // ny linje } } Programkode 1.6.4 c)
Flg. kodebit vil gi en utskrift som den i 1. eksempel i Figur 1.6.4 a):
int[][] a = {{1,2,3,4,5}, {6,7,8,9,10}, {11,12,13,14,15}}; skriv(a, 4); Programkode 1.6.4 d)
I metoden printf er tegnstrengen
utskriftsdirektiv og a[i][j] tallet som skrives ut. Direktivet
starter med % (prosenttegnet), så kommer feltbredden (en variabel) og til slutt
bokstaven d som forteller at det skal skrives ut et heltall på desimal form
(d for desimal). Hvis feltbredden er 4, blir direktivet lik "%4d".
Et utskriftsdirektiv kan inneholde mye mer.
Du finner mer om utskriftsdirektiver i
Vedlegg B om
formatert utskrift.
En metode som skriver ut en todimensjonal tabell med tegnstrenger kan lages nesten identisk med metoden i Programkode 1.6.4 c). For å få til en venstrejustert utskrift må det settes et minustegn i utskrifstdirektivet:
public static void skriv(String[][] a, int feltbredde) { for (int i = 0; i < a.length; i++) { for (int j = 0; j < a[i].length; j++) { System.out.printf("%-" + feltbredde + "s", a[i][j]); } System.out.printf("\n"); // ny linje } } Programkode 1.6.4 e)
Flg. eksempel viser hvordan dette virker:
String[][] a = {{"Petter","Bodil","Reidun"},
{"Ola","Anne","Siri"},
{"Anton","Jasmin","Siv"}};
skriv(a, 8); // venstrejustert utskrift:
// Petter Bodil Reidun
// Ola Anne Siri
// Anton Jasmin Siv
Programkode 1.6.4 f)
Speilinger En todimensjonal tabell kan speiles om en horisontal (vannrett) linje midt i tabellen (kan også kalles en horisontal rotasjon). Det betyr at første og siste rad bytter verdier, andre og nest siste rad bytter verdier, osv.
Før speiling: Etter speiling:
1 2 3 4 5 11 12 13 14 15
6 7 8 9 10 6 7 8 9 10
11 12 13 14 15 1 2 3 4 5
Figur 1.6.4 b) : Horisontal speiling
En todimensjonal tabell kalles regulær hvis den er på rektangulær form, dvs. at alle radene er like lange. En horisontal speiling av en todimensjonal tabell gir mening kun når den er regulær. I Java er det mulig å lage irregulære tabeller - se Avsnitt 1.6.5. En metode som utfører en horisontal speiling av en regulær todimensjonal tabell a kan kodes slik:
public static void horisontal(int[][] a) // horisontal speiling { int n = a[0].length; // antall kolonner int v = 0, h = a.length - 1; // v og h følger radene while (v < h) { if (a[v].length != n || a[h].length != n) throw new IllegalArgumentException("Tabellen a er ikke regulær!"); for (int j = 0; j < n; j++) // en og en kolonne { int temp = a[v][j]; // bytter a[v][j] og a[h][j] a[v][j] = a[h][j]; a[h][j] = temp; } v++; // øker v h--; // reduserer h } } Programkode 1.6.4 g)
Vi kan også speile (eller rotere) om en vertikal linje midt i tabellen. En vertikal speiling kan kodes på en tilsvarende måte som Programkode 1.6.4 g). Se Oppgave 1.
Hvis en bytter om rader og kolonner i en todimensjonal tabell, blir den transponert. Men da kan vi få dimensjonsproblemer. Tabellen i Figur 1.6.4 b) har 3 rader og 5 kolonner. En transponering av den vil gi en tabell med 5 rader og 3 kolonner. Dette kan vi dermed ikke få til ved å bytte om verdiene i en tabell. Vi må isteden opprette en ny tabell med korrekt dimensjon og så la den få resultatet av transponeringen. Det betyr at den originale tabellen ikke endres. Se Oppgave 2.
Hvis tabellen er kvadratisk (like mange rader som kolonner), kan tabellen transponeres. En slik tabell har en hoveddiagonal (elementene på skrå fra øverste venstre hjørne ned til nederste høyre hjørne). En transponering blir en speiling (eller rotasjon) om den diagonalen.
Før speiling: Etter speiling:
1 2 3 4 5 1 6 11 16 21
6 7 8 9 10 2 7 12 17 22
11 12 13 14 15 3 8 13 18 23
16 17 18 19 20 4 9 14 19 24
21 22 23 24 25 5 10 15 20 25
Figur 1.6.4 c) : Diagonal speiling
En diagonal speiling av en kvadratisk tabell kodes slik:
public static void diagonal(int[][] a) // diagonal speiling { for (int i = 0; i < a.length; i++) { if (a[i].length != a.length) throw new IllegalArgumentException("Tabellen er ikke kvadratisk!"); for (int j = 0; j < i; j++) { int temp = a[i][j]; // bytter om a[i][j] og a[j][i] a[i][j] = a[j][i]; a[j][i] = temp; } } } Programkode 1.6.4 h)
Bidiagonalen i en todimensjonal kvadratisk tabell består av elementene på skrå fra øverste høyre hjørne ned til nederste venstre hjørne. En speiling om bidiagonalen kan gjøres på en tilsvarende måte som for diagonalen. Se Oppgave 3.
Rotasjoner Vi kan rotere en todimensjonal tabell om midtpunktet. Hvis vi imidlertid skal rotere 90o eller 270o, kan vi på samme måte som for en transponering, få problemer med dimensjonen. Vi kan derfor lage to metoder. I den ene forutsettes det at tabellen er kvadratisk og dermed kan den roteres. Den andre, som må være regulær, kan returnere en en ny tabell som er rotasjonen av den gitte tabellen.
Flg. figur viser en rotasjon på 90o med klokken:
Før rotasjon: Etter rotasjon:
1 2 3 4 5 21 16 11 6 1
6 7 8 9 10 22 17 12 7 2
11 12 13 14 15 23 18 13 8 3
16 17 18 19 20 24 19 14 9 4
21 22 23 24 25 25 20 15 10 5
Figur 1.6.4 d) : Rotasjon 90o
Legg merke til at hvis vi først gjør en horisontal speiling og så en transponering (speiling om diagonalen), får vi en rotasjon med klokken på 90o. Sjekk at det stemmer. Dermed kan vi kode rotasjonen ved å kalle to andre metoder:
public static void rotasjon90(int[][] a) { horisontal(a); diagonal(a); } Programkode 1.6.4 i)
Rotasjoner på både 180o og 270o med klokken kan på en tilsvarende måte som en rotasjon på 90o utføres ved hjelp av to speilinger. Figur 1.3.17 i viser hvordan ulike speilinger og rotasjonen kan kombineres. Se også oppgavene nedenfor.
| 1. | Lag metoden public static void vertikal(int[][] a). Den skal speile
(eller rotere) den regulære tabellen a med hensyn på en vertikal linje
midt på tabellen.
|
| 2. | Lag metoden public static int[][] transponert(int[][] a). Den skal
returnere en tabell som er den transponerte av den regulære tabellen a, dvs. radene og kolonnene er
byttet om. Tabellen a skal ikke endres.
|
| 3. | Lag metoden public static void bidiagonal(int[][] a). Den skal speile
(eller rotere) tabellen a med hensyn på bidiagonalen.
Bidiagonalen består av elementene på skrå fra øverste høyre hjørne ned til nedre venstre
hjørne. Metoden skal kaste et unntak hvis a ikke er kvadratisk.
|
| 4. | Lag metoden public static int[][] roter90(int[][] a). Den skal returnere en tabell
som svarer til en rotasjon av
tabellen a med klokken 90o. Metoden skal virke for alle regulære tabeller, dvs.
også for de som ikke er kvadratiske. Tabellen a skal ikke endres.
|
| 5. | Lag metoden public static void roter180(int[][] a). Den skal rotere
tabellen a med klokken 180o. Metoden skal virke for alle regulære
tabeller, dvs. også for de som ikke er kvadratiske.
|
| 6. | Lag metoden public static void roter270(int[][] a). Den skal rotere
tabellen a med klokken 270o. Metoden skal kaste et unntak
hvis a ikke er kvadratisk.
|
| 7. | Lag metodene public static int[][] roter180(int[][] a). Den skal returnere en tabell
som svarer til en rotasjon av
tabellen a med klokken 180o. Metoden skal virke for alle regulære tabeller, dvs.
også for de som ikke er kvadratiske. Tabellen a skal ikke endres.
|
| 8. | Lag metodene public static int[][] roter270(int[][] a). Den skal returnere en tabell
som svarer til en rotasjon av
tabellen a med klokken 270o. Metoden skal virke for alle regulære tabeller, dvs.
også for de som ikke er kvadratiske. Tabellen a skal ikke endres.
|
![]() 1.6.5 Regulære og irregulære tabeller
1.6.5 Regulære og irregulære tabeller
En todimensjonal tabell kalles regulær hvis den har rektangulær form. Den
kalles irregulær hvis den ikke er regulær. I Figur 1.6.4 a) har vi
et eksempel en irregulær tabell:
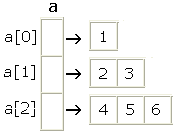 |
| Figur 1.6.5 a) : En irregulær tabell |
Også i en irregulær tabell a vil a.length står for antall rader. På figuren
over er den 3. Lengden på radene finner vi også som før, men nå behøver ikke de være like. Lengden
på første rad er som vanlig gitt ved a[0].length. På figuren er den 1. Osv.
Flg. kode oppretter tabellen på figuren over:
int[][] a = {{1},{2,3},{4,5,6}}; Programkode 1.6.5 a)
En generell tabell på «trekantform» med verdier fortløpnede fra 1 kan opprettes slik:
int n = 4, k = 1; int[][] a = new int[n][]; for (int i = 0; i < a.length; i++) { a[i] = new int[i+1]; // oppretter raden for (int j = 0; j < a[i].length; j++) a[i][j] = k++; // legger inn verdier } skriv(a,4); // utskrift (Programkode 1.6.4 c)) // Utskrift // 1 // 2 3 // 4 5 6 // 7 8 9 10 Programkode 1.6.5 b)
Det er ikke vanlig å bruke irregulære tabeller. Men i bestemte situasjoner kan de komme til nytte. En kvadratisk matrise kalles nedre triangulær hvis alle elementene over hoveddiagonaler er 0. Da vil det holde å lagre de verdiene som ligger på og under hoveddiagonalen, og disse kan lagres i en tabell maken til den i Figur 1.6.5 a).
Den todimensjonale tabellen i Figur 1.6.5 a) er irregulær, men har en trekantform. Vi kan ha mer irregulære tabeller enn det. Til venstre i Figur 1.6.5 b) under har vi en slik tabell. Den kan det være aktuelt å «sortere», dvs. la radene ha stigene lengde slik som til høyre i figuren.
4 5 6 1
11 12 13 14 15 2 3
1 -> 4 5 6
7 8 9 10 7 8 9 10
2 3 11 12 13 14 15
Figur 1.6.5 b)
En slik sortering kan vi få til ved hjelp av flg. kodebit:
int[][] a = {{4,5,6},{11,12,13,14,15},{1},{7,8,9,10},{2,3}}; Tabell.innsettingssortering(a, (x,y) -> x.length - y.length); skriv(a,4); // Programkode 1.6.4 c) // Utskrift // 1 // 2 3 // 4 5 6 // 7 8 9 10 // 11 12 13 14 15 Programkode 1.6.5 c)
| 1. | Lag en irregulær todimensjonal int-tabell der 1. rad har plass til 10 verdier, 2. rad plass til 9 verdier, osv. nedover til 10. og siste rad som skal ha plass til kun én verdi. Fyll tabellen med flg. verdier: Tallene fra 1 til 10 i 1. rad, tallene fra 11 til 19 i 2. rad, tallene fra 20 til 28 i 3. rad, osv. til kun tallet 55 i siste rad. Løs oppgaven på en tilsvarende måte som i Programkode 1.6.5 b). Skriv så ut tabellens innhold. |
| 2. | Lag en irregulær todimensjonal int-tabell med n rader. Første og siste rad skal inneholde 1 verdi, andre og nest siste rad 2 verdier, tredje og tredje siste rad 3 verdier, osv. Som verdier skal tallene fra 1 og utvover komme radvis. Hvis f.eks. n = 5, blir det tallet 1 på første rad, 2 og 3 på andre rad, 4, 5 og 6 på tredje rad, 7 og 8 på fjerde rad og 9 på femte rad. Skriv så ut tabellens innhold for ulike verdier av n. |
| 3. | Gjør om sorteringen i Programkode 1.6.5 c) slik at radene sorterses med synkende radlengder. Dvs. lengste rad øverst, osv. |
| 4. | Gjør om sorteringen i Programkode 1.6.5 c) slik at radene sorterses med hensyn på første verdi i hver rad. Dette får ikke effekt i tabellen som inngår i Programkode 1.6.5 c). Bruk derfor en annen tabell der dette vil gi en annen sortering. |
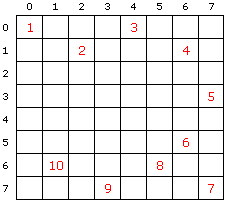 |
| Figur 1.6.6 a) : Et sjakkbrett |
I Figur 1.6.6 a) står starten på en mulig springer-tur med ruten (0.0) som utgangspunkt. Startruten er markert med 1, den neste ruten på turen med 2, osv. Foreløpig er (6,1) siste rute. Derfra er det 3 muligheter videre. Springeren kan gå til hvilken som helst av rutene (4,0), (4,2) eller (5,3). Den har allerede vært innom rute (7,3) og kan derfor ikke gå dit. Generelt vil det være opptil 8 mulige ruter som en springer kan gå videre til. Men hvis den er nær en av brettets kanter, blir det færre siden den må holde seg innenfor brettet.
Det er mulig å finne en springer-tur ved prøving og feiling. Når springeren har kommet til en rute vil det normalt være flere mulige ruter å gå videre til. Da er det bare å la den gå videre dit. Hvis den har kommet inn i en blindgate, dvs. det finnes ingen mulige ruter å gå videre til, så må vi trekke den tilbake til forrige rute der det var mer enn et valg for å gå videre. Dermed kan den prøve en ny mulighet derfra. Osv. Denne teknikken kalles prøving og feiling med tilbaketrekning. Det er nok nærmest umulig å finne en springer-tur på denne måten ved hjelp av papir og blyant, men en datamaskin klarer det utmerket.
Vi skal først bruke en heuristisk teknikk kalt Warnsdorffs regel (laget av H. C. Warnsdorff i 1823). Antallet utganger fra en rute er definert som antallet ruter det er mulig å gå videre til. Antallet utganger kan derfor variere fra 0 til 8. Warnsdorffs regel sier:
- La springeren hele tiden gå videre til den ruten som har færrest utganger.
- Hvis flere ruter har færrest utganger, velg den som er lengst fra sentrum av brettet
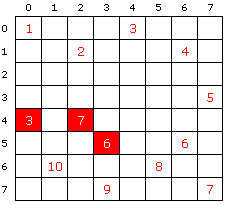 |
| Figur 1.6.6 b) : Start på en springertur |
Vi tar utgangspunkt i Figur 1.6.6 a). Videre fra rute (6,1) (nr. 10 på springer-turen) er det tre mulige ruter. Vi farger dem røde og for hver av dem angis antallet utganger ruten har. Se Figur 1.6.6 b). De tre røde rutene har henholdsvis 3, 6 og 7 utganger. I følge Warnsdorffs regel skal vi da flytte springen videre til den ruten som har færrest utganger, dvs. til rute (4,0).
Det er ikke garantert at Warnsdorffs regel gir en springer-tur, men som oftest vil den det. På internett ligger det mange Java-appletter der en kan «spille» seg frem til en springer-tur. Se Oppgave 1.
Hvis vi skal være helt sikre på å finne en springer-tur (hvis det finnes en) kan vi bruke prøving og feiling med tilbaketrekking. Hvis en springer står i rute (i, j), er det 8 mulige ruter den kan gå videre til. Det er:
1. (i + 1 , j - 2) 2. (i + 2 , j - 1) 3. (i + 2 , j + 1) 4. (i + 1 , j + 2) 5. (i - 1 , j + 2) 6. (i - 2 , j + 1) 7. (i - 2 , j - 1) 8. (i - 1 , j - 2)
Men en eller flere av disse kan være utenfor brettet eller springeren kan allerede ha besøkt en eller flere av dem. Dette må vi teste på forhånd. Flg. rekursive metoden finner en springer-tur ved å bruke systematisk prøving og feiling med tilbaketrekning:
public static boolean springer(int[][] brett, int i, int j, int k) { int n = brett.length; brett[i][j] = k; if (k == n*n) return true; if (i - 2 >= 0 && j + 1 < n && brett[i-2][j+1] == 0) if (springer(brett,i - 2,j + 1,k+1)) return true; if (i - 1 >= 0 && j + 2 < n && brett[i-1][j+2] == 0) if (springer(brett,i - 1,j + 2,k+1)) return true; if (i + 1 < n && j + 2 < n && brett[i+1][j+2] == 0) if (springer(brett,i + 1,j + 2,k+1)) return true; if (i + 2 < n && j + 1 < n && brett[i+2][j+1] == 0) if (springer(brett,i + 2,j + 1,k+1)) return true; if (i + 2 < n && j - 1 >= 0 && brett[i+2][j-1] == 0) if (springer(brett,i + 2,j - 1,k+1)) return true; if (i + 1 < n && j - 2 >= 0 && brett[i+1][j-2] == 0) if (springer(brett,i + 1,j - 2,k+1)) return true; if (i - 1 >= 0 && j - 2 >= 0 && brett[i-1][j-2] == 0) if (springer(brett,i - 1,j - 2,k+1)) return true; if (i - 2 >= 0 && j - 1 >= 0 && brett[i-2][j-1] == 0) if (springer(brett,i - 2,j - 1,k+1)) return true; brett[i][j] = 0; // setter 0 ved tilbaketrekning return false; // dette var en blindgate } Programkode 1.6.6 a)
Springer-metoden i Programkode 1.6.6 a) tar i mot ruten brett[i][j] og rutenummeret k som parametere. Rutenummeret settes inn i ruten. Brettet har dimensjon n x n og vi er ferdige hvis rutenummeret har blitt lik n*n. Hvis ikke, prøver vi først å gå to ruter oppover og en rute til høyre, dvs. til (i - 2, j + 1). Hvis den er innenfor brettet og springeren ennå ikke har vært der, flytter vi springeren dit, dvs. vi kaller metoden med den ruten som parameter og med et rutenummer som er én mer enn sist. Hvis det enten ikke var mulig å gå til den ruten eller det ledet oss inn i en blindgate, prøver vi neste mulige rute. Osv. Hvis vi har prøvd alle mulige veier videre fra rute (i, j) og ingen av dem fører til en springer-tur, så trekker vi oss tilbake. Men først setter vi en 0 i ruten.
Flg. metode skriver ut (til konsollet) innholdet av en todimensjonal tabell på en rektangulær og formatert måte:
public static void skriv(int[][] brett) { for (int i = 0; i < brett.length; i++) { for (int j = 0; j < brett[0].length; j++) { System.out.printf("%4d",brett[i][j]); } System.out.printf("\n"); } } Programkode 1.6.6 b)
Vi kan få skrevet ut en springer-tur som starter i det øverste venstre hjørnet, dvs. i rute (0.0), på et 8 x 8 brett, ved hjelp av flg. kodebit:
int[][] brett = new int[8][8]; if (springer(brett,0,0,1)) skriv(brett); // Utskrift: 1 54 39 48 59 44 31 50 38 47 56 53 32 49 60 43 55 2 33 40 45 58 51 30 34 37 46 57 52 25 42 61 3 20 35 24 41 62 29 14 36 23 18 11 26 15 8 63 19 4 21 16 9 6 13 28 22 17 10 5 12 27 64 7
| 1. | Søk på internett etter Java-appletter som bruker Warnsdorffs regel til å finne en springer-tur på et sjakkbrett.. |
| 2. | Lag en java-metode som finner en springer-tur ved hjelp av Warnsdorffs regel. |
![]() 1.6.7 Matriser
1.6.7 Matriser
Matriser er egentlig rektangulære oppstillinger av verdier. Men hvis verdiene er tall,
kan matriser også ses på som matematiske objekter. Dermed kan det lages regneregler
og formeler for matrisene.
To tallmatriser A og B kan adderes hvis de har samme dimensjon. Videre kan en en tallmatrise A multipliseres med en tallmatrise B hvis A har like mange kolonner som B har rader, dvs. hvis A er en m × n - matrise og B en n × k - matrise. Produktet når A multipliseres med B blir da en m × k - matrise.
Vi kan lage en class Matrise med metoder for både addisjon, multiplikasjon og andre regneoperasjoner. Her holder vi oss til heltallsmatriser. Klassen kan ha flg. grunnstruktur:
public class Matrise { private int m; // antall rader private int n; // antall kolonner private int w = 4; // feltbredde (width) for utskrift private int[][] a; // en todimensjonal heltallstabell public Matrise(int m, int n) // konstruktør { if (m < 0 || n < 0) throw new IndexOutOfBoundsException("Negativ dimensjon!"); this.m = m; this.n = n; a = new int[m][n]; } } // class Matrise Programkode 1.6.7 a)
Konstruktøren i Programkode 1.6.7 a) lager en matrise med m rader og n kolonner med en vanlig todimensjonal tabell som intern datastruktur. Dermed blir alle tabellelementene «nullet», dvs. de får 0 som verdi. Legg merke til at det bare er negative verdier på m og n som stoppes i konstruktøren. Med andre ord vil m = 0 eller n = 0 godtas. En matrise med 0 rader eller 0 kolonner kalles en tom matrise (eng: empty matrix). Dette betyr at vi i kodingen vår må passe på at tomme matriser behandles korrekt.
Det er fordelaktig å ha en metode som skriver ut en matrise. Dermed kan vi f.eks. se hvilke verdier den inneholder. Utskriften bør formateres, dvs. ha rette kolonner. Se Avsnitt 1.6.4. Klassen inneholder instansvariabelen w (w for width). Den angir feltbredden for kolonnene i utskriften. Den har 4 som standardverdi og det er normalt ok hvis ingen tall i matrisen har flere enn to siffer. Hvis ikke, kan vi finne det største tallet i matrisen og la antallet siffer der bestemme feltbredden. Det er også mulig å ha forskjellige bredder på kolonnene i matrisen. Se Oppgave 9. Her lager vi isteden en egen metode for å endre feltbredden:
public void settFeltbredde(int w) // legges i class Matrise { this.w = w; } Programkode 1.6.7 b)
En toString-metode kan brukes til utskrift:
public String toString() // toString legges i class Matrise { Formatter f = new Formatter(); // se vedlegg B for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { f.format("%"+ w +"d",a[i][j]); } if (n != 0) f.format("\n"); } return f.toString(); } Programkode 1.6.7 c)
Hvis metodene settFeltbredde og toString ligger i klassen Matrise, vil flg. programbit virke:
Matrise A = new Matrise(3,5); // 3 rader, 5 kolonner A.settFeltbredde(3); // ny feltbredde på 3 System.out.println(A); // Utskrift: // 0 0 0 0 0 // 0 0 0 0 0 // 0 0 0 0 0 Programkode 1.6.7 d)
Hvis vi allerede har en vanlig todimensjonal tabell, kan den brukes direkte som «innmat» i en matrise. Vi må imidlertid sjekke at den er regulær, dvs. at alle radene har samme lengde:
public Matrise(int[][] a) { m = a.length; n = m == 0 ? 0 : a[0].length; for (int i = 1; i < m; i++) { if (a[i].length != n) throw new IllegalArgumentException("Tabellen a er irregulær!"); } this.a = a; } Programkode 1.6.7 e)
Dimensjonen på matrisen som konstruktøren over lager, blir den samme som
dimensjonen til parametertabellen a. Legg merke til at en tom tabell er
tillatt. Hvis a.length er 0, dvs. a har ingen rader, blir
både m og n satt til 0. Formelt sett kan a ha 0 rader og
1 eller flere kolonner. F.eks. vil det skje i setningen:
int[][] a = new int[0][2];
Men det reserveres ikke noe plass i minnet så lenge antall rader er satt til 0. Da spiller
det ingen rolle om ønsket antall kolonner er 0, 1, 2 eller noe annet. I konstruktøren over
blir n satt til 0 i alle disse tilfellene. Hvis det ikke er 0 rader og
én eller flere av dem er null, får vi NullPointerException.
Det bør være mulig både å hente ut og endre på verdien til et tabellelement Dvs. vi trenger hent- og oppdater-metoder (eng: get og set):
public int hent(int i, int j) { if (i < 0 || i >= m) throw new IndexOutOfBoundsException("Indeks i(" + i + ") er utenfor matrisen"); if (j < 0 || j >= n) throw new IndexOutOfBoundsException("Indeks j(" + j + ") er utenfor matrisen"); return a[i][j]; } public int oppdater(int i, int j, int verdi) { if (i < 0 || i >= m) throw new IndexOutOfBoundsException("Indeks i(" + i + ") er utenfor matrisen"); if (j < 0 || j >= n) throw new IndexOutOfBoundsException("Indeks j(" + j + ") er utenfor matrisen"); int temp = a[i][j]; a[i][j] = verdi; return temp; // den gamle verdien returneres } Programkode 1.6.7 f)
Hvis vi ønsker å hente/returnere (eller oppdatere) en hel rad eller en hel kolonne, kan vi gjøre det ved at vi ser på en rad som en 1 × n - matrise og en kolonne som en m × 1 - matrise. En metode som henter en kolonne kan lages slik (se også Oppgave 4):
public Matrise kolonne(int j) { if (j < 0 || j >= n) throw new IllegalArgumentException("Indeks j(" + j +") er utenfor matrisen!"); Matrise K = new Matrise(m,1); for (int i = 0; i < m; i++) K.a[i][0] = a[i][j]; return K; } Programkode 1.6.7 g)
Flg. kodebit viser hvordan Programkode 1.6.7 e) og g) kan brukes:
int[][] a = {{1,2,3,4,5}, {6,7,8,9,10}, {11,12,13,14,15}}; Matrise A = new Matrise(a); System.out.println(A); Matrise K = A.kolonne(4); System.out.println(K); // Utskrift: // 1 2 3 4 5 // 6 7 8 9 10 // 11 12 13 14 15 // 5 // 10 // 15 Programkode 1.6.7 h)
Hvis vi ser på matriser som matematiske objekter, gir det mening å definere addisjon og multiplikasjon. To matriser kan adderes hvis de har samme dimensjon, dvs, begge er m × n - matriser. Vi finner summen ved å summere elementene parvis:
public Matrise pluss(Matrise B) { if (m != B.m || n != B.n) throw new IllegalArgumentException("Feil dimensjon - summen er udefinert!"); Matrise Sum = new Matrise(m,n); for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) Sum.a[i][j] = a[i][j] + B.a[i][j]; return Sum; } Programkode 1.6.7 i)
Flg. eksempel summeres to matriser:
int[][] a = {{1,2}, {3,4}}, b = {{4,3}, {2,1}}; Matrise S = (new Matrise(a)).pluss(new Matrise(b)); System.out.println(S); // Utskrift: // 5 5 // 5 5 Programkode 1.6.7 j)
Det er mange andre metoder det er aktuelt å lage for regning med matriser. Det tas opp i oppgavene nedenfor.
JAMA og JAMPACK Det finnes ikke noe bibliotek for matriseregning som en del av Java. Men det finnes klasser for dette laget av andre. De to mest kjente er og JAMA og JAMPACK. Det ser imidlertid ikke ut som om disse klassene har blitt oppdatert på noen år. EJML ser ut til å være nyere.
| 1. | Lag konstruktøren public Matrise(int m, int n, int verdi).
Den skal opprette en m × n - matrise
der alle elementene i matrisen får parameterverdien verdi som verdi. |
| 2. | Lag kopieringskonstruktøren public Matrise(Matrise A).
Den skal lage en ekte kopi av matrisen A. |
| 3. | Lag metoden public static Matrise enhet(int n). Den skal returnere
enhetsmatrisen, dvs.
n × n - matrisen
(den kvadratiske matrisen) som har 1-ere på hoveddiagonalen og 0 på alle
de andre plassene.
|
| 4. | Lag metoden public Matrise rad(int i). Den skal returnere
(som en 1 × n - matrise) matrisens rad
nr. i. |
| 5. | Lag metoden public Matrise minus(Matrise B). Den skal returnere
differansen mellom this og matrisen B. |
| 6. | Lag metoden public Matrise ganger(int k). Den skal returnere
matrisen vi får når tallet k ganges med this. |
| 7. | Lag metoden public Matrise ganger(Matrise B). Den skal returnere
matriseproduktet mellom this og matrisen B. |
| 8. | Lag metoden public Matrise transponer(). Den skal returnere den
transponerte til matrisen. |
| 9. | Gjør om metoden toString slik at den først finner hvor store tall matrisen innholder og så skriver ut med en feltbredde som er 2 enheter større enn det tallet som har flest siffer. |

|