Algoritmer og datastrukturer - Høgskolen i Oslo og Akershus

Vurderingskriterier De 10 bokstavpunktene (1A, 1B, 2A, osv) har samme vekt. På hvert gis det fra 0 til 10 poeng. Hvis det er svart riktig på det som det spørres etter, koden (i kodeoppgaver) virker som den skal, er effektiv og ikke bruker unødvendige hjelpestrukturer, er uten nevneverdige syntaksfeil og er brukbart forklart/dokumentert, så gis det 10 poeng. Hvis et bokstavpunkt er delt opp, vil vanskelighetsgraden normalt avgjøre delenes vekt.

Også ineffektiv og tungvint kode som er dårlig forklart/dokumentert, men som virker, vil kunne gi poeng, men ikke fullt hus. Ellers blir det fratrekk for alvorlige synstaksfeil, gal kode, mangler og logiske feil i koden, feil bruk av metoder og klasser og manglende forklaringer. Det gis 0 poeng hvis en oppgave er blank, misforstått eller er helt feil besvart.

Programkode kan være selvforklarende hvis det er enkle algoritmer med standard kodeteknikk. Men hvis algoritmen eller koden som lages er mer innfløkt, er det viktig med forklaringer. Det kan hende at en har en idé som ville ha virket, men som er kodet feil eller mangelfullt. Hvis en da ikke har forklaringer, kan det være vanskelig eller umulig å forstå det som er laget. Dermed risikerer en å få færre poeng (eller 0 poeng) enn det en ellers ville ha fått. Forklaringer kan være med ord og/eller tegninger.

I oppgaver der det ikke skal lages kode, må det være med begrunnelser for svarene - tekst og/eller tegninger. I oppgaver der det spørres etter en utskrift, er det spesielt viktig med forklaringer. Hvis det en har satt opp som utskrift er feil, kan en risikere å få 0 poeng hvis forklaringer mangler. Det kan jo hende at en har tenkt riktig, men kun gjort noen småfeil. Men uten forklaringer er det ikke mulig å vite om det er småfeil eller om en kun har gjettet.

Poengene på hvert av de 10 bokstavpunktene summeres. Maksimal poengsum er 100.

Følgende karakterskala brukes:

A: minst 90 poeng
B: minst 75 poeng
C: minst 60 poeng
D: minst 50 poeng
E: minst 40 poeng
F: færre enn 40 poeng

Oppgave 1A

I denne oppgaven brukes den grunnleggende datatypen char. Det er oppgitt at tabellen c kun inneholder bokstaver fra a til z (små eller store). Her må en kjenne til hvordan bokstavene er plassert i «alfabetet». Alle de første 128 tegnene (inklusiv bokstavene fra a til z) er felles for «alfabetene» ascii, iso-8859-1, unicode (Java bruker unicode), utf-8 og utf-16. Da er det helt fundamentalt å vite at de store bokstavene kommer først og så de små. Det bør også være velkjent at 'A' har tallverdi 65 og dermed 'Z' tallverdi 90 siden det er 26 bokstaver. Videre bør det være kjent at forskjellen mellom stor og liten bokstav er 32, dvs. at 'a' har tallverdi 65 + 32 = 97. Dermed: En bokstav er liten hvis den er større enn 'Z' (eller større enn eller lik 'a').

Men hvis en av en eller annen grunn ikke har fått med seg dette, kan en bruke metoden isLowerCase (eller isUpperCase) fra klassen Character. F.eks. slik for tabellelementet c[i]:

  if (Character.isLowerCase(c[i])) . . . .

I oppgaveteksten står det at «Målet (for å få best score) er å få metoden mest mulig effektiv med minst mulig bruk av hjelpestrukturer.»

1. Metoden kan lages på mange måter. En måte som flere nok har tenkt på, er å starte med en sortering. Da vil imidlertid de store bokstavene komme først. Men det kan repareres ved å snu tabellen. Deretter må antallet små bokstaver telles opp.

  // en hjelpemetode som kan brukes flere steder
  private static void bytt(char[] c, int i, int j)
  {
    char temp = c[i]; c[i] = c[j]; c[j] = temp;
  }

  public static int omorganiser(char[] c)
  {
    Arrays.sort(c);  // kvikksortering - orden n*log(n) i gjennomsnitt

    for (int v = 0, h = c.length - 1; v < h; )  // snur tabellen - orden n
    {
      bytt(c, v++, h--); // bytter om
    }

    int antall = 0;  // teller opp - orden n i gjennomsnitt
    while (antall < c.length && c[antall] > 'Z')  // c[antall] er en liten bokstav
    {
      antall++;
    }

    return antall;  // antallet små bokstaver
  }

Metoden over vil være av orden n*log(n) i gjennomsnitt (men av kvadratisk orden i det verste tilfellet). Det kommer av kvikksorteringen. Det å snu tabellen og å finne antallet små bokstaver, er av orden n og får dermed ingen betydning for metoden som helhet.

2. En annen måte er å bruke en hjelpetabell. Da holder det å gå gjennom tabellen c en gang. En liten bokstav legges i første del av hjelpetabellen og en stor i den andre delen. Dermed får vi automatisk antallet små bokstaver. Til slutt må vi imidlertid kopiere hjelpetabellens innhold tilbake til c. Dette gir en metode av orden n siden vi går gjennom c kun en gang. Kopieringen er også av orden n. Dermed blir hele metoden av orden n. Dette er så bra som det kan få blitt med tanke på effektivitet, men svakheten er at det inngår en hjelpetabell:

  public static int omorganiser(char[] c)
  {
    char[] d = new char[c.length];  // en hjelpetabell
    int v = 0, h = d.length - 1;    // hver sin ende av d

    for (char t : c)
    {
      if (t > 'Z') d[v++] = t;
      else d[h--] = t;
    }

    System.arraycopy(d,0,c,0,d.length);  // kopierer fra d til c
    return v;
   }

3. Den beste måten er å omorganisere tabellen c ved hjelp av en serie ombyttinger. Da trengs ingen hjelpetabell. Flg. metode går gjennom tabellen kun én gang. Dermed får den orden n:

  public static int omorganiser(char[] c)
  {
    int antall = 0;
    for (int i = 0; i < c.length; i++)
    {
      if (c[i] > 'Z') bytt(c, i, antall++);
    }
    return antall;
  }

Metoden over har en liten ulempe. Den gjør flere ombyttinger enn det som egentlig trengs. Hvis f.eks. tabellen kun har små bokstaver, gjøres det like mange ombyttinger som tabellen har størrelse.

En bedre måte er den som i undervisningen har blitt kalt «knipetangsteknikken». Dvs. at tabellen c «angripes» fra begge sider. Den er av orden n siden vi går gjennom c kun en gang og det inngår ingen hjelpetabell. I denne versjonen blir det ingen ombyttinger hvis tabellen kun har store (eller kun små) bokstaver:

  public static int omorganiser(char[] c)
  {
    int v = 0, h = c.length - 1;  // hver sin ende av c

    while (true)
    {
      while (v <= h && c[v] > 'Z') v++;   // så lenge c[v] er en liten bokstav
      while (v <= h && c[h] <= 'Z') h--;  // så lenge c[h] er en stor bokstav
      if (v < h) bytt(c, v++, h--);       // bytter om
      else return v;
    }
  }

Metoden over kan optimaliseres litt. Sammenligningen v <= h i while-løkkene trengs bare i starten for å takle muligheten at alle bokstavene er små eller alle er store:

  public static int omorganiser(char[] c)
  {
    int v = 0, h = c.length - 1;

    while (v <= h && c[v] >  'Z') v++;
    while (v <= h && c[h] <= 'Z') h--;

    while (true)
    {
      if (v < h) Tabell.bytt(c, v++, h--); else return v;
      while (c[v] >  'Z') v++;
      while (c[h] <= 'Z') h--;
    }
  }

Oppgave 1B

(1. del: 5 poeng) Etter åtte verdier ser datastrukturen slik ut:

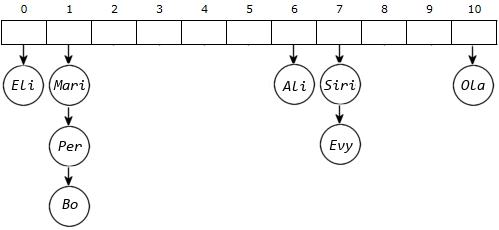(2. del: 5 poeng) Innleggingsmetoden starter med setningen: if (antall >= grense) { utvid(); }. Grensen er lik (int)(0.75 * hash.length) = (int)(0.75 * 11) = (int)(8.25) = 8 når 11 brukes som startdimensjon. Det betyr at når den niende verdien skal legges inn, blir antall >= grense sann og tabellen «utvides». Ny dimensjon blir 11*2 + 1 = 23 og grense = (int)(0.75 * 23) = (int)17.25 = 17. Etter utvidelsen (og omorganiseringen) og etter innleggingen av to nye verdier, vil datastruktueren se slik ut:

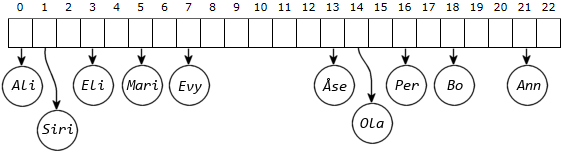Oppgave 2A

Begrepet leksikografisk sammenligning og ordning har blitt brukt bl.a. i forbindelse med permutasjoner (se Avsnitt 1.3.1) og komparatorer/lambda-uttrykk (se Avsnitt 1.4.8). I oppgavteksten står det også at en leksikografisk sammenligning er på samme måte som alfabetisk sammenligning av ord. F.eks. er Ola «mindre enn» Ole. Der er de to første bokstavene like, men på tredje plass er det forskjell. Dermed blir Ola «mindre enn» Ole siden a kommer foran e i alfabetet. Et spesialtilfelle får vi hvis det ene ordet utgjør første del av det andre. F.eks. er Andersen «større enn» enn Anders.

I kodingen av metoden compare() er det mange som starter med å sammenligne lengdene på de to listene. Hvis de har ulik lengde, tror mange at den korteste av dem da er minst. Men det blir helt galt. Husk hvordan det er for ord. Ta Anders og Anne som eksempel. De skiller seg på tredje bokstav. Siden d kommer foran n i alfabetet er Anders «mindre enn» Anne. Men Anne har færre bokstaver enn Anders.

1) Det at en leksikografisk sammenligning er på samme måte som alfabetisk sammenligning av ord, kan kanskje forlede noen til å kode dette ved å sammenligne det som toString-metodene returnerer. Dvs. en slik løsning:

  public static <T> int compare(Liste<T> a, Liste<T> b, Comparator<? super T> c)
  {
    return a.toString().compareTo(b.toString());  // sammenligner tegnstrenger
  }

Dette blir riktig i eksempel 1. Da sammenlignes [A, B, C] og [A, B, D] som tegnstrenger. Men det blir feil i eksempel 2 siden [1, 2, 3, 4, 5] er mindre enn [1, 2, 3, 4]. Det kommer av at kommategnet «alfabetisk» kommer foran tegnet ]. Men dette kunne repareres ved å lage tegnstrenger uten komma, mellomrom og parenteser. Da sammenlignes "ABC" med "ABD" og "12345" med "1234". Men dette vil likevel ikke virke generelt. Anta at listen a inneholder 1 og 2 og listen b 1 og 10. Da er a «mindre enn» b siden 2 er mindre enn 10, men som tegnstrenger er "12" større enn "110".

2) En korrekt løsning får vi ved å sammenligne (vha. komparatoren) verdiene parvis i de to listene. Da har man valget mellom å hente verdiene forløpende ved hjelp av hent-metoden eller ved hjelp av iteratorene. Flg. versjon bruker hent-metoden:

  public static <T> int compare(Liste<T> a, Liste<T> b, Comparator<? super T> comp)
  {
    int m = Math.min(a.antall(), b.antall());

    for (int i = 0; i < m; i++)
    {
      int cmp = comp.compare(a.hent(i), b.hent(i));
      if (cmp != 0) return cmp;         // ulike på plass i
    }

    // a er nå første del av b eller b første del av a
    return a.antall() - b.antall();     // den korteste er minst
  }

Versjonen over er effektiv nok for en TabellListe siden hent-metoden der er av konstant orden. Men det blir ineffektivt for en EnkeltLenketListe og en DobbeltLenketListe. Der er hent-metoden i gjennomsnitt av orden n og dermed vil metoden i de tilfellene bli i gjennomsnitt av kvadratisk orden.

3) Det er mest effektivt å hente ut verdiene ved hjelp av iteratorene. Da blir metoden av orden n i gjennomsnitt i alle tilfellene:

  public static <T> int compare(Liste<T> a, Liste<T> b, Comparator<? super T> comp)
  {
    Iterator<T> i = a.iterator(), j = b.iterator();
    int m = Math.min(a.antall(), b.antall());

    for (int k = 0; k < m; k++)
    {
      int cmp = comp.compare(i.next(), j.next());
      if (cmp != 0) return cmp;       // i.next() og j.next() er forskjellige
    }

    // a er nå første del av b eller b første del av a
    return a.antall() - b.antall();   // den korteste er minst
  }

Som nevnt foregår en leksikografisk sammenligning på samme måte som alfabetisk sammenligning av ord. Metoden compareTo() i klassen String er kodet slik (value er den interne char-tabellen):

  public int compareTo(String anotherString)
  {
    int len1 = value.length;
    int len2 = anotherString.value.length;
    int lim = Math.min(len1,len2);
    char v1[] = value;
    char v2[] = anotherString.value;

    int k = 0;
    while (k < lim)
    {
      char c1 = v1[k];
      char c2 = v2[k];
      if (c1 != c2)
      {
        return c1 - c2;
      }
      k++;
    }
    return len1 - len2;
  }

Oppgave 2B

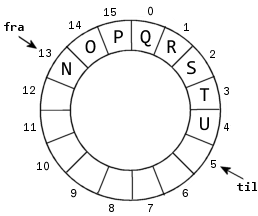i) (5 poeng)

  Utskrift: [I, J, K, L, M, N, O, P, Q]

ii) (5 poeng)

Køen har 16 + (til - fra) = 16 + 5 - 13
= 21 - 13 = 8.

  public int antall()
  {
    return fra <= til ? til - fra : a.length + til - fra;
  }

Oppgave 3A

a) 3 poeng for korrekt tre etter at de tre første verdiene er lagt inn, ytterligere 3 poeng for korrekt tre etter syv verdier og så ytterligere 4 poeng for korrekt tre etter alle verdiene er lagt inn.

Innlegging av 4:

Innlegging av 10:

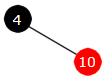a) Innlegging av 5: dobbel rotasjon og fargeskifte

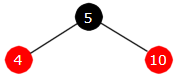Innlegging av 12: fargeskifte

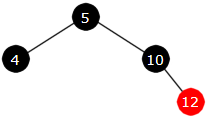Innlegging av 6:

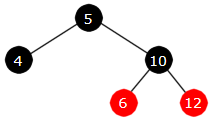Innlegging av 8: fargeskifte

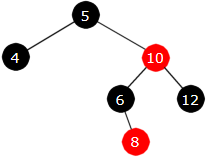b) Innlegging av 9: enkel rotasjon og fargeskifte

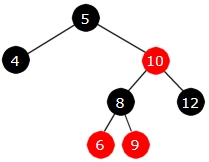Innlegging av 7:
Først et fargeskifte. Men det fører til en «forplantningsfeil». Dvs. at nå blir både 8-noden og 10-noden røde:

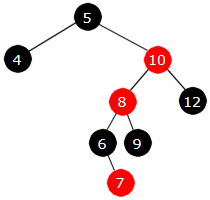c) Deretter repareres dette med en dobbel rotasjon og fargeskifte.

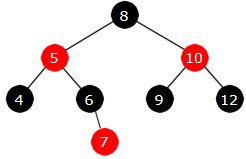Oppgave 3B

1) Dette kan løses på mange måter. Det enkleste er nok å bruke en hjelpestakk:

  public static <T> void omvendtkopi(Stakk<T> a, Stakk<T> b)
  {
    Stakk<T> c = new TabellStakk<>();  // hjelpestakk

    while (!a.tom())
    {
      T verdi = a.taUt();              // tar ut fra a
      b.leggInn(verdi);                // legger inn i b
      c.leggInn(verdi);                // legger inn i c
    }

    while (!c.tom()) a.leggInn(c.taUt());  // flytter fra c tilbake til a
  }

2) Mange vil velge å bruke en hjelpetabell. Det er mulig, men da må en huske at det ikke er mulig å opprette en generisk tabell. Vi må gå via en Object-tabell:

  @SuppressWarnings("unchecked")      // pga. Object[] -> T[]
  public static <T> void omvendtkopi(Stakk<T> a, Stakk<T> b)
  {
    T[] c = (T[]) new Object[a.antall()];  // hjelpetabell
    int i = 0;  // indeks i hjelpetabellen 

    while (!a.tom())
    {
      T verdi = a.taUt();               // tar ut fra a              
      b.leggInn(verdi);                 // legger inn i b
      c[i++] = verdi;                   // legger inn i c
    }

    while (i > 0) a.leggInn(c[--i]);    // flytter fra c tilbake til a
  }

Oppgave 4A

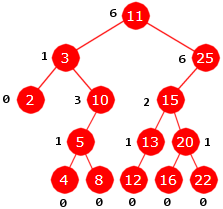
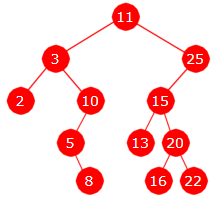Preorden: 11, 3, 2, 10, 5, 8, 25, 15, 13, 20, 16, 22
Postorden: 2, 8, 5, 10, 3, 13, 16, 22, 20, 15, 25, 11

Oppgave 4B

i) (4 poeng)

ii) (4 poeng for antall() og 2 poeng for tom())

  public int antall()
  {
    int antall = 0;
    Node<T> p = rot;

    while (p != null)
    {
      antall += (p.vAntall + 1);
      p = p.høyre;
    }

    return antall;
  }

Det er mange som koder metoden tom() ved hjelp av antall(). Dvs. slik:

  public boolean tom()
  {
    return antall() == 0;
  }

Koden vil virke, men er unødvendig ineffektiv. En metode som sjekker om en datastruktur er tom eller ikke (isEmpty() i java.util), er blant metodene som oftest brukes. Derfor er det viktig at den er effektiv. Slik som den er kodet over, må først antallet finnes og det er her en relativt kostbar operasjon. Her må en isteden bruke (se koden for SBinTre som er satt opp i vedlegget til eksamensoppgavene) at treet er tomt hvis og bare hvis rot er null. Dvs. slik:

  public boolean tom()
  {
    return rot == null;
  }

Oppgave 4C

1) Denne oppgaven løses enklest (og mest effektivt) ved å bruke samme idé som i den rekursive antall-metoden. Se Programkode 5.1.12 a). Vi bruker rett og slett resultatet av et metodekall på venstre subtre til å oppdatere vAntall. Da får vi en metode av orden n siden vi går gjennom treet i én gang og for hver node gjør vi en operasjon av konstant orden. Koden blir slik:

  private static <T> int settvAntall(Node<T> p)
  {
    if (p == null) return 0;
    return (p.vAntall = settvAntall(p.venstre)) + settvAntall(p.høyre) + 1;
  }

  public void settvAntall()
  {
    settvAntall(rot);  // bruker den rekursive metoden over
  }

2) Hvis en ikke skulle komme på idéen over, er det mulig å tenke annerledes. Det alle bør kunne få til er en metode som finner antallet noder i et subtre, f.eks. ved å bruke samme kode som i Programkode 5.1.12 a) (det gir kortest kode) eller ved å lage en iterativ metode. For eksempelets skyld lager vi her en iterativ versjon (obs: vi kan ikke bruke idéen i metoden antall() fra Oppgave 4B siden den virker kun når vAntall har korrekt verdi i alle noder):

  private int antall(Node<T> p)  // antallet i subtreet med p som rot
  {
    Stakk<Node<T>> stakk = new TabellStakk<>();  // en stakk
    int antall = 0;  // hjelpevariabel

    while (true)  // traverserer subtreet i preorden
    {
      antall++;                                       // øker antall
      if (p.venstre != null)                          // er det noe til venstre?
      {
        if (p.høyre != null) stakk.leggInn(p.høyre);  // legger på stakken
        p = p.venstre;                                // går til venstre
      }
      else if (p.høyre != null) p = p.høyre;          // går til høyre
      else if (!stakk.tom()) p = stakk.taUt();        // tar fra stakken
      else return antall;                             // tomt! - vi er ferdig
    }
  }

Deretter lager vi en metode som traverserer treet (denne gangen rekursivt i preorden) og bruker metoden over til å sette verdi på vAntall:

  // traverserer treet i preorden
  private static <T> void vAntall(Node<T> p)
  {
    if (p.venstre != null)
    {
      p.vAntall = antall(p.venstre);
      vAntall(p.venstre);
    }
    if (p.høyre != null) vAntall(p.høyre);
  }

  public void settvAntall()
  {
    if (rot != null) vAntall(rot);  // bruker den rekursive metoden over
  }

Det er litt vanskeligere å finne ut hvilken orden dette får. Den rekursive metoden går gjennom treet én gang, men for hver node kalles antall-metoden. Spørsmålet blir da hvor mye arbeid den metoden gjør i gjennomsnitt. For det første kalles den kun hvis venstre subtre ikke er tomt. I et binært søketre har i gjennomsnitt halvparten av nodene et tomt venstre subtre. Videre vil 1/6-del av nodene ha et venstre subtre med én node, 1/12-del av dem et subtre med to noder, osv. Se Avsnitt 5.2.15. Det viser seg at det gjennomsnittlige antallet noder i en nodes venstre subtre i et binært søketre med n noder er gitt ved:

(1 + 1/n)H_n − 2

Hvis n er stor, blir det tilnærmet lik H_n − 2 der H_n er det n-te harmoniske tallet (summen av de inverse heltallene fra 1 til n) og som kjent er H_n ≈ log(n) + 0,577. Det betyr at arbeidsmengden til antall-metoden i gjennomsnitt er av logaritmisk orden. Dermed blir denne versjonen av settvAntall() av orden n log(n).

Oppgave 4D

i) (2 poeng) Dette punktet var ment som et hint for hvordan metoden preorden(int indeks) kan kodes effektivt. Det står at en skal skrive opp «nodeverdi til nodene på veien fra roten og ned til p» og «nodeverdi til nodene på veien fra roten og ned til q». Dette burde være en svært enkel oppgave. Her har imidlertid noen misforstått og skrevet opp alle verdiene i preorden fra rot til henholdsvis p og q. Men det står «veien fra roten og ned til». I et binærtre er en vei (se Avsnitt 5.1.1) definert ved hjelp av kanter (piler). Det går en vei fra en node x ned til en node y hvis det er mulig å komme fra x til y ved å følge kanter (i kantenes retning). På en tegning er en kant den streken som går fra en node ned til nodens barn. En kants retning er alltid nedover. Rett svar er derfor:

p: 11, 3, 10, 5, 8
q: 11, 25, 15, 20, 22

ii) (8 poeng)

1) Den optimale løsningen her er å benytte verdien til vAntall i hver node. Ta utgangspunkt i treet fra Oppgave 4B. Anta at vi skal finne noden med indeks 6 i preorden. La rotnoden hete p. Den har indeks 0 i preorden. Dermed må noden vi leter etter ligge i et av subtrærne til p. Verdien til vAntall i p er 6. Det betyr at det venstre subtreet til p har 6 noder og dermed må nodene med indekser fra 1 til 6 i preorden ligge i det subtreet. La nå p være noden med verdi 3. Noden som har indeks 6 i hele treet, vil ha indeks 6 − 1 = 5 i treet med p som rot. Vi ser at vAntall i p er 1. Det betyr at i treet med p som rot, har p indeks 0, venstre barn til p indeks 1 og nodene i høyre subtre til p indekser fra 2 og videre. Med andre ord må vi dit for å finne noden med indeks 5. Men noden som har indeks 5, vil få indeks 5 − p.vAntall − 1 = 5 − 1 − 1 = 3 i det høyre subtreet. Vi går dit, dvs. vi lar p være lik noden med verdi 10. Osv.

Flg. metode er basert på beskrivelsen over. Den får logaritmisk orden i gjennomsnitt siden vi går rett nedover til den aktuelle noden. Husk at i et gjennomsnittlig binært søketre er den gjennomsnittlige nodedybden logaritmisk. Men hvis treet er ekstremt skjevt, vil den bli av lineær orden (orden n).

Det skal kastes en NoSuchElementException hvis indeks er utenfor treet. Da kan man velge om man vil teste indeksen på forhånd eller eventuelt gjøre det inne i algoritmen. Flg. metode tester på forhånd:

  public T preorden(int indeks)
  {
    if (indeks < 0 || indeks >= antall())
      throw new NoSuchElementException("Indeks er utenfor treet!");

    Node<T> p = rot;

    while (indeks > 0)
    {
      indeks--;

      if (indeks < p.vAntall) p = p.venstre;
      else
      {
        indeks -= p.vAntall;
        p = p.høyre;
      }
    }

    return p.verdi;
  }

I koden over kalles metoden antall() for å teste indeksen og det koster litt siden den er av logaritmisk orden. Vi kan isteden passe på at referansen p som vi bruker til å gå nedover i treet med, ikke blir null. Hvis den blir null, er vi ute av treet og dermed må også indeks være utenfor treet. Ekstrakostnaden er at p må sjekkes i hver iterasjon:

  public T preorden(int indeks)
  {
    Node<T> p = rot;

    while (p != null)
    {
      if (indeks == 0) return p.verdi;

      indeks--;

      if (indeks < p.vAntall) p = p.venstre;
      else
      {
        indeks -= p.vAntall;
        p = p.høyre;
      }
    }

    // kommer vi hit er vi ute av treet
    throw new NoSuchElementException("Indeks er utenfor treet!");
  }

Det er nok kun liten forskjell på effektivteten til de to versjonene av preorden() over. Men er det mulig å finne ut noe mer om det? Ja! Gjennomsnittlig nodedybde i et binært søketre er gitt ved 2H_n − 4 og det blir antallet ganger sammenligningen p != null i gjennomsnitt utføres. I antall() gås det ned til den siste noden i inorden. Men den gjennomsnittlige nodedybden til den siste i inorden er H_n − 1, dvs. halvparten av den gjennomsnittlige nodedybden. Antall iterasjoner i antall() er derfor halvparten så mange. Men i hver iterasjon er det flere operasjoner. Dette koster såpass mye at selv om det skjer halvparten så mange ganger, vil det i sum likevel koste mer. Faktisk viser testkjøringer at den andre av de to versjonene er 10 - 20 prosent raskere. Men hvis klassen hadde hatt en antall-variabel og det var den som ble returnert i metoden antall(), så viser testkjøringer at den første versjonen vil bli raskest.

Idéen i beskrivelsen over kan også kodes rekursivt. Da lager vi en rekursiv hjelpemetode og en metode som kaller den:

  private static <T> T preorden(Node<T> p, int indeks)
  {
    if (indeks == 0) return p.verdi;
    else if (indeks <= p.vAntall) return preorden(p.venstre, indeks - 1);
    else return preorden(p.høyre, indeks - 1 - p.vAntall);
  }

  public T preorden(int indeks)
  {
    if (indeks < 0 || indeks >= antall())
      throw new NoSuchElementException("Indeks er utenfor treet!");

    return preorden(rot, indeks);  // kaller metoden over
  }

2) Det er mulig å finne noden som har oppgitt indeks i preorden uten å benytte vAntall. En idé kunne være å traversere i preorden og så stoppe på den aktuelle noden. Den kan f.eks. løses iterativt. Flg. metode får lineær orden:

  public T preorden(int indeks)
  {
    if (indeks < 0 || indeks >= antall())
      throw new NoSuchElementException("Indeks er utenfor treet!");

    Stakk<Node<T>> stakk = new TabellStakk<>();
    Node<T> p = rot;
    int i = 0;

    while (true)
    {
      if (i++ == indeks) return p.verdi;

      if (p.venstre != null)
      {
        if (p.høyre != null) stakk.leggInn(p.høyre);
        p = p.venstre;
      }
      else if (p.høyre != null) p = p.høyre;
      else p = stakk.taUt();
    }
  }

3) En tredje måte som noen har brukt, er å traversere treet i preorden og så kopiere verdiene fortløpende over i en liste. Deretter hentes verdien med rett indeks fra listen. En slik løsning vil bli av orden n. Men dens store svakhet er at hele treet traverseres selv om det er den første (eller en av de første) i preorden som skal finnes:

  private static <T> void preorden(Node<T> p, Liste<T> liste)
  {
    liste.leggInn(p.verdi);
    if (p.venstre != null) preorden(p.venstre, liste);
    if (p.høyre != null) preorden(p.høyre, liste);
  }

  public T preorden(int indeks)
  {
    int antall = antall();

    if (indeks < 0 || indeks >= antall)
      throw new NoSuchElementException("Indeks er utenfor treet!");

    Liste<T> liste = new TabellListe<>(antall);
    preorden(rot, liste);  // bruker den rekursive metoden over
    return liste.hent(indeks);
  }