Oppgave 2

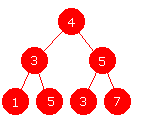
Definsjonen er ikke ekvivalent med Definisjon 5.2.1. Ethvert binært søketre vil oppfylle dette, men det omvendte er ikke sant. I figuren til venstre har vi et binærtre som oppfyller dette, men som åpenbart ikke er et binært søketre.

Oppgave 3

1. Ta utgangspunkt Definisjon 5.2.1. Da vil, som tidligere nevnt, verdiene komme sortert stigende i inorden. La p og q være to noder med samme verdi slik at p kommer etter q i inorden. Da kan ikke q ligge i det venstre subtreet til p siden de har like verdier. Hvis p ikke ligger i det høyre subtreet til q, må de to ha en nærmeste felles forfeder f. Men da må verdien i q være mindre enn den i f som igjen må være mindre enn eller lik den i p. Men det er umulig siden p og q har like verdier. Konklusjonen blir at p må ligge i det høyre subtreet til q. Definisjonen i Oppgave 3 er oppfylt.
2. Ta utgangspunkt i definisjonen i Oppgave 3. La noden q ligge i det venstre subtreet til noden p. Siden q da kommer foran p i inorden, må verdien til q være mindre enn eller lik den til p. Men de kan ikke være like. I så fall måtte p ligge i det høyre subtreet til q. Med andre ord er verdien i q mindre enn den i p. La så noden p ligge i det høyre subtreet til noden q. Da kommer p etter q i inorden og verdien til p er dermed større enn eller lik den til q. Definisjon 5.2.1 er oppfylt.

Oppgave 5

En node med verdien 2,5 må plasseres som venstre barn til noden med verdien 3.

Oppgave 6

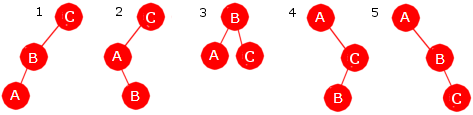
De tre verdiene A, B og C kan permuteres på 3! = 3·2·1 = 6 måter. Det er (A,B,C), (A,C,B), (B,A,C), (B,C,A), (C,A,B) og (C,B,A). Hvis vi lager et binært søketre ved å legge inn en og en verdi (se Avsnitt 5.2.3), vil vi få 6 trær. Da vil (B,A,C) og (B,C,A) gi like trær. Dermed blir det kun fem forskjellige. Senere, når vi bl.a. skal se på den gjennomsnittlige «oppførselen» til binære søketrær, vil vi normalt ta gjennomsnittet over de seks trærne.

Oppgave 7

De fire verdiene A, B, C og kan permuteres på 4! = 4·3·2·1 = 24 måter. Hvis vi bruke hver av dem til å bygge opp et binært søketre (se Avsnitt 5.2.3), vil vi få 24 trær. Men mange av dem vil være like. F.eks. (A,C,B,D) og (A,C,D,B) gi like trær. Det er kun 14 av dem som er forskjellige. Antallet forskjellige for n verdier er gitt ved formelen C(n). Flg. trær er de 14 som er forskjellige:

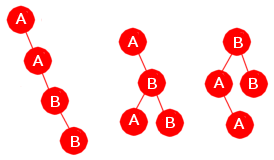
Oppgave 8

Det blir tre forskjellige trær: