![]() 9.2.1 B-tre av orden 4 eller 2-3-4 tre
9.2.1 B-tre av orden 4 eller 2-3-4 tre
Et 2-3-4 tre
(et B-tre av orden 4)
og et
rød-svart tre
er to ekvivalente datastrukturer. Et 2-3-4 tre kan omformes til et rød-svart tre og omvendt, et rød-svart tre
kan omformes til et 2-3-4 tre.
Rød-svarte trær er mest brukt, f.eks. i klassene
TreeSet og
TreeMap
i java.util. I et 2-3-4 tre må noder kunne «splittes» når treet bygges opp og det er litt
komplisert å kode på grunn av mange spesialtilfeller. I et
rød-svart tre brukes «farger» og rotasjoner og det er enklere å kode. Men det er imidlertid enklere
å forstå hva som skjer i et 2-3-4 tre og hvorfor det
blir balansert. Derfor kan det pedagogisk sett være lurt å starte med 2-3-4 trær og så gå over til
rød-svarte trær når en har forstått idéene.
Et 2-3-4 tre er ikke et binærtre. Det er et balansert tre der nodene kan ha flere enn to barn. I et binærtre kan en node ha ingen, ett eller to barn. Generelt gjelder at i et B-tre av orden m kan en node ha maksimalt m barn. En node kan der ha ingen barn (en bladnode), men aldri kun ett barn. I et B-tre av orden 4 kan dermed en indre node ha 2, 3 eller 4 barn. Derfor kalles det også et 2-3-4 tre. For et slikt tre gjelder:
- En node kan ha én, to eller tre verdier. En node med én verdi kalles en
2-node, en med to verdier kalles en3-nodeog en med tre verdier en4-node. - En indre node kan ha to, tre eller fire barn.
- Antallet verdier i en indre node er alltid én mindre enn antallet barn som noden har.
- Alle bladnoder ligger på samme nivå i treet.
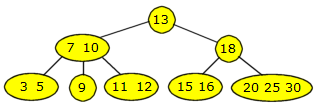 |
| Figur 9.2.1 a) : Et 2-3-4 tre med ellipseformede noder |
Figur 9.2.1 a) viser et 2-3-4 tre med 8 noder, 3 indre
noder (roten og to til)
og 5 bladnoder. Antallet verdier i en
indre node skal alltid være én mindre enn
antallet barn. Vi ser på figuren at rotnoden er en 2-node (én verdi) og dermed to barn.
Rotnodens venstre barn er en 3-node (to verdier) og tre barn, mens rotnodens høyre barn er en 2-node (én verdi) og har to barn.
Alle de 5 bladnodene ligger på samme nivå. Det er det kravet som gjør at det blir balansert.
Høyden til et 2-3-4 tre Det at det er balansert bør bety
at høyden er liten sammenlignet med antall verdier. Men er det mulig å si noe mer eksakt om dette? Ta n = 3
som eksempel, dvs. vi har tre verdier. La det være 1, 2 og 3. Da finnes det to mulige 2-3-4 trær:
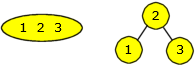 |
| Figur 9.2.1 b) : 2-3-4 trær med tre verdier |
Det første treet har høyde 0 og det andre høyde 1. Vi går et skritt videre. La n = 15
og med tallene fra 1 til 15 som verdier. Da er det mange muligheter, men dette er ytterpunktene:
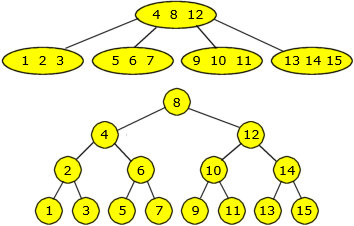 |
| Figur 9.2.1 c) : 2-3-4 trær med 15 verdier |
Det øverste treet, der alle nodene er 4-noder (tre verdier), har høyde 1, mens det andre, der alle nodene er 2-noder (én verdi),
har høyde 3. Neste mulighet for et 2-3-4 tre der alle nodene er 4-noder, får vi for n = 63.
Et slikt tre får da høyde 2. Det andre ytterpunktet for n = 63 er et 2-3-4 tre med formen til
et perfekt binærtre. Det vil ha høyde 5. I disse tilfellene (for n = 3, 15, 63) er høydene
gitt ved formlene ⌊log4(n)⌋ og ⌊log2(n)⌋
der symbolet ⌊ ⌋ betyr avrundet nedover. Sjekk at det stemmer! Vi kan bruke de samme
formlene for andre verdier av n til å gi en nedre og øvre grense for høyden til
et 2-3-4 tre med n verdier:
Høyden til et 2-3-4 tre med n verdier ligger mellom
⌊log4(n)⌋ og ⌊log2(n)⌋
Hvis f.eks. n = 1000 vil ⌊log4(n)⌋ = 4 og
⌊log2(n)⌋ = 9. Dermed vil et vilkårlig 2-3-4 tre med 1000 verdier ha en høyde
mellom 4 og 9. Se også Oppgave 2.
Sorteringsorden
I en node med flere verdier skal verdiene være sortert (stigende).
I slike trær kan vi imidlertid ikke, som for binære trær, snakke om en nodes venstre og høyre subtre
siden det kan være 2, 3 eller 4 subtrær.
Men for hver verdi i en indre node kan vi snakke om dens venstre og høyre
subtre. Se på noden med verdiene 7 og 10 i Figur 9.2.1 a):
Vi kan si at verdien 7 har to subtrær - det venstre består av noden med verdiene 3 og 5 og
det høyre av noden med verdien 9. På samme måte har verdien 10 to subtrær - det venstre
består av noden med verdien 9 og det høyre av noden med verdiene 11 og 12. Dette betyr spesielt
at noden/subtreet
med verdien 9 er høyre subtre til 7 og venstre subtre til 10.
Sorteringsrekkefølgen for verdiene i et 2-3-4 tre blir dermed slik:
- Verdiene i hver node skal være sortert stigende.
- Hvis x er en vilkårlig verdi i en indre node, skal største verdi i det venstre subtreet til x være mindre enn x, og x skal være mindre enn minste verdi i høyre subtreet til x.
Vi ser i Figur 9.2.1 a)
at rotnoden har verdien 13, at alle verdiene i dens venstre subtre
er mindre enn 13 og alle verdien i det høyre er større enn 13, osv. Sorteringsrekkefølgen blir dermed som forventet lik
3, 5, 7, 9, 10, 11, 12, 13, 15, 16, 18, 20, 25, 30.
Nodeform
Et binærtre tegnes så og si alltid med sirkelformede noder, mens nodene i et B-tre vanligvis lages rektangelformet.
Et 2-3-4 tre er egentlig et B-tre, men er, som nevnt over, ekvivalent med et rød-svart tre (som er et binærtre).
I 2-3-4 treet i Figur 9.2.1 a)
har nodene ellipseform (sirkel hvis det er kun én verdi). Mange liker å tegne det slik og her vil vi fortsette
med det. Men det er også vanlig å ha rektangelformede noder (kvadrat hvis det er kun én verdi). En tredje
mulighet er å bruke rektangler der hjørnene er avrundet.
Se også Oppgave 3.
Flg. figur viser hvordan treet vil se ut med rektangler:
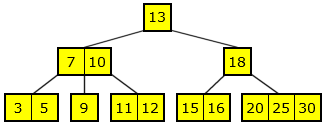 |
| Figur 9.2.1 d) : Et 2-3-4 tre med rektangelformede noder |
| 1. | Tegn et 2-3-4 tre med 15 verdier (f.eks. tallene fra 1 til 15) som har høyde 2.
Finnes det andre trær enn de to i Figur 9.2.1 c) som har
høyder på henholdsvis 1 og 3?
|
| 2. | Regn ut både ⌊log4(n)⌋ og ⌊log2(n)⌋ for n = 3, 15, 63 og 1000
og sjekk at det stemmer med det som er oppgitt i teksten. Vis også at
log2(n) = 2·log4(n).
|
| 3. | Bruk f.eks. Google med 2-3-4 tree som søkeord og velg så bilder (images). Hvis du da blar deg nedover, vil du finne tegninger med alle varianter av nodeformer. |
![]() 9.2.2 Innlegging og søking i et 2-3-4 tre
9.2.2 Innlegging og søking i et 2-3-4 tre
Vi skal nå lage en algoritme for innlegging av verdier i et 2-3-4 tre. Den vanlige algoritmen for innlegging
i et binært søketre gjør at innleggingsrekkefølgen bestemmer treets form. Hvis verdiene f.eks. legges inn
i sortert rekkefølge, blir treet ekstremt høyreskjevt. En algoritme for 2-3-4 trær må være slik at
kravene blir oppfylt og dermed får vi alltid balalanserte
trær uansett rekkefølge. Men to forskjellige rekkefølger vil kunne føre til litt ulik form på trærne.
En ny verdi skal alltid legges inn i den bladnoden som den sorteringsmessig hører til. Hvis bladnoden har en eller to verdier fra før, så går det greit. Anta at vi skal legge inn 6 i flg. tre:
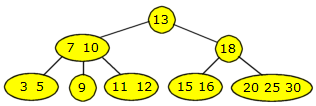 |
| Figur 9.2.2 a) : Et 2-3-4 tre |
Vi starter i rotnoden og ser at 6 er mindre enn 13. Dermed til venstre. Vi har at 6 er mindre enn 7 og dermed videre til venstre for 7. Bladnoden har plass. Det gir flg. tre:
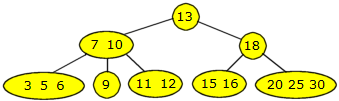 |
| Figur 9.2.2 b) : 6 er lagt inn |
Men hvis den aktuelle bladnoden er en 4-node (tre verdier), blir det mer komplisert. Anta at vi skal legge inn 22. Vi ser fort at den sorteringsmessig hører hjemme i bladnoden 20, 25 og 30. Da må den «splittes», dvs. deles i to. Midtverdien 25 skal rykke opp til foreldernoden:
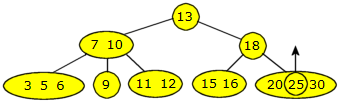 |
| Figur 9.2.2 c) : Noden 20, 25, 30 skal splittes |
Verdiene 20 og 30 skal utgjøre sine egne noder. Deretter legges 22 inn sammen med 20:
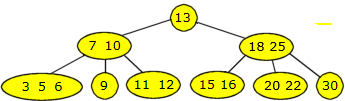 |
| Figur 9.2.2 d) : 22 er lagt inn |
I prosessen med å legge inn 22 måtte bladnoden splittes og midtverdien (dvs. 25) flyttes opp til
foreldernoden. Der var det plass. Hvis ikke, hadde vi også måttet splitte foreldernoden
og flytte dens midtverdi oppover. I verste fall kunne det ha fortsatt helt opp til rotnoden og
føre til at treet fikk en ny rotnode. Denne teknikken kalles
nedenifra og opp (eng: bottom up).
Det
er også mulig å gjøre det motsatte, dvs.
ovenifra og ned (eng: top down). I så fall
splittes alle 4-noder som passeres på veien ned til rett bladnode. I vår algoritme må vi her gjøre et valg.
Fordelen med ovenifra og ned er at den
er litt enklere å kode og kanskje litt enklere å illustrere. Men ulempen er at treet vil kunne få flere noder og
dermed i verste fall litt større høyde enn å bruke
nedenifra og opp. Men vi velger likevel
ovenifra og ned.
Innleggingsalgoritme (ovenifra og ned) for 2-3-4 trær
- Hvis treet er tomt, opprettes en bladnode og verdien legges inn i den.
- Finn den bladnoden som verdien sorteringsmessig hører til. Splitt alle 4-noder som passeres på veien ned dit (også bladnoden hvis den er en 4-node). En node splittes ved at midtverdien rykker opp til foreldernoden (på rett sortert plass) og ved at de to verdiene på hver siden inngår i sine egne noder. Hvis det er rotnoden som skal splittes, rykker midtverdien opp til en ny rotnode.
- Hvis bladnoden har plass, legges verdien inn på rett sortert plass. Hvis den ble splittet (var en 4-node), legges verdien inn i den noden som den etter splittingen hører til.
Hvis denne algoritmen følges, vil resultatet etter hver innlegging forbli å være et 2-3-4 tre. Det vil gi et balansert tre
uansett hvilken rekkefølge verdier legges inn. Vi skal nå teste dette ved å legge inn tallene fra treet i
Figur 9.2.2 a) i sortert rekkefølge, dvs. tallene
3, 5, 7, 9, 10, 11, 12, 13, 15, 16, 18, 20, 25 og 30:
Vi starter med et tomt tre. Dermed må første verdi 3 legges i en ny rotnode. De to neste verdiene (5 og 7) får også plass der og dermed flg. tre:
 |
| Figur 9.2.2 e) : Rotnoden inneholder 3, 5, 7 |
Neste verdi 9 er det imidlertid ikke plass til. Da må rotnoden først splittes og deretter legges 9 inn i den nye bladnoden sammen med 7:
 |
| Figur 9.2.2 f) : Splitting og innlegging |
Neste verdi er 10. Den legges inn i bladnoden som fra før inneholder 7 og 9. Når 11 deretter skal inn, må bladnoden med 7, 9 og 10 først splittes. Så legges 11 inn i den nye bladnoden sammen med 10:
 |
| Figur 9.2.2 g) : Innlegging, splitting og innlegging |
For de to neste verdiene 12 og 13 blir det på samme måte. Først legges 12 i tilhørende bladnode. Når 13 skal inn, må bladnoden først splittes. Deretter går 13 inn i ny bladnode sammen med 12:
 |
| Figur 9.2.2 h) : Verdien 12 er lagt inn |
Når 15 skal legges inn, gjelder det å huske algoritmen.
Den sier at alle 4-noder på veien ned til den bladnodnen som verdien sorteringsmessig hører til, skal splittes.
Verdien 15 hører hjemme i bladnoden som inneholder 12 og 13 fra før. Men på veien dit passerer vi rotnoden og
dermed må den splittes først. Så kan 15 legges inn:
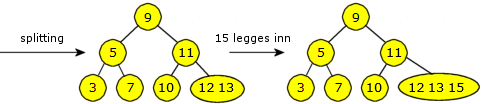 |
| Figur 9.2.2 i) : Splitting av rotnoden og innlegging av 15 |
Innlegging av resten av verdiene (16, 18, 20, 25 og 30) blir på samme måte. Da holder det sikkert med færre kommentarer:
 |
| Figur 9.2.2 j) : Splitting og innlegging av 16 og 18 |
Verdien 20 hører hjemme i bladnoden med verdiene 15, 16 og 18. Da må den først splittes. Så kan 20 legges inn i den nye bladnoden sammen med 18:
 |
| Figur 9.2.2 k) : Splitting og innlegging av 20 |
Vi må passere en 4-node (11, 13 og 16) for å finne plassen til 25. Da må den først splittes:
 |
| Figur 9.2.2 l) : Splitting og innlegging av 25 |
Til slutt 30 som hører hjemme i bladnoden nederst til høyre. Da må den splittes og så kan 30 legges inn i den nye noden sammen med 25. Da får vi dette 2-3-4 treet som sluttresultat:
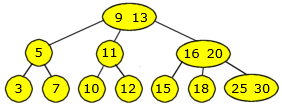 |
| Figur 9.2.2 m) : Alle verdiene er satt inn |
Treet over og det i Figur 9.2.2 a)
inneholder nøyaktig de samme verdiene. De har litt ulik form, men har samme høyde. De er likeverdige
som 2-3-4 trær.
Søking i et 2-3-4 tre er rett frem. Det er bare å bruke sorteringsrekkefølgen. Start
i rotnoden og gå eventuelt videre til et barn basert på størrelsen på søkeverdien i forhold
til nodeverdiene. Hvis en kommer til en bladnode og skal videre, er ikke verdien i treet.
| 1. | Lag et 2-3-4 tre ved fortløpende å legge inn flg. verdier i den gitte rekkefølgen: 18, 10, 25, 7, 5, 13, 15, 22, 9, 3, 11, 16, 30, 12.
Da skal du få Figur 9.2.2 a) som resultat.
|
| 2. | Gitt tallene fra 1 til 15. Finnes det noen rekkefølge (permutasjon) av tallene slik at hvis de fortløpende legges inn
i et 2-3-tre, så får vi det øverste treet i Figur 9.2.1 c).
Hva med det nederste treet?
|
![]() 9.2.3 Fjerning av verdier i et 2-3-4 tre
9.2.3 Fjerning av verdier i et 2-3-4 tre
Når en verdi skal fjernes må vi først finne den noden som inneholder verdien.
Da er det to muligheter: 1) Den ligger i en indre node eller 2) den ligger i en bladnode.
1) Den ligger i en indre node: Ta treet under som eksempel. 13 skal fjernes. Se den rød pilen:
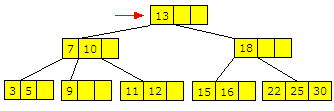 |
| Figur 9.2.3 a) : Verdien 13 skal fjernes |
Vi finner først den som kommer etter 13 i sortert rekkefølge. Det er 15. Som vi ser ligger den lengst til venstre i en bladnode. La disse bytte plass. Da får vi treet:
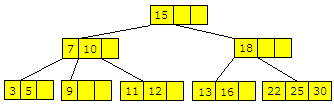 |
| Figur 9.2.3 b) : Verdiene 13 og 15 har byttet plass. |
Verdien 13 som skal fjernes, ligger nå i en bladnode. Med andre ord holder det å lage en regel (algoritme) for å fjerne verdier i bladnoder.
2) Verdien som skal fjernes ligger i en bladnode: Hvis det ikke er den enste verdien i bladnoden, fjerner vi verdien direkte. Hvis nodene i treet er tegnet som tre små bokser, må vi eventuelt flytte på den eller de gjenværende verdiene i noden slik at boksene er fylt opp fra venstre. Hvis vi fjerner 13 i treet i Figur 9.2.2 m), blir det slik:
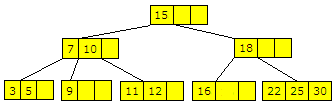 |
| Figur 9.2.3 c) : Verdiene 13 er fjernet fra treet. |
eller slik hvis vi tegner treet med «runde» noder:
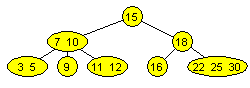 |
| Figur 9.2.3 d) : Verdiene 13 er fjernet fra treet. |
Da får vi flg. generelle regel: Hvis verdien som skal fjernes ligger i en bladnode og noden inneholder to eller tre verdier, så kan verdien fjernes uten videre.
Hvis den verdien som skal fjernes er en enslig verdi i en bladnode, kan vi «låne». Hvis en av de to nærmeste søskennodene har to eller flere verdier, kan vi først flytte ned disse to nodenes felles forelderveri og så flytte den næremste søskenverdien opp til forledernoden. Ta utgangspunkt i treet i Figur 9.2.3 c). Verdien 16 er enslig verdi. Da kan vi fjerne 16, flytte 18 ned og 22 opp. Det gir dette treet:
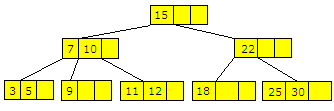 |
| Figur 9.2.3 e) : Verdiene 16 er fjernet fra treet. |
Neste problem oppstår hvis vi skal slette en enslig verdi i en bladnode og det ikke er noen søskennoder å «låne» av. Da blir det mer komplisert. Anta at verdien 3 er fjernet i treet i Figur 9.2.3 e), dvs. treet ser slik ut:
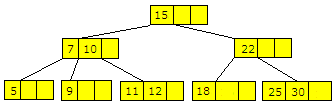 |
| Figur 9.2.3 f) : Verdiene 3 er fjernet fra treet. |
Hvis vi skal slette 5 i treet i Figur 9.2.3 f) får en situasjon der det ikke er noen søskennode å «låne» fra. Ta slår vi sammen verdien (5), søskenverdien (9) og de to verdienes felles forelderverdi (7) til én node, dvs. slik:
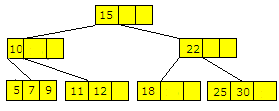 |
| Figur 9.2.3 g) : Verdiene 5 er fjernet fra treet. |
| 1. | xxxx |
![]() 9.2.4 Fra 2-3-4 tre til rød-svart tre
9.2.4 Fra 2-3-4 tre til rød-svart tre
I et rød-svart tre har nodene to farger. I et vanlig binærtre
vil venstre og/eller høyre peker i en node kunne være null. Her skal vi isteden si
at den peker til en svart «nullnode».
Et rød-svart tre (eng: red-black tree) er definert på følgende måte:
- Det er et binært søketre der det normalt ikke er tillatt med like verdier.
- Nodene er enten røde eller svarte. Rotnoden er svart.
- Barna til en rød node er svarte.
- Pekere som i et vanlig tre peker til null, skal her isteden peke til en svart «nullnode».
- La
pvære en vilkårlig node. Da er antall svarte noder på veien mellompog en nullnode i subtreet medpsom rot, det samme for alle slike nullnoder.
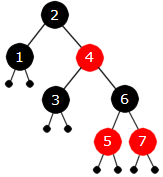 |
| Fig. 9.2.4 a) Et rød-svart tre |
Figuren til venstre viser et rød-svart binærtre med verdiene 1, 2, 3, 4, 5, 6 og 7. Vi ser at det er et binært søketre siden verdiene kommer sortert i inorden. Videre er det kun svarte og røde noder og rotnoden er svart. Barna til røde noder er svarte. Det som normalt er en nullpeker, er her en peker til en «nullnode» og den er markert med en liten svart sirkel.
Vi ser f.eks. at antall svarte noder på veien fra roten ned til en nullnode alltid er 3. Definisjonen gir også at ethvert subtre med en svart node som rotnode, er selv et rød-svart tre.
Dybden til en node er avstanden til roten. I et rød-svart tre har hver node også
en svart dybde. Det er den
svarte avstanden til roten, dvs.
én mindre enn antall svarte noder på veien til roten. Per definisjon har nullnoder samme svarte dybde.
Noen kaller denne dybden for treets svarte
høyde. Treet i figuren over har 2 som svart høyde. Vi skal senere se
at både den vanlige høyden og den svarte høyden til et rød-svart tre alltid er av orden
log2 n der n er antall noder i treet.
Vi skal i neste avsnitt se på en algoritme for å legge inn verdier i et rød/svart tre.
Treet i Figur 9.2.4 a) har oppstått ved at
1, 2, 3, 4, 5, 6 og 7 har blitt fortløpende lagt inn ved hjelp av algoritmen. En kan jo allerede nå lure på
hvordan treet vil bli etter en innlegging av 8. Hvordan tror du det blir? Du får svaret ved å klikke
her.
Et 2-3-4 tre og et rød-svart tre er to sider av samme sak. Et 2-3-4 tre kan «oversettes» til et rød-svart tre ved hjelp av flg. «omregningsformler» for 2-, 3- og 4-noder:
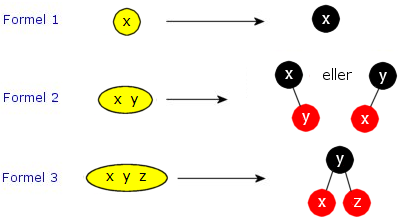 |
| Figur 9.2.4 b): «Omregningformler» fra 2-3-4 tre til rød-svart tre |
Omregningsformler:
Formel1: En 2-node i et 2-3-4 tre med verdix«oversettes» til en svart node med verdixi et rød-svart tre.Formel2: En 3-node i et 2-3-4 tre med verdienexogy«oversettes» enten til a) en svart foreldernode med verdixog et rødthøyrebarn med verdiyeller til b) en svart foreldernode med verdiyog et rødtvenstrebarn med verdix.Formel3: En 4-node i et 2-3-4 tre med verdienex,yogz«oversettes» til en svart foreldernode med verdiy, et rødtvenstrebarn med verdixog et rødthøyrebarn med verdiz.
I flg. eksempel skal vi «oversette» 2-3-4 treet
i Figur 9.2.4 c) under:
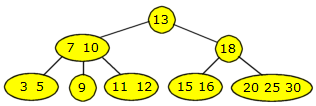 |
| Figur 9.2.4 c) : Et 2-3-4 tre |
Siden 2-3-4 treet har en rotnode med kun én verdi blir den gjort om til en svart nullnode i
det rød-svarte treet. Det venstre barnet til rotnoden i 2-3-4 treet har to verdier, dvs at det er
en 3-node. Da kan vi bruke enten a) eller b) i
Formel 2. Valget vil
påvirke treets utseende, men trærne blir likeverdige. Her velger vi å bruke muligheten a) for alle 3-noder.
Vi ser senere på hvordan treet vil bli hvis vi f.eks. isteden bruker b) for alle 3-noder. Det er også
mulig å blande, dvs. noen ganger a) og noen ganger b). Resultatene blir likeverdige.
Noden med verdiene 7 og 10 skal derfor gjøres om til en svart foreldernode (som blir venstre barn til roten) med verdi 7 og et rødt høyre barn til den med verdi 10. Osv. Resultatet blir:
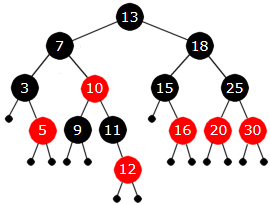 |
| Figur 9.2.4 d) : Formel 2a) for alle 3-noder |
Algoritmen for å «oversette» et 2-3-4 tre til et rød-svart tre er, som nevnt over, ikke
entydig. Formel 2 sier
at vi kan omskape en 3-node (som har to verdier) til to noder
der enten a) første verdi legges i en svart foreldernode
og den andre verdien i et rødt høyrebarn eller b) at
første verdi legges i et rødt venstrebarn og den andre verdien i en svart forelder.
Men alle trær får samme høyde og samme svarte høyde.
Treet Figur 9.2.4 d) ble til ved at a)
ble brukt i alle tilfellene. Hvis i isteden velger å bruke b) i alle tilfellene, får vi
flg. tre:
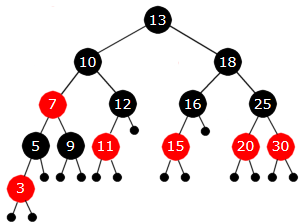 |
| Figur 9.2.4 e) : Formel 2b) for alle 3-noder |
| 1. |
«Oversett» flg. 2-3-4 tre til et rød-svart tre:
| ||
| 2. |
«Oversett» flg. 2-3-4 tre til et rød-svart tre:
|
![]() 9.2.5 Innlegging i et rød-svart tre
9.2.5 Innlegging i et rød-svart tre
Innleggingsalgoritmen er forholdsvis komplisert og
har mange spesialtilfeller. Vi starter derfor med et eksempel. Vi skal
fortløpende legge inn tallene 1, 2, 3, 4, 5, 6, 7 og 8. I et vanlig binært søketre
ville det ha resultert i et ekstremt høyreskjevt tre. Men her skal vi se (etter en del arbeid underveis)
at det blir et balansert tre.
Den første verdien (dvs. tallet 1) legges i en svart rotnode:
 |
||
| Figur 9.2.5 a): Første verdi | ||
Deretter gjør vi som i et vanlig binært søketre. Verdien (dvs. 2) legges på rett sortert plass i treet. En ny node skal alltid være rød. Her blir den nye noden høyre barn til rotnoden:
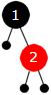 |
||
| Figur 9.2.5 b): Andre verdi | ||
Vi må sjekke om treet oppfyller definisjonen til et rød-svart tre. Algoritmen er heldigvis laget slik at det er kun punkt 3 som må sjekkes: En rød node kan ikke ha et rødt barn. Eller omvendt: En rød node kan ikke ha en rød forelder. Treet i Figur 9.2.5 b) er derfor ok.
Neste verdi, dvs. tallet 3, legges først på rett sortert plass i en rød node:
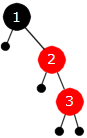 |
||
| Figur 9.2.5 c): Tredje verdi | ||
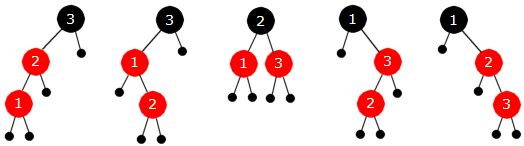
Treet i Figur 9.2.5 c) er i strid med punkt 3 i definisjonen (rød node har rød forelder). Legg merke til at hvis vi hadde lagt inn de tre verdiene 1, 2 og 3 i en annen rekkefølge, ville treet ha blitt annerledes. De seks permutasjonene av 1, 2 og 3 vil gi flg. fem forskjelige tilfeller:
 |
||
| Figur 9.2.5 d): Fem tilfeller for de seks permutasjonene av 1, 2 og 3 | ||
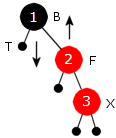
Rekkefølgen 2,1,3 og 2,3,1 gir det midterste treet i Figur 9.2.5 d). Det treet er ok. Men alle de fire andre trærne er i strid med punkt 3 i definisjonen. Det er en separat regel for hvert av de fire tilfellene. Her fortsetter vi imidlertid med treet i Figur 9.2.5 c). For å forklare dette grundig gir vi nodene navn som om det var et lite familietre. Den nye noden (det nye barnet) får navnet X siden dens endelige plassering foreløpig er ukjent. Dens forelder får navnet F, dens besteforelder B og dens «tante» T (tante siden noden T er søsken til forelder F):
 |
||
| Figur 9.2.5 e): X, F, B og S | ||
I Figur 9.2.5 e)
er T svart, F er høyre barn til B og X høyre barn til F.
Dette «repareres» ved hjelp av
venstrerotasjon
og fargeskifte. Vi roterer treet mot venstre om midtpunktet på kanten mellom
B og F. Det fører til at noden F heves (pil oppover) og noden B senkes (pil nedover). Deretter skifter de to farge - F blir svart og
B blir rød. Etterpå fjernes navnene X, F, B og T siden de ikke lenger gir mening:
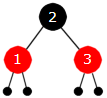 |
||
| Figur 9.2.5 f): En venstrerotasjon og fargeskifte | ||
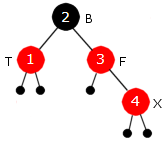
Neste verdi er 4 og den legges som normalt på rett sortert plass, dvs. som høyre barn til 3-noden. En ny node er alltid rød. Vi setter igjen navn på nodene. Den nye heter X, osv:
 |
||
| Figur 9.2.5 g): 4 på rett plass | ||
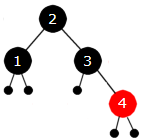
Treet i Figur 9.2.5 g) er «ulovlig» siden X og F er røde. Denne gangen er T rød. De fire tilfellene med rød T er de enkle tilfellene. Alle «repareres» på samme måte, dvs. ved kun å skifte farger: F og T blir svarte og B blir rød. Men siden B her er roten, settes den tilbake til svart. Roten skal alltid være svart. Hvis B ikke var roten, kunne vi ha fått et nytt problem. Forelderen til B kunne jo være rød og da får vi rødt barn med rød forelder. Et slikt tilfelle dukker opp når vi skal legge inn 8. Se lenger ned. Treet blir slik:
 |
||
| Figur 9.2.5 h): Treet er nå ok | ||
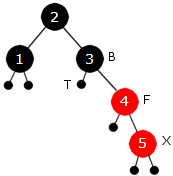
Neste verdi er 5 og den legges som vanlig i en rød node på rett sortert plass:
 |
||
| Figur 9.2.5 i): Tallet 5 er lagt inn | ||
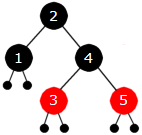
Vi får samme tilfelle som i Figur 9.2.5 e) og «reparerer» på samme måte - en venstrerotasjon og et fargeskifte. Her må vi imidlertid passe på at høyrepeker i 2-noden settes riktig:
 |
||
| Figur 9.2.5 j): Treet er ok | ||
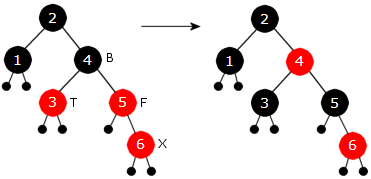
Når 6 legges inn vil vi få at X, F er T røde. Det er, som nevnt over, et enkelt tilfelle, dvs. kun et fargeskifte: F og T blir svarte og B blir rød:
 |
||
| Figur 9.2.5 k): Til venstre: 6 legges inn Til høyre: fargeskifte | ||
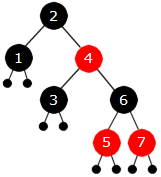
Når 7 legges inn ser vi at vi får det samme tilfellet som i Figur 9.2.5 e) en gang til. Dermed en venstrerotasjon og et fargeskifte:
 |
||
| Figur 9.2.5 l): 7 er lagt inn og treet er «reparert» | ||
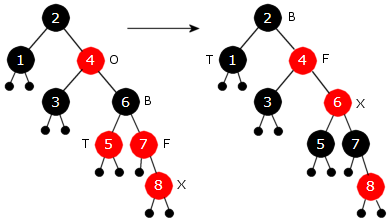
Siste verdi er 8. Den legges som vanlig i en rød node på rett sortert plass. Da får vi det venstre treet i figuren under. Her er T rød og da blir det fargeskifte: F og T blir svarte og B blir rød. Det gir treet til høyre i figuren under:
 |
||
| Figur 9.2.5 m): 8 er lagt inn og «problemet» er flyttet oppover | ||
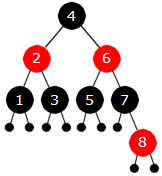
Men nå har vi fått et nytt problem. Siden oldeforelder O til X (forelder til B) er rød, får vi et tilfelle som er strid med punkt 3 i definisjonen. Dvs. rød node med rød forelder. I treet til høyre i figuren over er navnsettingen X, F, T og B flyttet oppover slik at de to røde nodene heter X og F. Men dette er en kjent tilfelle siden T nå er svart. Det betyr en venstrerotasjon og fargeskifte. Vi roterer om B - F (midpunktet på kanten mellom B og F). Det betyr at F heves og B senkes. Spesielt blir venstre subtre til F etterpå høyre subtre til B. Etter rotasjonen settes B til rød og F til svart. Dermed får vi (etter at navnene (bokstavene) er fjernet) dette vakre resultatet:
 |
||
| Figur 9.2.5 n): Verdiene fra 1 til 8 | ||
Ved innlegging av tallene fra 1 til 8 har kun to av de åtte tilfellene (der F og X er røde) oppstått. Vi skiller mellom hovedtilfellene T svart (fire tilfeller) og T rød (fire tilfeller). Som nevnt over er tilfellene med rød T enkle å behandle. Da er det kun fargeskifte - F og T blir svarte og B rød. Men som vist over (innlegging av 8) kan det føre til «problemer» oppover i treet. Det skjer hvis oldeforelder til X er rød. Da flyttes «navnene» X, F, T og B oppover og det nye tilfellet «repareres». Osv.
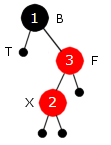
Hvis T derimot er svart, blir det rotasjoner og fargeskifte. Men da stopper det siden det da aldri blir rød node med rød forelder. Figur 9.2.5 d) viser de fem trærne som oppstår ved å legge inn tallene 1, 2 og 3 i en eller annen rekkefølge. Spesielt får vi dette treet hvis vi legger inn i rekkefølgen 1, 3, 2:
 |
||
| Figur 9.2.5 o): Inlegging av 1, 3, 2 | ||
Forskjellen mellom denne og den i Figur 9.2.5 e) er at nodene B - F - X nå danner en «knekk» eller en vinkel, mens nodene i Figur 9.2.5 d) går på skrå (ned mot høyre). Her «reparerer» vi ved å heve noden X to nivåer oppover og senke B ett nivå nedover. Deretter blir X svart og B rød. Dette kalles en dobbel venstrerotasjon med fargeskifte siden resultatet oppnås ved to rotasjoner. Først roterer vi mot høyre mhp. F - X, dvs. om midtpunktet på kanten mellom F og X. Da heves X og F senkes. Deretter (vi beholder nodenavnene) roterer vi mot venstre mhp. B - X. Flg. sekvens viser hva som skjer:
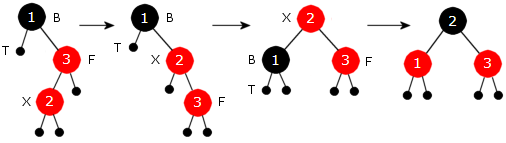 |
||
| Figur 9.2.5 p): Pil 1) Høyre rotasjon om F - X Pil 2) Venstre rotasjon om B - X Pil 3) Fargeskifte | ||
Huskeregler med illustrasjoner:
Hvis vi har det «ulovlige» tilfellet rød node med rød forelder, kaller vi noden X, dens forelder F, dens tante (søsken til forelder) T og dens besteforelder B. Vi har to hovedtilfeller: T er svart og T er rød.
Hvis T er svart trengs en rotasjon (og et fargeskifte). Ved en rotasjon kan et eller to subtrær bytte «eier». Det eller de dette gjelder er i tegningene under markert med en blå node. Et slikt subtre kan være både tomt og ikke tomt. Hvis det er tomt svarer det til en nullnode.
1) T er svart, B - F - X ligger på skrå (to tilfeller)
1a) B - F - X går på skrå ned mot høyre hvis F er høyre barn til B og X er høyre barn til F. Dette
repareres ved en venstrerotasjon mhp. B - F (F heves og B senkes) og et fargesifte (B blir rød og F svart).
Venstre subtre til F (symbolisert med en blå node) blir høyre subtre til B.
1b) B - F - X går på skrå ned mot venstre hvis F er venstre barn til B og X er venstre barn til F.
Dette repareres ved en høyrerotasjon mhp. B - F (F heves og B senkes) og et fargesifte (B blir rød og F svart).
Høyre subtre til F (symbolisert med en blå node) blir venstre subtre til B.
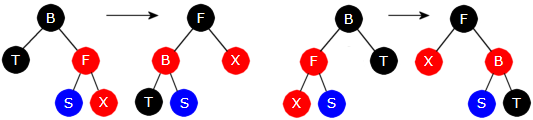 |
||
| 1a) En venstrerotasjon og fargeskifte 1b) En høyrerotasjon og fargeskifte | ||
2) T er svart, B - F - X har en knekk (to tilfeller)
2a) B - F - X har en «knekk» (eller vinkelspiss) mot høyre hvis
F er høyre barn til B og X er venstre barn til F. Dette
repareres ved en dobbel venstrerotasjon (X heves to nivåer og B senkes ett nivå) og et fargeskifte (B blir rød og X svart).
Venstre subtre til X (symbolisert med den blå noden S1) blir høyre subtre til B
og høyre subtre til X (symbolisert med den blå noden S2) blir venstre subtre til F.
2b) B - F - X har en «knekk» (eller vinkelspiss) mot venstre hvis
F er venstre barn til B og X er høyre barn til F. Dette
repareres ved en dobbel høyrerotasjon (X heves to nivåer og B senkes ett nivå) og et fargeskifte (B blir rød og X svart).
Venstre subtre til X (symbolisert med den blå noden S1) blir høyre subtre til F
og høyre subtre til X (symbolisert med den blå noden S2) blir venstre subtre til B.
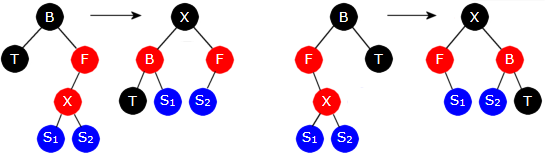 |
||
| 2a) Dobbel venstrerotasjon og fargeskifte 2b) Dobbel høyrerotasjon og fargeskifte | ||
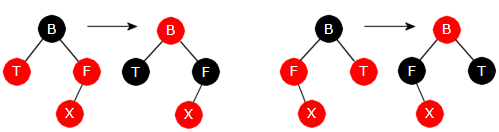
3) T er rød (fire tilfeller)
Dette er de enkle tilfellene. Alle sammen (fire tilfeller) behandles på samme måte. Dvs. et fargeskifte der B blir rød og F og T svarte. Men da kan det oppstå nye tilfeller oppover i treet. Hvis B har en forelder som er rød, vil både den og B etter fargeskiftet være røde. Da flyttes navnsettingen oppover ved at B settes til X, osv. Det en da får er et av de åtte mulige tilfellene og det behandles slik det tilfellet skal behandles.
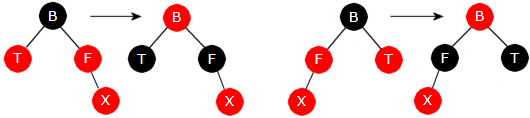 |
||
| De to tilfellene med rød T der B - F - X ligger på skrå. Det ene er en speilvending av det andre | ||
 |
||
| De to tilfellene med rød T der B - F - X har en knekk. Det ene er en speilvending av det andre | ||
Innleggingsalgoritmen:
- Treets første verdi legges i en svart rotnode.
- Generelt legges en ny verdi i en rød node på rett sortert plass i treet. La den hete X.
- Hvis forelder F til X er svart, stopper vi. Hvis F er rød, må F ha en svart forelder B (besteforelder til X) og X en tante T (søsken til forelder F).
- Hvis T er svart (en nullnode eller en vanlig node), er det fire mulige tilfeller. Avhengig av hviklet tilfelle det er (se huskereglene over) må det utføres en enkel eller en dobbel rotasjon (høyre eller venstre) og deretter et fargeskifte (F til svart og B til rød). Dermed er innleggingen ferdig.
- Hvis T er rød, må det utføres et fargeskifte (F og T til svart og B til rød). Hvis B er roten, settes den tilbake til svart og vi kan stoppe. Hvis ikke, omdøper vi B til X og går tilbake til pkt. 3.
| 1. |
Sjekk at nodenes rekkefølge i inorden bevares ved rotasjonene. Se f.eks. på tilfellet
1a). Der er rekkefølgen T - B - S - F - X før
rotasjonen. Som vi ser på figuren er den det samme etter rotasjonen. Sjekk at det også stemmer for tilfellene
1b),
2a) og
2b).
|
| 2. | Bruk animasjonen Red/Black Tree i flg. oppgaver. Legg merke til at du kan bruke muligheten SkipBack. Da settes treet tilbake til slik det var før en innlegging: |
a) Første del av Avsnitt 9.2.5 ble
brukt til å vise hvordan tallene fra 1 til 8 legges inn i et rød-svart tre. Gjør det samme
ved hjelp av animasjonen og sjekk at resultatet etter hver innlegging blir det samme.
| |
| b) Sett inn tallene 8, 7, 6, 5, 4, 3, 2, 1 (i den oppgitte rekkefølgen) i et på forhånd tomt rød-svart tre. Bruk animasjonen. Før hver innlegging finner du ut hva som må gjøres (se reglene og algoritmen). Deretter bruker du animasjonen til å gi deg fasiten. | |
| c) Gjør som i b), men legg inn 10, 4, 7, 14, 12, 6, 8, 9, 11. | |
| d) Gjør som i b), men legg inn 15, 18, 17, 3, 6, 10, 12, 13, 14. | |
| e) Gjør som i b), men legg inn 7, 5, 13, 9, 10, 12, 11, 6, 14. |
![]() 9.2.6 Java-kode for et rød-svart tre
9.2.6 Java-kode for et rød-svart tre
Nodene i et rød-svart skal
ha en farge. Til det brukes to fargekonstanter SVART og RØD. Vi trenger også
«nullnoder». I realiteten lager vi kun én nullnode (en konstant) med navn NULL som alle da kan peke til.
Klassen får navnet RSBinTre der R står for rød og S
for svart:
import java.util.*; public class RSBinTre<T> implements Beholder<T> { private static final boolean SVART = true; private static final boolean RØD = false; private static final class Node<T> // en indre nodeklasse { private T verdi; // nodens verdi private Node<T> venstre; // peker til venstre barn private Node<T> høyre; // peker til høyre barn private boolean farge; // RØD eller SVART private Node(T verdi, Node<T> v, Node<T> h, boolean farge) // konstruktør { this.verdi = verdi; venstre = v; høyre = h; this.farge = farge; } } // class Node private final Node<T> NULL; // en svart nullnode private Node<T> rot; // treets rot private int antall; // antall verdier private final Comparator<? super T> comp; // treets komparator public RSBinTre(Comparator<? super T> comp) // konstruktør { rot = NULL = new Node<>(null,null,null,SVART); this.comp = comp; } // konstruksjonsmetoder public static <T extends Comparable<? super T>> RSBinTre<T> rsbintre() { return new RSBinTre<>(Comparator.naturalOrder()); } public static <T> RSBinTre<T> rsbintre(Comparator<? super T> c) { return new RSBinTre<>(c); } // Instansmetodene skal inn her } // class RSBinTre Programkode 9.2.6 a)
Flere av metodene fra klassen SBinTre kan brukes i klassen RSBinTre. Men
pga. nullnoden NULL må vi gjøre noen små endringer. F.eks. slik i metoden inneholder(T verdi):
public boolean inneholder(T verdi) { for (Node<T> p = rot; p != NULL; ) // Obs: NULL istedenfor null { int cmp = comp.compare(verdi,p.verdi); if (cmp > 0) p = p.høyre; else if (cmp < 0) p = p.venstre; else return true; // funnet } return false; // ikke funnet } Programkode 9.2.6 b)
Utfordringen ligger i metoden leggInn(). Vi legger inn som i et vanlig binært søketre,
men hvis treet må «repareres» etterpå, må vi kunne gå oppover. Det kan vi løse
ved hjelp av en stakk. Alle nodene på veien nedover legges på stakken. Metoden starter derfor slik:
public boolean leggInn(T verdi) { if (rot == NULL) // treet er tomt { rot = new Node<>(verdi,NULL,NULL,SVART); // roten skal være svart antall++; return true; // vellykket innlegging } Stakk<Node<T>> stakk = new TabellStakk<>(); // en stakk Node<T> p = rot; // hjelpevariabel int cmp = 0; // hjelpevariabel while (p != NULL) { stakk.leggInn(p); // legger p på stakken cmp = comp.compare(verdi,p.verdi); // sammenligner if (cmp < 0) p = p.venstre; // til venstre else if (cmp > 0) p = p.høyre; // til høyre else return false; // duplikater ikke tillatt } Node<T> x = new Node<>(verdi,NULL,NULL,RØD); // en rød node antall++; Node<T> f = stakk.taUt(); // forelder til x if (cmp < 0) f.venstre = x; // x blir venstre barn else f.høyre = x; // x blir høyre barn if (f.farge == SVART) return true; // vellykket innlegging // Men hva hvis f er RØD? } Programkode 9.2.6 c)
Så langt er Programkode 9.2.6 c) omtrent som for et vanlig binært søketre. Men hvis
forelder f til x er rød, så blir det annerledes.
I så fall kan ikke f være rotnoden siden den alltid er svart. Da må x ha
en besteforelder b og den må da ligge øverst på stakken. Deretter må vi starte en løkke. I den finner
vi først «tanten» t til x. Så må vi avgjøre om t
er et venstre eller et høyre barn til b. Dvs. hvis f er er venstre barn
til b, så må t være høyre barn og omvendt.
Som beskrevet i
reglene er det to hovedtilfeller: t svart eller
t rød.
Flg. kode skal inn der det står // Men hva hvis f er RØD?
i Programkode 9.2.6 c):
Node<T> b = stakk.taUt(); // b for besteforelder til x while (true) { // Er t venstre eller høyre barn til b? Node<T> t = (f == b.venstre) ? b.høyre : b.venstre; if (t.farge == SVART) { // Rotasjoner og fargeskifte } else // t.farge == RØD { // Fargeskifte } } // while Programkode 9.2.6 d)
Hvis t.farge er SVART har vi fire undertilfeller -
se reglene. I hver av dem inngår en enkel eller
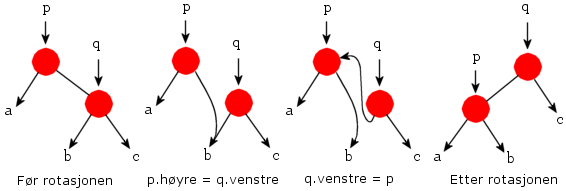
en dobbel rotasjon Doble rotasjoner består av to enkle rotasjoner. Koden for en generell enkel rotasjon er ikke vanskelig. Figuren under viser
gangen i en venstrerotasjon på p - q:
 |
||
| Figur 9.2.6 a): En venstrerotasjon | ||
Figuren viser gangen i en venstrerotasjon på p - q, dvs.
p er forelder og q er høyre barn. Rotasjonen foregår om
midtpunktet mellom p og q. Det fører til at p
senkes og q heves og dette kun ved hjelp av de to programsetningene
p.høyre = q.venstre og
q.venstre = p. De to siste trærne i Figur 9.2.6 a) er like. Det siste
er satt opp på en «penere» form.
En høyrerotasjon er en speilvending av en venstrerotasjon og utføres på
p - q (q er venstre barn til p)
ved hjelp av setningene p.venstre = q.høyre og
q.høyre = p. Vi setter dette opp i to metoder der
p og q er argumenter:
private static <T> Node<T> vRotasjon(Node<T> p, Node<T> q) // venstrerotasjon { p.høyre = q.venstre; q.venstre = p; return q; } private static <T> Node<T> hRotasjon(Node<T> p, Node<T> q) // høyrerotasjon { p.venstre = q.høyre; q.høyre = p; return q; } Programkode 9.2.6 e)
De fire tilfellene 1a), 1b), 2a) og 2b) fra reglene
må behandles hver for seg. For å finne hvem av dem som er aktuelle, må vi undersøke om x er
venstre eller høyre barn til f og om f er venstre eller høyre barn til b.
I alle tilfellene skal b bli rød. Det gir flg. kode:
En dobbel rotasjon utføres ved å kalle metodene over to ganger.
if (t.farge == SVART) { b.farge = RØD; // b skal uansett bli rød if (x == f.venstre) // 1b) eller 2a) { if (f == b.venstre) // 1b) { p = HR(b); f.farge = SVART; // høyrerotasjon + fargeskifte } else // f == b.høyre // 2a) { p = DVR(b); x.farge = SVART; // dobbel venstrerotasjon + fargeskifte } } else // x == f.høyre // 1a) eller 2b) { if (f == b.venstre) // 2b) { p = DHR(b); x.farge = SVART; // dobbel høyrerotasjon + fargeskifte } else // f == b.høyre // 1a) { p = VR(b); f.farge = SVART; // venstrerotasjon + fargeskifte } } if (b == rot) rot = p; // hvis b var rotnoden, må roten oppdateres else { Node<T> q = stakk.taUt(); if (b == q.venstre) q.venstre = p; else q.høyre = p; } return true; // to røde noder på rad er nå avverget } Programkode 9.2.6 f)
I tilfellet s.farge er RØD har vi også fire undertilfeller -
se illustrasjonene. Men denne gangen trengs det kun å skifte farger:
else // s.farge == RØD { f.farge = s.farge = SVART; // f og s blir svarte if (b == rot) return true; // vi stopper b.farge = RØD; // b blir RØD // Må sjekke om forelder til b (dvs. oldeforelder til x) er rød Node<T> o = stakk.taUt(); // oldeforelder til x if (o.farge == SVART) return true; // vi stopper // nå har den røde noden b en rød forelder // vi omdøper x, f og b og fortsetter oppover x = b; f = o; b = stakk.taUt(); } // else Programkode 9.2.6 g)
Vi kan sette sammen alt dette til en fullstendig kode for metoden leggInn(). Dette og kode for en del andre aktuelle metoder
ligger på RSBinTre. Hvis du flytter hele klassen over til deg selv, vil du kunne kjøre flg. programbit:
int[] a = Tabell.randPerm(10); RSBinTre<Integer> tre = RSBinTre.lagTre(); for (int k : a) tre.leggInn(k); System.out.println(tre); // bruker toString-metoden for (int k : tre) System.out.print(k + " "); // bruker iteratoren tre.nullstill(); for (int k = 1; k <= 1_000_000; k++) tre.leggInn(k); System.out.println("\n" + tre.høyde()); // treets høyde Programkode 9.2.6 h)
| 1. |
Legg inn RSBinTre hos deg og kjør Programkode 9.2.6 h).
|


