 |
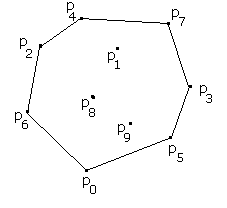
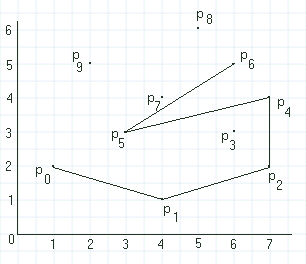
| Figur 2.2.1 a): Konvekst polygon |
Til venstre er det konvekse polygonet for de 10 punktene p0 , p1 , . . . . . p9 tegnet inn.
Vi ser at hvert punkt enten ligger på selve polygonet eller det ligger inne i polygonet. I tillegg ser vi at alle de indre vinklene i polygonet er mindre enn 180 grader.
Det å finne det konvekse polygonet til en samling punkter er et viktig problem i plangeometri. Da holder det selvfølgelig å finne de punktene som utgjør hjørnene i polygonet. Noen slike hjørner kan vi fort finne. I avsnitt 1.4.5 så vi på hvordan punkter kunne ordnes leksiografisk. Da kunne vi enten ordne med hensyn på x-koordinaten først, og så med hensyn på y-koordinaten, eller eventuelt omvendt. Hvis vi velger det minste og største punktet med hensyn på begge de to leksiografiske ordningene, så får vi hjørnepunkter. I figur 2.2.1 a) over ville vi på denne måten ha fått hjørnepunktene p6 , p3 , p0 og p4. I figur 2.2.1 b) nedenfor ville det ha blitt p5 , p7 , p6 og p1. Det er p7 og ikke p8 , som er størst. De har samme x-koordinat, og da er det størst som har størst y-koordinat.
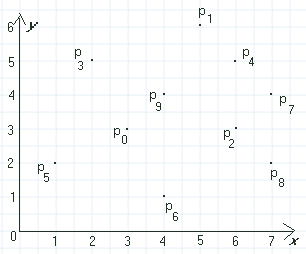 |
| Figur 2.2.1 b): Et koordinatsystem |
I avsnitt 1.4.5 laget vi en komparator som var basert på en leksiografisk ordning. Den var laget slik at vi først ordnet etter x-koordinaten, og så etter y-koordinaten.
Koden for class XkoordinatKomparator satt opp på nytt nedenfor. Den brukes et program som finner minste og største punkt mhp. komparatoren. Et punkt lager vi ved hjelp av class Point fra java.awt.
public class XkoordinatKomparator implements Comparator, Serializable { public int compare(Object o1, Object o2) { Point p1 = (Point)o1; // gjør om fra Object til Point Point p2 = (Point)o2; // gjør om fra Object til Point if (p1.x < p2.x) return -1; // p1 har minst x-koordinat if (p1.x > p2.x) return 1; // p1 har størst x-koordinat // Nå har p1 og p2 like x-koordinater if (p1.y < p2.y) return -1; // p1 har minst y-koordinat if (p1.y > p2.y) return 1; // p1 har størst y-koordinat return 0; } } // class XkoordinatKomparator Programkode 2.2.1 a)
I utgangspunktet er punktene representert ved hjelp av to heltallstabeller, en tabell for x-koordinater og en for y-koordinater:
int[] x = {3,5,6,2,6,1,4,7,7,4}; int[] y = {3,6,3,5,5,2,1,4,2,4}; Point[] p = new Point[x.length]; // en punkt-tabell for (int i = 0; i < p.length; i++) p[i] = new Point(x[i],y[i]); Comparator c = new XkoordinatKomparator(); Point a = p[Tabell.min(p,0,p.length,c)]; // finner minste Point b = p[Tabell.maks(p,0,p.length,c)]; // finner største System.out.println("(" + a.x + "," + a.y + ") er minst"); System.out.println("(" + b.x + "," + b.y + ") er størst"); Programkode 2.2.1 a)
Vi forutsetter her at det finnes to generisk metoder min og maks som tar en tabell, et fra/til interval og en komparator som parametere. I tillegg antas det at disse metodene ligger som statiske metoder i class Tabell.
![]() 2.2.2 Innpakkingsmetoden
2.2.2 Innpakkingsmetoden
Innpakkingsmetoden (engelsk: the gift wrapping algorithm) kalles også
Jarvis' marsj (engelsk: Jarvis' march) etter R.A.Jarvis som lanserte den
i 1973. Det er en metode som finner de punktene i en punktsamling
som utgjør hjørnene i det konvekse polygonet.
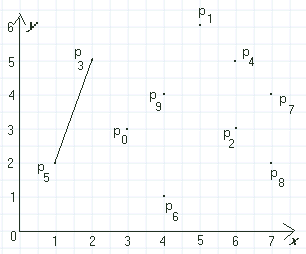 |
| Figur 2.2.2 a): Innpakkingsmetoden |
Vi tar utgangspunkt i figur 2.2.2 a). Der velger vi punktet med minst x-koordinat som ankerpunkt. Det er p5 = (1,2).
Deretter skal vi finne det største punktet med hensyn på en bestemt ordning. Gitt to punkter p og q som begge er forskjellige fra ankerpunktet a. Vi sier at p er mindre enn q mhp. a hvis p ligger på høyre side av den rette linjen som går gjennom a og q, orientert fra a til q, eller p ligger på denne linjen mellom a og q. Vi lager en komparator som gjenspeiler denne ordningen:
public class AnkerpunktKomparator implements Comparator, Serializable { private Point a; // et ankerpunkt public AnkerpunktKomparator(Point ankerpunkt) { a = ankerpunkt; } public int compare(Object o1, Object o2) { Point p = (Point)o1; // gjør om o1 til Point Point q = (Point)o2; // gjør om o2 til Point int d = (q.x - a.x)*(p.y - a.y) - (q.y - a.y)*(p.x - a.x); if (d != 0) return d; return (q.x - a.x)*(p.x - q.x) + (q.y - a.y)*(p.y - q.y); } } // AnkerpunktKomparator Programkode 2.2.2 a)
Det er a = p5 = (1,2) som er ankerpunkt. Hva er det største punktet blant resten mhp. vår nye ordning? Det er det punktet pk som er slik at når vi trekker en rett linje gjennom p5 og pk , vil alle de andre punktene ligge til høyre for linjen, eller eventuelt på linjen fra p5 og pk .
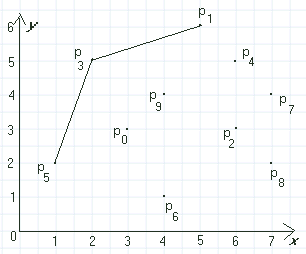 |
| Figur 2.2.2 b): Innpakkingsmetoden |
Vi finner så det største mhp. p1 , av resten av punktene. Det er p7 og ikke p4 . Den måten vi har definert «større enn» mhp. p1 gjør at p7 er «større enn» p4 .
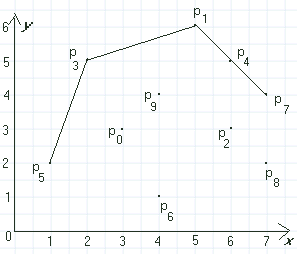
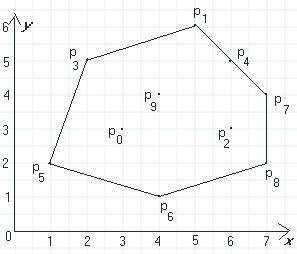
Det neste punktene vi finner på denne måten er p8 og p6 . Dermed er vi ferdige. Se figur 2.2.2 c) og figur 2.2.2 d). Dermed fant vi flg. hjørnepunkter: p5 , p3 , p1 , p7 , p8 og p6 .
|
|
|
| Figur 2.2.2 c): Avslutningen av innpakkingsmetoden | ||
Et problem som vi har underslått i diskusjonen ovenfor er hvordan algoritmen skal stoppe. Det må bli når vi kommer tilbake til ankerpunktet vi startet med. Ved ombytting legger vi startpunktet bakerst. Dermed deltar punktet under letingen etter nye "maks-punkter".
int[] x = {3,5,6,2,6,1,4,7,7,4}; int[] y = {3,6,3,5,5,2,1,4,2,4}; int n = x.length; // for å forenkle notasjonen Point[] p = new Point[n]; // en punkt-tabell for (int i = 0; i < n; i++) p[i] = new Point(x[i],y[i]); // Finner et startpunkt, f.eks. det minste punktet m.h.p // XkoordinatKomparatoren. Det blir punktet lengst ned til venstre. // Ved en ombytting legger vi punktet bakerst - i posisjon n-1. Tabell.bytt(p,n-1,Tabell.min(p,0,n,new XkoordinatKomparator())); // Finner det neste hjørnepunktet, d.v.s. det største punktet // mhp. startpunktet og legger det først - i posisjon 0. Tabell.bytt(p,0,Tabell.maks(p,0,n-1,new AnkerpunktKomparator(p[n-1]))); // Finner nye hjørner inntil vi er tilbake til startpunktet int k = 1; for ( ; k < n; k++) { int m = Tabell.maks(p,k,n,new AnkerpunktKomparator(p[k-1])); Tabell.bytt(p,k,m); if (m == n-1) break; // vi har kommet rundt } // hjørnepunktene ligger nå i p[0:k] for (int i = 0; i <= k; i++) System.out.println(p[i]); Programkode 2.2.2 b)
![]() 2.2.3 Graham's scan
2.2.3 Graham's scan
Graham's scan er oppkalt etter R.L. Graham som lanserte denne metoden i 1972.
Første skritt i algoritmen er å finne et ankerpunkt. Deretter sorteres punktene
mhp. ankerpunktet. Koden for dette er svært enkel. Under sorteringen bruker
vi her innsettingssortering, men senere, når vi har utviklet mer avanserte
sorteringsmetoder, vil vi naturligvis bruke dem isteden. Vi antar at
innsettingssortering ligger i class Tabell og har tre parametere -
en tabell, en dimensjon og en komparator.
int[] x = {3,5,6,2,6,1,4,7,7,4}; int[] y = {3,6,3,5,5,2,1,4,2,4}; int n = x.length; // for å forenkle notasjonen Point[] p = new Point[n]; // en punkt-tabell // legger inn x- og y-verdiene for (int i = 0; i < n; i++) p[i] = new Point(x[i],y[i]); Comparator c = new PunktKomparator(); // leksiografisk komparator // f.eks. minst etter leksiografisk ordning blir et ankerpunkt Point a = new Point(p[Tabell.min(p,0,n,c)]); // sorterer mhp. ankerpunktet - her kan en selvfølgelig // bruke en annen sorteringsmetode Tabell.innsettingssortering(p,new AnkerpunktKomparator(a)); // skriver ut punktene i sortert rekkefølge for (int i = 0; i < n; i++) System.out.println(p[i]); Programkode 2.2.3 a)
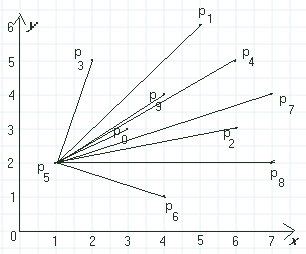 |
| Figur 2.2.3 a): Punktsortering |
Stigende sortering mhp. p5 gir rekkefølgen: (1,2) , (4,1) , (7,2) , (6,3) , (7,4) , (3,3) , (6,5) , (4,4) , (5,6) og (2,5).
Dette kan også ses på som en ordning med stigende vinkel. På Figur 2.2.3 a) er det trukket en linje fra ankerpunktet til de andre punktene. Der ser vi hvor store vinklene er. Lag et program som kjører Programkode 2.2.3 a) og sjekk at utskriften blir som påstått!
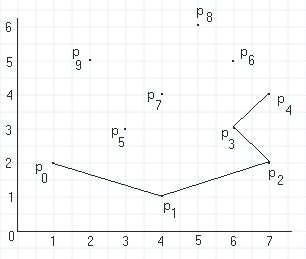 |
| Figur 2.2.3 b): Starten på Graham's scan |
Neste skritt i Graham's scan er å traversere og fortløpende tegne kanter i punktrekkefølgen. Vi trekker en kant fra p0 til p1 , så en fra p1 til p2 , osv. Så lenge som vi under denne traverseringen beveger oss mot klokken, så fortsetter vi.
Første gang det går galt er når vi går fra p3 til p4 . Da har vi "snudd oss" med klokken. Vi går da to posisjoner bakover - tilbake til p2, hopper så over p3 , og går rett til p4 . Fra p4 går vi videre til p5 . Når vi så går videre til p6 gjør vi en sving med klokken. Se figur 2.2.3 c). Dermed må vi trekke oss to posisjoner bakover - tilbake til p4 , hopper så over p5 og går rett til p6 . Vi får samme problemet på nytt når vi går fra p7 til p8. Dermed hopper vi over p7 , går rett til p8 , videre til p9 og til slutt til p0 . Vi har funnet det konvekse polygonet.
 |
| Figur 2.2.3 c): Starten på Graham's scan |
Det vil være situsjoner der det ikke er nok å trekke seg to posisjoner bakover. Det vi gjør er at for hver posisjon vi trekker oss bakover til, undersøker vi om vi får reist mot klokken ved å gå videre derfra direkte til det punktet der vi oppdaget at vi hadde gått med klokken.
Dette er ikke så vanskelig å få implementert. Vi trenger kun en enkel måte å kunne "trekke oss bakover". Det gjør vi ved fortløpende å legge de punktene vi besøker på en stakk (engelsk: stack). En stakk er en datastruktur der det vi sist la inn er det vi først får tatt ut. Datastrukturen stakk blir diskutert i kapitlet Stakker, køer og prioritetskøer.
Vi tar utgangspunkt i programkode 2.2.3 a) og fortsetter der vi sluttet:
Stack s = new Stack(); // Denne henter vi fra java.util // legger de tre første punktene på stakken s.push(p[0]); s.push(p[1]); s.push(p[2]); Point b, p1, p2; // hjelpevariabler Comparator bc; // en komparator for (int i = 3; i < n; i++) { p2 = p[i]; while (true) { p1 = (Point)s.pop(); // tar fra stakken b = (Point)s.peek(); // ser på den øverste bc = new AnkerpunktKomparator(b); if (bc.compare(p2,p1) > 0) { // ingen med klokken "knekk" - legger p1 tilbake s.push(p1); break; } } s.push(p2); // legger p2 på stakken } // Skriver ut hjørnepunktene while (!s.empty()) { p1 = (Point)s.pop(); System.out.println("(" + p1.x + "," + p1.y +")"); } Programkode 2.2.3 b)

Copyright © Ulf Uttersrud, 2009. All rights reserved.