2.1.1  Polygoner og internett
HTML-sider kan ha tegninger, grafikk o.l. med såkalte klikkbare områder (engelsk: hot spot). Det tillates tre typer klikkbare områder - rektangel, sirkel og polygon.

Figur 2.1.1 : Rektangel, sirkel og polygon er tillatt som klikkbart område

I web-leseren ligger det et program (en algoritme) som hele tiden registrerer posisjonen til markøren, og avgjør om den er innenfor eller utenfor et klikkbart område. Hvis området er et rektangel eller en sirkel, så er algoritmen svært enkel.

I html oppgis et rektangel ved hjelp av 4 heltall. Det er de to koordinatene til rektangelets øverste venstre hjørne, og de to koordinatene til det nederste høyre hjørne. La disse hete (x₁ , y₁) og (x₂ , y₂). Husk også at i Javas grafikksystem ligger origo i det øverste venstre hjørnet på skjermen, x-aksen går mot høyre og y-aksen nedover. Dette er det omvendte av hvordan vi normalt lager et xy-koordinatsystem. Da har vi også x-aksen mot høyre, men vi har normalt y-aksen oppover. Metoden som avgjør om et punkt (x₀ , y₀) ligger innenfor (eller på) rektangelet, blir slik:

  public static boolean
  innenforRektangel(int x0, int y0, int x1, int y1, int x2, int y2)
  {
    if (x0 < x1 || x0 > x2 || y0 < y1 || y0 > y2) return false;
    else return true;
  }
              Programkode 2.1.1 a)

En sirkel oppgis i HTML ved hjelp av tre heltall. Det er de to koordinatene til sirkelens senter og dens radius. Flg. metode avgjør om punktet (x₀ , y₀) ligger innenfor (eller på) sirkelen med senter i (x₁ , y₁) og med radius r:

  public static boolean
  innenSirkel(int x0, int y0, int x1, int y1, int r)
  {
    return (x0 - x1)*(x0 - x1) + (y0 - y1)*(y0 - y1) <= r*r;
  }
              Programkode 2.1.1 b)

Hvis vi har et polygon blir situasjonen langt vanskeligere. Det er ingen enkel oppgave å avgjøre om et punkt er innenfor et generelt polygon eller ikke. Det er imidlertid noe enklere hvis polygonet er konvekst. Måten vi gjør det på er å velge et punkt langt unna, d.v.s. et punkt vi helt sikkert vet ligger utenfor polygonet. Hvis vårt punkt heter (x₀ ,y₀ ) og punktet som ligger langt unna heter (u₀ ,v₀ ), så teller vi opp det antallet ganger linjesegmentet fra (x₀ ,y₀ ) til (u₀ ,v₀ ) skjærer polygonet. Hvis det skjer et odde antall ganger så er (x₀ ,y₀ ) innenfor polygonet, og ellers utenfor.

Siden polygonet består av en serie linjesegmenter eller kanter, må vi ha en måte å avgjøre om to linjesegmenter skjærer hverandre eller ikke. I tilegg må vi ta hensyn til at hvis skjæringen er gjennom et polygonhjørne, så skjæres polygonet egentlig bare en gang. Vi skal utvikle teori for dette i avsnittene som følger.

  2.1.2  Punkter og rette linjer
Et punkt p = (x,y) i et xy-plan er gitt ved to koordinater - x-koordinaten og y-koordinaten. Disse to koordinatene er normalt desimaltall, men her skal vi kun se på punkter med heltallige koordinater. Grunnen er at vi skal lage plangeometriske algoritmer til bruk på en dataskjerm, og der har alle punktene (pikslene) heltallige koordinater.

Vi vil normalt bruke p og q som navn på punkter. Hvis vi trenger flere punkter vil vi indeksere både punktene og punktenes koordinater - f.eks. p₁ = (x₁ ,y₁ ) og p₂ = (x₂ ,y₂ ).

Gitt to forskjellige punkter p₁ = (x₁ ,y₁ ) og p₂ = (x₂ ,y₂ ) i xy-planet. La tallene a, b og c være gitt ved

Likningen for den rette linjen L gjennom de to punktene er da gitt ved

  2.1.2 a)     ax + by - c = 0

La q = (x₀ ,y₀ ) være et vilkårlig punkt. Ved hjelp av likningen for L kan vi bestemme på hvilken side av L punktet q ligger. La

  2.1.2 b)     d = ax₀ + by₀ - c = (x₂ - x₁ )(y₀ - y₁ ) - (y₂ - y₁ )(x₀ - x₁ )

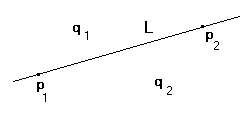Figur 2.1.2 : Linje gjennom to punkter

Vi vet at hvis d = 0 ligger q på linjen L. Vi orienterer linjen L slik at positiv retning er fra p₁ til p₂. Dermed er det veldefinert hva som er den høyre siden av L og hva som er den venstre siden. På tegningen til høyre blir dermed undersiden av L det samme som den høyre siden. Men dette er avhengig av hvordan koordinatsystemet vårt er orientert. I tegningen til høyre, og alle andre tegninger lenger nedover, er det underforstått at x-aksen er orientert mot høyre og y-aksen oppover. Det betyr at hvis d < 0 ligger q på høyre side og hvis d > 0 ligger q på venstre side.

I tegningen ligger q = q₁ til venstre for linjen L og punktet q = q₂ til høyre. Det betyr at d > 0 for q = q₁ og d < 0 for q = q₂.

Husk at hvis vi arbeider i grafikksystemet til Java så defineres origo til å være det øverste venstre hjørnet på skjermen, den positive x-aksen går mot høyre og den positive y-aksen går nedover. Dermed blir forholdet mellom fortegnet til d og høyre/venstre side av linjen snudd på hodet.

  2.1.3  Punkter og linjesegmenter

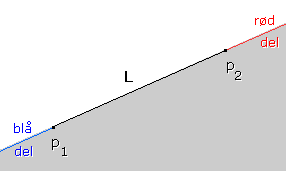Figur 2.1.3 a) : Et linjesegment

Vi bruker symbolet [ p₁ , p₂ ] for linjesegmentet fra p₁ til p₂. Linjesegmentet består av alle punktene på linjen fra og med p₁ til og med p₂.

Fortegnet til d definert i (2.1.2 b) avgjør om et punkt q ligger til venstre for den rette linjen L gjennom p₁ og p₂, til høyre for linjen eller på linjen. Hvis q ligger på L er det av interesse å avgjøre om q ligger på selve linjesegmentet [ p₁ , p₂ ] eller om q ligger utenfor linjesegmentet. Hvis q ligger utenfor linjesegmentet så er det to muligheter. Enten ligger q på p₁-siden av L (den blå delen på tegningen) eller på p₂-siden (den røde delen på tegningen).

Spørsmålet er nå om det finnes en enkel formel som avgjør om q ligger på den «blå» delen eller på den «røde» delen.

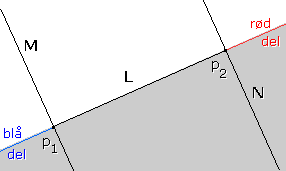Figur 2.1.3 b) : Vinkelrett på linjesegment

Vi kan lage en rett linje M gjennom p₁ vinkelrett på L og bruke likningen for denne rette linjen til å avgjøre problemet. Vi orienterer M oppover. Se tegningen til høyre. Vektoren p₁ - p₂ er en normalvektor på M. Likningen for M er da på formen ax + by = c der a = x₁ - x₂ og b = y₁ - y₂. Verdien til c kan vi bestemme siden M går gjennom p₁ og dermed blir c = ax₁ + by₁ . La q som før være punktet q = (x₀ , y₀ ) og la e være definert ved

  2.1.3 a)     e   =   ax₀ + by₀ - c   =   (x₁ - x₂ )(x₀ - x₁ ) + (y₁ - y₂ )(y₀ - y₁ )

Dermed får vi at q = (x₀ , y₀ ) ligger til venstre for M (obs M er orientert oppover) hvis e > 0, til høyre for M hvis e < 0 og på M hvis e = 0. Med andre ord ligger q på den blå delen av L hvis d = 0 (se (2.1.2 b)) og e > 0.

Kravet e > 0 kan forenkles til

  2.1.3 b)     (x₁ - x₂ )(x₀ - x₁ ) > 0   eller   (y₁ - y₂ )(y₀ - y₁ ) > 0

I utrykket for e (siste delen av (2.1.3 a)) er det en sum av to ledd. Hvis e > 0 må nødvendigvis minst ett av leddene være større enn 0. Dermed får vi at hvis e > 0 så må (2.1.3 b) være sann.

Anta omvendt at (2.1.3 b) er sann. Isolert sett må ikke dermed e > 0 være sann. Men hvis vi i tillegg har at d = 0 vil vi få at e > 0. For å se dette antar vi først at første del av (2.1.3 b) er sann - d.v.s. (x₁ - x₂ )(x₀ - x₁ ) > 0. Dermed er også (x₁ - x₂ )/(x₀ - x₁ ) > 0. Med andre ord hvis produktet av to heltall er positivt så er også kvotienten positiv. Hvis (y₁ - y₂ )(y₀ - y₁ ) = 0 er e > 0 oppfylt. Vi kan derfor anta at (y₁ - y₂ )(y₀ - y₁ ) er ulik 0 og dermed at kvotienten (y₁ - y₂ )/(y₀ - y₁ ) er ulik 0. Nå er d = 0 det samme som at (y₁ - y₂ )/(y₀ - y₁ ) = (x₁ - x₂ )/(x₀ - x₁ ). Dermed blir (y₁ - y₂ )/(y₀ - y₁ ) > 0. Altså hvis (x₁ - x₂ )(x₀ - x₁ ) > 0 så må (y₁ - y₂ )(y₀ - y₁ ) >= 0, og dermed blir e > 0. Hvis vi isteden starter med å anta at (y₁ - y₂ )(y₀ - y₁ ) > 0 så finner vi på samme måte at (x₁ - x₂ )(x₀ - x₁ ) >= 0 og dermed at e > 0.

Til slutt skal vi finne en formel for når q = (x₀ , y₀ ) ligger på den "røde" delen av L. Vi kan f.eks. finne likningen for den rette linjen N som går gjennom p₂ og står vinkelrett på L. Hvis vi orienterer N oppover finner vi fort at q ligger til høyre for N hvis

  2.1.3 c)     (x₂ - x₁ ) (x₀ - x₂ ) + (y₂ - y₁ )(y₀ - y₂ ) > 0

Setning 2.1.3:  La L være den rette linjen gjennom p₁ = (x₁ ,y₁ ) og p₂ = (x₂ ,y₂ ), orientert fra p₁ til p₂ . La q = (x₀ ,y₀ ) være et vilkårlig punkt i xy-planet. Da gjelder følgende regel for hvor q ligger i forhold til L:

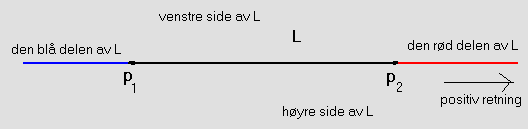Figur 2.1.3 : Rett linje med en blå, svart og rød del

1. Hvis   (x₂ - x₁ )(y₀ - y₁ )   <   (y₂ - y₁ )(x₀ - x₁ )   så ligger q på høyre side av L.
2. Hvis   (x₂ - x₁ )(y₀ - y₁ )   >   (y₂ - y₁ )(x₀ - x₁ )   så ligger q på venstre side L.
3. Hvis   (x₂ - x₁ )(y₀ - y₁ )   =   (y₂ - y₁ )(x₀ - x₁ )   og   (x₁ - x₂ )(x₀ - x₁ ) > 0   eller   (y₁ - y₂ )(y₀ - y₁ ) > 0   så ligger q på den blå delen av L.
4. Hvis   (x₂ - x₁ )(y₀ - y₁ )   =   (y₂ - y₁ )(x₀ - x₁ )   og
   (x₂ - x₁ ) (x₀ - x₂ ) + (y₂ - y₁ )(y₀ - y₂ ) > 0 så ligger q på den røde delen av L.
5. Hvis verken 1), 2), 3) eller 4) er oppfylt ligger q på linjesegmentet [ p₁ , p₂ ].

Vi lager en Java-metode som forteller oss om posisjonen til q = (x₀ ,y₀ ) i forhold til den rette linjen L gjennom p₁ = (x₁ ,y₁ ) og p₂ = (x₂ ,y₂ ). Den skal returnere -1 hvis q ligger på den høyre siden eller på den blå delen av L, returnere 1 hvis q ligger på den venstre siden eller på den rød delen og returnere 0 hvis q ligger på linjesegmentet [ p₁ , p₂ ].

  public static int posisjon(int x0, int y0, int x1, int y1, int x2, int y2)
  {
    // L er den rette linjen gjennom (x1,y1) og (x2,y2)
    // orientert fra (x1,y1) til (x2,y2)

    int d = (x2 - x1)*(y0  - y1) - (y2 - y1)*(x0  - x1);

    if (d < 0)   return -1;   // (x0,y0) på høyre side av L

    else if (d > 0)   return 1;  // (x0,y0) på venstre side av L

    else if ((x1 - x2)*(x0  - x1) > 0   // (x0,y0) på den blå delen av L
    || (y1 - y2)*(y0  - y1) > 0) return -1;

    else if ((x2 - x1 )*(x0 - x2 )      // (x0,y0) på den rød delen av L
    + (y2 - y1 )*(y0 - y2 ) > 0) return 1;

    else return 0;  // (x0,y0) på linjesegmentet
  }
              Programkode 2.1.3 a)

I hele utledningen over er det forutsatt at p₁ og p₂ er forskjellige punkter. Det er imidlertid ikke gjort slike forutsetninger i metoden posisjon. Hva skjer hvis p₁ = p₂ , d.v.s. hvis x₁ = x₂ og y₁ = y₂ ? Vi ser at returverdien blir 0 for dette tilfellet.

  2.1.4  Skjæring mellom linjesegmenter

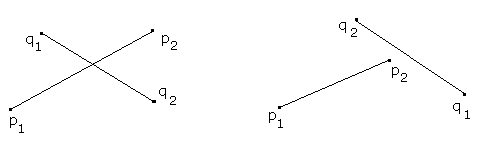Figur 2.1.4 a) : Skjæring og ikke skjæring mellom to linjesegmenter

I Figur 2.1.4 a) har vi to tilfeller med to linjesegmenter. I det første tilfellet (til venstre) har vi skjæring og i det andre er det ingen skjæring. Spørsmålet er nå om det kan settes opp en enkel formel for når to linjesegmenter skjærer hverandre?

Hvis vi tenker oss litt om finner vi at linjesegmentene [ p₁ , p₂ ] og [ q₁ , q₂ ] skjærer hverandre hvis q₁ og q₂ ligger på hver sin side av den rette linjen gjennom p₁ og p₂ samtidig med at p₁ og p₂ ligger på hver sin side av den rette linjen gjennom q₁ og q₂ .

Vi får også skjæring hvis q₁ eller q₂ ligger på linjesegmentet [ p₁ , p₂ ], og vi får skjæring hvis p₁ eller p₂ ligger på linjesegmentet [ q₁ , q₂ ]. Andre muligheter for skjæring er det ikke.

Dette kan vi sammenfatte i metoden skjæring:

  public static boolean
  skjæring(int x1, int y1, int x2, int y2,
  int u1, int v1, int u2, int v2)
  {
    // p1 = (x1,y1), p2 = (x2,y2), q1 = (u1,v1), q2 = (u2,v2)

    return
     posisjon(u1,v1,x1,y1,x2,y2) * posisjon(u2,v2,x1,y1,x2,y2) <= 0
     && posisjon(x1,y1,u1,v1,u2,v2) * posisjon(x2,y2,u1,v1,u2,v2) <= 0;
  }
              Programkode 2.1.4 a)

  2.1.5  Punkt i polygon
Gitt n punkter, d.v.s. p₀ , p₁ , p₂ . . . . p_n-1 som utgjør hjørnene i et polygon, og et punkt q som vi skal undersøke. Algoritmen for å avgjøre om q ligger inne i eller utenfor

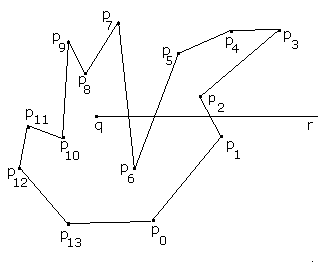Figur 2.1.5 a) : Et ikke-konvekst polygon

polygonet, gitt at polygonet ikke skjærer seg selv, blir nå:

1. Anta at y-koordinaten til q er forskjellig fra y-koordinatene til alle p-ene. Det betyr at en horisontal rett linje gjennom q ikke går gjennom noen av p-ene. La r være et punkt som har samme y-koordinat som q og som ligger så langt til høyre at det helt sikkert er utenfor polygonet. Finn det antallet ganger linjesegmentet fra q til r skjærer polygonet. Hvis antallet er odde er q inne i eller på polygonet og hvis antallet er jevnt er q utenfor polygonet.

På tegningen til høyre, der vi har 14 punkter, ser vi at linjesegmentet fra q til r skjærer polygonet 3 ganger - d.v.s. et odde antall ganger, og vi ser at det er i overenstemmelse med at q ligger inne i polygonet.

2. Hvis minst en av p-ene har samme y-koordinat som q, så er situsjonen mer kompleks. Tegningene nedenfor til høyre viser eksempler der det horisontale linjesegmentet fra q til r går gjennom en av p-ene. Poenget er at vår algoritme alltid skal returnere et odde tall når q ligger inne i eller på polygonet og et jevnt tall ellers - d.v.s. når q ligger utenfor.

Når vi skal implementere en algoritme som finner antallet skjæringer mellom polygonet og linjesegmentet fra q til r vil det være naturlig å bruke metoden ( programkode 2.1.4 ) som avgjør om to linjesegmenter skjærer hverandre eller ikke. Denne metoden anvender vi da fortløpende på linjesegmentene [ p₀ , p₁ ],

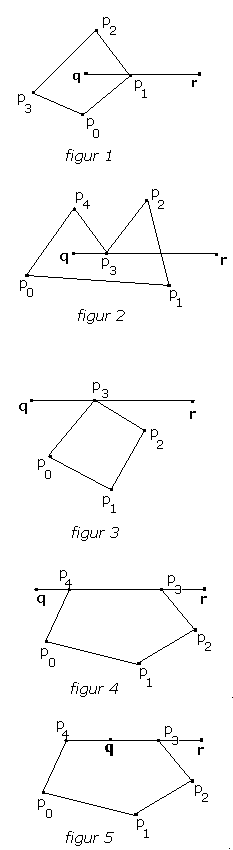Figur 2.1.5 b) : Forskjellige polygoner

[ p₁ , p₂ ], [ p₂ , p₃ ] o.s.v. til og med segmentet [ p_n-1 , p₀ ] der n er antallet hjørnepunkter i polygonet. Dette blir imidlertid problematisk når linjesegmentet [ q , r ] skjærer polygonet i et hjørnepunkt.

Figur 1 til venstre viser et eksempel der linjesegmentet [ q , r ] skjærer polygonet i et hjørnepunkt. Linjesegmentet skjærer både [ p₀ , p₁ ] og [ p₁ , p₂ ]. Vi får derfor registrert to skjæringer - noe som gir galt antall. Dette kunne vi håndtere ved å si at i et slikt tilfelle skal det bare telles opp som en skjæring. Dermed får vi i dette eksemplet at antallet skjæringer er en og det stemmer med at q ligger inne i polygonet.

I Figur 2 til høyre har vi en annen situasjon. Der skjærer (eller tangerer) [ q , r ] polygonet i hjørnet p₃ - d.v.s. segmentet skjærer [ p₂ , p₃ ] og [ p₃ , p₄ ]. Men nå kan ikke dette telles opp som kun en skjæring. Hvis vi gjør det vil antallet skjæringer mellom [ q , r ] og polygonet bli registrert som 2 siden vi også har en skjæring mellom [ q , r ] og [ p₁ , p₂ ]. Men det er et jevnt tall og dermed i strid med at q ligger inne i polygonet.

I Figur 3 har vi et tilsvarende tilfelle som i Figur 2. Linjesegmentet [ q , r ] skjærer (eller tangerer) både [ p₂ , p₃ ] og [ p₃ , p₀ ]. Registerer vi dette som bare en skjæring mellom [ q , r ] og polygonet, blir det galt siden q ligger utenfor polygonet.

Enda et problem er at [ q , r ] kan falle sammen med en av polygonets kanter. I Figur 4 har vi en slik situasjon. Vår algoritme vil her registrere at [ q , r ] skjærer både [ p₂ , p₃ ], [ p₃ , p₄ ] og [ p₄ , p₀ ]. Skal algoritmen vå fungere riktig må dette registreres som et jevnt antall skjæringer - f.eks. 0, 2 eller 4 - siden q nå ligger utenfor polygonet.

En måte vi kan takle dette på er å dele tilfellene der linjesegmentet fra q til r skjærer polygonet i ett eller flere hjørnepunkter, i to grupper. Den ene gruppen omfatter det vi kan kalle en slags tangeringer. Figur 2, Figur 3 og Figur 4 hører til i den gruppen. Den andre gruppen omfatter ekte skjæringer slik som i Figur 1. Har vi en tangering registrerer vi det som 0 skjæringer og har vi en ekte skjæring blir det registrert som 1. Men det vil være tilfeller som ikke uten videre kan plasseres i noen av gruppene. Hvis vi som i Figur 5 har q inne på kanten [ p₃ , p₄ ] blir det da skjæring eller "tangering"? I dette tilfellet ligger q på polygonet og vi må derfor registere det som 1 skjæring.

Konklusjon   Hvis vi skal få til en algoritme som virker korrekt også for alle spesialtilfellene må vi være meget nøye og omhyggelige under implementasjonen. Det som er enkelt å få til er å telle opp antallet skjæringer hvis linjesegmentet fra q til r ikke skjærer noen av polygonets hjørner. Men også de spesialtilfellene som er diskutert over må behandles på en korrekt måte, og det må sjekkes nøye om det finnes ytterligere spesialtilfeller utover de som er diskutert her.

Oppgave 1
Metoden skjæring i programkode 2.1.4 returnerer true/false avhengig av om linjesegmentene [ p₁ , p₂ ] og [ q₁ , q₂ ] skjærer hverandre eller ikke. Sjekk at metoden vil komme til å returnere korrekt svar for de 7 tilfellene i figur 1 - 7 ovenfor.

Copyright © Ulf Uttersrud, 2009. All rights reserved.