Oppgave 1

Setningen System.out.println(Arrays.toString(randPerm(10))); vil gi forskjellig utskrift hver gang den kjøres, men en vil se at det hele tiden blir en permutasjon av tallene fra 1 til 10.

Oppgave 2

Her vil svaret være avhenig av hvor rask maskin en bruker. Men n blir nok et femsifret tall?

Oppgave 3

Når det er «godtatt» k tall, vil det neste gang være en sannsynlighet på (n − k)/n at kallet nextInt(n) + 1 gir et av de som mangler. Det må derfor i gjennomsnitt gjøres n/(n − k) kall på nextInt for å få et slikt tall. I de n/(n − k) − 1 første av disse kallene vil det i gjennomsnitt bli letet halveis gjennom de «godtatte». Den siste gangen blir det letet gjennom alle. Det totale gjennomsnittet blir derfor lik:

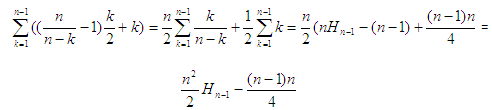Siden H_n-1 er av orden log(n), blir gjennomsnittet av orden n² log(n).

Oppgave 4

Også her vil setningen System.out.println(Arrays.toString(randPerm(10))); vil gi forskjellig utskrift hver gang den kjøres, men en vil se at det hele tiden blir en permutasjon av tallene fra 1 til 10.

Oppgave 5

Hvis en i Oppgave 2 fant en verdi på n som gav et tidsforbruk på ca. 5 sekunder, vil en her få et tidsforbruk på kansje bare 15 - 20 milliekunder. Med andre ord en enorm forbedring.

Oppgave 6

Når det er «godtatt» k tall, vil det neste gang være en sannsynlighet på (n − k)/n at kallet nextInt(n) + 1 gir et av de som mangler. Det må derfor i gjennomsnitt gjøres n/(n − k) kall på nextInt for å få et slikt tall. Gjennomsnittet blir derfor

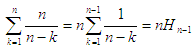Siden H_n-1 er av orden log(n), blir gjennomsnittet av orden n log(n).

Oppgave 7

  public static int[] randPerm(int n)
  {
    int[] a = new int[n];
    Random r = new Random();

    for (int i = 0; i < n; )
    {
      int k = r.nextInt(n);
      if (a[k] == 0) a[k] = ++i;
    }
    return a;

  } // randPerm

Oppgave 9

Hvis en i Oppgave 2 fant en verdi på n som gav et tidsforbruk på ca. 5 sekunder, vil en her få et tidsforbruk på kansje 0 milliekunder. Det betyr at du må øke verdien på n en god del for å få registert et tidsforbruk.

Oppgave 10

  public static int[] randPerm(int n)
  {
    Random r = new Random();
    int[] a = new int[n];
    for (int i = 0; i < n; i++) a[i] = i + 1;

    for (int i = 0; i < n; i++)
    {
      int k = r.nextInt(n - i) + i;
      bytt(a,i,k);
    }
    return a;
  } 

Oppgave 11

  public static void randPerm(int[] a, int v, int h)
  {
    if (v < 0 || h >= a.length)
      throw new IllegalArgumentException("Ulovlig intervall!");

    Random r = new Random();

    for (int k = h; k > v; k--)
    {
      int i = r.nextInt(k - v + 1);
      bytt(a,k,v + i);
    }
  }

Oppgave 12

  public static int[] randPerm(int n, int k)
  {
    if (k < 0 || k > n)
      throw new IllegalArgumentException("Ulovlig k!");

    int[] a = new int[n];   // fyller tabellen med 1, 2, . . , n
    for (int i = 0; i < n; i++) a[i] = i+1;

    Random r = new Random();

    for (int j = n-1; j >= n-k; j--)
    {
      int i = r.nextInt(j+1);
      bytt(a,i,j);
    }

    int[] b = new int[k];
    System.arraycopy(a,n-k,b,0,k);
    return b;   // tabellen med permutasjonen returneres
  }

Oppgave 13

  public static int[] randPerm(int n)
  {
    ArrayList<Integer> liste = new ArrayList<>(n);
    for (int i = 1; i <= n; i++) liste.add(i);

    Collections.shuffle(liste);

    int[] a = new int[n];
    int i = 0;
    for (int k : liste) a[i++] = k;

    return a;
  }