Oppgave 1A

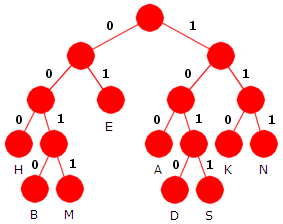Et Huffmantre blir alltid et fullt tre, dvs. alle indre noder har to barn. Hvis vi tegner et tre ved hjelp av de bitkodene som er oppgitt, vil en se at både B-noden og N-noden mangler søsken. Søskenen til B-noden vil få 4 som avstand til roten, mens søskenen til N-noden vil få 3 som avstand. Dermed må K bli søsken til N og M søsken til B:

Dekomprimeringen gir flg. resultat: EKSAMEN

Oppgave 1B

Verdiene 2, 5, 3, 1 og 4 legges fortløpende på stakken. Hver ny innlegging havner på toppen av stakken. Det betyr at stakkens innhold fra toppen og nedover til bunnen blir 4, 1, 3, 5 og 2. Ved et uttak er det alltid det på toppen som tas ut. Når verdiene fortløpende tas fra stakken og skrives ut, blir utskriften derfor 4 1 3 5 2. Med andre ord får vi verdiene i motsatt rekkefølge av hva den oprinnelig var.

Oppgave 1C

Oppgave 1D

  public static <T> T maks(Iterable<T> s, Comparator<? super T> c)
  {
    Iterator<T> i = s.iterator();
    if (!i.hasNext()) throw new NoSuchElementException("s er tom!");

    T maks = i.next();

    while (i.hasNext())
    {
      T verdi = i.next();
      if (c.compare(verdi,maks) > 0) maks = verdi;
    }
    return maks;
  }

Oppgave 2A

  public static <T> void forskyv(T[] a)
  {
    if (a.length < 2) return;

    T temp = a[a.length - 1];  // tar vare på den bakerste

    for (int i = a.length - 1; i > 0; i--) a[i] = a[i-1];

    a[0] = temp;  // legger inn forrest
  }

Oppgave 2B

Hvis k er større enn lengden til tabellen a, kan vi gjøre forenklinger. Eksempeltabellen i oppgaveteksten har lengde 10. La f.eks. k = 25. Men det blir det samme som å forskyve 5 ganger siden hver forskyvning på 10 enheter gjør at tabellen blir slik den var. Det blir tilsvarende med en negativ k. Hver forskyvning på -10, dvs. 10 enheter mot venstre, gjør at tabellen blir slik den var. Med andre ord kan vi erstatte k med k % a.length. Videre vil en forskyvning på f.eks. 3 mot venstre (k = −3), være det samme som en forskyvning på -3 + 10 = 7 mot høyre:

  public static void bytt(Object[] a, int v, int h)
  {
    Object temp = a[v]; a[v] = a[h]; a[h] = temp;
  }

  public static <T> void forskyv(T[] a, int k)
  {
    if (a.length < 2) return;

    k = k % a.length;

    if (k < 0) k += a.length;

    int v = 0, h = a.length - 1;
    while (v < h) bytt(a,v++,h--);  // snur hele tabellen

    v = 0; h = k - 1;
    while (v < h) bytt(a,v++,h--);  // snur de k første

    v = k; h = a.length - 1;
    while (v < h) bytt(a,v++,h--);  // snur resten
  }

Oppgave 3A

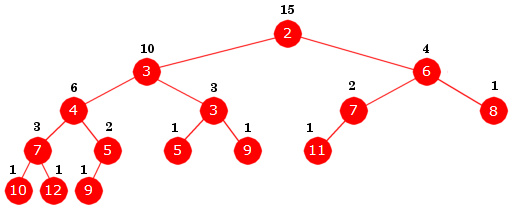Det er en gren for hver bladnode:

• 2, 3, 4, 7, 10
• 2, 3, 4, 7, 12
• 2, 3, 4, 5, 9
• 2, 3, 3, 5
• 2, 3, 3, 9
• 2, 6, 7, 11
• 2, 6, 8

Inorden: 10, 7, 12, 4, 9, 5, 3, 5, 3, 9, 2, 11, 7, 6, 8

Oppgave 3B

  public T kikk()
  {
    if (tom()) throw new NoSuchElementException("Treet er tomt!");
    return rot.verdi;
  }

  public int antall()
  {
    if (tom()) return 0;
    return rot.antall;
  }

  public boolean tom()
  {
    return rot == null;
  }

Oppgave 3C

Her må vi traversere treet og for hver node sjekke at antallet noder i venstre subtre er minst så stort som antallet i høyre subtre. Antallet i et tomt tre er 0. For å forenkle kodingen kan det være lurt å lage en hjelpemetode som finner antallet i et tre også i det tilfellet at det er tomt. Velger her en traversering i nivåorden:

  private static <T> int antall(Node<T> p)
  {
    if (p == null) return 0; else return p.antall;
  }

  public boolean erVenstretungt()
  {
    if (rot == null) return true;
    Kø<Node<T>> kø = new TabellKø<>();
    kø.leggInn(rot);

    while (!kø.tom())
    {
      Node<T> p = kø.taUt();

      if (antall(p.venstre) < antall(p.høyre))
        return false;  // ikke venstretungt

      if (p.venstre != null) kø.leggInn(p.venstre);
      if (p.høyre != null) kø.leggInn(p.høyre);
    }
    return true;
  }

Oppgave 3D

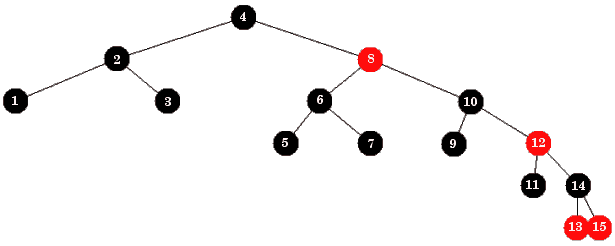
Verdien 10 skal først inn på rett sortert plass i treets høyre kant, dvs. som høyre barn til 8-noden. Men da vil ikke lenger 8-noden ha venstretyngde. Det repareres ved at nodens to subtrær bytter plass. Dermed blir 10-noden isteden venstre barn til 8-noden. De andre nodene på høyre kant (2-noden og 6-noden) vil da fortsatt ha venstretyngde:

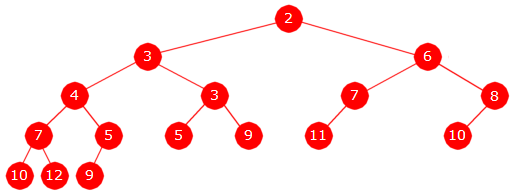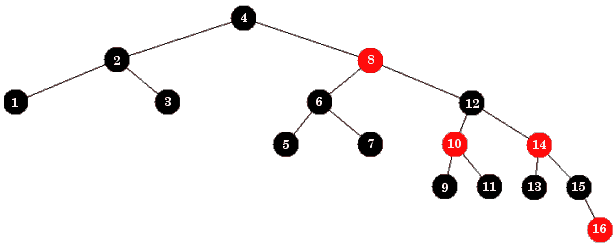
Verdien 12 settes inn på rett sortert plass i treets høyre kant når den settes inn som høyre barn til 8-noden. Da vil 8-noden fortsatt ha venstretyngde. Men det har ikke lenger 6-noden. Der må vi etterpå bytte om dens subtrær. Rotnoden blir ikke påvirket. Den vil fortsatt ha venstretyngde:

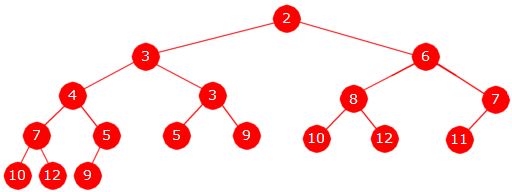Verdien 5 settes inn på rett sortert plass i treets høyre kant når den settes inn mellom 2-noden og 6-noden. Den nye noden får da 6-noden som høyre barn. Men da vil ikke den nye noden få venstretyngde. Det løses ved at nodens to subtrær bytter plass:

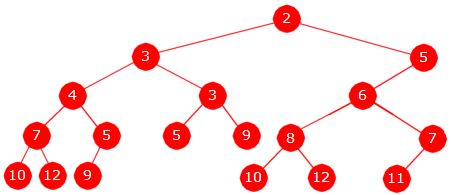Bytting av subtrær kan gjøres på vei nedover til rett plass fordi vi vet allerede da hvilke noder som ikke lenger vil ha venstretyngde. F.eks. hvis ny verdi er mindre enn eller lik verdien i rotnoden, vil den nye verdien bli ny rot og den gamle roten blir dens venstre barn. Osv.

  public void leggInn(T verdi)
  {
    if (rot == null)
      rot = new Node<>(verdi,1);
    else if (comp.compare(verdi,rot.verdi) <= 0)
      rot = new Node<>(verdi,rot.antall + 1,rot,null);
    else
    {
      Node<T> q = rot, p = rot.høyre;

      while (p != null && comp.compare(verdi, p.verdi) > 0)
      {
        q.antall++;
        if (q.venstre.antall == q.høyre.antall) byttSubtrær(q);
        q = p;
        p = p.høyre;
      }
      q.antall++;

      if (p == null)
      {
        if (q.venstre == null) q.venstre = new Node<>(verdi,1);
        else q.høyre = new Node<>(verdi,1);
      }
      else
      {
        q.høyre = new Node<>(verdi,p.antall + 1,p,null);
        if (q.venstre.antall < q.høyre.antall) byttSubtrær(q);
      }
    }
  }