Algoritmer og datastrukturer - Høgskolen i Oslo og Akershus

VIKTIG Programkode kan være selvforklarende hvis det er enkle algoritmer og en bruker standard kodeteknikk. Men hvis algoritmen eller koden som lages, er mer infløkt, er det viktig med forklaringer. Det kan hende at en har en idé som ville ha virket, men som er kodet feil eller mangelfullt. Hvis en da ikke har forklaringer, kan det være vanskelig eller umulig å forstå det som er laget. Dermed risikerer en å få færre poeng (eller 0 poeng) enn en ellers ville ha fått.

I oppgaver der det f.eks. spørres etter en utskrift, er det spesielt viktig med forklaringer. Hvis det en har satt opp som utskrift er feil, kan en riskikere å få 0 poeng hvis forklaringer mangler. Det kan jo hende at en har tenkt riktig, men kun gjort noen småfeil. Men uten forklaringer er det ikke mulig å vite om det er småfeil eller om feilen skyldes at en har bommet fullstendig.

Oppgave 1A

1. forslag Denne kan løses på mange måter. Det enkleste er å bruke en StringBuilder. Noen bruker konkatenering (+=), men for store strenger er det særdeles ineffektivt. En slik teknikk skal, så sant det er mulig, unngås. De som likevel bruker det, vil få trekk.

  public static int hash(String a, String b)
  {
    StringBuilder s = new StringBuilder();
    int m = Math.min(a.length(), b.length());  // minst lengde

    for (int i = 0; i < m; i++)
    {
      s.append(a.charAt(i));     // henter et tegn fra a
      s.append(b.charAt(i));     // og så et tegn fra b
    }

    s.append(a.substring(m));    // det som måtte være igjen i a
    s.append(b.substring(m));    // det som måtte være igjen i b

    return s.toString().hashCode();
  }

2. forslag En annen teknikk er å bruke tabeller hele veien:

  public static int hash(String a, String b)
  {
    char[] c = a.toCharArray();    // String til char-tabell
    char[] d = b.toCharArray();    // String til char-tabell

    int m = Math.min(c.length, d.length);       // minst lengde
    char[] h = new char[c.length + d.length];   // hjelpetabell

    for (int i = 0, k = 0; i < m; i++)
    {
      h[k++] = c[i];   // først en verdi fra c
      h[k++] = d[i];   // og så en verdi fra d
    }

    System.arraycopy(c, m, h, 2*m, c.length - m);  // det som måtte være igjen
    System.arraycopy(d, m, h, 2*m, d.length - m);  // det som måtte være igjen

    return String.valueOf(h).hashCode();  // valueOf er en String-metode
  }

Oppgave 1B

1. forslag I oppgaveteksten står det: «Vi sier at et ord er inneholdt i et annet ord hvis hver bokstav i det første ordet forekommer like mange ganger i det andre ordet som i det første, men ikke nødvendigvis i samme rekkefølge». En enkel, men ineffektiv løsning er da å finne for hver bokstav i a hvor mange ganger den finnes i a og så hvor mange ganger den finnes i b. Hvis en slik bokstav forekommer flere ganger i a enn i b, kan ikke a være inneholdt i b. Koden kan lages direkte etter denne oppskriften:

  public static boolean inneholdti(char[] a, char[] b)
  {
    if (a.length > b.length) return false;

    for (int i = 0; i < a.length; i++)
    {
      char tegn = a[i];  // ser på alle tegnene i a

      int aAntall = 0;   // hvor mange ganger finnes tegnet i a?
      for (int j = 0; j < a.length; j++) if (a[j] == tegn) aAntall++;

      int bAntall = 0;   // hvor mange ganger finnes tegnet i b?
      for (int j = 0; j < b.length; j++) if (b[j] == tegn) bAntall++;

      if (aAntall > bAntall) return false;
    }

    return true;
  }

Hvor effektiv er metoden over? La m og n være lengdene til tabellene a og b. For hver bokstav i a går vi gjennom hele a og hele b for å finne antallet av bokstaven. Det betyr at den er av orden m(m + n). Den første testen i koden gjør at m <= n. Dermed blir metoden av orden mn.

2. forslag En teknikk som er litt bedre enn den over, men fortsatt er ineffektiv, er å ta en og en bokstav fra tabellen a og så undersøke om den også ligger i tabellen b. Men da må vi passe på at hvis en bokstav forekommer flere ganger i a, så må den ligge minst like mange ganger i b. Det kan vi f.eks. få til ved å «blanke» bokstaven i b når den er funnet. Dermed hoppes den over neste gang vi leter etter den bokstaven. Det står ingenting i oppgaven om at tabellene ikke skal endres. Om det skjer, får en ikke noe trekk. I dette løsningsforslaget er det brukt en kopi hvis det er behov for endring i en tabell:

  public static boolean inneholdti(char[] a, char[] b)
  {
    if (a.length > b.length) return false;

    b = b.clone();  // lager en kopi

    for (int i = 0; i < a.length; i++)
    {
      char tegn = a[i];

      int j = 0;
      for (; j < b.length; j++) if (tegn == b[j]) break;

      if (j < b.length) b[j] = ' ';  // funnet og blankes
      else return false;             // ikke funnet
    }

    return true;
  }

I metoden over går vi, for hver bokstav i a, gjennom b. I gjennomsnitt vil vi nok ikke gå gjennom hele b. Men den vil nok likevel være av orden mn.

3. forslag En mulighet er å sortere tabellene først. Da kan vi bruke en fletteteknikk for å avgjøre om a er inneholdt i b. Hvis vi bruker en sorteringsalgoritme av lineæritmisk (n log(n)) orden, vil hele metoden bli av lineæritmisk orden. For å unngå endringer i de originale tabellene brukes kopier. Obs: En får ikke trekk hvis de originale tabellene endres.

  public static boolean inneholdti(char[] a, char[] b)
  {
    if (a.length > b.length) return false;

    a = a.clone();     // lager en kopi
    b = b.clone();     // lager en kopi

    Arrays.sort(a);    // kvikksortering
    Arrays.sort(b);    // kvikksortering

    int i = 0, j = 0;

    while (i < a.length && j < b.length)
    {
      if (a[i] > b[j]) j++;
      else if (a[i] == b[j])
      {
        i++; j++;
      }
      else return false;
    }

    return i == a.length;
  }

4. forslag Hvis vi teller opp (og lagrer i to tabeller) forekomstene av de forskjellige bokstavene i a og b først, vil vi få en metode av orden n der n er lengden til tabellen b. Det er oppgitt at det kun er store bokstaver i tabellene. Dermed kunne vi nøye oss med to opptellingstabeller av lengde 29 (A - Z + Æ, Ø, Å). Men hvis vi bruker en tabell med lengde 256, får vi litt enklere kode og en metode som virker også hvis a og b inneholder andre tegn.

  public static boolean inneholdti(char[] a, char[] b)
  {
    if (a.length > b.length) return false;

    int[] A = new int[256], B = new int[256];  // hjelpetabeller

    for (char c : a) A[c]++;     // teller opp tegnene i a
    for (char c : b) B[c]++;     // teller opp tegnene i b

    for (int i = 0; i < 256; i++) if (A[i] > B[i]) return false;

    return true;
  }

Oppgave 2A

I en prioritetskø vil taUt() ta ut den minste verdien, dvs. den minste med hensyn på ordningen gitt av komparatoren. I dette tilfellet ble komparatoren Komparator.naturlig() brukt. I kompendiet står den i Programkode 1.4.7 e) og den har blitt brukt systematisk i undervisningen. F.eks. var det den som inngikk i Oblig 3. Den virker bare for datatyper som er Comparable og bruker da den ordningen som gjelder for denne typen (metoden compareTo). For datatypen String som ble brukt i denne oppgaven, er det vanlig alfabetisk ordning. Dermed blir utskriften slik:

   Arne Berit Kari Ole Per

Obs: Det er generelt viktig å gi forklaringer og begrunnelser for løsninger og svar på oppgaver. Her i Oppgave 2B er det spesielt viktig. Hvis det en svarer er feil og det ikke er noen begrunnelser, kan det normalt ikke gis noen poeng. Men selvom svaret er feil kan en likevel få poeng hvis en har en forklaring. Det kan jo hende at en har tenkt riktig, men av ulike årsaker likevel fått feil svar.

Oppgave 2B

  public T kikk()
  {
    if (A.tom()) throw new NoSuchElementException("Køen er tom!");
    return A.kikk();
  }

Ordenen til metoden kikk() er avhengig av ordenen til metoden kikk() i stakken A. Den er av konstant orden både i en TabellStakk og i en LenketStakk. Generelt vil nok kikk() være av konstant orden i enhver stakkimplementasjon. Hvis ikke, er implementasjonen nærmest ubruklig. Det betyr at metoden kikk() som er laget over, er av konstant orden.

  public T taUt()
  {
    if (A.tom()) throw new NoSuchElementException("Køen er tom!");
    return A.taUt();
  }

Samme kommentar for metoden taUt() som for metoden kikk().

  public void leggInn(T verdi)
  {
    while (!A.tom() && c.compare(verdi, A.kikk()) > 0)
      B.leggInn(A.taUt());

    A.leggInn(verdi);

    while (!B.tom()) A.leggInn(B.taUt());
  }

Hvis den nye verdien er mindre enn den øverste på stakken A, vil metoden leggInn() være av konstant orden. Med andre ord er metoden av konstant orden i det beste tilfellet. Det verste tilfellet oppstår hvis den nye verdien er større enn alle verdiene på stakken A. Da må alle verdiene flyttes fra A til B og så etterpå fra B til A. Hvis det i utgangspunktet var n verdier, betyr det at metooden er av orden n i det verste tilfellet. I gjennomsnitt må vi flytte halvparten av verdiene fra A til B og så etterpå fra B til A. Det betyr at metoden også er av orden n i gjennomsnitt.

Oppgave 3A

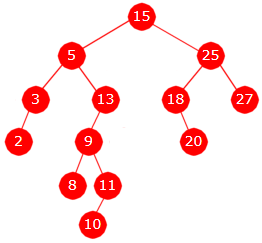Preorden: 15, 5, 3, 2, 13, 9, 8, 11, 10, 25, 18, 20, 27

Nivå 0: 1 node
Nivå 1: 2 noder
Nivå 2: 4 noder
Nivå 3: 3 noder
Nivå 4: 2 noder
Nivå 5: 1 node

Oppgave 3B

Det er flere som forsøker å løse denne oppgaven ved å starte i roten og så lete nedover i treet etter noden p. I letingen brukes da at treet er et binært søketre og dermed kan en sammenligne. Men denne teknikken kan ikke brukes her. Metoden er statisk og dermed er ikke variabelen rot tilgjengelig. F.eks. vil Netbeans gi flg. feilmelding: «non-static variable rot cannot be referenced from a static context». Eclipse sier: «Cannot make at static reference to the non-static field rot». Et annet problem er også at treet kan ha duplikater. Det betyr at ved vanlig søking finnes den første noden som har samme verdi som noden p. Men selv om det å referere til variabelen rot ikke vil virke, vil de som har løst det slik, likevel få en del utelling.

  private static <T> int nivå(Node<T> p)
  {
    int nivå = -1;

    while (p != null)
    {
      nivå++;
      p = p.forelder;
    }

    return nivå;
  }

Oppgave 3C

  private static <T> Node<T> nestePreorden(Node<T> p)
  {
    if (p.venstre != null)    return p.venstre;
    else if (p.høyre != null) return p.høyre;
    else
    {
      // Vi må oppover til den nærmeste noden som har
      // et høyre barn og som har p i sitt venstre subtre.
      // Hvis det ikke finnes en slik node, er p den siste.

      Node<T> f = p.forelder;
      while (f != null && (f.høyre == p || f.høyre == null))
      {
        p = f; f = f.forelder;
      }
      return f == null ? null : f.høyre;
    }
  }

Oppgave 3D

1. forslag Denne oppgaven kan løses på mange måter. En mulighet er å traversere treet og for hver node registere nodens nivå i en tabell. Dvs. hvis noden ligger på et bestemt nivå, øker vi antallet av noder som har det nivået. Nå vet vi ikke på forhånd hvor mange nivåer treet har, men hvis vi oppretter en nivåtabell som er like stor som antall noder, er vi på den sikre siden. En traversering i preorden kan vi gjøre ved hjelp av metoden i Oppgave 4C og en nodes nivå kan vi finne ved å bruke metoden i Oppgave 4B. Dermed får vi flg. kode:

  public int bredde()
  {
    int[] a = new int[antall];  // en hjelpetabell
    for (Node<T> p = rot; p != null; p = nestePreorden(p)) a[nivå(p)]++;
    return a[Tabell.maks(a)];   // en metode fra undervisningen
  }

En uheldig ting er at vi normalt lager tabellen a alt for stor. Det kan vi enkelt reparere ved å starte med en liten tabell og så «utvide» den hvis det er behov. Da blir koden slik:

  public int bredde()
  {
    int[] a = new int[8];       // en hjelpetabell
    for (Node<T> p = rot; p != null; p = nestePreorden(p))
    {
      int nivå  = nivå(p);      // finner nivået til p
      if (nivå == a.length) a = Arrays.copyOf(a,2*a.length);
      a[nivå]++;                // en mer på nivået
    }
    return a[Tabell.maks(a)];   // en metode fra undervisningen
  }

Anta at treet har n verdier. Da vil metoden over bli av orden n log(n). Selve traverseringen er av orden n, men for hver node vil det i gjennomsnitt være av orden log(n) å finne nivået.

2. forslag En rekursiv løsning som vil være av orden n:

Hvis vi traverserer treet rekursivt, kan vi bruke en heltallsparameter til å holde orden på hvilket nivå en node ligger på. Da kan vi bruke den til å telle opp antall noder på hvert nivå. Vi vet heller ikke her hvor mange nivåer treet har. For sikkerhets skyld kan vi opprette en nivåtabell som er like stor som antall noder:

  // rekursiv hjelpemetode
  private static <T> void bredde(Node<T> p, int nivå, int[] a)
  {
    a[nivå]++;   // en node til på dette nivået
    if (p.venstre != null) bredde(p.venstre, nivå + 1, a); // ned ett nivå
    if (p.høyre != null) bredde(p.høyre, nivå + 1, a);     // ned ett nivå
  }

  public int bredde()
  {
    if (tom()) return 0;
    int[] a = new int[antall];
    if (!tom()) bredde(rot, 0, a);
    return a[Tabell.maks(a)];
  }

Svakheten med den rekursive teknikken over, er at vi generelt bruker en altfor stor nivåtabell. Her er det ikke mulig å starte med en liten tabell og så utvide den ved behov. Det kommer av at det er verdioverføring av tabellreferansen. Men hvis vi isteden bruker en liste som jo er en slags «uendelig» tabell, så går det bra. Men i en liste kan vi ikke oppdatere verdien på en bestemt plass på samme måte som i en tabell. Vi må isteden bruke en kombinasjon av hent og oppdater:

  // rekursiv hjelpemetode
  private void bredde(Node<T> p, int nivå, Liste<Integer> liste)
  {
    if (liste.antall() == nivå) liste.leggInn(1);
    else liste.oppdater(nivå, liste.hent(nivå) + 1);

    if (p.venstre != null) bredde(p.venstre, nivå + 1, liste);
    if (p.høyre != null) bredde(p.høyre, nivå + 1, liste);
  }

  public int bredde()
  {
    Liste<Integer> liste = new TabellListe<>();
    if (!tom()) bredde(rot, 0, liste);

    int bredde = 0;
    for (int k : liste) if (k > bredde) bredde = k;

    return bredde;
  }

3. forslag som også vil være av orden n, dvs. traversering ved hjelp av en kø. Rett før den første noden på et nytt nivå tas ut fra køen, vil køen inneholde nøyaktig de nodene som ligger på dette nivået. Antallet får vi ved å bruke køens antall-metode. Da kan vi sjekke om det antallet er større enn det tidligere største antallet. Deretter tar vi ut (en etter en) nøyaktig så mange noder fra køen. Osv.

  public int bredde()
  {
    Kø<Node<T>> kø = new TabellKø<>();
    if (!tom()) kø.leggInn(rot);

    int bredde = 0;

    while (!kø.tom())
    {
      int pånivå = kø.antall();
      if (pånivå > bredde) bredde = pånivå;

      for (int i = 0; i < pånivå; i++)
      {
        Node<T> q = kø.taUt();
        if (q.venstre != null) kø.leggInn(q.venstre);
        if (q.høyre != null) kø.leggInn(q.høyre);
      }
    }

    return bredde;
  }

Oppgave 4A

Metoden public static int parter(int[] a, int v, int h, int skilleverdi) er den metoden som utgjør kjernen i kvikksortering. Den deler (parterer) tabellintervallet a[v:h] i to. Venstre del vil utgjøre alle verdiene som er mindre enn skilleverdi og høyre del resten (dvs. de som er større enn eller lik skilleverdi). Hvis skilleverdi også ligger i tabellen, er det ikke mulig å vite hvor i den høyre delen den vil havne. Metoden returnerer posisjonen til første verdi i høyre del. Det er viktig at en i svaret sitt prøver å forklare hva som foregår i denne algoritmen. Hvis en får feil utskrift, så kan en rett forklaring gjøre at en likevel kan få mange poeng.

  7  [2, 3, 6, 7, 5, 4, 1, 15, 11, 13, 10, 8, 12, 9, 14]

Oppgave 4B

Innsetting av 10:
Innsetting av 7: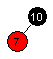
Innsetting av 4: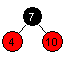
Innsetting av 13 og dermed fire verdier: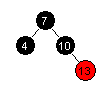
Innsetting av 12: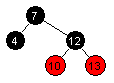
Innsetting av 6: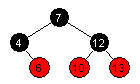
Innsetting av 8 og dermed syv verdier: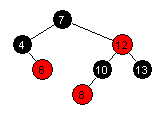
Innsetting av 9: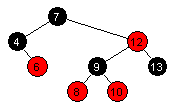
Innsetting av 11 og dermed alle verdiene: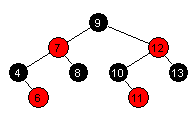