Eksamen høsten 1999 Datamaskinarkitektur
Les nøye gjennom oppgavene før du begynner og pass på å besvare alle spørsmålene. Alle hjelpemidler er tillatt. Deloppgavene vil bli vektlagt likt ved sensur, bortsett fra 3c, 3d, 4c og 4d som vil få vekt 2.

Oppgave 1

a) Skriv desimaltallet 24.600 på binær form. Ta med nok siffer etter komma til at nøyaktigheten blir omtrent den samme. Vis fremgangsmåten.

b) Skriv hei! som ASCII-kode med odde paritet.

c) Forenkle det boolske utrykket

\begin{eqnarray*} x + y\left(z + \overline{x+z}\right) \end{eqnarray*}



mest mulig ved hjelp av å bruke regneregler fra boolsk algebra.

d) Bruk Karnaugh-diagram til å forenkle følgende boolske funksjon mest mulig: 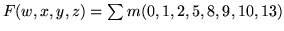$F(w,x,y,z)= \sum m(0,1,2,5,8,9,10,13)$. Skriv deretter funksjonen F enklest mulig som et produkt av summer.

e) Representer tallene A = -4 og B = 22 på 2'er komplement form med fortegn og utfør beregningen A + B. Vis at svaret stemmer.

f) Konstruer en komplett adderer (full adder) ved hjelp av to 4-til-1 linjers multipleksere og en NOT-port.

g) Konstruer en JK-vippe fra en D-vippe og logiske porter. Tegn kretsen.

Oppgave 2

a) Forklar kort forskjellen mellom en Moore og en Mealy sekvensiell krets.

Du skal nå designe en sekvensiell krets med ett input x og ett output U. Kretsen skal gi output U = 1 hvis og bare hvis antall enere den har mottatt via input x er delelig med 3. Den skal altså ha output lik 1 etter å ha mottatt 0, 3, 6, 9, ... etc. enere som input.

b) Tegn et tilstandsdiagram for kretsen. Bruk færrest mulig tilstander.

c) Kretsen skal designes med JK-vipper. Gi et binært nummer til hver tilstand og skriv ned tilstands-tabellen. Inkluder vippe-input i tabellen.

d) Bruk Karnaugh-diagram til å finne de boolske uttrykkene for vippe-inngangene og for output U. Bruk eventuelle ubrukte tilstander til å forenkle kretsen.

e) Tegn kretsen.

f) Er kretsen du har designet av Moore eller Mealy-type ? Begrunn svaret.


Oppgave 3

Fibonaccitall er en tallrekke som dukker opp i mange forskjellige sammenhenger i naturen, bl. a. i biologi. Rekken genereres ganske enkelt ved at neste ledd i rekken er summen av de to foregående. De to første tallene i rekken er satt til 1, 1 og resten kan da genereres. Tredje tall i rekken blir 1 + 1 = 2 som gir 1, 1, 2. Fjerde tall blir 1 + 2 = 3, femte tall blir 2 + 3 = 5 etc. slik at rekken blir 1, 1, 2, 3, 5, 8, 13, 21 ,34, $\cdots$.
I denne oppgaven skal du laget et digitalt system med en datapath og en kontrollenhet som genererer Fibonaccirekken. I de første deloppgavene skal en adderer og et register designes, som etterpå blir byggeklosser som skal brukes til å lage en datapath.

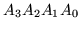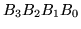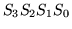a) Tegn en figur som viser hvordan man kan sette sammen fire komplette adderere (full adder) til en kombinatorisk krets som legger sammen de to positive 4-bits binære tallene $A_3A_2A_1A_0$ og $B_3B_2B_1B_0$ og leverer resultatet som tallet $S_3S_2S_1S_0$ gjennom fire output (Tegn de fire addererene som 'svarte bokser' med 3 input og 2 output, ikke ta med detaljene inni dem). Kretsen skal i tillegg ha et output V som er logisk 1 hvis det resulterer i en overflow når A og B legges sammen, og logisk 0 hvis summen ikke er for stor til å representeres med 4 bit.

b) Tegn en figur som viser hvordan man kan sette sammen fire D-vipper og NOT, AND og OR-porter til et 4-bits register med parallell load. I tillegg til 4 bit inn og ut skal registeret ha et input som må settes til logisk 1 for at registeret skal loades parallelt.

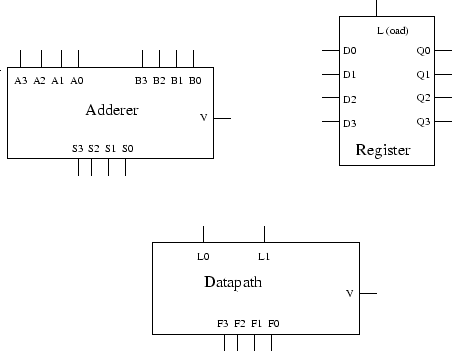
c) I design av datapath skal du betrakte og tegne enhetene i de forrige deloppgavene som 'svarte bokser' som vist i Fig. 1. Output og input til datapath skal være som i figuren. Sekvensen av Fibonaccitall skal kunne leses av fra de fire F-bitene. Sett sammen en slik adderer og to slike registere, R0 og R1, til en datapath som vil være i stand til å generere Fibonaccitall. Du kan anta at det binære tallet 1 er lagret i både R0 og R1 i utgangspunktet. Tegn inn alle koblinger mellom elementene i datapath og skriv navn på output og input.

Figure: 3c) Adderer, register og datapath
\begin{figure} \begin{center} \mbox{\psfig {figure=3c.ps,width=10cm}} \end{center}\end{figure}



d) Du skal nå designe en kontrollenhet som skal styre datapath. Den skal ha to output L0 og L1 og to input G og V. Output L0 og L1 skal styre datapath, slik at den genererer en sekvens av Fibonaccitall som kan leses fra datapaths fire F-output. Input G lik logisk 1 skal gi kontrollenheten beskjed om at prosessen med å generere Fibonaccitall skal begynne. Anta at det binære tallet 1 er lagret i begge registerne i datapath i utgangspunktet. Input V kommer fra datapath og betyr overflow; dette input skal gi beskjed om at prosessen er avsluttet og at kontrellenheten skal returnere til utgangspunktet. Tegn et ASM-diagram for en kontrollenhet som styrer datapath som skissert ovenfor.

e) Implementer ASM-diagrammet ved å bruke en D-vippe for hver tilstandsboks og oversette direkte til en tegning av en komplett og detaljert krets med vipper og porter. Husk å tegne inn outputene L0 og L1.

f) Lag en enkel tegning av det digitale systemet som viser hvordan du vil koble sammen datapath, representert ved en boks som i Fig. 1, og kontrollenhet representert ved en tilsvarende boks med input og output.

g) Hva er det største Fibonaccitallet denne kretsen kan lage ?

Oppgave 4

a) Forklar kort forskjellen mellom en prosedyre og en makro i et assemblerprogram.
b) Forklar hva som ligger i minnet etter at følgende assemblerprogram har blitt kjørt: 

DOSSEG
.MODEL SMALL
.STACK 100h
.DATA
.CODE
   mov ax,@data
   mov ds,ax
   mov bx,0
   mov cx,1
   Merke:
      mov ax,cx
      mul cl
      mul cx
      mov ds:[bx],ax
      add bx,2
      inc cx
      cmp cx,31
      jne Merke 
   mov  ah,4ch             
   int  21h      
END
c) Skriv et assemblerprogram som genererer alle Fibonacci tallene (se oppgave 3) som er mindre enn 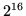$2^{16}$ og som legger dem etterhverandre i minnet som words.

d) Lag en assemblerprosedyre som finner ut hvilken av verdiene i ax, bx, cx og dx som er størst og returnerer med den største verdien i ax.

-SLUTT-

About this document ...

This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -show_section_numbers -split 0 -no_navigation exH99

The translation was initiated by Haarek Haugerud on 2000-05-29

Haarek Haugerud
2000-05-29