 Når programmet kjører, får vi opp vinduet som er vist til høyre. Etter en
liten stund blir det dessuten skrevet ut følgende feilmelding:
Når programmet kjører, får vi opp vinduet som er vist til høyre. Etter en
liten stund blir det dessuten skrevet ut følgende feilmelding:
Exception in thread "AWT-EventQueue-0" java.lang.StackOverflowError
.
.
.
Innholdsoversikt for programutvikling
Det er svært vanlig at det inni en metode blir foretatt kall på en eller flere andre metoder. Men kan en metode foreta et kall på seg selv? Ja, det er faktisk både tillatt og mulig. I en del situasjoner kan det til og med være fornuftig å gjøre det. For å se på hvilken virkning det har, skal vi først ta for oss følgende lille program, som du kan finne i fila Hei.java.
1 import javax.swing.*; 2 import java.awt.EventQueue; 3 4 public class Hei extends JFrame 5 { 6 private JTextArea utskrift; 7 8 public Hei() 9 { 10 super( "Hei!" ); 11 utskrift = new JTextArea( 20, 10 ); 12 getContentPane().add( new JScrollPane( utskrift ) ); 13 pack(); 14 setVisible( true ); 15 skrivHei(); 16 } 17 18 public void skrivHei() 19 { 20 utskrift.append( "Hei!\n" ); 21 skrivHei(); 22 } 23 24 public static void main( String[] args ) 25 { 26 EventQueue.invokeLater(new Runnable() 27 { 28 29 public void run() 30 { 31 final Hei heivindu = new Hei(); 32 heivindu.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); 33 } 34 }); 35 } 36 }
 Når programmet kjører, får vi opp vinduet som er vist til høyre. Etter en
liten stund blir det dessuten skrevet ut følgende feilmelding:
Når programmet kjører, får vi opp vinduet som er vist til høyre. Etter en
liten stund blir det dessuten skrevet ut følgende feilmelding:
Exception in thread "AWT-EventQueue-0" java.lang.StackOverflowError
.
.
.
Vi ser at metoden skrivHei() i dette programmet foretar
kall på seg selv. Det nye kallet vil bli utført hver gang metoden blir utført,
det vil si gjentatte ganger uten stans, så sant metoden i det hele tatt blir kalt opp.
Det blir den i dette programmet av vinduets konstruktør. Vi så altså at det
etter en tid likevel ikke ble utført nye kall på metoden. I programvinduet
vil vi se at det er et endelig antall Hei! som er skrevet ut.
Vi så altså dessuten at når programmet stoppet opp, fikk vi den feilmeldingen
som er gjengitt ovenfor. Det som har skjedd er at all lagerplass
som er tilgjengelig for programmet til å gjøre kall på metoder er brukt opp.
Det er nemlig slik at hver gang det foretas et metodekall, blir det lagret noe
informasjon om dette kallet. Blant annet blir hver av metodens lokale variable,
inklusive parametre, tildelt plass i memory. Det blir lagret separat
kall-informasjon for hvert kall, selv om det gjøres kall på samme metode, og
parametre og lokale variable har samme navn. Når det ikke er mer lagerplass
igjen på det område (stakken) som brukes til dette formål, kan det heller ikke
foretas nye kall. Derfor "kræsjer" programmet.
Metoder som foretar kall på seg selv, sier vi er rekursive. I eksemplet foran var rekursjonen ukontrollert: Det var ingen kontroll på om et nytt, rekursivt kall skulle foretas. Vi fikk derfor en "uendelig" rekursjon, som altså i praksis resulterte i program-kræsj.
Skal rekursive metoder fungere i praksis, må vi sørge for at det er kontrollert rekursjon:
Vi vil gjøre om programmet foran til en kontrollert rekursjon. Det
naturlige i dette tilfelle vil vel være å få skrevet ut tekstlinja
"Hei!\n" et ønsket antall ganger. Basistilfellet kan da være at
den enten skal skrives ut null ganger eller én gang. Hvilket av disse
alternativene vi velger får konsekvenser for noen detaljer i programkoden.
Programmet nedenfor bruker null ganger som basistilfelle. For å få eksemplet
enklest mulig, er antall tekstlinjer som skal skrives ut bestemt av programmet
selv, ikke av bruker. Programmet finnes i fila
Gjenta.java.
1 import javax.swing.*; 2 import java.awt.EventQueue; 3 4 public class Gjenta extends JFrame 5 { 6 private JTextArea utskrift; 7 8 public Gjenta() 9 { 10 super( "Gjenta" ); 11 utskrift = new JTextArea( 15, 10 ); 12 getContentPane().add( new JScrollPane( utskrift ) ); 13 pack(); 14 setVisible( true ); 15 skrivHei( 10 ); 16 } 17 18 public void skrivHei( int antallSomMangler ) 19 { 20 if ( antallSomMangler > 0 ) 21 { 22 utskrift.append( "Hei!\n" ); 23 skrivHei( antallSomMangler - 1 ); 24 } 25 } 26 27 public static void main( String[] args ) 28 { 29 EventQueue.invokeLater(new Runnable() 30 { 31 public void run() 32 { 33 final Gjenta heivindu = new Gjenta(); 34 heivindu.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); 35 } 36 }); 37 } 38 }
Problem: Skriv en rekursiv metode som returnerer summen
1 + 2 + 3 + ... + n
når n er gitt (som parameter).
Strategi:
Basistilfelle her: summere 1 eller 0 ledd. Velger vi 0, kan vi tolke summen som 0.
Et enklere problem: Det er enklere å summere (n - 1) ledd
enn det er å summere n ledd! Uttrykt i pseudo-kode kan vi derfor
skrive vår metode slik (når vi velger 0 ledd som basistilfelle):
public int sum( int n ) { if ( n <= 0 ) // basistilfelle return 0; else return < 1 + 2 + ... + (n - 1) > + n; }
Her ser vi at < 1 + 2 + ... + (n - 1) > ikke er noe
annet enn sum( n - 1 ), altså et rekursivt kall. Siden parameteren
minker med 1 for hvert nytt kall, vil den etter hvert nå basistilfellet
'parameter lik 0'. Rekursjonen vil da stoppe opp.
Den ferdige sum-metoden er brukt i programmet
RekursivSum.java.
nedenfor.
1 import java.awt.*; 2 import java.awt.event.*; 3 import javax.swing.*; 4 5 public class RekursivSum extends JFrame 6 { 7 8 private JTextField input, output; 9 10 public RekursivSum() 11 { 12 super("Rekursiv summering"); 13 14 Container c = getContentPane(); 15 c.setLayout(new FlowLayout()); 16 c.add(new JLabel("Beregner summen 1 + 2 + ... + n rekursivt.")); 17 c.add(new JLabel("Skriv n: ")); 18 input = new JTextField(4); 19 input.addActionListener(new Inputlytter()); 20 c.add(input); 21 c.add(new JLabel("Sum: ")); 22 output = new JTextField(10); 23 output.setEditable(false); 24 c.add(output); 25 setSize(275, 100); 26 setVisible(true); 27 } 28 29 public int sum(int n) 30 { 31 if (n <= 0) 32 return 0; 33 else 34 return sum(n - 1) + n; 35 } 36 37 public static void main(String[] args) 38 { 39 EventQueue.invokeLater(new Runnable() 40 { 41 42 public void run() 43 { 44 RekursivSum r = new RekursivSum(); 45 r.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); 46 } 47 }); 48 } 49 50 private class Inputlytter implements ActionListener 51 { 52 53 public void actionPerformed(ActionEvent e) 54 { 55 int n = Integer.parseInt(input.getText()); 56 output.setText(Integer.toString(sum(n))); 57 } 58 } 59 }
For å få forståelse for hvordan rekursive metoder virker, kan det være
instruktivt å foreta en sporing av et metodekall, for eksempel
sum(4). På en figur kan vi prøve å illustrere dette slik:
Vi ser her tydelig at kallene vil bli avsluttet i motsatt rekkefølge av
den rekkefølgen som kallene ble foretatt: Først avsluttes kallet
sum(0), som er basistilfelle, og returnerer 0. Dermed kan
sum(1) avslutte og returnere 0 + 1, det vil si 1.
sum(2) har dermed fått det dette kallet trenger og kan i sin tur
returnere 1 + 2, det vil si 3. Dette returneres til kallet
sum(3), som dermed kan avslutte ved å returnere 3 + 3,
det vil si 6. Denne returen går til kallet sum(4), som så kan
avslutte ved å returnere 6 + 4, altså 10 til sin "oppdragsgiver".
I matematikk er det ikke uvanlig å bruke rekursive definisjoner. Et
eksempel på dette har vi i definisjonen av fakultetsfunksjonen n!
for hele tall n, n >= 0:
(a) 0! = 1 (b) n! = n·(n - 1)! når n > 0, n helt tall.
Av denne definisjonen får vi for eksempel:
3! = 3·2! = 3·(2·1!) = 3·2 (1·0!) = 3·2·1·1 = 6.
Definisjonen definerer n! på en entydig måte for alle hele
tall n, n >= 0. Vi legger merke til at definisjonen er todelt:
del (b) er rekursiv, mens del (a) ikke er rekursiv:
den er et basistilfelle. Dette svarer nøyaktig til det som er tilfelle ved bruk
av rekursive metoder. Dersom den rekursive definisjonen ikke hadde hatt noe
basistilfelle, ville det ikke vært noen virkelig definisjon.
Vi skal nå definere en rekursiv metode som returnerer n!
for gitt verdi av n. Vi kan da faktisk foreta en direkte
oversettelse til Java av den rekursive definisjonen ovenfor:
long fakultet( long n ) { if ( n == 0 ) return 1; else return n * fakultet( n - 1 ); }
Vi bruker her datatype long fordi vi vet at fakultetsverdier
nokså fort blir temmelig store tall. En sporing av for eksempel kallet
fakultet(3) kan vi illustrere slik på en figur:
Metoden er lagt inn i vindusklassen
Fakultetstest
nedenfor.
1 import java.awt.*; 2 import javax.swing.*; 3 4 //Rekursiv fakultetsberegning 5 public class Fakultetstest extends JFrame 6 { 7 private JTextArea utskrift; 8 9 public Fakultetstest() 10 { 11 super( "Fakultetsberegning" ); 12 utskrift = new JTextArea( 24, 20 ); 13 utskrift.setEditable( false ); 14 Container c = getContentPane(); 15 c.add( new JScrollPane( utskrift ), BorderLayout.CENTER ); 16 setSize( 300, 450 ); 17 setVisible( true ); 18 skrivFakultetstabell(); 19 } 20 21 public void skrivFakultetstabell() 22 { 23 utskrift.setText( "Demonstrasjon av rekursiv fakultetsberegning\n" ); 24 for ( long i = 0; i <= 20; i++ ) 25 { 26 utskrift.append( i + "! = " + fakultet( i ) + "\n" ); 27 } 28 } 29 30 // Rekursiv fakultetsfunksjon 31 public long fakultet( long n ) 32 { 33 if ( n == 0 ) 34 return 1; 35 else 36 return n * fakultet( n - 1 ); 37 } 38 }
Driverklasse for programmet finnes i fila
Fakultetstester.java.
Ved kjøring gir programmet vinduet som er vist på følgende bilde.
Både sum-metoden i eksempel 2 og fakultet-metoden
i siste eksempel kan enkelt skrives uten bruk av rekursjon. For fakultetsmetoden
kan vi for eksempel skrive slik:
long fakultet( long n ) { long prod = 1; for ( int i = 2; i <= n; i++ ) prod *= i; return prod; }
Vi legger merke til at istedenfor det rekursive metodekallet har vi fått en løkke. Dette er svært typisk. Imidlertid er det ikke slik at alle rekursjoner lar seg erstatte av en enkel løkke.
Alle rekursive metoder lar seg skrive ikke-rekursivt. Noen ganger er det imidlertid svært komplisert og resulterer i programkode som det er vanskelig å forstå og få oversikt over. En rekursiv løsning vil da være både mye enklere å skrive, lettere å forstå, og den vil få fram idéen bak løsningen mye bedre. Derfor er det svært viktig å lære seg rekursiv tankegang og bli fortrolig med å skrive rekursive metoder. For å tilegne seg dette, er det sannsynligvis best å begynne med enkle eksempler, selv om vi kanskje normalt ville skrive disse ikke-rekursivt. Vi skal se på noen flere slike enkle eksempler på rekursjon.
Fibonacci-tallene, som har navn etter en italiensk matematiker som var
aktiv på begynnelsen av 1200-tallet, er definert ved at de to første tallene er 0 og 1. Alle
de etterfølgende Fibonacci-tallene er definert ved at hvert tall er lik summen
av de to nærmest foregående Fibonacci-tallene. Sekvensen av Fibonacci-tall vil
derfor se ut slik fra starten av (de to første tallene er skrevet om igjen)
og et lite stykke utover:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Ser vi nærmere på definisjonen av Fibonacci-tall, ser vi at det egentlig
er en rekursiv definisjon. Kaller vi Fibonacci-tall nummer n for
Fn, kan vi skrive definisjonen slik:
(a) Fn = n for n = 0, 1 (b) Fn = Fn-1 + Fn-2 for n > 1, n helt tall.
Dette kan vi oversette nærmest direkte til en java-metode:
long fibo( long n ) // forutsetter n >= 0 { if ( n == 0 || n == 1 ) return n; else return fibo( n - 1 ) + fibo( n - 2 ); }
Ser vi nærmere på denne koden, ser vi at når n er større
enn 1, så blir det for hvert kall på metoden gjort to rekursive kall.
Totalt antall kall blir derfor 2n-1 når
n > 1. Vi får altså eksponensiell vekst i antall kall. Vi
har for eksempel at 220 er omtrent lik en million.
Vi får altså et enormt stort antall kall, selv for forholdsvis moderate verdier
av metodeparameteren. Dessuten er det slik at fibo(n - 2)
allerede er beregnet i kallet fibo(n - 1).
For øvrig er det ganske lett å skrive en ikke-rekursiv versjon av denne metoden.
Dette er derfor
et eksempel der det ikke er så lurt å bruke rekursjon, selv om problemet i seg
selv er klart rekursivt.
Et palindrom er en tekststreng som gir samme resultat når den leses
baklengs som når den leses forlengs, det vil si som er symmetrisk.
Eksempler: radar, anna, otto.
For å teste om en gitt streng er et palindrom, kan vi derfor gå fram på den måten at vi først sammenlikner første og siste tegn i strengen. Dersom disse er like, kan vi gå videre ved å fjerne første og siste tegn fra strengen og så foreta samme test på den strengen som vi da får. Dette blir dermed en typisk rekursiv algoritme. Rekursjonen kan avsluttes når vi står igjen med en streng på bare ett eller ingen tegn.
Den bekrevne rekursive algoritmen er implementert i metoden
palindrom i programmet
Palindromtester.java
som er gjengitt nedenfor. Programmet er laget slik at det ikke skiller
mellom store og små bokstaver ved test på palindrom: Som parameter i kallet
på palindrom-metoden brukes den streng som man får når den
innleste strengen konverteres til bare store bokstaver.
1 import java.awt.*; 2 import java.awt.event.*; 3 import javax.swing.*; 4 5 public class Palindromtester extends JFrame 6 { 7 private JTextField input; 8 private JLabel output; 9 10 public Palindromtester() 11 { 12 super( "Palindromtester" ); 13 Container c = getContentPane(); 14 c.setLayout( new FlowLayout() ); 15 c.add( new JLabel( "Skriv teststreng: " ) ); 16 input = new JTextField( 30 ); 17 input.addActionListener( new Inputlytter() ); 18 c.add( input ); 19 output = new JLabel(); 20 c.add( output ); 21 setSize( 500, 100 ); 22 setVisible( true ); 23 } 24 25 public boolean palindrom( String str ) 26 { 27 if ( str.length() < 2 ) 28 return true; 29 else if ( str.charAt( 0 ) == str.charAt( str.length() - 1 ) ) 30 return palindrom( str.substring( 1, str.length() - 1 ) ); 31 else 32 return false; 33 } 34 35 public static void main( String[] args ) 36 { 37 EventQueue.invokeLater(new Runnable() 38 { 39 public void run() 40 { 41 Palindromtester t = new Palindromtester(); 42 t.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE ); 43 } 44 }); 45 } 46 47 private class Inputlytter implements ActionListener 48 { 49 public void actionPerformed( ActionEvent e ) 50 { 51 String teststr = input.getText(); 52 String resultat = teststr + " er"; 53 if ( !palindrom( teststr.toUpperCase() ) ) 54 resultat += " ikke"; 55 resultat += " palindrom."; 56 output.setText( resultat ); 57 } 58 } 59 }
Søking vil si å lete etter et element med gitt identifikasjon. Identifikasjonen kalles gjerne nøkkelverdi. Enkleste søkemetode i en liste er sekvensiell søking: elementene besøkes etter tur i den rekkefølge de står i lista. I snitt må da halve lista gjennomsøkes før det søkte element blir funnet, eller eventuelt det kan fastslås at det ikke finnes.
Sekvensiell søking er den mest ineffektive søkemetoden. Men dersom lista ikke er sortert, eller elementene ikke er plassert på en annen systematisk måte, er det ingen bedre måte å utføre søkingen på. I sorterte arrayer finnes det søkemetoder som er langt mer effektive enn sekvensiell søking, og som derfor bør foretrekkes, så sant lista ikke er ganske kort. En slik metode er binær søking, som vi nå skal se nærmere på.
For å kunne foreta binær søking, må følgende forutsetninger være oppfylte:
Søkestrategi:
Se først midt i arrayen. I tilfelle ikke funn:
Avgjør ved sammenlikning av nøkkelverdier om søkingen skal fortsette i venstre
eller høyre delarray.
Benytt samme strategi om igjen på denne delarray.
Vi ser at søkestrategien i sin natur er rekursiv, siden samme strategi benyttes om igjen og om igjen på nye (del)arrayer som vil bli mindre og mindre. Den delarrayen som det skal søkes videre i, vil bli halvert for hver gang søket skal fortsette. Søket, det vil si rekursjonen, vil opphøre når elementet blir funnet eller delarrayen det skal søkes i har skrumpet inn til en tom array.
Når vi skal programmere en metode som implementerer denne søkestrategien, er det klart at vi må tilføre metoden følgende informasjon:
Vi må derfor utstyre metoden med parametre som kan brukes til å tilføre metoden denne informasjonen. Dersom vi finner det søkte elementet, er det sannsynligvis arrayindeksen for hvor det befinner seg vi er interessert i å vite. Denne arrayindeksen passer det derfor å returnere fra metoden. Dersom elementet ikke blir funnet, må vi returnere en annen passende verdi. Det kan være -1, siden ingen arrayindeks kan være lik -1. Disse idéene er implementert i følgende rekursive metode:
//Foretar rekursiv binærsøking etter nøkkel i arrayen liste. //Returnerer indeksposisjon, eller -1 i tilfelle ikke funn. public int binsøk( int[] liste, int nøkkel, int venstre, int høyre ) { if ( venstre <= høyre ) { int mid = (venstre + høyre) / 2; //skal lete midt i lista if ( liste[ mid ] > nøkkel ) //leter videre i venstre listehalvdel return binsøk( liste, nøkkel, venstre, mid - 1 ); else if ( liste[ mid ] < nøkkel ) //leter videre i høyre listehalvdel return binsøk( liste, nøkkel, mid + 1, høyre ); else //funn! return mid; } else //tom liste, nøkkel finnes ikke return -1; }
Det kan være instruktivt å spore denne søkealgoritmen manuelt på et konkret eksempel. Det er gjort i de to søkene nedenfor med arrayen som inneholder verdiene
| 061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908 |
For enkelhets skyld inneholder
arrayen bare heltallsverdier, som vi også bruker som nøkkelverdier.
Arrayen er sortert med hensyn på disse, slik at betingelsene for å bruke
binærsøking er oppfylte. Vi søker først etter nøkkelverdien 653, som finnes
i arrayen, og så etter 400, som ikke finnes.
I oppstillingene nedenfor viser første rad arrayindeksene. Hakeparentesene
indikerer venstre og høyre arrayindeks som avgrenser den delarrayen som det søkes
i, det vil si indeksene som i metoden ovenfor er kalt venstre og høyre.
Nøkkelverdien som er uthevet representerer elementet midt i den delarray
som vi nå søker i, og som i metoden ovenfor er kalt liste[ mid ].
Hver ny rad representerer et nytt (rekursivt) kall på søkemetoden.
(Eksemplene er hentet fra boka til Donald E. Knuth: The Art of Computer
Programming, Volume 3: Sorting and Searching.)
a) Søk etter 653:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| [061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908] |
| 061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | [512 | 612 | 653 | 677 | 703 | 765 | 897 | 908] |
| 061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | [512 | 612 | 653] | 677 | 703 | 765 | 897 | 908 |
| 061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | 512 | 612 | [653] | 677 | 703 | 765 | 897 | 908 |
Vi ser at det søkte element ble funnet etter 4 "oppslag".
b) Søk etter 400:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| [061 | 087 | 154 | 170 | 275 | 426 | 503 | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908] |
| [061 | 087 | 154 | 170 | 275 | 426 | 503] | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908 |
| 061 | 087 | 154 | 170 | [275 | 426 | 503] | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908 |
| 061 | 087 | 154 | 170 | [275] | 426 | 503 | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908 |
| 061 | 087 | 154 | 170 | 275] | [426 | 503 | 509 | 512 | 612 | 653 | 677 | 703 | 765 | 897 | 908 |
Søkingen stoppet her opp fordi indeksen venstre fikk verdi 5,
mens indeksen høyre har verdi 4, slik at det ikke lenger er
tilfelle at venstre <= høyre. Metodens if-test
er derfor ikke oppfylt og rekursjonen stopper opp ved at metoden returnerer -1.
I begge de to eksemplene ovenfor stoppet søkingen opp etter 4 sammenlikninger av nøkkelverdier. (I den femte raden i siste eksempel blir det ikke foretatt noen sammenlikning av nøkkelverdier, raden indikerer bare at søkingen stoppet opp.) Antallet sammenlikninger har sammenheng med at antall elementer i arrayen er n = 16 = 24, det vil si 4 = log2 n. Dette er uttrykk for noe som gjelder generelt:
Maksimalt antall k av sammenlikninger av nøkkelverdier ved bruk av binær
søking på n elementer er lik det minste hele tall som er større enn eller lik
log2 n. For eksempel gir n = 1000 elementer et
maksimalt antall sammenlikninger k lik 10, siden 210 = 1024.
For n = 1 000 000 elementer får vi et maksimalt antall
sammenlikninger k lik 20, siden 220 = 1 048 576.
Generelt har vi at maksimalt antall sammenlikninger kmaks kan uttrykkes som
kmaks = ⌈log2 n⌉.
Den rekursive metoden for binær søking som er gitt ovenfor, er lagt inn
i programmet
BinarySearch.java
som er gjengitt nedenfor. Programmet oppretter en sortert array som inneholder alle
partall fra og med 0 til og med 1000. Hvert partall vil derfor ligge i en
indeksposisjon som er lik halvparten av tallet selv. Ingen oddetall finnes i
arrayen. I programvinduet kan brukeren skrive inn tall som det skal søkes etter.
Søkesultatet skrives ut. Programmets main-metode finnes i fila
Binsearchdriver.java.
1 import java.awt.*; 2 import java.awt.event.*; 3 import javax.swing.*; 4 5 public class BinarySearch extends JFrame 6 { 7 private JTextField input; 8 private JLabel output; 9 private int[] testliste; 10 private static final int ANTALL = 500001; //arraystørrelse 11 12 public BinarySearch() 13 { 14 super( "Binærsøking" ); 15 Container c = getContentPane(); 16 c.setLayout( new FlowLayout() ); 17 c.add( new JLabel( "Test på rekursiv binærsøking" ) ); 18 c.add( new JLabel( 19 "Søker i sortert array med alle partall fra 0 til " + 20 (ANTALL * 2 - 2) + "." ) ); 21 c.add(new JLabel("Dvs. partallet k befinner seg i posisjon k/2.")); 22 c.add( new JLabel( "Velg tall det skal søkes etter: " ) ); 23 input = new JTextField( 8 ); 24 input.addActionListener( new Inputlytter() ); 25 c.add( input ); 26 output = new JLabel(); 27 c.add( output ); 28 genererListe(); 29 setSize( 400, 200 ); 30 setVisible( true ); 31 } 32 33 private void genererListe() 34 { 35 testliste = new int[ ANTALL ]; 36 for ( int i = 0; i < testliste.length; i++ ) 37 testliste[ i ] = 2 * i; 38 } 39 40 //foretar rekursiv binærsøking etter nøkkel i liste. 41 //Returner indeksposisjon eller -1. 42 public int binsøk( int[] liste, int nøkkel, int venstre, int høyre ) 43 { 44 if ( venstre <= høyre ) 45 { 46 int mid = (venstre + høyre) / 2; //skal lete midt i lista 47 if (liste[ mid ] > nøkkel) //leter videre i venstre listehalvdel 48 return binsøk( liste, nøkkel, venstre, mid - 1 ); 49 else if (liste[mid] < nøkkel) //leter videre i høyre listehalvdel 50 return binsøk( liste, nøkkel, mid + 1, høyre ); 51 else //funn! 52 return mid; 53 } 54 else //tom liste, nøkkel finnes ikke 55 return -1; 56 } 57 58 private class Inputlytter implements ActionListener 59 { 60 public void actionPerformed( ActionEvent e ) 61 { 62 try 63 { 64 int nøkkel = Integer.parseInt( input.getText() ); 65 int pos = binsøk(testliste, nøkkel, 0, testliste.length - 1); 66 if ( pos >= 0 ) 67 output.setText( nøkkel + " finnes i posisjon " + pos ); 68 else 69 output.setText( nøkkel + " finnes ikke." ); 70 } 71 catch ( NumberFormatException ex ) 72 { 73 output.setText( "Skriv inn et heltall!" ); 74 } 75 } 76 } 77 }
Selv om binær søking i sin natur er en rekursiv algoritme, er det nokså rett fram programmering å skrive en ikke-rekursiv metode som implementerer algoritmen. (Dette er slett ikke tilfelle for alle algoritmer som i sin natur er rekursive!) I notatet Mer om arrayer kan du finne en ikke-rekursiv metode for binær søking.
Rekursjon brukt ved tegning av grafikk gjør det mulig å tegne grafikk som det ville ha vært svært vanskelig å tegne uten bruk av rekursjon. Tegning av grafikk forutsetter noe mer kjennskap til bruk og programmering av grafiske skjermkomponenter enn det vi har tatt for oss hittil. Enkelte eksempler krever også noe bruk av matematikk. Derfor blir det ikke gått nærmere inn på programkoden for konkrete eksempler på rekursiv grafikk i denne omgang. Men for å gi en indikasjon på mulighetene er det nedenfor lagt inn linker til noen appleter som demonstrerer slik rekursiv grafikk.
Den som vil se nærmere på rekursiv programmering av grafikk, kan her finne linker til programfilene til to av eksemplene ovenfor. Koden for programvinduene er imidlertid laget for et applikasjonsprogram, ikke for en applet. Tegnepanelene er de samme, enten de brukes i en applet eller i en applikasjon.
KochSnowflake
KochPanel.java
KochSnowflake.java
Kochtest.java
Diamantbokser
Diamantpanel.java
Diamantbokser.java
Diamanttest.java
Oppgaven går ut på å bruke rekursjon for å tegne komplisert grafikk. Som utgangspunkt tenker vi oss en trekant der det fra et "toppunkt" er trukket en rett linje til midtpunktet på motstående side, som på følgende figur.
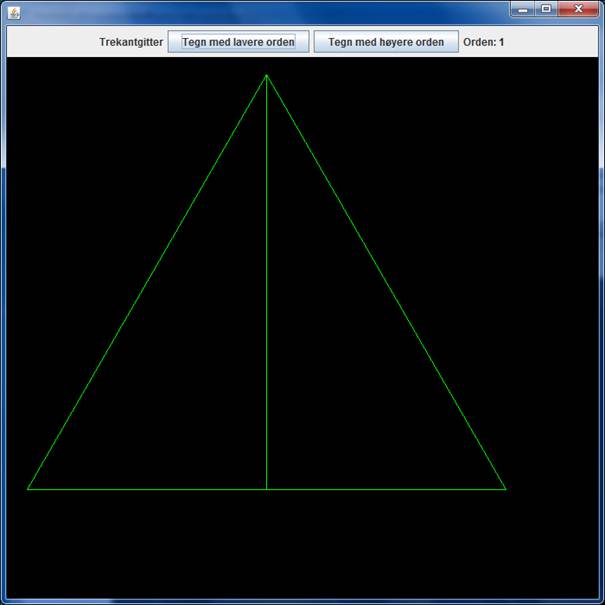
De to nye trekantene vi da får kan vi dele opp videre. Det gjør vi ved at vi nå oppfatter det nye punktet (det som var midtpunktet på motstående side) som "toppunkt" i hver av de to nye trekantene. Så trekker vi rette linjer til den motstående side i hver av disse, slik at vi får dette nye bilde:
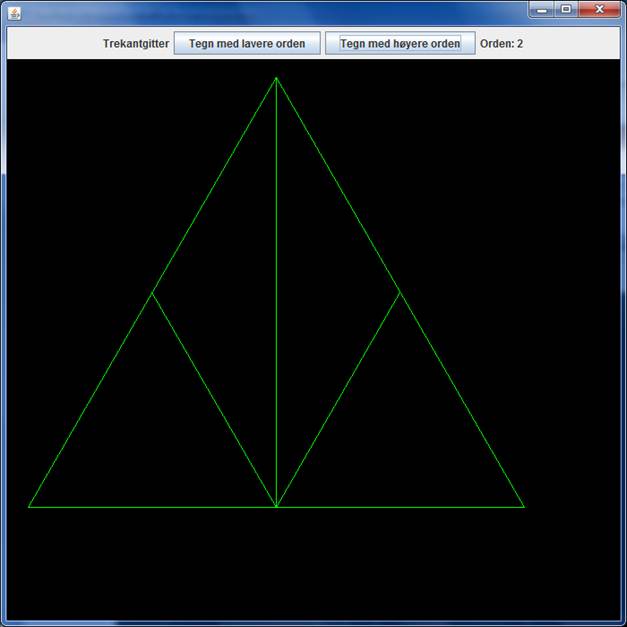
På denne måten fortsetter vi. Som figur nummer 7 vil vi da få følgende:
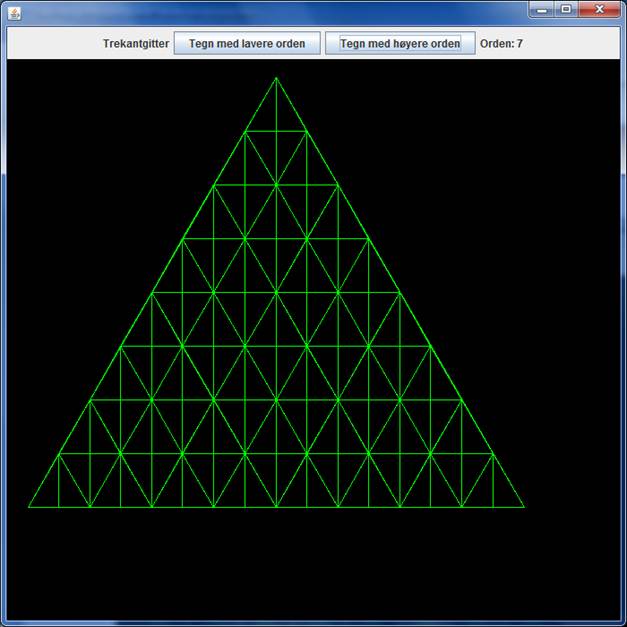
Du får som oppgave å lage et program som tegner ut slike figurer. Brukeren skal ved hjelp av knapper kunne manøvrere seg fra nivå til nivå fra utgangsfiguren (nivå 1) til nivå 14. Dersom din nettleser er satt opp til å vise appleter, kan du se hvordan programmet skal virke ved å klikke på følgende link: Trekantgitter.html. (Du skal imidlertid ikke lage appletprogram, men et vanlig applikasjonsprogram som virker på samme måte.)
Innholdsoversikt for programutvikling
Copyright © Kjetil Grønning og Eva Hadler Vihovde, revidert 2012