Kapittel 5 — Kontrollstrukturer, del 2

• for-løkker
• Tekst i eget tekstområde (JTextArea)
• Logiske operatorer
• Evaluering av logiske uttrykk
• do-while-løkker
• Feilsøking i løkker
• Løkker inni løkker
• switch-setningen
• Numeriske datatyper

for-løkker

Når vi trenger å bruke en løkke i et program, er det ofte slik at vi allerede før starten på løkka vet hvor mange ganger den skal gjennomløpes. Vi bruker da en tellevariabel som økes (eller minkes) med én for hvert løkkegjennomløp. Det er alltid mulig å bruke en while-løkke i slike situasjoner. Men den logiske strukturen kommer bedre fram ved å bruke en for-løkke, som på en måte er 'skreddersydd' for slike situasjoner og som derfor bør foretrekkes. En for-løkke har følgende form uttrykt i pseudo-kode:

  for ( < initialisering >; < test >; < oppdatering > )
    < instruksjon(er) >

Det som her er kalt initialisering, er vanligvis initialisering av en tellevariabel. Test er som regel test på om tellevariabelen har nådd sin maksimalverdi (eller minimalverdi). Oppdatering er økning (eller minking) av tellevariabelen. Dersom det er mer enn én instruksjon som skal utføres for hvert gjennomløp av løkka, må vi (selvsagt!) omslutte instruksjonene med blokkparenteser. Før vi går nærmere inn på hvordan en for-løkke virker, ser vi på et lite eksempel på en slik løkke.

Eksempel 1

Vi skal beregne summen 1 + 2 + 3 + ... + 99. Vi kan da skrive følgende kode:

  int sum = 0;  // skal inneholde summen
  for ( int i = 1; i < 100; i++ )
    sum += i;

Virkningen av en for-løkke vil være at følgende skritt utføres i den rekkefølge som er angitt:

1. Initialisering utføres først, og bare én gang. Eventuelle variable som deklareres ved initialiseringen (tellevariabelen i i eksemplet), vil bli lokale variable til for-løkka (de vil ikke eksistere utenfor den).
2. Løkke-instruksjonen(e) utføres så sant testen (i eksemplet: i < 100 ) gir true.
3. Oppdatering av tellevariabelen (i eksemplet: i++ ) utføres til slutt.
4. Så utføres testen på nytt for å sjekke om den gir true etc.
5. Programkontrollen hopper ut av for-løkka så snart testen gir false.

I eksemplet vil løkka bli gjennomløpt når tellevariabelen i har verdier lik 1, 2, 3, ..., 99. Altså i alt 99 ganger. For hvert løkkegjennomløp vil den nye verdien til i bli addert til variabelen sum. (Merk at vi foran løkka måtte passe på å gi sum en riktig startverdi!) Når i er blitt lik 100, vil testen gi false. Da vil programmet hoppe ut av løkka. Verdien 100 vil derfor ikke bli addert til summen. Resultatet blir at vi får beregnet akkurat den summen vi ønsket.

Eksempel 2

En student skal studere i 5 år og forventer å bruke 100 000 kroner første år og at forbruket øker med 10 000 kroner hvert år. Beregn totalt forbruk for de 5 år.

Følgende java-kode vil da kunne beregne det totale forbruket:

  int årsforbruk = 100000;
  int økning = 10000;
  int sum = årsforbruk;

  for ( int år = 2; år <= 5; år++ )
  {
    årsforbruk += økning;  //beregner ny verdi for årsforbruket
    sum += årsforbruk;   //adderer det nye årsforbruket til totalsummen
  }

Eksempel 3

I for-løkker er det ikke noe i veien for at tellevariabelen øker med noe annet enn 1 for hvert løkkegjennomløp. Som eksempel tenker vi oss at det i en dialogboks skal skrives ut følgende linjer:

2014
2017
2020
2023
2026
2029

Følgende instruksjoner kan da brukes:

  String utskrift = "";
  for ( int i = 14; i < 30; i += 3 )
  {
    utskrift += "20" + i;
    utskrift += "\n";  // for å få ny linje for neste årstall
  }
  JOptionPane.showMessageDialog( null, utskrift );

Oppgave 1

Lag et program som beregner og skriver ut (i en dialogboks) summen

  2 + 4 + 6 + 8 + ... + 98

Oppgave 2

Lag et program som leser inn 10 heltallsverdier fra brukeren og skriver ut (i en dialogboks) den største verdien som ble lest inn.

Oppgave 3

Utvid programmet fra oppgave 2 slik at det også skriver ut det nest største av de tallene som ble lest inn.

Oppgave 4

Lag et program som beregner og skriver ut summen av alle hele tall mellom to grenser som brukeren skriver inn. Programmet skal starte med å lese inn nedre og øvre grense for summen. Dersom innlest øvre grense er mindre enn eller lik nedre grense, skal programmet skrive ut en melding til brukeren om dette og deretter avslutte. Ellers skal programmet beregne nevnte sum - nedre grense skal tas med i summen, men ikke øvre grense - og summen skal skrives ut.

Tekst i eget tekstområde

Når vi skal vise tekst i vinduer på skjermen, er det ofte ønskelig å gruppere tekst som hører sammen, slik at den er klart atskilt fra annen tekst. Dette kan vi få til ved å plassere tekst i såkalte tekstområder. Et tekstområde er et objekt av type JTextArea, der JTextArea er navnet på en klasse i javas klassebibliotek. Når vi vil bruke et tekstområde, må vi derfor importere denne klassen fra klassebiblioteket. Det får vi gjort ved instruksjonen

import javax.swing.JTextArea;

Dessuten må vi opprette et objekt av denne typen. Det gjør vi på vanlig måte ved bruk av new-operatoren. Vi kan i dette tilfelle bruke default-konstruktøren, det vil si den som er uten parametre. For å kunne referere til tekstområdet vårt, blant annet for å putte tekst inn i det, må vi dessuten gi det et navn, det vil si tilordne JTextArea-objektet vårt som verdi til en variabel av type JTextArea. Vi kan altså skrive følgende instruksjon for å opprette og ta i bruk et tekstområde:

    JTextArea tekstområde = new JTextArea();

Plassere tekst i tekstområde

Like etter at vi har opprettet et tekstområde som forklart ovenfor, vil det være tomt, altså ikke inneholde noe tekst. Når vi skal plassere tekst i tekstområdet vårt, har vi to muligheter: enten erstatte eventuell eksisterende tekst med ny tekst, eller tilføye ny tekst til eksisterende tekst. Det første får vi til ved å skrive en instruksjon av denne type (uttrykt i pseudokode):

    tekstområde.setText( < tekststrengen vi ønsker som tekst > );
      // erstatter eventuell tekst i JTextArea-objektet tekstområde
      // med den tekst (av type String) som er parameter til
      // setText-metoden

Dersom vi vil beholde den teksten vi allerede har i tekstområdet vårt, og tilføye ny tekst til denne, kan vi skrive en instruksjon med følgende form (uttrykt i pseudokode):

    tekstområde.append( < tekststrengen vi ønsker å tilføye > );

I begge tilfeller kan den parameteren vi bruker (til setText eller append) enten være en konkret tekst avgrenset av doble sitattegn "..." på vanlig måte, eller en String-variabel som er blitt tilordnet den teksten vi ønsker å ha.

Vise tekstområde på skjermen

Som allerde nevnt, vil et tekstområde være en avgrenset del av et vindu på skjermen. I første omgang skal vi plassere et tekstområde i en dialogboks. Det får vi helt enkelt til ved at vi bruker JTextArea-objektet som parameter i showMessageDialog-metoden istedenfor den konkrete teksten eller String-variabelen som vi tidligere har brukt. Med det JTextArea-objektet vi har brukt ovenfor, kan vi altså skrive en instruksjon med følgende form (delvis uttrykt i pseudokode):

    JOptionPane.showMessageDialog( null, tekstområde,
         < tekst for tittellinje >, < kode for ikon > );

Eksempel 4

Programeksemplet nedenfor er en omarbeidet versjon av eksemplet i Fig. 5.6 i læreboka til Deitel & Deitel, 9. utgave. Programmet finnes i fila Renteberegning.java. Når programmet blir kjørt, vil det gi en utskrift som vist i følgende vindusbilde:

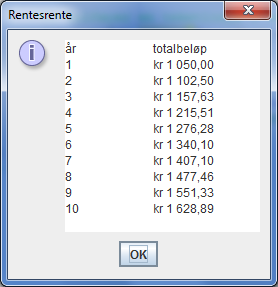
Det er her brukt et tekstområde som forklart ovenfor. For utskriften er det dessuten foretatt formatering av kronebeløpene. For å få til dette, er det gjort bruk av biblioteksklassen NumberFormat. Denne er derfor importert til programmet ved instruksjonen

import java.text.NumberFormat;

forrest i fila. Instruksjonen

NumberFormat kroneformat = NumberFormat.getCurrencyInstance();

vil opprette et formateringsobjekt for den pengeenheten som brukes i det landet der java er blitt installert, i vårt tilfelle for norske kroner. For å få den formateringen som er vist i utskriften er det da tilstrekkelig å bruke format-metoden til formateringsobjektet, slik det er gjort i programmets instruksjon

    kroneformat.format( beløp )

Legg merke til at da skrives automatisk ut benevningen kr foran beløpet og beløpet skrives ut med to desimaler med komma som desimaltegn, slik det er standard i Norge.

For beregningen av beløpene brukes instruksjonen

    beløp = grunnbeløp * Math.pow( 1.0 + rentefot, år );

Det gjøres her kall på metoden pow definert i klassebibliotekets klasse Math. Dersom variablene grunntall og eksponent er av type int eller double og på forhånd er blitt deklarert og tilordnet verdi, så vil instruksjonen

    Math.pow( grunntall, eksponent );

beregne og returnere potensen 'grunntall opphøyd i eksponent'. Klassen Math inneholder også metoder for de andre vanligste funksjonene vi kjenner fra matematikk (sinus, cosinus, eksponensialfunksjon, etc.).

 1 // Beregning av rentesrente.
 2 import java.text.NumberFormat;  // Klasse for numerisk formatering
 3 import javax.swing.JOptionPane;
 4 import javax.swing.JTextArea;
 5
 6 public class Renteberegning
 7 {
 8    public static void main( String args[] )
 9    {
10       double beløp;       // totalbeløp ved slutten av hvert år
11       double grunnbeløp = 1000.0;  // grunnbeløpet som blir forrentet
12       double rentefot = 0.05;         // rentefot pro anno
13
14       // oppretter formateringsobjekt for kronebeløp
15       NumberFormat kroneformat = NumberFormat.getCurrencyInstance();
16
17       // oppretter JTextArea for visning av utskrift
18       JTextArea tekstområde = new JTextArea();
19
20       // lager overskrift i tekstområdet
21       tekstområde.setText( "år\ttotalbeløp\n" );
22
23       // beregner totalbeløp for hvert år i 10 år
24       for ( int år = 1; år <= 10; år++ )
25       {
26          // beregner nytt beløp for gjeldende år
27          beløp = grunnbeløp * Math.pow( 1.0 + rentefot, år );
28
29          // tilføyer en tekstlinje i tekstområdet
30          tekstområde.append(
                       år + "\t" + kroneformat.format(beløp) + "\n");
31       } // end for
32
33       // viser resultater
34       JOptionPane.showMessageDialog( null, tekstområde,
35          "Rentesrente", JOptionPane.INFORMATION_MESSAGE );
36
37    } // end main
38 } // end klasse Renteberegning

Oppgave 5

Skriv et program som beregner og skriver ut andre og tredje potens av de hele tallene fra 0 til 10, sammen med tallene selv, slik at du får en tabell tilsvarende det som er vist i dialogboksen nedenfor.

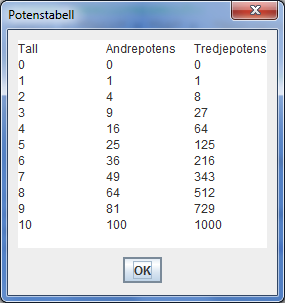
Bruk en løkke for å beregne potensene og tilføye verdiene i et tekstområde. For å få til pene kolonner, kan du på hver linje i tabellen tilføye strengen "\t" (et tabulatortegn) etter hver verdi (unntatt etter siste verdien på linja). Prøv å lage programmet slik at det er lett å endre det i tilfelle vi isteden ønsker å skrive ut tall og potenser for tall fra et annet intervall.

Oppgave 6

Lag et applikasjonsprogram som trekker 100 slumptall (hele tall) i intervallet fra 0 (inkludert) til 100 (ikke inkludert). Du får et slikt tall ved å skrive

  int tall = (int) (Math.random() * 100);

Programmet skal skrive ut i tabellform alle tall som blir trukket, med 10 tall per linje. Utskriften skal gjøres i et tekstområde som blir plassert i dialogboks. Programmet skal også finne og skrive ut det minste, det nest minste, det nest største og det største av tallene som blir trukket. På utskriften vil du kunne se om det er funnet riktige verdier for disse tallene!

Logiske operatorer

Et utsagn blir i matematikk definert som en setning eller påstand som er sann eller gal. I java-sammenheng svarer dette til et uttrykk som har verdi true eller false. Slike uttrykk kaller vi logiske uttrykk. Ved å bruke relasjonsoperatorene ( <, <= etc.) får vi laget enkle logiske uttrykk, det vil si uttrykk som ikke kan splittes opp i deler som hver for seg er logiske uttrykk.

I matematikk har vi lært å danne sammensatte utsagn ved å bruke de logiske bindeordene 'og' og 'eller', som det i matematikk brukes egne symboler for. Svarende til dette har vi i java logiske operatorer && og ||. Operatorene && og || returnerer true eller false på nøyaktig tilsvarende måte som de logiske bindeordene 'og' og 'eller' vil resultere i sanne eller gale utsagn:

Dersom p og q er logiske uttrykk, så vil uttrykket p && q få verdi true dersom både p og q har verdi true, ellers vil uttrykket få verdi false. Uttykket p || q vil få verdi true dersom minst én av p eller q har verdi true. Uttrykket vil ha verdi false bare i det tilfellet at både p og q har verdi false. Når vi leser kildekode, kan vi lese operatorene && og || som henholdsvis 'og' og 'eller'.

Negasjon

Negasjonen til et utsagn har motsatt sannhetsverdi av utsagnet selv. I java danner vi negasjon til et logisk uttrykk ved å sette operatortegnet ! foran uttrykket. Vanligvis vil det da være nødvendig å sette parentes rundt det logiske uttrykket. Når vi leser kildekode, kan vi lese operatoren ! som 'ikke'.

Eksempler

Vi forutsetter at variabelen x er blitt deklarert og har fått verdi.

Uttrykk: x == 1
Negasjon: !(x == 1) (som er ekvivalent med x != 1)
Uttrykk: x > 100
Negasjon: !(x > 100) (som er ekvivalent med x <= 100)
boolean ferdig = false;
Uttrykk: ferdig ( ferdig har verdi false)
Negasjon: !ferdig (!ferdig har verdi true)

I sammensatte logiske uttrykk kan det ofte være fornuftig å sette inn parenteser for å bedre lesbarheten og klargjøre strukturen, selv om parentesene strengt tatt ikke er nødvendige ut fra java-syntaksen.

Eksempel 5

Uttrykket

  ( m == 5 ) || ( n != 10 ) || ( p < 25 )

er lettere å lese med parenteser enn uten.

Eksempel 6: dobbeltulikhet uttrykt i java

Ofte er det krav om at en verdi skal være mellom gitte grenser, for eksempel mellom 0 og 100. I matematikk kan vi uttrykke dette som en dobbeltulikhet: 0 < x < 100.

I java må vi skrive det som et sammensatt logisk uttrykk:

  (0 < x) && (x < 100)

(parentesene er unødvendige, men øker lesbarheten).

Evaluering av logiske uttrykk

For operatorene && og || bruker java såkalt "short-circuit"-evaluering. Det betyr at dersom verdien til p && q eller p || q kan avgjøres allerede av verdien til p, så blir ikke q evaluert. Det er jo slik at dersom p har verdi false, kan umulig p && q få verdi true, selv om q har verdi true. Derfor blir verdien til q ikke sjekket. På liknende måte vil det være slik at dersom p har verdi true, så vil uttrykket p || q få verdi true uavhengig av om q er true eller false. Derfor blir verdien til q i dette tilfellet ikke sjekket. Denne virkemåten er av betydning i enkelte situasjoner.

Eksempel 7

Når x er en numerisk variabel større enn eller lik 0, så gir Math.sqrt( x ) kvadratrota til x. For negativ x er Math.sqrt( x ) ikke definert som en gyldig double-verdi. Returen fra metoden vil da være konstanten NaN, forkortelse for "Not a Number", som nettopp har som oppgave å indikere at et desimaltallsuttrykk ikke har noen gyldig verdi. På grunn av "short-circuit"-evaluering for operatoren && vil følgende if-test alltid gi en gyldig verdi, uavhengig av om x er positiv, 0 eller negativ:

  if ( x >= 0 && Math.sqrt( x ) < 100 )
    < en eller annen instruksjon >

Men merk at her kunne vi ikke byttet rekkefølge for de to ulikhetene i if-testen uten å risikere å få en ugyldig double-verdi.

For øvrig er det slik at aritmetiske operasjoner med noe som er NaN vil få som resultat noe som også er NaN. En sammenlikningsoperasjon med noe som er NaN vil alltid resultere i false.

Double-klassen har en static-metode isNaN som kan brukes til å sjekke om et double-uttrykk har verdien NaN:

  if (!Double.isNaN(< double-uttrykk >)) //uttrykket har gyldig verdi
    ...

Oppgave 7

Lag et program som leser inn hele tall fra brukeren inntil det blir lest inn et negativt tall. Programmet skal telle opp hvor mange av de innleste tallene som er mellom 10 og 50 (ingen av grensene inkludert) og skrive ut dette antallet.

Oppgave 8

Lag en utvidet versjon av programmet fra oppgave 7. I tillegg til det tidligere skal programmet nå beregne gjennomsnittsverdien for de innleste tallene mellom de nevnte grensene. Gjennomsnittet skal beregnes i form av et desimaltall. Programmet skal skrive ut det beregnede gjennomsnittet, formatert til to desimaler, samt hvor mange av de innleste tallene som var mellom de nevnte grensene. Divisjon med 0 skal unngås! Dersom ingen av de innleste tallene var mellom de nevnte grensene, skal programmet skrive ut en melding om dette istedenfor det som ellers skal skrives ut.

do-while-løkker

Dette er den tredje og siste løkketypen i java. Uttrykt i pseudo-kode har en do-while-løkke følgende form:

  do
  {
    < instruksjon(er) >
  } while ( < betingelse > ); //Merk at den avsluttes med ;

Betingelsen på slutten av løkka skal ha verdi true eller false. Den avgjør om løkka skal utføres på nytt eller ikke. Krøllparentesene er ikke nødvendig å ta med når det bare skal utføres én instruksjon, men de bør likevel tas med også i dette tilfellet for å unngå sammenblanding med while-løkke. Dessuten vil parentesene bidra til å øke lesbarheten. Nøkkelordet while bør plasseres etter parentesen } slik det er gjort ovenfor, ikke forrest på en ny linje. For da kunne vi lettere komme til å lese while som begynnelsen på en while-løkke istedenfor som slutten på en do-while-løkke.

Vi ser at det som skiller do-while-løkka fra while-løkka, er plasseringen av betingelsen. I while-løkka står den foran løkkekroppen, mens den i do-while-løkka står etter. Dette innebærer at do-while-løkka alltid vil bli utført minst én gang, mens while-løkka ikke trenger å bli utført en eneste gang. Derfor bør vi bruke do-while-løkke i tilfeller der vi ønsker at løkkekroppen skal utføres minst én gang og der vi dessuten på forhånd ikke vet hvor mange ganger den skal utføres. Et typisk eksempel på dette er innlesing av data fra brukeren. Der er det ofte slik at programmet ikke kommer videre før data er lest inn. Men de innleste data må som regel oppfylle visse betingelser, for eksempel være innenfor et bestemt intervall. Da må innlesing gjentas inntil dette er oppfylt. For øvrig må vi også i tilfelle do-while-løkke sørge for å unngå at programmet henger seg opp i en uendelig løkke.

Eksempel 8

Det skal leses inn gyldig verdi for månedsnummer, det vil si et tall fra 1 til 12. Følgende java-kode kan da brukes:

  int mnd;
  do
  {
    String input = JOptionPane.showInputDialog( "Skriv måned (1..12)" );
    mnd = Integer.parseInt( input );
    if ( mnd < 1 || mnd > 12 )
      JOptionPane.showMessageDialog( null, "Ugyldig verdi!" );
  } while ( mnd < 1 || mnd > 12 );

Oppgave 9

Lag en ny versjon av programmet du lagde til oppgave 4 ovenfor. I den nye versjonen skal innlesing av nedre og øvre grense foretas om igjen inntil det er lest inn en øvre grense som er minst like stor som nedre grense.

Feilsøking i løkker

En vanlig feil er at en løkke gjennomløpes en gang for lite eller en gang for mye i den ene enden, eller eventuelt i begge. Det betyr at det er brukt en gal grensebetingelse for løkka. Forviss deg derfor alltid om at grensebetingelsene er riktige. I tilfelle det er en løkke med styrevariabel (tellevariabel), vil det si å sjekke om styrevariabelen får riktig startverdi og sluttverdi. Skal det for eksempel brukes < eller <= i løkketesten?

En annen vanlig feil blant nybegynnere er gal bruk av semikolon. Vi så ovenfor at en do-while-løkke skal avsluttes med et semikolon, noe som kan være lett å glemme. Det er ingen tilsvarende avslutning for while-løkker og for-løkker. Men nybegynnere har lett for å plassere semikolon som ikke skal være der andre steder i slike løkker. Vi tar for oss et par eksempler på det.

Eksempel på feil i for-løkke

Vi skal skrive en løkke som beregner summene av alle (positive) partall og oddetall som er mindre enn 100. For det skriver vi følgende løkke:

  int parsum = 0, oddesum = 0;
  for (int i = 1; i < 100; i++);
  {
    if (i % 2 == 0)
      parsum += i;
    else
      oddesum += i;
  }

Legg merke til at det står et semikolon på slutten av den første linja i løkka ovenfor. Koden er derfor likeverdig med følgende:

  int parsum = 0, oddesum = 0;
  for (int i = 1; i < 100; i++) {//tom blokk!};
  {
    if (i % 2 == 0)
      parsum += i;
    else
      oddesum += i;
  }

Dette betyr faktisk at hele løkka blir avsluttet på sin første linje! En annen ting er for øvrig at denne koden ville resultere i en kompileringsfeil, for styrevariabelen i for løkka vil ikke være definert i den blokka som følger etter løkka, og som var ment å være dens innhold.

Eksempel på feil i while-løkke

Vi ønsker å finne ut hvor mange ledd vi må ta med i summen

  1 + 2 + 3 + 4 + ...

før vi får en sum som er minst lik 100. Til dette formål skriver vi følgende løkke:

  int i = 0, sum = 0;
  while (sum < 100);
  {
    i++;
    sum += i;
  }

Legg merke til at det står et semikolon på slutten av den første linja i løkka ovenfor. Koden er derfor likeverdig med følgende:

  int i = 0, sum = 0;
  while (sum < 100) {//tom blokk!};
  {
    i++;
    sum += i;
  }

Dette betyr faktisk at hele løkka blir avsluttet på sin første linje! Resultatet vil i dette tilfelle faktisk bli at vi får en såkalt uendelig løkke. Løkkebetingelsen sum < 100 nemlig aldri endre seg, den vil forbli true. Programmet vil komme til å 'henge'. Det kan være vanskelig å finne ut hvorfor, siden det ikke er noen syntaksfeil i denne koden.

Løkker inni løkker

Inni en løkkekropp kan vi ha hva som helst av instruksjoner, også en ny løkke, slik at vi får en løkke inni en løkke, eller med andre ord en indre løkke inni en ytre løkke. Da vil det bli slik at for hver verdi av styrevariabelen til den ytre løkka så vil den indre løkka bli gjennomført fullt ut så mange ganger som den skal. Det kan være et fast antall ganger, eller det kan være et antall ganger som er avhengig av hvilken verdi styrevariabelen til den ytre løkka har for øyeblikket. Vi kan selvsagt også ha løkker inni løkker på flere nivåer innover, så mange nivåer vi vil. Vi skal her begrense oss til å se på et eksempel der vi har to nivåer.

Eksempel 9

Vi tenker oss at vi skal lage et program som tegner ut et mønster tilsvarende som på følgende figur:

*
* *
* * *
* * * *
* * * * *

Vi ønsker dessuten at brukeren skal få velge hvor mange slike linjer med stjerner det skal være, men uansett antall skal det være slik at antall stjerner på hver linje øker med én for hver ny linje nedover.

Det står ikke noe i oppgaven om hvordan dette skal vises på skjermen. Vi velger å tilføye stjernene til et tekstområde som vi til slutt viser i en meldingsboks på skjermen, for det vet vi hvordan vi skal gjøre (se ovenfor). Stjernene kan vi i første omgang tilføye til en tekst som vi så legger inn på tekstområdet til slutt. Spørsmålet blir dermed hvordan vi skal gå fram for å få tilføyd stjernene til teksten. Med tanke på det vi skal fram til, kan vi lage en første skisse av programmet på denne måten:

< Les inn antall linjer. >
< Opprett tekstobjekt. >
< For hver linje: tilføy til teksten så mange stjerner det skal være på linja. >
< Vis på skjermen ferdig tekst i et tekstområde. >

I denne skissen er det noe som skal gjøres flere ganger, så mange ganger som antall linjer: Det er å tilføye til teksten stjerner for vedkommende linje. Denne operasjonen er det derfor naturlig å plassere i en løkke. Og siden vi vet hvor mange ganger dette skal utføres, er det naturlig å bruke en for-løkke. Vi kan derfor forfine vår skisse til følgende utkast:

  int n = < Les inn antall linjer >;
  String tekst = "";
  for (int i = 1; i <= n; i++)
  {
    < tilføy til teksten så mange stjerner det skal være på linja. >
  }
  < Vis på skjermen ferdig tekst i et tekstområde. >

Den vanskelige biten som gjenstår, er å oversette til javakode innholdet i løkkekroppen. Ser vi nærmere på situasjonen, så ser vi at antall stjerner som skal tilføyes for den linja som vi behandler for øyeblikket, er lik nummeret for linja, som er det samme som verdien til styrevariabelen i for løkka. Tenker vi oss at vi tilføyer én stjerne om gangen, vil det si at vi gjentatte ganger skal tilføye en stjerne, og vi skal gjøre det i ganger. Men dette kan vi få til ved å kjøre en løkke i ganger, der vi for hvert løkkegjennomløp tilføyer en stjerne til teksten vår! Dessuten må vi på et passende sted tilføye et escape-tegn \n for skifte av linje.

Ferdig program er gjengitt nedenfor. Legg spesielt merke til den indre for-løkka. I den må vi bruke et annet navn på styrevariabelen enn vi gjør i den ytre løkka. Legg dessuten merke til at vi bruker styrevariabelen til den ytre løkka til å bestemme hvor mange ganger den indre løkka skal gå. I tillegg til å legge til teksten en stjerne hvor hvert gjennomløp av den indre løkka, er det lagt til tre blanke tegn. Dette er for å få passe mellomrom mellom stjernene. Grunnen til at det ikke er brukt bare ett blankt tegn, er at det på utskriften til tekstområdet vil bli brukt en font der bredden til et blankt tegn er mindre enn bredden til et stjernetegn. (Det er mulig å velge en font der alle tegn har samme bredde, men det lærer vi først seinere.) Linjenummereringen på programmet nedenfor start på 5. På de fire første linjene lå det bare kommentarer. Du kan laste ned programmet fra følgende link: Stjernefigur.java.

 5 import javax.swing.*;
 6
 7 public class Stjernefigur
 8 {
 9   public static void main(String[] args)
10   {
11     String antall = JOptionPane.showInputDialog(
12             "Velg antall linjer med stjerner");
13     int n = Integer.parseInt(antall);
14     String tekst = "";
15     for (int i = 1; i <= n; i++)
16     {
17       for (int j = 1; j <= i; j++)
18       {
19         tekst += "*   ";
20       }
21       tekst += "\n"; //går over til neste linje
22     }
23     JTextArea tekstområde = new JTextArea();
24     tekstområde.setText(tekst);
25     JOptionPane.showMessageDialog(null, tekstområde);
26   }
27 }

Bildet under viser kjøring av programmet der det fra brukeren er lest inn verdien 15 for antall linjer.

Oppgave 5b

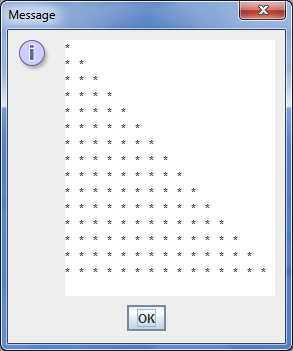
Dette er en nokså utfordrende oppgave!

Det skal lages et program som er en utvidelse og generalisering av programmet beskrevet i oppgave 5. Du skal gjøre følgende:
Definer en klasse Potenstabell med innhold som beskrevet i pseudo-kode nedenfor.

public class Potenstabell
{
  // Beregner og returnerer potensen med grunntall x og eksponenent y
  public int power(int x, int y)
  {
    < beregner og returnerer potens >
  }

  // Beregner potenser for tall og skriver ut potensene på tabellform
  // i et tekstområde. Parametrene har følgende betydning:
  // startverdi: første tall det beregnes potenser for.
  // makseksponenent: høyeste eksponent i potensene som beregnes.
  // antall: antall forskjellige tall det beregnes potenser for.
  // For hvert tall fra og med startverdi og oppover beregnes førstepotens,
  // andrepotens, ..., til og med potens med eksponent lik makseksponent.
  public void potenser(int startverdi, int makseksponent, int antall)
  {
    < beregner og skriver ut potenser >
  }
}

Definer en "driverklasse" til klassen Potenstabell beskrevet ovenfor, det vil si en klasse som inneholder en main-metode. Denne må opprette et Potenstabell-objekt og foreta et passsende metodekall for å få ut den potenstabell du ønsker. Det er altså meningen at både minste grunntall (1 i kjøringen nedenfor), eksponent for høyeste potens (5 i kjøringen nedenfor), og antall forskjellige grunntall (15 i kjøringen nedenfor) skal leses inn fra brukeren. Dersom du for eksempel ønsker å få skrevet ut første til femtepotens for tallene fra 1 til 15, skal du få ut en tabell tilsvarende som vist på følgende bilde:

Hint: Bruk en ytre løkke som går én gang for hvert grunntall det skal beregnes potenser for. For hvert av disse grunntallene, bruk en indre løkke som genererer potenser for vedkommende grunntall. Den øverste linja med overskrifter for kolonnene kan genereres ved hjelp av en egen løkke. Bruk escape-tegn \t (tabulatortegn) for å få pene kolonner.

switch-setningen

switch-setningen er noen ganger et alternativ til if-else-setninger, særlig når det er mange alternativer å teste på, slik at det ville blitt mange if-else etter hverandre. Uttrykt i pseudo-kode har en switch-setning følgende form:

  switch ( < testuttrykk > )
  {
    case verdi1:  < instruksjon(er) >
                  break;  // hopper ut av switch-blokka
    case verdi2:  < instruksjon(er) >
                  break;
    .
    .
    .                     // så mange case ... vi vil ha eller trenger
    default:      < instruksjon(er) > // default-del er frivillig
                  break;  // egentlig unødvendig med break her
  }

Testuttrykket som skal være i parentesen bak nøkkelordet switch kan ha datatype lik en av de primitive typene byte, short, char eller int. (Primitive datatyper er omtalt i kapittel 3.) Det kan også være av en opplistingstype eller av type String. (At det kan være av type String er nytt fra og med javaversjon 7.) Datatype char blir omtalt i kapittel 7, mens opplistingstyper blir omtalt i kapittel 6. String-typen er gitt en nærmere omtale i kapittel 7. Ved utførelse av en switch-setning vil programkontrollen hoppe til det første case-stedet som samsvarer med testuttrykkets verdi. (Verdiene som står bak case-ene må altså være verdier av samme datatype som testuttrykket.) På dette stedet vil utførelsen av instruksjoner begynne. Men merk at dersom vi ikke tar med break, så vil utførelsen av instruksjoner fortsette herfra og helt til slutten av switch-setningen. Nøkkelordet break har som virkning at programkontrollen hopper ut av switch-setningen og fortsetter med første instruksjon etter den. default-alternativet, som det er frivillig å ta med, vil bli utført dersom ingen av de andre alternativene slår til, men ikke ellers. break etter default er det unødvendig å ta med, siden vi likevel er kommet til slutten av switch-setningen. Men siden det er en vanlig feil å glemme break ellers, kan det være greit å ha som vane å ta den med også her.

Det som skal utføres etter en case-verdi, kan være den tomme instruksjonen, eller det kan være flere instruksjoner. Blokk-parenteser { } er i så fall ikke nødvendig.

Eksempel 9

Variabelen antDager skal tilordnes riktig antall dager for en måned, avhengig av månedsnummeret. (Vi tar ikke hensyn til skuddår.)

  int antDager, mnd;
  < mnd får tilordnet verdi fra 1 til 12, f.eks. ved innlesing >

  switch ( mnd )
  {
    case 4:
    case 6:
    case 9:
    case 11: antDager = 30;
             break;
    case 2:  antDager = 28;
             break;
    default: antDager = 31;
             break;
  }

Obs: I switch-setninger kan vi ikke teste på ulikheter, slik vi kan i if-else-setninger. Det er derfor ikke alle if-else-setninger som kan gjøres om til switch-setninger. Vi kunne for eksempel ikke ha skrevet portoberegningseksemplet ved hjelp av switch-setninger.

String-type som testuttrykk

Når en switch-setning blir utført, blir testuttrykket sammenliknet med case-alternativene. Ved sammenlikning av String-verdier er det viktig å være klar over at java skiller mellom små og store bokstaver. For eksempel vil "Mandag" og "mandag" ikke bli regnet for å være lik hverandre. Dersom vi ønsker at små og store bokstaver skal være likeverdige ved sammenlikning, kan vi før sammenlikningen konvertere eventuelle store bokstaver til små bokstaver, slik at vi vet at verdiene vi sammenlikner inneholder bare små bokstaver. Konvertering til små bokstaver kan vi få gjort ved å bruke String-metoden toLowerCase, som i følgende eksempel.

Eksempel: konvertering til små bokstaver

  String dag = "Mandag";
  dag = dag.toLowerCase(); // Nå er dag lik "mandag"

Metoden toLowerCase returner et nytt String-objekt som inneholder de samme bokstavene som det objektet dag som her brukes til å kalle opp metoden. Men i det returnerte objektet er alle bokstavene små. I eksemplet blir det returnerte objektet tilordnet som ny verdi til variabelen dag.

Istedenfor å konvertere til bare små bokstaver før sammenlikningen, kunne vi selvsagt like godt konvertert til bare store bokstaver før vi sammenliknet. Konvertering til store boskstaver får vi gjort ved bruk av String-metoden toUpperCase.

Eksempel 10

Vi skal skrive en kodebit som kan brukes til å avgjøre hvilken del av uka en dag tilhører.

  String dag = < f.eks. innlesing av navn >
  dag = dag.toLowerCase();
  String ukedel;
  switch (dag)
  {
    case "mandag":
        ukedel = "ukestart";
        break;
    case "tirsdag":
    case "onsdag":
    case "torsdag":
        ukedel = "midtuke";
        break;
    case "fredag":
        ukedel = "ukeslutt";
        break;
    case "lørdag":
    case "søndag":
        ukedel = "weekend";
        break;
    default:
        ukedel = "ukjent dag";
        break;  // unødvendig
  }

Merknad

Som nevnt tidligere, er switch-setningen i noen tilfeller et alternativ til if-else-konstruksjoner med mange greiner. Det er midlertid slik at java-kompilatoren generelt genererer mer effektiv bytekode fra switch-setninger som bruker String-objekter enn fra tilsvarende if-else-konstruksjoner med mange greiner.

Oppgave 10

Lag et program som gjentatte ganger leser inn nummeret til en ukedag, der 1 svarer til mandag, 2 til tirsdag, og så videre, inntil 7 for søndag. For hvert innlest nummer skal programmet skrive ut navnet på vedkommende ukedag, altså "mandag" i tilfelle det blir lest inn 1, "tirsdag" når det blir lest inn 2, og så videre. Dersom det blir lest inn et tall større enn 7, skal teksten "ukjent ukedag" skrives ut. Dersom det blir lest inn 0 eller en negativ verdi, skal programmet avslutte. Bruk en switch-setning til å avgjøre hva som skal skrives ut.

Oppgave 11

Lag et program som kan fortelle brukeren hvor mange dager det er i en måned. Brukeren skal skrive inn navnet på måneden. Du trenger ikke ta hensyn til skuddår.

Oppgave 12

Lag et program som kan fortelle brukeren om et år er skuddår eller ikke. Brukeren skal skrive inn årstallet. Et år er skuddår dersom årstallet er delelig med 4, men ikke delelig med 100, eller dersom årstallet er delelig med 400. For eksempel er 1992 og 2000 skuddår, men 1900 er ikke skuddår.

Numeriske datatyper

Vi har hittil brukt de numeriske datatypene int og double, som er standardtypene for henholdsvis hele tall og desimaltall. Begge typene er innebygget i javaspråket og kalles grunnleggende eller primitive datatyper. Ordet primitiv har i dette tilfelle sin opprinnelige betydning, som det har fått fra latin, nemlig noe som kommer først, eller med andre ord er grunnleggende.

Javaspråket har imidlertid flere andre numeriske datatyper innebygget i språket. Vi skal ta for oss en oversikt over dem og hvilke muligheter vi har for å tilordne dem verdier. Her er oversikten over typene:

• byte: Dette er en heltallstype på 8 biter med fortegn av type 2-komplement. Den kan ha verdier fra -2⁷ (-128) til 2⁷ - 1 (127), begge grenser inkludert.
• short: Typen er en heltallstype på 16 biter med fortegn av type 2-komplement. Den kan ha verdier fra -2¹⁵ (-32 768) til 2¹⁵ - 1 (32 767), begge grenser inkludert.
• int: Standardtypen for hele tall. Den er på 32 biter med fortegn av type 2-komplement og kan ha verdier fra -2³¹ (-2 147 483 648) til 2³¹ - 1 (2 147 483 647), begge grenser inkludert.
• long: Dette er en heltallstype på 64 biter med fortegn av type 2-komplement. Den kan ha verdier fra -2⁶³ (-9 223 372 036 854 775 808) til 2⁶³ - 1 (9 223 372 036 854 775 807), begge grenser inkludert.
• float: Desimaltallstype på 32 biter definert etter standarden IEEE 754. Den kan ha negative verdier i området -3.4028235E+38 til -1.4E-45 og positive verdier i området 1.4E-45 til 3.4028235E+38 (verdier uttrykt på eksponensiell form).
• double: Standardtypen for desimaltall. Den er på 64 biter definert etter standarden IEEE 754. Den kan ha negative verdier i området -1.7976931348623157E+308 til -4.9E-324 og positive verdier i området 4.9E-324 til 1.7976931348623157E+308.

Hvilken type man skal velge, avhenger av behovene, det vil si hvor store eller små verdier man har behov for å lagre, og når det gjelder desimaltall, hvor stort presisjonsnivå man har behov for. I dette programmeringskurset bruker vi standardtypene int og double, så sant det ikke er eksplisitt behov for å bruke noe annet. Vær klar over at double-typen bruker dobbelt så stor plass som float-typen og omtales også som dobbelt-presisjon, mens float kalles singel-presisjon. Vær for øvrig klar over at det bare er heltallstypene som gir eksakte beregninger uten avrundingsfeil, så lenge man holder seg innenfor de grensene som typene kan håndtere. For desimaltallstypene skjer det alltid en avrunding på grunn av konvertering mellom desimal og binær representasjon. (For hele tall skjer konverteringen eksakt.) Vær for øvrig klar over at dersom du for eksempel adderer 1 til den største int-verdien du kan bruke, så vi resultatet bli den største negative verdien! Tilsvarende gjelder for de andre typene.

Initialisering

Datafelt som blir deklarert på klassenivå, blir alltid automatisk initialisert til en standardverdi, dersom vi ikke selv gir dem en startverdi. For numeriske datatyper er det tallverdi null som er den automatiske startverdien. Lokale variable, det vil si variable som blir deklarert inni en metode, får ingen automatisk startverdi. For slike vil vi få en kompileringsfeil dersom vi glemmer å initialisere dem. Vi skal nå se på hvilke muligheter vi har for å tilordne numeriske variable konkrete verdier.

Literaler

En literal er en kildekoderepresentasjon av en fast verdi. For eksempel er 19 og 1.75 literaler i følgende instruksjoner:

  int alder = 19;
  double høyde = 1.75;

Heltallsliteraler

En heltallsliteral av type long må avsluttes med bokstaven L eller l, ellers vil den bli oppfattet til å være av type int. Det anbefales å bruke den store bokstaven L, siden den lille lett kan forveksles med sifferet 1.

Dersom en int-literal blir direkte tilordnet til en variabel av type short, og verdien er innenfor spennet som er tillatt for short-typen, så blir det hele tallet behandlet som om det var en short-literal. Tilsvarende gjelder for literaler tilordnet til byte-variable. I alle andre tilfelle må vi foreta eksplisitt typekonvertering (casting) for å tilordne en int-verdi til en variabel av type short eller byte.

Følgende instruksjoner er eksempler på korrekt tilordning:

  byte b = 120;
  short s = 15000;
  int i = 250000;
  long h = 17L; //nødvendig med L

Normalt uttrykker vi tallverdier i det desimale tallsystemet, det vil si med 10 som grunntall (basis). Men i java er det også tillatt å uttrykke heltallsliteraler som heksadesimale tall, det vil si med 16 som grunntall. Fra og med javaversjon 7 er det også tillatt å uttrykke dem på binær form, altså med 2 som grunntall. For heksadesimale verdier må vi bruke prefikset 0x, mens vi for binære verdier må bruke prefikset 0b. Her er noen eksempler:

  int dverdi = 28;  //verdi uttrykt desimalt
  int hverdi = 0x1c;  //samme verdi uttrykt heksadesimalt
  int bverdi = 0b11100;  //samme verdi uttrykt binært

Desimaltallsliteraler

Desimaltallsliteraler blir oppfattet til å være av type float dersom de ender på F eller f. Ellers blir de oppfattet til å være av type double, som er standardtypen for desimaltall. Literalene kan da ende på D eller d, men det er ikke nødvendig. For øvrig kan literalene uttrykkes på flere måter, men alltid så må de inneholde minst ett siffer. De kan inneholde et desimalpunktum (NB! ikke desimalkomma), men det er heller ikke nødvendig. De kan også uttrykkes på eksponensiell form ved at de inneholder en tier-eksponent bak E eller e. For eksempel så vil alle disse literalene uttrykke det samme desimaltallet:

  18.
  1.8e1
  .18E2

Her er noen flere eksempler:

  double d1 = 1234.56;
  double d2 = 1.23456e3;  //samme verdi som d1
  float f1 = 123.45f;

Tallet null kan være positivt 0.0 eller negativt -0.0. Disse blir oppfattet å være lik hverandre når de sammenliknes ved bruk av ==, men de gir ulike resultater når de brukes i enkelte beregninger. For eksempel så gir uttrykket 1d/0d som resultat +∞, mens 1d/-0d resulterer i -∞.

En double-konstant kan ikke tilordnes direkte til en float-variabel, selv om double-verdien er innenfor det tillatte float-intervallet. De eneste konstantene som kan tilordnes direkte til variable og datafelt av datatype float er float-konstanter.

Bruk av lav bindestrek i numeriske literaler

Fra og med javaversjon 7 er det tillatt å plassere lav bindestrek (_) hvor som helst mellom sifre i en numerisk literal. Dette gjør det mulig å gruppere sifre på tilsvarende måte som det er vanlig å gjøre ved formatering av utskrift. Hensikten er selvsagt å øke lesbarheten av programkoden og på den måten også bidra til å minske faren for feil. Her er noen eksempler på bruk av lav bindestrek:

  long kredittkortnummer = 1234_5678_9012_3456L;
  long fødselsnummer = 120911_123_45L;
  float kronekurs = 8.12_34F;
  long heksbyter = 0xEF_BC_DE_4A;
  long heksord = 0xBADE_CAFE;
  long makslong = 0x7fff_ffff_ffff_ffffL;
  byte oktett = 0b1010_0101;
  long biter = 0b11010110_01101011_10110101_10110011;

Merk at det bare er tillatt å plassere lav bindestrek mellom sifre, den kan ikke plasseres følgende steder:

• I starten eller slutten av en literal
• Ved sida av desimalpunktum i en desimaltallsliteral
• Foran F- eller L-suffiks. (Tilsvarende når det brukes små bokstaver)
• På steder der det forventes en sifferstreng

Følgende eksempler, stort sett hentet fra Oracles nettsider, viser korrekte og ukorrekte plasseringer av lav bindestrek i numeriske literaler.

  float pi1 = 3_.1415F;  //Ukorrekt; lav bindestrek ved sida av
                         //desimalpunktum
  float pi2 = 3._1415F;  //Ukorrekt; lav bindestrek ved sida av
                         //desimalpunktum
  long tlfnr = 12_34_56_78_L; //Ukorrekt; lav bindestrek foran L-suffiks

  int x1 = _52;  //Ukorrekt; dette er en identifikator, 
                 //ikke numerisk literal
  int x2 = 5_2;  //OK (desimal literal)
  int x3 = 52_;  //Ukorrekt; lav bindestrek på slutten av literal
  int x4 = 5_____2; //OK (desimal literal)

  int x5 = 0_x52;  //Ukorrekt; lav bindestrek i 0x-prefiks
  int x6 = 0x_52;  //Ukorrekt; lav bindestrek i begynnelsen av et tall
  int x7 = 0x5_2;  //OK (heksadesimal literal)
  int x8 = 0x52_;  //Ukorrekt; lav bindestrek på slutten av et tall

Innpakningsklasser

For hver av de numeriske typene finnes det en såkalt innpakningsklasse. Den kan brukes til å representere tallverdiene i form av objekter. I tillegg inneholder klassene konstanter for minste og største tillatte verdi av vedkommende datatype, samt diverse konverteringsmetoder. Vi har allerede gjort en del bruk av metodene Integer.parseInt og Double.parseDouble for konvertering fra sifferstreng til tallverdi i forbindelse med innlesing av verdier. Konstantene for minste og største int-verdi heter henholdsvis Integer.MIN_VALUE og Integer.MAX_VALUE. Tilsvarende gjelder for klassene Byte, Short, Long, Float og Double som er innpakningsklasser for de andre numeriske typene.

Desimaltallsklassene inneholder også konstanter for største og minste eksponent som er tillatt når tallene utrykkes på eksponensiell form. For double-typen heter disse konstantene Double.MIN_EXPONENT og Double.MAX_EXPONENT. For float-typen er det tilsvarende navn. Dessuten inneholder disse klassene konstanter som representerer pluss og minus uendelig. For double-typen er det Double.POSITIVE_INFINITY (representert av 0x7ff0000000000000L) og Double.NEGATIVE_INFINITY (representert av 0xfff0000000000000L). Tilsvarende gjelder for float-typen.

Copyright © Kjetil Grønning og Eva Hadler Vihovde, revidert 2014